Diskussion:Mathe für Nicht-Freaks: Abbildung, Funktion

Unklare Formulierung ganz zu Beginn

Fast ganz zu Beginn dieses Kapitels findet sich die für mich unklare Formulierung "Ein Beispiel hierfür ist die Quadratfunktion zwischen der Menge $\mathbb {R}$ in die Menge $\mathbb {R} _{0}^{+}$". Ich vermute, dass es heißen soll "Ein Beispiel hierfür ist die Quadratfunktion von der Menge $\mathbb {R}$ in die Menge $\mathbb {R} _{0}^{+}$".--Michael Oestreicher 19:57, 7. Nov. 2016 (CET)

@Michael Oestreicher: Ist korrigiert. Vielen Dank. -- Stephan Kulla 00:23, 14. Nov. 2016 (CET)

Irretierende Formulierung im Kapitel "Bild und Urbild"

Die Definitionsgleichung $f(A):=\cdots$ kann zu Mehrdeutigkeiten führen, wenn die Elemente im Definitionsbereich von $f$ Mengen enthalten. Z.B. kann man unter Beachtung der Definition der ganzen Zahlen: $0:=\{\},n:=\{i\}_{i=0}^{n-1}$ als Bild von $n$ der Funktion $f\colon \mathbb {N} \to \mathbb {N} \cup 2^{\mathbb {N} },i\mapsto i+1$ sowohl die Zahl $n+1$ als auch die Menge $\{i\}_{i=1}^{n}$ ansehen. Dieses Problem wird in der Fachliteratur umschifft, indem man z.B. das Bild von $A$ anstatt $f(A):=\cdots$ so definiert $f[A]:=\cdots$. -- Argetula 13:18, 10. Dez. 2017 (CET)

@Argetula: Guter Punkt. Da sich der Artikel an Studierende des ersten Semesters richtet, sollte man schauen, welche Schreibweise in den Vorlesungen vorherrscht. Mir ist zumindest $f(A)$ geläufiger. Wenn mal jemand Zeit hat, kann er/sie in der Fachliteratur des ersten Semesters schauen, welche Schreibweise hier am häufigsten verwendet wird. Im Artikel kann auf jeden Fall auf dieses Problem aufmerksam gemacht und die alternative Schreibweise vorgestellt werden (welche für Vorlesungen wie "Mengenlehre" wichtig ist). Magst du dies machen? -- Stephan Kulla 00:15, 11. Dez. 2017 (CET)

Ich möchte mich darauf beschränken, auf Problematisches in Artikeln hinzuweisen aber diese nicht zu bearbeiten, das können andere vermutlich viel besser als ich. --Argetula 12:02, 12. Dez. 2017 (CET)

@Argetula: Ich habe eine Todo notiert. -- Stephan Kulla 08:28, 20. Dez. 2017 (CET)

@Stephan Kulla: Todo erledigt -- Jürgen-Michael Glubrecht 16:16, 17. Sep. 2018 (CEST)

Anmerkung zur Formel $f:D\rightarrow Z:x\mapsto f(x)$

»$f(x)$« ist ein so zu sprechender Term: »Funktionswert von $f$ für das Argument $x$« oder »Bild von $x$ unter der Abbildung $f$«. Demnach lautet die Sprechweise der Formel

so: $\underbrace {f{\color {white}|}} _{{\text{Funktion }}f}:\underbrace {D\rightarrow Z{\color {white}|}} _{{\text{von }}D{\text{ nach }}Z,}:\underbrace {x\mapsto f(x){\color {white}|}} _{{\text{die }}x{\text{ auf den Funktionswert von }}f{\text{ für das Argument }}x{\text{ abbildet}}}$

oder so: $\underbrace {f{\color {white}|}} _{{\text{Abbildung }}f}:\underbrace {D\rightarrow Z{\color {white}|}} _{{\text{von }}D{\text{ nach }}Z,}:\underbrace {x\mapsto f(x){\color {white}|}} _{{\text{die }}x{\text{ auf das Bild von }}x{\text{ unter der Abbildung }}f{\text{ abbildet}}}$

Beide sind Tautologien. --Argetula 14:00, 8. Feb. 2018 (CET)

Den Begriff „Bild“ kenne ich eher als Bildmenge. Sprich ich würde nicht »Bild von $x$ unter der Abbildung $f$« sondern »$x$ wird unter der Abbildung $f$ abgebildet auf $f(x)$« sagen. Ansonsten: Ja, so kann man es ausdrucken. -- Stephan Kulla 20:47, 9. Feb. 2018 (CET)

Für mich ist irgendwie beides das Gleiche, weil bei einer einelementigen Menge gilt $f(\{x\})=\{f(x)\}$. Anders ausgedrückt: Die Abbildung $\varphi \colon M\to 2^{M},\varphi (x):=\{x\}$ ist eine Art Monomorphismus, so dass das Diagramm

${\begin{array}{ccc}D&{\stackrel {f}{\longrightarrow }}&Z\\\varphi \downarrow &&\varphi \downarrow \\2^{D}&{\stackrel {f}{\longrightarrow }}&2^{Z}\end{array}}$

kommutiert. Betrachtet man $\operatorname {Bild} (f,M):=f(M)$ und schönfinkelt das zu $\operatorname {Bild} (f)(M)$, dann ist $\operatorname {Bild} \colon \operatorname {Abb} (D,Z)\to \operatorname {Abb} (2^{D},2^{Z})$ ein injektiver Operator, der $\operatorname {Abb} (D,Z)$ in $\operatorname {Abb} (2^{D},2^{Z})$ einbettet. Im Diagramm muss unten streng genommen $2^{D}\;{\stackrel {\operatorname {Bild} (f)}{\longrightarrow }}\;2^{Z}$ stehen. Da $f$ beliebig ist, drückt das Diagramm die charakteristische Eigenschaft von Bild aus, durch welche über $f(\bigcup \nolimits _{k}M_{k})=\bigcup \nolimits _{k}f(M_{k})$ die Einbettung induziert wird. --Rumil 01:47, 10. Feb. 2018 (CET)

@Stephan: Ich definierte oben $f(x):=$ Bild von $x$ unter der Abbildung $f$. Du bevorzugst eine andere Definition: $f(x):=x$ wird unter der Abbildung $f$ abgebildet auf $f(x)$. Diese Definition lautet ausgeschrieben so: $f(x):=x$ wird unter der Abbildung $f$ abgebildet auf $x$ wird unter der Abbildung $f$ abgebildet auf $x$ wird unter der Abbildung $f$ abgebildet auf ... ad Infinitum.

Funktionen (Abbildungen) sind Zuordnungen mathematischer Objekte zu mathematischen Objekten, sie können mehrdeutig –– trigonometrische Arkusfunktionen, Quadratwurzelfunktion ––, eindeutig, eineindeutig, mehrparametrig –– $x^{y}$ (2 Parameter: $x,y$), $\textstyle {\int _{a}^{b}\!f(x)dx}$ (3 Parameter: $a,b,f$) –– sein, ihre Definitionsbereiche können echte Klassen sein –– Potenzmengenfunktion ––. All dies unter dem Wort ‘Abbildung’ zu subsummieren fällt mir nicht leicht.
Ich habe hier die Basis des Funktionsbegriff ausführlich dargelegt. -- Argetula 11:57, 16. Feb. 2018 (CET)

Argetula führt an der angegeben Stelle den Abbildungsbegriff auf Relationen zurück! Und das ist auch der einfachere Weg. Das Kapitel sollte in diesem Sinne umgeschrieben werden, dann wird vieles transparenter.

Definition (Abbildung, Funktion)

Eine Abbildung oder Funktion $f:A\rightarrow B$ aus der Menge $A$ in die Menge $B$ ist eine rechtseindeutige Relation $f\subseteq A\times B$. Die Relation $f$ hat also folgende Eigenschaft:

• zu einem Element $x\in A$ gibt es höchstens ein Element $y\in B$ mit $(x,y)\in f$.

Dieses eindeutige Element wird mit $f(x)$ bezeichnet und Funktionswert von $x$ genannt.

Mit dieser Definition ist auch die Gleichheit von Abbildungen klar, denn das ist nichts anderes als die Gleichheit von Relationen und das wiederum nichts anderes als die Gleichheit von Mengen. -- Jürgen-Michael Glubrecht 19:36, 25. Sep. 2018 (CEST)

@Jürgen-Michael Glubrecht: Die Definition mit der Relation ist besser, sollte aber hergeleitet werden. Ich schlage also vor, so wie in dem Artikel Mathe für Nicht-Freaks: Folge vorzugehen. Hier wird auch die formale Definition erst später aus der intuitiven Vorstellung hergeleitet. Insofern sollte man auch hier mit der intuitiven Formulierung starten, entdecken, welche Probleme sich ergeben und dann die formale Definition mit der Relation herleiten. Auch sollte der Artikel so geschrieben werden, dass er auch für Leserinnen verständlich ist, welche den Begriff der Relation nicht kennen. Der Relationsbegriff und Rechtseindeutigkeit sollten deswegen kurz wiederholt werden. -- Stephan Kulla 11:26, 30. Sep. 2018 (CEST)

@Stephan Kulla: Mache ich in einem zweiten Durchgang. Bin noch dabei, die Eigenschaften ausführlicher abzuhandeln. -- Jürgen-Michael Glubrecht 12:25, 30. Sep. 2018 (CEST)

@Jürgen-Michael Glubrecht: Super! Bei diesem Artikel lohnt sich ggf auch eine Neuplanung. Der Artikel ist recht alt und mehr Didaktik würde diesem Artikel gut tun   -- Stephan Kulla 12:44, 30. Sep. 2018 (CEST)

Beispiel für Nicht-Funktion

@ Zornsches Lemma: Aus welchem Grund hast du die Verständnisfrage entfernt? Jürgen-Michael Glubrecht 12:58, 22. Feb. 2019 (CET)

@ Jürgen-Michael Glubrecht: Die Antwort auf die Frage war falsch und damit macht es keinen Sinn dieses Beispiel zu behalten. Die Wurzelfunktion ist eine Funktion. Sie schickt jede nicht negative reelle Zahl $x$ auf die eindeutige nicht negative Zahl $y$, so dass $y^{2}=x$. Wenn wir ein Beispiel einer nicht eindeutigen Zuordnung wollen, müssen wir ein anderes angeben. Zornsches Lemma 13:38; 22. Feb. 2019 (CET)

Hallo Zornsches Lemma, gemeint war natürlich $g:\mathbb {R} \rightarrow \mathbb {R} :x\mapsto \pm {\sqrt {x}}$. Da aber ${\sqrt {x}}$ in der Tat oftmals - aber wie des Bild 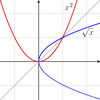zeigt keineswegs immer! - nur als positive Wurzel verstanden wird, ist das Beispiel nicht gut. Jürgen-Michael Glubrecht 19:46, 24. Feb. 2019 (CET)