Abbildung, Funktion – Serlo „Mathe für Nicht-Freaks“
Abbildung, Funktion
[Bearbeiten]Ein zentrales Konzept der Mathematik ist die Abbildung, die auch Funktion genannt wird. Abbildungen sind eindeutige Zuordnungen zwischen zwei Mengen und . Dies bedeutet, dass jedem Element durch die Abbildung genau ein Element zugeordnet wird. Ein Beispiel hierfür ist die Quadratfunktion von der Menge in die Menge , die jeder reellen Zahl ihre Quadratzahl zuordnet. Die Schreibweise für Abbildungen von nach ist:
Ausgesprochen wird dieser Ausdruck so:
Die Menge heißt Definitionsbereich von und ist die Zielmenge der Abbildung. Die Elemente aus dem Definitionsbereich von werden Argument genannt und jedes durch die Abbildung getroffene Element heißt Funktionswert zum Argument .
Hinweis
Die Begriffe „Abbildung“ und „Funktion“ sind beide in der Mathematik üblich und bedeuten genau dasselbe.
In der Zielmenge müssen nicht alle Elemente Funktionswerte sein.
Hier besteht der Definitionsbereich aus vier Elementen. Die Zielmenge ist . und sind Funktionswerte. Die Zahl dagegen nicht, denn keine Zahl ergibt bei Division durch den Rest . Also sind nicht alle Elemente in Funktionswerte.
Die Pfeile geben die Zuordnung wider: sie gehen vom Argument zum Funktionswert und verbinden so ein Paar. Wir können daher die Zuordnung als eine Menge von Paaren aus Argument und Funktionswert beschreiben: . Mengen von Paaren haben wir bereits im Kapitel Relation kennengelernt. Abbildungen sind also Relationen! Aber nicht jede Relation ist eine Abbildung. Damit eine Relation eine Abbildung ist, muss jedes Element in in Relation mit genau einem Element in sein
Fassen wir noch einmal zusammen, was eine Funktion ausmacht: Die Paare bilden eine Relation . Diese Relation hat eine spezielle Eigenschaft: zu jedem Element gibt es genau ein Element mit . Im Pfeildiagramm erkennst du dies daran, dass von jedem Element des Definitionsbereichs genau ein Pfeil ausgeht. Im Koordinatensystem muss es zu jedem -Wert genau einen -Wert geben.

Wir definieren daher Abbildungen als eine Relationen mit der oben genannten Eigenschaft:
Definition (Abbildung, Funktion)
Eine Abbildung oder Funktion aus der Menge in die Menge ist eine Relation mit folgender Eigenschaft:
- zu jedem Element gibt es genau ein Element mit .
Dieses eindeutige Element wird mit bezeichnet und Funktionswert von genannt. ist der Definitionsbereich, ist die Zielmenge der Funktion. Die Zuordnung kann zusätzlich angegeben werden: oder auch so .
Beispiel (Quadratfunktion)
Jeder reellen Zahl wird ihr Quadrat zugeordnet:
Funktionen werden häufig im Koordinatensystem veranschaulicht, wie in der Darstellung der Funktion rechts. Dabei werden die Paare als Koordinaten aufgefasst. Diese Punktemenge wird dann als Graph der Funktion bezeichnet.
Verständnisfrage: Welche der folgenden Pfeildiagramme stellen Abbildungen aus der Menge in die Menge dar?
-
Pfeildiagramm 1
-
Pfeildiagramm 2
-
Pfeildiagramm 3
-
Pfeildiagramm 4
Antwort:
- Pfeildiagramm 1: Abbildung
- Pfeildiagramm 2: partielle Abbildung (dem Objekt wird kein Element aus zugeordnet)
- Pfeildiagramm 3: keine Abbildung (dem Element werden mehrere Elemente aus zugeordnet und dem Objekt wird kein Element aus zugeordnet)
- Pfeildiagramm 4: Abbildung
Definitions- und Wertebereich
[Bearbeiten]Ist eine Funktion von nach , so ist der Definitionsbereich von
Der Wertebereich einer Funktion ist als die Menge der Funktionswerte definiert:
Definition (Wertebereich einer Funktion)
sei eine Funktion. Dann ist der Wertebereich von die Menge aller Elemente für die es ein Argument gibt, formalisiert:
Es gilt .
Einschränkung einer Funktion
[Bearbeiten]Definition (Einschränkung einer Funktion)
Sei eine Funktion und eine Teilmenge von . Dann ist die Einschränkung von auf die Funktion, die auf mit übereinstimmt:
Für die eingeschränkte Funktion gilt: .
ist tatsächlich eine Funktion.
Gleichheit von Abbildungen
[Bearbeiten]Es ist nicht sofort klar, wann zwei Abbildungen gleich sind. Ähnlich wie bei Mengen müssen wir definieren, wann zwei Abbildungen gleich sind.
Definition (Gleichheit von Abbildungen)
Zwei Abbildungen und sind gleich, wenn , und für alle gilt .
Sind zwei Funktionen gleich, so sind auch die Definitionsbereiche und die Wertebereiche gleich. Bei der Gleichheit kommt es nicht darauf an, ob die Zuordnungsvorschriften und gleich formuliert sind!
Beispiel
Die folgenden Funktionen sind gleich:
Bild und Urbild
[Bearbeiten]Zwei wesentliche Begriffe im Zusammenhang mit Abbildungen ist der Begriff des Bildes und der Begriff des Urbilds:
Definition (Bild)
Sei eine Funktion und eine Teilmenge. Das Bild ist die Menge aller Funktionswerte mit :
Notation: Es ist üblich, sowohl für den Funktionswert eines Elementes , als auch für das Bild einer Teilmenge die gleiche Schreibweise zu verwenden, nämlich mit runden Klammern. Aus dem Zusammenhang muss dann klar werden, was jeweils gemeint ist. Einige Autor*innen verwenden daher für das Bild einer Teilmenge eckige Klammern: .

Beispiel (Bild)
Sei . Es ist
Definition (Urbild)
Das Urbild einer Abbildung und einer Menge ist die Menge aller Argumente , die durch in die Menge abgebildet werden:
Beachte, dass auch Elemente enthalten kann, die durch nicht getroffen werden. Betrachte dazu die Abbildung auf der rechten Skizze. Die Zahl wird nicht getroffen und die Zahl besitzt als Funktionswert nur das Argument . Dementsprechend gilt für das Urbild .
Beispiel (Urbild)
Sei . Es ist
Warnung
Es besteht Verwechslungsgefahr zwischen dem Urbild , der Umkehrfunktion und dem multiplikativen Inversen .
Aufgabe
Sei
Bestimme folgende Bilder und Urbilder (beachte die unterschiedlichen Definitions- und Zielmengen der Abbildungen!):
Lösung
-
Da der gesamte Definitionsbereich von ist, müssen hier alle Funktionswerte bestimmt werden, die durch getroffen werden. Generell ist das Ergebnis der (reellwertigen) Quadratfunktion stets nicht negativ. Also ist das Bild eine Teilmenge von .
Nun kann man auch zeigen, dass alle nicht-negativen Zahlen durch getroffen werden.
Sei hierfür eine nicht negative Zahl. Es ist dann stets im Definitionsbereich von enthalten. Da ist, gibt es ein Argument, welches von auf abgebildet wird. Also gilt .
-
Wir müssen nur die Funktionswerte von und überprüfen. Es ist und .
Damit wird nur getroffen und es gilt .
-
Wenn wir alle Beträge der ganzen Zahlen bilden, erhalten wir die Menge der natürlichen Zahlen zusammen mit der Null, deshalb gilt:
-
Wir nutzen die Definition des Bildes . Da die Aussage immer falsch ist, folgt .
-
Bei der Quadratfunktion wird sowohl als auch auf abgebildet. Es ist nämlich sowohl sowie . Da beide Zahlen und im Defintionsbereich von sind, sind beide Zahlen im Urbild enthalten.
Nun suchen wir alle mit , also . Da nicht sein darf, bleibt nur die Möglichkeit übrig.
Damit ist das gesuchte Urbild.
-
Der Definitionsbereich von besteht nur aus der Menge . Diese Zahlen werden durch den Betrag auf die Menge abgebildet. Da die Menge in enthalten, ist der komplette Definitionsbereich das gesuchte Urbild, also
-
Bei der Betragsfunktion wird für ein beliebiges nicht-negatives sowohl als auch auf abgebildet. Damit ist das Urbild von .
-
Wir benutzen die Definition des Urbilds: . Die Aussage ist für alle falsch. Somit folgt .
Eigenschaften von Abbildungen
[Bearbeiten]sei eine Funktion von der Menge in die Menge . Es gelte also: .
Injektiv
[Bearbeiten]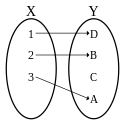

Wenn eine Funktion verschiedene Argumente stets auf verschiedene Funktionswerte abbildet, wird sie injektiv genannt. Im Pfeildiagramm injektiver Funktionen treffen niemals zwei Pfeilspitzen auf denselben Funktionswert.
Definition (Injektiv)
Eine Funktion ist injektiv, wenn sie verschiedene Argumente auf verschiedene Werte abbildet:
Zum Nachweis der Injektivität wird häufig die Kontraposition verwendet: .
Beispiel (Injektiv)
- ist nicht injektiv, denn alle Werte bis auf werden zweimal getroffen. Es gilt ja beispielsweise .
- ist injektiv, denn aus folgt .
Surjektiv
[Bearbeiten]
Eine Funktion ist surjektiv, wenn alle Elemente von von der Funktion getroffen werden. Anders ausgedrückt: zu jedem Element gibt es ein Argument , mit .
Definition (Surjektiv)
Eine Funktion ist surjektiv, wenn alle Elemente von getroffen werden:
Beispiel (Surjektiv)
- ist surjektiv, denn für ein beliebiges ist .
- ist nicht surjektiv, denn die Quadratfunktion auf wird niemals negativ.
Verständnisaufgabe: Ist surjektiv?
Nein, da weder noch in liegen. Das heißt liegt nicht im Bild von .
Satz (Surjektivität)
.
Beweis (Surjektivität)
Die Behauptung folgt mit der Definition des Wertebereichs: der umfasst alle Werte, die getroffen werden.
Bijektiv
[Bearbeiten]
Eine Funktion kann sowohl injektiv als auch surjektiv sein. Man nennt diese Eigenschaft bijektiv. Im Pfeildiagramm ist dann jedes Element von mit genau einem Element von verbunden. Mit Hilfe von bijektiven Funktionen können Mengen hinsichtlich ihre Größe verglichen werden: gibt es eine Bijektion von auf , so haben die beiden Mengen und gleichviele Elemente. Wir werden den Größenvergleich zwischen Mengen im Kapitel Mächtigkeit von Mengen ausführlich behandeln.
Definition (Bijektiv)
Eine Funktion ist bijektiv von auf , wenn sie injektiv und surjektiv ist. Das heißt, jedem Element von wird genau ein Element von zugeordnet:
Beispiel (Bijektiv)
- ist bijektiv.
- ist bijektiv.
- ist nicht bijektiv.
-
f : Gerade
-
g : Parabel 3. Grades
-
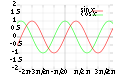
h : Sinuskurve
Beweis
- Im Koordinatenkreuz ist diese Funktion eine Gerade mit Steigung und um eine Einheit nach oben verschoben. Wir zeigen die Injektivität: aus folgt und daraus . Für die Surjektivität sei eine beliebige reelle Zahl gegeben. Dann definieren wir das Argument und rechnen nach: . Also werden alle reellen Zahlen getroffen.
- In gleicher Weise zeigt man die Bijektivität von , das ist eine Parabel 3. Grades.
- Der Graph von ist die Sinuskurve. Die nimmt bekanntlich alle Werte zwischen und an. Also ist surjektiv auf dem Intervall . ist aber nicht injektiv, denn ist periodisch, das heißt, diese Werte werden immer wieder angenommen.
Funktionskomposition
[Bearbeiten]
Seien zwei Abbildungen und gegeben. Dann können wir die beiden Funktionen nacheinander ausführen. Wir bilden zunächst ein mit ab und erhalten . Dann können wir darauf anwenden und erhalten . Insgesamt ergibt sich . Das führt zum Begriff der Komposition von Funktionen
Definition (Komposition von Abbildungen)
Die Komposition zweier Abbildungen und ist die Abbildung .
Gelesen wird so: erst , dann oder auch: nach .
Hinweis
Beachte, dass in der Schreibweise für die Funktionskomposition diejenige Funktion, die zuerst angewandt wird, rechts steht (Hier musst du also „von rechts nach links“ lesen). Die Schreibweise meint also, dass auf erst und danach angewandt wird. Es ist also .
Verständnisfrage: Sei und . Berechne
Antwort:
Verständnisfrage: Seien und zwei Abbildungen von nach . Gilt dann ? Wieso?
Nein, dies ist nicht der Fall. Sei zum Beispiel und . Dann ist nämlich
und
Hier sieht man, dass ist. Beispielsweise ist .
Satz (Existenz der Umkehrfunktion)
Ist bijektiv, so gibt es eine eindeutige Funktion mit für alle und für alle .
Beweis (Existenz der Umkehrfunktion)
Beweisschritt: Existenz
Wir definieren für das eindeutige mit . Die gewünschten Identitäten folgen unmittelbar.
Beweisschritt: Eindeutigkeit
Sind zwei solche Funktionen, so .
Definition (Umkehrfunktion)
Für eine bijektive Funktion bezeichnen wir mit die eindeutige Funktion aus obigem Satz. Diese Funktion nennen wir die Umkehrfunktion von .
Aufgaben
[Bearbeiten]Aufgabe (Komposition surjektiver Abbildungen)
Seien und zwei Abbildungen. Seien und surjektiv. Zeige, dass surjektiv ist.
Wie kommt man auf den Beweis? (Komposition surjektiver Abbildungen)
Da und sind, dann ist mit für alle (Nach Definition von Funktionskomposition).
Wir müssen überprüfen, dass alle Elemente durch getroffen werden:
Wir suchen für alle ein Element mit .
Da surjektiv ist, gibt es für alle ein Element mit .
Da surjektiv ist, gibt es für alle ein Element mit .
Nun kann man zeigen, dass für alle gilt:
Also ist die Funktion surjektiv.
Lösung (Komposition surjektiver Abbildungen)
ist surjektiv
ist surjektiv
Aus(*) und (**) gilt:
Dann für alle gibt es mit .Also ist surjektiv.
Aufgabe (Komposition injektiver Abbildungen)
Seien und zwei Abbildungen. Seien und injektiv. Zeige, dass injektiv ist.
Wie kommt man auf den Beweis? (Komposition injektiver Abbildungen)
Da und sind, dann ist mit für alle (Nach Definition von Funktionskomposition).
Wir müssen überprüfen, dass für alle zwei Elemente mit gilt :
ist injektiv, dann für alle zwei Elemente mit gilt .
ist injektiv, dann für alle zwei Elemente mit gilt .
Nun kann man zeigen, dass für alle zwei Elemente gilt:
Also ist die Funktion injektiv.
Lösung (Komposition injektiver Abbildungen)
ist injektiv ) ...(*)
ist injektiv ) ...(**)
Aus(*) und (**) gilt: .
Dann für alle gilt: .
Also ist die Funktion injektiv.
Aufgabe
Seien und zwei Abbildungen. Wenn und surjektiv sind, folgt daraus, dass surjektiv ist? Begründe deine Antwort.
Lösung
Wenn wir zeigen wollen, dass eine Funktion nicht surjektiv ist, reicht es ein einziges Gegenbeispiel zu finden. Seien die drei Mengen mit . Die formale Definition für Funktionskomposition lautet mit für alle . dann in unserem Gegenbeispiel haben wir . Beachte, dass die Funktionen und surjektiv sind, weil alle Elemente von durch und getroffen werden. Aber die Funktion ist nicht surjektiv, denn es gibt eine Element , die nicht Funktionswert durch ist. Es gilt, dass nicht unbedingt surjektiv ist.
Aufgabe
Seien und zwei Abbildungen. Wenn injektiv ist, folgt daraus, dass injektiv ist? Begründe deine Antwort.
Lösung
Die Antwort ist ja, was wir im Folgenden beweisen werden. Seien , wobei . Wir zeigen, dass . Weil , gilt
Da injektiv ist, folgt aus der Definition, dass . Somit ist injektiv.




































































![{\displaystyle f[A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35ed71bdb47bfe4c79812b2740415da6f8914c21)

























![{\displaystyle g^{-1}\left([0,5]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b944e43938aeca9b94cfd1a2397dd986ec82fdb5)
![{\displaystyle h^{-1}\left([0,5]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f09688ac278fa4775bea40b8ac54ad0c8045fd1)



























![{\displaystyle [0,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/466c74a63ec8b8422ccb96c6bc5140dca45b5593)
![{\displaystyle g^{-1}\left([0,5]\right)=\{-1,\,0,\,1\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9123bdd537a3aee9121c9bd7a29285fcc3de8967)


![{\displaystyle h^{-1}\left([0,5]\right)=[-5,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab05a5782fb7e4998d2d49b4fb464e6a30c198d2)


























![{\displaystyle h:\mathbb {R} \to [-1,1];x\mapsto \sin(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3ae4fb74e1253aac9059a8615f8b956964d73fb)







![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)

































































