MathemaTriX ⋅ Probetest. 01. KL6

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT

${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$	DEINE FESTE BEGLEITERIN
	FÜR DIE SCHULMATHEMATIK

EINFACH UND
VERSTÄNDLICH

GRATIS!^*

STARTEN!

MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS!

Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Anderen Test wählen

01 02 03 04 05 06 07 08

Die Form einer Rutsche wird vom folgenden Bild angenähert. Die Funktion 3. Grades h führt knickfrei zur Gerade g am Punkt (6|3). Die Funktion hat den Wert 3,2 an der Stelle 6,5. Die Tangente an diesem Punkt bildet zur Funktion einen Winkel von 5° zur Horizontalen (siehe Bild).
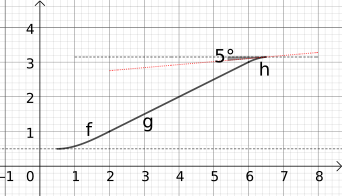
1. Erstellen Sie ein Gleichungssystem zur Berechnung der Koeffizienten der Funktion.
2. Berechnen Sie die Koeffizienten der Funktion.

Der Kosinus eines Winkels ist $\textstyle {\frac {21}{29}}$ $\textstyle {\frac {21}{29}}$ .
1. Wie viel ist der Sinus?
2. Wie groß ist der Winkel?
3. Wie groß ist die Hypotenuse eines rechtwinkeligen Dreiecks, wenn die Gegenkathete des Winkels mit Kosinus $\textstyle {\frac {21}{29}}\$ 13 cm ist?

Die zurückgelegte Strecke s ist das Produkt aus Geschwindigkeit v und Zeit t: $s=v\cdot t.$ $s=v\cdot t.$
Ein Auto fährt in einem Kreisverkehr mit 18 km/h und legt in 5 s die Hälfte seiner annäherungsweise kreisförmige Bahn zurück.
1. Wie viel ist der Radius dieser Bahn?
2. In der Mitte des Kreisverkehrs gibt es ein kreisförmiges Beet dessen Durchmesser 4 m ist. Wie weit vom Rand des Beets fährt das Auto?

Um ein Spiel zu beginnen gibt es folgenden Vorgang: Eine Person würfelt. Ist die Augenzahl mehr als 4, soll die nächste Person würfeln. Im Gegenfall darf die erste Person genau noch einmal würfeln. Ist die Summe der Augenzahlen mindestens 3, dann darf diese Person in der nächsten Runde mit dem Spiel anfangen, sonst ist die nächste Person dran.
1. Erstellen Sie das entsprechende Baumdiagramm!
2. Wie viel ist die Wahrscheinlichkeit für eine Person in einem Durchgang das Spiel anzufangen?
3. 5 Personen spielen. Wie viel ist die Wahrscheinlichkeit, dass zumindest drei Personen im ersten Durchgang mit dem Spiel anfangen dürfen?

Der Sexualverkehr bei einem Paar dauert durchschnittlich 10 min. Die Dauer wird von einer Normalverteilung mit 51 s Standardabweichung angenähert.
1. In wie viel Prozent der Fälle dauert der Sexualverkehr mehr als $8{,}62\ min$ ?
2. Die ideale Dauer für dieses Paar liegt in einem symmetrischen Intervall und umfasst 95% der Fälle. Welche ist die kürzeste bzw. längste ideale Dauer?
3. Füllen Sie die fehlenden Werte in den Kästchen aus!
4. Welche Eigenschaften hat der Punkt E?
5. Zeichnen Sie eine Verteilung mit größerem $\mu$ und größerem $\sigma$
6. Veranschaulichen Sie in der Abbildung die Wahrscheinlichkeit, dass die Dauer kleiner als 9 min ist!

Bei 4 Personen wurde die Häufigkeit des Sexualverkehrs pro Jahr gemessen und eine Prognose in Abhängigkeit von den folgenden Jahren mit Hilfe von exponentiellen Funktionen gemacht.
1. Bei welcher Funktion lässt die Häufigkeit am schnellsten nach?
2. Die Funktion R für Reinhard lautet: $f(x)=d\cdot e^{-k\cdot x}.\$ Lesen Sie aus dem Diagramm den Parameter $d$ ab!
3. Die Halbwertszeit für Gregor (Funktion G) ist 13,5 Jahre. Stellen Sie die entsprechende Exponentialfunktion auf!
4. Gregor hat eine Prostata-OP gehabt, sobald die Häufigkeit auf 120 mal pro Jahr gesunken war. Zum welchen Zeitpunkt war das? Benutzen Sie für die Lösung die Antwort der vorherigen Frage!
5. Die Halbwertszeit für eine andere Person, bei der die Häufigkeit zum gleichen Anfangspunkt bei 360 mal pro Jahr lag, ist 12 Jahre. Zeichnen Sie die entsprechende Exponentialfunktion (in dieses Diagramm)!
6. Die Gleichung B für Barbara lautet: $320\ e^{x\cdot (\ln(9)-\ln(10))}$ . Um wie viel reduziert sich die Häufigkeit des Sexuelverkehrs nach 45 Monaten? (kein Prozent, sondern wie viel mal pro Jahr wird es weniger)
7. Wie viel ist die mittlere Änderungsrate zwischen der Stellen 5 und 35 der Funktion B?
8. Die allgemeine Gleichung für die hier dargestellte Vorgänge lautet: $M(t)=M_{0}\cdot a^{t}$ . Geben Sie die Intervalle für a, t und M an!
9. Wie viel ist die Halbwertszeit für Barbara (Funktion B)?

Rechnen Sie 15 m/s in km/h um!

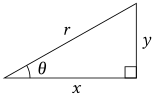
1. Schreiben Sie eine Formel für den Winkel $\theta$ in Bezug auf die Seiten r und y auf!
2. Wie groß ist der Winkel $\theta$ im Bild, wenn x=37 cm und r=500 mm sind?

Beim Vergleich von zwei ausgedehnten Kondomen geht man von einer Zylinder-Form aus. Der Durchmesser des Kondoms A ist das 1,2-fache des Kondoms B, seine Höhe (Länge) ist zwei drittel des Kondoms B.
1. Jemand behauptet, dass das Volumen des Kondoms A 4% weniger als das Volumen des Kondoms B ist. Stimmt diese Aussage, ja oder nein und warum?
2. Wie viel Prozent mehr ist das Volumen des Kondoms B als das Volumen des Kondoms A?

Nehmen wir an, dass es in einer Klasse 40 Personen (Frauen oder Männer) gibt, von denen eine unbekannte Anzahl b Männer sind.
1. Wie lautet die Formel (mit Hilfe von b) für die Wahrscheinlichkeit, dass eine Person ein Mann ist? ${\text{P}}(''{\text{Mann}}'')={\qquad }$
2. Es wird zwei mal eine Person zufällig gewählt und aus der Klasse raus gebracht. Erstellen Sie das entsprechende Baumdiagramm!
3. Es wird zwei mal eine Person zufällig gewählt und in die Klasse zurück gebracht. Erstellen Sie das entsprechende Baumdiagramm!
4. Die Wahrscheinlichkeit, dass im ersten Fall (Person wird raus gebracht) zumindest eine Frau gewählt wird, ist ${\tfrac {9}{10}}.\$ Wie viele sind die Frauen?

Die Gleichung der Konzentration einer Glückshormone nach dem Orgasmus lautet: $M(t)=24,5\cdot 0{,}957^{t}$ (t in Minuten, M(t) in $mg/\ell$ ). Um wie viele $mg/\ell$ reduziert sich die Konzentration nach 1 Minute?

Schreiben Sie

17{,}2\cdot 10^{-5}

in Gleitkommadarstellung auf! Welchen der folgenden Möglichkeiten entspricht diese Zahl?

$1720\cdot 10^{-7}$	$\quad$	$0,00172\cdot 10^{-1}$
$0{,}00000172\cdot 10^{2}$	$\quad$	$17200\cdot 10^{-11}\ {\text{Tausende}}$
$1{,}72\cdot 10^{-4}$

Die sogenannte Genüßkurve einer Person beim Sexualverkehr in Abhängigkeit von der Zeit in Minuten wird im folgenden Diagramm dargestellt. Der steigende Teil ist eine als r abgebildete Polynomfunktion 3. Grades. Sie führt am Punkt (4|4) knickfrei zur sogenannten Hochebene des Genüsses. Nach 3,2 min haben wir den Genüßwert 3,584. Es gilt dazu: $r'(3{,}1547)=1.$ $r'(3{,}1547)=1.$
1. Erstellen Sie ein Gleichungssystem zur Berechnung der Koeffizienten der Funktion.
2. Berechnen Sie die Koeffizienten der Funktion.

Die Schallgeschwindigkeit ist ca. 1224 km/h. 5,4 s nach einem Blitz wird der entsprechende Donner gehört. Wie weit weg ist der Blitz gefallen? (Wir können schon davon ausgehen, dass wir den Blitz annäherend sofort sehen)

Welche der folgenden Ausdrücke sind zueinander gleich?

${\sqrt[{100}]{a^{75}}}$	A	$\quad$	$a^{\frac {3}{4}}$	D	$\quad$	$a^{0{,}75}$	F
$\left({\tfrac {3}{4}}\right)^{a}$	B	$\quad$	${\tfrac {1}{0{,}75^{-a}}}$	E	$\quad$	${\sqrt[{20}]{\tfrac {1}{a^{-15}}}}$	G
${\tfrac {1}{a^{-0{,}75}}}$	C

Für die sexuelle Häufigkeit einer Person gilt folgende Gleichung:

H(t)=0,87\cdot 0,97^{t}

t die Zeit in Jahren
H(t) die Häufigkeit in Tausenden pro Jahr

Kreuzen Sie die zutreffende(n) Aussage(n) an!

Die Häufigkeit nimmt linear ab
Die Häufigkeit nimmt um 13% pro Minute ab
Die Häufigkeit am Anfang ist 870 mal pro Jahr
Die Häufigkeit nimmt um 3% pro Jahr zu
Die Häufigkeit nimmt im Laufe der Zeit immer langsamer ab
Die Häufigkeit nimmt um 97% pro Jahr ab

Die Steigung einer 790 m langer Straße ist 12%. Berechnen Sie
1. den Winkel zwischen Straße und Horizontale,
2. den Winkel zwischen Straße und Vertikale,
3. den Höhenunterschied zwischen den beiden Rändern der Straße,
4. den horizontalen Abstand zwischen den beiden Rändern der Straße.

Die Temperatur beim Sexualverkehr in der Vagina einer Frau in °C in Abhängigkeit von der Zeit in Minuten wird durch eine kubische Funktion (Polynomfunktion 3. Grades) angegeben. Am Anfang ist die Temperatur 37,2°C. An dieser Stelle hat die Funktion auch einen lokalen Tiefpunkt. Nach 0,1 Stunden erreicht die Temperatur ihren höchsten Wert. Nach 210 s ist die Temperatur 38,7°C.
1. Erstellen Sie ein Gleichungssystem zur Berechnung der Koeffizienten der Funktion.
2. Berechnen Sie die Koeffizienten der Funktion.

Im folgenden Diagramm ist der Erwartungswert der "flächeren" Funktion 70 und die Standardabweichung 9.
1. Wie viel ist der Erwartungswert der anderen Funktion?
2. Die Standardabweichung der spitzeren Funktion ist 5. Beschriften Sie die Stellen und die Punkte, die eine Standardabweichung vom Erwartungswert abweichen!

Eine blaue und eine gelbe Würfel werden gleichzeitig gewürfelt und die Augensumme berechnet.
1. Schreiben Sie in einer Tabelle alle mögliche Ergebnisse und die entsprechenden Wahrscheinlichkeiten auf! Benutzen Sie dafür erst ein geeignetes Diagramm!
2. Das Ergebnis "größer" bedeutet, dass die Augenzahl des blauen Würfels größer als die Augenzahl des gelben ist. Was ist mehr, die Wahrscheinlichkeit des Ergebnisses "größer" oder die Wahrscheinlichkeit, dass die Augensumme mehr als 8 ist?
3. Sie wiederholen den Vorgang (die zwei Würfeln gleicheitig würfeln) 7 mal. Wie viel ist die Wahrscheinlichkeit, dass eine Augensumme von weniger als 6 zumindest zwei mal vorkommt?

Die Masse m ist das Produkt aus Dichte $\rho$ $\rho$ und Volumen V:
$m=\rho \cdot V.$ $m=\rho \cdot V.$
1. Die Masse einer Kugel ist 403 kg, seine Dichte 21,8 $kg/\ell .\$ Wie viel ist der Durchmesser der Kugel in m?
2. Die Masse eines Zylinders ist 80 g, seine Höhe 4,5 mm und der Durchmesser der Basis 1,1 cm. Wie viel ist seine Dichte in $kg/\ell .{\text{?}}$

Das Diagramm zeigt die Geschwindigkeit $v$ $v$ in km/h eines Fußgängers in Abhängigkeit von der Zeit t in h.
1. Was bedeutet die gekennzeichnete Fläche in diesem Sachzusammenhang?
2. Was bedeutet in diesem Sachzusammenhang ${\tfrac {v(t_{2})-v(t_{1})}{t_{2}-t_{1}}}$ ?
3. An welchem Zeitpunk ungefähr ist die Beschleunigung null?
4. Geben Sie eine Einschätzung der zurückgelegte Strecke ab Anfang der 1. bis Ende der 5. Stunde an!
5. Wie viel ungefähr ist die größte Geschwindigkeit im Intervall $[0;3]$ in m/s?

Eine Frau hat in ihrem Leben mit 25 Österreichern, 30 Deutschen, 10 Südeuropäer und 15 Männern von anderen Ländern geschlafen. Mit 70% der Deutschen war das ein One-Night-Stand, mit den restlichen Nationalitäten war das so bei 80% der Fälle.
1. Vervollständigen Sie das der Situation entsprechende nachstehende Diagramm!
2. Beschreiben Sie das Ereignis, dessen Wahrscheinlichkeit durch $0{,}30\cdot 0{,}375\$ berechnet wird!
3. Beschreiben Sie das Ereignis, dessen Wahrscheinlichkeit durch $0{,}125\cdot 0{,}2+0{,}375\cdot 0{,}3+0{,}2\cdot 0{,}1875+0{,}2\cdot 0{,}3125\$ berechnet wird!
4. Beschreiben Sie das Ereignis, dessen Wahrscheinlichkeit durch $0{,}125\cdot 0{,}2+0{,}8\cdot 0{,}125\$ berechnet wird!
5. Berechnen Sie die Wahrscheinlichkeit, dass ein zufällig ausgewählte Liebhaber nicht Österreicher und nicht One-Night-Stand ist!

Antworten (klicken)

1. - $3=a\cdot 6^{3}+b\cdot 6^{2}+c\cdot 6+d$
  - $0{,}5=3\cdot a\cdot 6^{2}+2\cdot b\cdot 6+c$
  - $3{,}2=a\cdot 6{,}5^{3}+b\cdot 6{,}5^{2}+c\cdot 6{,}5+d$
  - $\tan(5^{\circ })=3\cdot a\cdot 6{,}5^{2}+2\cdot b\cdot 6{,}5+c\quad (\tan 5^{\circ }\approx 0{,}08749)$
2. Geogebra→CAS→löse({})→ a≈−0,85 ; b≈15,53 ; c≈−94,01 ; d≈191,71
1. ${\tfrac {20}{29}}$
2. ca. 43,60°
3. ca. 18,85 cm
1. ca. 7,96 m
2. ca. 5,96 m
1. S: spielen, NS: Nicht spielen A:Augenzahl
```
          1    2    3    4    5    6
         / \   -----------    ------
        1  A>1   S(3/6)       NS(2/6)
 NS(1/36)  S(5/36)
```
2. ${\tfrac {23}{36}}$
3. Geogebra→Statistik→Binomial mit n=5 und $p={\tfrac {23}{36}}$ →P(3≤X≤5)≈74,73%
1. Geogebra→Statistik→Normal mit μ=10 und σ=0,85→P(8,62≤X)≈94,78%
2. Geogebra→Statistik→Normal mit μ=10 und σ=0,85→P(X≤?)=2,5%→ 8,334 min und →P(?≤X)=2,5%→ 11,666 min
3. 8,3 - 10 -11,7
4. Höhepunkt (f'=0), wobei x-Wert ist Median, Modus und Erwartungswert
5. nach rechts verschieben und flacher
6. Fläche links von 9
1. B
2. 220 (mal pro Jahr)
3. $N(t)=400\cdot 0{,}94995^{t}$
4. ca. 23,45 Jahre nach Anfang der Messung
5. wird gemacht
6. ca. 104,45 mal pro Jahr weniger
7. ca. 6 mal pro Jahr weniger jedes Jahr
8. 0<a<1, t>0, $0<M<M_{0}$
9. ca. 6,5 Jahre
54 km/h
1. $\theta =\arcsin {\tfrac {y}{r}}$
2. $\theta \approx 42{,}27^{\circ }$
1. Sei r=5 und H=4, dann
  $V_{1}=\pi \ 5^{2}4$
  $V_{2}=\pi \ 6^{2}{\tfrac {8}{3}}$
  ${\tfrac {V_{2}}{V_{1}}}=0{,}96$ also ja^[1]
2. $4{,}1{\dot {6}}$

$P(Mann)={\tfrac {b}{40}}$

          M: b/40               F:(40−b)/40
         /       \                /     \
M: (b−1)/39  F: (40−b)/39    M: b/39   F: (39−b)/39

          M: b/40               F:(40−b)/40
         /       \                /     \
  M: b/40     F: (40−b)/40    M: b/40   F: (40−b)/40

27

ca. 1,05 mg/Liter
Alle
1. - $4=a\cdot 4^{3}+b\cdot 4^{2}+c\cdot 4+d$
  - $0=3\cdot a\cdot 4^{2}+2\cdot b\cdot 4+c$
  - $3{,}584=a\cdot 3{,}2^{3}+b\cdot 3{,}2^{2}+c\cdot 3{,}2+d$
  - $1=3\cdot a\cdot 3{,}1547^{2}+2\cdot b\cdot 3{,}1547+c$
2. Geogebra→CAS→löse({})→ a≈−0,125 ; b≈0,75 ; c≈0 ; d≈0
ca. 1,84 km
A=C=D=F=G, B=E
das 3. und das 5.
1. ca. 6,84°
2. ca. 83,16°
3. ca. 94,8 m
4. ca. 784,4 m
1. - $37{,}2=a\cdot 0^{3}+b\cdot 0^{2}+c\cdot 0+d$
  - $0=3\cdot a\cdot 0^{2}+2\cdot b\cdot 0+c$
  - $38{,}7=a\cdot 3{,}5^{3}+b\cdot 3{,}5^{2}+c\cdot 3{,}5+d$
  - $0=3\cdot a\cdot 6^{2}+2\cdot b\cdot 6+c$
2. Geogebra→CAS→löse({})→ a≈−0,02226 ; b≈0,20037 ; c≈0 ; d≈37,2
1. gleich also 70
2. 67 - 83

2	3	4	5	6	7	8	9	10	11	12
$\ {\tfrac {1}{36}}\$	$\ {\tfrac {1}{18}}\$	$\ {\tfrac {1}{12}}\$	$\ {\tfrac {1}{9}}\$	$\ {\tfrac {5}{36}}\$	$\ {\tfrac {1}{6}}\$	$\ {\tfrac {5}{36}}\$	$\ {\tfrac {1}{9}}\$	$\ {\tfrac {1}{12}}\$	$\ {\tfrac {1}{18}}\$	$\ {\tfrac {1}{36}}\$

"größer"
Geogebra→Statistik→Binomial mit n=7 und $p={\tfrac {10}{36}}$ →P(2≤X)≈62,16%

1. ca. 0,328 m
2. ca. 187 kg/Liter
1. Zurückgelegte Strecke zwischen Anfang 2. und Ende 5. Stunde.
2. Mittlere Beschleunigung zwischen $t_{1}$ und $t_{2}$
3. ca. 0 bzw. 3,3 h
4. ca. 8 km
5. $0{,}8{\dot {3}}\ km/h$

N One-Night-Stand
      Ö 0,3125    D 0,375    S 0,125     R 0,1875
         / \        / \        / \         / \
    N:0,8  0,2  N:0,7  0,3  N:0,8  0,2  N:0,8  0,2

Deutscher und kein One-Night-Stand
Kein One-Night-Stand
Südeuropäer

93,75%

BILDERVERZEICHNIS

ÖFFNE DEIN HORIZONT!
LERNE MIT MATHEMATRIX!

\quad

\quad

\quad

$\mathbf {MATHE} \mu \alpha T\mathbb {R} ix$
LOGO	CH DE AT

SPENDEN
Der Hauptautor ggf. das Team verdient zwar nicht viel, braucht allerdings dein Geld eigentlich nicht. Wenn du aber doch meinst, dass gute Arbeit belohnt werden soll und dieses Projekt gut findest, kannst du immer in diesem Link spenden. Das ist allerdings vielleicht die einzige Einrichtung mit völliger Transparenz, wo du genau weißt, was mit deinem Geld passiert.

↑ Allgemeine Lösung: $1{,}2^{2}\cdot {\tfrac {2}{3}}=0{,}96$

[1] Allgemeine Lösung: $1{,}2^{2}\cdot {\tfrac {2}{3}}=0{,}96$

[1]