MathemaTriX ⋅ Probetest. 02. KL6

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT

${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$	DEINE FESTE BEGLEITERIN
	FÜR DIE SCHULMATHEMATIK

EINFACH UND
VERSTÄNDLICH

GRATIS!^*

STARTEN!

MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS!

Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Anderen Test wählen

01 02 03 04 05 06 07 08

Die Form eines Turms wird annähernd durch eine Funktion 2. Grades angegeben. Der Gipfel des Turms befindet sich 180 Meter oberhalb der Ebene und in einer horizontale Entfernung von 300 dm vom westlichen Rand des Turms.
1. Erstellen Sie ein Gleichungssystem zur Berechnung der Koeffizienten der Funktion.
2. Berechnen Sie die Koeffizienten der Funktion.

In einem Sonnensystem kreisen um den Planet A 10 Monde, um den Planet B 25, um den Planet C 45 und um den Planet D 20 Monde. Beim Planet D haben 5% der Monde Wasser, bei den restlichen ist der entsprechende Prozentsatz 40%.
1. Vervollständigen Sie das der Situation entsprechende nachstehende Diagramm!
2. Beschreiben Sie das Ereignis, dessen Wahrscheinlichkeit durch $0{,}10\cdot 0{,}4\$ berechnet wird!
3. Beschreiben Sie das Ereignis, dessen Wahrscheinlichkeit durch $0{,}1\cdot 0{,}4+0{,}4\cdot 0{,}45+0{,}05\cdot 0{,}2+0{,}4\cdot 0{,}25\$ berechnet wird!
4. Beschreiben Sie das Ereignis, dessen Wahrscheinlichkeit durch $0{,}25\cdot 0{,}4+0{,}95\cdot 0{,}2\$ berechnet wird!
5. Berechnen Sie die Wahrscheinlichkeit, dass ein zufällig ausgewählter Mond sowohl kein Wasser hat als auch nicht um den Planet C kreist!

Die Punkte, die die 110 Student*innen in zwei Tests A und B erreicht haben, wurden in den folgenden Boxplots erfasst.
1. Wie können wir interpretieren, dass im zweiten Boxplot die linke "Antenne" völlig fehlt?
2. Eine Stundentin hat im Test A 31 Punkte und im Test B 30. Im welchen Test, A oder B, hat sie mit ihrer Punktenanzahl einen größeren Anteil ihrer Mitstudent*innen überragt?
3. Nehmen wir an, dass ein Wert als Ausreißer nach unten oder nach oben gilt, wenn er mehr als das 1,5-Fache des Interquartilsabstands links vom zweiten bzw. rechts vom dritten Quartil liegt. Unterhalb von welchem Wert gilt eine Produktionszahl im zweiten Diagramm als Ausreißer nach unten?
Um Sternkarten zu erzeugen werden oft rechtwinkleige Dreiecke benutzt.
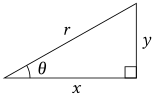
1. Schreiben Sie eine Formel für den Winkel $\theta$ in Bezug auf die Seiten x und y auf!
2. Wie groß ist der Winkel $\theta$ im Bild, wenn ihre Steigung 80% ist?
3. Wie groß ist der Winkel $\theta$ im Bild, wenn x=20 m und r=210 dm sind?

Bei 4 Sternen wurde der Wasserstoff-Vorrat ("Brennstoff" der Sterne) im Gt seit Entstehung des Sterns in Abhängigkeit von der Zeit in Millionen Jahren mit Hilfe von exponentiellen Funktionen modelliert.
1. Bei welcher Funktion lässt die Häufigkeit am langsamsten nach?
2. Die Funktion für den Stern B lautet: $f(x)=c\cdot e^{-m\cdot x}.\$ Lesen Sie aus dem Diagramm den Parameter $c$ ab!
3. Die Halbwertszeit für den Stern S (Funktion S) ist 46 Jahre. Stellen Sie die entsprechende Exponentialfunktion auf!
4. Bei diesem Stern S findet ein Supernova statt (Ende des Sterns), sobald der Vorrat 110 Gt war. Zum welchen Zeitpunkt war das? Benutzen Sie für die Lösung die Antwort der vorherigen Frage!
5. Die Halbwertszeit für einen anderen Stern, dessen Vorrat am Anfang 290 Gt war, ist 16 Jahre. Zeichnen Sie die entsprechende Exponentialfunktion (in dieses Diagramm)!
6. Die Gleichung für den Stern B lautet: $320\ e^{x\cdot (\ln(9)-\ln(10))}$ . Um wie viel Gt reduziert sich der Vorrat nach 7050000 Jahren?
7. Wie viel ist die mittlere Änderungsrate zwischen den Stellen 2 und 50 für den Stern G?
8. Die allgemeine Gleichung für die hier dargestellte Vorgänge lautet: $V(m)=V_{0}\cdot b^{m}$ . Geben Sie die Intervalle für b, m und V an!
9. Lesen Sie die Halbwertszeit für den Stern R ab!

Nehmen wir an, dass es in einem Sternhaufen 4000 Sterne gibt, von denen eine unbekannte Anzahl b sogenannte rote Riesen sind.
1. Wie lautet die Formel (mit Hilfe von b) für die Wahrscheinlichkeit, dass ein Stern ein roter Riese ist? ${\text{P}}(''RR'')={\qquad }$
2. In einem Bild wird zwei mal ein Stern zufällig gewählt und aus dem Bild entfernt. Erstellen Sie das entsprechende Baumdiagramm!
3. in einem Bild wird zwei mal ein Stern zufällig gewählt, ohne dass er aus dem Bild entfernt wird (das Bild bleibt dann unverändert). Erstellen Sie das entsprechende Baumdiagramm!
4. Die Wahrscheinlichkeit, dass im ersten Fall (Stern wird aus dem Bild entfernt) kein roter Riese gewählt wird, ist ${\tfrac {9}{16}}.\$ Wie viele sind die roten Riesen?

Die Form der Bahn eines Raumschiffs im Vordergrund des Sternbilds Orion wird vom folgenden Bild angenähert. Polynomfunktion 4. Grades im Intervall [-5;0] schneidet die Vertikale Achse bei 8 und führt dort knickfrei zur dargestellten Gerade g(x)=x+8. Die Funktion hat den Tiefpunkt (−2|7) und hat an der Stelle −4 den Wert 8,5.
1. Erstellen Sie ein Gleichungssystem zur Berechnung der Koeffizienten der Funktion (OHNE diese Koeffizienten zu berechnen!).
2. Wie viel ist der Tangens?
3. Wie groß ist der Winkel?
4. Wie groß ist die Hypotenuse eines rechtwinkeligen Dreiecks, wenn die Ankathete des Winkels mit Sinus ${\tfrac {119}{169}}\$ 15 cm ist?

Die zurückgelegte Strecke s ist das Produkt aus Geschwindigkeit v und Zeit t: $s=v\cdot t.$ $s=v\cdot t.$
Die Strecke eines Busses hat die Form eines Rechtecks, dessen Breite ${\tfrac {2}{5}}\$ ${\tfrac {2}{5}}\$ seiner Länge ist. Nehmen wir an, dass der Bus mit einer konstanten Geschwindigkeit von 7 m/s fährt. Für die Länge des Rechtecks braucht der Bus 24 Minuten.
1. Wie viel ist die Geschwindigkeit in km/h?
2. Wie viel Prozent größer als die Breite ist die Länge?
3. Wie viel Prozent kleiner als die Länge ist die Breite?
4. Wie viele km mehr als die Breite ist die Länge?
5. Wie lang ist die Strecke des Busses?

Um ein Spiel zu beginnen gibt es folgenden Vorgang: Eine Person würfelt. Ist die Augenzahl weniger als 2, soll die nächste Person würfeln. Im Gegenfall darf die erste Person genau noch einmal würfeln. Ist die Summe der Augenzahlen höchstens 11, dann (und nur dann) darf diese Person in der nächsten Runde mit dem Spiel anfangen, sonst ist die nächste Person dran.
1. Erstellen Sie das entsprechende Baumdiagramm!
2. Wie viel ist die Wahrscheinlichkeit für eine Person in einem Durchgang das Spiel anzufangen?
3. 6 Personen spielen. Wie viel ist die Wahrscheinlichkeit, dass mehr als zwei Personen im ersten Durchgang mit dem Spiel anfangen dürfen?

Sterne bestehen aus Gasen, vor allem aus Wasserstoff. Die Geschwindigkeit der Teilchen eines Gases hängt von der Temperatur ab: Je wärmer ein Gas ist, desto höhere sind die Geschwindigkeiten seiner Teilchen. Diese Geschwindigkeiten sind bei einer bestimmten Temperatur (näherungsweise) normalverteilt. Bei einem bestimmten Gas ist die mittlere Geschwindigkeit der Teilchen 25200 km/h und die Standardabweichung 2000 km/h.
1. In welchem symmetrischen Intervall liegen 38% der Geschwindigkeiten?
2. In wie viel Prozent der Fälle ist die Geschwindigkeit weniger als $2{,}8\$ bzw. $6{,}8\ km/s?$
3. Rechnen Sie die mittlere Geschwindigkeit in m/s um!
4. Skizzieren Sie eine Verteilung mit größerer Standardabweichung und 28000 km/h mittlere Geschwindigkeit!
5. Veranschaulichen Sie in der Abbildung die Wahrscheinlichkeit, dass die Geschwindigkeit kleiner als 22000 km/h ist!
6. Welche Eigenschaften hat der Punkt E?

Beim Vergleich von zwei Teleskopen geht man von einer Zylinder-Form aus. Der Durchmesser des Teleskops A ist das 1,4-fache des Teleskops B, seine Höhe (Länge) ist zwei fünftel des Teleskops B.
1. Jemand behauptet, dass das Volumen des Teleskops A 21,6% weniger als das Volumen des Teleskops B ist. Stimmt diese Aussage, ja oder nein und warum?
2. Wie viel Prozent mehr ist das Volumen des Teleskops B als das Volumen des Teleskops A?

Die Gleichung der Konzentration von Helium in einem Stern lautet: $K(z)=24,5\cdot 1{,}087^{z}$ (z in Millionen Jahre, K(t) in $mg/\ell$ ). Um wie viele $mg/\ell$ erhöht sich die Konzentration nach einem Million Jahren?

Schreiben Sie

43{,}2\cdot 10^{-6}

in Gleitkommadarstellung auf! Welchen der folgenden Möglichkeiten entspricht diese Zahl?

$4320\cdot 10^{-8}$	$\quad$	$0,00432\cdot 10^{-1}$
$0{,}00000432\cdot 10^{2}$	$\quad$	$43200\cdot 10^{-11}\ {\text{Tausende}}$
$4{,}32\cdot 10^{-4}$

Die erreichten Punkte der gleichen 130 Stundent*innen in drei verschiedenen Tests werden in den hier dargestellten Boxplot-Diagrammen zusammengefasst. Welche der folgenden Ausdrücken stimmt? (mehrere richtige Antworten möglich)

Der Median in den ersten zwei Diagrammen ist gleich
Die Spannweite ist im zweiten Diagramm größer
Der Quartilabstand ist im zweiten Diagramm größer
Der Wert 34 gehört in alle drei Fällen zum Intervall mit den größten Werten.
Es gibt mit Sicherheit eine Person, die insgesamt 100 Punkte hatte.
Eine Person, die 30 Punkte im ersten Diagramm hatte, gehört zu den 25% mit den meisten Punkten.
Wir ordnen die Personen nach absteigender Punktenanzahl ein. Die 30. Person gehört zu den 25% mit den meisten Punkten.

Die Schallgeschwindigkeit ist ca. 1224 km/h. 5,4 s nach einem Blitz wird der entsprechende Donner gehört. Wie weit weg ist der Blitz gefallen? (Wir können schon davon ausgehen, dass wir den Blitz annäherend sofort sehen)

Für die vorhandene Wassermenge auf einem Planeten gilt folgende Gleichung:

W(m)=0,96\cdot 0,987^{m}

m die Zeit in Millionen Jahren
W(m) die Menge in Tt (Teratonnen)

Kreuzen Sie die zutreffende(n) Aussage(n) an!

Die Menge am Anfang ist 960 Milliarden Tonnen
Die Menge nimmt linear ab
Die Menge nimmt um 1,3% pro eine Millione Jahre ab
Die Menge nimmt um 4% pro eine Millione Jahre zu
Die Menge nimmt im Laufe der Zeit immer langsamer ab
Die Menge nimmt um 98,7% pro eine Millione Jahre ab

Im folgenden Diagramm ist der Erwartungswert der "flächeren" Funktion 70 und die Standardabweichung 2,6.
1. Wie viel ist der Erwartungswert der "spitzeren" Funktion?
2. Die Standardabweichung der "spitzeren" Funktion ist 1. Beschriften Sie die Stellen und die Punkte, die eine Standardabweichung vom Erwartungswert abweichen!

Die Masse m ist das Produkt aus Dichte $\rho$ $\rho$ und Volumen V:
$m=\rho \cdot V.$ $m=\rho \cdot V.$
1. Die Masse eines Würfels ist 403 kg, seine Dichte 21,8 $kg/\ell .\$ Wie viel ist seine Kante in m?^[1]
2. Die Masse eines Zylinders ist 8 kg, seine Höhe 4,5 mm und der Durchmesser der Basis 1,1 cm. Wie viel ist seine Dichte in $kg/\ell .{\text{?}}$ ^[2]

Das Diagramm zeigt die Geschwindigkeit $v$ $v$ in km/h eines Fußgängers in Abhängigkeit von der Zeit t in h.
1. Was bedeutet die gekennzeichnete Fläche in diesem Sachzusammenhang?
2. Was bedeutet in diesem Sachzusammenhang ${\tfrac {v(t_{2})-v(t_{1})}{t_{2}-t_{1}}}$ ?
3. An welchem Zeitpunk ungefähr ist die Beschleunigung null?
4. Geben Sie eine Einschätzung der zurückgelegte Strecke ab Anfang der Zeitmessung bis Ende der 2. Stunde an!

Welche der folgenden Ausdrücke sind zueinander gleich?

${\sqrt[{200}]{c^{75}}}$	A	$\quad$	$\left({\tfrac {3}{8}}\right)^{c}$	D	$\quad$	$c^{0{,}375}$	F
$b^{\frac {3}{8}}$	B	$\quad$	${\tfrac {1}{0{,}375^{-c}}}$	E	$\quad$	${\sqrt[{20}]{\tfrac {1}{c^{-7,5}}}}$	G
${\tfrac {1}{c^{-0{,}375}}}$	C

Antworten (klicken)

1. - $0=a\cdot 0^{2}+b\cdot 0+c$
  - $180=a\cdot 30^{2}+b\cdot 30+c$
  - $0=2\cdot a\cdot 30+b$
2. Geogebra→CAS→löse({...})→ a=−0,2 ; b=12 ; c=0

   A: 0,1            B: 0,25         C: 0,45           D: 0,2
   /     \           /     \         /     \           /     \
W:0,4   KW:0,6    W:0,4   KW:0,6   W:0,4   KW:0,6   W:0,05   KW:0,95

ist aus Planet A und hat Wasser
hat Wasser
sowohl hat Wasser als auch kommt aus Planet B oder D

$0{,}73$

1. zumindest 25% der Student*innen habe 22 Puntke gehabt.
2. B
3. 11,5
1. $\theta =\arctan {\tfrac {y}{x}}$
2. $38{,}66^{\circ }$
3. $17{,}75$
1. S
2. 320 (Gt)
3. $N(t)=160\cdot 0{,}985^{t}$
4. ca. 24,86 Jahre nach Entstehung des Sternes
5. wird gemacht
6. ca. 167,75 Gt weniger
7. ca. 7,3 Gt weniger pro Jahr
8. 0<b<1, m>0, $0<V<V_{0}$
9. ca. 34,5 Jahre

$P(''RR'')={\tfrac {b}{4000}}$

        RR: b/4000                       KRR:(4000−b)/4000
         /       \                           /       \
RR:(b−1)/3999  KRR:(4000−b)/3999    RR:b/3999    KRR:(3999−b)/3999

        RR: b/4000                       KRR:(4000−b)/4000
         /       \                           /       \
RR: b/4000  KRR:(4000−b)/4000        RR:b/4000    KRR:(4000−b)/4000

ca. 1000

1. - $8=a\cdot 0^{4}+b\cdot 0^{3}+c\cdot 0^{2}+d\cdot 0+e$
  - $1=4\cdot a\cdot 0^{3}+3\cdot b\cdot 0^{2}+2\cdot c\cdot 0+d$
  - $7=a\cdot (-2)^{4}+b\cdot (-2)^{3}+c\cdot (-2)^{2}+d\cdot (-2)+e$
  - $0=4\cdot a\cdot (-2)^{3}+3\cdot b\cdot (-2)^{2}+2\cdot c\cdot (-2)+d$
  - $8{,}5=a\cdot (-4)^{4}+b\cdot (-4)^{3}+c\cdot (-4)^{2}+d\cdot (-4)+e$
2. ${\tfrac {119}{120}}=0{,}991{\dot {6}}$
3. $\approx 44{,}76^{\circ }$
4. 21,125 cm
1. 25,2 km/h
2. 250%
3. <60%/li>
4. 6,048 km
5. 28,224 km
1. S: spielen, NS: Nicht spielen A:Augenzahl
```
          6    5    4    3    2    1
         / \   -----------    ------
        6  A<12   S(3/6)       NS(2/6)
 NS(1/36)  S(5/36)
```
2. ${\tfrac {23}{36}}$
3. Geogebra→Statistik→Binomial mit n=6 und $p={\tfrac {23}{36}}$ →P(3≤X≤6)≈87,01%
1. Geogebra→Statistik→Normal mit μ=25200 und σ=2000→P(Min≤X)≈0,31% und P(X≤Max)≈0,31%→Min=24208,3 nd Max=26191,7 km/h
2. Geogebra→Statistik→Normal mit μ=25200 und σ=2000→P(X≤10080)≈0% bzw. P(X≤24480)≈35,94%
3. 7000 m/s
4. nach rechts verschieben und flacher
5. Das erste Kästchen von links ist 21200, ein bischen rechts davon Strecke zeichnen und Fläche links der Strecke schrafieren.
6. Höhepunkt (f'=0), wobei x-Wert ist Median, Modus und Erwartungswert
1. Sei r=5 und H=4, dann
  $V_{1}=\pi \ 5^{2}4$
  $V_{1}=\pi \ (1{,}4\cdot 5)^{2}{\tfrac {8}{5}}$
  ${\tfrac {V_{1}}{V_{2}}}=0{,}784$ also ja^[3]
2. ${\tfrac {27}{98}}\approx 27{,}551\%$
8,7% von 24,5 also ca. 0,213 $mg/\ell$
$4{,}32\cdot 10^{-5}\$ also nur das erste
das 3., das 4., das 6. und das 7.
1836 m
das 1., das 3. und das 5.
1. 70
3. 27
1. ca. 0,264 m
2. ca. $18707\ kg/\ell$
1. zurückgelegte Strecke
2. Beschleunigung zwischen $t_{1}$ und $t_{2}$
3. ca. 0 bzw. 3.2 h
4. ca. 5 km
A=C=F=G, D=E, B

BILDERVERZEICHNIS

ÖFFNE DEIN HORIZONT!
LERNE MIT MATHEMATRIX!

\quad

\quad

\quad

$\mathbf {MATHE} \mu \alpha T\mathbb {R} ix$
LOGO	CH DE AT

SPENDEN
Der Hauptautor ggf. das Team verdient zwar nicht viel, braucht allerdings dein Geld eigentlich nicht. Wenn du aber doch meinst, dass gute Arbeit belohnt werden soll und dieses Projekt gut findest, kannst du immer in diesem Link spenden. Das ist allerdings vielleicht die einzige Einrichtung mit völliger Transparenz, wo du genau weißt, was mit deinem Geld passiert.

↑ So ein Dichte ist typisch für Metalle auf der Erde
↑ So ein Dichte könnte typisch für das innere eines Sterns sein
↑ Allgemeine Lösung: $V_{1}=1{,}4^{2}\cdot {\tfrac {2}{5}}=0{,}784\ von\ V_{2}$

[1] So ein Dichte ist typisch für Metalle auf der Erde

[2] So ein Dichte könnte typisch für das innere eines Sterns sein

[3] Allgemeine Lösung: $V_{1}=1{,}4^{2}\cdot {\tfrac {2}{5}}=0{,}784\ von\ V_{2}$

[1]

[2]

[3]