Physik Oberstufe/ Anhang/ Aufgaben und Übungen Elektrizitätslehre

| ↑ Inhaltsverzeichnis | Aufgaben Schwingungen und Wellen >

Grundbegriffe und -wissen

Ladung, Strom und Elektrolyse

Bei der Elektrolyse von Wasser entstehen durch den Ladungsfluss von vier Elektronen zwei Wasserstoff- (H₂) und ein Sauerstoffmolekül (O₂):

Anode (+): 2 H₂O (l) → O₂ (g) + 4 H⁺ (aq) + 4e¯, Kathode (-): 4 H⁺ (aq) + 4e¯ → 2 H₂ (g)

Die Mischung der entstehenden Gase heißt Knallgas. Unter „normalen“ Bedingungen, d.h. 100,000 kPa und 25°C nimmt ein Mol des Gases ungefähr 24,79 × 10⁻³ m³/mol ein. Dieses Volumen wird molares Volumen oder auch Molvolumen $V_{\mathrm {m} }$ genannt.

Wir messen, wie viel Gasvolumen pro Sekunde bei einem konstanten Strom entsteht. Dazu tragen wir das Volumen in Abhängigkeit von der Zeit bei fest eingestellter Stromstärke auf und bestimmen die Steigung der Ausgleichsgeraden.

Bestimme für vier Stromstärken $I$ das Volumen des pro Sekunde entstehenden Gases ${\frac {\Delta V}{\Delta t}}$ .
Zeige, dass das Volumen des pro Sekunde entstehenden Gases ${\frac {\Delta V}{\Delta t}}$ proportional zum Strom $I={\frac {\Delta Q}{\Delta t}}$ ist.
Untersuche, was sich bei der Reihen- bzw. der Parallelschaltung von Knallgaszellen ändert.
Berechne aus der Messung das molare Volumen $V_{\mathrm {m} }$ .

Beachte: Es sei $\Delta N_{e}$ die Anzahl der transportierten Elektronen und $\Delta N_{G}$ die Anzahl der dabei entstandenen Gasmoleküle. Dann gilt mit $\Delta N_{e}={\frac {I\cdot \Delta t}{e}}$ und ${\frac {\Delta N_{G}}{3}}={\frac {\Delta N_{e}}{4}}$ für das Molare Volumen $V_{\mathrm {m} }$ ( $N_{A}$ ist die Avogadro Konstante):

V_{\mathrm {m} }={\frac {\Delta V}{\Delta N_{G}}}\cdot N_{A}={\frac {4\Delta V}{3\Delta N_{e}}}\cdot N_{A}={\frac {4\Delta V}{3}}\cdot {\frac {e}{I\cdot \Delta t}}\cdot N_{A}={\frac {4}{3}}\cdot {\frac {\Delta V}{\Delta t}}\cdot {\frac {e\cdot N_{A}}{I}}\,.

Schaltung von Widerstanden

Betrachte die abgebildeten Schaltungen von Widerständen.

Bearbeite für jede der Schaltungen die folgenden Aufgaben:

Zeichne die Schaltung ab.
Berechne den resultierenden Widerstand $R_{\mathrm {r} es}$ der Schaltung.
Wo überall in der Schaltung fließt der maximale Strom?
Zeichne Messgeräte ein:

Spannungsmessung am $470\,\Omega$ großen Widerstand,
Messung des Stroms, der durch den $470\,\Omega$ großen Widerstand fließt.

Berechne die Spannung am und den Strom durch den $470\,\Omega$ großen Widerstand.
Welche Widerstände darf man jeweils vertauschen, ohne dass sich eines der Ergebnisse ändert?

Falls Labor vorhanden:

Baue die Schaltung auf und vergleiche Messung und Rechnung. Trage dazu die Werte in eine Tabelle ein.
Berechne die prozentuale Abweichung von Rechnung und Messung.

✘ Lösung ✔

Teilergebnisse resultierende Widerstände: 143 Ω, 2150 Ω, 363 Ω und 831 Ω.

← Grundschaltung von Widerständen

Parallelschaltung

Für die parallele Schaltung von zwei Widerständen gilt:

R_{\mathrm {res} }={\frac {R_{1}\cdot R_{2}}{R_{1}+R_{2}}}

.

Stelle eine entsprechende Formel für drei parallel geschaltete Widerstände auf.

✘ Lösung ✔

Für die parallele Schaltung von drei Widerständen gilt:

R_{\mathrm {res} }={\frac {R_{1}\cdot R_{2}\cdot R_{3}}{R_{1}\cdot R_{2}+R_{1}\cdot R_{3}+R_{2}\cdot R_{3}}}

.

← Grundschaltung von Widerständen

Das elektrische Feld

Feld- und Äquipotentiallinien

Studiere unterschiedliche Ladungsanordnungen mit einem Simulationsprogramm.

← Superpositionsprinzip, Feld- und Äquipotentiallinien

Superpositionsprinzip

Gegeben sind zwei Punktladungen $Q_{1}$ und $Q_{2}$ im Abstand $a$ .

Bestimme für $Q_{1}=Q_{2}=2{\rm {nC}}$ und eine Abstand der Ladungen von $a=5\,{\rm {cm}}$ das elektrische Feld nach Betrag und Richtung an einem Punkt, der von $Q_{1}$ $4\,{\rm {cm}}$ und von $Q_{2}$ $3.5\,{\rm {cm}}$ entfernt ist.
Bestimme allgemein den Ort, an dem das resultierende Feld der Ladungen verschwindet, d.h. ${\vec {E}}=0$ gilt.

✘ Lösung ✔

Lösung zweiter Teil
1. Fall: Die Ladungen sind gleichnamig: $Q_{1}\cdot Q_{2}>0$
Das Feld kann nur zwischen den Ladungen verschwinden, da dort die Felder entgegengesetzt verlaufen und sich damit auslöschen können.
Für ${\vec {E}}=0$ muss gelten:

{\frac {Q_{1}}{r_{1}^{2}}}={\frac {Q_{2}}{r_{2}^{2}}}={\frac {Q_{2}}{(a-r_{1})^{2}}}\qquad \implies \qquad {\frac {Q_{1}}{Q_{2}}}={\frac {r_{1}^{2}}{(a-r_{1})^{2}}}\,,

wobei wir $r_{2}=a-r_{1}$ gesetzt haben. Da alle Terme positiv sind können wir die Wurzel ziehen:

{\sqrt {\frac {Q_{1}}{Q_{2}}}}={\frac {r_{1}}{a-r_{1}}}\,.

Für $r_{i}$ ergibt sich damit:

r_{1}={\frac {\sqrt {|Q_{1}|}}{{\sqrt {|Q_{1}|}}+{\sqrt {|Q_{2}|}}}}\cdot a\,,\qquad r_{2}={\frac {\sqrt {|Q_{2}|}}{{\sqrt {|Q_{1}|}}+{\sqrt {|Q_{2}|}}}}\cdot a\,.

2. Fall: Die Ladungen sind verschiedennamig: $Q_{1}\cdot Q_{2}<0$
Das Feld kann nur abseits der Ladungen verschwinden, und nur für $|Q_{1}|\neq |Q_{2}|$ auf der Seite der betraglich kleineren Ladung. Ohne Beschränkung der Allgemeinheit gelte im Folgenden: $|Q_{1}|>|Q_{2}|$ .
Für ${\vec {E}}=0$ muss dann gelten:

{\frac {|Q_{1}|}{r_{1}^{2}}}={\frac {|Q_{2}|}{r_{2}^{2}}}\quad \implies \quad {\frac {|Q_{1}|}{(a+r_{2})^{2}}}={\frac {|Q_{2}|}{r_{2}^{2}}}\qquad \implies \qquad {\frac {|Q_{1}|}{|Q_{2}|}}={\frac {(a+r_{2})^{2}}{r_{2}^{2}}}\,,

wobei wir $r_{1}=a+r_{2}$ gesetzt haben. Wir können wieder die Wurzel ziehen:

{\sqrt {\frac {|Q_{1}|}{|Q_{2}|}}}={\frac {a+r_{2}}{r_{2}}}\,.

Auflösen nach $r_{2}$ und ausrechnen von $r_{1}$ ergibt:

r_{1}={\frac {\sqrt {|Q_{1}|}}{{\sqrt {|Q_{1}|}}-{\sqrt {|Q_{2}|}}}}\cdot a\,,\qquad r_{2}={\frac {\sqrt {|Q_{2}|}}{{\sqrt {|Q_{1}|}}-{\sqrt {|Q_{2}|}}}}\cdot a\,.

← Coulombsches Gesetz

Bahnkurve und Braunsche Röhre

Erläutere die Funktionsweise der in der Abbildung mit ①…⑤ nummerierten Komponenten.
Berechne die erforderlichen Ablenkspannungen $U_{C_{1}}$ und $U_{C_{2}}$ für die dargestellte Bahnkurve mit den im Bild angegebenen Daten.

← Braunsche Röhre

Braunsche Röhre und Energieerhaltung

Löse die folgende Problematik auf: Nach den diskutierten Überlegungen haben die Elektronen nach dem Durchfliegen des Kondensators eine offensichtlich größere kinetische Energie als vorher. Dies widerspricht dem Energieerhaltungssatz und man könnte bei entsprechender Anordnung demnach ein Perpetuum mobile bauen.

← Braunsche Röhre

Kondensator

Schaltung von Kondensatoren

Leite die Formeln für Reihen- und Parallelschaltung von Kondensatoren her.

✘ Lösung ✔

Ansatz: Bei der Reihenschaltung muss die Ladung beider Kondensatoren gleich groß sein, da die Ladungsbilanz auf der „Insel“ zwischen den Kondensatoren ausgeglichen sein muss (Ladungserhaltung). Außerdem addieren sich die Spannungen der Kondensatoren (Maschenregel).
Es gilt also:

Q_{1}=Q_{2}=Q

und

U=U_{1}+U_{2}

.

Damit erhält man für die resultierende Kapazität:

C_{\mathrm {res} }={\frac {Q}{U}}={\frac {Q}{U_{1}+U_{2}}}

.

Für das Inverse erhält man die bekannte Formel:

{\frac {1}{C_{\mathrm {res} }}}={\frac {U_{1}+U_{2}}{Q}}={\frac {U_{1}}{Q}}+{\frac {U_{2}}{Q}}={\frac {1}{C_{1}}}+{\frac {1}{C_{2}}}

.

Dabei wurde im letzten Schritt wieder $Q_{1}=Q_{2}=Q$ verwendet.

Bei der Parallelschaltung muss wegen der Maschenregel für die Spannungen an den Kondenstoren gelten:

U_{1}=U_{2}=U

.

Die gesamte gespeicherte Ladung ist:

Q=Q_{1}+Q_{2}

.

Daraus erhalten wir mit $Q_{i}=C_{i}\cdot U$ das gesuchte Ergebnis:

Q=C_{\mathrm {res} }\cdot U=(C_{1}+C_{2})\cdot U\quad \Rightarrow \quad C_{\mathrm {res} }=C_{1}+C_{2}

.

Dielektrikum

Ein Plattenkondensator der Kapazität $C_{0}$ wird teilweise mit einem Dielektrikum ( $\epsilon _{r}$ ) gefüllt. Berechne die neue Kapazität, wenn

eine Platte komplett mit einem Dielektrikum der Dicke des halben Plattenabstands bedeckt ist;

✘ Lösung ✔

Der Aufbau entspricht einer Reihenschaltung zweier Kondensatoren $C_{1}$ und $C_{2}$ , wobei $C_{1}$ dem Kondensator $C_{0}$ mit halbiertem Plattenabstand entspricht. $C_{2}$ ist ein ebensolcher Kondensator, jedoch mit Dielektrikum.
Es gilt:

C={\frac {C_{1}\cdot C_{2}}{C_{1}+C_{2}}}

.

Aus obigen Überlegungen folgt:

C_{1}=2\cdot C_{0}

.

C_{2}=\epsilon _{r}\cdot C_{1}=2\cdot \epsilon _{r}\cdot C_{0}

.

Damit ergibt sich:

C={\frac {C_{1}\cdot C_{2}}{C_{1}+C_{2}}}={\frac {4\cdot \epsilon _{r}\cdot C_{0}^{2}}{2C_{0}\cdot (1+\epsilon _{r})}}=C_{0}{\frac {2\epsilon _{r}}{1+\epsilon _{r}}}

.

die halbe Platte mit einem Dielektrikum der Dicke des Plattenabstands gefüllt wird.

✘ Lösung ✔

Der Aufbau entspricht einer Parallelschaltung zweier Kondensatoren $C_{1}$ und $C_{2}$ , wobei $C_{1}$ dem Kondensator $C_{0}$ mit halbierter Plattenfläche und Dielektrikum entspricht. $C_{2}$ ist ein ebensolcher Kondensator, jedoch ohne Dielektrikum.
Es gilt:

C=C_{1}+C_{2}

.

Aus obigen Überlegungen folgt:

C_{1}=\epsilon _{r}\cdot {\frac {C_{0}}{2}}

.

C_{2}={\frac {C_{0}}{2}}

.

Damit ergibt sich:

C=C_{1}+C_{2}=\epsilon _{r}\cdot {\frac {C_{0}}{2}}+{\frac {C_{0}}{2}}=C_{0}\cdot {\frac {1+\epsilon _{r}}{2}}

.

← Schaltungen von Kondensatoren

Variation Plattenabstand

Ein Plattenkondensator der Kapazität $C_{0}$ wird auf die Spannung $U_{0}$ aufgeladen. Anschließend werden die Platten auf den doppelten Plattenabstand auseinander gezogen. Berechne die neue Kapazität des Kondensators $C_{1}$ , die Ladung auf den Platten sowie die Spannung am Kondensator, wenn:

die Spannungsquelle nach dem Aufladen des Kondensators entfernt wird,
die Spannungsquelle angeschlossen bleibt.

Betrachte die im Kondensator gespeicherte Energie in beiden Fällen vor und nach dem auseinander ziehen. Warum gilt der Energieerhaltungssatz?

✘ Lösung ✔

Nach dem Zusammenhang:

C={\frac {\varepsilon _{0}A}{d}}

halbiert sich die Kapazität bei Verdopplung des Plattenabstands $d$ :

C_{1}=C_{2}={\frac {C_{0}}{2}}

.

Für die Spannung gilt:
1. Da die Ladung in diesem Fall auf den Platten konstant ist, d.h. $Q_{1}=Q_{0}=Q$ ist, gilt mit $Q=C\cdot U$ :

U_{1}={\frac {Q}{C_{1}}}=2{\frac {Q}{C_{0}}}=2\cdot U_{0}

.

Andere Erklärung: Das Feld

{\vec {E}}

bleibt bei gleicher Ladung konstant (gleiche Flächenladungsdichte

\sigma

), aber der Weg und damit die Überführungsarbeit einer Ladung verdoppelt sich entsprechend.

2. In diesem Fall ist die Spannung konstant, $U_{2}=U_{0}=U$ . Durch die geringere Kapazität gilt für die Ladung:

Q_{2}=C_{2}\cdot U={\frac {C_{0}}{2}}\cdot U={\frac {Q_{0}}{2}}

.

Andere Erklärung: Die Spannung

U

und damit die Überführungsarbeit einer Ladung bleibt wegen der angeschlossenen Spannungsquelle konstant. Da der Weg sich aber verdoppelt, muss sich zum Ausgleich die elektrische Kraft, d.h. das Feld und damit die Flächenladungsdichte

\sigma

, entsprechend verringern.

← Kondensator als elektrisches Bauelement

Kondensatoren zusammenschalten

Zwei Kondensatoren $C_{1}$ und $C_{2}$ werden getrennt auf die Spannung $U_{1}$ bzw. $U_{2}$ aufgeladen und anschließend ihre Anschlüsse verbunden. Berechne die Spannung $U_{\mathrm {n} }$ an den Kondensatoren nach dem Verbinden und untersuche die Energie des Systems.

← Kondensator als elektrisches Bauelement

Lösung der Differentialgleichung

Für Auf- und Entladung eines Kondensators haben wir mit $I(t)={\dot {Q}}(t)$ für $Q(t)$ eine Differentialgleichung (DGL) erhalten:

{\dot {Q}}(t)={\frac {U_{0}}{R}}-{\frac {Q(t)}{RC}}\,.

Löse die Differentialgleichung mit dem Ansatz:

Q(t)=A+B\cdot e^{D\cdot t}\;.

Dabei sind A, B und D Konstanten, deren Wert durch die Anfangsbedingung und Einsetzen des Ansatzes in die DGL bestimmt wird. Im Falle der Entladung gilt $U_{0}=0$ und für die Anfangsbedingung:

Q(0)=Q_{0}\;,

bei Aufladung:

U_{C}(0)={\frac {Q(0)}{C}}=0\,.

✘ Lösung ✔

Für die Ableitung des Ansatzes gilt:

{\dot {Q}}(t)=B\cdot e^{D\cdot t}\cdot D\;,

eingesetzt in die DGL ergibt sich:

{\dot {Q}}(t)=B\cdot e^{D\cdot t}\cdot D={\frac {U_{0}}{R}}-{\frac {A+B\cdot e^{D\cdot t}}{RC}}\;.

Entladung
Wegen der Anfangsbedingung $U_{0}=0$ folgt für Entladung:

B\cdot e^{D\cdot t}\cdot D=-{\frac {A+B\cdot e^{D\cdot t}}{RC}}\;.

Umstellen ergibt:

B\cdot e^{D\cdot t}\cdot \left(RCD+1\right)=-A\;.

Damit diese Gleichung für alle Zeiten $t$ erfüllte ist, muss gelten:

D=-{\frac {1}{RC}}

und

A=0\;.

Unser Ansatz ergibt mit $Q(0)=Q_{0}$ (d.h. $B=Q_{0}$ ) also:

Q(t)=Q_{0}\cdot e^{-{\frac {t}{RC}}}\;.

Aufladung
Im Falle der Aufladung findet man analog:

B\cdot e^{D\cdot t}\cdot D={\frac {U_{0}}{R}}-{\frac {A+B\cdot e^{D\cdot t}}{RC}}\;.

Umstellen ergibt:

B\cdot e^{D\cdot t}\cdot \left(RCD+1\right)=U_{0}\cdot C-A\;.

Auch diese Gleichung muss für alle Zeiten $t$ gelten. Daraus folgt:

D=-{\frac {1}{RC}}

und

A=U_{0}\cdot C\;.

Mit $U_{0}\cdot C=Q_{0}$ findet man:

Q(t)=Q_{0}+B\cdot e^{-{\frac {t}{RC}}}\;.

Zur Zeit $t=0$ soll der Kondensator ungeladen sein:

Q(0)=0=Q_{0}+B\;\Rightarrow \;B=-Q_{0}\;.

Somit finden wir als Lösung:

Q(t)=Q_{0}\cdot \left(1-e^{-{\frac {t}{RC}}}\right)\;.

← Auf- und Entladung eines Kondensators

Energie des elektrischen Feldes

Bestimme die in einem Kondensator gespeicherte Energie, indem du den Spannungsverlauf $U(t)$ beim Entladen über einen Widerstand $R$ :

U(t)=U_{0}e^{-{\frac {t}{RC}}}

in die Formel für die Leistung:

P=U\cdot I={\frac {U^{2}}{R}}

einsetzt und über die Zeit integrierst.

✘ Lösung ✔

W=\int _{0}^{\infty }\!\!P(t)\,{\mathrm {d} }t=\int _{0}^{\infty }\!{\frac {U(t)^{2}}{R}}{\mathrm {d} }t={\frac {U_{0}^{2}}{R}}\int _{0}^{\infty }\!e^{-{\frac {2t}{RC}}}{\mathrm {d} }t={\frac {1}{2}}CU_{0}^{2}\,.

← Energie elektrischer Felder

Das magnetische Feld

Magnetfeld um stromdurchflossene Leiter

Durch einen geraden Leiter fließt ein Strom von $I=10{\rm {A}}$ . In welchem Abstand $r$ vom Leiter ist das Magnetfeld genauso groß wie das Erdmagnetfeld $(B\approx 50\mu {\rm {T)}}$ ?

✘ Lösung ✔

Aus der Formel für das Magnetfeld im Abstand $r$ eines stromdurchflossenen Leiters folgt:

B=\mu _{0}\mu _{r}{\frac {I}{2\pi \cdot r}}\quad \Rightarrow \quad r=\mu _{0}\mu _{r}{\frac {I}{2\pi \cdot B}}

r=2\times 10^{-7}{\frac {10\,{\rm {A\,Vs\,m^{2}}}}{50\times 10^{-6}\,{\rm {Vs\,Am}}}}={\frac {1}{25}}\,{\rm {m=4\,{\rm {cm}}}}

Durch einen zweiten Leiter fließt der Strom $I_{2}=5{\rm {A}}$ . Wie kann man den Leiter anbringen, damit das Magnetfeld längs einer parallelen Geraden mit Abstand $r$ zum ersten Leiter verschwindet? Wie, damit es in einem Punkt mit Abstand $r$ zum ersten Leiter verschwindet? Wo überall verschwindet das Magnetfeld im letzten Fall?

← Das Feld stromdurchflossener Leiter

Kraft auf einen Leiter

Ein Leiter wird um den Winkel $\varphi$ aus der senkrechten Position zu den Feldlinien gedreht. Wie groß ist anschließend die auf ihn wirkende Kraft?

✘ Lösung ✔

Wird ein Leiterstück der Länge $b$ um $\varphi$ aus der senkrecht zu den Feldlinien stehenden Richtung gekippt, so ist für die magnetische Kraft $F_{\rm {m}}$ die senkrecht zum Feld stehende Komponente $b_{\rm {eff}}$ des Leiterstücks relevant.

{\displaystyle b} — Wird ein Leiterstück der Länge $b$ um $\varphi$ aus der senkrecht zu den Feldlinien stehenden Richtung gekippt, so ist für die magnetische Kraft $F_{\rm {m}}$ die senkrecht zum Feld stehende Komponente $b_{\rm {eff}}$ des Leiterstücks relevant.

Relevant ist der Anteil des Leiters, der senkrecht zu den Feldlinien verläuft. Wird ein Leiterstück der Länge $b$ um $\varphi$ geneigt, so gilt für die senkrecht zum Feld stehende Komponente $b_{\rm {eff}}$ :

b_{\rm {eff}}=b\cdot \cos \varphi \,.

Für die Kraft auf das Leiterstück gilt damit:

F_{\rm {m}}=B\cdot I\cdot b_{\rm {eff}}=B\cdot I\cdot b\cdot \cos \varphi \,.

← Ein Maß für die Stärke des Magnetfelds

Kräfte zwischen parallelen Leitern

Durch zwei im Abstand $2\,{\rm {cm}}$ parallel angebrachte Leiter fließt ein Strom von $12\,{\rm {A}}$ . Bestimme die zwischen den Leitern wirkende Kraft pro Länge nach Betrag und Richtung für parallele und antiparallele Ströme.

✘ Lösung ✔

Magnetisches Feld bei antiparallelem Strom.
Magnetisches Feld bei parallelem Strom.

Aus der Formel für das Magnetfeld im Abstand $r$ eines stromdurchflossenen Leiters:

B=\mu _{0}\mu _{r}{\frac {I}{2\pi \cdot r}}

und der Definition der magnetischen Induktion:

B={\frac {F_{m}}{I\cdot b}}\quad \Rightarrow \quad {\frac {F_{m}}{b}}=B\cdot I

folgt:

{\frac {F_{m}}{b}}=\mu _{0}\mu _{r}{\frac {I^{2}}{2\pi \cdot r}}=4\pi \times 10^{-7}{\frac {\rm {Vs}}{\rm {Am}}}\cdot {\frac {12^{2}\,{\rm {A^{2}}}}{2\pi \cdot 2\times 10^{-2}\,{\rm {m}}}}=1.44\times 10^{-3}\,{\frac {\rm {N}}{\rm {m}}}\,.

Für die Richtungen der Kräfte findet man im Fall paralleler (gleich gerichteter) Ströme mit der Rechte-Faust-Regel und der UVW-Regel anziehende Kräfte. Bei antiparallelen Strömen stoßen die Leiter sich ab.

← Ein Maß für die Stärke des Magnetfelds

Elektrisches und magnetisches Feld im Vergleich

Vergleiche elektrisches und magnetisches Feld bezüglich:

der Definition der Feldrichtung und Feldstärke;
einfacher Felder: Punktladung und stromdurchflossener, gerader Leiter;
homogener Felder: Kondensator und lange Spule.

✘ Lösung ✔

Definition der Feldrichtung und Feldstärke

Das elektrische Feld hat die Richtung der Kraft auf eine Probeladung $q$ . Die Feldstärke folgt aus:

{\vec {E}}:={\frac {{\vec {F}}_{\rm {el}}}{q}}\,.

Das magnetische Feld hat die Richtung, in die sich eine Kompassnadel ausrichtet. Die Feldstärke folgt aus der Kraft eines senkrecht zu den Feldlinien verlaufenden Leiters der Länge $b$ mit $n$ Windungen:

B:={\frac {F_{m}}{I\cdot n\cdot b}}\,.

Einfache Felder: Punktladung und gerader Leiter

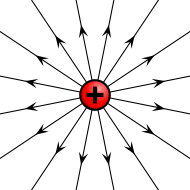
Feld einer positiven Ladung $+Q$
Feld einer negativen Ladung $-Q$ .

Für die elektrische Feldstärke im Abstand $r$ einer Punktladung $Q$ gilt:

E={\frac {Q}{4\pi \epsilon _{0}\cdot r^{2}}}\,.

Strom $I$ aus der Zeichenebene heraus.
$I$ in die Zeichenebene hinein.

Für die magnetische Feldstärke im Abstand $r$ eines vom Strom $I$ durchflossenen Leiters gilt:

B=\mu _{0}\mu _{r}{\frac {I}{2\pi \cdot r}}\,.

Homogene Felder: Kondensator und lange Spule

Für die elektrische Feldstärke in einem Kondensator mit Plattenabstand $d$ , an dem die Spannung $U$ anliegt, gilt:

E={\frac {U}{d}}\,.

Für die magnetische Feldstärke in einer langen Spule der Länge $l$ und der Windungszahl $n$ , durch die der Strom $I$ fließt, gilt:

B=\mu _{0}\mu _{r}{\frac {I\cdot n}{l}}\,.

← Das Magnetfeld der langen Spule

Elektronenstrahl im magnetischen Feld

Ein Elektronenstrahl wird mit $v=8.4\times 10^{6}{\frac {\rm {m}}{\rm {s}}}$ in ein homogenes Magnetfeld mit $B=10^{-3}{\rm {T}}$ geschossen. Der Winkel $\varphi$ zwischen ${\vec {B}}$ und ${\vec {v}}$ beträgt $70^{\circ }$ . Das Elektron legt einen spiralförmigen Weg zurück. Bestimme die Ganghöhe und den Radius der Spirale. Zeige, dass die Umlauffrequenz in der Spirale nicht von der Geschwindigkeit und damit auch nicht vom Winkel $\varphi \neq 0$ abhängt.

✘ Lösung ✔

Wir zerlegen den Vektor ${\vec {v}}$ der Geschwindigkeit in ein Komponente parallel und eine Komponente senkrecht zu ${\vec {B}}$ :

v_{||}=v\cdot \cos \varphi =2.873\times 10^{6}{\frac {\rm {m}}{\rm {s}}}\,,

v_{\perp }=v\cdot \sin \varphi =7.893\times 10^{6}{\frac {\rm {m}}{\rm {s}}}\,.

Die Komponente $v_{\perp }$ unterliegt der Lorentzkraft, die Komponente $v_{||}$ ist vom Magnetfeld unbeeinflusst und steht in direktem Zusammenhang mit der Ganghöhe der Spirale.

Für den Radius $r$ der Spirale erhält man mit $v=v_{\perp }$ :

r={\frac {m\cdot v_{\perp }}{e\cdot B}}\approx 44.88\,{\rm {mm\,.}}

Für eine Windung braucht das Elektron die Umlaufdauer $T$ :

T={\frac {2\pi \,r}{v_{\perp }}}\approx 35.73\times 10^{-9}{\rm {s\,.}}

In dieser Zeit $T$ bewegt sich das Elektron um die Ganghöhe $s$ parallel zu ${\vec {B}}$ weiter:

s=v_{||}\cdot T\approx 0.103\,{\rm {m\,.}}

Unabhängigkeit der Umlauffrequenz von ${\vec {v}}$ :
Für die Umlauffrequenz $f$ gilt wie oben:

f={\frac {v_{\perp }}{2\pi \,r}}.

Aus $F_{Z}=F_{L}$ haben wir schon den Zusammenhang zwischen $r$ und $v_{\perp }$ gefunden:

r={\frac {m\cdot v_{\perp }}{e\cdot B}}.

Eingesetzt erhält man damit:

f={\frac {e\cdot B}{2\pi \,m}},

die sog. Zyklotronfrequenz.

← Bewegung von Ladungen im Magnetfeld

Induktion

Rähmchen und Magnetfeld

Ein geschlitztes, quadratisches Leiter-Rähmchen mit Seitenlänge $l=4\,{\rm {cm}}$ werde mit $v=3\,{\rm {\frac {\rm {cm}}{\rm {s}}}}$ durch ein $5\,{\rm {cm}}$ breites, homogenes Magnetfeld $B=10\,{\rm {mT}}$ geschoben.

Skizziere die in den einzelnen Abschnitten vom Magnetfeld durchflossene Fläche $A(t)$ und bestimme daraus unter Verwendung des Induktionsgesetzes die induzierte Spannung $U_{\rm {ind}}$ .
Der Schlitz wird nun verlötet, sodass ein Strom $I_{\rm {ind}}$ fließt. Berechen $I_{\rm {ind}}$ , wenn der Widerstand des Rähmchens $1\,\Omega$ beträgt.
Bestimme jeweils Richtung und Betrag der Kraft, die auf das Rähmchen während der Bewegung durch das Magnetfeld einwirkt.
Berechne die mechanische Energie, die erforderlich ist, um das verlötete Rähmchen mit konstanter Geschwindigkeit ${\vec {v}}$ durch das Magnetfeld zu bringen. Vergleiche sie mit der elektrischen Energie, die das Rähmchen erwärmt.

✘ Lösung ✔

Mit dem Magnetfeld überlappende Fläche $A(x)$ und daraus resultierende Induktionsspannung $U_{\rm {ind}}.$

Befindet sich das Rähmchen außerhalb des Magnetfelds, wird keine Spannung induziert.
Für $A(x)$ gilt im Abschnitt $0\,{\rm {cm}}\leq x<4\,{\rm {cm}}$ :

A(x)=l\cdot x\,.

Mit $x=v\cdot t$ erhalten wir:

A(t)=l\cdot v\cdot t\,.

Die Induktionsspannung $U_{\rm {ind}}$ beträgt demnach in diesem Abschnitt:

U_{\rm {ind}}=-{\dot {\Phi }}=B\cdot {\dot {A}}(t)=-B\cdot l\cdot v

\qquad \,=-12\,{\rm {\mu V\,.}}

Im Abschnitt $4\,{\rm {cm}}\leq x\leq 5\,{\rm {cm}}$ ist $A$ konstant, die Ableitung verschwindet, damit ebenso die Induktionsspannung.

Im Abschnitt $5\,{\rm {cm}}<x<9\,{\rm {cm}}$ nimmt $A(x)$ mit der negativen Rate des ersten Abschnitts ab. Die Induktionsspannung entspricht der des ersten Abschnitts, weist aber entgegengesetztes Vorzeichen auf.

Der induzierte Strom beträgt:

I_{\rm {ind}}={\frac {U_{\rm {ind}}}{R}}=12\,\mu A\,.

Er fließt erst gegen, dann im Uhrzeigersinn.

Die Kraft wirkt in den Abschnitten, in denen ein Strom fließt und stets gegen die Bewegungsrichtung ${\vec {v}}$ .
Für den Betrag erhält man:

F_{\rm {m}}=B\cdot I\cdot l=48\times 10^{-10}\,{\rm {N\,.}}

Für die aufzubringende Arbeit gilt:

W_{\rm {mech}}=F\cdot s=F_{\rm {m}}\cdot 2\cdot l=384\times 10^{-12}\,{\rm {Nm\,.}}

Auf dem Weg wir die elektrische Energie:

W_{\rm {el}}=U_{\rm {ind}}\cdot I_{\rm {ind}}\cdot {\frac {2\cdot l}{v}}=384\times 10^{-12}\,{\rm {J}}

frei. Dabei wurde die Zeitspanne $t={\frac {2\cdot l}{v}}$ , in der der Strom fließt, verwendet.

Man nutzt genau dieses Prinzip in Wirbelstrombremsen.

← Das Induktionsgesetz im allgemeinen Fall

Erzeugung von Wechselspannung

Erkläre die Induktionsspannung einer sich drehenden Leiterschleife mithilfe der Lorentzkraft auf bewegte Ladungen. Bestimme die Richtung des Drehmoments auf die Leiterschleife, wenn ein Induktionsstrom fließt.

Es sei $B=2\times 10^{-4}{\rm {T}}$ und $l=b=2\,{\rm {cm}}$ . Mit welcher Frequenz $f$ muss eine Spule mit $n=100$ Windungen gedreht werden, damit die Wechselspannung ${\hat {U}}_{\rm {ind}}=5\,{\rm {mV}}$ entsteht?