Quadriviale Kuriositäten/ Die Stele vom Rocher des Doms

Die Umgebung der französischen Stadt Avignon.

Dieses Kapitel beschreibt einige archäoastronomische Aspekte in Bezug auf die Darstellungen der Stele vom Felsen Rocher des Doms in der französischen Stadt Avignon. Der Felsen am Ufer der Rhône wurde bereits im Neolithikum genutzt, und das bewohnte Gebiet in Avignon beschränkte sich noch im frühen Mittelalter auf diesen Felsen.

Ergänzend werden die säkularen mesonychischen (altgriechisch für "in der Mitte der Nacht") Aufgänge von einigen hellen Sternen am südlichen Meridian betrachtet und ein entsprechendes Java-Programm vorgestellt, mit dem die Erstaufgänge (englisch: "first rise", latein: "ortus primus") von beliebigen Gestirnen an beliebigen Orten über dem südlichen Horizont berechnet werden können.

Beschreibung[Bearbeiten]

Stele vom Rocher des Doms
Vorderseite der Stele vom Rocher des Doms.
Rückseite der Stele vom Rocher des Doms.

Die 26 Zentimeter hohe Stele aus Kalkstein befindet sich in einer Dauerausstellung für Vorgeschichte im Museum Calvet in Avignon.^[1] Sie wurde in den Jahren 1960 und 1961 bei Ausgrabungen am linken Rhône-Ufer nördlich von Avignon im nördlichen Teil des kleinen Massivs Rocher des Doms gefunden. Auf der Vorderseite ist möglicherweise ein Gesicht darstellt.^[2] Die Stele stammt aus der Lagozza-Kultur und wurde wie die Himmelstafel von Tal-Qadi ebenfalls am Ende des Neolithikums hergestellt. Im unteren Bereich der Vorderseite befindet sich etwas nach rechts versetzt eine sternartige Darstellung mit acht Strahlen und einer kleinen zentralem Bohrung, die als Sonnenfigur interpretiert wurde.^[3]

Der Rocher des Doms ist ein freistehender Felsen am Ufer der Rhône, der in alle Himmelsrichtungen eine ausgezeichnete Sicht auf den Himmel ermöglicht. Ohne die heute durch die Städte Avignon und Saint-Rémy-de-Provence vorherrschende Lichtverschmutzung muss die Sicht in Richtung auf das 50 Kilometer südlich gelegene Mittelmeer und auf die sich davor erstreckende 22 Kilometer entfernte Kalksteinkette der Alpillen in früheren Nächten hervorragend gewesen sein.

Die Darstellungen[Bearbeiten]

Sur le roc d'Avignion l'on y s'étonnait, l'on y s'étonnait.

Die Darstellungen auf den beiden Seiten der Stele lassen in der Tat astronomische Deutungen zu, die auf astronomischen Beobachtungen am prähistorischen Observatorium Rocher des Doms beruhen könnten.

Vorderseite[Bearbeiten]

Die Ekliptik verläuft im Goldenen Tor der Ekliptik im Sternbild Stier (Taurus) zwischen dem Roten Riesen Aldebaran ("Ochsenauge") und dem offenen Sternhaufen der Plejaden (Siebengestirn). Diese beiden Objekte sowie der offene Sternhaufen der Hyaden, in welchem der Stern Aldebaran zu sehen ist, haben geringe ekliptikale Breiten und werden deswegen regelmäßig innerhalb eines drakonitischen Zyklus mit der Dauer von 18,6 Jahren von der Mondscheibe bedeckt. Die beiden genannten Sternhaufen bilden die beiden Pfosten des Goldenen Tores.

Der Frühlingspunkt lag 3000 vor Christi Geburt etwas östlich vom Goldenen Tor auf der Ekliptiklinie. Die Öffnung des Trichters der Thuraya (arabisch al-thurayya = "Plejaden") wird durch die Sterne Menkar im Sternbild Walfisch (Cetus), die Plejaden in der Spitze und den Stern Hamal im Sternbild Widder (Aries) gebildet. Alle sieben Wandelgestirne (Sonne, Mond, Merkur, Venus, Mars, Jupiter und Saturn) wandern im Laufe der Zeit regelmäßig durch diesen Trichter der Thuraya in das Goldene Tor der Ekliptik.

Diese sehr auffälligen vier genannten Himmelsobjekte lassen sich zwanglos der Geometrie der Darstellung auf der Vorderseite der Stele zuordnen:

Vorderseite der Kalksteinstele vom Rocher des Doms
Vorderseite
Die Ekliptiklinie (rot gestrichelt) vom Trichter der Thuraya (unten) durch das Goldene Tor der Ekliptik im Sternbild Stier (Taurus) oben.

Rückseite[Bearbeiten]

Auf der Rückseite befinden sich zahlreiche, verschieden große und meist gebohrte Vertiefungen, die die Himmelsregion um den Asterismus des Wintersechsecks darzustellen scheinen. Das Wintersechseck besteht aus dem hellsten Stern überhaupt, nämlich Sirius im Sternbild Großer Hund (Canis Major), sowie den Sternen Prokyon im Sternbild Kleiner Hund (Canis Minor), Pollux im Sternbild Zwillinge (Gemini), Capella im Sternbild Fuhrmann (Auriga), Aldebaran im Sternbild Stier (Taurus) und dem sehr hellen Stern Rigel im Sternbild Orion.

Das Sternbild Orion wird vom Wintersechseck umrundet und ist über den im Sternbild Orion unten rechts liegenden Stern Rigel in das Wintersechseck eingebunden. Orion besteht ferner aus den drei Gürtelsternen Alnitak (ζ Orionis), Alnilam (ε Orionis) und Mintaka (δ Orionis) (von links nach rechts) sowie darüber dem Roten Riesen Beteigeuze (oben links), dem Stern Bellatrix (oben rechts), der durch eine eher natürlich aussehende Vertiefung markiert ist, und dem Stern Saiph (unten links). "Der Helle im Schwert" heißt auf Arabisch Nair Al Saif (oder auch Hatysa) und befindet sich unterhalb des Gürtels des Orions und direkt unterhalb der Orionnebels an der Spitze des Schwertes.

Das Sternbild Orion mit seinen sieben Hauptsternen und der Schwertregion unterhalb der drei Gürtelsterne Alnitak (ζ Orionis), Alnilam (ε Orionis) und Mintaka (δ Orionis) (von links nach rechts).
Die Schwertregion im Sternbild Orion mit dem Orionnebel und dem halb links darunterliegenden hellen Stern Nair Al Saif (oder Hatysa) mit der Größenklasse 2,75^m<7sup>.

Zu den hellsten und auffälligsten Sternen der Umgebung des Wintersechsecks gehören Adhara im Sternbild Großer Hund (Canis Major), Alphard im Sternbild Wasserschlange (Hydra), Castor im Sternbild Zwillinge (Gemini), Hamal im Sternbild Widder (Aries) und Menkar im Sternbild Walfisch (Cetus). Der Stern Castor ist in der Darstellung durch eine geritzte gradlinige Furche mit seinem "Zwillingsbruderstern" Pollux verbunden; diese beiden Sterne bilden heute die Köpfe des Sternbilds Zwillinge (Gemini).

In der folgenden Tabelle sind alle genannten Sterne samt ihrer astronomischen Bezeichnung und ihrer scheinbaren Helligkeit enthalten. Der Stern Capella ist der sechste, auf der Stele nicht dargestellte Stern des Wintersechsecks und ist hier nur der Vollständigkeit halber aufgeführt. Die Plejaden sind ebenfalls nicht repräsentiert. Der Stern Phakt wird weiter unten näher betrachtet. Zwischen Phakt und Menkar befindet sich auf der Stele eventuell noch eine weitere Bohrung, die rechts unterhalb vom Stern Rigel mit dem hellsten in dieser Region befindlichen Stern Zaurak (γ Eridani, 3^m) im sehr ausgedehnten Sternbild des Flusses Eridanus identifiziert werden könnte.

Eigenname	Astronomische Bezeichnung	Scheinbare Helligkeit
Sirius	α Canis Majoris	-1,5^m
Capella	α Aurigae	0,0^m
Rigel	β Orionis	0,0^m
Beteigeuze	α Orionis	0,5^m bis 1,5^m
Prokyon	α Canis Minoris	0,5^m
Aldebaran	α Tauri	1,0^m
Pollux	β Geminorum	1,0^m
Adhara	ε Canis Majoris	1,5^m
Alnilam	ε Orionis	1,5^m
Alnitak	ζ Orionis	1,5^m
Bellatrix	γ Orionis	1,5^m
Castor	α Geminorum	1,5^m
Alphard	α Hydrae	2,0^m
Hamal	α Arietis	2,0^m
Mintaka	δ Orionis	2,0^m
Saiph	κ Orionis	2,0^m
Menkar	α Ceti	2,5^m
Phakt	α Columbae	2,5^m
Nair Al Saif	ι Orionis	2,75^m

Rückseite der Kalksteinstele vom Rocher des Doms
Rückseite
Darstellung der Himmelsregion um den Asterismus des Wintersechsecks mit den Sternen Aldebaran (α Tauri ) im Stier (Taurus), Rigel (β Orionis) im Orion, Sirius (α Canis Majoris) im Großen Hund (Canis Major), Prokyon (α Canis Minoris) im Kleinen Hund (Canis Minor), Pollux (β Geminorum) in den Zwillingen (Gemini) und Capella (α Aurigae) im Fuhrmann (Auriga). Der Stern Capella ist auf der Stele nicht dargestellt.
Astronomische Aufnahme des Wintersechsecks.

Extinktion[Bearbeiten]

Die Helligkeit von dicht über dem Horizont befindlichen Gestirnen wird durch atmosphärische Einflüsse vermindert, und zwar umso mehr, je dichter sich das Gestirn am Horizont befindet. Das Licht wird auf dem mehrere hundert Kilometer langen Weg durch die Atmosphäre nicht nur gebrochen (Refraktion), sondern auch an Teilchen gebeugt (Diffraktion) oder gestreut (Diffusion) sowie abgeschwächt (Absorption), wodurch die scheinbare Heiligkeit um einige Größenklassen verringert wird (Extinktion).

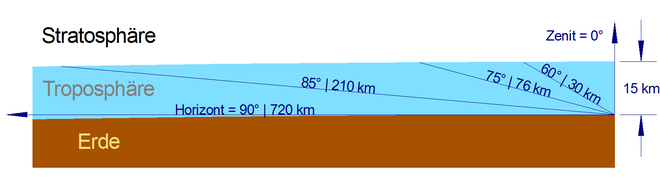
Weglängen für Lichtstrahlen in der 15 Kilometer hohen Troposphäre in Abhängigkeit von der Zenitdistanz $z$ .

Die astronomische Extinktion ergibt sich durch Beugung, Streuung und Vernichtung von Photonen (Lichtteilchen) an Atomen, Molekülen und Aerosolen in der Atmosphäre, und diese hängen in erster Linie von der Weglänge in der Troposphäre, allerdings auch von der Zusammensetzung der Luft, vom Luftdruck und von der Temperatur ab.

Die Weglänge ergibt sich in Abhängigkeit von der Zenitdistanz $z$ . Der Zusammenhang zwischen der Zenitdistanz und Höhe über dem Horizont $h$ ergibt sich wiederum sehr einfach aus der folgenden Winkelbeziehung:

h=90^{\circ }-z

Mit Hilfe der Luftmasse $m_{a}$ lässt sich die Abschwächung der scheinbaren Helligkeit in Größenklassen $\Delta _{m}$ in Abhängigkeit vom Zenitwinkel $z$ berechnen:^[4]

m_{a}={\frac {1}{\cos {z}+0,025\cdot e^{-11\cdot {\cos {z}}}}}

\Delta _{m}=0,28\cdot m_{a}

Der Extinktionskoeffizient von 0,28 stellt einen für Beobachtungen auf Meereshöhe stattfindenden realistischen Wert dar. Bei größeren Beobachtungshöhen, wie zum Beispiel auf Bergen, kann sich der Extinktionskoeffizient bis auf die Hälfte dieses Wertes verringern.

In der folgenden Tabelle sind die Abschwächungen in Größenklassen beziehungsweise als Abschwächungsfaktor für verschiedene Höhen h über dem Horizont angegeben:

Atmosphärische Extinktion in Abhängigkeit von der Höhe über dem Horizont
Höhe über dem Horizont $h$ in Bogengrad	Abschwächung der scheinbaren Helligkeit $\Delta _{m}$ in Größenklassen	Scheinbare Helligkeit $m$ eines freiäugig gerade noch sichtbaren Gestirns in Größenklassen	Abschwächungsfaktor
0,0	11,2	-4,7	0,000033
0,5	8,9	-2,4	0,00028
1,0	7,4	-0,9	0,0011
1,5	6,2	0,3	0,0033
2,0	5,4	1,1	0,0069
2,5	4,7	1,8	0,013
3,0	4,2	2,3	0,021
4,0	3,4	3,1	0,044
5,0	2,9	3,6	0,069
6,0	2,5	4,0	0,10
7,0	2,2	4,3	0,13
8,0	1,9	4,6	0,17
10	1,6	4,9	0,23
16	1,0	5,5	0,40
20	0,8	5,7	0,48
25	0,7	5,8	0,52
30	0,6	5,9	0,58
35	0,5	6,0	0,63
50	0,4	6,1	0,69
90	0,3	6,2	0,76

Venus-Untergang im Sternbild Zwillinge (Gemini) bei hohem Glanz (-4,3 mag) am 21. Mai 2023 um 0:19 Uhr in Berlin. Der Planet stand im Dunst noch 3,5 Bogengrad über dem Horizont und war gerade noch mit bloßem Auge zu erkennen (Venusphase = 57,5 Prozent, östliche Elongation = 44°40', Farbtemperatur = 4100 Kelvin).

Ab einer Höhe von zirka 30 Bogengrad ist die Abschwächung geringer als eine halbe Größenklasse und spielt bei der freiäugigen Beobachtung kaum noch eine Rolle. Direkt am Horizont können in völliger Dunkelheit jedoch nur Objekte gesehen werden, die mindestens eine scheinbare Helligkeit von -4,7^m haben, da deren Licht um 11,2 Größenklassen auf 6,5^m abgeschwächt wird, so dass sie bei der Abwesenheit von Lichtverschmutzung freiäugig gerade noch zu erkennen sind. Dies betrifft in der Realität nur die Sonne, den Mond und die Venus, die eine maximale scheinbare Helligkeit von genau diesen -4,7^m erreichen kann. Der hellste Stern des Himmels ist Sirius mit einer scheinbaren Helligkeit von -1,7^m. Er kann demnach erst bei Höhen ab knapp einem Bogengrad über dem Horizont gefunden werden.

Durch die Rayleigh-Streuung ergibt sich stets eine besonders starke Abschwächung bei den Lichtanteilen mit kürzerer Wellenlängen, also im Blauen, so dass das Licht der Gestirne rötlicher erscheint. Dies ist besonders deutlich bei Sonnenaufgängen und Sonnenuntergängen aber auch bei den Auf- und Untergängen von Mond, Planeten und sehr hellen Sternen zu beobachten.

Sterne am Horizont[Bearbeiten]

Auch Aristoteles hat im vierten vorchristlichen Jahrhundert in seinem Werk Peri uranú (Περὶ οὐρανοῦ) beschrieben, dass es Sterne gibt, die von Ägypten oder von Zypern aus beim Auf- und Untergang zu beobachten sind, die aber in weiter nördlich gelegenen Regionen nie zu sehen sind.^[5] Hiermit hat er sich sicherlich auch auf den zweithellsten Stern des gesamten Himmels Canopus (siehe unten) bezogen, der zu seinen Lebzeiten in Athen nicht sichtbar war, aber durchaus auf Zypern und erst recht in Ägypten. Ferner stellt er fest, dass die Begrenzung des Schattens auf der Oberfläche des Mondes bei einer Mondfinsternis kreisförmig ist und von der Erde hervorgerufen werden muss, die das Sonnenlicht verschattet. Er schließt aus all diesen Beobachtungen folgerichtig, dass die Erde eine runde Form haben muss, und dass die Erdkugel erheblich kleiner sein muss als die Himmelssphäre.

Anhand der folgenden Landkarte kann abgelesen werden, auf welchen Breitengraden sich verschiedene Orte und Regionen von Westeuropa über Zentraleuropa bis nach Osteuropa sowie im Orient und in Nordafrika befinden.

Somit können die Breitengrade der Orte und der ersten und letzten Erscheinungen von den Sternen innerhalb der letzten Jahrtausende, die in den folgenden Tabellen aufgeführt sind, den entsprechenden geographischen Regionen zugeordnet werden.

Süd- und Mitteleuropa, Nordafrika sowie der vordere Orient.

Landkarte vom nördlichen Wendekreis bei 23,4 Bogengrad (weiß gestrichelt, unten) bis zum 60. nördlichen Breitengrad im Bereich Europa, Nordafrika und Naher Osten.

Neuerschienene Sterne[Bearbeiten]

Hier sind einige markante Beispiele von Sternen aufgeführt, die im Laufe der letzten Jahrtausende bei ihrer oberen Kulmination auf dem südlichen Meridian plötzlich über dem Horizont aufgetaucht sind.

Phakt[Bearbeiten]

Animierte Darstellung des Sterns **Phakt** bei der oberen Kulmination vor 4300 Jahren in Richtung Mittelmeer direkt über dem südlichen Horizont vom **Rocher des Doms** aus gesehen. Die Stadt Avignon existierte damals noch nicht, und es gab keine Lichtverschmutzung.

Man stelle sich vor, was in den Köpfen der Mitglieder einer archaischen Gesellschaft vorgegangen ist, nachdem am Himmel eines Jahres ein Stern zu sehen war, der zuvor zirkumpolar um den Himmelssüdpol und deswegen permanent unter dem Horizont verborgen war.

Am 11. November 1572 sah der dänische Astronom Tycho Brahe eine neue, in Bezug auf den Fixsternhimmel ortsfeste und sehr helle Leuchterscheinung im Sternbild Kassiopeia. Im Laufe eines Jahres nahm die Leuchtstärke dies Objekts immer weiter ab. Er dokumentierte seine Beobachtungen in der Schrift De nova et nullius ævi memoria prius visa Stella (zu Deutsch: "Über den neuen und durch keine Erinnerung der Ewigkeit früher gesehen Stern"). Darin widersprach und widerlegte er Aristoteles, der noch von einem unveränderlichen Fixsternhimmel ausgegangen war. Wenige Jahre später war ein ähnliches Ereignis auch für den deutschen Astronomen Johannes Kepler noch so ungewöhnlich, dass er das Erscheinen der Supernova 1604 in seinem Buch "De Stella Nova in Pede Serpentarii" (zu Deutsch: "Über den neuen Stern im Fuß des Sternbilds Schlangenträger (Ophiuchus)") thematisierte.

Ähnlich aufgebracht muss die Reaktion der gebildeten und den Sternenhimmel beobachtenden Bewohner des Rocher des Doms im heutigen Avignon vor einigen tausend Jahren gewesen sein, als einige Wochen vor der Wintersonnenwende zum ersten Mal ein heller neuer Stern dicht über dem südlichen Horizont auftauchte. Allerdings konnten sie dieses Ereignis in Ermangelung einer Schrift noch nicht in Textform festhalten.

Die im Folgenden angegebenen Berechnungen berücksichtigen folgende Einflussfaktoren, um das damalige Geschehen nachzuvollziehen:

Den Breitengrad des Beobachtungspunkts (die Stadt Avignon befindet sich auf 43,95 Bogengrad nördlicher Breite).
Die Höhe des Beobachtungspunkts über dem Meeresspiegel (Höhe vom Rocher des Doms über dem Meeresspiegel 55 Meter).
Die Präzession der Erdachse zur Epoche J2000, wodurch sich die äquatorialen Koordinaten des Sterns zum Beobachtungszeitpunkt verändern.
Die äquatorialen Koordinaten zur Epoche J2000:
- Rektaszension (Phakt: 5h 39m 39s = 84,912°).
- Deklination (Phakt: -34° 04' 27" -34,074°).
Die Eigenbewegung des Sterns gegenüber dem Fixsternhimmel, wodurch sich die äquatorialen Koordinaten ebenfalls verändern:
- Eigenbewegung Rektaszension pro Jahr (Phakt: 4,6 mas/a).
- Eigenbewegung Deklination pro Jahr (Phakt: -29.9 mas/a.).
Die scheinbare Helligkeit im Zenit (Phakt: 2,6^m).
Die atmosphärische Refraktion, wodurch sich die tatsächlich beobachtete Höhe in Horizontnähe etwas vergrößert.
Die atmosphärische Extinktion, durch die sich die visuelle Helligkeit in Horizontnähe deutlich verringert.

→ Zur Deklination im äquatorialen Koordinatensystem siehe auch Astronomische Bezugssysteme.

→ Siehe auch Wikibook „Digitale bildgebende Verfahren“ / Kapitel „Bildaufnahme“ / Abschnitt „Atmosphärische Störungen“.

Ein Stern wie Phakt mit der Größenklasse 2,65^m erscheint erst bei einer Höhe von über 3 Bogengrad über dem Horizont mit einer visuellen Helligkeit von 6^m und ist dann mit bloßem Auge erkennbar – diese maximale Höhe erreichte Phakt vor knapp 4000 Jahren. Der kurzwellige Lichtanteil wird in der Atmosphäre durch die Rayleigh-Streuung stärker gestreut als der langwellige, so dass sich dicht über dem Horizont zusätzlich eine rötliche Verfärbung des Sternenlichts ergibt.

Die folgende Tabelle gibt die maximalen Deklinationen an, auf denen in den letzten 4500 Jahren der Stern Phakt bedingt durch die Präzession der Erde zu beobachten war. Daraus abgeleitet ergeben sich die nördlichsten Breitengrade einer möglichen Beobachtung (dieser ergibt sich aus der Deklination, indem diese zu 90 Bogengrad addiert wird). Für den Beobachtungspunkt (Rocher des Doms) werden ferner die maximalen Höhne über dem Horizont und die maximale visuelle Helligkeit angegeben

Phakt (α Columbae)
Beobachtungsjahr	-4000	-3500	-3000	-2500	-2000	-1000	0000	1000	2000
Deklination	-51,1°	-48,8°	-46,6°	-44,6°	-42,6°	-39,3°	-36,8°	-35,0°	-34,1°
Nördlichste Breite der Beobachtung	38,9°	41,2°	43,4°	45,4°	47,4°	50,7°	53,2°	55,0°	55,9°
Maximale Höhe der Beobachtung vom Rocher des Doms	-	-	0,3°	2,1°	3,5°	7°	9,5°	11°	12°
Maximale visuelle Helligkeit vom Rocher des Doms	-	-	12^m	8^m	6,5^m	5^m	4,5^m	4^m	4^m

Der hellste Stern im Sternbild Taube (Columba) Phakt (α Columbae) tauchte vom Rocher des Doms aus gesehen für die Bewohner also vor knapp 4000 Jahren zum ersten Mal in südlicher Richtung sichtbar über dem geographischen Horizont auf. Seitdem ist er in jedem Jahr über der gut 20 Kilometer entfernten Kalksteinkette Massif des Alpilles (Höhe über dem Meeresspiegel in dieser Richtung bis zu knapp 300 Meter) zu sehen. Zwischen dem frühen Morgen (gegen 3 Uhr) bei der Tag-und-Nacht-Gleiche im Herbst und dem Abend (gegen 21 Uhr) bei der Wintersonnenwende war er damals bei klarer Sicht zunächst nur wenige Minuten bei der oberen Kulmination auf dem südlichen Meridian, also exakt in Richtung Süden zu sehen.

Die geometrische Bahn des Sternes **Phakt** bei der oberen Kulmination auf dem südlichen Meridian vor 4700 Jahren, wie sie ohne atmosphärische Störungen vom **Rocher des Doms** aus in Richtung Süden ausgesehen hätte. Durch die Atmosphäre wird das Licht eines sehr dicht über dem Horizont stehenden Himmelsobjekts gebrochen, so dass dieses dunkler erscheint und eine etwas größere scheinbare Höhe hat, als sich aus der Deklination ergibt. Der Stern Phakt erreichte damals noch nicht einmal die Größenklasse 10^m, so dass er mit bloßem Auge nicht sichtbar war.

Darstellung der Rückseite der Stele vom **Rocher des Doms** mit der Lage des Horizonts und des Meridians bei der oberen Kulmination von **Phakt**.

Alle vier Jahre erhöhte sich die maximale Höhe über dem Horizont um ungefähr eine Bogenminute, nach 250 Jahren war es dann bereits ein Bogengrad mehr, und die maximale Sichtbarkeitsdauer betrug schon ungefähr zwei Stunden. Im Augenblick der maximalen Höhe über dem Horizont befand sich Stern Phakt wie alle anderen Gestirne auf dem senkrecht auf dem Horizont stehenden südlichen Meridian. Zu diesem Zeitpunkt lag der Meridian damals im weiteren Verlauf in Richtung Zenit zwischen den Zwillingssternen Castor und Pollux, den beiden Hauptsternen im Sternbild Zwillinge (Gemini), so wie es auf der Skizze zur Rückseite der Stele vom Rocher des Doms angedeutet ist.

Ähnliche Verhältnisse wie für den freistehenden Rocher des Doms ergeben sich für den ebenfalls freistehenden, rund 450 Meter hohen Magura-Hügel mit den neolithischen Höhlenmalereien, der sich im heutigen Bulgarien nur wenige Kilometer näher am Äquator befindet als Avignon (die nördliche Breite beträgt 43,73 Bogengrad). Von diesem Hügel aus wird die Südrichtung durch den knapp 13 Kilometer entfernten und gut 1100 Meter hohen Berg Vedernk markiert, über dem Phakt vor ungefähr 4000 Jahren zum ersten Mal auftauchte. Da Phakt nur eine Größenklasse von 2,6^m hat, wird er freiäugig erst bei einer Höhe über dem Horizont von mindestens dreieinhalb Bogengrad sichtbar, so dass er dann schon höher steht als der Gipfel vom Vedernk, der vom Magura-Hügel aus nur eine Höhe von knapp drei Bogengrad über dem Horizont hat.

Bis heute hat sich die Steigerungsrate der maximalen Horizonthöhe immer mehr verlangsamt und ist fast zum Stillstand gekommen. Heute erreicht Phakt in Avignon über dem Horizont eine Höhe von 12 Bogengrad und kulminiert während der Wintersonnenwende gegen Mitternacht auf dem südlichen Meridian. In Norddeutschland ist er wegen seiner geringen maximalen Höhe über dem Horizont auch heute praktisch nicht zu beobachten, denn in Flensburg beträgt die Höhe während der oberen Kulmination nur gut ein Bogengrad und in Berlin sind es ebenfalls nur knapp dreieinhalb Bogengrad. In fünfhundert Jahren wird die maximale Horizonthöhe erreicht sein, die nur einige Bogenminuten höher ist als heute. Danach beginnt die maximale Höhe über dem Horizont zu fallen, bis Phakt in 6000 Jahren bei der Beobachtung vom Rocher des Doms wieder verschwunden sein wird.

Der Asterismus **Ägyptisches Kreuz** über dem südlichen Horizont in Ägypten mit dem zentralen Stern Sirius auf dem Meridian sowie den vier Armsternen **Prokyon**, **Beteigeuze**, **Phakt** und **Naos** (im Uhrzeigersinn). **Canopus** (α Carinae) liegt im südlichen Sternbild Kiel des Schiffs (Carina), ist der zweithellste Stern am gesamten Sternenhimmel und ist von Europa aus praktisch nicht zu sehen,

Im Arabischen existiert für Phakt der historische Name Suhail Hadar, was soviel wie "der brüllend Helle" bedeuten könnte. Phakt befindet sich in seiner Eigenschaft als markanter Stern am rechten unteren Ende des Asterismus Ägyptisches Kreuz, das von Ägypten aus gesehen symmetrisch zum Meridian steht, wenn der zentrale und hellste Stern des Fixsternhimmels Sirius gut eine Stunde später als Phakt genau im Süden steht. Das Ende des gegenüberliegenden Arms wird durch Prokyon markiert. Der andere Arm des Kreuzes wird durch die Linie Beteigeuze (rechts oben) über Sirius zum Stern Naos (ζ Puppis, scheinbare Helligkeit 2,0^m) im Sternbild Achterdeck des Schiffs (Puppis) gebildet. Der Begriff "Ägyptisches Kreuz" beziehungsweise "Egyptian X" ist allerdings erst in der Neuzeit belegt.^[6]^[7]

Das Ägyptische Kreuz ein großflächiger Asterismus, die vertikale Ausdehnung des Ägyptischen Kreuzes beträgt rund 40 Bogengrad. Dieser Asterismus ist zwar nicht historisch, jedoch sehr prägnant und durch die fünf einzubeziehenden hellen Sterne leicht zu erkennen. Der zweithellste Stern des Fixsternhimmels Canopus ist auf dem Meridian 36 Bogengrad fast senkrecht unterhalb des hellsten Sterns Sirius zu sehen, sofern er über dem Horizont steht:

Prokyon (α Canis Minoris, 0,4m) im Sternbild Kleiner Hund
Beteigeuze (α Orionis, 0,4m) im Sternbild Orion
Sirius (α Canis Majoris, -1,5m) im Sternbild Großen Hund
Naos (ζ Puppis, 2,2m) im Sternbild Achterdeck des Schiffs
Phakt (α Columbae, 2,6m) im Sternbild Taube
Canopus (α Carinae, -0,7m) im Sternbild Kiel des Schiffs

Canopus[Bearbeiten]

Die ungefähren Winkelabstände zwischen Canopus und dem wegen der Präzession der Erdachse wandernden Himmelssüdpol von 6000 vor Christus bis 8000 nach Christus.

Die heutige Lage von Syrien und Irak im ehemaligen Zweistromland (Mesopotamien) am Euphrat und am Tigris.

Die Betrachtung zur wachsenden Deklination von Sternen kann auch für den nach Sirius zweithellsten Stern des Nachthimmels Canopus (α Carinae, scheinbare Helligkeit = -0,65^m) südlich des Ägyptischen Kreuzes im Sternbild Kiel des Schiffes (Carina) durchgeführt werden. Nicht nur wegen seiner großen Helligkeit, sondern auch wegen seine Lage ist Canopus sehr auffällig, da er die beiden etwas nördlicheren Sterne Naos (ζ Puppis, scheinbare Helligkeit = 2,2^m) und Phakt (α Columbae, scheinbare Helligkeit = 2,65^m) im rechten Winkel zu einem markanten Dreieck ergänzt. Wegen seiner südlichen Deklination ist Canopus von der Erde aus allerdings nur in südlicheren Breiten zu beobachten.

Die Berechnungen berücksichtigen folgende Einflussfaktoren:

Den Breitengrad des Beobachtungspunkts (die Stadt Uruk befand sich auf 31,322 Bogengrad nördlicher Breite).
Die Höhe des Beobachtungspunkts über dem Meeresspiegel = 0 Meter.
Die äquatorialen Koordinaten zur Epoche J2000:
- Rektaszension (Canopus: 6h 23m 57s = 95,988°).
- Deklination (Canopus: -52° 41' 44" = -52,696°).
Die Eigenbewegung des Sterns gegenüber dem Fixsternhimmel, wodurch sich die äquatorialen Koordinaten ebenfalls verändern:
- Eigenbewegung Rektaszension pro Jahr (Canopus: 21,4 mas/a).
- Eigenbewegung Deklination pro Jahr (Canopus: 26,7 mas/a).
Die scheinbare Helligkeit im Zenit (Canopus: -0,65^m).

Canopus (α Carinae) von Uruk
Beobachtungsjahr	-4000	-3000	-2000	-1000	0000	1000	2000
Deklination	-58,5°	-56,3°	-54,6°	-53,4°	-52,6°	-52,4°	-52,7°
Nördlichster Breitengrad der Beobachtung	31,5°	33,7°	35,4°	36,6°	37,4°	37,6°	37,3°
Maximale Höhe der Beobachtung von Uruk aus	0,5°	2,5°	4°	5°	6°	6°	6°
Maximale visuelle Helligkeit von Uruk aus	8^m	4^m	3^m	2^m	2^m	2^m	2^m

Vom Pynx-Hügel in Athen, auf einer nördlichen geographischen Breite von knapp 38 Bogengrad, wo Meton im fünften vorchristlichen Jahrhundert astronomische Beobachtungen durchgeführt hat, war Canopus zum Beispiel nie zu sehen. In den letzten 2500 Jahren stand er im äquatorialen Koordinatensystem im Bereich des nördlichen Maximums seiner Deklination von dort aus gesehen immer gerade so unterhalb des Horizonts.

500 Jahre vor Christi Geburt erreichte der Stern Canopus eine Deklination von -53 Bogenrad, so dass er dann dank seiner großen Helligkeit auf der nördlichen Breite von zirka 37 Bogengrad bei einer Größenklasse von 6^mzum ersten Mal beobachtet werden konnte. Auf Kreta (mittelminoische Zeit) und auf Zypern sowie in Aleppo (Syrien) war er ab dieser Zeit also sichtbar. Dieser Breitengrad verläuft nördlich der Insel Malta, wo sich die Tempelanlagen von Mnajdra mir freier Sicht nach Süden befinden, von denen während der Tarxien-Phase der Insel bereits mehrere tausend Jahre zuvor astronomische Beobachtungen ausgeführt wurden, als der Stern Canopus von dort aus noch lange nicht zu beobachten war.

Interessant ist das Detail, dass ein gegenüberliegendes Paar der Seitenwände der annähernd würfelförmigen Kaaba in Mekka auf einer nördlichen geographischen Breite von gut 21,4 Bogengrad (also etwas südlich des Wendekreises) zum Azimut des Sonnenuntergangs zur Wintersonnenwende (244 Bogengrad) beziehungsweise zum Azimut des Sonnenaufgangs zur Sommersonnenwende (64 Bogengrad) ausgerichtet ist. Die beiden senkrecht dazu stehenden Außenwände zeigen in Richtung des Azimuts des Aufgangs von Canopus (154 Bogengrad).^[8] Wegen der fast gleichbleibenden Deklination innerhalb der letzten 2000 Jahre stand Canopus in dieser südsüdöstlichen Richtung stets sechs bis sieben Bogengrad über dem Horizont. In dieser Höhe war und ist er mit einer für diese horizontnahen Verhältnisse sehr großen scheinbaren Helligkeit von rund 1,5^m zu sehen. Von der Kaaba selbst aus ist dies allerdings nicht zu beobachten, weil sich diese im Innenhof der al-Harām-Moschee befindet und von deren Gebäudewänden umgeben ist. Bei der Kulmination auf dem südlichen Meridian (die Richtung des Azimuts beträgt hier 180 Bogengrad) erreicht Canopus eine scheinbare Helligkeit von immerhin 0,3^m, jedoch nie eine Horizonthöhe von mehr 17 Bogengrad.

Mesopotamien[Bearbeiten]

Der Stern Canopus wurde von den Sumerern mit MUL.NUN^KI bezeichnet, was mit "Stern der Stadt Eridu" übersetzt wird.^[9]^[10] Die älteste und südlichste Stadt Mesopotamiens war Eridu, deren sumerische Schreibweise NUN^KI (wörtlich "Ort der Erde") lautet. Die ältesten archäologischen Funde aus dieser Gegend datieren auf das sechste vorchristliche Jahrtausend, und Eridu darf als der Ausgangspunkt der sumerischen Zivilisation gelten.

In Eridu befand sich der Tempel des Süßwasserozeans Eapsu, an dem der sumerische Weisheitsgott Enki verehrt wurde, der auch als der Herrscher des Süßwasserozeans Abzu galt. Die sumerische Königsliste, die die ältesten sumerischen Herrscher aus der Zeit vom Ende des vierten Jahrtausends vor Christus benennt, beginnt mit dem Satz:

Als das Königtum vom Himmel herabkam, war das Königtum in Eridu.

Der prototypische mesopotamische Tempel, von dem heute nur noch ein Ruinenhügel übrig ist, befand sich im Zentrum von Eridu, das auf 30,816 Bogengrad nördlicher Breite liegt. Die ältesten Schichten des Tempels stammen aus der späten Obed-Kultur, und diese werden auf die ersten Hälfte des vierten vorchristlichen Jahrtausends datiert. Zu dieser Zeit waren die beiden Ströme Euphrat und Tigris noch nicht vereinigt, der Persische Golf war durch deren Sedimente noch nicht so stark verlandet, und die Küste lag deswegen noch viel weiter nördlich als heute.

Von Eridu aus ergibt sich wegen des flachen Geländes mit wenigen Metern Höhe über dem Meeresspiegel eine vollkommen freie Sicht zum südlichen Horizont. Irgendwann vor rund 6000 Jahren wurde der Stern Canopus von dort aus zum ersten Mal in ganz Mesopotamien am südlichen Horizont sichtbar, so dass es einen Zusammenhang zwischen diesem Ereignis und der sumerischen Benennung des Sterns MUL.NUN^KI mit der Stadt NUN^KI geben dürfte. Eridu lag am äußersten südöstlichen Ende des fruchtbaren Halbmondes. Im Westen und im Süden von Eridu befand sich die weit ausgedehnte Wendekreiswüste auf der Arabischen Halbinsel, und im Osten lag der Persische Golf, der sich in dieser Richtung auf über 200 Kilometer ausdehnte. Daraus ergibt sich, dass es von Mesopotamien aus damals nicht ohne weiteres möglich war, auf dem Landweg bewohnte Orte zu bereisen, die südlicher als Eridu lagen.^[11]

In der folgenden Tabelle sind die säkularen oberen Kulminationen für die Stadt Eridu (30,816 Bogengrad nördliche Breite) angegeben:

Canopus (α Carinae) von Eridu
Beobachtungsjahr	-4500	-4000	-3500	-3000	-2500	-2000
Deklination	-59,7°	-58,5°	-57,4°	-56,3°	-55,4°	-54,6°
Nördlichster Breitengrad der Beobachtung	30,3°	31,5°	32,6°	33,7°	34,6°	35,4°
Maximale Höhe der Beobachtung von Eridu aus	0,1°	1,2°	2,2°	3,1°	4,0°	4,8°
Maximale visuelle Helligkeit von Eridu aus	10,0^m	6,2^m	4,5^m	3,5^m	2,8^m	2,3^m

Canopus von Eridu aus gesehen
Künstliche Darstellung einer Gruppe von Menschen, die vor gut 6000 Jahren bei der Stadt Eridu direkt über dem Horizont die Kulmination des Sternes Canopus auf dem südlichen Meridian (Bildmitte) beobachtet haben.
Die Kulmination des Sterns Canopus auf dem südlichen Meridian im Altertum von Eridu aus gesehen. Der Horizont befindet sich an der unteren Kante der Darstellung bei der Höhe 0 Bogengrad, auf der Horizontalen ist der Azimut aufgetragen (die Südrichtung liegt bei 180 Bogengrad). Die sechs eingezeichneten Bahnen stehen von unten nach oben für die Jahre 4500, 4000, 3500, 3000, 2500 und 2000 vor Christus und zeigen die zunehmende scheinbare Helligkeit von Canopus im jeweils höchsten Punkt seiner Bahn.

Die Aufgangspunkte, die Kulminationen und die Untergangspunkte des Sterns Canopus im Altertum von Eridu aus gesehen. Der Horizont befindet sich an der unteren Kante der Darstellung bei der Höhe 0 Bogengrad, auf der Horizontalen ist der Azimut aufgetragen (die Südrichtung liegt bei 180 Bogengrad). Die sechs eingezeichneten Bahnen stehen von unten nach oben ebenfalls für die Jahre 4500, 4000, 3500, 3000, 2500 und 2000 vor Christus.

Das heutige irakische Gebiet zwischen Ninive im Norden und Eridu im Süden.

In diesem Zusammenhang sei darauf hingewiesen, dass Canopus in der rund 0,15 Bogengrad nördlicheren Stadt Ur sowie in der rund 0,5 Bogengrad nördlicheren Stadt Uruk zu dieser Zeit noch nicht zu sehen war. In Ur war dies erst über 60 Jahre später, in Uruk erst über 200 Jahre später und in Babylon sogar erst rund 800 Jahre später der Fall.

Zwischen Eridu und Ur dürfte es zu Fuß beziehungsweise per Boot eine Tagesreise gewesen sein, so dass davon ausgegangen werden kann, dass sich die Einwohner der beiden Städte über den Sachverhalt austauschen konnten, dass in der Stadt Eridu in Richtung Süden ein ungewöhnlich heller Stern direkt über dem Horizont zu sehen war, der in der Stadt Ur nicht zu sehen war. Um zu Fuß weiter nach Uruk zu reisen, musste der Euphrat überquert werden, der in diesem Bereich heute eine Breite von 50 bis 100 Metern hat. Vor 6000 Jahren lagen sowohl Eridu als auch Ur wegen des etwas höheren Meeresspiegels und der noch nicht so weit fortgeschrittenen Verlandung allerdings am Persischen Golf, so dass die Reise eventuell auch durch eine Bootsfahrt entlang des Ufers und stromaufwärts des Flusses Euphrat bewerkstelligt werden konnte. Auf welchem Weg auch immer betrug die Reisezeit nach Uruk sicherlich mehrere Tage, so dass ein Austausch der Einwohner zwar nicht so häufig, aber dennoch regelmäßig stattgefunden haben dürfte.

In der folgenden Tabelle sind die säkularen oberen Kulminationen für die Stadt Ur (30,962 Bogengrad nördliche Breite), für die Stadt Uruk (31,322 Bogengrad nördliche Breite) und für die Stadt Babylon (32,542 Bogengrad nördliche Breite) angegeben:

Canopus (α Carinae) von Ur, Uruk und Babylon
Beobachtungsjahr	-4500	-4000	-3500	-3000	-2500	-2000
Deklination	-59,7°	-58,5°	-57,4°	-56,3°	-55,4°	-54,6°
Nördlichster Breitengrad der Beobachtung	30,3°	31,5°	32,6°	33,7°	34,6°	35,4°

Maximale Höhe der Beobachtung von Eridu aus	0,1°	1,2°	2,2°	3,1°	4,0°	4,8°
Maximale visuelle Helligkeit von Eridu aus	10,0^m	6,2^m	4,5^m	3,5^m	2,8^m	2,3^m

Maximale Höhe der Beobachtung von Ur aus	0,0°	1,0°	2,0°	2,9°	3,8°	4,6°
Maximale visuelle Helligkeit von Ur aus	10,5^m	6,7^m	4,7^m	3,7^m	2,9^m	2,4^m

Maximale Höhe der Beobachtung von Uruk aus	-	0,7°	1,7°	2,6°	3,5°	4,2°
Maximale visuelle Helligkeit von Uruk aus	-	7,6^m	5,2^m	4,0^m	3,1^m	2,7^m

Maximale Höhe der Beobachtung von Babylon aus	-	-	0,6°	1,5°	2,3°	3,1°
Maximale visuelle Helligkeit von Babylon aus	-	-	7,9^m	5,6^m	4,3^m	3,5^m

Ninive lag noch deutlich weiter nördlich und zudem auf einer Höhe von rund 200 Metern über dem Meeresspiegel, dort wo sich heute die Stadt Mossul befindet. Südlich des Ortes, am rechten Ufer des Tigris, befindet sich ein gut 300 Meter hohes Plateau, das die freie Sicht auf den geometrischen und astronomischen Horizont in Richtung Süden verdeckt, die freiäugige Sichtbarkeit des Sternes Canopus jedoch nicht beeinträchtigt, da dieser hoch genug steht. In der folgenden Tabelle sind die säkularen oberen Kulminationen von Canopus zwischen 1200 und 600 vor Christus für die Stadt Ninive (36,367 Bogengrad nördliche Breite) angegeben:

Canopus (α Carinae) von Ninive
Beobachtungsjahr	-1200	-1100	-1000	-900	-800	-700	-600
Deklination	-53,6°	-53,5°	-53,4°	-53,3°	-53,2°	-53,1°	-53,0°
Nördlichster Breitengrad der Beobachtung	36,4°	36,5°	36,6°	36,7°	36,8°	36,9°	37,0°
Maximale Höhe der Beobachtung von Ninive aus	0,9°	1,0°	1,1°	1,2°	1,3°	1,4°	1,5°
Maximale visuelle Helligkeit von Ninive aus	7,0^m	6,7^m	6,4^m	6,2^m	6,0^m	5,8^m	5,7^m

Aufgrund der Präzession der Erdachse hat Canopus von Ninive aus gesehen bis zum Mittelalter nur knapp die fünfte Größenklasse überschritten und ist bis heute schon wieder etwas schwächer sichtbar geworden.

Es ist festzuhalten, das Canopus vor der Entstehungszeit der Himmelsscheibe von Ninive in Ninive am südlichen Meridian über dem Horizont sichtbar wurde. Diese Scheibe soll hergestellt worden sein, als Ninive im 7. Jahrhundert vor Christus als Hauptstadt des Assyrischen Reiches die größte Bedeutung erlangte. Auf der Himmelsscheibe ist in einem der acht Segmente, das dem Stern Sirius zugeordnet wird, ein großes diagonales Kreuz zu sehen, welches sehr an das "Ägyptische Kreuz" (bestehend aus den auffälligen Sternen Prokyon, Beteigeuze, Naos und Phakt, siehe oben) mit dem darunter liegenden Stern zweithellsten Stern Canopus erinnert. Der hellste Stern Sirius befindet sich im Schnittpunkt der beiden Kreuzachsen und wurde in der sumerischen Sprache als KAK.SI.SÁ (Pfeil) sowie in der akkadischen Sprache meist als „šu-ku-du“ ((Rohr-)Pfeil) oder auch als „šil-ta-ḫu“ (Pfeil) bezeichnet. Auf der Himmelsscheibe zeigt ein großer Pfeil vom Schnittpunkt der Kreuzachsen in Richtung Mittelpunkt der Scheibe. Ferner sind in diesem Segment mehrere kleine Kreuze zu erkennen.

Das Kreuz auf der Himmelsscheibe von Ninive
Die auf um 650 vor Christus in die Amtszeit des assyrischen Königs Aššur-bāni-apli datierte Himmelsscheibe von Ninive aus Ton (Durchmesser rund 14 Zentimeter, Dicke rund 3 Zentimeter) im Britischen Museum (Inventarnummer K.8538, ausgestellt in G55/dc8). Sie wurde im 19. Jahrhundert vom britischen Archäologen Austen Henry Layard in Ninive gefunden.^[12]
Bei zwei Uhr auf dem Ziffernblatt befindet sich in der Abbildung ein großes diagonales Kreuz mit Pfeil, das mit den Sternen Sirius und Beteigeuze in Verbindung gebracht werden kann. Von dort aus entgegen dem Uhrzeigersinn:^[13]^[14]^[15]
- Sternbild Pflug (zwei Dreiecke: Pegasus / Andromeda)
- [Vermutung: Sternbild Schaf (Widder)]
- Sternbild Stier mit den Plejaden
- Sternbilder Zwillinge und Orion (gegenüber Sirius)
- Sternbilder Wasserschlange und/oder Becher (und Regulus im Löwen)
- Sternbilder Rabe und Jungfrau
- Sternbild Waage (und eventuell Sternbild Zentaur)
Das "Ninive-Kreuz" mit den hellsten Sternen am südlichen Meridian während der oberen Kulmination von Canopus um 650 vor Christus. Canopus erschien in Ninive zu dieser Zeit zum ersten Mal am Nachthimmel.

Achernar[Bearbeiten]

In südlicheren Breiten findet sich als Beispiel im Sternbild (Fluss) Eridanus dessen südlichster und der neunthellste Stern am Himmel Achernar (α Eridani).

Die Berechnungen berücksichtigen folgende Einflussfaktoren:

Die Stadt Teotihuacán

Den Breitengrad des Beobachtungspunkts: die Sonnenpyramide von Teotihuacán befindet sich nordöstlich von Mexiko-Stadt bei 19,693 Bogengrad nördlicher Breite.
Die Höhe des Beobachtungspunkts: die Sonnenpyramide von Teotihuacán befindet sich 2300 Meter über dem Meeresspiegel.
Die äquatorialen Koordinaten zur Epoche J2000:
- Rektaszension (Achernar: 1h 37m 43s = 24,429°).
- Deklination (Achernar: -57° 14' 12" = -57,237°).
Die Eigenbewegung des Sterns gegenüber dem Fixsternhimmel, wodurch sich die äquatorialen Koordinaten ebenfalls verändern:
- Eigenbewegung Rektaszension pro Jahr (Achernar: 97,1 mas/a).
- Eigenbewegung Deklination pro Jahr (Achernar: -41,7 mas/a).
Die scheinbare Helligkeit im Zenit (Achernar: 0,5^m).

Achernar (α Eridani)
Beobachtungsjahr	-4000	-3500	-3000	-2500	-2000	-1500	-1000	-600	-500	-400	-300	-200	-100	000	500	1000	1500	2000
Deklination	-82°	-83°	-83°	-81°	-79°	-76°	-74°	-71,3°	-70,8°	-70,2°	-69,7°	-69,1°	-68,5°	-68,0°	-65,2°	-62,5°	-59,8°	-57,2°
Nördlichster Breitengrad der Beobachtung	8°	7°	7°	9°	11°	14°	16°	18,7°	19,2°	19,8°	20,3°	20,9°	21,5°	22,0°	24,8°	27,5°	30,2°	32,8°
Maximale Höhe der Beobachtung von der Sonnenpyramide von Teotihuacán aus	-	-	-	-	-	-	-	1,0°	1,5°	2,0°	2,5°	3,0°	3,5°	4,0°	6,7°	9,3°	12,0°	14,5°
Maximale visuelle Helligkeit von der Sonnenpyramide von Teotihuacán aus	-	-	-	-	-	-	-	8,0^m	6,5^m	6,0^m	5,5^m	5,0^m	4,5^m	4,0^m	2,8^m	2,2^m	1,8^m	1,6^m

Das Gebiet von Teotihuacán war seit dem sechsten Jahrhundert vor Christus bewohnt. Bald nach der Gründung wurde für die Bewohner am südlichen Meridian zum ersten Mal der helle Stern Achernar und somit das vollständige Sternbild Fluss Eridanus sichtbar. Seit 100 nach Christus war die Stadt über 500 Jahre lang ein wichtiges Zentrum in Mesoamerika. Von der aus dieser Zeit stammenden Sonnenpyramide aus konnte insbesondere der Sonnenuntergang zur Tag-und-Nacht-Gleiche trotz des bergigen Geländes direkt auf dem westlichen Horizont beobachtet werden.

Selbst in der südägyptischen Stadt Assuan, die sich sich bei 24,094 Bogengrad nördlicher Breite befindet, ging Achernar bis ungefähr 600 nach Christus nie auf. Dies bedeutet, dass das heutige Sternbild Fluss Eridanus, das in Nord-Süd-Richtung eine sehr große Ausdehnung hat, im Altertum weder von Mesopotamien aus noch von Ägypten aus vollständig beobachtet werden konnte. Erst in heutiger Zeit wird Achernar auf dem Breitengrad von Alexandria an der ägyptischen Mittelmeerküste beziehungsweise vom prähistorischen Uruk (31,322 Bogengrad nördliche Breite) im flachen Land des heutigen Iraks sichtbar.

Sirius[Bearbeiten]

Abschließend soll die zeitliche Entwicklung der Sichtbarkeit des hellsten Sterns am Himmel Sirius (α Canis Majoris) anhand der nördlichsten Breitengrade der Beobachtung auf Meereshöhe in den letzten 10000 Jahren dargestellt werden. Beim Auftauchen über der Horizontlinie ist Sirius seit jeher der einzige Stern, der schon bei einer Höhe von weniger als einem Bogengrad über dem Horizont gesehen werden kann.

Die Berechnungen berücksichtigen folgende Parameter:

Die äquatorialen Koordinaten zur Epoche J2000:
- Rektaszension (Sirius: 6h 45m 9s = 101,2875°).
- Deklination (Sirius: -16° 42' 58" = -16,7161°).
Die Eigenbewegung des Sterns gegenüber dem Fixsternhimmel, wodurch sich die äquatorialen Koordinaten ebenfalls verändern:
- Eigenbewegung Rektaszension pro Jahr (Sirius: -546,01 mas/a).
- Eigenbewegung Deklination pro Jahr (Sirius: -1223,07 mas/a).
Die scheinbare Helligkeit im Zenit (Sirius: -1,5^m).

Sirius (α Canis Majoris)
Beobachtungsjahr	-8000	-7500	-7000	-6500	-6000	-5500	-5000	-4500	-4000	-3500	-3000	-2500	-2000	-1500	-1000	-500	000	500	1000	1500	2000
Deklination	-46,5°	-43,9°	-41,2°	-38,6°	-35,9°	-33,4°	-30,9°	-28,6°	-26,4°	-24,4°	-22,5°	-20,8°	-19,4°	-18,2°	-17,2°	-16,4°	-16,0°	-15,8°	-15,8°	-16,1°	-16,7°
Nördlichster Breitengrad der Beobachtung	43,5°	46,1°	48,8°	51,4°	54,1°	56,6°	59,1°	61,4°	63,6°	65,6°	67,5°	69,2°	70,6°	71,8°	72,8°	73,6°	74,0°	74,2°	74,2°	73,9°	73,3°

Sirius ist also selbst in höheren nördlichen Breiten schon seit langem sichtbar, und er verliert seit etwa 1000 Jahren wieder langsam an Höhe.

In Sachsen-Anhalt war er zur Zeit der Fertigstellung des Sonnenobservatoriums in Goseck um 4900 vor Christus bereits seit rund eintausend Jahren gut sichtbar. Da die Sicht von der Kreisgrabenanlage nach Süden durch einen leichten Hügel mit einer Höhe von knapp 4 Bogengrad über dem Horizont verdeckt ist, konnte Sirius von dort ab dem Jahr 5900 vor Christus beobachtet werden. Bei freier Sicht zum südlichen Horizont war dies auf dieser geographischen Breite bereits mehrere hundert Jahre früher der Fall.

Der Ort Goseck befindet sich auf 51,198 Bogengrad nördlicher Breite und auf einer Höhe von 152 Meter über dem Meeresspiegel.

Sirius (α Canis Majoris) von Goseck
Beobachtungsjahr	-6800	-6700	-6600	-6500	-6400	-6300	-6200	-6100	-6000	-5900	-5800	-5700	-5600	-5500
Deklination	-40,2°	-39,6°	-39,1°	-38,6°	-38,0°	-37,5°	-37,0°	-36,5°	-35,9°	-35,4°	-34,9°	-34,4°	-33,9°	-33,4°
Nördlichster Breitengrad der Beobachtung	49,8°	50,4°	50,9°	51,4°	52,0°	52,5°	53,0°	53,5°	54,1°	54,6°	55,1°	55,6°	56,1°	56,6°
Maximale Höhe der Beobachtung von Goseck aus	-	-	0,6°	1,0°	1,5°	2,0°	2,5°	2,9°	3,4°	3,9°	4,4°	4,9°	5,4°	5,9°
Maximale visuelle Helligkeit von Goseck aus	-	-	7,0^m	6,0^m	4,7^m	3,9^m	3,2^m	2,8^m	2,4^m	2,0^m	1,7^m	1,4^m	1,2^m	1,0^m

Der Stern Sirius wurde also innerhalb weniger hundert Jahre über der Kreisgrabenanlage in Goseck sehr gut sichtbar, obwohl er sich am südlichen Horizont nur wenige Grad über den Horizont erhob. Bei der ersten Sichtbarkeit um 5900 vor Christus über dem südlichen Hügel hatte er von Zentrum der Kreisgrabenanlage gesehen eine visuelle Helligkeit von 2^m, so dass er damals bereits zu den drei Dutzend hellsten sichtbaren Sternen überhaupt zählte, obwohl sein Licht wegen der geringen Horizonthöhe noch stark abgeschwächt war.

360-Grad-Panorama im Zentrum der Kreisgrabenanlage eine gute Stunde vor Sonnenuntergang am 3. Februar 2015.

Aus digitalem Geländemodell berechnetes 360-Grad-Panorama im Zentrum der Kreisgrabenanlage. Der Himmelsäquator schneidet den natürlichen Horizont im Osten (Azimut 90 Bogengrad) exakt auf dem geometrischen Horizont (Zenitdistanz 90 Bogengrad). Die Vertikale ist vierfach überhöht dargestellt.

Vorübergehend verschwundene Sterne[Bearbeiten]

Hier sind einige markante Beispiele von Sternen aufgeführt, die im Laufe der letzten Jahrtausende bei ihrer oberen Kulmination auf dem südlichen Meridian nur mit einer langjährigen Unterbrechung über dem Horizont zu sehen waren.

Fomalhaut[Bearbeiten]

Die Lage der vier Königssterne Aldebaran, Regulus, Antares und **Fomalhaut**. Letzterer liegt im Gegensatz zu den drei anderen Sternen deutlich südlich der Ekliptik.

Das Belchen-System.

Eine noch stärker sich ändernde Deklination kann zum Beispiel für den hellsten Stern im Sternbild Südlicher Fisch Fomalhaut (α Piscis Austrini) festgestellt werden. Bei den alten Persern gehörte er als hellster Stern der Sternregion in der Nähe Ekliptik zusammen mit Antares (α Scorpii) , Regulus (α Leonis) und Aldebaran (α Tauri) zu den vier Königssternen, die vier Quadranten entlang der Ekliptik markieren.

Die Berechnungen berücksichtigen folgende Einflussfaktoren:

Den Breitengrad des Beobachtungspunkts (der Elsässer Belchen befindet sich auf 47,822 Bogengrad nördlicher Breite).
Die Höhe des Beobachtungspunkts über dem Meeresspiegel (der Elsässer Belchen befindet sich 1247 Meter über dem Meeresspiegel).
Die äquatorialen Koordinaten zur Epoche J2000:
- Rektaszension (Fomalhaut: 22h 57m 39s = 344,413°).
- Deklination (Fomalhaut: -29° 37' 20" = -29,622°).
Die Eigenbewegung des Sterns gegenüber dem Fixsternhimmel, wodurch sich die äquatorialen Koordinaten ebenfalls verändern:
- Eigenbewegung Rektaszension pro Jahr (Fomalhaut: 356,4 mas/a).
- Eigenbewegung Deklination pro Jahr (Fomalhaut: -162,5 mas/a).
Die scheinbare Helligkeit im Zenit (Fomalhaut: 1,15^m).

Fomalhaut (α Piscis Austrini)
Beobachtungsjahr	-4000	-3000	-2000	-1000	-0500	0000	0500	1000	1500	2000
Deklination	-42,6°	-44,2°	-44,2°	-42,4°	-40,9°	-39,1°	-37,0°	-34,7°	-32,2°	-29,6°
Nördlichster Breitengrad der Beobachtung	47,4°	45,8°	45,8°	47,6°	49,1°	50,9°	53,0°	55,3°	57,8°	60,4°
Maximale Höhe der Beobachtung vom Elsässer Belchen aus	1,2°	-	-	1,3°	2,5°	4,5°	6,5°	8,5°	11,0°	13,5°
Maximale visuelle Helligkeit vom Elsässer Belchen aus	8,0^m	-	-	8,0^m	6,0^m	4,5^m	3,5^m	3,0^m	2,5^m	2,5^m

Fomalhaut war vor 7000 Jahren in Avignon, aber auch noch vom Elsässer Belchen aus noch gut sichtbar. Damals wurde die Deklination noch von Jahr zu Jahr südlicher, so dass er nur noch in zunehmend südlicheren Breiten sichtbar war. Vor rund 4000 Jahren lag der nördlichste Breitengrad bei 45,8 Bogengrad - das entspricht ungefähr dem Ort Mailand -, und danach fing Fomalhaut wieder an zu steigen.

Vor 2500 Jahren erreichte die Deklination von Fomalhaut eine so große Höhe und scheinbare Helligkeit, dass er von der Zugspitze und vom prähistorischen Observatorium auf dem Elsässer Belchen aus gesehen wieder den Horizont überstieg und beobachtet werden konnte. Seit 1000 vor Christi Geburt gab es in der Gegend bereits die Urnenfelderkultur (Hallstadt B), und die ersten Kelten tauchten kurz danach dort auf. In Richtung Süden liegt vom Elsässer Belchen aus der bei guten atmosphärischen Verhältnissen sichtbare, 221 Kilometer entfernte und mit 4810 Metern Höhe höchste Berg der Alpen, der Mont Blanc. Der Elsässer Belchen konnte wegen der guten Sicht auf andere Berggipfel als Sonnenobservatorium verwendet werden, vielleicht wurden von den keltischen Astronomen des Nachts ja auch die Bewegungen der Sterne beobachtet und die Erkenntnisse immer wieder mündlich an die nachfolgenden Druiden tradiert.

Siehe auch Das Belchen-System.

Vor rund 1500 Jahren war Fomalhaut dann von Köln aus und vor etwa 500 Jahren sogar von Kopenhagen aus zu sehen.

Alnair[Bearbeiten]

Der hellste Stern im Sternbild Kranich (Grus) ist Alnair (α Gruis, scheinbare Helligkeit 1,7^m).

Die Berechnungen berücksichtigen folgende Einflussfaktoren:

Die Lage von Mnajdra an der Südküste von Malta.

Den Breitengrad des Beobachtungspunkts (Mnajdra befindet sich auf 35,827 Bogengrad nördlicher Breite).
Die Höhe des Beobachtungspunkts über dem Meeresspiegel (Mnajdra befindet sich an der Südwestküste Maltas nur unwesentlich über dem Meeresspiegel).
Die äquatorialen Koordinaten zur Epoche J2000:
- Rektaszension (Alnair: 22h 08m 14s = 332,058°).
- Deklination (Alnair: -46° 57' 40" = -46,961°).
Die Eigenbewegung des Sterns gegenüber dem Fixsternhimmel, wodurch sich die äquatorialen Koordinaten ebenfalls verändern:
- Eigenbewegung Rektaszension pro Jahr (Alnair: 146,0 mas/a).
- Eigenbewegung Deklination pro Jahr (Alnair: -169,1 mas/a).
Die scheinbare Helligkeit im Zenit (Alnair: 1,7^m).

Alnair (α Gruis)
Beobachtungsjahr	-4000	-3900	-3800	-3700	-3600	-3500	-3400	-3300	-3200	-3100	-3000	-2000	-1000	0000	1000	2000
Deklination	-49,6°	-50,0°	-50,5°	-50,9°	-51,3°	-51,7°	-52,1°	-52,5°	-52,8°	-53,2°	-53,5°	-55,8°	-56,3°	-54,7°	-51,4°	-47,0°
Nördlichster Breitengrad der Beobachtung	40,4°	40,0°	39,5°	39,1°	38,7°	38,3°	37,9°	37,5°	37,2°	36,8°	36,5°	34,2°	33,7°	35,3°	38,6°	43,0°
Maximale Höhe der Beobachtung von Mnajdra aus	4,9°	4,5°	4,1°	3,7°	3,3°	2,9°	2,5°	2,2°	1,9°	1,6°	1,3°	-	-	0,2°	3,2°	7,5°
Maximale visuelle Helligkeit von Mnajdra aus	4,6^m	4,8^m	5,1^m	5,3^m	5,7^m	6,0^m	6,4^m	6,8^m	7,2^m	7,7^m	8,3^m	-	-	12^m	5,7^m	3,8^m

Alnair war vor 5500 Jahren vom maltesischen Mnajdra aus also noch beobachtbar. Mnajdra liegt an der Südwestküste Maltas auf einer Terrassenfelsen am Mittelmeer mit völlig freier Sicht nach Süden. Vor 6000 Jahren war dort aufgrund des niedrigeren Wasserstandes der einzige flache Küstenstreifen in der Region, an welchem angelandet werden konnte.^[16] In der zweiten Hälfte des vierten vorchristlichen Jahrtausends, also in der Frühphase der dortigen megalithischen Tempelkultur, verschwand Alnair vom maltesischen Nachthimmel und war dann über 4000 Jahre lang nicht mehr beobachtbar. Heute steht er wieder siebeneinhalb Bogengrad über dem südlichen Horizont und erreicht eine visuelle Helligkeit von 4^m.

→ Ausführungen zum Kalenderstein der Tempelanlage von Mnajdra finden sich hier: „Der Kalenderstein vom Tempel Mnajdra“.

Verschwundene zirkumpolare Sterne[Bearbeiten]

Hier sind einige markante Beispiele von zirkumpolaren Sternen aufgeführt, die im Laufe der letzten Jahrtausende bei der unteren Kulmination auf dem nördlichen Meridian auf einmal verschwanden.

Arktur[Bearbeiten]

Umgekehrt verhält es sich beim dritthellsten Stern des Nachthimmels Arktur (α Bootis, scheinbare Helligkeit 0^m) im Sternbild Bärenhüter (Bootes). Er hat eine große Deklination und ist daher in hinreichend nördlichen Breiten zirkumpolar. Er sinkt dort also niemals unter den Horizont, und somit kann in Richtung Norden die untere Kulmination auf dem nördlichen Meridian beobachtet werden. Die Deklination hat sich in den letzten 5000 Jahren stark verringert, so dass er in immer nördlicher werdenden Breiten zirkumpolar blieb.

Die Berechnungen berücksichtigen folgende Einflussfaktoren:

Die äquatorialen Koordinaten zur Epoche J2000:
- Rektaszension (Arktur: 14h 15m 40s = 213,917°).
- Deklination (Arktur: 19° 10' 57" = 19.182°).
Die Eigenbewegung des Sterns gegenüber dem Fixsternhimmel, wodurch sich die äquatorialen Koordinaten ebenfalls verändern:
- Eigenbewegung Rektaszension pro Jahr (Arktur: -1312.1 mas/a).
- Eigenbewegung Deklination pro Jahr (Arktur: -2342.9 mas/a).

Arktur (α Bootis)
Beobachtungsjahr	-4000	-3000	-2000	-1000	0000	1000	2000
Deklination	54,3°	49,1°	43,1°	36,9°	30,7°	24,7°	19,2°
Südlichster Breitengrad der Zirkumpolarität	35,7°	40,9°	46,9°	53,1°	59,3°	65,3°	70,8°

Im zwölften vorchristlichen Jahrhundert wurde Arktur demnach auf dem Breitenkreis von Nebra (Unstrut, zirka 51,2 Bogengrad nördliche Breite) und der Kreisgrabenanlage von Goseck eines Herbstes gegen Mitternacht plötzlich unsichtbar, nachdem er als zirkumpolarer Stern Jahrtausende lang nie so dicht zum Horizont gekommen war. In südlicheren Breiten erfolgte dieses Phänomen schon entsprechend früher. Vom Rocher des Doms (zirka 44 Bogengrad nördliche Breite) war er vor über 4300 Jahren beispielsweise noch zirkumpolar. Heute ist er nur noch in sehr hohen Breiten zirkumpolar zu beobachten, wie zum Beispiel vom nördlichsten Zipfel des norwegischen Festlands (bei über 71 Bogengrad nördliche Breite).

Wegen der sehr großen Eigenbewegung von Arktur sind die äquatorialen Koordinaten in der prähistorischen Vergangenheit nicht ganz so zuverlässig bestimmbar wie bei den anderen hier untersuchten Sternen.

Capella[Bearbeiten]

Ähnlich ist es beim sechsthellsten Stern des Nachthimmels Capella (α Aurigae, scheinbare Helligkeit 0,1^m) im Sternbild Fuhrmann (Auriga). Er hat eine nicht ganz so große Deklination wie Arktur und ist in entsprechend nördlichen Breiten zirkumpolar. Die Deklination hat sich in den letzten 5000 Jahren allerdings stark erhöht, so dass er im Laufe dieser Zeitspanne in immer südlicher werdenden Breiten zirkumpolar blieb.

Die Berechnungen berücksichtigen folgende Einflussfaktoren:

Die äquatorialen Koordinaten zur Epoche J2000:
- Rektaszension (Capella: 5h16m42s = 79,175°).
- Deklination (Capella: 45°59'53" = 45.998°).
Die Eigenbewegung des Sterns gegenüber dem Fixsternhimmel, wodurch sich die äquatorialen Koordinaten ebenfalls verändern:
- Eigenbewegung Rektaszension pro Jahr (Capella: 56,2 mas/a).
- Eigenbewegung Deklination pro Jahr (Capella: -542.1 mas/a).

Capella (α Aurigae)
Beobachtungsjahr	-4000	-3000	-2000	-1000	0000	1000	2000
Deklination	20,6°	26,1°	31,6°	36,7°	41,0°	44,3°	46,0°
Südlichster Breitengrad der Zirkumpolarität	69,4°	63,9°	58,4°	53,3°	49,0°	45,7°	44,0°

Capella erreichte demzufolge von Norddeutschland aus gesehen (nördliche Breitengrade zwischen 50 und 54 Bogengrad) im ersten vorchristlichen Jahrtausend seine Zirkumpolarität.

Programm zur Berechnung säkularer Aufgänge[Bearbeiten]

Mit dem unten abrufbaren Java-Programm können für beliebige Sterne die säkularen Aufgänge bestimmt werden. Unter säkularer Aufgang ist gemein, ob und wie hoch ein Gestirn von einem bestimmten Beobachtungspunkt der Erde aus den Horizont übersteigt.

Zirkumpolare Sterne gehen nie unter, wenn die untere Kulmination auf dem nördlichen Meridian sichtbar ist. Falls die obere Kulmination auf dem südlichen Meridian unterhalb des Horizonts liegt, geht das entsprechende zirkumpolare Gestirn nie auf.

Das hier vorgestellt Java-Programm benötigt die folgenden Parameter der Beobachtung, die in Klassenvariablen gespeichert sind:

Klassenvariablen[Bearbeiten]

	/* Beobachtungszeitpunkt */
	private static final long firstObservationYear = -3000; // erstes Beobachtungsjahr
	private static final long yearIncrement = 500;          // Schrittweite fuer die Jahre
	private static final long lastObservationYear = -4000;  // letztes Beobachtungsjahr
	private static final long epoch = 2000;                 // astronomische Epoche J2000

	/* Beobachtungsort */
	private static double phi = java.lang.Math.toRadians (43.95); // geographischer Breitengrad in Radiant
	private static double REarth = 6371000;                       // Erdradius in Metern
	private static double elevation = 55;                         // Hoehe ueber Normalnull in Metern
	private static double chineInDegrees = java.lang.Math.toDegrees (java.lang.Math.acos (REarth / (REarth + elevation))); // Kimmwinkel in Bogengrad
	private static double altitudeIncrement = 0.1; // Schrittweite fuer die Hoehe ueber dem Horizont in Bogengrad

	/* Gestirn */
	private static java.lang.String name = "Phakt"; 
	private static double apparentMagnitude = 2.6; // Scheinbare Helligkeit in Groesssenklassen
	/* Aequatoriale Koordinaten zur Epoche in Radiant */
	private static double alpha0 = java.lang.Math.toRadians (15 * (5 + 39/60.0 + 38.95/3600.0)); // Rektaszension
	private static double delta0 = java.lang.Math.toRadians (-(34 + 4/60.0 + 26.6/3600.0));      // Deklination

Ferner ergeben sich geringe Änderungen der äquatorialen Koordinaten eines Gestirns durch dessen Eigenbewegung. Diese wird in der Regel in Millibogensekunden angegeben und kann in astronomischen Katalogen oder Datenbanken nachgeschlagen werden, wie zum Beispiel im Hipparcos-Katalog aus dem Jahr 1997 oder im Tycho-2-Katalog aus dem Jahr 2000.

Diese Einflüsse auf die Rektaszension (RA, englisch = "right ascension") und die Deklination (DE) eines Gestirns wird mit Hilfe der beiden linear unabhängige Parameter $\mu _{RA}$ und $\mu _{DE}$ beachtet, die im Java-Programm ebenfalls als Klassenvariablen gespeichert werden:

	/* Jaehrliche Veraenderung der aequatorialen Koordinaten zur Epoche in Millibogensekunden */
	private static double mu_RA =   4.6; // Eigenbewegung Rektaszension
	private static double mu_DE = -29.9; // Eigenbewegung Deklination

	/* Aequatoriale Koordinaten zum Beobachtungszeitpunkt in Radiant */
	private static double alpha; // Rektaszension zum Beobachtungszeitpunkt
	private static double delta; // Deklination zum Beobachtungszeitpunkt

Unterprogramme[Bearbeiten]

Extinktion[Bearbeiten]

Das Unterprogramm "extinction" dient zur Bestimmung der Luftmasse "airMass" in Abhängigkeit der Zenitdistanz $z$ , die anhand der Höhe $h$ über dem Horizont bestimmt werden kann:

z=90^{\circ }-h

Aus der Luftmasse kann anschließend die proportionale Extinktion berechnet werden:

	/*
	 Berechnung der Extinktion in Abhaengigkeit von der astronomischen Hoehe "heightInDegrees" als Reduktion der scheinbaren Helligkeit
	 Formel nach https://asterism.org/resources/atmospheric-extinction-and-refraction/
	 */
	private static double extinction (double heightInDegrees)
	{
		double z = java.lang.Math.toRadians (90 - heightInDegrees); // Zenithoehe
		double cosz = java.lang.Math.cos (z);
		double airMass = 1 / (cosz + 0.025 * java.lang.Math.exp (-11 * cosz)); // Luftmassen
		double extinction = 0.28 * airMass; // Extinktion
		return extinction;
	}

Wenn die äquatorialen Koordinaten eines Gestirns Jahrhunderte oder gar Jahrtausende vor oder nach der Epoche der Katalogisierung bestimmt werden sollen, muss die Präzession der Erdachse berücksichtigt werden. Nach knapp 26000 Jahren sind die beiden Himmelspole während einer Präzessionsperiode beziehungsweise innerhalb eines Platonischen Jahres einmal um den Pol der Ekliptik gekreist.

→ Siehe auch Präzession und Nutation.

Präzession[Bearbeiten]

Die Präzession der Erdachse wird im Unterprogramm "precession" für ein beliebiges Zieljahr "year" mit einem Formelsatz nach der Internationalen Astronomischen Union (IAU) von 2006 bestimmt:^[17]

	/* Berechnung der Praezession fuer das Jahr "year" nach IAU 2006 */
	private static void precession (long year)
	{
		/* Jahre in Bezug auf die Epoche */
		double jahre = year - epoch;

		/* Eigenbewegung beruecksichtigen */
		alpha = alpha0 + jahre * java.lang.Math.toRadians (mu_RA / 3600 / 1000);
		delta = delta0 + jahre * java.lang.Math.toRadians (mu_DE / 3600 / 1000);

		/* Praezessionsformel arbeitet mit Jahrhunderten */
		double jahrhunderte = jahre / 100.0;

		/* IAU 2006 */
		double zeta = (((((-0.0000003173 * jahrhunderte - 0.000005971) * jahrhunderte + 0.01801828)
				* jahrhunderte + 0.2988499) * jahrhunderte + 2306.083227) * jahrhunderte + 2.650545);
		double z = (((((-0.0000002904 * jahrhunderte - 0.000028596) * jahrhunderte + 0.01826837)
				* jahrhunderte + 1.0927348) * jahrhunderte + 2306.077181) * jahrhunderte - 2.650545);
		double theta = ((((-0.00000011274 * jahrhunderte - 0.000007089) * jahrhunderte - 0.04182264)
				* jahrhunderte - 0.4294934) * jahrhunderte + 2004.191903) * jahrhunderte;

		zeta = java.lang.Math.toRadians (zeta / 3600);
		z = java.lang.Math.toRadians (z / 3600);
		theta = java.lang.Math.toRadians (theta / 3600);

		double A = java.lang.Math.cos (delta) * java.lang.Math.sin (alpha + zeta);
		double B = java.lang.Math.cos (theta) * java.lang.Math.cos (delta) * java.lang.Math.cos (alpha + zeta) - java.lang.Math.sin (theta) * java.lang.Math.sin (delta);
		double C = java.lang.Math.sin (theta) * java.lang.Math.cos (delta) * java.lang.Math.cos (alpha + zeta) + java.lang.Math.cos (theta) * java.lang.Math.sin (delta);

		alpha = java.lang.Math.atan2 (A, B) + z;
		if (alpha < 0)
		{
			alpha = alpha + 2 * java.lang.Math.PI;
		}
		delta = java.lang.Math.asin (C);
	}

Kimmtiefe[Bearbeiten]

Von der Horizontalen gemessene Kimmtiefe $\tau$ bei der Beobachtung in der Höhe $H$ über der Erdoberfläche (Erdradius = $R$ ).

Für Beobachtungsorte, die nicht auf der Meeresspiegelhöhe liegen, muss die auf offenem Meer die Kimmlinie (englisch: "chine line") zum sichtbaren Horizont zwischen Wasser und Himmel berücksichtigt werden. Der Horizontwinkel $H_{Kimm}$ muss um die Kimmtiefe $\tau$ korrigiert werden, die sich aus dem Erdradius $R_{Erde}\approx 6371000{\text{ m}}$ und der Beobachtungshöhe $H$ ergibt:

\tau =\arccos \left({\frac {R_{Erde}}{R_{Erde}+H}}\right)

H_{Kimm}=H-\tau

Anmerkung zu einer Näherungslösung[Bearbeiten]

Im rechtwinkligen Dreieck mit der Gegenkathete der Länge $s$ gilt der Satz des Pythagoras:

R_{Erde}^{2}+s^{2}=(R_{Erde}+H)^{2}=R_{Erde}^{2}+2\cdot R_{Erde}\cdot H+H^{2}

Der Term $H^{2}$ ist im Verhältnis zu den anderen Termen so klein, das er ohne großen Fehler vernachlässigt werden kann:

s^{2}\approx 2\cdot R_{Erde}\cdot H

Damit kann die Gleichung nach der Länge der Gegenkathete $s$ aufgelöst werden, die auch als Sichtweite vom erhöhten Standpunkt bis zum sichtbaren Horizont interpretiert werden kann:

s\approx {\sqrt {2\cdot R_{Erde}\cdot H}}

Die unter der Gegenkathete befindlichen Bogenlänge entlang der Erdoberfläche ergibt sich im Bogenmaß zu:

b=\tau \cdot R_{Erde}

Für kleine Winkel $\tau$ gilt ohne großen Fehler:

s\approx b

Und daraus folgt wiederum:

{\sqrt {2\cdot R_{Erde}\cdot H}}\approx \tau \cdot R_{Erde}

Beziehungsweise nach $\tau$ aufgelöst:

\tau \approx {\sqrt {\frac {2\cdot H}{R_{Erde}}}}

Atmosphärische Refraktion[Bearbeiten]

Diagramm mit der atmosphärischen Refraktion über der Höhe über der Erdoberfläche nach Bennett.

Ferner ergibt sich durch die atmosphärische Refraktion eine weitere Verringerung des wahren Horizonts $H_{Refr}$ um den in Bogenminuten bestimmten Winkel $\rho$ , der durch folgende Näherungsformel von George G. Bennet^[18] bestimmt werden kann, wobei die Höhe über der Erdoberfläche $H$ in Meter einzusetzen und das Winkelargument des Kotangens in Bogengrad zu verwenden ist:

\rho =\cot \left(H+{\frac {7,31}{H+4,4}}\right)

H_{Refr}=H_{Kimm}-\rho

Meteorologische Korrektur[Bearbeiten]

Die oben angegebene Formel gilt für einen Luftdruck von 1010 Hektopascal und eine Temperatur von 10° Celsius (283 Kelvin). Falls der atmosphärische Luftdruck und die atmosphärische Temperatur an der Erdoberfläche genauer berücksichtigt werden sollen, muss die Refraktion $\rho (p,T)$ mit einem Korrekturfaktor $c$ multipliziert werden, der vom Luftdruck $p$ und von der Temperatur $T$ anhängt:

\rho (p,T)=c\cdot \rho ={\frac {p}{T}}\cdot {\frac {283{\text{ K}}}{1010{\text{ hPa}}}}\cdot \rho

Java-Code[Bearbeiten]

Mit dem folgenden Java-Programm, das über das Hauptprogramm "main" aufgerufen wird, können die säkularen Aufgänge eines Gestirns für ein beliebiges Jahr in Bezug auf die astronomische Standardepoche J2000 berechnet werden:

→ Java-Programm "SaekularerAufgang"

Weblinks[Bearbeiten]

Commons: Stèle anthropomorphe 22.615 – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise[Bearbeiten]

↑ Stèle du rocher des Doms, Avignon Musée Calvet, Collections permanentes Préhistoire
↑ Sylvain Gagnière, Jacques Granier: Les stèles anthropomorphes du musée Calvet d'Avignon, in: Gallia préhistoire, tome 6, 1963. Seiten 31 bis 62
↑ Jean-Pierre Girault, Jean Gascó: DEUX STÈLES PROTOHISTORIQUES REDÉCOUVERTES AU PUY D’ISSOLUD (VAYRAC, LOT), PDF-Datei, französisch
↑ Mike Luciuk: Atmospheric Extinction and Refraktion, Amateur Astronomers, Garwood, New Jersey, Vereinigte Staaten von Amerika
↑ Siehe Aristoteles: Peri uranú (Περὶ οὐρανοῦ), Buch 2, Kapitel 14
↑ William Tyler Olcott: A Field Book of the Stars, Seite 104, New York, 1907
↑ David H. Kelley, Eugene F. Milone: Exploring Ancient Skies - A Survey of Ancient and Cultural Astronomy, 16. Februar 2011, Seite 276, Springer, New York, ISBN 9781441976246
↑ David A. King: Astronomical Alignments in Medieval Islamic Religious Architecture, in: Annals of the New York Academy of Sciences, Volume 385, Issue 1, Seiten 303 bis 312, Wiley-Blackwell, 1982
↑ Bartel Leendert van der Waerden: Erwachende Wissenschaft Band 2: Die Anfänge der Astronomie, in: Wissenschaft und Kultur, Band 23, Verlag Birkhäuser, Basel und Stuttgart, 1968
↑ Rita Gautschy-Loidl: Babylonische Astronomie, Abschnitt 7.2 Identifikation der genannten Sternbilder: Die Serie ^MULAPIN, in: Knaurs Neuer Historischer Weltatlas
↑ Markus Bautsch, Friedhelm Pedde: Canopus, der "Stern der Stadt Eridu". In: Dem Himmel nahe.. Nr. 17, Berlin, ISSN 2940-9330, S. 8-9 (https://wfs.berlin/wp-content/uploads/2023/05/BROplanet-juni2023ff_www.pdf).
↑ tablet K.8538, British Museum
↑ Johannes Koch: Neuere Untersuchungen zur Topographie des babylonischen Fixsternhimmels, Kapitel 7 bis 16, Verlag Otto Harrassowitz, Wiesbaden, 1989, ISBN 978-3447029438
↑ Hermann Hunger: Astrological Reports to Assyrian Kings, State Archives of Assyria, Band VIII, Seite 46, Helsinki University Press, 1992, ISBN 978-1-57506-331-7
↑ Gary D. Thompson: E: Late Mesopotamian Constellations / 9: Late Babylonian (Neo-Assyrian) planisphere, Episodic Survey of the History of the Constellations
↑ Reuben Grima: Landscape, Territories, and the Life-Histories of Monuments in Temple Period Malta, in: Journal of Mediterranean Archaeology, 21.1 (2008), Seiten 35 bis 56, ISSN (Print) 0952-7648 ISSN (Online) 1743-1700
↑ George H. Kaplan: The IAU Resolutions on Astronomical Reference Systems, Time Scales, and Earth Rotation Models Explanation and Implementation, Chapter 5: Precession and Nutation, U.S. Naval Observatory, Washington, D.C., 20 October 2005
↑ George G. Bennett: The Calculation of Astronomical Refraction in Marine Navigation, in: The Journal of Navigation, Volume 35, Issue 2, pp. 255–259, The Royal Institute of Navigation, May 1982

[calvet-1] Stèle du rocher des Doms, Avignon Musée Calvet, Collections permanentes Préhistoire

[2] Sylvain Gagnière, Jacques Granier: Les stèles anthropomorphes du musée Calvet d'Avignon, in: Gallia préhistoire, tome 6, 1963. Seiten 31 bis 62

[3] Jean-Pierre Girault, Jean Gascó: DEUX STÈLES PROTOHISTORIQUES REDÉCOUVERTES AU PUY D’ISSOLUD (VAYRAC, LOT), PDF-Datei, französisch

[4] Mike Luciuk: Atmospheric Extinction and Refraktion, Amateur Astronomers, Garwood, New Jersey, Vereinigte Staaten von Amerika

[5] Siehe Aristoteles: Peri uranú (Περὶ οὐρανοῦ), Buch 2, Kapitel 14

[6] William Tyler Olcott: A Field Book of the Stars, Seite 104, New York, 1907

[7] David H. Kelley, Eugene F. Milone: Exploring Ancient Skies - A Survey of Ancient and Cultural Astronomy, 16. Februar 2011, Seite 276, Springer, New York, ISBN 9781441976246

[8] David A. King: Astronomical Alignments in Medieval Islamic Religious Architecture, in: Annals of the New York Academy of Sciences, Volume 385, Issue 1, Seiten 303 bis 312, Wiley-Blackwell, 1982

[9] Bartel Leendert van der Waerden: Erwachende Wissenschaft Band 2: Die Anfänge der Astronomie, in: Wissenschaft und Kultur, Band 23, Verlag Birkhäuser, Basel und Stuttgart, 1968

[10] Rita Gautschy-Loidl: Babylonische Astronomie, Abschnitt 7.2 Identifikation der genannten Sternbilder: Die Serie ^MULAPIN, in: Knaurs Neuer Historischer Weltatlas

[11] Markus Bautsch, Friedhelm Pedde: Canopus, der "Stern der Stadt Eridu". In: Dem Himmel nahe.. Nr. 17, Berlin, ISSN 2940-9330, S. 8-9 (https://wfs.berlin/wp-content/uploads/2023/05/BROplanet-juni2023ff_www.pdf).

[12] tablet K.8538, British Museum

[13] Johannes Koch: Neuere Untersuchungen zur Topographie des babylonischen Fixsternhimmels, Kapitel 7 bis 16, Verlag Otto Harrassowitz, Wiesbaden, 1989, ISBN 978-3447029438

[14] Hermann Hunger: Astrological Reports to Assyrian Kings, State Archives of Assyria, Band VIII, Seite 46, Helsinki University Press, 1992, ISBN 978-1-57506-331-7

[15] Gary D. Thompson: E: Late Mesopotamian Constellations / 9: Late Babylonian (Neo-Assyrian) planisphere, Episodic Survey of the History of the Constellations

[16] Reuben Grima: Landscape, Territories, and the Life-Histories of Monuments in Temple Period Malta, in: Journal of Mediterranean Archaeology, 21.1 (2008), Seiten 35 bis 56, ISSN (Print) 0952-7648 ISSN (Online) 1743-1700

[17] George H. Kaplan: The IAU Resolutions on Astronomical Reference Systems, Time Scales, and Earth Rotation Models Explanation and Implementation, Chapter 5: Precession and Nutation, U.S. Naval Observatory, Washington, D.C., 20 October 2005

[18] George G. Bennett: The Calculation of Astronomical Refraction in Marine Navigation, in: The Journal of Navigation, Volume 35, Issue 2, pp. 255–259, The Royal Institute of Navigation, May 1982

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]