Exercises: Continuity – Serlo

Lipschitz continuous functions are uniformly continuous

Exercise

Let $f:\mathbb {R} \rightarrow \mathbb {R}$ be Lipschitz continuous with Lipschitz constant $K\in \mathbb {R} ^{+}$. That is

$|f(x)-f(y)|\leq K\cdot |x-y|$

for all $x,y\in \mathbb {R}$. Prove that $f$ is uniformly continuous.

How to get to the proof?

We need to show that for all $\epsilon >0$ , there is a $\delta >0$ , such that for all $x,y\in \mathbb {R}$ with $|x-y|<\delta$ there is $|f(x)-f(y)|<\epsilon$. By our assumption, we have

$|f(x)-f(y)|\leq K\cdot |x-y|<K\cdot \delta$

In order for $|f(x)-f(y)|<\epsilon$ to hold, it suffices to have $K\cdot \delta =\epsilon$. We can reach this by taking $\delta ={\tfrac {\epsilon }{K}}$.

Proof

Let $\epsilon >0$ be arbitrary. We choose $\delta ={\tfrac {\epsilon }{K}}$. Then, for all $x,y\in \mathbb {R}$ with $|x-y|<\delta ={\tfrac {\epsilon }{K}}$:

$|f(x)-f(y)|\leq K\cdot |x-y|<K\cdot {\frac {\epsilon }{K}}=\epsilon$

Continuity at the origin

Exercise

Prove that the following function is continuous at the origin $x=0$:

$f:\mathbb {R} \to \mathbb {R} ,~f(x)={\begin{cases}K\cdot x\cdot \sin \left({\frac {1}{x}}\right),&x\neq 0\\0,&x=0\end{cases}}$

with a real number $K>0$

How to get to the proof?

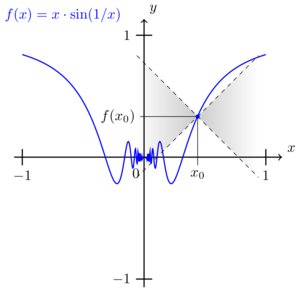
In order to establish continuity at the origin $x=0$ , we make use of the epsilon-delta criterion. That means, for all $\epsilon >0$ we have to find a $\delta >0$ such that the inequality $|f(x)-f(0)|<\epsilon$ holds at all $x$ with $|x|<\delta$ . The question now is how to find a suitable $\delta$ for any given $\epsilon >0$ . To answer this question, we take a look at the function $f$ around $x=0$:

Since at $x\neq 0$ $\left\vert \sin \left({\frac {1}{x}}\right)\right\vert \leq 1$, there is

$|f(x)-f(0)|=|f(x)|=\left\vert K\cdot x\cdot \sin \left({\frac {1}{x}}\right)\right\vert =K\cdot |x|\left\vert \sin \left({\frac {1}{x}}\right)\right\vert \leq K\cdot |x|$

This inequality also holds at $x=0$, since $|f(0)|=|0|$. Visually, the inequality above means that the graph of the function $f$ fits inside the "double wedge" given by $|f(x)|\leq K\cdot |x|$, where $K>0$ tells us, how much the wedge is "stretched" in $y$-direction. So if we choose $K\cdot \delta =\epsilon \Leftrightarrow \delta ={\tfrac {\epsilon }{K}}$, then at any $x$ with $|x|<\delta$ , there is

$|f(x)-f(0)|\leq K\cdot |x-0|<K\cdot \delta =\epsilon$

Which we can use to carry through the proof (see below).

Note: We can also "move the double wedge" to any $(x_{0},f(x_{0}))$ when investigating continuity at $x_{0}$ . If the graph fits inside the "moved double wedge" $|f(x)-f(x_{0})|\leq K\cdot |x-x_{0}|$ , then for any $|x-x_{0}|<\delta ={\tfrac {\epsilon }{K}}$, there is

$|f(x)-f(x_{0})|\leq K\cdot |x-x_{0}|<K\cdot \delta =\epsilon$

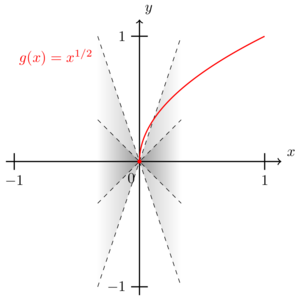
So any function fitting in such a double wedge is continuous. The converse does not hold true. There are functions which do not fit in any double wedge around $|f(x)-f(x_{0})|\leq K\cdot |x-x_{0}|$ but are continuous at $x_{0}$. An example is the square root function $g:[0,\infty )\to \mathbb {R} ,\quad g(x)={\sqrt {x}}$ around $x_{0}=0$.

• 
  The function $f(x)=x\cdot \sin \left({\frac {1}{x}}\right)$ is continuous at $x=0$.
• 
  The function $f(x)=x\cdot \sin \left({\frac {1}{x}}\right)$ is continuous at any $x_{0}=0$.
• 
  The function $g(x)={\sqrt {x}}$ is not Lipschitz-continuous at $x=0$

Proof

Let $\epsilon >0$. We choose $\delta =\epsilon$. Let $x$ be any real number with $|x|<\delta$. Then:

${\begin{aligned}\left|f(x)-f(0)\right|&=\left|x\cdot \sin \left({\frac {1}{x}}\right)-0\right|\\[0.3em]&=\left|x\cdot \sin \left({\frac {1}{x}}\right)\right|\\[0.3em]&\quad {\color {Gray}\left\downarrow \ |\sin(\cdot )|\in [0,1]\right.}\\[0.3em]&\leq |x|\\[0.3em]&\quad {\color {Gray}\left\downarrow \ {\text{by assumption }}|x|<\delta \right.}\\[0.3em]&<\delta \\[0.3em]&\quad {\color {Gray}\left\downarrow \ {\text{by choice }}\delta =\epsilon \right.}\\[0.3em]&=\epsilon \\[0.3em]\end{aligned}}$

This shows that $f$ is continuous at $x=0$ .

Extreme value theorem

Exercise (Maximum and minimum of a function)

Prove that the function $f(x)={\frac {6x^{2}+x}{x^{3}+x^{2}+x+1}}$ defined on $[1,\infty )$ attains a maximum, but not a minimum.

Solution (Maximum and minimum of a function)

Proof step: $f$ attains a maximum

The function $f$ is continuous on $[1,\infty )$, since it is composed by continuous functions and the denominator is strictly positive ($>0$). The enumerator is also strictly positive, so $f(x)>0$ for $x\geq 1$, $f(1)={\frac {7}{4}}>1$, and

$\lim _{x\to \infty }f(x)=\lim _{x\to \infty }{\frac {6x^{2}+x}{x^{3}+x^{2}+x+1}}=\lim _{x\to \infty }{\frac {{\frac {6}{x}}+{\frac {1}{x^{2}}}}{1+{\frac {1}{x}}+{\frac {1}{x^{2}}}+{\frac {1}{x^{3}}}}}={\frac {0}{1}}=0$

That means, there is an $x_{0}>1$ with $f(x)<1$ for all $x\geq x_{0}$. The extreme value theorem implies that $f$ attains a maximum on $[1,x_{0}]$ . One may even show that the maximum is even global. However, computing the maximum explicitly would require us to solve $f(x)'=0$ , which is quite a computational effort and can be even harder for other functions $f$. The extreme value theorem just allowed us to quickly show that there is a maximum - and saved us from the tedious solution of $f(x)'=0$.

Proof step: $f$ does not attain a minimum

There is $f>0$ on $[1,\infty )$ . And indeed, $f$ approaches 0 (see the previous proof step). But it does not attain 0. Since $\lim _{x\to \infty }f(x)=0$ and by continuity, there can not be a minimum (if there was an attained minimum $f(x_{\epsilon })=\epsilon >0$, then by $\lim _{x\to \infty }f(x)=0$, there would by $f(x)={\tfrac {\epsilon }{2}}$ for some $x$, which is a contradiction ).

Exercise (How often is a value attained #1)

1. Show that there is no continuous function $f:\mathbb {R} \to \mathbb {R}$ , which attains each of its function values exactly twice.
2. Is there a continuous function $f:\mathbb {R} \to \mathbb {R}$ , which attains each of its function values exactly three times?

Exercise (How often is a value attained #2)

Let $n\in \mathbb {N}$ with $n>1$. Show: There is no continuous function $f:[0,1]\to \mathbb {R}$ , which attains each of its function values exactly $n$ times.

Intermediate value theorem and zeros

Exercise (Zero of a function)

Prove that the function

$f:\mathbb {R} \to \mathbb {R} ,\ f(x)=\sin(x)-e^{-x}$

has exactly one zero inside the interval $[0,{\tfrac {\pi }{2}}]$ .

Solution (Zero of a function)

Proof step: $f$ has at least one zero

$f$ is continuous as it is composed by the continuous functions $\sin$ and $\exp$. In addition,

$f(0)=\sin(0)-e^{0}=-1<0$

and

$f({\tfrac {\pi }{2}})=\sin({\tfrac {\pi }{2}})-e^{-{\tfrac {\pi }{2}}}=1-\underbrace {e^{-{\tfrac {\pi }{2}}}} _{<1}>0$

By means of the intermediate value theorem, there must be an ${\tilde {x}}\in [0,{\tfrac {\pi }{2}}]$ with $f({\tilde {x}})=0$.

Proof step: $f$ has exactly one zero

$\sin$ is strictly monotonously increasing on $[0,{\tfrac {\pi }{2}}]$ . The function $x\mapsto \exp$ is also monotonously increasing on $[0,{\tfrac {\pi }{2}}]$ , so $x\mapsto \exp(-x)$ is decreasing and $x\mapsto -\exp(-x)$ again increasing. Hence there can be only one zero ${\tilde {x}}\in [0,{\tfrac {\pi }{2}}]$ with $f({\tilde {x}})=0$ , since a function with two zeros $f({\tilde {x}}_{1})=f({\tilde {x}}_{2})=0$ is never strictly monotonously increasing (it would either have to stay constant or go "down again" between ${\tilde {x}}_{1}$ and ${\tilde {x}}_{2}$).

Exercise (Solution of an equation)

Let $a,b,c\in \mathbb {R}$ with $a<b<c$. Prove that the equation

${\frac {1}{x-a}}+{\frac {1}{x-b}}+{\frac {1}{x-c}}=2$

Has at least three solutions.

Solution (Solution of an equation)

It is a powerful trick in mathematics, to transform the problem of finding solutions $x$ to $f(x)=g(x)$ as zeros of an auxiliary function $h(x)=f(x)-g(x)$ (if $h(x)=0$, then $f(x)=g(x)$ and vice versa). In our case, the continuous auxiliary function is

$h:\mathbb {R} \setminus \{a,b,c\}\to \mathbb {R} ,\ h(x)={\frac {1}{x-a}}+{\frac {1}{x-b}}+{\frac {1}{x-c}}-2$

When approaching $a$ and $b$, this function goes to

$\lim _{x\to a+}h(x)=\infty$

and

$\lim _{x\to b-}h(x)=-\infty$

Therefore, there must be two arguments $x_{1},x_{2}\in (a,b)$ with $h(x_{1})>0$ and $h(x_{2})<0$ ($x_{1}$ is close to $a$ and $x_{2}$ close to $b$). By the intermediate value theorem, there must hence be a zero ${\tilde {x}}\in [x_{1},x_{2}]\subset (a,b)$ with $h({\tilde {x}})=0$. This zero ${\tilde {x}}$ is one solution of the above equation.

The same argument works between $b$ and $c$. Since $\lim _{x\to b+}h(x)=\infty$ and $\lim _{x\to c-}h(x)=-\infty$ , we can use the intermediate value theorem and get a zero ${\tilde {y}}\in (b,c)$ with $h({\tilde {y}})=0$ .This is the second solution we have been looking for.

The third solution follows by a similar argument. There is $\lim _{x\to c+}h(x)=\infty$ and $\lim _{x\to \infty }h(x)=-2<0$. So the intermediate value theorem renders a ${\tilde {z}}\in (c,\infty )$ with $h({\tilde {z}})=0$ . The equation has therefore at least three solutions.

Exercise (Solution of an equation)

Let $f:[0,1]\to \mathbb {R}$ be continuous with $f(0)=f(1)$. Prove that there is a $c\in [0,1]$ with $f(c)=f\left(c+{\tfrac {1}{2}}\right)$ .

Solution (Solution of an equation)

We consider the following auxiliary function:

$h:[0,{\tfrac {1}{2}}]\to \mathbb {R} ,\ h(c)=f(x+{\tfrac {1}{2}})-f(x)$

Finding a $c\in [0,1]$ with $f(c)=f\left(c+{\tfrac {1}{2}}\right)$ now amounts to finding a zero of $h$. Since $f$ is continuous, so is $h$ . In addition, at the endpoints of the interval, there is

$h(0)=f({\tfrac {1}{2}})-f(0)$

and

$h({\tfrac {1}{2}})=f(1)-f({\tfrac {1}{2}}){\overset {\text{Vor.}}{=}}f(1)-f({\tfrac {1}{2}})=-(f({\tfrac {1}{2}})-f(0))=-h(0)$

Fall 1: $h(0)=0$

This means $f({\tfrac {1}{2}})-f(0)=0$, or equivalently

$f(0)=f({\tfrac {1}{2}})$

So we have found a solution $c=0$ to $f(c)=f\left(c+{\tfrac {1}{2}}\right)$.

Fall 2: $h(0)\neq 0$

We will first consider the case $h(0)>0$. Since $h(0)>0$ , there is $h({\tfrac {1}{2}})=-h(0)<0$. The intermediate value theorem now yields a $c\in [0,{\tfrac {1}{2}}]\subset [0,1]$ with

$h(c)=f(c+{\tfrac {1}{2}})-f(c)=0$

This $c$ is a zero of $h$ and hence a desired solution for $f(c)=f(c+{\tfrac {1}{2}})$. The other case $h(0)<0$ can be treated using exactly the same arguments.

So for any choice of $h(0)$, there is a $c\in [0,1]$ with $f(c)=f(c+{\tfrac {1}{2}})$.

Exercise (Existence of exactly one zero)

Let $n\in \mathbb {N}$ be a natural number. We define the function $f_{n}:\mathbb {R} \to \mathbb {R} ,x\mapsto x^{n}+4n^{2}x-10$. Prove that $f_{n}$ has exactly one positive zero.

Solution (Existence of exactly one zero)

We need to show two things: At first, we need to show that a zero exists inside the interval $]0;+\infty [$. Second, we need to assure that there is indeed only one such zero.

The function $f_{n}$ is a polynomial function and hence continuous. At the beginning of the interval $x=0$ , there is $f(0)=-10<0$ i.e. the graph of the function runs below the $x$-axis. At infinity, there is $\lim _{x\to \infty }f_{n}(x)=+\infty$, meaning that for large $x$ , the graph runs above the $x$-axis. As $f_{n}$ is continuous, we can apply the intermediate value theorem and get a zero $x_{1}\in ]0;+\infty [$.

Now we need to show that there is at most one zero. Both $x\mapsto x^{n}$ and $x\mapsto x$ are strictly monotonously increasing functions for $x>0$ . So we may assume that $f_{n}$ is also strictly monotonous, there. We can prove this assumption be taking the first derivative:

For $x>0$ there is: $f_{n}'(x)=\underbrace {nx^{n-1}} _{>0}+\underbrace {4n^{2}} _{>0}>0$.

One may show with a bit of effort that differentiable functions with positive derivative $f_{n}(x)>0$ are strictly monotonous in the sense that $f_{n}(y)>f_{n}(x)$ for $y>x$. If there were two zeros $x_{1}<x_{2}$, we would have $f_{n}(x_{2})=f_{n}(x_{1})=0$ although there is $x_{2}>x_{1}$ . This would contradict $f_{n}$ being monotonous and in hence excluded. Therefore, $f_{n}$ can have at most one zero (as all strictly monotonous functions).

Note: We could also prove that $f_{n}$ has at most one zero, only using that $f_{n}$ is differentiable with $f_{n}'(x)>0$:

Assume that, the function $f_{n}$ would have two zeros $x_{1},x_{2}\in ]0;+\infty [$ with $x_{1}<x_{2}$. Since the function $f_{n}$ is differentiable and $f_{n}(x_{1})=0=f_{n}(x_{2})$, we may use Rolle's theorem and get that some $\xi \in ]x_{1};x_{2}[$ exists wit $f_{n}'(\xi )=0$. But this is a contradiction to the first derivative of $f_{n}$ being strictly positive $f_{n}'(x)>0$ . So this is a second way to exclude the existence of two zeros.

Continuity of the inverse function

Exercise (Continuity of the inverse function 1)

Let $f:(-1,1)\to \mathbb {R}$ be defined by

$f(x)={\frac {2x}{1-x^{2}}}$

1. Prove that $f$ is continuous, strictly monotonous and injective.
2. Prove that $f$ ist surjectiive (so it is a 1-to-1-map from $(-1,1)$ to $\mathbb {R}$ an inverse function exists).
3. Why is the inverse function $f^{-1}:f(\mathbb {R} )\to \mathbb {R}$ continuous, monotonously increasing and bijective? Explicitly determine $f^{-1}$.

Solution (Continuity of the inverse function 1)

Part 1: $f$ is continuous on $(-1,1)$ since it is the quotient of the continuous polynomials $x\mapsto 2x$ and $x\mapsto 1-x^{2}$. Note that $1-x^{2}\neq 0$ for all $x\in (-1,1)$.

Let $x,y\in \mathbb {R}$ with $x<y$. Then, strict monotony holds:

$x<y\Rightarrow \left\{{\begin{array}{c}2x<2y\\1-y^{2}<1-x^{2}\end{array}}\right\}\Rightarrow 2x(1-y^{2})<2y(1-x^{2})\Leftrightarrow \underbrace {\frac {2x}{1-x^{2}}} _{=f(x)}<\underbrace {\frac {2y}{1-y^{2}}} _{=f(y)}$

Therefore, $f$ is also injective.

Part 2: The function runs towards infinity at the end points of the open interval $(-1,1)$ as follows:

$\lim _{x\to 1-}f(x)=\lim _{x\to 1-}{\frac {2x}{1-x^{2}}}=\lim _{x\to 1-}{\frac {2}{{\frac {1}{x}}-x}}{\overset {\frac {2}{0+}}{=}}\infty$ and $\lim _{x\to -1+}f(x)=\lim _{x\to -1+}{\frac {2x}{1-x^{2}}}=\lim _{x\to -1+}{\frac {2}{{\frac {1}{x}}-x}}{\overset {\frac {2}{0-}}{=}}-\infty$

Since $f$ is continuous, the intermediate value theorem ensures that for each $y\in \mathbb {R}$ there is a $x\in (-1,1)$ mapped onto it: $f(x)=y$. Therefore, $f(x)$ is also surjective: $f[(-1,1)]=\mathbb {R}$.

Part 3: Since $f$ is bijective, the inverse map exists and is bijective, as well:

$f^{-1}:\mathbb {R} \to (-1,1)$

The theorem about continuity of the inverse function tells us that $f^{-1}$ is continuous and strictly monotonously increasing. Now, let us compute $f^{-1}$. That means, we need to bring $f(x)=y$ into the form $x=f^{-1}(y)$ - i.e. we need to get $x$ standing alone on the left side of the equation:

$y={\frac {2x}{1-x^{2}}}\Leftrightarrow y-yx^{2}=2x\Leftrightarrow yx^{2}+2x-y=0$

Fall 1: $y=0$

$2x=0\iff x=0$

Fall 2: $y\neq 0$

We can use the quadratic solution formula in order to solve for $x$:

$yx^{2}+2x-y=0\iff x_{1/2}={\frac {-2\pm {\sqrt {4+4y^{2}}}}{2y}}={\frac {-1\pm {\sqrt {1+y^{2}}}}{y}}$

Since $y=f(x)>0$ for $x>0$, the only reasonable solution is $x={\frac {-1+{\sqrt {1+y^{2}}}}{y}}$ . Putting all together, the full definition for the inverse function reads

$f^{-1}(y)={\begin{cases}{\frac {-1+{\sqrt {1+y^{2}}}}{y}}&{\text{ für }}y\neq 0,\\0&{\text{ für }}y=0\end{cases}}$

Hint

The distinction of two cases above is not very convenient. We can avoid it using a little trick: In case $y\neq 0$ enumerator and denominator of $f^{-1}$ can be multiplied by a factor of $(-1-{\sqrt {1+y^{2}}})$:

$f^{-1}(y)={\frac {(-1+{\sqrt {1+y^{2}}})(-1-{\sqrt {1+y^{2}}})}{y(-1-{\sqrt {1+y^{2}}})}}={\frac {1-(1+y^{2})}{-y(1+{\sqrt {y^{2}+1}})}}={\frac {-y^{2}}{-y(1+{\sqrt {y^{2}+1}})}}={\frac {y}{1+{\sqrt {y^{2}+1}}}}$

Plugging in $y=0$ , we get that $f^{-1}(0)={\tfrac {0}{1+{\sqrt {1+0^{2}}}}}={\tfrac {0}{2}}=0$ is described correctly. So we can use the definition above for all $y\in \mathbb {R}$ and avoid the case distinction.

Exercise (Continuity of the inverse function 2)

Let

$g:[0,\infty )\to \mathbb {R} ,\ g(x)=\ln(x+e)+\cos \left({\frac {1}{\ln(x+e)}}\right)$

1. Prove that $g$ is injective.
2. Determine the range $g([0,\infty ))$ of all attained values.
3. Why is the inverse function $g^{-1}:g([0,\infty ))\to [0,\infty )$ continuous?

Solution (Continuity of the inverse function 2)

Part 1:

$g$ is continuous, as it is composed by the continuous functions $x\mapsto x+e$, $x\mapsto {\frac {1}{x}}$, $x\mapsto \ln(x)$ and $x\mapsto \cos(x)$ on $[0,\infty )$.

The logarithm is strictly monotonously increasing (and its inverse is decreasing): for $x,y\in [0,\infty )$ with $x<y$ , there is:

${\underset {\text{sms}}{\overset {\ln }{\Longrightarrow }}}\quad \ln(x+e)<\ln(y+e)\quad \Longrightarrow \quad {\frac {1}{\ln(x+e)}}>{\frac {1}{\ln(y+e)}}$

Now, ${\frac {1}{\ln(x+e)}}\in (0,1]$ for $x\in [0,\infty )$. Since in addition, $\cos$ is strictly monotonously decreasing on $(0,1]$, we have

$\cos \left({\frac {1}{\ln(x+e)}}\right)<\cos \left({\frac {1}{\ln(y+e)}}\right)$

So the $\cos$-term is also strictly monotonously increasing and so is $g$:

$\underbrace {\ln(x+e)+\cos \left({\frac {1}{\ln(x+e)}}\right)} _{=g(x)}<\underbrace {\ln(y+e)+\cos \left({\frac {1}{\ln(y+e)}}\right)} _{=g(y)}$

Therefore, $g$ is also injective.

Part 2:

At the ends of the domain of definition, there is

$g(0)=\ln(e)+\cos \left({\frac {1}{\ln(e)}}\right)=1+\cos(1)$

and

$\lim _{x\to \infty }\ln(x+e)=\infty {\text{ und }}\lim _{x\to \infty }{\frac {1}{\ln(x+e)}}=0$

this implies

$\lim _{x\to \infty }g(x)=\lim _{x\to \infty }[\underbrace {\ln(x+e)} _{\to \infty }-\underbrace {\cos \left({\frac {1}{\ln(x+e)}}\right)} _{\to \cos(0)=1}]=\infty$

$g$ is continuous on the interval $[0,\infty )$. Hence, we can use a corollary of the intermediate value theorem, and get that $g([0,\infty ))$ is again an interval. Since $g$ is strictly monotonously increasing and $\lim _{x\to \infty }g(x)=\infty$ , we can conclude

$g([0,\infty ))=[g(0),\infty )=[1+\cos(1),\infty )$

Part 3:

Since $D=[0,\infty )$ is an interval and $g:[0,\infty )\to [1+\cos(1),\infty )$ in bijective, we can use the theorem about continuity of the inverse function. I tells us that

$g^{-1}:[1+\cos(1),\infty )\to [0,\infty )$

is indeed continuous.