Extreme value theorem – Serlo
In the following we are going to deal with continuous functions on compact intervals. These are intervals that are closed and bounded, i.e. have the form . We will see that such functions are always bounded and attain a minimum and maximum. This theorem is called the Extreme Value Theorem. It is used in mathematics to prove the existence of relative extrema, i.e. points of a function that are "at the extreme" of being the lowest point in the graph (the minimum) or the highest point in the graph (the maximum).
Motivation
[Bearbeiten]Let's take a continuous function which is defined on a compact interval . I.e. we are considering a function . This function has the value at the point and the value at the point .
Now is defined for every intermediate point between and . Intuitively, for functions without gaps in the domain of definition, continuity means that we are able to draw the graph without lifting the pen from the paper. Hence, the graph of connects the points and by a continuous path without jumps. The following graph provides an example for such a function :
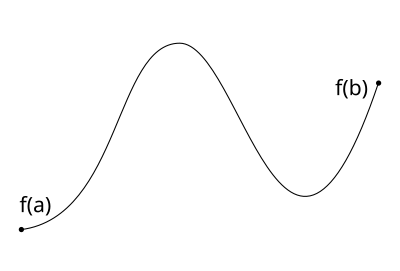
We note that the function above is bounded. And it attains a maximum and minimum value:

Is it always that way? Try for yourself to connect the points and by different graphs without lifting the pen. Could you imagine to draw the graph of an unbounded function - even if your paper was infinitely large?
Intuitively, the answer is no. No matter how far your graph goes up or down, you need to return to the end points at or . Going to infinity "forces you to lift the pen" and is therefore not allowed. However, the function can attain very large values (like or more) while staying bounded, as long as you return in order to reach the end point. This situation is illustrated in the following figure:

So our first intuition tells us that when connecting the two points and without lifting the pen, our function stays bounded. And it attains a maximum and a minimum. Now let's think about what could go wrong when phrasing this intuition in a mathematical way. The end points and of the domain of definition could become problematic: For an open domain of definition , the function could run towards at or , or it could converge towards a value without attaining it. Including the boundary points in the domain of definition excludes these cases as it "catches the function" at the end points and . If we move a boundary to infinity, let's say by considering the domain of definition , the function could have "infinitely much time" and might run towards infinity while being continuous. This happens for instance for . So we also expect problems with unbounded domains of definition. A statement like "the maximum and minimum are attained" can only be expected to hold true on a compact interval . Now, in between and , the function could also "break out" and tend towards (like near ). This scenario will be prevented by assuming continuity of the function .
In the following, we will mathematically verify that our intuition is true. That means we prove a statement like "the maximum and minimum are attained" for continuous functions defined on a compact interval and discuss what may go wrong if we choose other domains of definition.
Extreme value theorem
[Bearbeiten]Theorem (Extreme value theorem)
Every continuous function defined on a compact interval is bounded and attains a maximum and a minimum (extreme values). That means, if with and is a continuous function, then there are arguments , such that for all arguments the inequality holds.
Example (Extreme value theorem)

Consider with . The domain of definition is a compact interval. In addition, is continuous as it is composed out of continuous functions , , and with domains of definition . Hence, must attain a maximum and a minimum.
Proof (Extreme value theorem)
Let be a continuous function with and . We will only prove explicitly that is bounded from above and attains a maximum. The analogous statement that is bounded from below and attains a minimum can be shown the same way.
So let us consider the image . This is the the set of all function values, which are attained by . Let us take the supremum of the set , where we explicitly allow for use of the extended definition of the supremum . If is bounded from above, then and else, (since , the case cannot occur).
Now, we know that there is a sequence in , which tends towards the supremum (for each nonempty set there is a subsequence in , tending towards ). Hence there is a sequence of arguments in with .
We now make use of the Bolzano-Weierstraß theorem. This theorem tells us that each sequence in a compact interval with and has a converging subsequence. Hence, also has a convergent subsequence . Let be the limit of the convergent subsequence . Since for all , there is also and therefore . So, must be an argument of the function . Since is continuous, we can make use of the sequential definition of continuity
is a function value of and hence a real number. Therefore we know that is bounded from above. And we have shown that attains its upper bound at the argument . Therefore, for all and indeed, is the maximum among all function values of .
Assumptions of the theorem
[Bearbeiten]Let's take a look at the assumptions made within the extreme value theorem:
- is a continuous function
- is defined on a compact interval
Are those assumptions really necessary or can we relax them without losing validity of the extreme value theorem?
Assumption of continuity
[Bearbeiten]
First, we note that continuity prevents the function from "breaking out" to or within its domain of definition. Ij we just allow any function , no matter whether it is continuous or not, we will find non-continuous functions which are violating the extreme value theorem. The following function is unbounded (so it does not attain any extrema) and non-continuous at :
So we cannot simply drop the assumption that is continuous.
Interval-assumption
[Bearbeiten]
The domain of definition is also important. It must include its boundary (i.e. be closed). This way we "catch" the function at the interval boundary and make sure it does not "run away" towards infinity. The function is an example which "runs away" as we approach .
Unboundedly large domains are also problematic, since the function has "infinitely much time" to run away. An easy example is the function . And there are functions, which are defined on a bounded domain of definition, continuous and do not "run away" towards infinity, but do not attain an extremum. This happens if there are open boundaries or gaps within the domain of definition. The extremum would then be attained at the boundary (or the gap) - but this argument has been removed from the domain of definition.
Question: Does the continuous function always attain a maximum or a minimum, if it is defined on a bounded interval?
No. For instance, the function , does not. There is: . So the infimum and maximum of the image are 0 and 1, which would be attained at the boundary ( and ), if was defined there. However, we removed 0 and 1 from the domain of definition, so does no longer attain an extremum.
The same may happen when removing a maximum or minimum from the interior of the domain of definition instead of the boundary - which creates a gap. Of course, the function may also "run away" at such a gap. An example for this effect is the continuous but unbounded function . The argument is excluded from the domain of definition . So this function is well defined and continuous, but it "runs away" at the gap. In a mathematical language, the function is unbounded and hence violates the conclusion of the extreme value theorem.
Outlook: Generalization of the theorem
[Bearbeiten]So far, we only considered intervals (possibly with gaps) as candidates for the domain of definition. Is this restriction really necessary? This time, the answer is no. For instance, we can take the union of two intervals with and define some continuous and real-valued function on . If we restrict to only or , we can apply the extreme value theorem. Both the functions and with restricted domain of definition are bounded and hence attain a maximum and a minimum. The function must therefore also be bounded. Its maximum is the larger of the both maxima of and , so also attains a maximum (the same holds for the minimum). Therefore, every continuous function defined on the union of two closed intervals fulfills the conclusion of the extreme value theorem. The same holds if we consider three or more closed intervals - or an even larger class of domains of definition. In fact, we can precisely state what this larger class of domains of definition is:
If we take a second look at the proof, we note that the domain of definition is only mentioned at one point: where we make use of the Bolzano-Weierstraß theorem. We used it to show that any sequence from the domain of definition contains a convergent subsequence. Hence, the proof arguments hold true, as long as the domain of definition allows for the usage of the Bolzano-Weierstraß theorem.
So we can generalize the above theorem. It will hold not only on closed intervals , but on all sets satisfying the Bolzano-Weierstraß theorem. We will call these sets satisfying the Bolzano-Weierstraß theorem sequentially closed sets:
Definition (Sequential closedness)
A subset of the real numbers is called sequentially closed iff any sequence out of this set has a convergent subsequence.
If the domain of definition of a continuous function is sequentially compact, then the function must fulfill the extreme value theorem. The generalization of sequential compactness from real numbers to other sets of mathematical objects is one of the topics dealt with in topology.
Exercise: Image of polynomials of even degree
[Bearbeiten]Exercise (Image of polynomials)
Let
be a polynomial function with and . Let further have an even degree . Show that the image of is given by
Here, (an case ) and (in case ) are real numbers.
Proof (Image of polynomials)
We will consider the case . The proof for the case works analogously. At first, we note that the polynomial is a composition of continuous functions and hence continuous itself on . It is temping to use the extreme value theorem in order to show that attains a minimum. However, is not a compact interval. However, we can cut it off at very large values and make it compact this way. For even , there is , da . The -term dominates the other ones, so there is also
Now, let us take any function value of – for instance . Since there is an , such that for all . Analogously, since there is an , such that for arguments smaller than . Both on and , the polynomial is larger than the function value .
We can hence cut off the real number axis and restrict to the interval . Since on the function is larger than , the argument does not belong to this set and . Analogously, . Therefore, is a nonempty, closed and bounded interval. Hence it is compact an we can apply the extreme value theorem. The polynomial indeed attains a minimum on . Now, (since ) and therefore, is also a global minimum of the polynomial.
The intermediate value theorem additionally yields that the image of is an interval (see also Conclusions from the intermediate value theorem). Since and is a global minimum of , the image of must be of the form .
Exercise: Continuous functions on [0,1]
[Bearbeiten]Exercise (There is no continuous function on a compact interval attaining all function values exactly twice)
Show that there is no continuous function attaining all its function values exactly twice. That means, there is no continuous function , such that for all exactly two numbers with exist.
Solution (There is no continuous function on a compact interval attaining all function values exactly twice)
We perform a proof by contradiction. Let be a continuous function attaining all its values exactly twice. Since is continuous and is a compact interval, has to be bounded and to attain a maximum . By assumption, this maximum is attained exactly twice. So there are two arguments with . Let without loss of generality be .
Now, must also attain a minimum on the interval , which we call . Since is the maximum of , it is also the maximum of the restriction . Therefore, . In case , the function would have to be constant on and hence attain exactly one value infinitely often. Therefore, .
Since the minimum is attained by on the interval and the function attains the maximum on both ends of the interval, there is an with and . And we know that is attained at some second argument . This argument mab be situated on the inside of the interval or on the outside.
Fall 1:
First, we consider the case where is not in on consider - without loss of generality - the case . The mean of and is an intermediate value and will hence be attained by the function between and by means of the intermediate value theorem. Analogously, is attained in the intervals and . So is attained at least at three arguments, which leads to a contradiction to the function attaining each value exactly twice:

Fall 2:
Now, we consider the case where is situated inside the interval . Without loss of generality, we assume . Within the interval , must attain a maximum . Since is the minimum on , there will be . In addition, has already been attained twice, so we need the strict inequality (else, the function would be constant on ). As is the maximum of , which was already attained twice at and , there is .
Now, the intermediate value theorem tells us that is attained within the interval (since ). For the same reason (), the value is also attained on . So is a value attained at least three times: inside the open interval , inside of and inside of . This is a contradiction to every value being attained exactly twice:

In addition, the statement of the above exercise can be generalized in multiple ways:
- We have shown that on a compact interval , there is no continuous function attaining each value twice.
- Similarly, one may show that there is no continuous function attaining each of its values twice.
- And for each given number , , one can show that there is no continuous function attaining each of its values exactly times.
Exercise for understanding: Give an example for:
- A continuous function , attaining each of its function values exactly once.
- A function (non-continuous) attaining all of its function values exactly twice.
Possible solution:
- with
- with


![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)
















![{\displaystyle {\tilde {x}},{\hat {x}}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d35d5c9736d3ac4a078bad9bf0f0068482a827a)
![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)

![{\displaystyle f:[0,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2de6d0d4c98d4ca7ad937c772dc3e3e914b062f5)

![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)




![{\displaystyle f([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e8bf1526030f5a9f1564d4ef14c5d63350dfe9a)
![{\displaystyle \sup f([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a65626183645ac3fe6c0204a9d1e4197e9daa0a)
![{\displaystyle \sup f([a,b])=\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/33ff8e1849b616c364c8cf865d2e45e97ecac4b5)
![{\displaystyle \sup([a,b])\in \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e738a90cb42d96196ca5915eb2a86ad09556838)
![{\displaystyle f([a,b])\neq \emptyset }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b74c580b64922dc1cf3ac1217ce77e61a48b58e9)




![{\displaystyle \lim _{n\to \infty }f(x_{n})=\sup f([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604956c3ed94dba3f0022eacc941121a95efab02)





![{\displaystyle {\tilde {x}}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7a70e57f199d3304bbe0964d741eeafd3ee2e32)
![{\displaystyle f\left({\tilde {x}}\right)=f\left(\lim _{k\to \infty }x_{n_{k}}\right)=\lim _{k\to \infty }f\left(x_{n_{k}}\right)=\sup f([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df91bd626d705848daeb06815783109280e9da96)


![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)



![{\displaystyle f:[-1,1]\to \mathbb {R} :x\mapsto {\begin{cases}{\frac {1}{x}}&;x\neq 0\\0&;x=0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd5ae3a79a40126b1fb2f0aa6a8b578459a49156)
![{\displaystyle (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e70f9c241f9faa8e9fdda2e8b238e288807d7a4)
![{\displaystyle g:(0,1]\to \mathbb {R} :x\mapsto {\tfrac {1}{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab202566a18373eba5c870db8e8c51cff818f1de)





![{\displaystyle j:[-1,1]\setminus \{0\}\to \mathbb {R} :x\mapsto {\tfrac {1}{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26da6ee14303c41bac398da1e25b826bafe46477)
![{\displaystyle [-1,1]\setminus \{0\}=[-1,0)\cup (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/426931c78973d59cf31c2f402678b46aba8b78c9)
![{\displaystyle D=[a,b]\cup [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a14698de03f1e6c8d46222e97fcc61e1e93d23e0)



![{\displaystyle [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85b3b21d6d891d97f85e263d394e3c90287586f)
![{\displaystyle j_{1}=j|_{[a,b]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5fb6eff5a0c60db7e65cf8bc388b7ea55f0a33c)
![{\displaystyle j_{2}=j|_{[c,d]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28fc5503e9a9b3470331f0eb9fd4eae5eaf98ce6)


![{\displaystyle [a,b]\cup [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b212df8832496863465ec0b2e1802daf819aab35)






![{\displaystyle p(\mathbb {R} )={\begin{cases}[y_{\min },\infty )&{\text{ for }}a_{n}>0,\\(-\infty ,y_{\max }]&{\text{ for }}a_{n}<0.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94279d404bb45fcdbdd0b21c607a31c16419daf1)


















![{\displaystyle (-\infty ,s]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5359f53052d0f8481329cddd4d46ccb35457e73)

![{\displaystyle [s,S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa89eaacbc711abc21f726338470978db420e117)




![{\displaystyle 0\in [s,S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72c226681244620ddbb4043ef5c606fe51b8dcdd)

![{\displaystyle y\in f([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17a97446e5940ea18ee0eb5f218cac4f5ce6c28b)
![{\displaystyle x_{1},x_{2}\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b866ca024d3b7214deb13b31212a98e7573b15c)

![{\displaystyle x_{M},{\tilde {x}}_{M}\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee63b71586999e23401a27af1a19af201d899b36)


![{\displaystyle [x_{M},{\tilde {x}}_{M}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d54807bbb89629a6fd8c8e857c810131ab5ed1ed)

![{\displaystyle f|_{[x_{M},{\tilde {x}}_{M}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/572d1aaefe87494aff3e92701e6c40e58ec4687b)






![{\displaystyle {\tilde {x}}_{m}\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49bd4d48269519d9759474006d9b8252e5b75444)

![{\displaystyle {\tilde {x}}_{m}\notin [x_{M},{\tilde {x}}_{M}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d35b8f5b263058fed64bd74d7fbe677229681bd0)



![{\displaystyle [x_{m},{\tilde {x}}_{M}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/966b409858e26dcc84be6b24ef293a662c4a9cfc)
![{\displaystyle [{\tilde {x}}_{M},{\tilde {x}}_{m}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f34fbcfed64f90e9390fea12d6871b97ac13c09)
![{\displaystyle {\tilde {x}}_{m}\in [x_{M},{\tilde {x}}_{M}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1720afc065716ce021ea09c483ab801bb353f33e)

![{\displaystyle [x_{m},{\tilde {x}}_{m}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bcf0d5ef1688536cd7b184f6d78eb0562f1c79c)





![{\displaystyle [x_{M},x_{m}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecaa53169a3f57b79d4c87635b4834620c6f044c)


![{\displaystyle [{\tilde {x}}_{m},{\tilde {x}}_{M}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a1b6df65c8e49b262d0610c3f31cc58a517ea92)






![{\displaystyle f:(0,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/49ab7b661669309684d09744c1f199e3f4c9702b)

