Zwischenwertsatz – Serlo „Mathe für Nicht-Freaks“

Der Zwischenwertsatz besagt, dass jede stetige Funktion $f:[a,b]\to \mathbb {R}$ alle Werte zwischen $f(a)$ und $f(b)$ mindestens einmal annimmt. Stetige Funktionen nehmen also alle Zwischenwerte zwischen $f(a)$ und $f(b)$ an (wenn es zwischen $a$ und $b$ keine Lücken im Definitionsbereich gibt). Der Zwischenwertsatz kann somit genutzt werden, um die Existenz von Funktionswerten zu beweisen.

Motivation

Zwischenwertsatz: Intuition und Praxis

Sei $f:[a,b]\to \mathbb {R}$ eine beliebige stetige Funktion. An der Stelle $a$ besitzt sie den Funktionswert $f(a)$ und an der Stelle $b$ den Funktionswert $f(b)$. Nehmen wir an, dass $f(a)\leq f(b)$ ist. Sei außerdem $s$ ein beliebiger Wert zwischen $f(a)$ und $f(b)$, also $f(a)\leq s\leq f(b)$:

Die Funktionswerte f(a) und f(b) an den Stellen a und b zusammen mit der Geraden beim Zwischenwert s

Nach unserer Vorstellung besitzen stetige Funktionen innerhalb des Definitionsbereichs keine Sprünge. Da $f$ auf dem gesamten Intervall $[a,b]$ definiert ist und somit ihr Definitionsbereich zusammenhängend ist, verbindet der Graph die Punkte $(a,f(a))$ und $(b,f(b))$ ohne Sprünge. Wenn wir $f(a)$ und $f(b)$ ohne Absetzen des Stifts verbinden, müssen wir irgendwann die Gerade $y=s$ kreuzen. Es gibt also mindestens einen Schnittpunkt zwischen der Geraden $y=s$ und dem Graphen von $f$:

Der Graph f schneidet die Gerade y=s in verschiedenen Schnittpunkten. Dort gilt f(x)=s

Für die $x$-Werte ${\tilde {x}}$ der Schnittpunkte gilt $f({\tilde {x}})=s$. Der Zwischenwert $s$ wird also mindestens einmal durch die Funktion $f$ angenommen. Wir haben intuitiv gesehen, dass stetige Funktionen alle Werte zwischen zwei Funktionswerten mindestens einmal annehmen, wenn der Definitionsbereich keine Lücken zwischen den beiden Argumenten besitzt.

Der Zwischenwertsatz

Erklärung der Definition des Zwischenwertsatzes. (YouTube-Video vom Kanal Quatematik)

Satz (Zwischenwertsatz)

Sei $f:[a,b]\to \mathbb {R}$ eine stetige Funktion mit $a,b\in \mathbb {R}$ und $a<b$. Sei $s$ ein Wert zwischen den beiden Funktionswerten $f(a)$ und $f(b)$. Es gilt also $f(a)\leq s\leq f(b)$ oder $f(b)\leq s\leq f(a)$. Dann gibt es mindestens eine reelle Zahl $x\in [a,b]$ mit $f(x)=s$. Der Zwischenwert $s$ wird also mindestens einmal von der Funktion $f$ angenommen.

Nullstellensatz von Bolzano

Für den Beweis des Zwischenwertsatzes reicht es aus, diesen nur für den Spezialfall $s=0$ zu beweisen. Dieser Spezialfall wird auch „Nullstellensatz von Bolzano” genannt:

Satz (Nullstellensatz von Bolzano)

Sei $h:[a,b]\to \mathbb {R}$ eine stetige Funktion mit $a,b\in \mathbb {R}$ und $a<b$. Sei außerdem die Null ein Zwischenwert von $h(a)$ und $h(b)$, also $h(a)\leq 0\leq h(b)$ oder $h(a)\geq 0\geq h(b)$. Dann besitzt $h$ mindestens eine Nullstelle. Es gibt also mindestens ein Argument ${\tilde {x}}\in [a,b]$ mit $h({\tilde {x}})=0$.

Wieso reicht es, nur diesen Spezialfall zu betrachten? Nehmen wir eine stetige Funktion $f:[a,b]\to \mathbb {R}$ und einen Wert $s\in \mathbb {R}$ zwischen den Funktionswerten $f(a)$ und $f(b)$. Nach dem Zwischenwertsatz müssen wir nun ein ${\tilde {x}}\in [a,b]$ mit $f({\tilde {x}})=s$ finden. Nun gilt:

$f({\tilde {x}})=s\iff f({\tilde {x}})-s=0$

Damit ist genau dann $f({\tilde {x}})=s$, wenn $f({\tilde {x}})-s=0$ ist. Wir definieren nun die Hilfsfunktion $h:[a,b]\to \mathbb {R}$ mit $h(x)=f(x)-s$. Wie wir gerade festgestellt haben, ist genau im Fall $f({\tilde {x}})=s$ die Gleichung $h({\tilde {x}})=0$ erfüllt. Wenn wir also eine Nullstelle von $h$ finden, dann nimmt auch die Funktion $f$ den Wert $s$ an.

Nun erfüllt die Funktion $h$ alle Voraussetzungen des Nullstellensatz von Bolzano. Es ist eine Funktion der Form $[a,b]\to \mathbb {R}$ mit dem abgeschlossenen Intervall $[a,b]$ als Definitionsbereich. Als Verkettung stetiger Funktionen ist die Funktion $h$ stetig. Im Fall $f(a)\leq s\leq f(b)$ ist:

${\begin{aligned}f(a)\leq s\iff f(a)-s\leq 0\iff h(a)\leq 0\\[0.3em]f(b)\geq s\iff f(b)-s\geq 0\iff h(b)\geq 0\end{aligned}}$

Damit folgt aus $f(a)\leq s\leq f(b)$ die Ungleichungskette $h(a)\leq 0\leq h(b)$. Betrachten wir nun den Fall $f(a)\geq s\geq f(b)$:

${\begin{aligned}f(a)\geq s\iff f(a)-s\geq 0\iff h(a)\geq 0\\[0.3em]f(b)\leq s\iff f(b)-s\leq 0\iff h(b)\leq 0\end{aligned}}$

Es folgt insgesamt, dass Null ein Zwischenwert von $h(a)$ und $h(b)$ ist. Somit erfüllt $h$ die Voraussetzungen des Nullstellensatz von Bolzano. Nach diesem Nullstellensatz gibt es ein ${\tilde {x}}\in [a,b]$ mit $h({\tilde {x}})=0$. Für dieses ${\tilde {x}}$ ist dann $f({\tilde {x}})=s$. Dies zeigt, dass aus dem Nullstellensatz von Bolzano der allgemeinere Zwischenwertsatz folgt. Wir müssen also nur den Nullstellensatz von Bolzano beweisen.

Beweis des Nullstellensatz von Bolzano

Beweis (Nullstellensatz von Bolzano)

Sei $h:[a,b]\to \mathbb {R}$ eine stetige Funktion mit $h(a)\leq 0\leq h(b)$ oder $h(a)\geq 0\geq h(b)$. Im Folgenden betrachten wir den Fall $h(a)\leq 0\leq h(b)$. Der andere Fall $h(a)\geq 0\geq h(b)$ kann analog bewiesen werden. Wir müssen nun eine Nullstelle von $h$ finden. Dies kann durch eine geeignete Intervallschachtelung gezeigt werden. Als Startintervall wählen wir $[a_{1},b_{1}]=[a,b]$, also $a_{1}=a$ und $b_{1}=b$. Wir wissen nämlich, dass sich im Intervall $[a,b]$ die gesuchte Nullstelle befinden muss.

Für $h(a_{1})=0$ oder $h(b_{1})=0$ haben wir bereits eine Nullstelle bei $x=a_{1}$ bzw. $x=b_{1}$ gefunden und sind fertig. Falls $h(a_{1})<0$ und $h(b_{1})>0$ ist, verkleinern wir unser Intervall. Wir betrachten hierzu den Mittelpunkt ${\tfrac {a_{1}+b_{1}}{2}}$ des Startintervalls. Ist der Wert von $h$ an diesem Punkt gleich Null, so haben wir wieder eine Nullstelle gefunden und sind fertig.

Wenn $h\left({\tfrac {a_{1}+b_{1}}{2}}\right)\neq 0$ ist, so wählen wir nun ein anderes Intervall, in dem sich eine Nullstelle befinden muss. Nehmen wir an, es sei $h\left({\tfrac {a_{1}+b_{1}}{2}}\right)>0$. Dann ergibt sich folgendes Bild:

Illustration für den Fall, dass der Funktionswert in der Mitte positiv ist.

Wir sehen, dass der Graph im ersten Intervall von $a_{1}$ bis ${\tfrac {a_{1}+b_{1}}{2}}$ die $x$-Achse überqueren muss. Da $h$ als stetige Funktion keine Sprünge aufweist und in diesem Intervall keine Definitionslücken aufweist, sollte sich in diesem Intervall also eine Nullstelle von $h$ befinden. Da beide Funktionswerte $h\left({\tfrac {a_{1}+b_{1}}{2}}\right)$ und $h(b_{1})$ positiv sind, können wir nicht sagen, ob sich im Bereich von ${\tfrac {a_{1}+b_{1}}{2}}$ bis $b_{1}$ eine Nullstelle befindet oder nicht. Deswegen wählen wir als zweites Intervall $[a_{2},b_{2}]=\left[a_{1},{\tfrac {a_{1}+b_{1}}{2}}\right]$.

Wenn demgegenüber $h\left({\tfrac {a_{1}+b_{1}}{2}}\right)$ kleiner als Null ist, muss der Graph von $h$ im zweiten Intervall von ${\tfrac {a_{1}+b_{1}}{2}}$ bis $b_{1}$ einen Vorzeichenwechsel vollführen. Dementsprechend sollte sich dort eine Nullstelle befinden und wir wählen in diesem Fall $\left[{\tfrac {a_{1}+b_{1}}{2}},b_{1}\right]$ als zweites Intervall $[a_{2},b_{2}]$:

Illustration für den Fall, dass der Funktionswert in der Mitte negativ ist.

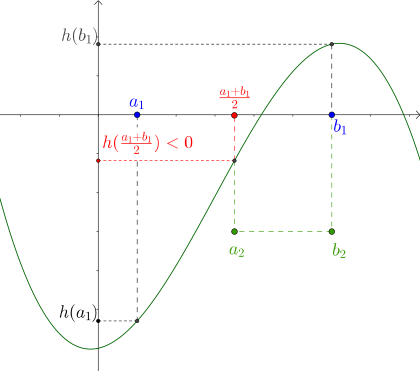
Insgesamt bestimmen wir $[a_{2},b_{2}]$ folgendermaßen:

$[a_{2},b_{2}]={\begin{cases}\left[a_{1},{\frac {a_{1}+b_{1}}{2}}\right]&;h\left({\frac {a_{1}+b_{1}}{2}}\right)>0\\\left[{\frac {a_{1}+b_{1}}{2}},b_{1}\right]&;h\left({\frac {a_{1}+b_{1}}{2}}\right)<0\end{cases}}$

Diesen Vorgang wiederholen wir nun immer wieder: Im $n$-ten Schritt berechnet wir den Mittelpunkt ${\tfrac {a_{n}+b_{n}}{2}}$ des Intervalls $[a_{n},b_{n}]$. Nimmt $h$ hier den Wert $0$ an, sind wir fertig und können ${\tfrac {a_{n}+b_{n}}{2}}$ als Nullstelle zurückgeben. Ansonsten wählen wir analog zu vorher ein neues Intervall $[a_{n+1},b_{n+1}]$ mit folgender Definition

$[a_{n+1},b_{n+1}]={\begin{cases}\left[a_{n},{\frac {a_{n}+b_{n}}{2}}\right]&;h\left({\frac {a_{n}+b_{n}}{2}}\right)>0\\\left[{\frac {a_{n}+b_{n}}{2}},b_{n}\right]&;h\left({\frac {a_{n}+b_{n}}{2}}\right)<0\end{cases}}$

Durch dieses Vorgehen erhalten wir entweder nach irgendeinem Schritt $n$ eine gesuchte Nullstelle, oder wir bekommen eine Folge von Intervallen $([a_{n},b_{n}])_{n\in \mathbb {N} }$. So wie wir die Folgenglieder gewählt haben, ist die Folge $(a_{n})_{n\in \mathbb {N} }$ monoton wachsend, und die Folge $(b_{n})_{n\in \mathbb {N} }$ monoton fallend. Da jedes Folgenglied im Intervall $[a,b]$ liegt, sind die Folgen auch beschränkt. Daraus können wir nach dem Monotoniekriterium für Folgen folgern, dass beide Folgen konvergieren. Beachte, dass die Länge des Intervalls bei jedem Schritt halbiert wird. Das heißt:

${\begin{aligned}\lim _{n\rightarrow \infty }{(b_{n}-a_{n})}&=\lim _{n\rightarrow \infty }{{\frac {1}{2}}\cdot (b_{n-1}-a_{n-1})}\\[0.3em]&=\lim _{n\rightarrow \infty }{{\frac {1}{2}}\cdot {\frac {1}{2}}\cdot (b_{n-2}-a_{n-2})}\\[0.3em]&\vdots \\[0.3em]&=\lim _{n\rightarrow \infty }{{\frac {1}{2^{n}}}\cdot (b_{1}-a_{1})}=0\end{aligned}}$

Und damit folgt: $\lim _{n\rightarrow \infty }{a_{n}}=\lim _{n\rightarrow \infty }{b_{n}}$. Damit konvergieren die Folgen der unteren bzw. oberen Intervallgrenzen gegen den gleichen Wert $c\in [a;b]$. Außerdem gilt mit unserer Wahl, dass $h(a_{n})<0$ sowie $h(b_{n})>0$ für alle $n\in \mathbb {N}$ gilt. Deswegen gilt für die Grenzwerte: $\lim _{n\rightarrow \infty }{h(a_{n})}\leq 0$ und $\lim _{n\rightarrow \infty }{h(b_{n})}\geq 0$. Weil $h$ stetig ist, gilt

$\lim _{n\rightarrow \infty }{h(a_{n})}=h\left(\lim _{n\rightarrow \infty }{a_{n}}\right)=h(c)=h\left(\lim _{n\rightarrow \infty }{b_{n}}\right)=\lim _{n\rightarrow \infty }{h(b_{n})}$

Mit der oberen Zeile folgt also $h(c)\leq 0$ und $h(c)\geq 0$, damit muss $h(c)=0$ gelten und wir haben auch in diesem Fall eine Nullstelle der Funktion $h$ gefunden.

Folgerungungen aus dem Zwischenwertsatz

Stetige Funktionen bilden Intervalle auf Intervalle ab

Mit Hilfe des Zwischenwertsatzes können wir beweisen, dass stetige Funktionen Intervalle auf Intervalle abbilden:

Satz (Folgerung aus Zwischenwertsatz)

Sei $I\subseteq \mathbb {R}$ ein Intervall und $f:I\to \mathbb {R}$ stetig. Dann ist auch $f(I)$ ein Intervall.

Beweis (Folgerung aus Zwischenwertsatz)

Wir setzen $A=\inf f(I)$ und $B=\sup f(I)$. Dabei erlauben wir $A=-\infty$ (wenn $f(I)$ nach unten unbeschränkt ist) und $B=\infty$ (wenn $f(I)$ nach oben unbeschränkt ist). Nehmen wir nun eine reelle Zahl $y$ mit $A<y<B$. Aus der Definition vom Infimum folgt aus $A<y$, dass es ein $a\in I$ mit $f(a)<y$ gibt. Analog gibt es ein $b\in I$ mit $y<f(b)$. Ingesamt ist damit $f(a)<y<f(b)$.

$y$ ist damit ein Zwischenwert zweier Funktionswerte von $f$. Da $f$ stetig ist, gibt es nach dem Zwischenwertsatz ein $x\in I$ mit $f(x)=y$. Da $y\in (A,B)$ beliebig war, folgt $(A,B)\subseteq f(I)$. Nun können noch $A$ oder $B$ Elemente von $f(I)$ sein. Damit muss $f(I)$ eines der folgenden vier Intervalle sein:

${\begin{aligned}f(I)={\begin{cases}[A,B]&A{\text{ und }}B{\text{ werden von }}f{\text{ angenommen}}\\[0.5em][A,B)&A{\text{ wird von }}f{\text{ angenommen, }}B{\text{ nicht}}\\[0.5em](A,B]&B{\text{ wird von }}f{\text{ angenommen, }}A{\text{ nicht}}\\[0.5em](A,B)&A{\text{ und }}B{\text{ werden von }}f{\text{ nicht angenommen}}\end{cases}}\end{aligned}}$

Wir sehen, dass $f(I)$ ein Intervall ist.

Wertebereich von Potenzfunktionen

Beispiel (Wertebereich der Potenzfunktionen $x\mapsto x^{k}$)

Die Potenzfunktionen $f:\mathbb {R} \to \mathbb {R}$ mit $f(x)=x^{k}$ für $k\in \mathbb {N}$ sind stetig. Weiter gilt

$\lim _{x\to \infty }f(x)=\lim _{x\to \infty }x^{k}=\infty$

Damit ist $\sup f(\mathbb {R} )=\infty$. Außerdem ist

$\lim _{x\to -\infty }f(x)=\lim _{x\to -\infty }x^{k}={\begin{cases}\infty &{\text{ für gerade }}k\\-\infty &{\text{ für ungerade }}k\end{cases}}$

Bei ungeraden $k$ ist $\inf f(\mathbb {R} )=-\infty$. Für gerade $k$ ist $\inf f(\mathbb {R} )=0$, denn für alle $x\in \mathbb {R}$ ist $f(x)=x^{k}\geq 0$ und die Null wird wegen $f(0)=0^{k}=0$ angenommen. Nach dem Zwischenwertsatz ist damit

$f(\mathbb {R} )={\begin{cases}\mathbb {R} _{0}^{+}=[0,\infty )&{\text{ für gerade }}k\\\mathbb {R} =(-\infty ,\infty )&{\text{ für ungerade }}k\end{cases}}$

Wertebereich der Exponentialfunktion

Beispiel (Wertebereich der Exponentialfunktion)

Die Exponentialfunktion $\exp :\mathbb {R} \to \mathbb {R}$ ist stetig. Außerdem gilt $\exp(x)>0$ für alle $x\in \mathbb {R}$. Es ist $\lim _{x\to -\infty }\exp(x)=0$ und $\lim _{x\to \infty }\exp(x)=\infty$. Es ist damit $\inf \exp(\mathbb {R} )=0$ und $\sup \exp(\mathbb {R} )=\infty$. Da weder $0$ noch $\infty$ durch die Exponentialfunktion angenommen werden, folgt aus dem Zwischenwertsatz

$\exp(\mathbb {R} )=\mathbb {R} ^{+}=(0,\infty )$

Aufgabe (Wertebereich der verallgemeinerten Exponentialfunktion)

Für $a\in \mathbb {R} \setminus \{1\}$ definiert

$\exp _{a}:\mathbb {R} \to \mathbb {R} ,\ \exp _{a}(x)=a^{x}=\exp(x\ln(a))$

die verallgemeinerte Exponentialfunktion. Zeige: $\exp _{a}(\mathbb {R} )=\mathbb {R} ^{+}$.

Hinweis: Unterscheide die Fälle $a>1$ und $0<a<1$.

Lösung (Wertebereich der verallgemeinerten Exponentialfunktion)

Da $\exp$ und $x\mapsto x\cdot \ln(a)$ stetig auf $\mathbb {R}$ stetig sind, ist auch $\exp _{a}$ als Komposition dieser Funktionen stetig auf $\mathbb {R}$. Weiter ist $\exp _{a}(x)>0$, da $\exp(x)>0$ ist.

Fall 1: $a>1$

Hier gilt $\ln a>0$, und damit ist $\lim _{x\to \infty }x\ln a=\infty$. Daraus folgt $\lim _{x\to \infty }\exp _{a}(x)=\lim _{x\to \infty }\exp(x\ln a)=\infty$. Andererseits ist $\lim _{x\to -\infty }x\ln a=-\infty$, und somit $\lim _{x\to -\infty }\exp _{a}(x)=\lim _{x\to -\infty }\exp(x\ln a)=0$. Insgesamt ergibt sich in diesem Fall $\exp _{a}(\mathbb {R} )=(0,\infty )=\mathbb {R} ^{+}$.

Fall 2: $0<a<1$

Hier ist $\ln a<0$, und daher $\lim _{x\to \infty }x\ln a=-\infty$. Also folgt $\lim _{x\to \infty }\exp _{a}(x)=\lim _{x\to \infty }\exp(x\ln a)=0$. Andererseits gilt $\lim _{x\to -\infty }x\ln a=\infty$, und somit $\lim _{x\to -\infty }\exp _{a}(x)=\lim _{x\to -\infty }\exp(x\ln a)=\infty$. Also gilt auch sich diesem Fall $\exp _{a}(\mathbb {R} )=(0,\infty )=\mathbb {R} ^{+}$.

Übungsaufgabe: Fixpunktsatz

Beweis eines Fixpunktsatzes

In der folgenden Aufgabe beweisen wir einen Fixpunktsatz. Fixpunkte sind Argumente $x$ einer Funktion $f$, die die Gleichung $f(x)=x$ erfüllt. Fixpunkte werden also durch eine Funktion nicht verändert. Fixpunktsätze sind wiederum Sätze, die die Existenz von Fixpunkten in gewissen Situationen beweisen. Für die Mathematik sind solche Sätze wichtig, weil manchmal die Existenz eines Objekts auf die Existenz eines Fixpunktes zurückgeführt werden kann. Beispielsweise ist das Argument $x$ genau dann Nullstelle einer Funktion $f:\mathbb {R} \to \mathbb {R}$, wenn die Funktion $g:\mathbb {R} \to \mathbb {R}$ mit der Zuordnungsvorschrift $g(x)=x-f(x)$ einen Fixpunkt besitzt. Aus der Existenz eines Fixpunkts der Funktion $g$, folgt die Existenz einer Nullstelle für $f$. In der folgenden Aufgabe werden wir einen Zwischenwertsatz beweisen:

Aufgabe (Fixpunktsatz)

Sei $f:[a,b]\to [a,b]$ eine stetige Funktion. Beweise, dass $f$ mindestens einen Fixpunkt besitzt. Fixpunkte sind Stellen $x\in [a,b]$ mit $f(x)=x$.

Wie kommt man auf den Beweis? (Fixpunktsatz)

Durch Umstellung der Gleichung $f(x)=x$ erhalten wir $f(x)-x=0$. Damit ist $x$ genau dann ein Fixpunkt von $f$, wenn $x$ eine Nullstelle der Funktion $h(x)=f(x)-x$ ist. Definieren also die Hilfsfunktion $h:[a,b]\to \mathbb {R}$ mit $h(x)=f(x)-x$. Wie sich herausstellt, können wir den Nullstellensatz von Bolzano einsetzen, um die Existenz einer Nullstelle zu beweisen. Hierfür müssen wir die Voraussetzungen dieses Satzes beweisen:

• $h$ ist stetig.
• Null ist ein Zwischenwert von $h(a)$ und $h(b)$.

$h$ ist stetig als Verknüpfung stetiger Funktionen und wir können außerdem beweisen, dass $h(b)\leq 0\leq h(a)$ ist. Der Nullstellensatz liefert damit die Existenz des Grenzwerts.

Beweis (Fixpunktsatz)

Sei $f:[a,b]\to [a,b]$ eine stetige Funktion. Wir definieren die Hilfsfunktion $h:[a,b]\to \mathbb {R} :x\mapsto h(x)=f(x)-x$. Für diese gilt:

• $h$ ist stetig auf $[a,b]$ als Differenz der stetigen Funktionen $f$ und ${\text{id}}:[a,b]\to [a,b]:x\mapsto x$.
• Es ist $h(b)\leq 0\leq h(a)$, weil:
  • $h(a)=\underbrace {f(a)} _{\in [a,b]}-a\geq 0$
  • $h(b)=\underbrace {f(b)} _{\in [a,b]}-b\leq 0$.

Damit erfüllt $h$ die Voraussetzungen des Nullstellensatzes. Es gibt daher ein ${\tilde {x}}\in [a,b]$ mit $h({\tilde {x}})=f({\tilde {x}})-{\tilde {x}}=0$. Es folgt $f({\tilde {x}})={\tilde {x}}$. Also besitzt $f$ einen Fixpunkt.

Voraussetzungen zum Fixpunktsatz

Im obigen Fixpunktsatz ist die Stetigkeit eine notwendige Voraussetzung des bewiesenen Fixpunktsatzes. Wenn wir diese weglassen, finden wir eine Funktion $g:[a,b]\to [a,b]$, für die der Fixpunktsatz nicht mehr gilt. Dies zeigt folgende Aufgabe:

Aufgabe (Fixpunktsatz)

Gib eine Funktion $g:[0,1]\to [0,1]$ mit $g(x)\neq x$ für alle $x\in [0,1]$ an.

Beweis (Fixpunktsatz)

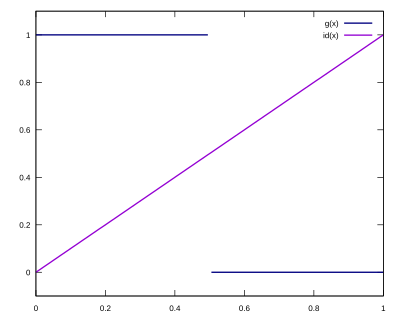
Zum Beispiel besitzt die Funktion

$g:[0,1]\to [0,1]:x\mapsto g(x)={\begin{cases}1&{\text{ für }}0\leq x\leq {\tfrac {1}{2}},\\0&{\text{ für }}{\tfrac {1}{2}}<x\leq 1\end{cases}}$

keinen Fixpunkt. Dies zeigt der folgende Graph der Funktion $g$. Es gibt nämlich keinen Schnittpunkt des Graphen von $g$ mit dem Graphen der Identitätsfunktion ${\text{id}}:[0,1]\to [0,1],\ x\mapsto x$:

Graphen der Funktion g und der Identitätsfunktion f

Übungsaufgabe: Nullstellen und Wertebereich von Polynomen

Nullstellen von Polynomen

Die folgende Aufgabe stellt einen Spezialfall des Fundamentalsatzes der Algebra dar. Dieser besagt, dass eine nicht-konstante Polynomfunktion

$p(z)=a_{n}z^{n}+a_{n-1}z^{n-1}+\ldots +a_{1}z+a_{0}$

mit komplexen Koeffizienten $a_{0},a_{1},\ldots ,a_{n-1},a_{n}$ mindestens eine komplexe Nullstelle hat. Im Reellen stimmt diese Aussage im Allgemeinen nicht. Ein Polynom mit reellen Koeffizienten muss keine reelle Nullstelle haben. Eine Polynomfunktion ohne reelle Nullstellen ist zum Beispiel $p(x)=x^{2}+1$. Für gewisse Polynome können wir jedoch die Existenz einer Nullstelle beweisen:

Aufgabe (Nullstellen von Polynomen)

Sei

$p:\mathbb {R} \to \mathbb {R} ,\ p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\ldots +a_{1}x+a_{0}$

eine Polynomfunktion mit $a_{0},a_{1},\ldots ,a_{n-1},a_{n}\in \mathbb {R}$ und $a_{n}\neq 0$. Wenn $n$, also der Grad von $p$, ungerade ist, besitzt $p$ mindestens eine Nullstelle.

Zusammenfassung des Beweises (Nullstellen von Polynomen)

Wir werden die Aufgabe mit Hilfe des Nullstellensatzes beweisen. Hierzu müssen wir zwei reelle Zahlen $x_{1},x_{2}\in \mathbb {R}$ mit $p(x_{1})\leq 0\leq p(x_{2})$ oder $p(x_{1})\geq 0\geq p(x_{2})$ finden. Dies folgt nun aus $\lim _{x\to \infty }p(x)=\infty$ und $\lim _{x\to -\infty }p(x)=-\infty$, was wir mit einem einfachen Umformungstrick $p$ für den Fall $a_{n}>0$ zeigen können. Wir werden nur den Fall $a_{n}>0$ ausführlich behandeln. Der Fall $a_{n}<0$ kann analog geführt werden.

Lösung (Nullstellen von Polynomen)

Wir führen den Beweis für $a_{n}>0$. Im Fall $a_{n}<0$ kann analog der Satz bewiesen werden. Für $x\neq 0$ erhalten wir durch Ausklammern von $x^{n}$:

$p(x)=x^{n}(a_{n}+a_{n-1}x^{-1}+\ldots +a_{1}x^{-n+1}+a_{0}x^{-n})$

Der Ausdruck $a_{n}+a_{n-1}x^{-1}+\ldots +a_{1}x^{-n+1}+a_{0}x^{-n}$ in den Klammern konvergiert für $x\to \pm \infty$ gegen $a_{n}$. Dies gilt, da die Terme $x^{-1},\ldots ,x^{-n}$ für $x\to \pm \infty$ gegen $0$ konvergieren. Da $n$ ungerade ist, folgt:

$\lim _{x\to \infty }p(x)=\lim _{x\to \infty }\underbrace {x^{n}} _{\to \infty }(\underbrace {a_{n}+a_{n-1}x^{-1}+\ldots +a_{1}x^{-n+1}+a_{0}x^{-n}} _{\to a_{n}>0})=\infty$

und

$\lim _{x\to -\infty }p(x)=\lim _{x\to -\infty }\underbrace {x^{n}} _{\to -\infty }(\underbrace {a_{n}+a_{n-1}x^{-1}+\ldots +a_{1}x^{-n+1}+a_{0}x^{-n}} _{\to a_{n}>0})=-\infty$

Damit muss es aber $x_{1},x_{2}\in \mathbb {R}$ mit $p(x_{1})\leq 0\leq p(x_{2})$ geben. Weiter ist $p$ als Polynomfunktion stetig als Komposition der stetigen Funktionen $x\mapsto x^{k}$ für $k=0,\ldots n$. Aus dem Nullstellensatz von Bolzano folgt, dass es ein $x_{0}\in \mathbb {R}$ mit $p(x_{0})=0$ gibt. Die Polynomfunktion hat also mindestens eine Nullstelle.

Wertebereich von Polynomen

Aufgabe (Wertebereich von Polynomen)

Sei

$p:\mathbb {R} \to \mathbb {R} ,\ p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\ldots +a_{1}x+a_{0}$

eine Polynomfunktion mit $a_{0},a_{1},\ldots ,a_{n-1},a_{n}\in \mathbb {R}$ und $a_{n}\neq 0$, und $n$ ungerade. Zeige, dass $p(\mathbb {R} )=\mathbb {R}$.

Lösung (Wertebereich von Polynomen)

Fall 1: $a_{n}>0$

Für $x\neq 0$ ist:

$\lim _{x\to \infty }p(x)=\lim _{x\to \infty }\underbrace {x^{n}} _{\to \infty }(\underbrace {a_{n}+a_{n-1}x^{-1}+\ldots +a_{1}x^{-n+1}+a_{0}x^{-n}} _{\to a_{n}>0})=\infty$

und

$\lim _{x\to -\infty }p(x)=\lim _{x\to -\infty }\underbrace {x^{n}} _{\to -\infty }(\underbrace {a_{n}+a_{n-1}x^{-1}+\ldots +a_{1}x^{-n+1}+a_{0}x^{-n}} _{\to a_{n}>0})=-\infty$

Da $p$ stetig ist, folgt $p(\mathbb {R} )=\mathbb {R}$.

Fall 2: $a_{n}<0$

Analog zum ersten Fall.

Übungsaufgabe: Existenz von Wurzeln

Der Zwischenwertsatz bietet eine weitere Möglichkeit die Existenz von Wurzeln zu beweisen. Im Kapitel „Wurzel reeller Zahlen“ haben wir dies bereits mit Hilfe einer Intervallschachtellung bewiesen. Wir werden nun einen alternativen Beweis mit Hilfe des Zwischenwertsatzes kennen lernen. Zur Erinnerung: Die $n$-te Wurzel ${\sqrt[{n}]{\alpha }}$ für eine positive Zahl $\alpha$ ist eine positive reelle Zahl $x$ mit $x^{n}=\alpha$.

Aufgabe (Existenz der Wurzel)

Sei $n\in \mathbb {N}$. Zeige, dass es für alle $\alpha >0$ eine positive reelle Zahl $x$ mit $x^{n}=\alpha$ gibt.

Lösung (Existenz der Wurzel)

Es ist genau dann $x^{n}=\alpha$, wenn $x^{n}-\alpha =0$ ist. Die gesuchte Zahl $x$ muss also eine positive Nullstelle des Polynoms $p:\mathbb {R} \to \mathbb {R}$ mit $p(x)=x^{n}-\alpha$ sein. Zunächst ist $p$ als Polynom auf ganz $\mathbb {R}$ stetig. Damit ist $p$ auch auf den Intervall $[0,\alpha +1]$ stetig. Weiter gilt

$p(0)=0^{n}-\alpha =-\alpha <0$

sowie

${\begin{aligned}p(1+\alpha )&=(1+\alpha )^{n}-\alpha \\[0.3em]&\quad {\color {Gray}\left\downarrow \ {\text{Bernoulli-Ungleichung}}\right.}\\[0.3em]&\geq 1+n\alpha -\alpha \\&=1+\underbrace {(n-1)} _{\geq 0}\alpha \\&\geq 1\end{aligned}}$

Damit ist $p(0)<0<p(1+\alpha )$. Nach dem Zwischenwertsatz besitzt $p$ im Intervall $(0,1+\alpha )$ mindestens eine Nullstelle. Weil alle Zahlen aus $(0,1+\alpha )$ positiv sind, ist auch die Nullstelle positiv. Außerdem erfüllt sie die Gleichung $x^{n}=\alpha$.

Übungsaufgabe: Lösung einer Gleichung

Der Zwischenwert- beziehungsweise Nullstellensatz kann verwendet werden, die Existenz einer Lösung für eine Gleichung zu begründen. Hier wird aus der Gleichung eine stetige Funktion gebildet, auf die der Zwischenwert- beziehungsweise der Nullstellensatz angewandt werden kann.

Aufgabe (Lösung einer Gleichung)

Zeige, dass es genau ein $x\in \mathbb {R}$ mit $\cos x=x$ gibt.

Lösung (Lösung einer Gleichung)

Funktionen $f(x)=\cos x$ und $g(x)=x$

Beweisschritt: Die Gleichung besitzt eine Lösung

Wir bilden die Hilfsfunktion

$h:\mathbb {R} \to \mathbb {R} ,\ h(x)=x-\cos x$

Diese ist stetig, als Differenz der stetigen Funktionen $x\mapsto x$ und $x\mapsto \cos x$. Weiter gilt

$h(0)=0-\cos 0=-1<0$

sowie

$h({\tfrac {\pi }{2}})={\tfrac {\pi }{2}}-\cos({\tfrac {\pi }{2}})={\tfrac {\pi }{2}}>0$

Nach dem Nullstellensatz gibt es also ein ${\tilde {x}}\in \mathbb {R}$ mit $h({\tilde {x}})={\tilde {x}}-\cos {\tilde {x}}=0$. Für dieses ${\tilde {x}}$ gilt dann $\cos {\tilde {x}}={\tilde {x}}$. Es löst also unsere Gleichung.

Beweisschritt: Es gibt genau eine Lösung der Gleichung

Wir unterscheiden vier Fälle

Fall 1: $x\leq -{\tfrac {\pi }{2}}$

Es ist $x\leq -{\tfrac {\pi }{2}}<-1\leq \cos(x)$. Damit gibt es kein $x$ mit $\cos x=x$ geben.

Fall 2: $-{\tfrac {\pi }{2}}<x\leq 0$

Es ist $x\leq 0<\cos x$. Also kann es kein $x$ mit $\cos x=x$ geben.

Fall 3: $0<x<{\tfrac {\pi }{2}}$

Oben haben wir bereits gezeigt, dass es ein $x$ mit $\cos x=x$ gibt. Nun ist $x\mapsto x$ streng monoton steigend $x\mapsto \cos x$ für $0<x<{\tfrac {\pi }{2}}$ streng monoton fallend. Also kann es kein weiteres $x$ mit $\cos x=x$ geben.

Fall 4: ${\tfrac {\pi }{2}}\leq x$

Es ist $\cos x\leq 1<{\tfrac {\pi }{2}}\leq x$. Also kann es kein $x$ mit $\cos x=x$ geben.

Aus beiden Beweisschritten folgt, dass es genau ein $x\in \mathbb {R}$ mit $\cos x=x$ gibt.