Unstetigkeit beweisen: Epsilon-Delta-Kriterium und Folgenkriterium – „Mathe für Nicht-Freaks“

Überblick

Um die Unstetigkeit einer Funktion zu beweisen, muss man zeigen, dass diese mindestens eine Unstetigkeitsstelle besitzt. Für den Nachweis einer Unstetigkeitsstelle kann man eine von mehreren Methoden verwenden:

Folgenkriterium: Man kann nachweisen, dass die Funktion an der betrachteten Stelle das Folgenkriterium nicht erfüllt.
Betrachtung des links- und rechtsseitigen Grenzwert: Man kann den linksseitigen und rechtsseitigen Grenzwert der Funktion an der betrachteten Stelle ausrechnen. Wenn entweder einer dieser beiden Grenzwerte nicht existiert oder wenn diese Grenzwerte unterschiedlich sind, dann ist die Funktion an der betrachteten Stelle unstetig.
Epsilon-Delta-Kriterium: Man kann nachweisen, dass die Funktion an der betrachteten Stelle das Epsilon-Delta-Kriterium nicht erfüllt.

Folgenkriterium

→ Hauptartikel: Folgenkriterium der Stetigkeit: Folgenstetigkeit

Wiederholung: Folgenkriterium

Definition (Folgenkriterium der Stetigkeit an einer Stelle)

Eine Funktion $f : D \to ℝ$ mit $D \subseteq ℝ$ ist stetig an der Stelle $x_{0} \in D$ , wenn für alle Folgen $(x_{n})_{n \in ℕ}$ mit $\forall n \in ℕ : x_{n} \in D$ und $lim_{n \to \infty} x_{n} = x_{0}$ gilt:

lim_{n \to \infty} f (x_{n}) = f (lim_{n \to \infty} x_{n}) = f (x_{0})

Beweisskizze

Unstetigkeit mit Hilfe des Folgenkriteriums zeigen (Beweisschema)

Um mit dem Folgenkriterium zu zeigen, dass eine Funktion $f : D \to ℝ$ an der Stelle $x_{0} \in D$ unstetig ist, muss man eine Argumentenfolge $(x_{n})_{n \in ℕ}$ mit $x_{n} \in D$ für alle $n \in ℕ$ und dem Grenzwert $x_{0}$ finden, so dass die Funktionswertfolge ${(f (x_{n}))}_{n \in ℕ}$ nicht gegen $f (x_{0})$ konvergiert. Es soll also $lim_{n \to \infty} x_{n} = x_{0}$ und $lim_{n \to \infty} f (x_{n}) \neq f (x_{0})$ gelten. Für $lim_{n \to \infty} f (x_{n}) \neq f (x_{0})$ gibt es zwei Möglichkeiten:

Die Funktionswertfolge ${(f (x_{n}))}_{n \in ℕ}$ divergiert.
Die Funktionswertfolge ${(f (x_{n}))}_{n \in ℕ}$ konvergiert, jedoch ist ihr Grenzwert ungleich $f (x_{0})$ .

Ein Unstetigkeitsbeweis über das Folgenkriterium könnte zum Beispiel folgende Form aufweisen:

Sei $f : \dots$ eine Funktion mit $f (x) = \dots$ . Diese Funktion ist unstetig an der Stelle $x_{0} = \dots$ . Wählen wir nämlich die Folge $(x_{n})_{n \in ℕ}$ mit $x_{n} = \dots$ , so liegen alle Folgenglieder im Definitionsbereich von $f$ , und wir haben

lim_{n \to \infty} x_{n} = \dots = x_{0}

Jedoch ist $lim_{n \to \infty} f (x_{n}) \neq f (x_{0})$ . Es ist nämlich ...Beweis, dass ${(f (x_{n}))}_{n \in ℕ}$ divergiert oder dass der Grenzwert von ${(f (x_{n}))}_{n \in ℕ}$ ungleich $f (x_{0})$ ist...

Beispielaufgabe

Beweis der Unstetigkeit der topologischen Sinusfunktion mit Hilfe des Folgenkriteriums

Aufgabe (Unstetigkeit der topologischen Sinusfunktion)

Beweise die Unstetigkeit der folgenden Funktion:

f : ℝ \to ℝ : x \mapsto {\begin{matrix} \sin (\frac{1}{x}) & x \neq 0 \\ 0 & x = 0 \end{matrix}

Wie kommt man auf den Beweis? (Unstetigkeit der topologischen Sinusfunktion)

Damit $f$ eine unstetige Funktion ist, muss sie mindestens eine Unstetigkeitkeitsstelle besitzen. Für jedes $x \neq 0$ entspricht $f$ in einer hinreichend kleinen Umgebung von $x$ der Funktion $\sin (\frac{1}{x})$ . Da die Funktion $\sin (\frac{1}{x})$ als Komposition stetiger Funktionen stetig ist, muss auch $f$ für alle $x \neq 0$ stetig sein. Damit muss die Unstetigkeitsstelle bei $x = 0$ liegen.

Um mit dem Folgenkriterium zu zeigen, dass $f$ an der Stelle $x = 0$ unstetig ist, müssen wir eine Argumentenfolge $(x_{n})_{n \in ℕ}$ mit $lim_{n \to \infty} x_{n} = 0$ und $lim_{n \to \infty} f (x_{n}) \neq f (0)$ finden. Um diese Argumentenfolge zu finden, schauen wir uns zunächst den Graphen der Funktion $f$ an:

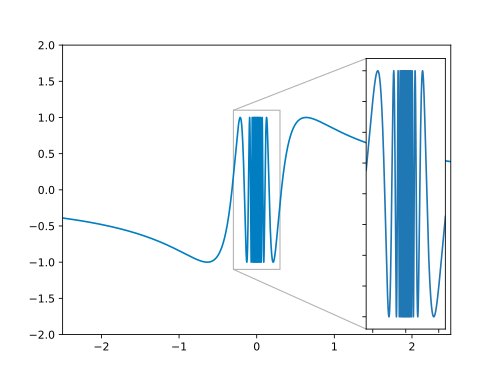
In der Graphik sehen wir, dass die Funktion $f$ in jeder Umgebung des Nullpunkts jeden Wert zwischen $- 1$ und $1$ beliebig oft annimmt. Also können wir $(x_{n})_{n \in ℕ}$ so wählen, dass $f (x_{n})$ immer gleich $1$ ist. Dann ist nämlich garantiert, dass $lim_{n \to \infty} f (x_{n}) = 1 \neq 0 = f (0)$ ist. Dabei wählen wir $x_{n}$ so, dass $x_{n}$ von oben gegen Null konvergiert.

In der folgenden Graphik sind neben dem Graphen von $f$ auch die Funktionswerte der Folge $x_{n}$ eingetragen. Man sieht, dass für $x_{n} \to 0$ die Funktionswerte gegen $1$ konvergieren, was ungleich dem Funktionswert $f (0) = 0$ ist:

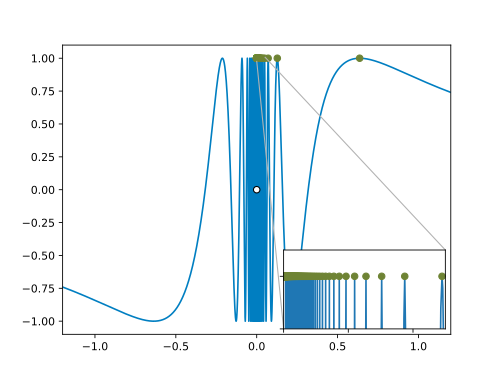
Wie lauten die Werte für $x_{n}$ ? Formen wir hierzu die Gleichung $f (x) = 1$ nach $x$ um:

\begin{matrix} \begin{matrix} f (x) & = 1 \\ \overset{f (0) \neq 0}{⟺} & \sin (\frac{1}{x}) & = 1 \\ ⟺ & \exists k \in ℤ : & \frac{1}{x} & = \frac{π}{2} + 2 k π \\ ⟺ & \exists k \in ℤ : & x & = \frac{1}{\frac{π}{2} + 2 k π} \end{matrix} \end{matrix}

Für alle $x = \frac{1}{\frac{π}{2} + 2 k π}$ mit $k \in ℤ$ gilt also $f (x) = 1$ . Damit unsere Argumente $x_{n}$ positiv sind und von oben gegen Null konvergieren, wählen wir $x_{n} = \frac{1}{\frac{π}{2} + 2 n π}$ . Es gilt dann:

lim_{n \to \infty} x_{n} = lim_{n \to \infty} \frac{1}{\frac{π}{2} + 2 n π} = 0

Jedoch haben wir gesehen, dass $lim_{n \to \infty} f (x_{n}) = 1 \neq 0 = f (0)$ ist. Wir haben also eine Argumentenfolge $(x_{n})_{n \in ℕ}$ gefunden, welche die Unstetigkeit von $f$ an der Stelle $x = 0$ beweist.

Beweis (Unstetigkeit der topologischen Sinusfunktion)

Sei $f : ℝ \to ℝ$ mit $f (x) = \sin (\frac{1}{x})$ für $x \neq 0$ und $f (0) = 0$ . Wir betrachten die Folge $(x_{n})_{n \in ℕ}$ mit $x_{n} = \frac{1}{\frac{π}{2} + 2 n π}$ . Für diese Folge ist:

lim_{n \to \infty} x_{n} = lim_{n \to \infty} \frac{1}{\frac{π}{2} + 2 n π} = 0

Außerdem gilt:

\begin{matrix} lim_{n \to \infty} f (x_{n}) & = lim_{n \to \infty} f (\frac{1}{\frac{π}{2} + 2 n π}) \\ = lim_{n \to \infty} \sin (\frac{1}{\frac{1}{\frac{π}{2} + 2 n π}}) \\ = lim_{n \to \infty} \sin (\frac{π}{2} + 2 n π) \\ = lim_{n \to \infty} 1 = 1 \end{matrix}

Damit ist $lim_{n \to \infty} f (x_{n}) = 1 \neq 0 = f (0)$ , obwohl $lim_{n \to \infty} x_{n} = 0$ ist. Dies beweist, dass $f$ an der Stelle $x = 0$ und somit auch insgesamt unstetig ist.

Baustelle: Betrachtung des links- und rechtsseitigen Grenzwerts

To-Do:

In diesem Abschnitt sollte man an einem Beispiel einer Funktion mit Fallunterscheidung zeigen, wie man durch die Betrachtung des links- und rechtsseitigen Grenzwerts die Unstetigkeit einer Funktion beweisen. Jedoch sollte zunächst im Kapitel Mathe für Nicht-Freaks: Grenzwert von Funktionen der links- und rechtsseitige Grenzwert eingeführt werden. Auch muss dort bewiesen werden, dass eine Funktion an einem Punkt genau dann stetig ist, wenn der links- und rechtsseitige Grenzwert existiert und dem Funktionswert an einer Stelle entspricht.

Epsilon-Delta-Kriterium

→ Hauptartikel: Epsilon-Delta-Kriterium der Stetigkeit

Wiederholung: Epsilon-Delta-Kriterium

Definition (Epsilon-Delta-Definition der Unstetigkeit)

Eine Funktion $f : D \to ℝ$ mit $D \subseteq ℝ$ ist genau dann unstetig an der Stelle $x_{0} \in D$ , wenn es ein $ϵ > 0$ gibt, so dass es für alle $δ > 0$ ein $x \in D$ mit $| x - x_{0} | < δ$ und $| f (x) - f (x_{0}) | \geq ϵ$ gibt. $f$ ist also genau dann in $x_{0} \in D$ unstetig, wenn gilt

\exists ϵ > 0 \forall δ > 0 \exists x \in D : | x - x_{0} | < δ \land | f (x) - f (x_{0}) | \geq ϵ

Allgemeine Beweisstruktur

Epsilon-Delta-Kriterium der Unstetigkeit kann folgendermaßen in Prädikatenlogik formuliert werden:

\exists ϵ > 0 \forall δ > 0 \exists x \in D : | x - x_{0} | < δ \land | f (x) - f (x_{0}) | \geq ϵ

Daraus ergibt sich ein Schema, mit dem die Unstetigkeit einer Funktion nach dem Epsilon-Delta-Kriterium bewiesen werden kann:

\begin{matrix} \underset{\exists ϵ > 0}{\underset{⏟}{Wähle ϵ = \dots}} \underset{\forall δ > 0}{\underset{⏟}{Sei δ > 0 beliebig.}} \\ \underset{\exists x \in D}{\underset{⏟}{Wähle x = \dots Es ist x \in D, weil \dots}} \\ Es ist: \\ Beweis für | x - x_{0} | < δ \\ Beweis für | f (x) - f (x_{0}) | \geq ϵ \end{matrix}

Beispielaufgabe

Aufgabe (Unstetigkeit der topologischen Sinusfunktion)

Beweise die Unstetigkeit der folgenden Funktion an der Stelle $x_{0} = 0$ :

f : ℝ \to ℝ : x \mapsto {\begin{matrix} \sin (\frac{1}{x}) & x \neq 0 \\ 0 & x = 0 \end{matrix}

Wie kommt man auf den Beweis? (Unstetigkeit der topologischen Sinusfunktion)

Bei dieser Aufgabe soll die Unstetigkeit einer Funktion gezeigt werden. Wir betrachten hierzu die Negation des Epsilon-Delta-Kriteriums. Unser Ziel ist es sowohl ein $ϵ > 0$ , als auch ein $x \in ℝ$ so zu wählen, dass $| x - x_{0} | < δ$ und $| f (x) - f (x_{0}) | \geq ϵ$ ist. Dabei darf $x$ in Abhänigigkeit von $δ$ gewählt werden, während $ϵ$ unabhängig für alle $δ > 0$ sein muss. Für eine Lösung können wir folgendermaßen vorgehen:

Schritt 1: Zielungleichungen vereinfachen

Zunächst können wir beide Ungleichungen, die erfüllt sein müssen, umschreiben, denn in unserem Fall ist $x_{0} = 0$ und $f (x_{0}) = 0$ . Dadurch können wir schreiben: $| x | < δ$ und $| f (x) | \geq ϵ$ .

Schritt 2: Wahl eines geeigneten $ϵ > 0$

Wir betrachten nun den Graphen der Funktion $f$ – dieser hilft uns nämlich unsere „Beweisbausteine“ zu finden:

Wir müssen ein $ϵ > 0$ finden, so dass es stets Funktionswerte im Bereich $(x_{0} - δ, x_{0} + δ) = (- δ, δ)$ gibt, die einen Abstand größer gleich $ϵ$ von $f (x_{0}) = f (0) = 0$ haben – egal wie klein $δ$ ist. Sprich: Egal, welches $δ$ wir wählen, es gibt immer Punkte die oberhalb oder unterhalb des $2 ϵ$ - $2 δ$ -Rechtecks liegen.

In der Grafik erkennen wir, dass die Funktion in der Nähe des Nullpunkts unendlich oft zwischen $- 1$ und $1$ oszilliert. Damit bietet sich ein $ϵ \leq 1$ an. Dann gibt es nämlich immer Funktionswerte in jeder noch so kleinen Umgebung von der Null mit $| f (x) | \geq 1$ . Wir wählen $ϵ = \frac{1}{2}$ . In der folgenden Grafik ist dies illustriert:

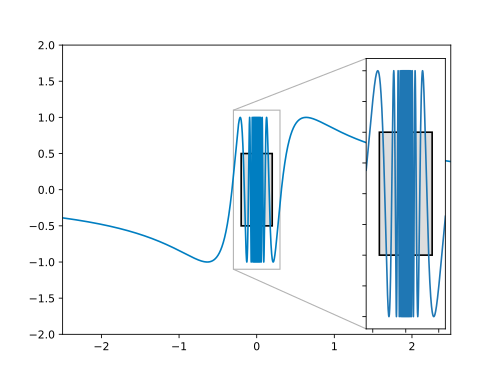
Im Beweis müssen wir nach der Wahl von $ϵ$ das $δ$ beliebig größer Null wählen. Das machen wir dann auch.

Schritt 3: Wahl eines geeigneten $x \in ℝ$

Wir haben $ϵ = \frac{1}{2}$ gesetzt. Es muss nun gelten $| \sin (\frac{1}{x}) | \geq \frac{1}{2}$ . Damit diese Bedingung erfüllt ist, können wir solche $x$ mit $\sin (\frac{1}{x}) = 1$ wählen. Nun ist $\sin (a) = 1$ genau dann, wenn $a = \frac{π}{2} + 2 k π$ für ein $k \in ℤ$ ist. Für die gesuchten $x$ gilt also:

\frac{1}{x} = \frac{π}{2} + 2 k π ⟺ x = \frac{1}{\frac{π}{2} + 2 k π}

Damit haben wir verschiedene $x$ gefunden, für die $| f (x) | \geq ϵ$ gilt. Jetzt muss noch die erste Bedingung $| x | < δ$ beachtet werden. Unsere $x$ hängen von $k$ ab. Wir müssen ein geeignetes $k$ mit $k \in ℤ$ finden, so dass $| x | < δ$ erfüllt ist. Setzen wir also in diese Ungleichung $| x | < δ$ die gefundene Gleichung $x = \frac{1}{\frac{π}{2} + 2 k π}$ ein und stellen sie nach $k$ um:

\begin{matrix} | x | < δ & ⟺ | \frac{1}{\frac{π}{2} + 2 k π} | < δ \\ ⟺ \frac{1}{\frac{π}{2} + 2 k π} < δ \\ ⟺ 2 k π + \frac{π}{2} > \frac{1}{δ} \\ ⟺ 2 k π > \frac{1}{δ} - \frac{π}{2} \\ ⟺ k > \frac{1}{2 π} (\frac{1}{δ} - \frac{π}{2}) \end{matrix}

Dies liefert den Ausdruck $k > \frac{1}{2 π} (\frac{1}{δ} - \frac{π}{2})$ . Wählen wir also eine natürliche Zahl $k$ , die größer als $\frac{1}{2 π} (\frac{1}{δ} - \frac{π}{2})$ ist, so ist $| x | < δ$ erfüllt. Ein solches $k$ muss nach dem archimedischen Axiom existieren. Wählen wir ein solches $k$ und definieren damit das $x$ über $x = \frac{1}{\frac{π}{2} + 2 k π}$ , haben wir sowohl $| x | < δ$ als auch $| f (x) | \geq ϵ$ gegeben. Damit sind alle Bausteine für den Beweis gefunden und dieser muss nur noch sauber aufgeschrieben werden.

Beweis (Unstetigkeit der topologischen Sinusfunktion)

Wähle $ϵ = \frac{1}{2}$ und sei $δ > 0$ beliebig. Wähle eine natürliche Zahl $k$ , so dass $k > \frac{1}{2 π} (\frac{1}{δ} - \frac{π}{2})$ . Eine solche natürliche Zahl $k$ muss nach dem Archimedischen Axiom existieren. Weiter sei $x = \frac{1}{\frac{π}{2} + 2 k π}$ . So gilt:

\begin{matrix} k > \frac{1}{2 π} (\frac{1}{δ} - \frac{π}{2}) & ⟹ 2 k π > \frac{1}{δ} - \frac{π}{2} \\ ⟹ 2 k π + \frac{π}{2} > \frac{1}{δ} \\ ↓ \frac{1}{a} > \frac{1}{b} > 0 ⟺ 0 < a < b \\ ⟹ \frac{1}{\frac{π}{2} + 2 k π} < δ \\ ↓ \frac{1}{\frac{π}{2} + 2 k π} > 0 \\ ⟹ | \frac{1}{\frac{π}{2} + 2 k π} | < δ \\ ↓ x = \frac{1}{\frac{π}{2} + 2 k π} \\ ⟹ | x | < δ \end{matrix}

Weiter ist:

\begin{matrix} | f (x) - f (0) | & = | \sin (\frac{1}{x}) - 0 | \\ ↓ x = \frac{1}{\frac{π}{2} + 2 k π} \\ = | \sin (\frac{π}{2} + 2 k π) | \\ ↓ \sin (\frac{π}{2} + 2 k π) = 1 \\ = | 1 | \geq \frac{1}{2} = ϵ \end{matrix}

Damit ist die Funktion unstetig an der Stelle $x_{0} = 0$ .

Übungsaufgaben

Epsilon-Delta-Kriterium: Vorzeichenfunktion

Aufgabe (Unstetigkeit der Vorzeichenfunktion)

Beweise, dass die Vorzeichenfunktion $sgn : ℝ \to ℝ$ mit folgender Zuordnungsvorschrift unstetig ist:

sgn (x) = {\begin{matrix} 1 & x > 0 \\ 0 & x = 0 \\ - 1 & x < 0 \end{matrix}

Wie kommt man auf den Beweis? (Unstetigkeit der Vorzeichenfunktion)

Um die Unstetigkeit zu beweisen, müssen wir eine Unstetigkeitsstelle der Funktion finden. Schauen wir uns hierzu den Graphen der Funktion an:

Man sieht, dass die Funktion an der Nullstelle einen Sprung aufweist. Bei $x_{0} = 0$ sollte sich also eine Unstetigkeitsstelle befinden. Nun müssen wir ein $ϵ > 0$ finden, für welches kein $δ > 0$ gefunden werden kann, so dass die Funktion komplett im $2 ϵ$ - $2 δ$ -Rechteck liegt. Hier müssen wir $ϵ$ kleiner als die Sprunghöhe $1$ wählen – zum Beispiel $ϵ = \frac{1}{2}$ . Egal welches $δ > 0$ wir nun vorgeben, es muss Funktionswerte unter- oder oberhalb des $2 ϵ$ - $2 δ$ -Rechtecks geben.

Sei also $δ > 0$ beliebig. Wir müssen nun zeigen, dass es ein $x$ mit $| x - x_{0} | < δ$ und $| f (x) - f (x_{0}) | \geq ϵ$ gibt. Schauen wir uns zunächst die Ungleichung $| x - x_{0} | < δ$ an:

| x - x_{0} | < δ \overset{x_{0} = 0}{⟺} | x | < δ

Bei der Ungleichung $| f (x) - f (x_{0}) | \geq ϵ$ ergibt sich:

\begin{matrix} \begin{matrix} | f (x) - f (x_{0}) | & \geq ϵ \\ ⟺ & | sgn (x) - sgn (x_{0}) | & \geq \frac{1}{2} \\ ⟺ & | sgn (x) - sgn (0) | & \geq \frac{1}{2} \\ ⟺ & | sgn (x) | & \geq \frac{1}{2} \end{matrix} \end{matrix}

Das $x$ muss damit so gewählt werden, dass $| x | < δ$ und $| sgn (x) | \geq \frac{1}{2}$ ist. Beginnen wir mit der zweiten Ungleichung $| sgn (x) | \geq \frac{1}{2}$ . Für $x \neq 0$ ist $sgn (x)$ entweder $1$ oder $- 1$ . Für $x \neq 0$ gilt somit immer $| sgn (x) | = 1 \geq \frac{1}{2}$ .

Blicken wir nun auf die Ungleichung $| x | < δ$ . Wie wir gerade geschlossen haben, soll $x \neq 0$ sein. Dies ist zum Beispiel für alle $x$ mit $0 < x < δ$ erfüllt. Wählen wir also für $x$ den Mittelwert zwischen $0$ und $δ$ mit $x = \frac{0 + δ}{2} = \frac{δ}{2}$ .

Dies sehen wir auch in folgender Grafik. Hier haben wir das $2 ϵ$ - $2 δ$ -Rechteck mit $ϵ = \frac{1}{2}$ und $δ = \frac{1}{2}$ eingetragen. Alle Punkte, die unter- oder oberhalb des Rechtecks liegen, sind rot markiert. Dies sind alle $x$ im Intervall $(- δ, δ)$ mit $x \neq 0$ . Unsere Wahl $x = \frac{δ}{2}$ ist gesondert markiert und liegt oberhalb des Rechtecks:

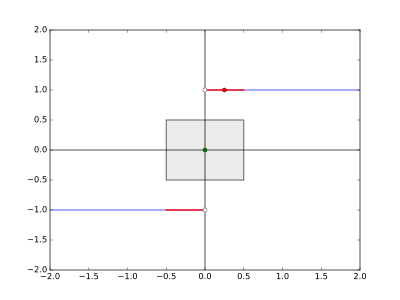
Die Wahl von $x = \frac{δ}{2}$ reicht aus.

Beweis (Unstetigkeit der Vorzeichenfunktion)

Wir setzen $x_{0} = 0$ . Außerdem wählen wir $ϵ = \frac{1}{2}$ . Sei $δ > 0$ beliebig. Wählen wir $x = \frac{δ}{2}$ . Zum einen ist:

\begin{matrix} \begin{matrix} \frac{1}{2} & < 1 \\ ⟹ & \frac{1}{2} δ & < δ \\ ⟹ & | \frac{1}{2} δ | & < δ \\ ⟹ & | \frac{1}{2} δ - 0 | & < δ \\ ⟹ & | x - x_{0} | & < δ \end{matrix} \end{matrix}

Zum anderen ist

\begin{matrix} | f (x) - f (x_{0}) | & = | sgn (x) - sgn (x_{0}) | \\ = | sgn (\frac{δ}{2}) - sgn (0) | \\ = | 1 - 0 | \\ = 1 \\ \geq \frac{1}{2} = ϵ \end{matrix}

Damit ist $sgn$ an der Stelle $x_{0} = 0$ unstetig und somit insgesamt unstetig.

Zwischenwertsatz →

„Analysis Eins“ ist jetzt als Buch verfügbar!

Den Bereich zur Analysis 1 gibt es jetzt auch als Buch! Bestelle dir dein Exemplar oder lade dir das Buch gleich kostenlos als PDF herunter:

Buch kaufen PDF downloaden

Über 150 ehrenamtliche Autorinnen und Autoren – die meisten davon selbst Studierende – haben daran mitgewirkt. Wir wollen, dass alle Studierende die Konzepte der Hochschulmathematik verstehen und dass hochwertige Bildungsangebote frei verfügbar sind. Bei dieser Mission kannst du mitmachen oder uns mit einer Spende unterstützen.

Fragen? Feedback? Interesse an der Mitarbeit?

Wenn du Fragen zum Inhalt hast oder etwas nicht verstanden hast, kontaktiere uns. Wir werden dir deine Fragen gerne beantworten! Auch für Kritik und Anmerkungen sind wir sehr dankbar! Unsere Artikel sind gewissenhaft recherchiert, aber vereinzelte Fehler können nicht ausgeschlossen werden und wir sind sehr dankbar für alle Hinweise. Melde dich auch bei uns, wenn du unsere Vision, Hochschulmathematik verständlich zu erklären, unterstützen möchtest! Unsere Kontaktmöglichkeiten:

E-Mail: mfnf@kulla.me

Telegram-Gruppe: https://t.me/serlo_hochschule

Hinweis: Telegram ist ein externer Chatdienst, der nicht von Serlo oder der Wikimedia betrieben wird. Bitte informiere dich selbstständig, ob du mit ihren Datenschutzbestimmungen einverstanden bist.

Dieser Artikel steht unter einer freien CC-BY-SA 3.0 Lizenz. Damit kannst du ihn frei verwenden, bearbeiten und weiterverbreiten, solange du „Mathe für Nicht-Freaks“ als Quelle nennst und deine Änderungen am Text unter derselben CC-BY-SA 3.0 oder einer dazu kompatiblen Lizenz stellst. Auf der Seite „Kopier uns!“ erklären wir dir detailliert, was du bei der Benutzung unsere Texte, Bilder und Videos beachten musst.