Stetigkeit von Funktionen – Serlo „Mathe für Nicht-Freaks“
Einleitung
[Bearbeiten]Grobe Intuition zur Stetigkeit
[Bearbeiten]Betrachten wir die Graphen verschiedener Funktionen, so stellen wir fest, dass einige von ihnen Sprünge aufweisen und andere nicht:
-
Die Normalparabel der Funktion kann ohne Absetzen gezeichnet werden.
-
Auch die Graphen der Sinus- und Kosinus-Funktion sind ohne Absetzen des Stifts zeichenbar.
-
Die Vorzeichenfunktion hat einen Sprung bei .
-
Auch der Graph der Aufrundungsfunktion , die eine Zahl zur größeren ganzen Zahl aufrundet, besitzt Sprünge.
Wir könnten nun vermuten, dass wir Funktionen in zwei Kategorien klassifizieren können: einerseits in stetige Funktionen, deren Graphen man ohne Absetzen des Stiftes kontinuierlich zeichnen kann und andererseits in unstetige Funktionen, welche Sprünge besitzen. Dieses Unterscheidungskriterium liefert oft brauchbare Ergebnisse, es hat aber auch seine Probleme und ist deswegen nur eine grobe Intuition für das Konzept der Stetigkeit.
Probleme der groben Intuition der Stetigkeit
[Bearbeiten]Betrachten wir als erstes Beispiel die Funktion und die spezielle Vorzeichenfunktion
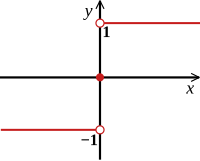
Beide Funktionen sind stetig, obwohl ihre Graphen einen „Sprung“ bei aufweisen:
-
Die Funktion ist stetig, obwohl ihr Graph nicht ohne Absetzen des Stifts gezeichnet werden kann.
-
Auch die Vorzeichenfunktion, die keinen Funktionswert an der Stelle besitzt, ist stetig.
Die grobe Intuition der Stetigkeit führt uns bei beiden Funktionen in die Irre. Der entscheidende Punkt ist, dass beide Funktionen an der Stelle nicht definiert sind. Eine Untersuchung auf Stetigkeit ergibt nämlich nur an den Stellen einen Sinn, wo die Funktion auch einen Funktionswert besitzt. Die „Sprungstelle“ hat somit für beide Funktionen keinen Einfluss darauf, ob sie stetig sind oder nicht, weil sie nicht zum Definitionsbereich gehört. Wir müssen daher bei der Anwendung der groben Intuition auf den Definitionsbereich der Funktion achten.
Die grobe Intuition ist außerdem nicht ausreichend, um bei jeder Funktion eine Entscheidung zu ihrer Stetigkeit treffen zu können. Betrachten wir dazu die beiden Funktionen:
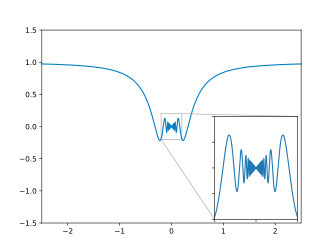
Beide Funktionen oszillieren in jeder Umgebung von sehr stark, wie folgende Abbildungen zeigen:
-
Die Funktion , welche in jeder Umgebung der Null stark oszilliert.
-
Auch die Funktion oszilliert in jeder Umgebung der Null stark.
Sind diese Funktionen stetig oder nicht? Die grobe Intuition, dass Graphen stetiger Funktionen ohne Absetzen des Stiftes gezeichnet werden können, liefert hier keine klare Antwort. Diese Probleme zeigen, dass wir eine mathematisch präzise Definition für die Stetigkeit von Funktionen benötigen.
Wozu braucht man Stetigkeit?
[Bearbeiten]Wir haben nun gesehen, warum wir eine mathematisch strikte Definition der Stetigkeit brauchen. Aber warum beschäftigen wir uns eigentlich mit Stetigkeit?
- Stetige Funktionen sind „nette“ Funktionen. Sie haben einige nützliche Eigenschaften, welche wir für weitere Betrachtungen oder Beweise nutzen können.
- Wenn wir Funktionswerte annähern, nutzen wir das Konzept der Stetigkeit (auch wenn wir uns dessen nicht bewusst sind). Anstatt zu bestimmen, kann auch die Annäherung verwendet werden, wenn hinreichend nah an liegt. Diese Approximation ist jedoch nur dann sinnvoll, wenn die Funktion an der Stelle stetig ist.
- Viele Vorgänge oder Beziehungen zwischen Größen in den Naturwissenschaften sind stetig. Es gibt aber auch unstetige Vorgänge, wie zum Beispiel Veränderungen an der Börse, Phasenübergänge oder das Verhalten chaotischer Systeme wie gewisse Wetterphänomene.
- Die Stetigkeit ist ein wichtiges Konzept der Topologie. Sie erhält nämlich Nachbarschaftsbeziehungen. Dies bedeutet, dass durch stetige Funktionen benachbarte Punkte „nicht auseinandergerissen“ werden.
- Die Beweistechniken, die wir im Zusammenhang mit der Stetigkeit nutzen, sind auch nützlich für andere Themen der Analysis.
Formale Definition der Stetigkeit
[Bearbeiten]Wie kommt man auf eine formale Definition?
[Bearbeiten]Wir haben bereits festgestellt, dass es stetige Funktionen gibt, welche sich nicht ohne Absetzen des Stiftes zeichnen lassen. Dementsprechend benötigen wir eine klare Definition für die Stetigkeit. Um diese zu finden, können wir folgendermaßen vorgehen: Wir überlegen uns, welche Eigenschaften stetige Funktionen haben sollten. Dann wählen wir diejenige Eigenschaft als Definition, die wir als charakteristisch für Stetigkeit ansehen. Diese Eigenschaft sollte eine sein, die wir gut formal durch eine Definition beschreiben können. Folgende Eigenschaften sollten stetige Funktionen besitzen:
- Kleine Ursachen haben kleine Wirkung: Bei stetigen Funktionen sollte eine hinreichend kleine Änderung des Arguments nur eine kleine Änderung des Funktionswerts verursachen.
- Bei stetigen Funktionen kann man den Limes in die Funktion ziehen. Es sollte also gelten: .
- Benachbarte Punkte werden durch stetige Funktionen nicht „auseinandergerissen“ (der Graph besitzt keine Sprünge). Das heißt, dass Nachbarschaftsbeziehungen der Punkte untereinander erhalten bleiben.
- Zwischenwerteigenschaft: Eine stetige Funktion nimmt alle Funktionswerte zwischen und mindestens einmal an, wenn sie auf dem kompletten Intervall definiert ist.
Später werden wir sehen, dass diese Eigenschaften für stetige Funktionen Sinn ergeben. Es hat sich im Laufe der Zeit gezeigt, dass die ersten beiden Eigenschaften eine gute Ausgangsbasis für eine formale Definition liefern. Diese werden wir als „Epsilon-Delta-Kriterium“ beziehungsweise als „Folgenkriterium“ der Stetigkeit kennenlernen.
Epsilon-Delta-Kriterium
[Bearbeiten]→ Hauptartikel: Epsilon-Delta-Kriterium der Stetigkeit
Das Epsilon-Delta-Kriterium formalisiert die Intuition, dass hinreichend kleine Änderungen des Arguments beliebig kleine Änderungen im Funktionswert verursachen bzw. dass benachbarte Punkte nicht auseinander gerissen werden. Die Definition für Stetigkeit in einem Punkt lautet:
Definition (Epsilon-Delta-Definition der Stetigkeit)
Eine Funktion mit ist genau dann stetig an der Stelle , wenn es zu jedem ein gibt, so dass für alle mit ist. ist also genau dann in stetig, wenn gilt
Folgenkriterium
[Bearbeiten]→ Hauptartikel: Folgenkriterium der Stetigkeit: Folgenstetigkeit
Äquivalent lässt sich Stetigkeit über das Folgenkriterium definieren. Stetige Funktionen werden dabei als die Funktionen charakterisiert, bei denen der Limes in die Funktion gezogen werden kann. Die Definition der Stetigkeit in einem Punkt lautet dann:
Definition (Folgenkriterium der Stetigkeit an einer Stelle)
Eine Funktion mit ist stetig an der Stelle , wenn für alle Folgen mit und gilt:
Beide Definitionen beschreiben die Stetigkeit an einem Punkt. Damit die Funktion insgesamt stetig ist, muss sie in jedem Argument stetig sein.
Warum wählt man nicht die Zwischenwerteigenschaft als Definition?
[Bearbeiten]Die Zwischenwerteigenschaft sagt aus, dass eine auf einem Intervall stetige Funktion alle Werte zwischen und annehmen muss. Bis ins 19. Jahrhundert glaubte man, dass Funktionen mit der Zwischenwerteigenschaft stetig wären[1]. Schließlich lässt die Tatsache, dass eine Funktion jeden Zwischenwert annimmt, intuitiv den Schluss zu, dass sie keine Sprünge besitzt. Nur schwer kann man sich nicht stetige Funktion vorstellen, die die Zwischenwerteigenschaft erfüllen.
Unsere Intuition führt uns hier in die Irre. Die Zwischenwerteigenschaft ist nämlich zu schwach, um als Definition der Stetigkeit zu dienen. Ein Gegenbeispiel ist die Conway Funktion zur Basis 13. Diese Funktion nimmt für jedes Intervall jede reelle Zahl als Funktionswert an, egal wie klein das Intervall ist. Jede noch so kleine Änderung des Arguments kann so beliebig große Änderungen des Funktionswerts verursachen. Die Conway Funktion zur Basis 13 erfüllt damit die Zwischenwerteigenschaft, ist aber in keinem Punkt stetig.
Übersicht zu den Eigenschaften stetiger Funktionen
[Bearbeiten]Nun wo wir die Definition stetiger Funktionen kennengelernt haben, können wir uns anschauen, welche nützlichen Eigenschaften sie besitzen.
Kleine Ursachen haben kleine Wirkung
[Bearbeiten]→ Hauptartikel: Epsilon-Delta-Kriterium der Stetigkeit
Unsere grobe Intuition sagt uns, dass stetige Funktionen ohne Absetzen des Stifts gezeichnet werden können und keine Sprünge besitzen. Betrachten wir dazu eine stetige Funktion, die an der Stelle den Wert besitzt. Ändern wir um den Betrag , bekommen wir den neuen Funktionswert :

Wenn stetig ist, dann kann der Abstand von zu beliebig klein gemacht werden, indem hinreichend klein gewählt wird. Dies ist möglich, weil bei stetigen Funktionen hinreichend kleine Änderungen des Arguments nur kleine Änderungen des Funktionswertes verursachen. Aus folgt also . Diese Eigenschaft stetiger Funktionen haben wir im sogenannten „Epsilon-Delta-Kriterium“ formalisiert.
Limes kann in die Funktion hineingezogen werden
[Bearbeiten]→ Hauptartikel: Folgenkriterium der Stetigkeit: Folgenstetigkeit
Stetige Funktionen erfüllen auch das sogenannte Folgenkriterium: Betrachten wir die Funktion und eine konvergente Folge mit . Was ist ? Bei stetigen Funktionen kann man den Limes in die Funktion ziehen und wir erhalten so:
Dies erleichtert Grenzwertberechnungen ungemein. Der Grund dafür ist, dass beliebig nah an liegt, wenn hinreichend nah bei ist. Das hängt damit zusammen, dass bei stetigen Funktionen hinreichend kleine Änderungen im Argument nur kleine Änderungen im Funktionswert verursachen.
Das können wir gut am Beispiel der Exponentialfunktion mit nachvollziehen. Es gilt nämlich
Das folgende Diagramm illustriert diesen Umstand:

Nachbarschaftsbeziehungen bleiben erhalten
[Bearbeiten]Die Intuition, dass hinreichend kleine Änderungen im Argument nur kleine Änderungen im Funktionswert hervorrufen, kann auch anders formuliert werden: Benachbarte Punkte werden durch stetige Funktionen nicht „auseinandergerissen“ (der Graph besitzt keine Sprünge). Man kann auch sagen, dass Nachbarschaftsbeziehungen der Punkte untereinander erhalten bleiben. Die Topologie beschäftigt sich näher mit diesen Phänomenen.
Zwischenwertsatz
[Bearbeiten]→ Hauptartikel: Zwischenwertsatz
Betrachten wir folgende Ausgangssituation: Sei ein beliebiger Wert und sei eine Funktion, die an der Stelle den Wert und an der Stelle den Funktionswert besitzt (wir nehmen dabei an):

Wenn stetig und im gesamten Intervall definiert ist, können wir unseren Graphen ohne Absetzen des Stifts von nach zeichnen. Dabei muss dieser zwangsweise mindestens einmal die Gerade schneiden. Es muss also mindestens eine Stelle geben, wo ist:

Das gilt nicht nur für , sondern für alle Funktionswerte zwischen und . Alle Funktionswerte zwischen und werden also mindestens einmal angenommen.
Mit dem Zwischenwertsatz können wir beispielsweise beweisen, dass die Gleichung mindestens eine Lösung besitzt. Es ist nämlich . Weil die Sinusfunktion stetig ist, muss es nach dem Zwischenwertsatz mindestens eine Stelle zwischen und geben, wo ist. Auf ähnliche Art und Weise können wir für viele andere Gleichungen beweisen, dass sie mindestens eine Lösung besitzen.
Verkettungen stetiger Funktionen sind wieder stetig
[Bearbeiten]→ Hauptartikel: Komposition stetiger Funktionen
Beliebige Verkettungen wie Kompositionen, Summen oder Produkte stetiger Funktionen sind ebenfalls stetig. Somit können wir aus der Tatsache, dass die Identitätsfunktion und die konstante Funktion stetig sind, schließen, dass auch die aus diesen Funktionen verkettete Funktion stetig ist.
Intuition der Stetigkeit
[Bearbeiten]Wie wir bereits festgestellt haben, spiegelt unsere ursprüngliche, anschauliche Intuition der Stetigkeit – Graphen stetiger Funktionen besitzen keine Sprünge – nur grob den Begriff der Stetigkeit wider. Um falsche Diagnosen zu vermeiden, sollten wir unsere grobe Intuition demnach entsprechend der formalen Definition umformulieren:
Bei stetigen Funktionen führen hinreichend kleine Änderungen des Arguments zu beliebig kleinen Änderungen des Funktionswerts.
Eine alternative Intuition liefert das Folgenkriterium:
Stetige Funktionen sind genau die Funktionen, bei denen man den Limes in die Funktion ziehen kann. Bei ihnen gilt .
Hinweis
Beachte, dass die wahre Intuition der Stetigkeit nur ungefähr der ursprünglichen Intuition entspricht, dass stetige Funktionen keine Sprünge besitzen. Für stetige Funktionen solltest du besser eine der beiden obigen Intuitionen wählen.
Wichtige Aspekte der Stetigkeit
[Bearbeiten]Nachdem wir die Intuition und die Definition der Stetigkeit kennengelernt haben, betrachten wir nun einige wichtige Aspekte dieses Konzepts.
Stetigkeit ist eine lokale Eigenschaft
[Bearbeiten]Nach unserer groben und ungenauen Intuition scheint Stetigkeit eine globale Eigenschaft der gesamten Funktion zu sein. Aus der formalen Definition der Stetigkeit an einer Stelle können wir jedoch folgern, dass es sich um eine lokale Eigenschaft handelt. Das heißt, dass die Kenntnis über den Funktionsverlauf in einer beliebig kleinen Umgebung eines Arguments ausreicht, um entscheiden zu können, ob sie dort stetig ist oder nicht. Stimmen zwei Funktionen in einer beliebig kleinen Umgebung um ein Argument überein, müssen entweder beide an dieser Stelle stetig sein, oder bei diesem Argument eine Unstetigkeitsstelle aufweisen.
So können wir die Stetigkeit der speziellen Vorzeichenfunktion zeigen, die bei nicht definiert ist:
Diese Funktion ist lokal konstant. Das bedeutet, dass es für jeden Punkt eine Umgebung gibt, auf der konstant ist:

Da es um jeden Punkt der speziellen Vorzeichenfunktion eine Umgebung gibt, in der die Funktion konstant ist, muss sie auch an jedem Punkt dasselbe Stetigkeitsverhalten wie eine konstante Funktion besitzen. Da konstante Funktionen nach unserer Intuition stetig sind, sollte dies auch für die spezielle Vorzeichenfunktion an jeder Stelle gelten. Sowohl mit dem Folgenkriterium, als auch mit dem Epsilon-Delta-Kriterium, kann die Stetigkeit einfach bewiesen werden.
Warum ist Stetigkeit eine lokale Eigenschaft?
[Bearbeiten]Um besser zu verstehen, warum Stetigkeit eine lokale Eigenschaft ist, können wir die Negation der Stetigkeit betrachten. Nach unserer groben Vorstellung ist eine Funktion genau dann an einer Stelle unstetig, wenn ihr Graph dort einen Sprung besitzt. Insofern bedeutet Stetigkeit an einer Stelle die Abwesenheit eines Sprungs im Graphen am betrachteten Argument. Nun ist die Sprungstelle eines Graphen eine lokale Eigenschaft. Die Kenntnis einer Funktion in einer beliebig kleinen Umgebung um diese Stelle reicht aus, um festzustellen, ob es dort eine Sprungstelle gibt oder nicht. Dementsprechend ist auch deren Negation, also die Abwesenheit eines Sprungs beziehungsweise die Stetigkeit an einer Stelle, eine lokale Eigenschaft.
Bedeutung des Definitionsbereichs für die Stetigkeit
[Bearbeiten]

Anhand der speziellen Vorzeichenfunktion können wir sehen, wie wichtig der Definitionsbereich bei Entscheidungen zur Stetigkeit ist. Während nämlich die Vorzeichenfunktion
die auf dem kompletten Zahlenbereich definiert ist, unstetig ist, ist die spezielle Vorzeichenfunktion
die an der Stelle nicht definiert ist, stetig. Auch mit gleicher Zuordnungsvorschrift können Funktionen mit unterschiedlichen Definitionsbereichen ein unterschiedliches Stetigkeitsverhalten aufweisen. Dieses Beispiel zeigt, wie wichtig die Kenntnis des Definitionsbereichs ist, um die Frage nach Stetigkeit und Unstetigkeit zu beantworten.
Stetigkeit ist nur im Definitionsbereich definiert
[Bearbeiten]
Stetigkeit ist nur für Argumente einer Funktion definiert. Aussagen über Stetigkeits- oder Unstetigkeitsstellen sind also nur sinnvoll, wenn die Funktion an der ausgewählten Stelle auch definiert ist. Sowohl im Epsilon-Delta-Kriterium, als auch im Folgenkriterium wird auf den Funktionswert an der betrachteten Stelle zurückgegriffen. Somit muss die Funktion hier definiert sein, um diese Definitionen anwenden zu können.
Betrachten wir die Funktion . Sie ist an der Stelle nicht definiert. Zu fragen, ob die Funktion an dieser Stelle stetig ist, wäre ungefähr genauso sinnvoll wie die Frage, ob sie am Mount Everest oder am Mond stetig ist. Also schlicht unsinnig. Sinnvoll und richtig ist dagegen: „Die Funktion kann in nicht stetig fortgesetzt werden.“ Es ist wichtig, dass wir zwischen stetiger Fortsetzbarkeit und Stetigkeit sauber unterscheiden.
Halten wir fest: Stetigkeit ist nur für Punkte im Definitionsbereich einer Funktion definiert. Außerhalb des Definitionsbereichs sind Aussagen zur Stetigkeit einer Funktion sinnlos.
Ausblick auf die nächsten Kapitel
[Bearbeiten]In den nächsten Kapiteln werden wir die verschiedenen Definitionen der Stetigkeit behandeln. Außerdem werden wir lernen, die Stetigkeit einer Funktion nachzuweisen und wichtige Eigenschaften stetiger Funktionen (wie beispielsweise die Zwischenwerteigenschaft) zu beweisen.













![{\displaystyle {\begin{aligned}h&:\mathbb {R} \to \mathbb {R} :x\mapsto h(x)={\begin{cases}\sin \left({\tfrac {1}{x}}\right)&;x\neq 0\\0&;x=0\end{cases}}\\[0.5em]g&:\mathbb {R} \to \mathbb {R} :x\mapsto g(x)={\begin{cases}x\sin \left({\tfrac {1}{x}}\right)&;x\neq 0\\0&;x=0\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f9d3a3bea768248f4c8c9d4669d39afa07b73a6)












![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)















































