Folgenkriterium der Stetigkeit: Folgenstetigkeit – Serlo „Mathe für Nicht-Freaks“
Motivation und Herleitung
[Bearbeiten]Erste Beispiele
[Bearbeiten]Betrachte den Grenzwert . In der Schule würde man diesen Grenzwert folgendermaßen ausrechnen:
Diese Rechnung ergibt intuitiv Sinn: Wenn , dann sollte sein. Doch können wir so argumentieren? Ist es erlaubt, den Limes in die Funktion reinzuziehen? Betrachte hierzu die Vorzeichenfunktion , welche das Vorzeichen von zurückgibt:
Wegen gilt:
Also ist . Dies zeigt, dass man den Limes nicht ohne Weiteres in eine Funktion hineinziehen kann. Im Funktionsplot sieht man, warum dies bei , jedoch nicht bei möglich ist. Bei konvergiert nämlich die Folge gegen , wenn geht:

Bei der Vorzeichenfunktion gibt es einen Sprung im Graphen bei , und deswegen konvergiert die Folge nicht gegen :
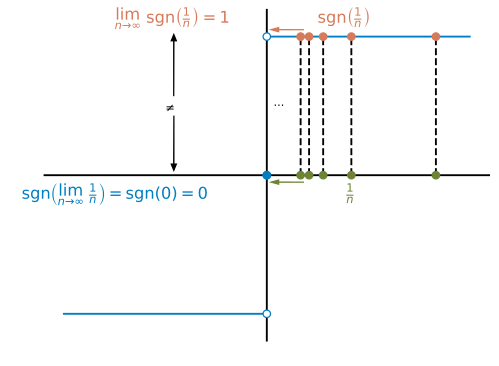
Wir stellen fest: Es gibt Funktionen, bei denen der Limes hineingezogen werden kann, und Funktionen, bei denen es nicht (immer) geht.
Sprungstellen und Stetigkeit
[Bearbeiten]Wir erkennen, dass wir deswegen den Limes nicht in hineinziehen können, weil der Graph der Vorzeichenfunktion an der Stelle „einen Sprung macht“. Wir überlegen uns nun, warum das Hineinziehen des Limes nicht möglich ist, wenn der Graph beim Grenzwert der Argumentenfolge einen Sprung macht. Nehmen wir an, dass folgenden Graphen besitzt:
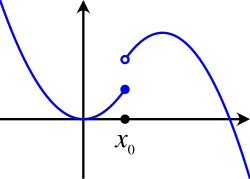
Wenn wir uns von links an annähern, dann nähern sich die Funktionswerte auch an an. Wenn also die Argumentenfolge fast ausschließlich (sprich: bis auf endlich viele Ausnahmen) nur aus reellen Zahlen kleiner gleich besteht, können wir den Limes hineinziehen. Dies schlägt jedoch fehl, wenn in der Argumentenfolge unendlich viele Zahlen größer als auftreten. Ihre Funktionswerte nähern sich nämlich nicht an, weil der Graph bei in die rechte Richtung einen Sprung macht. Durch den Sprung gibt es einen Mindestabstand, den die Funktionswerte in der Nähe und rechts von nicht unterschreiten. Der Sprung der Funktion an der Stelle verhindert, dass bei jeder Argumentenfolge der Limes hineingezogen werden kann.
Ähnliches passiert, wenn der Graph bei in die linke Richtung einen Sprung besitzt:

Hier schlägt das Hineinziehen des Limes fehl, wenn die Argumentenfolge unendlich viele Zahlen kleiner als besitzt. Die Funktionswerte links von nähern sich aufgrund des Sprungs nämlich nicht an.
Im Übrigen ist die Situation eine andere, wenn an der Sprungstelle nicht definiert ist:

Hier ergibt der Ausdruck keinen Sinn, weil die Funktion an der Stelle nicht definiert ist. Deswegen müssen wir nicht betrachten, ob dort der Limes hineingezogen werden kann. An allen anderen Stellen ist der Graph von kontinuierlich und damit stetig. Wir sehen: Ein Sprung macht nur dann eine Funkion unstetig, wenn die Funktion an der Sprungstelle definiert ist.
Übergang zur formalen Definition
[Bearbeiten]Nehmen wir eine Funktion mit Sprungstelle im Punkt . Wenn man sich dem Argument von der einen Seite nähert, wird ein gewisser Abstand zwischen und nie unterschritten. Dieser Mindestabstand zwischen und wurde durch den Sprung an der Stelle verursacht. Wenn man sich von der anderen Seite an nähert, gehen die -Werte beliebig nah an heran (vorausgesetzt, dass hier keine zweite Sprungstelle vorliegt).
Für -Werte, die beliebig (=„unendlich“) nahe an herankommen sollen, können wir den Folgenbegriff verwenden. Dafür beschreiben wir die -Werte als Folge , die gegen konvergiert. Die Verwendung des Folgenbegriffs ist auch deswegen sinnvoll, weil wir für die Annäherung oft unendlich viele -Werte benötigen und Folgen ebenfalls unendlich viele Glieder besitzen.
Gehen wir nun davon aus, dass wir uns von der Seite nähern, bei der unsere gegenüber einen gewissen Mindestabstand in der Nähe von nicht unterschreiten. Dieser bleibt auch im Limes erhalten. Falls existiert, so wissen wir damit sicher, dass ist.
Nun haben wir nur die Annäherung von der Seite betrachtet, wo nicht gegen strebt. In unseren Beispielen können wir jedoch die Folge so wählen, dass ist. Dies ist zum Beispiel der Fall, wenn unsere von der anderen Seite an streben. Damit erfüllt ist, können wir unsere gegen konvergierende Folge also nicht beliebig wählen. Jedoch existiert zumindest eine Folge , für die nicht gegen strebt.
Herleitung des Folgenkriteriums
[Bearbeiten]Fassen wir das bisher Gefundene zusammen:
Wenn eine Funktion an der Stelle einen Sprung besitzt, gibt es mindestens eine Folge von Argumenten mit und .
Sprich: Im Fall eines Sprungs an der Stelle gilt für mindestens eine Folge von Argumenten mit Grenzwert . Nun ist nach unserer Intuition eine Funktion genau dann unstetig an einer Stelle, wenn ihr Graph dort einen Sprung macht. Wir können also definieren:
Der Graph einer Funktion ist unstetig an der Stelle , wenn es mindestens eine Folge von Argumenten mit und gibt.
Um die Definition der Stetigkeit an einer Stelle zu finden, müssen wir die Negation der obigen Aussage nehmen. Nach dieser Überlegung können wir uns die Stetigkeit an einer Stelle als Abwesenheit eines Sprungs an der betrachteten Stelle vorstellen, und wir erhalten:
Eine Funktion ist an der Stelle stetig, wenn für alle Folgen aus mit gilt:
Bei Stetigkeit einer Funktion an einer Stelle kann der Limes hineingezogen werden, wenn die Argumentenfolge gegen diese Stelle konvergiert. Diese Definition der Stetigkeit ist das Folgenkriterium der Stetigkeit. Nun ist eine Funktion genau dann stetig, wenn sie an jeder Stelle ihres Definitonsbereichs stetig ist. Damit erhalten wir für die Stetigkeit einer Funktion:
Eine Funktion ist stetig, wenn für alle konvergenten Folgen gilt . Dabei müssen alle Folgenglieder und der Grenzwert Elemente des Definitionsbereiches von sein, damit die Gleichung Sinn ergibt.
Wir können zusammenfassen: Bei einer stetigen Funktion kann man den Limes in die Funktion hineinziehen – unabhängig vom Grenzwert der Argumentenfolge. Weil beispielsweise die Exponentialfunktion stetig ist, kann man immer den Limes in diese Funktion hineinziehen. Die Vorzeichenfunktion ist bei unstetig, und damit kann der Limes nicht in die Funktion gezogen werden, wenn die Argumentenfolge gegen null konvergiert.
Definition
[Bearbeiten]Im obigen Abschnitt haben wir bereits die Definition der Stetigkeit kennengelernt. Hier haben wir festgelegt:
Definition (Folgenkriterium der Stetigkeit an einer Stelle)
Eine Funktion mit ist stetig an der Stelle , wenn für alle Folgen mit und gilt:
Darauf aufbauend haben wir definiert, dass eine Funktion stetig ist, wenn sie an jeder Stelle stetig ist:
Definition (Folgenkriterium der Stetigkeit)
Eine Funktion mit ist stetig, wenn für alle und für alle Folgen mit und gilt:
Stetigkeit garantiert uns also, dass wir den Limes in die Funktion hineinziehen können. Dies kann die Grenzwertberechnung ungemein vereinfachen, und somit ist Stetigkeit ein Konzept, auf das man bei Grenzwertberechnungen stößt.
Auswirkungen der Definition
[Bearbeiten]Wir haben über unsere Vorstellung von Sprungstellen eine formale Definition von Stetigkeit gefunden. Diese hat sich im Laufe der Zeit als sinnvoll herausgestellt und wird in der mathematischen Community als Definition der Stetigkeit akzeptiert. Deswegen werden auch wir sie im Folgenden heranziehen. Somit ist die Grundlage für Entscheidungen, ob eine Funktion stetig ist, nicht mehr unsere Intuition – sondern das von uns gefundene Folgenkriterium. Dies hat gewisse Nebeneffekte. Betrachte die topologische Sinusfunktion:
Ihr Graph ist:

Bei dieser Funktion ist man sich intuitiv nicht sicher, ob sie an der Stelle stetig ist, denn in der Nähe davon schwingt die Funktion immer stärker. Schaut man sich den Graphen an, so sieht es (für mich) nicht nach einer gewöhnlichen Sprungstelle aus. Wenn wir aber unser Folgenkriterium der Stetigkeit heranziehen, können wir zeigen, dass die topologische Sinusfunktion an der Nullstelle trotzdem unstetig ist (Übungsaufgabe).
Als Nebenprodukt unserer Definition haben wir also neben der Sprungstelle eine andere Art der Unstetigkeit erhalten. Im Englischen wird sie essential discontinuity genannt. Diese werden bzw. müssen wir akzeptieren, sofern wir das Folgenkriterium als die Definition der Stetigkeit benutzen wollen. Es sei erwähnt, dass dies eine der Standarddefinitionen ist und wir mit einer Ablehnung wohl ziemlich einsam und verloren in der Welt der Mathematik wären.
Beispiel für das Folgenkriterium
[Bearbeiten]Quadratfunktion ist stetig
[Bearbeiten]Aufgabe (Stetigkeit der Quadratfunktion)
Zeige, dass die Quadratfunktion stetig ist.
Beweis (Stetigkeit der Quadratfunktion)
Sei . Wir betrachten nun eine beliebige Folge , die gegen konvergiert. Es ist
Bei der Quadratfunktion kann der Limes also immer hineingezogen werden, womit diese Funktion stetig ist.
Anwendung des Folgenkriteriums
[Bearbeiten]Nachdem wir bewiesen haben, dass die Quadratfunktion stetig ist, können wir immer den Limes in diese Funktion hineinziehen, ohne großartig darüber nachdenken zu müssen. Dies ist das Schöne an der Stetigkeit, wie es folgende Beispielaufgabe zeigt:
Aufgabe (Anwendung des Folgenkriteriums)
Berechne .
Lösung (Anwendung des Folgenkriteriums)
Wir können die bewiesene Stetigkeit der Quadratfunktion ausnutzen, indem wir den Limes in die Quadratfunktion hineinziehen. Nach dem Folgenkriterium können wir dies machen. Damit erhalten wir:
Allgemeine Beweisskizzen
[Bearbeiten]Stetigkeitsbeweise mit dem Folgenkriterium
[Bearbeiten]Um die Stetigkeit einer Funktion an einer Stelle zu beweisen, müssen wir zeigen, dass für jede Folge von Argumenten mit gilt, dass ist. Dementsprechend könnte ein Beweis lauten:
Sei eine Funktion mit und sei gegeben. Sei eine beliebige Folge von Argumenten mit . Es gilt:
Um die Stetigkeit der Funktion zu beweisen, muss das Beweisschema etwas angepasst werden:
Sei eine Funktion mit und sei eine beliebige Zahl aus dem Definitionsbereich von . Sei eine beliebige Folge von Argumenten mit . Es gilt:
Unstetigkeitsbeweise mit dem Folgenkriterium
[Bearbeiten]Um mit dem Folgenkriterium zu zeigen, dass eine Funktion an der Stelle unstetig ist, muss man eine Argumentenfolge mit für alle und dem Grenzwert finden, so dass die Funktionswertfolge nicht gegen konvergiert. Es soll also und gelten. Für gibt es zwei Möglichkeiten:
- Die Funktionswertfolge divergiert.
- Die Funktionswertfolge konvergiert, jedoch ist ihr Grenzwert ungleich .
Ein Unstetigkeitsbeweis über das Folgenkriterium könnte zum Beispiel folgende Form aufweisen:
Sei eine Funktion mit . Diese Funktion ist unstetig an der Stelle . Wählen wir nämlich die Folge mit , so liegen alle Folgenglieder im Definitionsbereich von , und wir haben
Jedoch ist . Es ist nämlich ...Beweis, dass divergiert oder dass der Grenzwert von ungleich ist...
Zusammenhang zum Epsilon-Delta-Kriterium
[Bearbeiten]Es gibt zwei Definitionen der Stetigkeit: das Epsilon-Delta-Kriterium und das Folgenkriterium. Um zu zeigen, dass beide Definitionen das gleiche Konzept beschreiben, müssen wir beweisen, dass beide Kriterien äquivalent zueinander sind. Wenn das Folgenkriterium erfüllt ist, muss auch das Epsilon-Delta-Kriterium erfüllt sein und umgekehrt.
Epsilon-Delta-Kriterium impliziert Folgenkriterium
[Bearbeiten]Satz (Das Epsilon-Delta-Kriterium impliziert das Folgenkriterium)
Sei mit eine Funktion. Wenn diese Funktion an der Stelle das Epsilon-Delta-Kriterium erfüllt, dann ist auch das Folgenkriterium an der Stelle erfüllt.
Wie kommt man auf den Beweis? (Das Epsilon-Delta-Kriterium impliziert das Folgenkriterium)
Nehmen wir an, dass die Funktion an der Stelle das Epsilon-Delta-Kriterium erfüllt. Es gilt also:
Zu jedem gibt es ein , sodass für alle mit ist.
Wir wollen nun zeigen, dass auch das Folgenkriterium erfüllt ist. Für jede Argumentenfolge mit Grenzwert soll also gelten. Sei also eine Folge von Argumenten mit . Wir müssen nun zeigen, dass der Grenzwert der Funktionswertfolge gleich ist. Es soll also gelten:
Zu jedem gibt es ein mit für alle .
Sei beliebig. Wir müssen nun ein finden, so dass für alle erfüllt ist. Wir kennen die Ungleichung aus der Konklusion des Epsilon-Delta-Kriteriums. Der Unterschied liegt darin, dass wir anstelle des Arguments das Folgenglied haben. Wenden wir also das Epsilon-Delta-Kriterium auf unseren speziellen Fall mit dem vorgegebenen an. Wir erhalten:
Es gibt ein , so dass für alle Folgenglieder mit ist.
Wir kommen dem Ziel näher. Wenn ein Folgenglied die Ungleichung erfüllt, erfüllt es auch die Zielungleichung . Nun wissen wir wegen , dass beliebig klein wird. Damit gibt es ein , so dass für alle erfüllt ist. Dieses können wir als unser wählen. Ist nämlich , so ist und damit nach dem Epsilon-Delta-Kriterium.
Beweis (Das Epsilon-Delta-Kriterium impliziert das Folgenkriterium)
Sei eine Funktion, die an der Stelle das Epsilon-Delta-Kriterium erfüllt. Sei eine Folge mit für alle und . Wir wollen zeigen, dass für beliebiges ein existiert, sodass für alle gilt.
Sei beliebig. Nach dem Epsilon-Delta-Kriterium gibt es ein , sodass für alle mit ist. Wegen der Konvergenz von gegen können wir ein finden, sodass für alle ist.
Sei beliebig. Es ist damit . Nach dem Epsilon-Delta-Kriterium gilt damit . Dies beweist und damit das Folgenkriterium.
Folgenkriterium impliziert Epsilon-Delta-Kriterium
[Bearbeiten]Satz (Das Folgenkriterium impliziert das Epsilon-Delta-Kriterium)
Sei mit eine Funktion. Wenn an der Stelle das Folgenkriterium erfüllt, erfüllt sie auch das Epsilon-Delta-Kriterium.
Wie kommt man auf den Beweis? (Das Folgenkriterium impliziert das Epsilon-Delta-Kriterium)
Wir müssen folgende Implikation beweisen:
Wir beweisen diese Implikation über Kontraposition. Wir werden also zeigen, dass folgende Implikation gilt:
Also:
Sei also eine Funktion, die das Epsilon-Delta-Kriterium an der Stelle nicht erfüllt. Damit erfüllt die Unstetigkeitsversion des Epsilon-Delta-Kriteriums an der Stelle . Es existiert ein , so dass es für jedes ein mit und gibt. Wir müssen nun zeigen, dass das Folgenkriterium nicht erfüllt ist. Hierzu müssen wir eine Folge von Argumenten finden, so dass und ist.
Um die gesuchte Folge zu finden, müssen wir die Unstetigkeitsversion des Epsilon-Delta-Kriteriums geschickt nutzen. Hier wird uns ein vorgegeben, so dass für gewisse Argumente die Ungleichung gilt. Wenn wir als Folgenglieder nur solche Argumente verwenden, dann ist automatisch wegen dieser Ungleichung .
Nun brauchen wir eine Argumentenfolge , die gegen konvergiert. Hierzu suchen wir uns eine Nullfolge . Bespielsweise kann gewählt werden. Für jedes finden wir ein Argument mit und . Aus diesen bilden wir die gesuchte Argumentenfolge . Diese erfüllt zum einen und wegen damit . Zum anderen kann wegen die Funktionswertfolge nicht gegen konvergieren.
Beweis (Das Folgenkriterium impliziert das Epsilon-Delta-Kriterium)
Wir beweisen den Satz über Kontraposition. Hierzu müssen wir zeigen, dass eine Funktion , die das Epsilon-Delta-Kriterium an der Stelle nicht erfüllt, auch das Folgenkriterium an der Stelle nicht erfüllt. Sei also mit eine Funktion, die an der Stelle das Epsilon-Delta-Kriterium nicht erfüllt. Es gibt also ein , so dass für alle ein mit und existiert.
Für jedes gibt es damit ein mit und . Aus der Ungleichung folgt . Da ist, ist sowohl als auch . Nach dem Sandwichsatz konvergiert damit die Folge gegen .
Jedoch kann wegen für alle die Folge nicht gegen konvergieren. Damit ist das Folgenkriterium an der Stelle für die Funktion nicht erfüllt. Es gibt nämlich eine Argumentenfolge mit und .
Übungsaufgaben
[Bearbeiten]Stetigkeit der Betragsfunktion
[Bearbeiten]Aufgabe (Stetigkeit der Betragsfunktion)
Beweise die Stetigkeit der Betragsfunktion.
Beweis (Stetigkeit der Betragsfunktion)
Sei mit die Betragsfunktion. Sei eine beliebige Zahl und sei eine Folge reeller Zahlen mit . Im Kapitel „Grenzwertsätze: Grenzwert von Folgen berechnen“ haben wir die Betragsregel bewiesen. Diese besagt, dass ist, wenn ist. Also haben wir:
Dies beweist die Stetigkeit von nach dem Folgenkriterium.
Unstetigkeit der topologischen Sinusfunktion
[Bearbeiten]Aufgabe (Unstetigkeit der topologischen Sinusfunktion)
Beweise die Unstetigkeit der folgenden Funktion:
Wie kommt man auf den Beweis? (Unstetigkeit der topologischen Sinusfunktion)
Damit eine unstetige Funktion ist, muss sie mindestens eine Unstetigkeitkeitsstelle besitzen. Für jedes entspricht in einer hinreichend kleinen Umgebung von der Funktion . Da die Funktion als Komposition stetiger Funktionen stetig ist, muss auch für alle stetig sein. Damit muss die Unstetigkeitsstelle bei liegen.
Um mit dem Folgenkriterium zu zeigen, dass an der Stelle unstetig ist, müssen wir eine Argumentenfolge mit und finden. Um diese Argumentenfolge zu finden, schauen wir uns zunächst den Graphen der Funktion an:
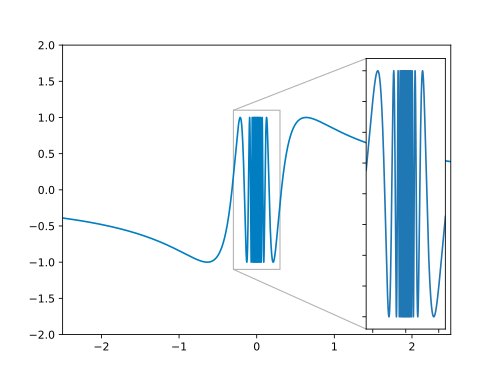
In der Graphik sehen wir, dass die Funktion in jeder Umgebung des Nullpunkts jeden Wert zwischen und beliebig oft annimmt. Also können wir so wählen, dass immer gleich ist. Dann ist nämlich garantiert, dass ist. Dabei wählen wir so, dass von oben gegen Null konvergiert.
In der folgenden Graphik sind neben dem Graphen von auch die Funktionswerte der Folge eingetragen. Man sieht, dass für die Funktionswerte gegen konvergieren, was ungleich dem Funktionswert ist:
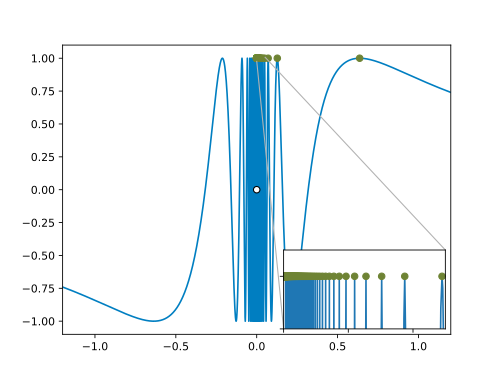
Wie lauten die Werte für ? Formen wir hierzu die Gleichung nach um:
Für alle mit gilt also . Damit unsere Argumente positiv sind und von oben gegen Null konvergieren, wählen wir . Es gilt dann:
Jedoch haben wir gesehen, dass ist. Wir haben also eine Argumentenfolge gefunden, welche die Unstetigkeit von an der Stelle beweist.
Beweis (Unstetigkeit der topologischen Sinusfunktion)
Sei mit für und . Wir betrachten die Folge mit . Für diese Folge ist:
Außerdem gilt:
Damit ist , obwohl ist. Dies beweist, dass an der Stelle und somit auch insgesamt unstetig ist.




![{\displaystyle {\begin{aligned}\lim _{n\to \infty }\exp \left({\frac {1}{n}}\right)&=\exp \left(\lim _{n\to \infty }{\frac {1}{n}}\right)\\[0.5em]&{\color {OliveGreen}\left\downarrow \ \lim _{n\to \infty }{\frac {1}{n}}=0\right.}\\[0.5em]&=\exp(0)\\&=1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9033e78c163e21a94fa543848169f60d4d2131a6)
















































![{\displaystyle {\begin{aligned}\lim _{n\to \infty }f(x_{n})&=\lim _{n\to \infty }x_{n}^{2}\\&=\lim _{n\to \infty }x_{n}\cdot x_{n}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ \lim _{n\to \infty }a_{n}\cdot b_{n}=\lim _{n\to \infty }a_{n}\cdot \lim _{n\to \infty }b_{n}\right.}\\[0.5em]&=\left(\lim _{n\to \infty }x_{n}\right)\cdot \left(\lim _{n\to \infty }x_{n}\right)\\&{\color {OliveGreen}\left\downarrow \ {\text{Voraussetzung}}\lim _{n\to \infty }x_{n}=x\right.}\\[0.5em]&=x\cdot x=x^{2}=f(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3ae5ae0caf809de6b9e9a96c1043d1a13b3de95)

![{\displaystyle {\begin{aligned}&\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{2}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Quadratfunktion ist stetig}}\right.}\\[0.3em]=\ &\left(\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)\right)^{2}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ \lim _{n\to \infty }\left(a_{n}+b_{n}\right)=\lim _{n\to \infty }a_{n}+\lim _{n\to \infty }b_{n}\right.}\\[0.3em]=\ &\left(\lim _{n\to \infty }1+\lim _{n\to \infty }{\frac {1}{n}}\right)^{2}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ \lim _{n\to \infty }{\frac {1}{n}}=0\right.}\\[0.3em]=\ &(1+0)^{2}=1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c582a39ed00e26885a646b4afa917cf9ce4ae4d2)




















































![{\displaystyle {\begin{aligned}{\begin{array}{rrrl}&&f(x)&=1\\[0.5em]{\overset {f(0)\neq 0}{\iff {}}}&&\sin \left({\frac {1}{x}}\right)&=1\\[0.5em]\iff {}&\exists k\in \mathbb {Z} :&{\frac {1}{x}}&={\frac {\pi }{2}}+2k\pi \\[0.5em]\iff {}&\exists k\in \mathbb {Z} :&x&={\frac {1}{{\frac {\pi }{2}}+2k\pi }}\end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ee2a00a2f43e5e9d665e22fb3757d1c17b30b5e)





![{\displaystyle {\begin{aligned}\lim _{n\to \infty }f(x_{n})&=\lim _{n\to \infty }f\left({\frac {1}{{\frac {\pi }{2}}+2n\pi }}\right)\\[0.5em]&=\lim _{n\to \infty }\sin \left({\frac {1}{\frac {1}{{\frac {\pi }{2}}+2n\pi }}}\right)\\[0.5em]&=\lim _{n\to \infty }\sin \left({\frac {\pi }{2}}+2n\pi \right)\\[0.5em]&=\lim _{n\to \infty }1=1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a891cfa8167534da2fbdc7f3ff20d74e618118ce)
