Integral einer Funktion – Serlo „Mathe für Nicht-Freaks“
Dieser Abschnitt ist noch im Entstehen und noch nicht offizieller Bestandteil des Buchs. Gib den Autoren Zeit, den Inhalt anzupassen!
Das Integral ist neben der Ableitung eines der wichtigsten Konzepte der Analysis. Es handelt sich um eine Art Umkehrung der Differentialrechnung. Mit ihm ist es möglich, viele interessante Fragestellungen aus der Flächenberechnung und der Physik zu beantworten.
Wir wollen in diesem Kapitel eine anschauliche Vorstellung des Integrals einführen, bevor wir diese im nächsten Kapitel mithilfe von Riemannintegralen präzisieren.
Motivation
[Bearbeiten]Wir können das Integral im Grunde auf zwei verschiedenen Weisen motivieren. Die erste Möglichkeit sind Probleme aus der Flächenberechnung, zum Beispiel „Wie groß ist die Fläche einer Ellipse?“. Das heißt, wir wollen komplizierte krummlinige Flächeninhalte berechnen.
Beim zweiteren geht es um Fragestellungen wie „Wie groß ist der zurückgelegte Weg meines Autos, wenn die Geschwindigkeit zu jedem Zeitpunkt bekannt ist?“. Wir wollen also, dass wir bei bekannter Ableitung Rückschlüsse auf die Gesamtänderung einer Funktion ziehen können.
Damit sind wir auch an einer Art Verallgemeinerung von Summen und Reihen interessiert. Würde sich nämlich die Geschwindigkeit deines Autos nicht von Moment zu Moment ändern, sondern nur alle 10 Zeiteinheiten, dann wäre es möglich, mithilfe einer Summe den zurückgelegten Weg auszurechnen. Ebenso wäre es möglich, von Flächen, die sich aus Rechtecken unterschiedlicher Größe zusammensetzen, den Flächeninhalt mit einer Summe zu berechnen. Während man also bei Summen über eine endliche Anzahl und bei Reihen über eine abzählbare Menge von Zahlen summiert, wollen wir nun über eine überabzählbare Menge, nämlich alle Funktionswerte einer Funktion, summieren. Dies ist aber mit den konventionellen Methoden nicht möglich. Wir benötigen daher ein neues mathematisches Instrument, das Integral.
Intuitionen des Integrals
[Bearbeiten]Für das Integral gibt es mehrere Intuitionen, die alle eng zusammenhängen:
- Integral als orientierter Flächeninhalt: Das Integral ist der orientierte Flächeninhalt zwischen dem Graphen einer Funktion und der -Achse. Orientiert bedeutet, dass Flächenstücke oberhalb der -Achse positiv und Flächenstücke unterhalb der -Achse negativ gezählt werden.
- Integral als Gesamtänderung einer Funktion: Das Integral ist gleich der Gesamtänderung einer Funktion zwischen den Argumenten und , die an jeder Stelle die Ableitung besitzt.
- Integral als verallgemeinerte Summe: Das Integral ist eine Summe über eine überabzählbare Menge an Summanden.
Definition als Fläche unter dem Graphen
[Bearbeiten]Möglicherweise kennst du bereits die Vorstellung, dass das Integral einer Funktion gleich dem orientierten Flächeninhalt unter dem Graphen dieser Funktion ist. In der folgenden Abbildung ist eine positive und stetige Funktion eingezeichnet. Das Integral der Funktion entspricht dem Inhalt der grauen Fläche, die nach oben durch den Funktionsgraphen, nach unten durch die -Achse sowie nach links und rechts durch die Senkrechten und begrenzt wird:

Ist die Funktion jedoch nicht überall positiv, ist bei dieser Vorstellung die Betonung auf dem orientierten Flächeninhalt wichtig. „Orientiert“ bedeutet, dass Flächenstücke, die unterhalb der -Achse liegen (wo die Funktion negative Funktionswerte annimmt), negativ zum Flächeninhalt beitragen. In der folgenden Abbildung entspricht das Integral der Differenz zwischen der blauen Fläche und der gelben Fläche:
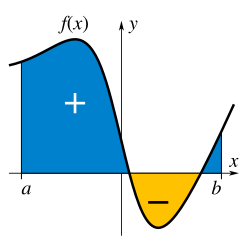
Während also in der Geometrie der Inhalt einer Fläche immer positiv ist, kann das Integral als orientierte Fläche auch negativ werden (wenn die Funktion beispielsweise nur negative Funktionswerte besitzt).
Wir können damit das Integral anschaulich wie folgt definieren:
Definition (Integral als Fläche unter dem Graphen)
Beispiele
[Bearbeiten]Anhand der Definition können wir schon eine Reihe von Integralen berechnen.
Beispiel (Konstante Funktion)
Seien mit . Ferner sei definiert durch für alle . Die Funktion ist somit konstant.
Offensichtlich stellt die Fläche unter dem Graphen von und der x-Achse ein Rechteck mit der Breite und der Höhe dar. Der Flächeninhalt beträgt also . Damit gilt gemäß unserer Definition:

Beispiel (Lineare Funktion)
Sei definiert durch für alle . Die Funktion ist somit linear.
Offensichtlich besteht die Fläche unter dem Graphen von und der x-Achse aus zwei Dreiecken, wobei sich das kleinere unterhalb und das größere Dreieck oberhalb der x-Achse befindet. Das kleine Dreieck hat (siehe Grafik) den Flächeninhalt und das größere den Flächeninhalt . Damit gilt gemäß unserer Definition:
Beachte, dass wir unter dem Integral den orientierten Flächeninhalt verstehen, womit das kleinere Dreieck einen negativen Beitrag zum Integral leistet.
Definition über Stammfunktion
[Bearbeiten]Wir betrachten nun eine andere Vorstellung des Integrals: Sei eine stetige Funktion und eine Stammfunktion von . Eine Stammfunktion von ist dabei eine Funktion, deren Ableitung gleich ist. Es gilt also für alle . Wenn nun eine Stammfunktion von ist, dann können wir definieren:
Definition (Integral über Stammfunktion)
Das Integral ist damit gleich der Veränderung der Stammfunktion zwischen den Argumenten und .
Aufgabe (Wohldefiniertheit)
Zeige, dass die Definition wohldefiniert ist. Das heißt, dass das Ergebnis des Integrals nicht von der Wahl der Stammfunktion abhängt.
Lösung (Wohldefiniertheit)
Sei eine stetige Funktion mit zwei beliebig gewählten Stammfunktionen und . Falls nun gilt , so haben wir gezeigt, dass die Definition des Integrals für jede Stammfunktion zu dem gleichen Ergebnis führt. Das heißt, die Definition ist wohldefiniert, macht also Sinn.
Für beide Stammfunktionen gilt per Definition . Aus dieser Eigenschaft folgt, dass beide Stammfunktionen sich höchstens durch eine additive Konstante unterscheiden können. Es muss also gelten: mit . Durch Benutzung dieser Beziehung folgt nun direkt die Behauptung, denn:Beispiele
[Bearbeiten]Wir zeigen zunächst, dass diese Definition bei konstanten Funktionen zu dem gleichen Ergebnis führt wie die Definition über Flächeninhalte. Wie wir später beim Hauptsatz der Differential- und Integralrechnung sehen werden, gilt dies sogar für alle stetigen Funktionen.
Beispiel (Konstante Funktion)
Seien mit . Ferner sei definiert durch für alle . Die Funktion ist somit konstant.
Die Funktion mit der Funktionsvorschrift ist eine mögliche Stammfunktion von , da gilt. Es folgt gemäß der oben eingeführten Definition:
Dies ist wie erwartet das gleiche Ergebnis wie beim identischen Beispiel aus dem vorherigen Abschnitt.
Probleme mit der Definition
[Bearbeiten]Die Definitionen im vorangegangen Abschnitt sind anschaulich, jedoch zu unexakt. Sie eignen sich nicht dafür, Beweise zu führen und Eigenschaften des Integrals nachzuweisen. Aus diesem Grund wird im Mathematikstudium das Riemannintegral eingeführt, mit dem eine mathematisch präzise Definition für den Ausdruck festgelegt wird. Mit dieser Definition ist es dann vergleichsweise einfach, die charakteristischen Eigenschaften von Integralen exakt herzuleiten.
Eine weitere bisher unbeantwortete Frage lautet, warum die beiden anschaulichen Definitionen vom Integral zum selben Integralbegriff führen. Auch hier wird das Riemannintegral Abhilfe schaffen und die beiden Definitionen durch den Hauptsatz der Differential- und Integralrechnung vereinigen.
Ablage
[Bearbeiten]Um die Frage nach dem Sinn des Integrals beantworten zu können, müssen wir einen Schritt zurückgehen. Betrachten wir hierzu folgendes Grundproblem:
Sei eine unbekannte reellwertige Funktion, die auf einem Intervall definiert ist. Sei die Funktion die Ableitung von , welche uns bekannt ist. Das bedeutet, dass wir an jeder Stelle die momentane Änderungsrate von der Funktion (bezüglich der Variablen ) kennen. Wie können wir nun von diesem Wissen über die aktuelle Änderungsrate an jeder Stelle im Intervall auf die globale Änderung von in diesem Intervall schließen? Wenn wir doch an jeder Stelle aus dem Intervall die aktuelle Änderungsrate von kennen, dann sollte es möglich sein, die Gesamtänderung von in diesem Intervall zu bestimmen. Aber wie groß ist diese?
Mit Hilfe des Integrals können wir das obige Problem lösen. Wir sagen hierzu:
Das Integral ist gleich der Gesamtänderung einer Funktion zwischen den Argumenten und , die an jeder Stelle die Ableitung besitzt.
Das Integral ist damit eine Art der Umkehrung der Ableitung. Während die Ableitung einer Funktion ihre momentane Änderungsrate angibt, können wir mit Hilfe des Integrals die Gesamtänderung einer Funktion bestimmen, wenn wir an jeder Stelle ihre aktuelle Änderungsrate, sprich ihre Ableitung, kennen.
In dieser Intuition des Integrals erkennen wir bereits eine Grundvorstellung des Intregrals: Die Gesamtänderung von im Intervall ist gleich der Differenz . Wenn nun das Integral gleich dieser Gesamtänderung ist, dann muss gelten:
Wenn nun an jeder Stelle aus dem Intervall die Ableitung von gleich ist (wenn also ist), dann ist eine Stammfunktion von . Damit entspricht unsere obige Intuition der Grundvorstellung, dass das Integral gleich der Veränderung der Stammfunktion ist.
Im Folgenden benötigen wir noch analog zum Ableitungszeichen eine Notation. Dazu verwenden wir:
Wir sagen dazu: Das Integral von bis über nach .
Die genaue Bedeutung des Symbols soll uns noch unbekannt sein. Erst durch eine Definition bekommt der Ausdruck schließlich einen Sinn. Wir werden im Folgenden zwei unterschiedliche Möglichkeiten betrachten, dem Symbol eine Bedeutung zuzuschreiben. Dabei orientieren wir uns an die Problemstellungen aus der Motivation.
Im nächsten Kapitel über Riemannintegrale einfügen:
- Bezeichnung Unterteilung/Stützpunkte prüfen?
Wir wissen nun, wozu wir das Integral einsetzen können: Um die Gesamtänderung einer Funktion über ein Intervall zu bestimmen, deren Ableitung wir an jeder Stelle des Definitionsbereichs kennen. Sei die bekannte Ableitung von . Als erste Annäherung an dieses Ziel könnten wir die Änderungsrate am Startpunkt (also ) betrachten und mit der Länge des Intervall multiplizieren um eine Approximation an die Gesamtänderung zu erhalten. Es sollte also gelten:

Für kleine Intervalle ist dies auch tatsächlich eine gute Näherung, wie wir aus der Definition der Ableitung als Steigung der bestmöglichen linearen Approximation sehen können.
Zur Wiederholung: Eine differenzierbare Funktion können wir in der Nähe eines Punktes durch ihre Ableitung an diesem Punkt approximieren:
Diese Approximation ist gut, wenn der Abstand zwischen und klein ist, und wird im Allgemeinen schlechter, wenn dieser Abstand größer wird.
Um die Näherung der Gesamtänderung zu verbessern, können wir das Gesamtintervall in zwei kleinere Teilintervalle und einteilen. Dann verwenden wir für jedes der beiden die obige Approximation und addieren die Ergebnisse.

Ganz allgemein können wir das Gesamtintervall in Teilintervalle unterteilen, auf jedem davon eine Näherung für die Gesamtänderung bestimmen und all diese aufsummieren. Dies führt uns zum Begriff der Unterteilung:
Definition ((Riemann-)Zerlegung)
Eine (Riemann-)Zerlegung eines Intervalles ist eine Menge von Intervallen mit zusammen mit einer Menge von Stützstellen , sodass in jedem Intervall genau eine Stützstelle liegt, d.h. .
Als Feinheit der Zerlegung bezeichnen wir dann die Breite des größten Intervalls der Zerlegung, also die Zahl .
Für jede solche Zerlegung können wir dann wie folgt eine Approximation an die Gesamtänderung der Funktion unter ausschließlicher Verwendung ihrer Ableitung definieren:
Definition (Riemannsumme)
Sei eine Funktion und eine Zerlegung. Dann ist die Riemannsumme von bezüglich definiert als
Wir erwarten nun, dass sich die Riemannsumme für immer feiner werdende Zerlegungen immer weiter dem tatsächlichen Wert der Gesamtänderung annähert. Es sollte also gelten:
Dies ist - wie wir gleich sehen werden - auch tatsächlich der Fall. Und wie du siehst benötigen wir zum Berechnen der linken Seite ausschließlich die Ableitung , nicht jedoch die ursprüngliche Funktion . Daher können wir versuchen die linke Seite ganz allgemein für beliebige Funktionen zu definieren. Auch solche, die nicht als Ableitung einer anderen Funktion gegeben sind. Wir nennen diesen Grenzwert - so er denn existiert - dann das Integral von .
Bevor wir diese Definition jedoch formalisieren, sollten wir aber noch kurz über eine andere Frage nachdenken: Warum müssen wir den Grenzwert über alle Zerlegungen betrachten? Genügt es nicht den Grenzwert über eine feste Folge von immer feiner werdenden Zerlegungen zu betrachten? Etwa Zerlegungen in gleich große Intervalle, wobei immer größer wird?
Dazu betrachten wir die sogenannte Dirichlet-Funktion:
Diese Funktion bildet also alle rationalen Zahlen auf und alle irrationalen Zahlen auf ab. Für die Zerlegungen
erhalten wir die Riemannsumme
Der Grenzwert über diese Zerlegungen wäre daher ebenfalls .
Verwenden wir jedoch Zerlegungen , deren Stützstellen lauter irrationale Zahlen sind, so gilt:
Also wäre der über diese Zerlegungen berechnete Grenzwert .
In Fall der Dirichlet-Funktion würde also das Integral von der Wahl der Folge von Zerlegungen abhängen, die wir zu seiner Bestimmung verwenden. Um derartige Probleme zu vermeiden, wollen wir das Integral einer Funktion nur in dem Fall definieren, dass jede Folge immer feiner werdender Zerlegungen zum selben Grenzwert führen.
Definition (Riemann-Integral)
Eine Funktion heißt Riemann-integrierbar, wenn es eine Zahl gibt, sodass gilt
d.h. wenn die Riemannsumme für (beliebige) immer feiner werdene Zerlegungen gegen den Wert konvergiert.
Wir bezeichnen dann als (Riemann-)Integral von von bis .
Zusammenhang hzur Intuition?









![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)





![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)




![{\displaystyle f:[-2,3]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/44dbb8a4897b96ce21023eb414a28509d63358ca)

![{\displaystyle x\in [-2,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51fcc4cace3afb6b2d2b6701df837ee9f25fcd12)



![{\displaystyle F:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cacd74b0bb95ed9ddf45676b1ad0f3d618c4cdc)





















![{\displaystyle [a,c]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70b45aa26fb924cdd37786af1adcf5d58cfe15af)
![{\displaystyle [c,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07f3f774df12e18b9f2bb94333ff320bbd2c308d)



![{\displaystyle {\mathcal {Z}}=\{[x_{0},x_{1}],[x_{1},x_{2}],\dots ,[x_{n-1},x_{n}]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/030fa7485d5f52029ba6a3b0cd5647741ea98a0b)


![{\displaystyle t_{i}\in [x_{i-1},x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82811fdf676362991070d2ed9c835e61f95590f6)



![{\displaystyle D:[0,1]\to \mathbb {R} :x\mapsto {\begin{cases}1,&x\in \mathbb {Q} \\0,&x\notin \mathbb {Q} \end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afae18add98633afbf8761c48e71da1a24399e61)


![{\displaystyle ({\mathcal {Z}},{\mathcal {T}}):=\left(\{[0,{\tfrac {1}{n}}],[{\tfrac {1}{n}},{\tfrac {2}{n}}],\dots ,[{\tfrac {n-1}{n}},1]\},\{0,{\tfrac {1}{n}},\dots ,{\tfrac {n-1}{n}}\}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7606bf2be66b1fb186395ac11eb75e79bb4a2d35)







