Ableitung und Differenzierbarkeit – Serlo „Mathe für Nicht-Freaks“
Mit der Ableitung werden wir eines der wichtigsten Konzepte der Analysis kennenlernen. Die Ableitung entspricht der Änderungsrate einer Funktion. Sie wird in den Naturwissenschaften oft genutzt, um in mathematischen Modellen die Veränderung eines Systems zu modellieren. Mit Hilfe der Ableitung können wir eine Funktion auf viele ihrer Eigenschaften untersuchen.
Intuitionen der Ableitung
[Bearbeiten]Für die Ableitung gibt es mehrere Intuitionen, die alle eng zusammenhängen:
- Ableitung als momentane Änderungsrate: Die Ableitung entspricht dem, was wir intuitiv als momentane Änderungsrate einer Funktion verstehen. Eine Änderungsrate beschreibt dabei, wie stark sich eine Größe bezüglich einer anderen Bezugsgröße ändert. Bei der momentanen Änderungsrate wird diese Bezugsgröße als „unendlich klein“ angenommen. Es wird also der Grenzwert der Änderungsrate betrachtet, wenn die Bezugsgröße gegen Null konvergiert. Ein Beispiel hierfür ist die Geschwindigkeit. Diese ist die momentane Änderungsrate des Ortes bezüglich der Zeit und gibt an, wie stark sich der Ort eines Objekts zu einem bestimmten Zeitpunkt mit der Zeit ändert.
- Ableitung als Tangentensteigung: Die Ableitung entspricht der Steigung, die die Tangente des Graphen an der Stelle der Ableitung besitzt. Damit löst die Ableitung das geometrische Problem, die Tangente an einen Graphen durch einen Punkt zu bestimmen.
- Ableitung als Steigung der lokal besten linearen Approximation: Jede an einer Stelle ableitbare Funktion kann in einer Umgebung um diesen Punkt gut durch eine lineare Funktion approximiert werden. Die Ableitung entspricht der Steigung dieser linearen Funktion. Damit kann die Ableitung genutzt werden, um Funktionen lokal durch lineare Funktionen gut anzunähern.
- Ableitung als verallgemeinerte Steigung: Zunächst ist der Begriff der Steigung einer Funktion nur für lineare Funktionen definiert. Man kann die Ableitung aber benutzen, um die Steigung auch für nicht-lineare Funktionen zu definieren.
Diese Intuitionen werden wir im Folgenden detailliert besprechen und aus ihnen eine formale Definition der Ableitung herleiten. Außerdem werden wir sehen, dass ableitbare Funktionen „knickfrei“ sind, weshalb sie auch glatte Funktionen genannt werden.
Ableitung als momentane Änderungsrate
[Bearbeiten]Berechnung der Ableitung
[Bearbeiten]Die Ableitung entspricht der momentanen Änderungsrate einer Funktion . Wie kann diese momentane Änderungsrate einer Funktion bestimmt oder definiert werden? Sei zum Beispiel eine reellwertige Funktion, die folgenden Graph besitzt:
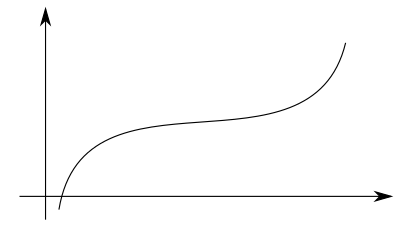
So kann eine physikalische Größe in Abhängigkeit von einer anderen Größe beschreiben. Beispielsweise könnte dem zurückgelegten Weg eines Objekts zum Zeitpunkt entsprechen. könnte auch der Luftdruck in der Höhe oder die Populationsgröße einer Art zum Zeitpunkt sein. Nehmen wir nun das Argument , an dem die Funktion den Funktionswert besitzt:

Nehmen wir einmal an, dass der zurückgelegte Weg eines Autos zum Zeitpunkt ist. Dann ist die momentane Änderungsrate von an der Stelle gleich der Geschwindigkeit des Objekts zum Zeitpunkt . Wie kann diese Geschwindigkeit bestimmt werden?
Anstatt die Geschwindigkeit direkt zu berechnen, können wir sie schätzen. Wir nehmen einen Zeitpunkt in der Zukunft und schauen, welchen Weg das Auto im Zeitraum von bis zurückgelegt hat. Der in dieser Zeit zurückgelegte Weg ist gleich der Differenz , während die Zeitdifferenz gleich ist. Nun ist die Geschwindigkeit gleich dem Quotienten . Damit hat das Auto im Zeitraum von nach die durchschnittliche Geschwindigkeit
Dieser Quotient, der die durchschnittliche Änderungsrate von der Funktion im Intervall angibt, wird Differenzenquotient genannt. Entsprechend seines Namens ist er ein Quotient von zwei Differenzen. In folgender Abbildung sehen wir, dass dieser Differenzenquotient gleich der Steigung derjenigen Sekante ist, die durch die Punkte und geht:
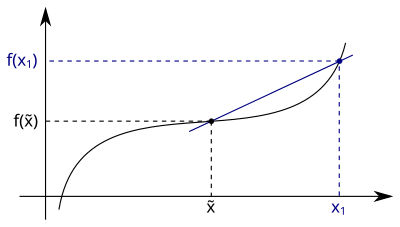
Diese durchschnittliche Geschwindigkeit ist eine erste Approximation der aktuellen Geschwindigkeit unseres Autos zum Zeitpunkt . Nun muss die Bewegung des Autos zwischen den Zeitpunkten und nicht gleichförmig verlaufen sein – es kann beschleunigen oder abbremsen. Die momentane Geschwindigkeit zum Zeitpunkt ist also im Allgemeinen eine andere als die durchschnittliche Geschwindigkeit im Zeitraum zwischen und . Ein besseres Ergebnis sollten wir erhalten, wenn wir den Zeitraum für die Berechnung der durchschnittlichen Geschwindigkeit verkürzen. Wir betrachten also einen Zeitpunkt , der näher an liegt, und bestimmen die durchschnittliche Geschwindigkeit für den neuen Zeitraum zwischen und :

Diesen Prozess wiederholen wir beliebig oft. Wir betrachten also eine Folge von Zeitpunkten, die alle von verschieden sind und die gegen konvergieren. Für jedes berechnen wir die durchschnittliche Geschwindigkeit des Autos im Zeitraum von bis . Je kürzer ist, desto weniger sollte das Auto in diesem Zeitraum beschleunigen oder abbremsen können und umso mehr entspricht dann die durchschnittliche Geschwindigkeit der momentanen Geschwindigkeit des Autos zum Zeitpunkt :

Weil der Zeitabstand beliebig klein wird (es ist ), sollte die Folge der Durchschnittsgeschwindigkeiten gleich der momentanen Geschwindigkeit des Autos zum Zeitpunkt sein.
Damit haben wir eine Methode gefunden, um die momentane Änderungsrate von an der Stelle zu bestimmen: Wir nehmen eine beliebige Folge von Argumenten , die alle verschieden von sind und für die ist. Für jedes bestimmen wir den Quotienten . Die momentane Änderungsrate ist der Grenzwert dieser Quotienten:
Für die Ableitung von an der Stelle schreiben wir . Damit können wir notieren:
Konkretisierung
[Bearbeiten]Nun haben wir in unserem Beispiel stets Zeitpunkte in der Zukunft von betrachtet. Was passiert, wenn wir einen Zeitpunkt in der Vergangenheit von betrachten? Hier erhalten wir folgendes Bild:

Die durchschnittliche Geschwindigkeit im Zeitraum von bis ist dann gleich . Wenn wir diesen Quotienten um erweitern, erhalten wir:
Wir erhalten denselben Term wie im vorherigen Abschnitt. Dieser gibt die durchschnittliche Geschwindigkeit an, egal ob oder ist. Damit sollte dessen Wert im Fall auch nah an der momentanen Geschwindigkeit des Autos zum Zeitpunkt liegen, wenn nur hinreichend nah an liegt. Es ist also
wobei eine beliebige Folge von Argumenten ungleich mit ist. Die Folgenglieder von können dabei je nach Index manchmal größer und manchmal kleiner als sein:

Verfeinerung der Definition
[Bearbeiten]Sei nun eine beliebige reellwertige Funktion und sei . Wie wir im obigen Abschnitt gesehen haben, ist
wobei eine Folge von Argumenten ungleich ist, die gegen konvergiert. Damit es mindestens eine solche Folge von Argumenten gibt, muss ein Häufungspunkt vom Definitionsbereich sein (eine Zahl ist genau dann Häufungspunkt einer Menge, wenn es eine Folge in dieser Menge ungleich dieser Zahl gibt, die gegen diese Zahl konvergiert). Das hört sich jetzt vielleicht komplizierter an, als es häufig ist. In den meisten Fällen ist ein Intervall und dann ist jedes ein Häufungspunkt von . Für die Definition des Differentialquotienten soll es egal sein, welche Folge wir wählen. Dementsprechend können wir die Ableitung definieren:
Sei mit und sei ein Häufungspunkt von . Die Funktion ist an der Stelle ableitbar mit der Ableitung , wenn für jede Folge von Argumenten ungleich und mit gilt:
Nun können wir diese Definition abkürzen, indem wir die Grenzwertdefinition für Funktionen benutzen. Zur Erinnerung: Es ist nach Definition genau dann , wenn für alle Folgen von Argumenten ungleich mit ist. Also:
Sei mit und sei ein Häufungspunkt von . Die Funktion ist an der Stelle ableitbar mit der Ableitung , wenn gilt:
Die h-Methode
[Bearbeiten]
Es gibt eine weitere Möglichkeit, die Ableitung zu definieren. Hierzu gehen wir vom Differentialquotienten aus und führen die Variablenersetzung durch. Die neue Variable ist also der Unterschied zwischen der Stelle , bei der die Ableitung bestimmt werden soll, zu dem Punkt, wo der Differenzenquotient gebildet wird. Für geht . Damit können wir die Ableitung auch definieren als
Sei mit und sei ein Häufungspunkt von . Die Funktion ist an der Stelle ableitbar mit der Ableitung , wenn gilt:
Anwendungen in den Naturwissenschaften
[Bearbeiten]Die Ableitung haben wir als momentane Änderungsrate einer Größe kennengelernt. Als solche tritt sie in den Naturwissenschaften häufig auf. Folgende Größen sind beispielsweise als Änderungsraten definiert:
- Geschwindigkeit: Die Geschwindigkeit ist die momentane Änderungsrate des zurückgelegten Wegs eines Objekts.
- Beschleunigung: Die Beschleunigung ist die momentane Änderungsrate der Geschwindigkeit eines Objekts.
- Druckänderung: Sei der Luftdruck in der Höhe . Die Ableitung ist die Änderungsrate des Luftdrucks mit der Höhe. Dieses Beispiel zeigt, dass die Änderungsrate nicht immer auf die Zeit bezogen sein muss. Es kann auch die Änderungsrate bezüglich einer anderen Größe, wie zum Beispiel der Höhe, sein.
- Chemische Reaktionsrate: Betrachten wir eine chemische Reaktion . Sei die Konzentration des Stoffs zum Zeitpunkt . Die Ableitung ist die momentane Änderungsrate der Stoffkonzentration von und damit gibt sie an, wie viel des Stoffs in den Stoff umgesetzt wird. Damit gibt die chemische Reaktionsrate für die Reaktion an.
- Änderung der Population: Oft betrachtet man die Anzahl an Individuen in einer Population (zum Beispiel die Anzahl an Menschen auf dem Planeten, die Anzahl an Bakterien in einer Petrischale, die Anzahl an Tieren einer Gattung oder die Anzahl der Atome eines radioaktiven Stoffs). Die Ableitung gibt die momentane Änderungsrate der Individuen zum Zeitpunkt wieder.
Definitionen
[Bearbeiten]Ableitung und Differenzierbarkeit
[Bearbeiten]Definition (Ableitung)
Sei mit und sei ein Häufungspunkt von . Die Funktion ist an der Stelle ableitbar mit der Ableitung , wenn gilt:
Äquivalent kann in der Definition auch gefordert werden:
Eine an der Stelle ableitbare Funktion nennt man an der Stelle differenzierbar. Eine Funktion heißt ableitbar oder differenzierbar, wenn an jeder Stelle ihres Definitionsbereichs der obige Grenzwert existiert. Differenzierbare Funktionen sind also überall, wo sie definiert sind, differenzierbar.
Differenzenquotient und Differentialquotient
[Bearbeiten]Die Begriffe „Differenzenquotient“ und „Differentialquotient“ sind folgendermaßen definiert:
Definition (Differenzenquotient)
Der Differenzenquotient einer Funktion mit im Intervall ist der Quotient
Dieser Quotient entspricht der Steigung der Sekanten zwischen den Punkten und .
Definition (Differentialquotient)
Sei mit . Sei ein Häufungspunkt des Definitionsbereichs . Der Differentialquotient dieser Funktion an der Stelle ist der Grenzwert:
Wenn dieser Grenzwert existiert und eine reelle Zahl ist, entspricht er der Ableitung .
Ableitungsfunktion
[Bearbeiten]
Ist eine Funktion mit an jeder Stelle ihres Definitionsbereichs differenzierbar, so besitzt an jedem Punkt in eine Ableitung. Die Funktion, die jedem Argument ihre Ableitung zuordnet, heißt Ableitungsfunktion von :
Definition (Ableitungsfunktion)
Sei eine differenzierbare Funktion mit . Wir definieren die Ableitungsfunktion durch
Ist die Ableitungsfunktion zusätzlich noch stetig, so nennt man stetig differenzierbar.
Warnung
Die Begriffe „stetig differenzierbar“ und „differenzierbar“ sind nicht äquivalent. Die Stetigkeit der Ableitungsfunktion ist eine echte zusätzliche Forderung.
Notationen
[Bearbeiten]Geschichtlich bedingt wurden unterschiedliche Notationen entwickelt, um die Ableitung einer Funktion darzustellen. In diesem Artikel haben wir bisher nur die Notation für die Ableitung von kennengelernt. Sie geht auf den Mathematiker Joseph-Louis Lagrange zurück, der sie 1797 einführte[1]. Mit dieser Notation wird die zweite Ableitung von mit und die -te Ableitung mittels notiert.
Isaac Newton - neben Leibniz der Begründer der Differentialrechnung - notierte die erste Ableitung von mit , entsprechend notierte er die zweite Ableitung durch . Heutzutage wird diese Schreibweise hauptsächlich in der Physik für die Ableitung nach der Zeit verwendet.
Gottfried Wilhelm Leibniz führt für die erste Ableitung von nach der Variablen die Notation ein. Gelesen wird diese Schreibweise als „d f von x nach d x“. Für die zweite Ableitung notierte Leibniz und die -te Ableitung wird mittels notiert.
Bei den Schreibweisen von Leibniz handelt es sich nicht um einen Bruch! Die Symbole und werden als Differentiale bezeichnet, welche aber in der modernen Analysis (abgesehen von der Theorie der sogenannten „Differentialformen“) lediglich eine symbolische Bedeutung haben. Sie sind nur in dieser Schreibweise als formaler Differentialquotient erlaubt. Nun gibt es Anwendungen der Ableitung (wie zum Beispiel die „Kettenregel“ oder „Integration durch Substitution“), in denen man mit den Differentialen beziehungsweise so umgehen kann, als seien sie gewöhnliche Variablen und in denen man so zu richtigen Lösungen kommt. Da es aber in der modernen Analysis keine Differentiale gibt, handelt es sich bei solchen Rechnungen nicht um formal richtige Argumentationen.
Die Notation oder für die erste Ableitung von geht auf Leonhard Euler zurück. In dieser Notation wird die zweite Ableitung durch oder und die -te Ableitung durch oder geschrieben.
Übersicht zu allen Notationen
[Bearbeiten]| Schreibweise von … | 1. Ableitung | 2. Ableitung | -te Ableitung |
|---|---|---|---|
| Lagrange | |||
| Newton | |||
| Leibniz | |||
| Euler |
Ableitung als Tangentensteigung
[Bearbeiten]

Die Ableitung entspricht dem Grenzwert . Dabei ist der Differenzenquotient die Steigung der Sekante zwischen den Punkten und . Bei der Grenzwertbildung geht diese Sekante in die Tangente über, die den Graphen von im Punkt berührt:
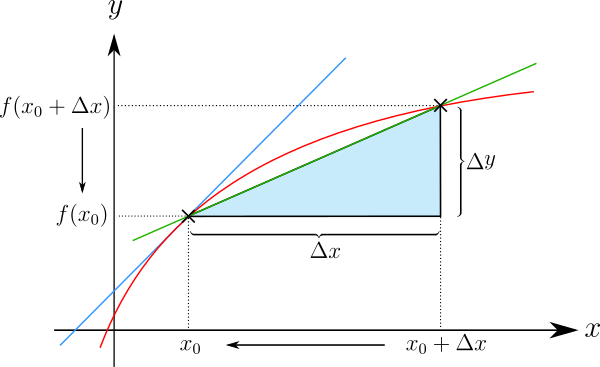
Damit ist die Ableitung gleich der Steigung der Tangente am Graphen durch den Punkt . Die Ableitung kann also genutzt werden, um die Tangente an einem Graphen zu bestimmen. Somit löst sie auch ein geometrisches Problem. Mit kennen wir die Steigung der Tangente und mit einen Punkt auf der Tangente. Damit können wir die Funktionsgleichung dieser Tangente bestimmen.
Verständnisfrage: Wie lautet die Tangentengleichung, wenn ihre Steigung gleich und sie durch den Punkt geht?
Die allgemeine Formel einer linearen Funktion ist . Dabei ist die Steigung von und ist der Schnittpunkt von mit der y-Achse. Sei nun die gesuchte Tangente. Diese besitzt die Steigung und damit gilt .
Wir müssen noch bestimmen. Weil durch den Punkt geht, ist
Damit ist
Durch Kenntnis der Ableitung kann also die Tangengleichung bestimmt werden.
Ableitung als Steigung der lokal besten linearen Approximation
[Bearbeiten]Approximation einer differenzierbaren Funktion
[Bearbeiten]Die Ableitung kann auch zur Approximation einer Funktion genutzt werden. Um diese Approximation zu finden gehen wir von der Grenzwertdefinition der Ableitung aus:
Der Differenzenquotient liegt also beliebig nah an der Ableitung , wenn hinreichend nah an ist. Für können wir schreiben:
Im Folgenden nehmen wir an, dass der Ausdruck für „ ist ungefähr so groß wie “ wohldefiniert ist und den üblichen Rechengesetzen für Gleichungen gehorcht. Damit können wir diese Gleichung umstellen zu
Wenn hinreichend nah an liegt, dann ist ungefähr gleich dem Wert . Dieser Wert kann somit in der Nähe der Ableitungsstelle als Approximation von verwendet werden. Dabei ist die Funktion mit der Zuordnungsvorschrift eine lineare Funktion, da ein beliebiger aber fester Punkt ist.
Die Zuordnungsvorschrift beschreibt dabei die Tangente, die den Funktionsgraphen an der Stelle der Ableitung berührt. Die Tangente ist also in der Nähe des Berührungspunkts eine gute Approximation des Funktionsgraphen. Dies zeigt auch das folgende Diagramm. Wenn man in einer differenzierbaren Funktion an einer Stelle nah genug reinzoomt, so sieht der Funktionsgraph näherungsweise wie eine Gerade aus:
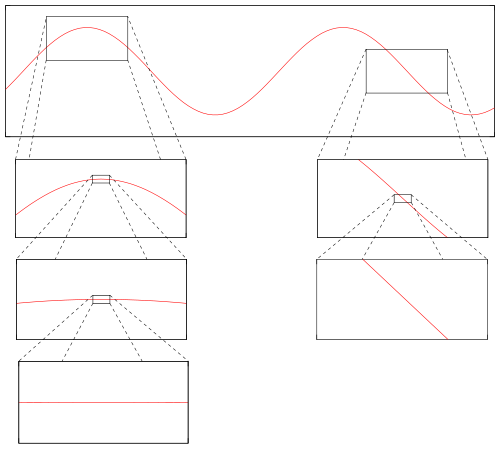
Diese Gerade wird durch die Zuordnungsvorschrift beschrieben und entspricht der Tangente des Graphen an dieser Stelle.
Beispiel: Kleinwinkelnäherung des Sinus
[Bearbeiten]Schauen wir uns das gerade Besprochene an einem Beispiel an. Hierfür betrachten wir die, für gewöhnlich aus der Schule bekannte, Sinusfunktion . Ihr Graph ist

Wie wir noch sehen werden, ist die Ableitung des Sinus der Kosinus und damit ist
Nach dem Abschnitt zur Approximation gilt damit
In der Nähe der Null ist also . Dies ist die sogenannte Kleinwinkelnäherung. So kann durch angenähert werden. Mit ist diese Annäherung auch recht gut. Im folgenden Diagramm sieht man, dass in der Nähe des Nullpunkts die Sinusfunktion ungefähr durch beschrieben werden kann:

Das Diagramm zeigt aber auch, dass diese Approximation nur in der Nähe der Ableitungstelle gut ist. Bei Werten weit weg von der Null unterscheidet sich stark von . Die Approximation ist folglich nicht immer sinnvoll.
Qualität der Approximation
[Bearbeiten]Wie gut ist die Approximation ? Um dies zu beantworten, sei derjenige Wert mit
Der Wert ist damit der Unterschied zwischen dem Differenzenquotienten und der Ableitung . Dieser Unterschied verschwindet für den Grenzübergang , weil für diesen Grenzübergang der Differenzenquotient in den Differentialquotienten, also der Ableitung , übergeht. Es gilt also . Nun können wir die obige Gleichung umstellen und erhalten so
Der Fehler zwischen und ist damit gleich dem Term . Wegen ist auch
Der Fehler verschwindet also für . Wir können aber noch mehr sagen: fällt schneller als ein linearer Term gegen Null ab. Selbst wenn wir durch teilen und so diesen Term in der Nähe von stark vergrößern, verschwindet für . Es ist nämlich
Der Fehler in der Approximation fällt also für schneller als linear gegen Null ab. Fassen wir die bisherige Argumentation in einem Satz zusammen:
Satz (Approximation einer differenzierbaren Funktion)
Sei und sei ein Häufungspunkt von . Sei außerdem an der Stelle differenzierbar mit der Ableitung . Seien und so definiert, dass für alle gilt
Dann verschwindet der Fehlerterm für , das heißt . Für gilt dementsprechend .
Alternative Definition der Ableitung
[Bearbeiten]Dass differenzierbare Funktionen durch lineare Funktionen approximiert werden können, charakterisiert den Begriff der Ableitung. Jede Funktion ist an der Stelle ableitbar, wenn eine reelle Zahl sowie eine Funktion existieren, so dass und gelten. Ihre Ableitung ist dann . Es gilt nämlich
Somit können wir die Ableitung auch wie folgt definieren:
Definition (Alternative Definition der Ableitung)
Sei eine Funktion und ein Häufungspunkt von . Die Funktion ist genau dann im Punkt differenzierbar mit der Ableitung , wenn eine Funktion existiert, so dass
und gelten.
Beschreibung der Ableitung über stetige Funktion
[Bearbeiten]Es gibt eine weitere Charakterisierung der Ableitung. Wir beginnen hierfür mit der Formel
Dabei ist der Unterschied zwischen dem Differenzenquotienten und der Ableitung, welcher für verschwindet. Wenn wir diese Formel umstellen erhalten wir:
Dabei erfüllt für die Eigenschaft
Damit kann in eine an der Stelle stetige Funktion erweitert werden, wobei der Funktionswert gewählt wird. Diese Darstellung einer ableitbaren Funktion ermöglicht eine weitere Charakterisierung stetiger Funktionen:
Satz (Äquivalente Charakterisierung der Ableitung)
Eine Funktion ist in genau dann differenzierbar, wenn es eine in stetige Abbildung gibt, die folgende Gleichung erfüllt:
In diesem Fall ist .
Beweis (Äquivalente Charakterisierung der Ableitung)
Beweisschritt: mit mit
Gelte also , wobei eine Funktion mit sei. Nun gilt für
Setzen wir nun . So folgt
Also ist stetig (fortsetzbar) in mit .
Beweisschritt: mit mit
Gelte nun mit einer in stetigen Funktion , wobei . Für gilt dann
Setzen wir nun . So folgt
Ableitung als verallgemeinerte Steigung
[Bearbeiten]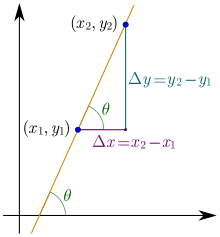
Die Steigung ist zunächst nur für lineare Funktionen mit der Zuordnungsvorschrift mit definiert. Bei solchen Funktionen ist die Steigung gleich dem Wert und kann über den Differenzenquotienten berechnet werden. Für zwei verschiedene Argumente und aus dem Definitionsbereich von gilt nämlich
Nun ist auch die Ableitung von an jedem Häufungspunkt des Definitionsbereichs:
Die Ableitung linearer Funktionen ist daher stets gleich ihrer Steigung. Der Begriff der Ableitung stimmt also bei linearen Funktionen mit jenem der Steigung überein. Außerdem ist er bei allen differenzierbaren Funktionen definiert. Somit stellt die Ableitung eine Verallgemeinerung der Steigung dar. Zur Erinnerung: Ein Begriff ist genau dann eine Verallgemeinerung eines anderen Begriffs , wenn überall dort mit übereinstimmt, wo definiert ist und auf weitere Fälle angewandt werden kann.
Somit können wir die Ableitung als momentane Steigung einer Funktion ansehen. Der Steigungsbegriff geht damit von einer globalen Eigenschaft (die Steigung bei linearen Funktionen ist für die gesamte Funktion definiert), in eine lokale Eigenschaft über (die Ableitung ist die momentane Änderungsrate einer Funktion).
Beispiele
[Bearbeiten]Beispiel einer differenzierbaren Funktion
[Bearbeiten]

Beispiel (Quadratfunktion ist an der Stelle ableitbar)
Die Quadratfunktion ist ableitbar an der Stelle mit der Ableitung . Dieses Resultat erhalten wir, wenn wir den Differentialquotienten an der Stelle auswerten:
Der letzte Ausdruck zeigt, dass der Differenzenquotient gleich für ist (für ist der Differenzenquotient nicht definiert, weil sonst durch Null geteilt wird). Nun müssen wir den Grenzwert von für bestimmen:
Damit ist die Ableitung von an der Stelle gleich , also . Analog können wir die Ableitung von an einer beliebigen Stelle bestimmen:
Damit ist die Ableitung der Quadratfunktion an der Stelle gleich . Die Ableitungsfunktion von ist damit die Funktion .
Beispiel einer nicht differenzierbaren Funktion
[Bearbeiten]
Beispiel (Betragsfunktion ist nicht differenzierbar)
Wir betrachten die Betragsfunktion und prüfen, ob sie an der Stelle ableitbar ist. Hier wählen wir die Folgen , und mit
Diese konvergieren alle gegen . Nun betrachten wir die Differentialquotienten zu den einzelnen Folgen. Für ergibt sich:
Für bekommen wir:
Für gilt:
Dieser Grenzwert für die Folge existiert nicht. Wir sehen daher, dass je nach gewählter Folge der Grenzwert unterschiedlich ist oder nicht existiert. Damit existiert nach Definition auch nicht der Grenzwert , womit die Funktion an der Stelle nicht ableitbar ist. Die Betragsfunktion besitzt am Nullpunkt keine Ableitung.
Links- und rechtsseitige Ableitung
[Bearbeiten]Definition
[Bearbeiten]Die Ableitung einer Funktion ist der Grenzwert des Differenzenquotienten für . Der Differenzenquotient kann dabei als eine Funktion aufgefasst werden, die für alle außer für definiert ist. Damit handelt es sich beim Grenzwert um einen Grenzwert einer Funktion.
Die Begriffe „linksseitiger und rechtsseitiger Grenzwert“ können auch für den Differenzenquotienten betrachtet werden. So erhalten wir die Begriffe „linksseitige“ beziehungsweise „rechtsseitige“ Ableitung. Bei der linksseitigen Ableitung werden nur Sekanten links von der betrachteten Stelle evaluiert. Es werden also nur Differenzenquotienten betrachtet, bei der ist. Dann wird überprüft, ob diese Differenzenquotienten für den Grenzübergang gegen eine Zahl konvergieren. Wenn ja, dann ist diese Zahl der linksseitige Grenzwert. Also:
Dabei ist die Schreibweise für die linksseitige Ableitung von an der Stelle . Damit dieser Grenzwert Sinn ergibt, muss es mindestens eine Folge von Argumenten geben, die von links gegen konvergiert. Es muss also ein Häufungspunkt der Menge sein.
Definition (Linksseitige Ableitung)
Sei eine Funktion und ein Häufungspunkt der Menge . Die Zahl ist die linksseitige Ableitung von an der Stelle , wenn gilt
Dies ist äquivalent dazu, dass für alle Folgen aus mit und sowie gilt
Auf analoge Weise kann die rechtsseitige Ableitung folgendermaßen definiert werden:
Definition (Rechtsseitige Ableitung)
Sei eine Funktion und ein Häufungspunkt der Menge . Die Zahl ist die rechtsseitige Ableitung von an der Stelle , wenn gilt
Dies ist äquivalent dazu, dass für alle Folgen aus mit und sowie gilt
Funktionen besitzen an einer Stelle in ihrem Definitionsbereich nur dann einen Grenzwert, wenn sowohl der linksseitige als auch der rechtsseitige Grenzwert an dieser Stelle existieren und beide Grenzwerte übereinstimmen. Diesen Satz können wir direkt auf Ableitungen anwenden:
Eine Funktion ist an einer Stelle in ihrem Definitionsbereich genau dann ableitbar, wenn dort sowohl die linksseitige als auch die rechtsseitige Ableitung existieren und beide Ableitungen übereinstimmen.
Beispiel
[Bearbeiten]Wir haben bereits gezeigt, dass die Betragsfunktion an der Stelle nicht differenzierbar ist. Jedoch können wir zeigen, dass die rechtsseitige Ableitung an dieser Stelle existiert und gleich ist:
Analog können wir zeigen, dass die linksseitige Ableitung an derselben Stelle gleich ist:
Weil die rechtsseitige und die linksseitige Ableitung nicht übereinstimmen, ist die Betragsfunktion an der Stelle nicht ableitbar. Sie besitzt dort zwar links- und rechtsseitige Ableitungen, aber keine Ableitung.
Differenzierbare Funktionen sind knickfrei
[Bearbeiten]Im obigen Beispiel haben wir gesehen, dass die Betragsfunktion nicht differenzierbar ist. Dies liegt daran, dass die Betragsfunktion an der Stelle „einen Knick hat“, so dass die linksseitige und die rechtsseitige Ableitung verschieden ist. Wenn wir von links an gehen, ist die Ableitung gleich , während die Ableitung von der rechten Seite aus gleich ist. Der Knick in der Betragsfunktion verhindert also die Differenzierbarkeit.
Wenn also eine Funktion einen Knick besitzt, ist sie an dieser Stelle nicht ableitbar. Sprich: Ableitbare Funktionen sind knickfrei. Man nennt sie deswegen auch glatte Funktionen. Dies heißt aber nicht, dass knickfreie Funktionen automatisch ableitbar sind. Betrachten wir als Gegenbeispiel die Vorzeichenfunktion mit der Definition
Ihr Graph ist

Diese ist an der Nullstelle nicht ableitbar, da dort wegen dem Sprung in der Funktion der Differenzenquotient gegen Unendlich konvergiert. Für die rechtsseitige Ableitung gilt beispielsweise:
Auch besitzt die Vorzeichenfunktion an der Nullstelle keinen Knick. Schließlich macht die Funktion dort einen Sprung und es wäre daher sinnlos dort von einem „Knick in der Funktion“ zu sprechen. Hierzu müsste die Funktion an der betrachteten Stelle stetig sein.
Am Beispiel der Vorzeichenfunktion sehen wir, dass Knickfreiheit und Ableitbarkeit nicht dasselbe sein kann. Knickfreiheit ist allerdings eine Voraussetzung für Ableitbarkeit. Folglich sind ableitbare Funktionen glatt (=knickfrei).
Zusammenhang zwischen Differenzierbarkeit, Stetigkeit und stetiger Differenzierbarkeit
[Bearbeiten]Stetige Differenzierbarkeit einer Funktion impliziert ihre Differenzierbarkeit, woraus wiederum ihre Stetigkeit folgt. Die Umkehrungen gelten im Allgemeinen nicht, wie wir im Laufe dieses Abschnitts sehen werden:
Die erste Implikation folgt direkt aus der Definition: Eine Funktion heißt genau dann stetig differenzierbar, wenn sie differenzierbar ist und die Ableitungsfunktion stetig ist. Damit sind stetig differenzierbare Funktionen auch differenzierbar. Die zweite Implikation zeigen wir im Folgenden.
Jede differenzierbare Funktion ist stetig
[Bearbeiten]Wir zeigen nun, dass jede an einer Stelle differenzierbare Funktion an dieser Stelle auch stetig ist. Damit ist Differenzierbarkeit eine stärkere Forderung an eine Funktion als Stetigkeit:
Satz
Sei mit eine Funktion, die an der Stelle differenzierbar ist. Dann ist im Punkt stetig. Damit gilt auch: Jede differenzierbare Funktion ist stetig.
Beweis
Sei eine beliebige Folge in , die gegen konvergiert. Da in differenzierbar ist, gibt es eine Funktion mit , so dass für alle in gilt
Wir haben uns bereits überlegt, dass dann auch gilt. Wegen muss also gelten. Insgesamt erhalten wir somit:
Den Limes durften wir hier auseinanderziehen, da die Grenzwerte , und existieren. Nach dem Folgenkriterium für Stetigkeit gilt wegen , dass an der Stelle stetig ist.
Alternativer Beweis
Sei eine Folge aus , die gegen konvergiert und deren Folgenglieder ungleich sind. Es ist also und für alle . Da in differenzierbar ist, gilt . Die Ableitung von im Punkt ist eine reelle Zahl. Dann gilt:
Den Limes durften wir hier auseinanderziehen, da die Grenzwerte und existieren. Damit ist solange die Folge maximal endlich oft den Wert aufweist und geht.
Sei nun eine beliebige Folge aus , die gegen konvergiert und deren Folgenglieder unendlich oft gleich dem Wert sind. Nun haben wir gezeigt, dass der Grenzwert der Teilfolge von mit Folgenglieder ungleich gleich ist. Auch die Teilfolge von Folgeglieder gleich konvergiert als konstante Folge gegen . Somit kann man die Folge in zwei Teilfolgen zerlegen, die beide gegen konvergieren. Insgesamt ergibt sich so .
Für jede Folge aus , die gegen konvergiert, ist somit . Nach dem Folgenkriterium für Stetigkeit gilt dann, dass an der Stelle stetig ist.
Anwendung: Unstetige Funktionen sind nicht differenzierbar
[Bearbeiten]Aus dem vorherigen Abschnitt wissen wir, dass jede differenzierbare Abbildung stetig ist. Also:
Wenn wir auf diese Implikation das Prinzip der Kontraposition anwenden, dann folgt: Unstetige Funktionen sind nicht differenzierbar:
Beispiel: Unstetige Funktionen sind nicht differenzierbar
[Bearbeiten]Nehmen wir als Beispiel die Vorzeichenfunktion
Diese ist im Punkt nicht stetig. Also ist sie dort auch nicht differenzierbar. Nehmen wir die Folge . Diese konvergiert gegen Null. Wenn die Vorzeichenfunktion differenzierbar wäre, dann müsste der Grenzwert existieren. Jedoch ist
Der Grenzwert existiert nicht in . Damit ist die Vorzeichenfunktion – wie erwartet – nicht differenzierbar im Punkt .
Nicht jede differenzierbare Funktion ist stetig differenzierbar
[Bearbeiten]Im folgenden Beispiel greifen wir Kenntnisse über Ableitungsregeln vor, die wir erst im nächsten Kapitel ausführlicher behandeln werden. Da jene allerdings meist schon aus der Schule bekannt sind, führen wir das Beispiel bereits jetzt vor:
Beispiel (Beispiel einer differenzierbaren, aber nicht stetig differenzierbaren Funktion)
Wir werden zeigen, dass folgende Funktion überall differenzierbar ist, aber die Ableitungsfunktion nicht an jedem Punkt stetig ist:
Für ist die Funktion nach der Produkt- und Kettenregel in jedem Punkt unendlich oft stetig differenzierbar. Wir werden nun die Differenzierbarkeit an der Stelle betrachten. Es gilt
Also ist an der Stelle differenzierbar mit dem Ableitungswert . Jedoch ist die Ableitungsfunktion an der Stelle nicht stetig. Um dies zu zeigen, müssen wir die Ableitungsfunktion ermitteln. Für folgt aus der Produkt- und Kettenregel:
Zusammen mit dem Ableitungswert erhalten wir somit die Ableitungsfunktion
Um die Unstetigkeit von bei zu zeigen, verwenden wir die Folgendefinition von Stetigkeit. Sei dazu die Folge mit . Es gilt . Wenn stetig wäre, müsste nach dem Folgenkriterium gelten. Nun ist aber
Der Grenzwert existiert nicht, denn die Folge besitzt die beiden Häufungspunkte und . Damit folgt, dass an der Stelle nicht stetig ist. ist somit zwar differenzierbar, aber nicht stetig differenzierbar.
Übungsaufgaben
[Bearbeiten]Hyperbelfunktion
[Bearbeiten]Aufgabe (Hyperbelfunktion ist an der Stelle 2 ableitbar)
Zeige, dass die Hyperbelfunktion an der Stelle differenzierbar ist, und berechne dort die Ableitung. Wie lautet die Ableitung von an einer beliebigen Stelle ?
Lösung (Hyperbelfunktion ist an der Stelle 2 ableitbar)
Hier lautet der Differentialquotient an der Stelle :
Also ist an der Stelle mit der Ableitung differenzierbar. Für ein allgemeines gilt
Wurzelfunktion
[Bearbeiten]Aufgabe (Wurzelfunktion ist im Nullpunkt nicht differenzierbar)
Zeige, dass die Wurzelfunktion
in nicht differenzierbar ist.
Lösung (Wurzelfunktion ist im Nullpunkt nicht differenzierbar)
Wir müssen zeigen, dass der Differentialquotient von in nicht existiert. Dieser lautet
Wir wählen die positive Nullfolge . Für diese gilt
Damit existiert kein Grenzwert des Differentialquotienten . Die Funktion ist daher in nicht differenzierbar.
Bestimmung von Grenzwerten
[Bearbeiten]Aufgabe (Bestimmung von Grenzwerten mit Differentialquotienten)
Sei in differenzierbar. Zeige die folgenden Grenzwerte
- Gilt auch die umgekehrte Aussage zum Grenzwert : Existiert der Grenzwert , so ist in differenzierbar, und ist gleich diesem Grenzwert.
Lösung (Bestimmung von Grenzwerten mit Differentialquotienten)
Lösung Teilaufgabe 1:
Da in differenzierbar ist, gilt
Substituieren wir , so gilt . Damit gilt
Lösung Teilaufgabe 2:
Hier gilt
Lösung Teilaufgabe 3:
Die Umkehrung ist falsch. Wir betrachten dazu die Funktion in . Für diese existiert der Grenzwert
Die Betragsfunktion ist jedoch an der Stelle Null nicht differenzierbar.
Kriterium für Differenzierbarkeit
[Bearbeiten]Aufgabe (Kriterium für Differenzierbarkeit einer allgemeinen Funktion in Null)
Sei . Zeige: Gilt für ein , so ist in Null differenzierbar mit .
Lösung (Kriterium für Differenzierbarkeit einer allgemeinen Funktion in Null)
Es gilt
Damit ist dann wegen
Mit dem Einschnürungssatz folgt daher













![{\displaystyle [{\tilde {x}},x_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc5043777ec906bd72d0ecf9ca136a9489dfe801)





















































![{\displaystyle [{\tilde {x}},x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/405c0d85ca3635f5ffb1d59a9b2144c81c4f91cb)





































![{\displaystyle {\begin{aligned}&&f'({\tilde {x}})&\approx {\frac {f(x)-f({\tilde {x}})}{x-{\tilde {x}}}}\\[0.3em]&\implies {}&f'({\tilde {x}})\cdot (x-{\tilde {x}})&\approx f(x)-f({\tilde {x}})\\[0.3em]&\implies {}&f({\tilde {x}})+f'({\tilde {x}})\cdot (x-{\tilde {x}})&\approx f(x)\\[0.3em]&\implies {}&f(x)&\approx f({\tilde {x}})+f'({\tilde {x}})\cdot (x-{\tilde {x}})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29b0a1732aaaa27ce71c7b12bec4be7b11e15c0c)














![{\displaystyle {\begin{aligned}&&{\frac {f(x)-f({\tilde {x}})}{x-{\tilde {x}}}}&=f'({\tilde {x}})+\epsilon (x)\\[0.3em]&\implies {}&f(x)-f({\tilde {x}})&=f'({\tilde {x}})\cdot (x-{\tilde {x}})+\epsilon (x)\cdot (x-{\tilde {x}})\\[0.3em]&\implies {}&f(x)&=f({\tilde {x}})+f'({\tilde {x}})\cdot (x-{\tilde {x}})+\underbrace {\epsilon (x)\cdot (x-{\tilde {x}})} _{:=\ \delta (x)}\\[0.3em]&\implies {}&f(x)&=f({\tilde {x}})+f'({\tilde {x}})\cdot (x-{\tilde {x}})+\delta (x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4c7302ebc33ca2c6af1c4f867476240e332c27b)









![{\displaystyle {\begin{aligned}f(x)&=f({\tilde {x}})+f'({\tilde {x}})\cdot (x-{\tilde {x}})+\epsilon (x)\cdot (x-{\tilde {x}})\\[0.3em]&=f({\tilde {x}})+f'({\tilde {x}})\cdot (x-{\tilde {x}})+\delta (x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9cab53ff84835e4c795cb810b094522bcc90d61)




![{\displaystyle {\begin{aligned}f'({\tilde {x}})&=\lim _{x\to {\tilde {x}}}{\frac {f(x)-f({\tilde {x}})}{x-{\tilde {x}}}}\\[0.3em]&=\lim _{x\to {\tilde {x}}}{\frac {f({\tilde {x}})+c\cdot (x-{\tilde {x}})+\delta (x)-f({\tilde {x}})}{x-{\tilde {x}}}}\\[0.3em]&=\lim _{x\to {\tilde {x}}}{\frac {c\cdot (x-{\tilde {x}})+\delta (x)}{x-{\tilde {x}}}}\\[0.3em]&=\lim _{x\to {\tilde {x}}}c+\underbrace {\frac {\delta (x)}{x-{\tilde {x}}}} _{\to 0}\\[0.3em]&=c\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64b3c1a3b7c4d4848448ebecf7fbc6b0566758cd)



![{\displaystyle {\begin{aligned}&&{\frac {f(x)-f({\tilde {x}})}{x-{\tilde {x}}}}&=f'({\tilde {x}})+\epsilon (x)\\[0.3em]&\implies {}&f(x)-f({\tilde {x}})&=f'({\tilde {x}})\cdot (x-{\tilde {x}})+\epsilon (x)\cdot (x-{\tilde {x}})\\[0.3em]&\implies {}&f(x)&=f({\tilde {x}})+(f'({\tilde {x}})+\epsilon (x))\cdot (x-{\tilde {x}})\\[0.3em]&&&\ {\color {Gray}\left\downarrow \ \varphi (x)=f'({\tilde {x}})+\epsilon (x)\right.}\\[0.3em]&\implies {}&f(x)&=f({\tilde {x}})+\varphi (x)\cdot (x-{\tilde {x}})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8687b6114178763448e91342a6a076c7d6e9b1d9)







![{\displaystyle {\begin{aligned}f(x)&=f({\tilde {x}})+f'({\tilde {x}})\cdot (x-{\tilde {x}})+\delta (x)\\[0.3em]&=f({\tilde {x}})+f'({\tilde {x}})\cdot (x-{\tilde {x}})+{\tfrac {\delta (x)(x-{\tilde {x}})}{x-{\tilde {x}}}}\\[0.3em]&=f({\tilde {x}})+\left(f'({\tilde {x}})+{\tfrac {\delta (x)}{x-{\tilde {x}}}}\right)\cdot (x-{\tilde {x}})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45776e0914fee6a07c7f11182c1c93ee9de2b3e5)



![{\displaystyle {\begin{aligned}f(x)&=f({\tilde {x}})+\varphi (x)\cdot (x-{\tilde {x}})\\[0.3em]&=f({\tilde {x}})+(\varphi (x)+\varphi ({\tilde {x}})-\varphi ({\tilde {x}}))\cdot (x-{\tilde {x}})\\[0.3em]&=f({\tilde {x}})+\varphi ({\tilde {x}})\cdot (x-{\tilde {x}})+(\varphi (x)-\varphi ({\tilde {x}}))\cdot (x-{\tilde {x}})\\[0.3em]&=f({\tilde {x}})+f'({\tilde {x}})\cdot (x-{\tilde {x}})+(\varphi (x)-\varphi ({\tilde {x}}))\cdot (x-{\tilde {x}})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2131c11be30c781372dc249e141f4ffda7fd86f)





![{\displaystyle {\begin{aligned}{\frac {g(x)-g({\tilde {x}})}{x-{\tilde {x}}}}&={\frac {(mx+b)-(m{\tilde {x}}+b)}{x-{\tilde {x}}}}\\[0.3em]&={\frac {mx-m{\tilde {x}}}{x-{\tilde {x}}}}\\[0.3em]&={\frac {m(x-{\tilde {x}})}{x-{\tilde {x}}}}\\[0.3em]&=m\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cfc5858ba6512366ee926f8f380469553180b35)
![{\displaystyle {\begin{aligned}g'({\tilde {x}})&=\lim _{x\to {\tilde {x}}}{\frac {g(x)-g({\tilde {x}})}{x-{\tilde {x}}}}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Siehe obige Rechnung}}\right.}\\[0.3em]&=\lim _{x\to {\tilde {x}}}m=m\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66f5a9735167df5ecbd93e1658e93e36fc9f456b)





![{\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{\frac {f(3+h)-f(3)}{h}}=\lim _{h\to 0}{\frac {(3+h)^{2}-3^{2}}{h}}\\[0.3em]&=\lim _{h\to 0}{\frac {9+6h+h^{2}-9}{h}}=\lim _{h\to 0}{\frac {6h+h^{2}}{h}}=\lim _{h\to 0}{(6+h)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb6c7566af2b644ee0070166593c8e8ce26c7d32)






![{\displaystyle {\begin{aligned}f'({\tilde {x}})&=\lim _{h\to 0}{\frac {f({\tilde {x}}+h)-f({\tilde {x}})}{h}}=\lim _{h\to 0}{\frac {({\tilde {x}}+h)^{2}-{\tilde {x}}^{2}}{h}}\\[0.3em]&=\lim _{h\to 0}{\frac {{\tilde {x}}^{2}+2{\tilde {x}}h+h^{2}-{\tilde {x}}^{2}}{h}}=\lim _{h\to 0}{\frac {2{\tilde {x}}h+h^{2}}{h}}\\[0.3em]&=\lim _{h\to 0}{(2{\tilde {x}}+h)}=2{\tilde {x}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f052a60ffcabe05eebbfc4ddfb556284f3eae7c2)








![{\displaystyle {\begin{aligned}\lim _{n\rightarrow \infty }{\frac {f(x_{n})-f(x_{0})}{x_{n}-x_{0}}}&=\lim _{n\rightarrow \infty }{\frac {|{\frac {1}{n}}|-|0|}{{\frac {1}{n}}-0}}=\lim _{n\rightarrow \infty }{\frac {\frac {1}{n}}{\frac {1}{n}}}\\[0.3em]&=\lim _{n\rightarrow \infty }{1}=1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0f6d1508fa7390e0d02874b6c812359c7a19619)
![{\displaystyle {\begin{aligned}\lim _{n\rightarrow \infty }{\frac {f({\tilde {x}}_{n})-f(x_{0})}{{\tilde {x}}_{n}-x_{0}}}&=\lim _{n\rightarrow \infty }{\frac {|-{\tfrac {1}{n}}|-|0|}{-{\tfrac {1}{n}}-0}}=\lim _{n\rightarrow \infty }{\frac {\tfrac {1}{n}}{-{\tfrac {1}{n}}}}\\[0.3em]&=\lim _{n\rightarrow \infty }{-1}=-1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86be70df4e44a50d24d254c9e5afbca72df306ba)
![{\displaystyle {\begin{aligned}\lim _{n\rightarrow \infty }{\frac {f({\hat {x}}_{n})-f(x_{0})}{{\hat {x}}_{n}-x_{0}}}&=\lim _{n\rightarrow \infty }{\frac {|(-1)^{n}{\tfrac {1}{n}}|-|0|}{(-1)^{n}{\tfrac {1}{n}}-0}}\\[0.3em]&=\lim _{n\rightarrow \infty }{\frac {\tfrac {1}{n}}{(-1)^{n}{\tfrac {1}{n}}}}=\lim _{n\rightarrow \infty }{(-1)^{n}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9538f68a6fc3330f2ed5cb86fa2920f209ee2fe6)



















![{\displaystyle {\begin{aligned}{f_{+}}'(0)&=\lim _{x\downarrow 0}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\downarrow 0}{\frac {|x|-|0|}{x}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ x>0\implies |x|=x\right.}\\[0.3em]&=\lim _{x\downarrow 0}{\frac {x-0}{x}}=\lim _{x\downarrow 0}1=1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/050e452f972119883e0d82aecf009cafa1aaeb05)
![{\displaystyle {\begin{aligned}{f_{-}}'(0)&=\lim _{x\uparrow 0}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\uparrow 0}{\frac {|x|-|0|}{x}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ x<0\implies |x|=-x\right.}\\[0.3em]&=\lim _{x\uparrow 0}{\frac {-x-0}{x}}=\lim _{x\uparrow 0}-1=-1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3022cc131313897b1251dc2d4641b47eb1a8dab6)








![{\displaystyle {\begin{aligned}&\lim _{n\to \infty }{f(x_{n})}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ f(x)=f({\tilde {x}})+f'({\tilde {x}})\cdot (x-{\tilde {x}})+\delta (x)\right.}\\[0.3em]=\ &\lim _{n\to \infty }{f({\tilde {x}})+f'({\tilde {x}})\cdot (x_{n}-{\tilde {x}})+\delta (x_{n})}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Limes auseinanderziehen}}\right.}\\[0.3em]=\ &\lim _{n\to \infty }\underbrace {f({\tilde {x}})} _{\to f({\tilde {x}})}+\lim _{n\to \infty }f'({\tilde {x}})\cdot \underbrace {(x_{n}-{\tilde {x}})} _{\to 0}+\lim _{n\to \infty }\underbrace {\delta (x_{n})} _{\to 0}\\[0.3em]=\ &f({\tilde {x}})+0+0\\[0.3em]=\ &f({\tilde {x}})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c9caeac927078226c9912285880559e31531b18)







![{\displaystyle {\begin{aligned}&\lim _{n\rightarrow \infty }{f(x_{n})-f({\tilde {x}})}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ \forall n\in \mathbb {N} :x_{n}-{\tilde {x}}\neq 0\right.}\\[0.3em]=\ &\lim _{n\rightarrow \infty }{\frac {(f(x_{n})-f({\tilde {x}}))\cdot (x_{n}-{\tilde {x}})}{x_{n}-{\tilde {x}}}}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Limes auseinanderziehen}}\right.}\\[0.3em]=\ &\lim _{n\rightarrow \infty }\underbrace {\frac {f(x_{n})-f({\tilde {x}})}{x_{n}-{\tilde {x}}}} _{\to f'({\tilde {x}})}\cdot \lim _{n\rightarrow \infty }\underbrace {(x_{n}-{\tilde {x}})} _{\to 0}\ \\[0.3em]=\ &f'({\tilde {x}})\cdot 0\\[0.3em]=\ &0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d875560546a6f6c1a71da05e2189b1b942bc73d)















![{\displaystyle f'(0)=\lim _{h\to 0}{\frac {h^{2}\sin \left({\frac {1}{h}}\right)-0}{h}}=\lim _{h\to 0}\underbrace {h} _{\to 0}\cdot \underbrace {\sin \left({\frac {1}{h}}\right)} _{\in [-1,1]}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b60efaea08b799eeb61b5534b5178ad7491f0929)

![{\displaystyle {\begin{aligned}f'({\tilde {x}})&=\left(x^{2}\cdot \sin \left({\frac {1}{x}}\right)\right)'\\[0.3em]&=2x\sin \left({\frac {1}{x}}\right)+x^{2}\cos \left({\frac {1}{x}}\right)\left(-{\frac {1}{x^{2}}}\right)\\[0.3em]&=2x\cdot \sin \left({\frac {1}{x}}\right)-\cos \left({\frac {1}{x}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c057129bebea2f9f216e3d8513b5ec490421e17)




![{\displaystyle {\begin{aligned}\lim _{n\to \infty }f'(x_{n})&=\lim _{n\to \infty }\left(2x_{n}\cdot \sin \left({\frac {1}{x_{n}}}\right)-\cos \left({\frac {1}{x_{n}}}\right)\right)\\[0.3em]&=\lim _{n\to \infty }\left(2{\frac {1}{n\pi }}\cdot \sin(n\pi )-\cos(n\pi )\right)\\[0.3em]&=\lim _{n\to \infty }\left(2{\frac {1}{n\pi }}\cdot 0-(-1)^{n}\right)\\[0.3em]&=\lim _{n\to \infty }-(-1)^{n}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16313c2244bfb36d7df8066627ff5b96099c1692)





![{\displaystyle {\begin{aligned}g'(2)&=\lim _{h\to 0}{\frac {g(2+h)-g(2)}{h}}=\lim _{h\to 0}{\frac {{\frac {1}{2+h}}-{\frac {1}{2}}}{h}}\\[0.3em]&=\lim _{h\to 0}{\frac {\frac {2-(2+h)}{2\cdot (2+h)}}{h}}=\lim _{h\to 0}{\frac {-h}{2h(h+2)}}\\[0.3em]&=\lim _{h\to 0}{\frac {-1}{2h+4}}={\frac {-1}{0+4}}=-{\frac {1}{4}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60333530450384e7d5cbd79bc8c481ea4e63ef4c)

![{\displaystyle {\begin{aligned}g'({\tilde {x}})&=\lim _{h\to 0}{\frac {g({\tilde {x}}+h)-g({\tilde {x}})}{h}}=\lim _{h\to 0}{\frac {{\frac {1}{{\tilde {x}}+h}}-{\frac {1}{\tilde {x}}}}{h}}\\[0.3em]&=\lim _{h\to 0}{\frac {\frac {{\tilde {x}}-({\tilde {x}}+h)}{{\tilde {x}}\cdot ({\tilde {x}}+h)}}{h}}=\lim _{h\to 0}{\frac {-h}{{\tilde {x}}h(h+{\tilde {x}})}}\\[0.3em]&=\lim _{h\to 0}{\frac {-1}{{\tilde {x}}h+{\tilde {x}}^{2}}}={\frac {-1}{0+{\tilde {x}}^{2}}}=-{\frac {1}{{\tilde {x}}^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8e52958275ae63676fe78f6b3798d2d7adb6466)
















![{\displaystyle {\begin{aligned}\lim _{h\to 0}{\frac {f(a-h)-f(a)}{h}}&{\overset {{\tilde {h}}=-h}{=}}\lim _{{\tilde {h}}\to 0}{\frac {f(a+{\tilde {h}})-f(a)}{-{\tilde {h}}}}\\[0.3em]&=-\lim _{{\tilde {h}}\to 0}{\frac {f(a+{\tilde {h}})-f(a)}{\tilde {h}}}=-f'(a)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc162e6dad7e471b15cc32039012acc573ff3640)
![{\displaystyle {\begin{aligned}\lim _{h\to 0}{\frac {f(a+h)-f(a-h)}{2h}}&=\lim _{h\to 0}{\frac {f(a+h)-f(a)-(f(a-h)-f(a))}{2h}}\\[0.3em]&={\frac {1}{2}}\cdot \underbrace {\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}} _{=f'(a)}-{\frac {1}{2}}\cdot \underbrace {\lim _{h\to 0}{\frac {f(a-h)-f(a)}{h}}} _{=-f'(a)}\\[0.3em]&={\frac {1}{2}}f'(a)+{\frac {1}{2}}f'(a)=f'(a)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf1a3274cd70bd5596aab459a0741f5ac2f75bbe)


![{\displaystyle {\begin{aligned}\lim _{h\to 0}{\frac {f(0+h)-f(0-h)}{h}}&=\lim _{h\to 0}{\frac {|h|-|-h|}{h}}\\[0.3em]&=\lim _{h\to 0}{\frac {|h|-|h|}{h}}=\lim _{h\to 0}{\frac {0}{h}}=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af58842e2b9c1b30c0486128fbcc4644e92c3974)







