Sinus und Kosinus – Serlo „Mathe für Nicht-Freaks“
In diesem Kapitel behandeln wir die beiden trigonometrischen Funktionen Sinus und Kosinus. Sie bilden die wichtigsten trigonometrischen Funktionen und werden unter anderem in der Geometrie für Dreiecksberechnungen sowie der Trigonometrie benötigt. Wellen wie elektromagnetische Wellen sowie harmonische Schwingungen lassen sich über Sinus- beziehungsweise Kosinusfunktionen beschreiben, sodass diese in der Physik allgegenwärtig sind.
Definition über Einheitskreis
[Bearbeiten]Es gibt mehrere Möglichkeiten, den Sinus und den Kosinus zu definieren. Aus der Schule wird dir möglicherweise schon die Definition vom Sinus und Kosinus am Einheitskreis bekannt sein. Dabei wird ein Punkt betrachtet, der sich auf einem Kreis um den Ursprung mit Radius befindet. Die -Achse schließt mit der Strecke vom Nullpunkt zu den Winkel ein:

Der Winkel legt eindeutig fest, wo sich der Punkt befindet. Damit kann die -Koordinate und die -Koordinate jeweils durch eine von abhängige Funktion beschrieben werden. Diese Funktionen und nennen wir die Sinusfunktion beziehungsweise Cosinusfunktion :

Im Folgenden nehmen wir als Winkel und schreiben anstelle von beziehungsweise anstatt . Damit ergibt sich folgende Definition:
Definition (Definition Sinus und Kosinus am Einheitskreis)
Sei der Punkt auf dem Einheitskreis, dessen Ortsvektor mit der horizontalen Koordinatenachse den Winkel einschließt. Die Koordinaten von werden dann genannt. Dabei nennt man den Kosinus von und den Sinus von .
Graph der Sinus und Kosinusfunktion
[Bearbeiten]Die folgende Animation zeigt, wie die Graphen der Sinus- beziehungsweise Kosinusfunktion schrittweise konstruiert werden:

Damit ergibt sich folgender Graph für die Sinusfunktion:
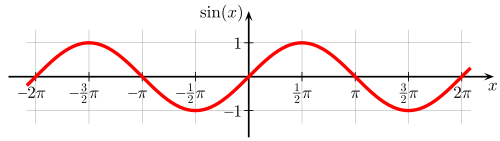
Für die Kosinusfunktion erhalten wir:

Definition über Exponentialfunktion
[Bearbeiten]Darstellung über komplexe Exponentialfunktion
[Bearbeiten]Die Sinus- und Kosinusfunktion kann auch als Summe von gewissen komplexen Exponentialfunktionen definiert werden. Mit dieser Darstellung können besonders elegant Eigenschaften vom Sinus und Kosinus nachgewiesen werden.
Definition (Sinus und Kosinus über komplexe Exponentialfunktion)
Wir definieren die Funktionen (Sinus) und (Kosinus) durch
Diese Funktionen sind wohldefiniert: Für jede reelle Zahl ist die komplexe Zahl die komplex Konjugierte von . Damit ist eine reelle Zahl und es gilt . Auf analoge Art kann man zeigen, dass ist.
Herleitung der Exponentialdefinition
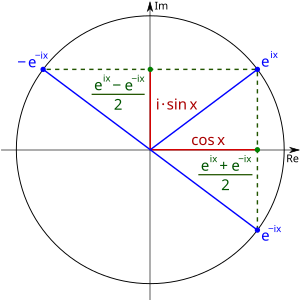
[Bearbeiten]Man kann zeigen, dass der Punkt auf dem Einheitskreis ist, dessen Ortsvektor mit der -Achse den Winkel einschließt:

Der Realteil der komplexen Zahl ist damit , und der Imaginärteil ist . Es gilt also . Bei betrachten wir den Winkel . Der Punkt liegt gespiegelt an der reellen Achse auf der anderen Seite:

Damit ist der Realteil von derselbe wie bei , also . Jedoch ist der Imaginärteil gegenüber um die Zahl multipliziert und damit gleich . Wir erhalten . Also haben wir:
Durch Addition beider Gleichungen erhalten wir:
Und durch Subtraktion der beiden Gleichungen ergibt sich:
Damit haben wir die beiden Definitionen und hergeleitet. Diese Herleitung ist noch einmal in folgender Grafik illustriert:
Reihendarstellung vom Sinus und Kosinus
[Bearbeiten]Definition als Reihe
[Bearbeiten]
In der Vorlesung wird oft eine andere Definition bevorzugt, nämlich die sogenannte Reihendarstellung, bei der der Sinus und Kosinus über eine Reihe definiert wird. Die Reihendarstellung ist zwar weniger anschaulich als die Definition über dem Einheitskreis, mit ihr können aber einige Eigenschaften des Sinus und Kosinus leichter bewiesen werden. Außerdem kann mit ihr der Sinus und Kosinus auf komplexe Zahlen erweitert werden.
Definition (Sinus und Kosinus)
Wir definieren die Funktionen (Sinus) und (Kosinus) durch
Wohldefiniertheit der Reihendarstellung
[Bearbeiten]Wir müssen nachweisen, dass unsere Reihendarstellung der Sinus- und Kosinusfunktion wohldefiniert ist. Sprich: Wir müssen zeigen, dass für alle die Reihen beziehungsweise gegen eine reelle Zahl konvergieren.
Satz
Für alle reelle Zahlen konvergieren die Reihen und .
Beweis
Wir beweisen den Satz für die Reihe der Sinusfunktion. Der Beweis für die Reihe der Kosinusfunktion kann analog geführt werden. Für finden wir zunächst:
Für konvergiert die Reihe demnach. Für wenden wir das Quotientenkriterium an. Sei hierzu für alle , so dass wir haben. Es gilt:
Wegen konvergiert die Reihe nach dem Quotientenkriterium.
Äquivalenz der Exponential- und Reihendarstellung
[Bearbeiten]Wir haben mehrere Definitionen der Sinus- und Kosinusfunktion kennen gelernt. Einen Zusammenhang zwischen der Exponentialdarstellung und der Definition am Einheitskreis haben wir bereits hergestellt. Nun müssen wir noch zeigen, dass die Exponential- und die Reihendarstellung äquivalent zueinander sind.
Satz
Es gilt für alle :
Damit ist es egal, ob die Sinus- bzw. Kosinusfunktion über ihre Reihendarstellung oder über ihre Exponentialdarstellung definiert wird.
Beweis
Wir wissen bereits vom Kapitel über die Exponentialfunktion, dass die Exponentialfunktion die Reihendarstellung hat. Wenn wir nun für in die Reihendarstellung einsetzen, erhalten wir:
Nun setzen wir in die Reihendarstellung der Exponentialfunktion ein:
Schreiben wir und . So haben wir gezeigt, dass
Es folgt für die Differenz
Damit ist:
Analog ist:
Es folgt:


















![{\displaystyle {\begin{aligned}&\sin :\mathbb {R} \to \mathbb {R} :x\mapsto {\frac {1}{2\mathrm {i} }}\left(\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}\right)\\[0.3em]&\cos :\mathbb {R} \to \mathbb {R} :x\mapsto {\frac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18fea4d6273aa2215edb762bc859c1a7cb1a071f)












![{\displaystyle {\begin{aligned}e^{\mathrm {i} \theta }&=\cos(\theta )+\sin(\theta )\mathrm {i} \\[0.3em]e^{-\mathrm {i} \theta }&=\cos(\theta )-\sin(\theta )\mathrm {i} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aff8b06ff43c4b3ef1375f75e521471f69091aa8)







![{\displaystyle {\begin{aligned}&\sin :\mathbb {R} \to \mathbb {R} ,x\mapsto \sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k+1)!}}x^{2k+1}\\[0.3em]&\cos :\mathbb {R} \to \mathbb {R} ,x\mapsto \sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k)!}}x^{2k}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe8c17ff3511f1dab32e72316bb4b1f31f754f32)




![{\displaystyle {\begin{aligned}&\sum _{k=0}^{\infty }{{\frac {(-1)^{k}}{(2k+1)!}}x^{2k+1}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ x=0\right.}\\[0.3em]=\ &\sum _{k=0}^{\infty }{{\frac {(-1)^{k}}{(2k+1)!}}0^{2k+1}}\\[0.3em]=\ &\sum _{k=0}^{\infty }{0}=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/372ae50417058d96933aab61faa49ed58b3b05c5)




![{\displaystyle {\begin{aligned}&\lim _{k\to \infty }{\left|{\frac {a_{k+1}}{a_{k}}}\right|}\\[0.3em]=\ &\lim _{k\to \infty }{\left|-{\frac {x^{2(k+1)+1}\cdot (2k+1)!}{x^{2k+1}\cdot (2(k+1)+1)!}}\right|}\\[0.3em]=\ &\lim _{k\to \infty }{\left|-{\frac {x^{2k+3}\cdot (2k+1)!}{x^{2k+1}\cdot (2k+3)!}}\right|}\\[0.3em]=\ &\lim _{k\to \infty }{\left|{\frac {x^{2}}{(2k+2)(2k+3)}}\right|}=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d1d4cf3d12509d03e5e2a4abe8227bbf48e17e9)

![{\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k+1)!}}x^{2k+1}&={\frac {1}{2\mathrm {i} }}\left(\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}\right)\\[0.5em]\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k)!}}x^{2k}&={\frac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a78644e97a0c9226c1a8999da18e8db69fd455)


![{\displaystyle {\begin{aligned}\mathrm {e} ^{\mathrm {i} {\tilde {x}}}&=\sum _{k=0}^{\infty }{\frac {(\mathrm {i} {\tilde {x}})^{k}}{k!}}\\[0.5em]&\ {\color {OliveGreen}\left\downarrow \ {\text{absolute Konvergenz}}\implies {\text{Reihe aufspalten}}\right.}\\[0.5em]&=\sum _{l=0}^{\infty }{\frac {(\mathrm {i} {\tilde {x}})^{2l}}{(2l)!}}+\sum _{l=0}^{\infty }{\frac {(\mathrm {i} {\tilde {x}})^{2l+1}}{(2l+1)!}}\\[0.5em]&\ {\color {OliveGreen}\left\downarrow \ \mathrm {i} ^{2l}=(-1)^{l}{\text{und }}\mathrm {i} ^{2l+1}=\mathrm {i} \cdot (-1)^{l}\right.}\\[0.5em]&=\sum _{l=0}^{\infty }{\frac {(-1)^{l}}{(2l)!}}{\tilde {x}}^{2l}+\mathrm {i} \sum _{l=0}^{\infty }{\frac {(-1)^{l}}{(2l+1)!}}{\tilde {x}}^{2l+1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8c4dfac6c3ee81cd73636012ea19349377dcbb7)

![{\displaystyle {\begin{aligned}\mathrm {e} ^{-\mathrm {i} {\tilde {x}}}&=\sum _{k=0}^{\infty }{\frac {(-\mathrm {i} {\tilde {x}})^{k}}{k!}}\\[0.5em]&\ {\color {OliveGreen}\left\downarrow \ {\text{absolute Konvergenz}}\implies {\text{Reihe aufspalten}}\right.}\\[0.5em]&=\sum _{l=0}^{\infty }{\frac {(-\mathrm {i} {\tilde {x}})^{2l}}{(2l)!}}+\sum _{l=0}^{\infty }{\frac {(-\mathrm {i} {\tilde {x}})^{2l+1}}{(2l+1)!}}\\[0.5em]&\ {\color {OliveGreen}\left\downarrow \ (-\mathrm {i} )^{2l}=(-1)^{l}{\text{und }}(-\mathrm {i} )^{2l+1}=-\mathrm {i} \cdot (-1)^{l}\right.}\\[0.5em]&=\sum _{l=0}^{\infty }{\frac {(-1)^{l}}{(2l)!}}{\tilde {x}}^{2l}-\mathrm {i} \sum _{l=0}^{\infty }{\frac {(-1)^{l}}{(2l+1)!}}{\tilde {x}}^{2l+1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2223c9a4cc217f53e66e30b777387cf5d507d9a2)







