Lipschitz continuity – Serlo
Lipschitz continuity is an even stronger form of uniform continuity and is often used in the theory of differential equations.
Derivation
[Bearbeiten]By introducing the notion of Lipschitz continuity, we will be able to say more about the rate at which a function changes. As we already know, continuous functions have the neat property that sufficiently small changes in the arguments will result in arbitrary small changes in the function value. On top of that, Lipschitz continuity allows us give an estimate of that change. We can thus talk very precisely about how "fast" the changes of the output become smaller. For better understanding, let us first recap what we mean by changes of a function. Let be an function with domain .
Let's take two arbitrary points and from the domain of and form the straight line through the points und . The slope of the line increases, as the difference between the values and gets bigger. The mean rate of change between function values is equal to the slope of the secant through those points and can be calculated with the so-called slope triangle:

Let's assume now that the rate of change is bounded, i.e. the slopes of the secants cannot get arbitrary large or small. Thus the absolute value has an upper bound (because the absolute value is bounded, both positive and negative values are bounded). There exists a constant , so that for all with the inequality holds: This number is called the Lipschitz constant. By multiplying both sides of the equation with , we get:
This inequality is the basis for the definition of Lipschitz continuity. If we can find such a constant that satisfies this inequality for all , then we have also found an absolute bound for the rate of change of the function. Because the inequality is still true even for this will result in a nice simplification of the definition, because we can drop the assumption that , which we otherwise would have needed, had we tried to work with the original mean rate of change .
Definition
[Bearbeiten]Definition (Lipschitz continuity)
Let be a subset of and let be a function. Then we say is Lipschitz continuous in , if and only if there exists a constant , which satisfies for all .
More formally the definition could be written using quantifiers:
The right-hand side of the above equivalence can be translated as follows:
Why do we need Lipschitz continuity?
[Bearbeiten]The Lipschitz constant of a Lipschitz continuous functions gives us an absolute upper bound for the rate of change. This is useful if we want to estimate function values.
Let us assume we are given a point from the domain and the corresponding function value . Now imagine you want to estimate the value for a new point . We can obtain such an estimate if we use our Lipschitz constant to find an upper and lower bound for . From Lipschitz continuity it follows that:
By adding we obtain:
This way we have found a lower and upper bound and know that must be located somewhere in between.
Intuition
[Bearbeiten]Picturing Lipschitz continuity with cones
[Bearbeiten]Let's try to visualize the Lipschitz condition: Given a Lipschitz continuous function we draw the straight lines and through the point and make their slope be equal to our Lipschitz constant and respectively. Above we already have seen that the Lipschitz condition is given by , which means that the slope of all secants through is bounded. This means that the graph of the function must run between those two lines:

This constraints is true for all in the domain. In the picture we could let the lines move along the graph of and in turn the graph of will always lie between those two lines:
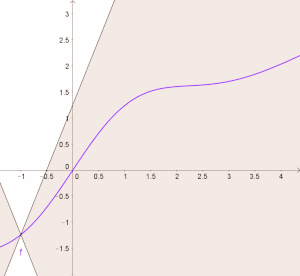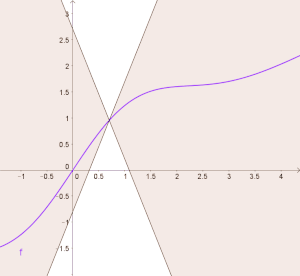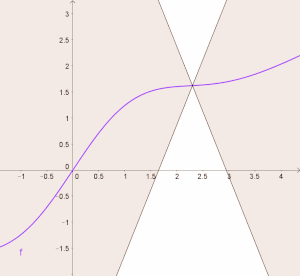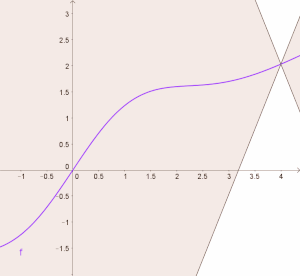
If the function is differentiable the derivative of the function taken at a point will match the slope of the tangent at that point. Using this visualization we can see that the derivative of a Lipschitz continuous function cannot get bigger than (or less than ). This means that the absolute value of the derivative is bounded by the Lipschitz constant.
Difference between Lipschitz and uniform continuity
[Bearbeiten]
Both the Lipschitz and uniform continuity are so-called global properties of a function (normal continuity is only a local property!). In contrast to Lipschitz continuity, uniform continuity gives no information about the rate of change. This could be a disadvantage if you are trying to estimate a value from another value .
Lipschitz continuity implies a linear relationship between the distance of the arguments and the output values . This is not the case with uniform continuity because the constraint is the same for all with . Hence the cones of Lipschitz continuity that become progressively smaller as we approach give us a much better estimate than the „--rectangle“ of uniform continuity. We could try choose arbitrary small, to improve the approximation of . But this could mean that our values must become really small too, i.e. we have to be really close the the original point . You can observe this phenomenon by studying the behaviour of the square-root function near .
Link to uniform continuity
[Bearbeiten]How is this new notion of Lipschitz continuity linked to the old concepts of normal and uniform continuity? We already made the claim that Lipschitz continuity is stronger than uniform continuity: Every Lipschitz continuous function is also uniform continuos. But the converse is not generally true.
Lipschitz continuous functions are uniformly continuous
[Bearbeiten]Theorem (Lipschitz continuity implies uniform continuity)
Let and be a function which is Lipschitz continuous in . Then is also uniformly continuous in .
Proof (Lipschitz continuity implies uniform continuity)
Let's recall the definition of uniform continuity: A function is uniformly continuous, if and only if for all we can find a , so that for all with , it follows that .
Thus let . Our job is to find a , so that for all arguments that are less than apart from one another, i.e. , also the distance of the outputs is smaller than , so should be satisfied. Our starting point is that is Lipschitz continuous, and we are trying to show that must be uniformly continuous also. We remember that being Lipschitz continuous means, that there exists a constant , so that for all .
The question we need to ask ourself is: How large can the distance between the arguments be, so that the outputs still satisfy ? Maybe you will soon realize that we can choose the distance to be smaller than . So we choose our . But be wary! The Lipschitz constant could be zero (we would divide by zero). Here we need a case-by-case analysis:
Fall 1:
If , then the Lipschitz condition tells us that for all . But this implies that and thus for all . That means must be a constant function, and is therefore uniformly continuous. For an arbitrary you could choose any .
Fall 2:
The interesting case is . We already hinted at the solution. Choose . Let with . Now everything will follow from our Lipschitz condition:
Not all uniformly continuous functions are Lipschitz continuous
[Bearbeiten]To show this fact we only need to find a counterexample, i.e. a function which we know is uniformly continuous, but not Lipschitz continuous. We will see that the square root function in is such a counterexample. It was already proven previously that this function is uniformly continuous. We now will show that it is not Lipschitz continuous. Thus consider the function:
We will give a prove by contradiction. Let's assume this function is Lipschitz continuous. By definition there must be a constant , so that for all the following holds: . But this would have further implications for all with or :
But by choosing and , we see that:
This is a contradiction! Therefore the assumption that is Lipschitz continuous in must be false.
Lipschitz continuity implies (normal) continuity
[Bearbeiten]From the previous section we see that Lipschitz continuity implies (normal) continuity: Since Lipschitz continuous functions are uniformly continuous, they are also continuous (remember that uniform continuity is stronger than normal continuity). To view it from a different angle, we can ask ourself why a discontinuous function cannot be Lipschitz continuous:
Let's re-evoke the first intuitive image we had about continuity: A function is continuous if there aren't any "jumps" or "gaps":

The pictured function is discontinuous at . Imagine tracing a straight line through the point at the -value of the graph, and through another point . This line is a secant of that graph.

If you imagine moving the right intersection point of that secant closer and closer to the point which is the jump point, you will observe that the slope of the secant gets bigger and bigger and will eventually reach infinity. This means that there cannot be any constant that will bound the absolute value of the slope of the secant. If you think you have found such a constant just move the intersection point of the secant even closer to , until you will eventually reach a point where the slope will be greater than .
So now it should be clear why every discontinuous function cannot be Lipschitz continuous. You can reverse this proposition logically by contraposition and obtain the original proposition that Lipschitz continuity implies (normal) continuity. In summary, functions which rate of change is bounded are Lipschitz continuous and cannot have any points of discontinuity.

Examples
[Bearbeiten]Example (The identity is Lipschitz continuous)
The identity with is Lipschitz continuous on all of with Lipschitz constant , because for all it follows that:
Example (The restricted Square function is Lipschitz continuous)
Consider the Square function on the closed interval :
The values are chosen at will, but with . We claim that this function is Lipschitz continuous because for all it follows that:
Thus we can choose as our Lipschitz constant.
Example (The (unrestricted) Square function is not Lipschitz continuous)
In contrast consider the unrestricted Square function with . By dropping the condition that the interval must be closed, we lose the Lipschitz continuity. Assume that there is a Lipschitz constant with for all . We start by observing that:
Because of the inequality must be true for all . But it's clear that such a Lipschitz constant cannot possibly exist. We easily find that by setting and (after trying to choose a fixed ) the inequality doesn't hold. By this contradiction we see that the Square function cannot be Lipschitz continuous on all of
Exercises
[Bearbeiten]Lineare Funktionen sind Lipschitz-stetig
[Bearbeiten]Exercise (Linear functions are Lipschitz continuous)
Show that every linear function with is Lipschitz continuous.
Solution (Linear functions are Lipschitz continuous)
Let be at will. Then we see:
The linear function is therefore Lipschitz continuous with Lipschitz constant .
Quadratic functions and Lipschitz continuity
[Bearbeiten]Exercise (Quadratic functions and Lipschitz continuity)
Prove that every quadratic function with for and Is Lipschitz continuous on the compact interval , but not on .
Solution (Quadratic functions and Lipschitz continuity)
We use a binomial expansion:
Let now . The triangle inequality implies:
So the graph of the function can never be steeper than and this is a suitable Lipschitz constant.
But what happens if we take the entire real axis as domain ? The function is getting infinitely steep as runs towards so we expect that it is not Lipschitz-continuous, i.e. there is no upper bound for the steepness. Assume, was Lipschitz continuous with upper bound on the steepness , for all The computation above yields
So the steepness should be at most for all . But if we choose and , then we exceed the maximum steepness:
This is a contradiction and hence, is not Lipschitz continuous on .
Lipschitz-Continuity and the hyperbola
[Bearbeiten]Exercise
Let with .
- Prove that is Lipschitz continuous and determine the Lipschitz constant for this function (on this interval).
- Is the function still Lipschitz cotinuous if we extend its domain of definition to ?
Solution
Solution sub-exercise 1:
Let . Then,
So is Lipschitz-continuous on with Lipschitz constant (= maximal steepness). There is no better constant, since the first derivative at 1 is , so the function has steepness 1 there.
Solution sub-exercise 2:
Assume, would be Lipschitz continuous . Then there is a Lipschitz constant with for all . For this is equivalent to . Now, we distinguish the two cases and :
Fall 1:
For and there is . ↯
Fall 2:
For and we get a contradiction:
A useful criterion for Lipschitz continuity
[Bearbeiten]The Mean value theorem can be used to show that on a compact interval, every continuous differentiable function is Lipschitz continuous:
Theorem (Lipschitz continuity of differentiable functions on compact intervals)
Let be continuous and further differentiable in . The derivative function is assumed to be bounded (this is especially the case, if is continuous). Then, is Lipschitz continuous with Lipschitz constant .
The derivative being bounded by intuitively corresponds to having a maximum steepness, which in turn implies Lipschitz continuity. However, there are non-differentiable functions with maximum steepness, so Lipschitz continuity actually requires less than being differentiable and classifies more functions.



















![{\displaystyle {\begin{aligned}&&\left|{\frac {f(x)-f({\tilde {x}})}{x-{\tilde {x}}}}\right|&\leq L\\[0.3em]&\iff &\left|f(x)-f({\tilde {x}})\right|&\leq L|x-{\tilde {x}}|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a832717e6411cdeb9a88e8e25caa24bb60dbbeb)









![{\displaystyle {\begin{array}{cc}&f:D\rightarrow \mathbb {R} {\text{ is Lipschitz continuous }}\\[1em]\iff &\exists L\geq 0\,\forall x,{\tilde {x}}\in D:|f(x)-f({\tilde {x}})|\leq L\cdot |x-{\tilde {x}}|\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26bcc29b9f774be0744134c87bf32db3d85ea6ca)

































![{\displaystyle {\begin{aligned}|f(x)-f(y)|&\leq L\cdot |x-y|<L\cdot \delta \\[0.5em]&=L\cdot {\frac {\epsilon }{L}}=\epsilon \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/941384ad0bb3a0ec890bda94770a2579e440e133)






![{\displaystyle {\begin{aligned}&&|{\sqrt {x}}-{\sqrt {y}}|&<L\cdot |x-y|\\[0.3em]&\implies &{\frac {|{\sqrt {x}}-{\sqrt {y}}|\cdot |{\sqrt {x}}+{\sqrt {y}}|}{|{\sqrt {x}}+{\sqrt {y}}|}}&<L\cdot |x-y|\\[0.3em]&\implies &{\frac {1}{|{\sqrt {x}}+{\sqrt {y}}|}}\cdot |x-y|&<L\cdot |x-y|\\[0.3em]&\implies &{\frac {1}{|{\sqrt {x}}+{\sqrt {y}}|}}&<L\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29da71a9bccf6e3a8a79681e23db686978a6b577)


![{\displaystyle {\begin{aligned}{\frac {1}{|{\sqrt {x}}+{\sqrt {y}}|}}&={\frac {1}{{\frac {1}{\sqrt {4L^{2}}}}+0}}\\[0.5em]&={\frac {1}{\frac {1}{2L}}}=2L>L\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7139e39e14b1b47d76d3c597d7ac6601136c13e9)







![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle {\begin{aligned}f:[a,b]&\to \mathbb {R} \\x&\mapsto x^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea31b7b7e80ae4e3c53f3c5bdd3ecca38780b815)


![{\displaystyle x,y\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e14f38807bc231b9e43d45c8e909d463afb17b5)
![{\displaystyle {\begin{aligned}|f(x)-f(y)|&=|x^{2}-y^{2}|\\[0.3em]&=|(x+y)\cdot (x-y)|\\[0.3em]&=|x+y|\cdot |x-y|\\[0.3em]&\leq \left(\left|x\right|+\left|y\right|\right)\cdot \left|x-y\right|\\[0.3em]&\leq 2\cdot \max\{\left|x\right|,\left|y\right|\}\cdot \left|x-y\right|\\[0.3em]&\leq 2\cdot \max\{|a|,|b|\}\cdot |x-y|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c7596d1375f555a2ae852ee7568c884dfd28aff)







![{\displaystyle {\begin{aligned}|f(x)-f(y)|&=|a\cdot x+b-(a\cdot y+b)|\\[0.3em]&=|a\cdot (x-y)|=|a|\cdot |x-y|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/399e0f80c0c8ca39510581c9f5728cd77a0423ca)




![{\displaystyle [-2,2]\subseteq \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae62cde2c2776c5c544d576b2f2499c3e67f0c1)
![{\displaystyle {\begin{aligned}|f(x)-f(y)|&=|ax^{2}+bx+c-(ay^{2}+by+c)|\\[0.3em]&=|a(x^{2}-y^{2})+b(x-y)|\\[0.3em]&=|a(x+y)(x-y)+b(x-y)|\\[0.3em]&=|a(x+y)+b|\cdot |x-y|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f27f899cfaa85609769b8686e77ed5c081381eb)
![{\displaystyle x,y\in [-2,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dcf93923fba30c5021c0156a8ad5c66c5e40e68)
![{\displaystyle {\begin{aligned}|f(x)-f(y)|&=|a(x+y)+b|\cdot |x-y|\\[0.3em]&\leq (|a(x+y)|+|b|)\cdot |x-y|\\[0.3em]&\leq (|a|\cdot |x+y|+|b|)\cdot |x-y|\\[0.3em]&\leq (|a|\cdot (|x|+|y|)+|b|)\cdot |x-y|\\[0.3em]&\leq (4|a|+|b|)\cdot |x-y|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e1c07bd5c4bfadecd79404fe6e8c5e84ce6af1b)



![{\displaystyle {\begin{aligned}|f(x)-f(y)|&=|a(x+y)+b|\cdot |x-y|\\[0.3em]&\leq L\cdot |x-y|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63193e8a8d2fb7768ae5c981946f728026f84627)


![{\displaystyle {\begin{aligned}|a(x+y)+b|&=\left|a\left({\frac {L-b+1}{a}}+0\right)+b\right|\\[0.3em]&=|L+1|>L\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abdafdd771ff0ace1755cd67cdd045db779082f2)



![{\displaystyle (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e70f9c241f9faa8e9fdda2e8b238e288807d7a4)

![{\displaystyle {\begin{aligned}|f(x)-f(y)|&=\left|{\frac {1}{x}}-{\frac {1}{y}}\right|=\left|{\frac {y-x}{xy}}\right|\\[0.3em]&={\frac {1}{xy}}\cdot |x-y|\\[0.3em]&{\color {OliveGreen}\left\downarrow \ x,y\geq 1\right.}\\[0.3em]&\leq 1\cdot |x-y|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52a16ccccbe937089e72808ccc36a99070f62c12)


![{\displaystyle f|_{(0,1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/221a5e5788ff3672911cf7eabc32f3e9b323ab43)

![{\displaystyle x,y\in (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53ed60a602ababea356ccb07866f0c33ae8180b1)




![{\textstyle x={\frac {1}{2L}}\in (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ba32fe53ed1369d83b64159f7ad4a033b728200)


![{\displaystyle x=2L\in (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a47a2c70fb14c7ff8b23b8ebb2e73d877b2294fb)

![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)





