Diffgeo: Beispiele: Kugel

Aus Wikibooks

Wechseln zu: Navigation, Suche

Zurück zum Inhaltsverzeichnis

Inhaltsverzeichnis

[Bearbeiten] Die Fläche

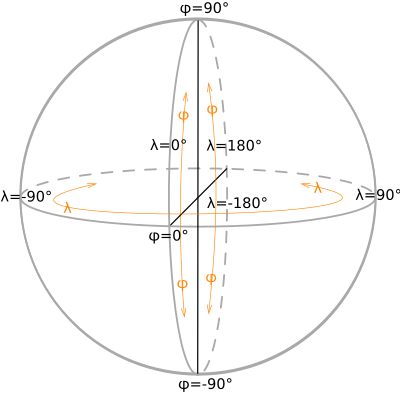
Geographische Koordinaten auf der Kugel

Parametrisiert wie in Geodätische Koordinatensysteme Geographische Koordinaten geschildert. Statt λ und φ werden U und V verwendet.

[Bearbeiten] Parametrisierung

\begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} R \cdot cos{U}\cdot cos{V} \\ R \cdot sin{U} \cdot cos{V} \\ R \cdot sin{V} \end{pmatrix}
V \in (-\frac{\pi}{2};\frac{\pi}{2})\, U \in [-\pi;\pi)

[Bearbeiten] (Gaußsche) Tangentenvektoren

Siehe Gaußsches Dreibein


\vec{g}_1 = \vec{x}_u=-R \cdot sin{u}\cdot cos{v} \cdot \vec{e_x}+R \cdot cos{u} \cdot cos{v} \cdot \vec{e_y}
\vec{g}_2 = \vec{x}_v=-R \cdot cos{u}\cdot sin{v} \cdot \vec{e_x}-R \cdot sin{u} \cdot sin{v} \cdot \vec{e_y}+R \cdot cos{v} \cdot \vec{e_z}
\vec g_3 = \frac{\vec{x}_u(u) \times \vec{x}_v(v)} {|| \vec{x}_u(u) \times \vec{x}_v(v) ||} =

[Bearbeiten] erste Fundamentalform

[Bearbeiten] erste Fundamentalgrößen

Siehe hier:

g_{11} = \vec{x}_u \cdot \vec{x}_u = \vec{x}_u = R^2 \cos{v}^2
g_{12}=G_{21}=\vec{x}_u \cdot \vec{x}_v = 0
g_{22}=\vec{x}_v \cdot \vec{x}_v = R^2

[Bearbeiten] erster Fundamentaltensor

\mathbf{G} = \begin{pmatrix} g_{11} & g_{12} \\ g_{21} & g_{22} \end{pmatrix} = \begin{pmatrix} R^2 \cos{V}^2 & 0 \\ 0 & R^2 \end{pmatrix}

[Bearbeiten] Inverser erster Fundamentaltensor

\mathbf{G}^{-1} = \begin{pmatrix} g^{11} & g^{12} \\ g^{21} & g^{22} \end{pmatrix} = \begin{pmatrix} \frac{1}{\cos^2V \cdot R^2} & 0 \\ 0 & \frac{1}{R^2} \end{pmatrix}


[Bearbeiten] zweite Fundamentalform

[Bearbeiten] zweifache Ableitungen

\vec{x}_{uu} =
\vec{x}_{uv} =
\vec{x}_{vv} =

[Bearbeiten] zweite Fundamentalgrößen

Hier nachschauen!

b_{11} = \vec{x}_{uu} \cdot \vec n =
b_{12} = b_{21} = \vec{x}_{uv} \cdot \vec n
b_{21} = \vec{x}_{vv} \cdot \vec n =


[Bearbeiten] zweiter Fundamentaltensor

\mathbf{B} = \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} = \begin{pmatrix} L & M \\ M & N \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}

[Bearbeiten] Christoffelsymbole

Siehe hier. Mit u1 = u, u2 = v. α = 1, β = 1, γ = 1

\Gamma_{11}^{1} := \frac{1}{2} g^{11} (\frac{\partial g_{11}}{\partial u^{1}} + \frac{\partial g_{11}}{\partial u^{1}} - \frac{\partial g_{11}}{\partial u^{1}}) + \frac{1}{2} g^{12} (\frac{\partial g_{12}}{\partial u^{1}} + \frac{\partial g_{21}}{\partial u^{1}} - \frac{\partial g_{11}}{\partial u^{2}}) =

α = 2, β = 1, γ = 1

\Gamma_{12}^{1} := \frac{1}{2} g^{11} (\frac{\partial g_{11}}{\partial u^{2}} + \frac{\partial g_{12}}{\partial u^{1}} - \frac{\partial g_{21}}{\partial u^{1}}) + \frac{1}{2} g^{12} (\frac{\partial g_{12}}{\partial u^{2}} + \frac{\partial g_{22}}{\partial u^{1}} - \frac{\partial g_{21}}{\partial u^{2}}) =

α = 1, β = 2, γ = 1

\Gamma_{11}^{2} := \frac{1}{2} g^{21} (\frac{\partial g_{11}}{\partial u^{1}} + \frac{\partial g_{11}}{\partial u^{1}} - \frac{\partial g_{11}}{\partial u^{1}}) + \frac{1}{2} g^{22} (\frac{\partial g_{12}}{\partial u^{1}} + \frac{\partial g_{21}}{\partial u^{1}} - \frac{\partial g_{11}}{\partial u^{2}}) =

α = 1, β = 1, γ = 2

\Gamma_{21}^{1} = \Gamma_{12}^{1}

α = 2, β = 1, γ = 2,

\Gamma_{12}^{2} := \frac{1}{2} g^{11} (\frac{\partial g_{21}}{\partial u^{2}} + \frac{\partial g_{12}}{\partial u^{2}} - \frac{\partial g_{22}}{\partial u^{1}}) + \frac{1}{2} g^{12} (\frac{\partial g_{22}}{\partial u^{2}} + \frac{\partial g_{22}}{\partial u^{2}} - \frac{\partial g_{22}}{\partial u^{2}}) =

α = 1, β = 2, γ = 2

\Gamma_{21}^{2} =\Gamma_{12}^{2}

α = 2, β = 2, γ = 2

\Gamma_{22}^{2} := \frac{1}{2} g^{21} (\frac{\partial g_{21}}{\partial u^{2}} + \frac{\partial g_{12}}{\partial u^{2}} - \frac{\partial g_{22}}{\partial u^{1}}) + \frac{1}{2} g^{22} (\frac{\partial g_{22}}{\partial u^{2}} + \frac{\partial g_{22}}{\partial u^{2}} - \frac{\partial g_{22}}{\partial u^{2}}) =

Zurück zum Inhaltsverzeichnis

Von „http://de.wikibooks.org/wiki/Diffgeo:_Beispiele:_Kugel“
Persönliche Werkzeuge