Ordnungsrelation – „Mathe für Nicht-Freaks“

Ordnungen sind eine besondere Klasse binärer, homogener Relationen. Sie sind eine Verallgemeinerung der Ordnungsrelationen wie $\le$ oder $<$, die du bereits für die Zahlbereiche $\mathbb{N}$, $\mathbb{Z}$ und $ℝ$ kennst. Mit Hilfe von Ordnungsrelationen können Elemente einer Grundmenge ihrer Größe nach geordnet und miteinander verglichen werden.

Um eine Ordnung auf einer Menge zu definieren, reicht es, eine der beiden Relationen $\le$ oder $<$ zu definieren. Die jeweils andere Relation lässt sich dann mit den folgenden Beziehungen darauf zurückführen:

• $x<y$ genau dann, wenn $x\le y$ und $x\ne y$,
• $x\le y$ genau dann, wenn $x<y$ oder $x=y$.

Ordnungsrelationen lassen sich umdrehen: so wird aus der Kleiner-Gleich-Relation $\le$ die Grösser-Gleich-Relation $\ge$ und aus der Echt-Kleiner-Relation $<$ wird die Echt-Größer-Relation $>$. In Listen im Internet kann in der Regel gewählt werden, ob die Ergebnisse aufsteigend oder absteigend sortiert werden sollten.

Ordnungsrelationen gibt es auch außerhalb der Zahlen. So sind beispielsweise die Wörter im Lexikon alphabetisch geordnet.

Totalordnung

Transitivität: Aus $a\le b$ und $b\le c$ folgt $a\le c$

Totalordnungen sind direkte Verallgemeinerungen der Kleiner-Gleich-Relation auf den Zahlen. Genau wie andere binäre homogene Relationen wird die Totalordnung über ihre Eigenschaften bestimmt.

Frage: Welche Eigenschaft besitzt die Relation $\le$ auf den Zahlbereichen $\mathbb{N}$, $\mathbb{Z}$ und $ℝ$?

Eigenschaft der Relation $\le$	Begründung
reflexiv	Für alle $x$ ist $x\le x$.
antisymmetrisch	Aus $x\le y$ und $y\le x$ folgt $x=y$
transitiv	Aus $x\le y$ und $y\le z$ folgt $x\le z$
linear	Für alle reellen Zahlen $x$ und $y$ ist $x\le y$ oder $y\le x$
nicht irreflexiv	Diese Relation ist reflexiv und die Grundmenge ist nicht leer
nicht symmetrisch	Gegenbeispiel: Es ist $23\le 42$ aber $42\le ̸23$ und damit kann die Relation nicht symmetrisch sein

Eine Relation ist dann eine Totalordnung, wenn sie diejenigen vier Eigenschaften hat, die auch die Kleiner-Gleich-Relation für die Zahlen besitzt:

Definition (Totalordnung)

Eine Totalordnung $\le$ auf $M$ ist eine binäre und homogene Relation auf der Grundmenge $M$, die folgende Eigenschaften besitzt:

• $\mathrm{\forall }x\in M:x\le x$ (Reflexivität)
• $\mathrm{\forall }x,y\in M:x\le y\wedge y\le x\Rightarrow x=y$ (Antisymmetrie)
• $\mathrm{\forall }x,y,z\in M:x\le y\wedge y\le z\Rightarrow x\le z$ (Transitivität)
• $\mathrm{\forall }x,y\in M:x\le y\vee y\le x$ (Linearität)

Da eine Totalordnung die direkte Verallgemeinerung der Ordnung auf der Zahlengeraden ist, welche eine „Linie“ ist, wird eine Totalordnung auch lineare Ordnung genannt.

Hinweis

In der Mathematik wird das Adjektiv „linear“ mehrfach verwendet. So kennst du „lineare Funktionen“ aus der Schule und in der linearen Algebra gibt es den Begriff der „linearen Abbildung”. Diese Begriffe haben aber nichts mit dem Begriff der „linearen Ordnung“ zu tun!

Beispiel (Totalordnung)

• Die $x\le y$ Relation auf der Grundmenge $\mathbb{N}$ ist eine Totalordnung.
• Die $x\le y$ Relation auf der Grundmenge $\mathbb{Z}$ ist eine Totalordnung.
• Die $x\le y$ Relation auf der Grundmenge $ℝ$ ist eine Totalordnung.
• Die alphabetische Ordnung der Wörter in einem Lexikon ist eine Totalordnung

Die Ordnungen $\le$ auf den Zahlbereichen $\mathbb{N}$, $\mathbb{Z}$ und $ℝ$ sind zwar alle Totalordnungen, aber sie unterscheiden sich auch! So hat $\mathbb{N}$ ein kleinstes Element, nämlich die $1$, aber weder $\mathbb{Z}$ noch $ℝ$ haben ein kleinstes Element. In $ℝ$ gibt es zwischen zwei verschiedenen Elementen $x\ne y$ mit $x\le y$ immer ein weiteres Element $z$ mit $z\ne x$, $z\ne y$ und $x\le z\le y$. Das gilt für $\mathbb{N}$ und $\mathbb{Z}$ nicht.

Satz

Sei $\le$ eine Totalordnung auf der Menge $M$ und $A\subseteq M$ eine Teilmenge von $M$. Dann ist die Einschränkung von $\le$ auf $A$ eine Totalordnung auf $A$.

Beweis

Die Einschränkung von $\le$ auf $A$ ist $\{x,y\in A|x\le y\}$. Die vier Eigenschaften der Totalordnung auf $M$ gelten natürlich auch für die Teilmenge $A\subseteq M$. Also ist $\{x,y\in A|x\le y\}$ eine Totalordnung auf $A$.

Wie bereits gesagt, ist auch die Umkehrung $\ge$ einer Totalordnung $\le$ wieder eine Totalordnung:

Aufgabe: Sei $\le$ eine Totalordnung. Beweise, dass dann auch die konverse Relation $\ge$ definiert durch $x\ge y:\iff y\le x$ eine Totalordnung ist.

Beweisschritt: $\ge$ ist reflexiv

Wir müssen beweisen, dass für alle $x$ aus der Grundmenge $x\ge x$ gilt. Nun gilt $x\ge x$ nach Definition genau dann, wenn $x\le x$ ist. Wir wissen aber bereits, dass $\le$ reflexiv ist, und damit auch, dass $x\le x$ für alle $x$ gilt. Es folgt die Reflexivität von $\ge$.

Beweisschritt: $\ge$ ist antisymmetrisch

Auch dies folgt aus der Antisymmetrie von $\le$. Für $\le$ gilt nämlich $x\le y\wedge y\le x\Rightarrow x=y$. Setzen wir $x\ge y\iff y\le x$ ein, folgt $y\ge x\wedge x\ge y\Rightarrow x=y$ für alle $x$ und $y$ der Grundmenge. Dies ist die Antisymmetrieeigenschaft von $\ge$.

Beweisschritt: $\ge$ ist transitiv

Sei $x\ge y$ und $y\ge z$. Nach Definition ist dann $y\le x$ und $z\le y$. Es folgt $z\le x$ aus der Transitivität von $\le$. Damit gilt aber auch $x\ge z$ nach der Definition von $\ge$. Ingesamt haben wir so $x\ge y\wedge y\ge z\Rightarrow x\ge z$ gezeigt und damit die Transitivität von $\ge$.

Beweisschritt: $\ge$ ist linear

Von $\le$ wissen wir bereits, dass es linear ist. Also gilt für zwei $x$ und $y$: $x\le y$ oder $y\le x$. Nach Definition von $\ge$ gilt dann auch für alle $x$ und $y$: $y\ge x$ oder $x\ge y$. Dies ist die Linearitätseigenschaft von $\ge$.

Definition (Weitere Ordnungsrelationen auf Grundlage der Totalordnung)

Sei $\le$ eine Totalordnung auf der Grundmenge $M$. Dann sind die weiteren Ordnungsrelationen $<$ und $>$ auf $M$ folgendermaßen definiert:

• $x<y:\iff x\le y\wedge x\ne y$
• $x>y:\iff y<x$

Während $\ge$ ebenfalls eine Totalordnung ist, ist das bei $<$ und $>$ nicht der Fall. Diese beiden Relationen sind strikte Totalordnungen:

Strikte Totalordnung

Analog zur Totalordnung, soll auch die Relation $<$ die Kleiner-Relation der reellen Zahlen verallgemeinern. Wenn eine Relation das tut, nennt man sie strikte Totalordnung. Welche Eigenschaften muss nun aber $<$ besitzen, um als strikte Totalordnung zu gelten?

Frage: Welche Eigenschaften besitzt die Relation $<$ auf den Zahlbereichen $\mathbb{N}$, $\mathbb{Z}$ und $ℝ$ ?

Eigenschaft der Relation $<$	Begründung
irreflexiv	Für alle $x$ ist $x≮x$.
antisymmetrisch	Ist $x<y$, so folgt automatisch $y≮x$. Damit kann $x<y$ und $y<x$ nie gleichzeitig auftreten. Somit ist die Implikation $x<y\wedge y<x\Rightarrow x=y$ stets wahr, weil die Prämisse $x<y\wedge y<x$ stets falsch ist (siehe Abschnitt zur Implikation).
asymmetrisch	Die Kleiner-Relation ist antisymmetrisch und irreflexiv.
transitiv	Aus $x<y$ und $y<z$ folgt $x<z$.
konnex	Für zwei verschiedene Zahlen $x$ und $y$ gilt entweder $x<y$ oder $y<x$.
trichotom	Die Kleiner-Relation ist asymmetrisch und konnex.
nicht linear	Für die Zahlen $x=1$ und $y=1$ gilt weder $x<y$ noch $y<x$.
nicht reflexiv	Es ist beispielsweise $1≮1$.
nicht symmetrisch	Es ist beispielsweise $23<42$, aber nicht auch $42<23$.

Aus dem Abschnitt zu den Eigenschaften binärer Relationen wissen wir, dass eine binäre Relation genau dann trichotom ist, wenn sie gleichzeitig irreflexiv, asymmetrisch, konnex und antisymmetrisch ist. Dementsprechend müssen wir von einer binären Relation nur die Trichotomie und die Transitivität fordern und es folgt dann bereits, dass diese Relation genau dieselben Eigenschaften wie die Echt-Kleiner-Relation besitzt. Deswegen wählen wir die Trichotomie und die Transitivität als die charakteristischen Eigenschaften einer strikten Totalordnung:

Definition (strikte Totalordnung)

Eine binäre und homogene Relation $<$ auf der Grundmenge $M$ heißt strikte Totalordnung, wenn $<$ folgende Eigenschaften besitzt:

• $\mathrm{\forall }x,y,z\in M:x<y\wedge y<z\Rightarrow x<z$ (Transitivität)
• $\mathrm{\forall }x,y\in M:x<y\dot{\vee }x=y\dot{\vee }y<x$ (Trichotomie)

Das Symbol $\dot{\vee }$ ist dabei die Kontravalenz, also die Entweder-Oder-Verknüpfung zwischen Aussagen. Wir zeigen nun, dass die mit Hilfe einer Totalordnung $\le$ definierte Relation $<$ eine strikte Totalordnung ist.

Satz

Sei $\le$ eine Totalordnung auf $M$ und die Relation $<$ wie folgt definiert: $x<y:\iff x\le y\wedge x\ne y$. Dann ist $<$ eine strikte Totalordnung auf $M$.

Beweis

Zu zeigen ist, dass $<$ transitiv und trichotom ist.

Beweisschritt: $<$ ist transitiv

Gelte $x<y\wedge y<z$. Nach Definition von $<$ gilt dann: $(x\le y\wedge x\ne y)\wedge (y\le z\wedge y\ne z)$. Mit der Transitivität von $\le$ folgt $x\le z$. Weiterhin folgt aus $x\ne y$ mit der Antisymmetrie von $\mathrm{\neg }(x\le y)\vee \mathrm{\neg }(y\le x)$. Da $x\le y$ gilt, muss $\mathrm{\neg }(y\le x)$ gelten. Wäre nun $x=z$, würde daraus $\mathrm{\neg }(y\le z)$ folgen - Widerspruch! Also gilt $x\ne z$. Insgesamt haben wir $x\le z\wedge x\ne z$ gezeigt, was nach Definition von $<$ gerade $x<z$ ist.

Beweisschritt: $<$ ist trichotom

Gelte $x=y$, dann gilt nach Definition von $<$ weder $x<y$ noch $y<x$. Gelte nun $x\ne y$. Mit der Linearität von $\le$ gilt $x\le y\vee y\le x$. Wegen der Antisymmetrie von $\le$ kann aber wegen $x\ne y$ nicht beides gelten, also: $x\le y\dot{\vee }y\le x$. Daraus folgt $x<y\dot{\vee }y<x$. In beiden Fällen gilt also $x<y\dot{\vee }x=y\dot{\vee }y<x$.

Aufgabe: Sei $\le$ eine Totalordnung. Beweise, dass dann auch die Relation $>$ definiert durch $x>y:\iff y\le x\wedge y\ne x$ eine strikte Totalordnung ist.

Sei $\le$ eine Totalordnung auf $M$. Wie im vorigen Abschitt gezeigt ist dann auch $\ge$ mit $x\ge y:\iff y\le x$ eine Totalordnung auf $M$. Die Definition von $>$ lässt sich wie folgt umschreiben: $x>y:\iff y\le x\wedge x\ne y$, also gilt $x>y\iff x\ge y\wedge x\ne y$. Nunmehr folgt der Beweis genauso wie eben für $<$ gezeigt.

Sobald eine strikte Totalordnung $<$ definiert wurde, können ähnlich wie bei der Totalordnung weitere Ordnungsrelationen auf $<$ zurückgeführt werden:

Definition (Weitere Ordnungsrelationen auf Grundlage der strikten Totalordnung)

Sei $<$ eine strikte Totalordnung auf der Grundmenge $M$. Dann sind die weiteren Ordnungsrelationen $\le$, $\ge$ und $>$ auf $M$ folgendermaßen definiert:

• $x\le y:\iff x<y\vee x=y$
• $x\ge y:\iff y>x\vee x=y$
• $x>y:\iff y<x$

Aufgabe: Sei $<$ eine strikte Totalordnung. Beweise, dass dann auch die Relation $\le$ definiert durch $x\le y:\iff y<x\vee y=x$ eine Totalordnung ist.

Zu zeigen ist, dass $\le$ reflexiv, antisymmetrisch, transitiv und linear ist.

Beweisschritt: $\le$ ist reflexiv

Es gilt $x=x$, also auch $x\le x$.

Beweisschritt: $\le$ ist antisymmetrisch

Gelte $x\le y\wedge y\le x$. Nach Definition von $\le$ gilt dann: $(x<y\vee x=y)\wedge (y<x\vee y=x)$. Wegen der Trichotomie von $<$ können aber nicht $x<y$ und $y<x$ gemeinsam gelten oder eine der beiden Ungleichungen zusammen mit der Gleichung, also folgt $x=y$.

Beweisschritt: $\le$ ist transitiv

Gelte $x\le y\wedge y\le z$. Dann gilt nach Definition von $\le$ $(x<y\vee x=y)\wedge (y<z\vee y=z)$. Ist $x=y$ folgt $x=z$, also gilt $x\le z$. Ist $y=z$, folgt ebenfalls $x=z$ und damit $x\le z$. Gelte also $x\ne y$ und $y\ne z$. Dann gelten $x<y$ und $y<z$ und mit der Transitivität von $<$ folgt $x<z$ und somit auch $x\le z$.

Beweisschritt: $\le$ ist linear

Mit der Trichotomie von $<$ gilt entweder $x<y$ oder $x=y$ oder $y<x$. Im ersten Fall gilt $x\le y$, ebenso im zweiten Fall. Im zweiten Fall gilt zusätzlich $y\le x$. Im dritten Fall gilt $y\le$. Insgesamt gilt $x\le y\vee y\le x$.

Die Beweis, dass $\ge$ eine Totalordnung ist verläuft analog.

Aufgabe: Sei $<$ eine strikte Totalordnung. Beweise, dass dann auch die Relation $>$ definiert durch $x>y:\iff y<x$ eine strikte Totalordnung ist.

Zu zeigen ist, dass $>$ transitiv und trichotom ist.

Beweisschritt: $>$ ist transitiv

Sei $x>y\wedge y>z$. Nach Definition von $>$ gilt dann auch: $y<x\wedge z<y$. Mit der Transitivität von $<$ folgt daraus $z<x$, also gilt $x>z$.

Beweisschritt: $>$ ist trichotom

Es gilt $x>y\dot{\vee }x=y\dot{\vee }y>x$. Nach Definition von $>$ folgt daraus: $y>x\dot{\vee }x=y\dot{\vee }x>y$, das ist die Trichotomie von $>$.

Aufgabe: Sei $\le$ eine Totalordnung auf der Menge $M$ und $<$ wie üblich definiert. Zeige:

$\mathrm{\forall }x,y\in M:(x<y\iff y\nleqq x)$

Beweis:

Gilt $x<y$, so gilt nach Definition $x\le y$ und $x\ne y$. Aus $x\ne y$ folgt wegen der Antisymmetrie $x\nleqq y\vee y\nleqq x$. Da $x\nleqq y$ nicht gilt, muss $y\nleqq x$ gelten. Gelte nun $y\nleqq x$. Dann folgt mit der Linearität $x\le y$. Gälte $x=y$, dann folgte mit der Reflexivität $y\le x$ ↯. Also gilt $x\ne y$ und insgesamt folgt $x<y$.

Aufgabe: Sei $\le$ eine transitive binäre Relation auf der Menge $M$ und $<$ wie üblich definiert. Zeige: Gilt $\mathrm{\forall }x,y\in M:(x<y\iff y\nleqq x)$, so ist $\le$ eine Totalordnung auf $M$.

Beweis:

Mit der Definition von $<$ lautet die Voraussetzung:

$(\ast )x\le y\wedge x\ne y\iff y\nleqq x$

Da $\le$ transitiv ist, sind nur noch die drei anderen Eigenschaften zu zeigen.

Beweisschritt: Reflexivität

Für den Spezialfall $y=x$ ist die linke Seite von (*) immer falsch. Also ist auch die rechte Seite falsch und es gilt die Reflexivität: $x\le x$.

Beweisschritt: Antisymmetrie

Gelte $x\le y\wedge y\le x$. Dann ist (*) nur wahr, wenn $x=y$ gilt. Das zeigt die Antisymmetrie.

Beweisschritt: Linearität

Gilt $y\le x$, dann gilt auch $x\le y\vee y\le x$, also die Linearität. Gelte nun $y\nleqq x$. Dann liefert (*) $x\le y\wedge x\ne y$, also ebenfalls die Linearität.

Also ist $\le$ eine Totalordnung. ✔

Zusammenhang von strikter Totalordnung zur Totalordnung

In den vorherigen beiden Abschnitten haben wir dargelegt, wie man aus einer Totalordnung und einer strikten Totalordnung einer Menge die jeweils andere Ordnung definieren kann. Es fehlt aber noch der Beweis, dass beide Wege gleichwertig sind, dass es also egal ist, welchen Weg man geht. Um dies zu zeigen, muss Zweierlei gezeigt werden:

1. Sei ${\le }_1$ eine Totalordnung, von der man die strikte Totalordnung $<$ über $x<y:\iff x{\le }_{1}y\wedge x\ne y$ bildet. Wenn man nun wieder die von $<$ induzierte Totalordnung ${\le }_2$ über $x{\le }_{2}y:\iff x<y\vee x=y$ bildet, dann müssen die beiden Relationen ${\le }_1$ und ${\le }_2$ identisch sein. Es muss also gelten $x{\le }_{2}y\iff x{\le }_{1}y$.
2. Analoges muss gelten, wenn man bei einer strikten Totalordnung ${<}_1$ beginnt und über den Zwischenschritt der von ${<}_1$ induzierten Totalordnung $\le$ die von $\le$ induzierte strikte Totalordnung ${<}_2$ bildet: $x{<}_{2}y\iff x{<}_{1}y$.

Beweis

Sei ${\le }_1$ eine Totalordnung und ${\le }_2$ definiert über $x{\le }_{2}y:\iff x<y\vee x=y$, wobei $<$ definiert ist über $x<y:\iff x{\le }_{1}y\wedge x\ne y$.

Beweisschritt: $x{\le }_{2}y\iff x{\le }_{1}y$

Es gilt:

$\begin{array}{cc}& x{\le }_{2}y\\ & \updownarrow 𝖣𝖾𝖿𝗂𝗇𝗂𝗍𝗂𝗈𝗇𝗏𝗈𝗇{\mathsf{\le }}_{\mathrm{𝟤}}\\ \iff & x<y\vee x=y\\ & \updownarrow x<y\iff x{\le }_{1}y\wedge x\ne y\\ \iff & (x{\le }_{1}y\wedge x\ne y)\vee x=y\\ & \updownarrow 𝖣𝗂𝗌𝗍𝗋𝗂𝖻𝗎𝗍𝗂𝗏𝗀𝖾𝗌𝖾𝗍𝗓\mathsf{:}(A\wedge B)\vee C\iff (A\vee C)\wedge (B\vee C)\\ \iff & (x{\le }_{1}y\vee x=y)\wedge (x\ne y\vee x=y)\\ & \updownarrow A\vee \mathrm{\neg }A𝗂𝗌𝗍𝖾𝗂𝗇𝖾𝖳𝖺𝗎𝗍𝗈𝗅𝗈𝗀𝗂𝖾\mathsf{(}𝗂𝗆𝗆𝖾𝗋𝗐𝖺𝗁𝗋\mathsf{)}\\ \iff & (x{\le }_{1}y\vee x=y)\wedge 𝖶\\ & \updownarrow A\wedge 𝖶\iff A\\ \iff & x{\le }_{1}y\vee x=y\\ & \updownarrow {\le }_1𝗂𝗌𝗍𝗋𝖾𝖿𝗅𝖾𝗑𝗂𝗏\\ \iff & x{\le }_{1}y\end{array}$

Den letzten Beweisschritt wollen wir näher ausführen: Um die Äquivalenz $x{\le }_{1}y\iff x{\le }_{1}y\vee x=y$ zu zeigen, müssen wir die beiden Implikationen $x{\le }_{1}y\Rightarrow x{\le }_{1}y\vee x=y$ und $x{\le }_{1}y\vee x=y\Rightarrow x{\le }_{1}y$ beweisen. Die erste Implikation ist klar, weil $A\Rightarrow A\vee B$ unabhängig von der Aussage $B$ stets wahr ist. Wenn wir in der zweiten Implikation mit der Prämisse $x{\le }_{1}y\vee x=y$ starten, dann ist einer der beiden Fälle $x{\le }_{1}y$ und $x=y$ wahr. In beiden Fällen gilt $x{\le }_{1}y$, denn im ersten Fall gilt es sowieso und im zweiten Fall folgt es aus der Reflexivität von ${\le }_1$.

Sei nun ${<}_1$ eine strikte Totalordnung. Sei $\le$ die von ${<}_1$ induzierte Totalordnung mit $x\le y\iff x{<}_{1}y\vee x=y$. Sei wiederum ${<}_2$ definiert über $x{<}_{2}y\iff x\le y\wedge x\ne y$.

Beweisschritt: $x{<}_{2}y\iff x{<}_{1}y$

Es gilt:

$\begin{array}{cc}& x{<}_{2}y\\ & \updownarrow 𝖣𝖾𝖿𝗂𝗇𝗂𝗍𝗂𝗈𝗇𝗏𝗈𝗇{<}_{\mathrm{𝟤}}\\ \iff & x\le y\wedge x\ne y\\ [0.3em]& \updownarrow x\le y\iff x{<}_{1}y\vee x=y\\ \iff & (x{<}_{1}y\vee x=y)\wedge x\ne y\\ & \updownarrow 𝖣𝗂𝗌𝗍𝗋𝗂𝖻𝗎𝗍𝗂𝗏𝗀𝖾𝗌𝖾𝗍𝗓\mathsf{:}(A\vee B)\wedge C\iff (A\wedge C)\vee (B\wedge C)\\ \iff & (x{<}_{1}y\wedge x\ne y)\vee (x=y\wedge x\ne y)\\ & \updownarrow A\wedge \mathrm{\neg }A𝗂𝗌𝗍𝗂𝗆𝗆𝖾𝗋𝖿𝖺𝗅𝗌𝖼𝗁(𝖥)\\ \iff & (x{<}_{1}y\wedge x\ne y)\vee 𝖥\\ & \updownarrow A\vee F\iff A𝗂𝗌𝗍𝖾𝗂𝗇𝖾𝖳𝖺𝗎𝗍𝗈𝗅𝗈𝗀𝗂𝖾\\ \iff & (x{<}_{1}y\wedge x\ne y)\\ & \updownarrow {<}_1𝗂𝗌𝗍𝗂𝗋𝗋𝖾𝖿𝗅𝖾𝗑𝗂𝗏\\ \iff & x{<}_{1}y\end{array}$

Halbordnung

Es gibt Relationen, die bis auf die Linearität alle Eigenschaften der Totalordnung erfüllen. Damit verhalten sie sich fast wie Totalordnungen. Jedoch können bei diesen Relationen nicht alle Paare von Elemente der Grundmenge miteinander verglichen werden. Diese Relationen werden Halbordnungen oder partielle Ordnungen genannt (eben weil diese Ordnungen nur „zur Hälfte“ Totalordnungen sind):

Definition (Halbordnung)

Eine Halbordnung $R\subseteq M\times M$ ist eine binäre und homogene Relation auf der Grundmenge $M$, die folgende Eigenschaften besitzt:

• reflexiv
• antisymmetrisch
• transitiv

Beispiel (Halbordnung)

• Die Ist-Teiler-von-Beziehung auf $\mathbb{N}$ ist eine Halbordnung.
• Die Teilmengenbeziehung auf jeder Menge von Mengen ist eine Halbordnung.

Aus der Definition folgt, dass jede Totalordnung eine Halbordnung ist. Aber nicht jede Halbordnung ist eine Totalordnung.

Aufgabe: Gib ein Beispiel für eine Halbordnung an, die keine Totalordnung ist.

Die Teilmengenbeziehung $\subseteq$ auf der Potenzmenge $𝒫(\{1,2\})=\{\varnothing ,\{1\},\{2\},\{1,2\}\}$ ist eine Halbordnung, aber keine Totalordnung. So gilt für die Mengen $\{1\}$ und $\{2\}$ weder $\{1\}\subseteq \{2\}$ noch $\{2\}\subseteq \{1\}$ und damit ist $\subseteq$ keine totale Relation.

Quasiordnung

Quasiordnungen sind sowohl Verallgemeinerungen der Halbordnung als auch der Äquivalenzrelation

Noch allgemeiner sind Quasiordnungen, auch Präordnungen genannt. Bei ihnen wird die Antisymmetrie nicht mehr verlangt.

Definition (Quasiordnung)

Eine Quasiordnung $R\subseteq M\times M$ ist eine binäre und homogene Relation auf der Grundmenge $M$, die folgende Eigenschaften besitzt:

• reflexiv
• transitiv

Beispiel (Quasiordnung)

• Die Ist-Teiler-von-Beziehung $x\mid y$ auf $\mathbb{Z}$ ist eine Quasiordnung.

Diese Relation ist nicht antisymmetrisch, denn es gilt beispielsweise $3\mid -3$ und $3\mid -3$ aber nicht $3=-3$. Auf $\mathbb{N}$ dagegen ist die Relation $|$ eine Halbordnung.

Der Begriff der Quasiordnung verallgemeinert nicht nur den der Halbordnung, sondern zugleich auch den der Äquivalenzrelation.

Nachweis von Ordnungsrelationen

Wenn du die Aufgabe hast zu entscheiden, ob eine gegebene Relation eine Totalordnung bzw. eine Halbordnung ist, so musst du schauen, ob diese Relation alle notwendigen Eigenschaften für diese Art von Relation erfüllt. Der folgende Entscheidungsbaum demonstriert dir die Vorgehensweise:

Entscheidungsbaum zum Nachweis von Ordnungsrelationen

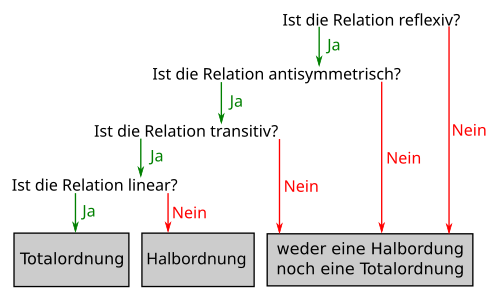
Beispielaufgabe

Aufgabe

Ist die Relation „$x$ ist eine Teilmenge von $y$“ auf der Grundmenge $𝒫(ℝ)$, der Menge aller Teilmengen von $ℝ$, eine Halbordnung bzw. eine Totalordnung?

Lösung

Hier kannst du schrittweise vorgehen:

Beweisschritt: Ist die Relation reflexiv?

Ja, die Relation ist reflexiv, denn jede Menge ist nach Definition eine Teilmenge von sich selbst (Für alle Mengen $M$ gilt $M\subseteq M$).

Beweisschritt: Ist die Relation antisymmterisch?

Ja, die Relation ist antisymmetrisch, weil aus $A\subseteq B$ und $B\subseteq A$ die Gleichheit $A=B$ folgt.

Beweisschritt: Ist die Relation transitiv?

Ja, die Relation ist transitiv, weil aus $A\subseteq B$ und $B\subseteq C$ die Beziehung $A\subseteq C$ folgt.

Beweisschritt: Ist die Relation linear?

Nein, die Relation ist nicht linear. So ist weder $\{1,2,3\}\subseteq \{4,5,6\}$ noch ist $\{4,5,6\}\subseteq \{1,2,3\}$.

Beweisschritt: Ist die Relation eine Halbordnung bzw. eine Totalordnung?

Da die Relation reflexiv, antisymmetrisch und transitiv ist, ist sie eine Halbordnung. Da die Relation aber nicht linear ist, ist sie keine Totalordnung.