- Paarmengen und kartesisches Produkt (Kreuzprodukt)
Wie allgemein bekannt lässt sich die Lage eines Punktes in der Ebene durch zwei Zahlen beschreiben. Dazu benutzt man ein rechtwinkliges (kartesisches) Koordinatensystem mit einer  -Achse und
-Achse und  -Achse, die senkrecht aufeinander stehen. Bezeichnet man beispielsweise mit
-Achse, die senkrecht aufeinander stehen. Bezeichnet man beispielsweise mit  den Abstand eines Punktes
den Abstand eines Punktes  von der
von der  -Achse (dieser ist negativ, wenn
-Achse (dieser ist negativ, wenn  links der
links der  -Achse liegt) und mit
-Achse liegt) und mit  man den Abstand eines Punktes
man den Abstand eines Punktes  von der
von der  -Achse (dieser ist negativ, wenn
-Achse (dieser ist negativ, wenn  unterhalb der
unterhalb der  -Achse liegt), so wird durch das Zahlenpaar
-Achse liegt), so wird durch das Zahlenpaar  die Lage des Punktes im Koordinatensystem beschrieben. Bei dem Zahlenpaar
die Lage des Punktes im Koordinatensystem beschrieben. Bei dem Zahlenpaar  ist die Reihenfolge wesentlich. So beschreiben beispielsweise die Zahlenpaare
ist die Reihenfolge wesentlich. So beschreiben beispielsweise die Zahlenpaare  und
und  unterschiedliche Punkte im Koordinatensystem, es gilt also
unterschiedliche Punkte im Koordinatensystem, es gilt also  .
.
Diese Paarbildung wird mit den folgenden Definitionen auf allgemeine Mengen erweitert:
- Definition
- Seien
 und
und  Mengen und sei
Mengen und sei  und
und 
- geordnetes Paar:
 heißt geordnetes Paar.
heißt geordnetes Paar.
- Gleichheit von geordneten Paaren
Zwei geordnete Paare " und
und  sind gleich" ⇔ "
sind gleich" ⇔ " und
und  "
"
- Paarmenge
Die Paarmenge (kartesisches Produkt, Kreuzprodukt) von  und
und  wird wie folgt definiert:
wird wie folgt definiert:
 und
und 
Normalerweise spricht man nur von Paaren (statt von geordneten Paaren), die Reihenfolge der Elemente ist aber wesentlich.
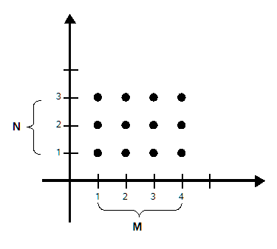
Die Menge  nennt man auch Rechteckmenge. Man kann die Elemente von nennt man auch Rechteckmenge. Man kann die Elemente von  in Form von Rechtecken im kartesischen Koordinatensystem aufschreiben. Hierzu folgendes Beispiel: in Form von Rechtecken im kartesischen Koordinatensystem aufschreiben. Hierzu folgendes Beispiel:  und und  . Die dazugehörige Rechteckmenge lautet dann: . Die dazugehörige Rechteckmenge lautet dann:


Die Abbildung rechts veranschaulicht diese Rechteckmenge.
|
|
|
|
Rechteckmenge 
|
In vielen mathematischen Sachverhalten stehen Objekte in bestimmten Zusammenhängen z. B. " ist größer als
ist größer als  ". Der Zusammenhang "
". Der Zusammenhang " ist größer als
ist größer als  " kann auch in der ungewöhnlichen Weise "
" kann auch in der ungewöhnlichen Weise " steht in der Relation größer" dargestellt werden. Das Beispiel zeigt aber, wie der Begriff der Relation auf den Mengenbegriff zurückgeführt werden kann.
steht in der Relation größer" dargestellt werden. Das Beispiel zeigt aber, wie der Begriff der Relation auf den Mengenbegriff zurückgeführt werden kann.
- Definition
 und
und  seien Mengen.
seien Mengen.
 heißt eine Relation zwischen
heißt eine Relation zwischen  und
und  ⇔
⇔  .
.
Ist  so ist
so ist  eine Relation auf
eine Relation auf  .
.
- Gilt
 dann "erfüllen
dann "erfüllen  und
und  die Relation
die Relation  " oder "stehen in der Relation
" oder "stehen in der Relation  ". Oft wird hierfür auch "
". Oft wird hierfür auch " " geschrieben.
" geschrieben.
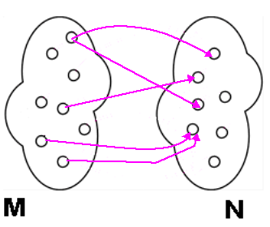
Stellt man sich zwei Mengen  und und  als Punktmengen in einer Ebene vor, kann man die Relation als Punktmengen in einer Ebene vor, kann man die Relation  durch Verbindungslinien zwischen den in Relation stehenden Punktepaaren kennzeichnen. Ein Pfeil von einem durch Verbindungslinien zwischen den in Relation stehenden Punktepaaren kennzeichnen. Ein Pfeil von einem  zu einem zu einem  bedeutet bedeutet  . .
|
|
|
|
Relation zwischen  und und 
|
Beispiel:
Sei  eine beliebige Menge. Durch eine beliebige Menge. Durch  ist eine Relation auf ist eine Relation auf  definiert: die Gleichheitsrelation. Diese lässt sich anschaulich als Diagonale darstellen. definiert: die Gleichheitsrelation. Diese lässt sich anschaulich als Diagonale darstellen.
|

|
|
|
Gleichheitsrelation
|
Beispiel:
 und
und  und
und  ist groesser als
ist groesser als 
ist eine Relation zwischen  und
und  und definiert die oben erwähnte "Größer-Relation".
und definiert die oben erwähnte "Größer-Relation".
Viele Probleme lassen sich vereinfachen, indem man Objekte, die gewissen gemeinsamen Kriterien genügen, als äquivalent betrachtet, obwohl sie sich hinsichtlich anderen Kriterien unterscheiden können. Hierzu benutzt man in der Mathematik die Äquivalenzrelation.
- Definition
- Seien
 eine Menge und
eine Menge und  eine Relation auf
eine Relation auf  .
.
- Äquivalenzrelation:
 ist eine Äquivalenzrelation auf
ist eine Äquivalenzrelation auf  , wenn für alle
, wenn für alle  gilt:
gilt:
- Reflexivität:

- Symmetrie:
 ⇒
⇒ 
- Transitivität:
 und
und  ⇒
⇒ 
- Äquivalenzklasse
Sei  eine Äquivalenzrelation auf
eine Äquivalenzrelation auf  . Die Menge der zu
. Die Menge der zu  äquivalenten Elemente von
äquivalenten Elemente von 
![{\displaystyle [x]:=\lbrace y\in M\mid x\sim y\rbrace }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9577f7f99d949ad7e14c56a4ac5996c272dc7cce)
- nennt man die Äquivalenzklasse oder Faser von
 bezüglich
bezüglich  . Das Element
. Das Element  heißt Repräsentant von
heißt Repräsentant von ![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d) .
.
Beispiel:
Die oben erwähnte Gleichheitsrelation  ist die "klassische" Äquivalenzrelation. Reflexivität, Symmetrie und Transitivität sind die bekannten Eigenschaften der Gleichheit. Außerdem gilt für alle
ist die "klassische" Äquivalenzrelation. Reflexivität, Symmetrie und Transitivität sind die bekannten Eigenschaften der Gleichheit. Außerdem gilt für alle  :
:  . Die Äquivalenzklassen von
. Die Äquivalenzklassen von  bezüglich
bezüglich  sind also Mengen mit genau einem Element, d.h.
sind also Mengen mit genau einem Element, d.h. ![{\displaystyle [x]=\lbrace x\rbrace }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3970a4ea37164ffa92ea1ab369602f036ee8583) .
.
In diesem Zusammenhang der Hinweis, dass eine Menge eine "Zusammenfassung wohl unterschiedener Objekte" ist.
Beispiel und Übung:
Etwas spannender ist schon die Entscheidung, ob es sich bei der Relation
 und
und  oder
oder  um eine Äquivalenzrelation handelt. Es ist also zu prüfen, ob
um eine Äquivalenzrelation handelt. Es ist also zu prüfen, ob  auf der Menge
auf der Menge  reflexiv, symmetrisch und transitiv ist.
reflexiv, symmetrisch und transitiv ist.
- Satz
- Sei
 eine Äquivalenzrelation auf
eine Äquivalenzrelation auf  , dann gilt
, dann gilt
![{\displaystyle [x]\cap [y]\not =\emptyset \Leftrightarrow [x]=[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4c9905e338a0c83b12fe93b4d92dcd9fe8fabc0)
- Beweis
- Sei
![{\displaystyle z\in [x]\cap [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/815ef00d294b6a9fdaaa892145581fbd553be9f1) . Dann ist
. Dann ist  und
und  , und wegen der Transitivität und der Symetrie gilt daher
, und wegen der Transitivität und der Symetrie gilt daher  . Für jedes
. Für jedes ![{\displaystyle a\in [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05b02437c238452a7cd8dbb82cd1cd934c8e380b) gilt daher
gilt daher  und wegen der Transitivität auch
und wegen der Transitivität auch  . Daraus folgt
. Daraus folgt ![{\displaystyle [x]\subseteq [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4044b09c892280324baed37803bc2090935cedf8) . Ganz analog zeigt man
. Ganz analog zeigt man ![{\displaystyle [y]\subseteq [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac2e8afc1de2256507f713d34dc61c6cc7c3b7a5) . Damit gilt
. Damit gilt ![{\displaystyle [x]=[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c34866e2a1216182b168dc1e272b0b02f1aab3a) .
.
- Dass
![{\displaystyle [x]=[y]\Rightarrow [x]\cap [y]\not =\emptyset }](https://wikimedia.org/api/rest_v1/media/math/render/svg/822eeb31d5b2bcc0479b358f32b09edceed25b66) gilt ist klar.
gilt ist klar.
Bemerkung: Dieser Satz besagt, dass Äquivalenzklassen disjunkt oder gleich sein müssen. D.h. eine Äquivalenzrelation auf der Menge  , bildet eine disjunkte Partition der Menge
, bildet eine disjunkte Partition der Menge  .
.
Mengen kann man über die Teilmengenbeziehung " " der Größe nach ordnen. Solche Ordnungen werden durch Eigenschaften wie Reflexivität, Antisymmetrie und Transitivität charakterisiert. Dies führt zu der sehr allgemeinen Definition der Ordnungsrelation.
" der Größe nach ordnen. Solche Ordnungen werden durch Eigenschaften wie Reflexivität, Antisymmetrie und Transitivität charakterisiert. Dies führt zu der sehr allgemeinen Definition der Ordnungsrelation.
- Definition
- Seien
 eine Menge und
eine Menge und  eine Relation auf
eine Relation auf  .
.
- Ordnungsrelation:
 ist eine Ordnungsrelation auf
ist eine Ordnungsrelation auf  , wenn für alle
, wenn für alle  gilt:
gilt:
- Reflexivität:

- Antisymmetrie:
 und
und 
- Transitivität:
 und
und 
- Ist
 eine Ordnungsrelation auf
eine Ordnungsrelation auf  , so heißt das Paar
, so heißt das Paar  eine geordnete Menge und
eine geordnete Menge und  eine Ordnung auf
eine Ordnung auf  . Die Namensgebung ist hier leider nicht sehr einheitlich. Man sagt statt Ordnung auch Halbordnung, Partialordnung oder teilweise Ordnung.
. Die Namensgebung ist hier leider nicht sehr einheitlich. Man sagt statt Ordnung auch Halbordnung, Partialordnung oder teilweise Ordnung.
- Statt
 schreibt man oft
schreibt man oft  , und auch, wie sicherlich vertraut,
, und auch, wie sicherlich vertraut,  (sprich
(sprich  kleiner oder gleich
kleiner oder gleich  ).
).
 ist linear (total) geordnet, wenn für alle
ist linear (total) geordnet, wenn für alle  gilt:
gilt:  oder
oder  .
.
- Definition
- Eine nichtleere Teilmenge
 einer geordneten Menge
einer geordneten Menge  heißt Kette von
heißt Kette von  , falls
, falls  eine total Ordnung ist.
eine total Ordnung ist.
Die vertraute Schreibweise " " könnte zu dem Fehlschluss verleiten, dass die Definition nur "gut bekannte" geordnete Mengen, wie z. B. die natürlichen Zahlen beschreibt. Das ist nicht der Fall, der Begriff ist viel allgemeiner. Das sollen die folgenden Beispiele verdeutlichen:
" könnte zu dem Fehlschluss verleiten, dass die Definition nur "gut bekannte" geordnete Mengen, wie z. B. die natürlichen Zahlen beschreibt. Das ist nicht der Fall, der Begriff ist viel allgemeiner. Das sollen die folgenden Beispiele verdeutlichen:
Beispiel:
Die oben erwähnte Gleichheitsrelation  ist eine Ordnungsrelation auf
ist eine Ordnungsrelation auf  .
Wie schon gesagt ist
.
Wie schon gesagt ist  eine Äquivalenzrelation, also ist sie reflexiv und transitiv. Falls
eine Äquivalenzrelation, also ist sie reflexiv und transitiv. Falls  und
und  folgt aus der Definition der Gleicheitsrelation
folgt aus der Definition der Gleicheitsrelation  , d. h. auch die Antisymmetrie ist erfüllt.
, d. h. auch die Antisymmetrie ist erfüllt.
Beispiel und Übung:
Potenzmenge:
Sei  eine Menge und
eine Menge und  die Potenzmenge von
die Potenzmenge von  . Durch
. Durch  wird eine Ordnungsrelation auf
wird eine Ordnungsrelation auf  definiert. Beweisen lässt sich dies mit den Rechenregeln der Teilmengenbeziehung.
definiert. Beweisen lässt sich dies mit den Rechenregeln der Teilmengenbeziehung.
Zum Schluss dieses Abschnitts noch eine Übungsaufgabe, bei der vielleicht erst mit dem "zweiten Blick" klar wird, was hier eigentlich definiert wird:
Übungsaufgabe:
Zeige:
Sei  eine Menge und
eine Menge und  eine Ordnung auf
eine Ordnung auf  .
Für jede Teilmenge
.
Für jede Teilmenge  wird durch
wird durch  eine Ordnung auf
eine Ordnung auf  definiert.
definiert.  läßt sich also auf Teilmengen
läßt sich also auf Teilmengen  einschränken.
einschränken.
Hinweise:
Es wird vorausgesetzt, dass  eine Menge und
eine Menge und  eine geordnete Menge ist.
Sei nun
eine geordnete Menge ist.
Sei nun  eine Teilmenge von
eine Teilmenge von  .
.  ist dann eine Relation auf
ist dann eine Relation auf  , bei der alle Elemente von
, bei der alle Elemente von  miteinander in Beziehung stehen, d. h. für alle
miteinander in Beziehung stehen, d. h. für alle  gilt
gilt  .
"
.
" " steht als Symbol für die vorausgesetzte Ordnungsrelation, d. h. "
" steht als Symbol für die vorausgesetzte Ordnungsrelation, d. h. " " symbolisiert eine Relation oder Teilmenge von
" symbolisiert eine Relation oder Teilmenge von  , also insbesondere ist "
, also insbesondere ist " " eine Paarmenge.
Aus den beiden Paarmengen
" eine Paarmenge.
Aus den beiden Paarmengen  und
und  wird dann der Durchschnitt "
wird dann der Durchschnitt " " gebildet. Dieser Durchschnitt ist wieder eine Paarmenge. Und genau für diese Paarmenge soll gezeigt werden, dass sie eine Ordnungsrelation, d. h. reflexiv, antisymmetrisch und transitiv, ist.
" gebildet. Dieser Durchschnitt ist wieder eine Paarmenge. Und genau für diese Paarmenge soll gezeigt werden, dass sie eine Ordnungsrelation, d. h. reflexiv, antisymmetrisch und transitiv, ist.
Im Folgenden werden ausgezeichnete Elemente geordneter Mengen bezüglich gegebener Teilmengen beschrieben. Diese Begriffe werden in der Analysis und auch vielen anderen Gebieten der Mathematik häufig verwendet.
- Definition
 sei eine geordnete Menge und
sei eine geordnete Menge und  eine Teilmenge von
eine Teilmenge von  :
:
- "
 heißt Maximum oder größtes Element von
heißt Maximum oder größtes Element von  " :
" :  "
" und
und  gilt
gilt  "
"
- "
 heißt Minimum oder kleinstes Element von
heißt Minimum oder kleinstes Element von  " :
" :  "
" und
und  gilt
gilt  ".
".
- Satz
- Eine Teilmenge einer geordneten Menge besitzt höchstens ein Maximum (Minimum).
- Beweis
- Seien also
 und
und  Maxima von
Maxima von  . Dann gilt
. Dann gilt  und
und  (
( ist Maximum) sowie
ist Maximum) sowie  (
( ist Maximum). Daraus folgt wegen der Antisymmetrie der Ordnungsrelation sofort
ist Maximum). Daraus folgt wegen der Antisymmetrie der Ordnungsrelation sofort  .
.
Eine geordnete Menge muss kein Maximum oder Minimum besitzen, z.B. die Menge  , besitzt weder ein Maximum noch ein Minimum, obwohl sie geordnet ist.
, besitzt weder ein Maximum noch ein Minimum, obwohl sie geordnet ist.
Da Maximum und Minimum einer Teilmenge  eindeutig bestimmt sind (vorausgesetzt sie existieren!) definiert man weiter:
eindeutig bestimmt sind (vorausgesetzt sie existieren!) definiert man weiter:
- Definition
- Sei
 eine Teilmenge einer geordneten Menge
eine Teilmenge einer geordneten Menge  und
und  sei ein Maximum von
sei ein Maximum von  , so setzt man:
, so setzt man: 
Im Allgemeinen existieren zu einer Teilmenge  einer geordneten Menge
einer geordneten Menge  weder Minimum noch Maximum. Für solche Teilmengen
weder Minimum noch Maximum. Für solche Teilmengen  ist die obige Definition nicht anwendbar. Mit der folgenden Definition erweitert man die Menge der "möglichen Elemente" indem man auch Elemente der Menge
ist die obige Definition nicht anwendbar. Mit der folgenden Definition erweitert man die Menge der "möglichen Elemente" indem man auch Elemente der Menge  zuläßt.
zuläßt.
- Definition
 sei eine geordnete Menge und
sei eine geordnete Menge und  eine Teilmenge von
eine Teilmenge von 
- "
 heißt obere Schranke von
heißt obere Schranke von  " :
" :  "
" und
und  gilt
gilt  "
"
- "
 heißt untere Schranke von
heißt untere Schranke von  " :
" :  "
" und
und  gilt
gilt  "
"
- Sei
 ist obere Schranke von
ist obere Schranke von  .
.
" heißt nach oben beschränkt" :
heißt nach oben beschränkt" :  "
" , d. h.
, d. h.  hat (mindestens) eine obere Schranke"
hat (mindestens) eine obere Schranke"
- Sei
 ist untere Schranke von
ist untere Schranke von  .
.
" heißt nach unten beschränkt " :
heißt nach unten beschränkt " :  "
" , d. h. "
, d. h. " hat (mindestens) eine untere Schranke"
hat (mindestens) eine untere Schranke"
- "
 heißt beschränkt " :
heißt beschränkt " :  "
" ist nach oben und unten beschränkt"
ist nach oben und unten beschränkt"
Falls ein minimales Element der Menge  ist obere Schranke von
ist obere Schranke von  existiert, so ist es nach dem oben bewiesenen Satz eindeutig und dieses Element nennt man dann Supremum von
existiert, so ist es nach dem oben bewiesenen Satz eindeutig und dieses Element nennt man dann Supremum von  . Die Existenz eines solchen Elementes ist jedoch keinesfalls gesichert und im "Einzelfall" nachzuweisen. Erst nachdem dieser Nachweis geglückt ist, dürfen also die folgende Definitionen benutzt werden:
. Die Existenz eines solchen Elementes ist jedoch keinesfalls gesichert und im "Einzelfall" nachzuweisen. Erst nachdem dieser Nachweis geglückt ist, dürfen also die folgende Definitionen benutzt werden:
- Definition
 sei eine geordnete Menge und
sei eine geordnete Menge und  eine Teilmenge von
eine Teilmenge von 
- "
 heißt Supremum oder kleinste obere Schranke oder sup
heißt Supremum oder kleinste obere Schranke oder sup  von
von  " :
" :  "
" " .
" .
- "
 heißt Infimum oder größte untere Schranke oder inf
heißt Infimum oder größte untere Schranke oder inf  von
von  " :
" :  "
" "
"
- Satz
 sei eine geordnete Menge,
sei eine geordnete Menge,  eine Teilmenge von
eine Teilmenge von  und
und  . Dann gilt:
. Dann gilt:
 und
und 

 und
und 
 und
und  und
und 
 muss im Gegensatz zum
muss im Gegensatz zum  nicht zur Teilmenge
nicht zur Teilmenge  gehören. Ein Beispiel hierfür ist die Menge
gehören. Ein Beispiel hierfür ist die Menge  (
( steht für die Menge der reellen Zahlen). Später werden wir solche Beispiele genauer untersuchen.
steht für die Menge der reellen Zahlen). Später werden wir solche Beispiele genauer untersuchen.
Zum Schluss dieses Abschnitts wird noch der Begriff der Wohlordnung eingeführt. Ein Beispiel für eine wohlgeordnete Menge sind die natürlichen Zahlen mit der "natürlichen" Ordnung. Dagegen sind die "normalen" Ordnungen der ganzen oder positiven reellen Zahlen nicht wohlgeordnet.
- Definition
- Eine Ordnung
 auf einer Menge
auf einer Menge  heißt Wohlordnung :
heißt Wohlordnung :  mit
mit  existiert
existiert  .
.
►___weiter: Funktionen
▲___zum Inhaltsverzeichnis
◄___zurück: Mengen



















































![{\displaystyle [x]:=\lbrace y\in M\mid x\sim y\rbrace }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9577f7f99d949ad7e14c56a4ac5996c272dc7cce)
![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)




![{\displaystyle [x]=\lbrace x\rbrace }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3970a4ea37164ffa92ea1ab369602f036ee8583)



![{\displaystyle [x]\cap [y]\not =\emptyset \Leftrightarrow [x]=[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4c9905e338a0c83b12fe93b4d92dcd9fe8fabc0)
![{\displaystyle z\in [x]\cap [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/815ef00d294b6a9fdaaa892145581fbd553be9f1)
![{\displaystyle a\in [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05b02437c238452a7cd8dbb82cd1cd934c8e380b)


![{\displaystyle [x]\subseteq [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4044b09c892280324baed37803bc2090935cedf8)
![{\displaystyle [y]\subseteq [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac2e8afc1de2256507f713d34dc61c6cc7c3b7a5)
![{\displaystyle [x]=[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c34866e2a1216182b168dc1e272b0b02f1aab3a)
![{\displaystyle [x]=[y]\Rightarrow [x]\cap [y]\not =\emptyset }](https://wikimedia.org/api/rest_v1/media/math/render/svg/822eeb31d5b2bcc0479b358f32b09edceed25b66)






















































