Physikalische Grundlagen der Nuklearmedizin: Druckversion
Dieser Text ist sowohl unter der „Creative Commons Attribution/Share-Alike“-Lizenz 3.0 als auch GFDL lizenziert.
Eine deutschsprachige Beschreibung für Autoren und Weiternutzer findet man in den Nutzungsbedingungen der Wikimedia Foundation.
Atom-und Kernstruktur
Einleitung
Der Großteil der Inhalte dieses Kapitels entspricht dem Stoff des Fachs Physik an Gymnasien. Um die Grundlage für die nachfolgenden Kapitel zu bilden, wird dieser Stoff hier nochmals behandelt. Dieses Kapitel soll also vorrangig dazu dienen, bereits Erlerntes wieder aufzufrischen.
Atomstruktur
Das Atom ist ein grundlegender Baustein der gesamten Materie. Ein einfaches Modell des Atoms besagt, dass es aus zwei Komponenten besteht: Einem Atomkern, welcher von einer Hülle aus Elektronen (siehe auch Elektronenhülle) umgeben ist.
Der Atomkern ist elektrisch positiv geladen, die Elektronen sind hingegen negativ geladen. Weil sich positive und negative Ladungen gegenseitig anziehen, ist die Elektronenhülle an den Kern gebunden.
Diese Situation hat eine gewisse Ähnlichkeit mit der „Hülle“ aus Planeten, die unsere Sonne umkreisen und durch die Schwerkraft an sie gebunden sind.
Der Radius eines Atoms beträgt ungefähr 10-10 Meter, während der Radius eines Atomkerns circa 10-14 Meter beträgt. Der Kern ist also etwa zehntausend mal kleiner als die Hülle. Analog dazu kann man sich einen Golfball in der Mitte eines Fußballstadions vorstellen. Der Golfball ist der Atomkern, das Stadion das Atom, und die Elektronen schwirren irgendwo im Bereich der Zuschauerplätze um das Stadion herum. Das bedeutet, dass das Atom hauptsächlich aus leerem Raum besteht. Jedoch ist die Situation weitaus komplexer als dieses einfache Modell, und wir werden uns später mit den physikalischen Kräften beschäftigen, welche das Atom zusammenhalten.
Chemische Phänomene sind die Wechselwirkungen zwischen den Elektronen verschiedener Atome. Verbinden sich zum Beispiel zwei Wasserstoffatome zu einem Wasserstoffmolekül so sind nur die Elektronen an der Bindung beteiligt, die Kerne bleiben von der Bindung weitgehend unbehelligt und tragen auch nicht zu ihr bei. Radioaktivität entsteht dagegen durch Veränderungen innerhalb eines Kerns . An ihr sind die Elektronen daher üblicherweise nicht beteiligt. (Eine Ausnahme ist der Zusammenstoß eines Elektrons mit einem Kern, den wir später unter Begriff Elektroneneinfang behandeln werden.)
Der Atomkern
Eine einfache Beschreibung des Atomkerns besagt, dass er aus Protonen und Neutronen zusammengesetzt ist. Diese zwei Bausteine werden kollektiv Nukleonen genannt, was bedeutet, dass sie Bausteine des Atomkerns (Latein. nucleus „Kern“) sind.
Wenn man die Massen der Nukleonen vergleicht, hat ein Proton etwa gleich viel Masse wie ein Neutron, aber beide sind 2000 mal schwerer als ein Elektron. Also ist der Großteil der Masse eines Atoms in seinem kleinen Kern konzentriert.
Elektrisch gesehen ist das Proton positiv geladen und das Neutron hat keine Ladung. Insgesamt ist ein Atom für sich gesehen elektrisch neutral (wobei freie Atome praktisch nur in Edelgasen vorkommen). Die Anzahl Protonen im Kern muss daher gleich der Anzahl der Elektronen, die den Atomkern umkreisen, sein.
Klassifikation der Atomkerne
Der Begriff Ordnungszahl (oder auch Kernladungszahl) ist in der Kernphysik als die Anzahl der Protonen im Atomkern definiert und hat das Symbol Z. Da es in einem Atom gleich viele Elektronen wie Protonen gibt, ist die Ordnungszahl gleich der Anzahl Elektronen im Atom. Ebenfalls werden in der Chemie die Elemente nach dieser Zahl im Periodensystem geordnet.
Die Massenzahl ist definiert als die Anzahl Nukleonen, also der Anzahl Protonen plus der Anzahl Neutronen. Sie hat das Symbol A.
Es ist möglich, dass Atomkerne eines bestimmten Elements zwar die gleiche Anzahl Protonen haben (was ja ein Element definiert), aber nicht unbedingt die gleiche Anzahl Neutronen, das heißt, dass sie dieselbe Ordnungszahl haben, aber nicht unbedingt die gleiche Massenzahl. Solche Atome nennt man Isotope. Alle Elemente haben Isotope und die Anzahl reicht von drei Wasserstoffisotopen bis zu über 30 Isotopen für Cäsium und Barium. Die Chemie bezeichnet die verschiedenen Elemente auf eine relativ einfache Art mit Symbolen wie H für Wasserstoff (engl. hydrogen) oder He für Helium. Das Klassifikationsschema zur Identifikation unterschiedlicher Isotope basiert darauf, vor das Elementsymbol die hochgestellte Massenzahl und die tiefgestellte Kernladungszahl zu schreiben; die Kernladungszahl kann auch weggelassen werden, weil sie durch das Elementsymbol bereits festgelegt ist. Man verwendet also folgende Schreibweise, um ein Isotop vollständig zu identifizieren:
wobei X das Elementsymbol des chemischen Elementes bezeichnet.
Wir nehmen den Wasserstoff als Beispiel. Wie bereits gesagt, hat er drei Isotope:
- Das häufigste Isotop besteht aus einem einzigen Proton, welches von einem Elektron umkreist wird,
- das zweite Isotop hat im Atomkern ein zusätzliches Neutron,
- und das dritte hat zwei Neutronen im Kern.
Eine einfache Illustration dieser drei Isotope ist in der Abbildung unten gezeigt. Sie ist jedoch nicht maßstabsgetreu, man beachte die obige Bemerkung bezüglich der Größe des Kerns im Vergleich zur Größe des Atoms. Nichtsdestotrotz ist diese Abbildung nützlich, um zu zeigen wie Isotope klassifiziert und benannt werden.
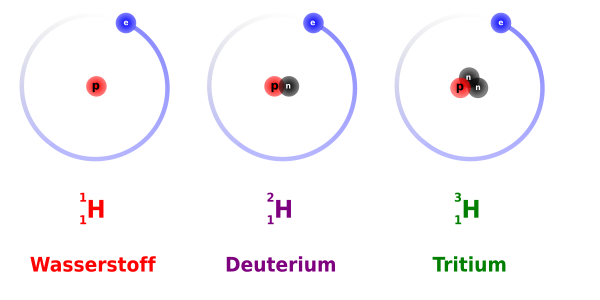
Das erste Isotop, bekannt als Wasserstoff, hat die Massenzahl 1, die Ordnungszahl 1 und wird folgendermaßen geschrieben:
Das zweite Isotop, genannt Deuterium, hat die Massenzahl 2, die Ordnungszahl 1 und wird so geschrieben:
Und als dritten im Bunde haben wir ein Isotop namens Tritium mit (Massenzahl 3, Ordnungszahl 1):
Genau nach dem selben Schema bezeichnet man alle anderen Isotope. Der Leser sollte nun in der Lage sein, zu erkennen, dass das Uranisotop 92 Protonen, 92 Elektronen und 236 - 92 = 144 Neutronen hat.
Zum Abschluss dieser Klassifikation müssen wir noch eine weitere Notation erklären. Man bezeichnet Isotope auch mit dem ausgeschriebenen Namen ihres Elements gefolgt von ihrer Massenzahl. Zum Beispiel können wir Deuterium ebenso gut als Wasserstoff-2 und als Uran-236 bezeichnen.
Bevor wir das Thema der Klassifikationsschemata abschließen, wollen wir uns noch mit den Unterschieden zwischen Chemie und Kernphysik beschäftigen. Man erinnert sich, dass ein Wassermolekül aus zwei an ein Sauerstoffatom gebundenen Wasserstoffatomen besteht. Die chemische Bindung zwischen diesen Atomen entsteht, indem die Elektronenhüllen der Atome miteinander wechselwirken. Theoretisch könnten wir ein Glas Wasser herstellen, wenn wir Sauerstoff und Wasserstoffatome millionenfach zu solchen Molekülen zusammenfügten. Wir könnten auf dieselbe Art und Weise auch ein Glas mit schwerem Wasser herstellen, indem wir Deuterium anstelle von Wasserstoff verwenden. Chemisch betrachtet wäre das zweite Wasserglas dem ersten sehr ähnlich. Aus der Sicht des Physikers fiele jedoch sofort auf, dass das zweite Glas schwerer ist als das erste, da der Deuteriumkern zweimal so schwer wie der Wasserstoffkern ist. Deshalb wird diese Art von Wasser in der Tat auch schweres Wasser genannt.
Vereinfacht gesagt, befasst sich der Chemiker mit der Veränderung und Interaktion von Elektronenhüllen als Voraussetzung für den Aufbau komplexer Moleküle, während sich der Kernphysiker eher für die Eigenschaften der Atomkerne interessiert.
Atommasseneinheit
Die SI-Einheit der Masse ist das Kilogramm. Zur Beschreibung der Eigenschaften von Atomen und Kernen ist es jedoch zu groß. Daher verwendet man die Atomare Masseneinheit (amu), die der Einheit Dalton entspricht. Sie kann als ein Zwölftel der Masse eines Kohlenstoffatoms (12C) definiert werden und entspricht damit ungefähr der Masse eines Protons oder Neutrons. Ihr Zahlenwert in Kilogramm ist 1,6605387313 · 10 -27. Dies ist ein Millionstel Millionstel Millionstel Millionstel Tausendstel Kilogramm.
Die Massen des Protons mp und des Neutrons mn sind:
und
wobei ein Elektron lediglich eine Masse von nur 0,00055 amu besitzt.
Bindungsenergie
Wir müssen uns nun mit der Stabilität der Kerne auseinandersetzen. Bisher wissen wir, dass ein Kern ein winzig kleines Gebiet im Zentrum eines Atoms füllt und aus neutralen und positiv geladenen Teilchen besteht. Bei großen Kernen wie zum Beispiel Uran (Z=92) befindet sich also eine große Anzahl von Protonen im einem winzigen Gebiet im Zentrum des Atoms. Man kann sich daher fragen warum ein Kern mit so einer großen Anzahl von positiven Ladungen auf so engem Raum nicht auseinander fliegt. Wie kann ein Kern bei so einer starken Abstoßung zwischen seinen Komponenten stabil sein? Sollten die negativ geladenen Elektronen in der Atomhülle nicht die Protonen vom Kern wegziehen?
Betrachten wir zum Beispiel den Kern Helium-4 (4He). Er besteht aus zwei Protonen und zwei Neutronen, so dass wir uns aus dem bisher Gelernten seine Masse wie folgt berechnen würden:
plus die
Somit würden wir eine
erwarten.
Die experimentell bestimmte Masse von 4He ist etwas geringer - nämlich nur 4,00260 amu. Es gibt also einen Unterschied von 0,03038 amu zwischen unserer Erwartung und der tatsächlich gemessenen Masse. Man kann diesen Unterschied von lediglich 0,75% als vernachlässigbar ansehen. Jedoch sollte man bedenken, dass dieser Massenunterschied immerhin der Masse von 55 Elektronen entspricht und somit Anlass zur Verwunderung bietet.
Man kann sich die fehlende Masse als eine Form von umgewandelter Energie vorstellen, welche den Kern zusammenhält. Diese nennt man Bindungsenergie.
Wie das Kilogramm als Einheit der Masse im Bezug auf Kerne, ist auch das Joule als Einheit zu groß, um die Energien zu beschreiben, die den Kern zusammenhalten. Die Einheit um Energien in der atomaren Größenordnung zu messen ist das Elektronenvolt (eV).
Ein Elektronenvolt ist definiert als die Menge an Energie, die ein Teilchen mit der Ladung 1 e (Elementarladung) gewinnt, wenn es durch ein Potential von einem Volt beschleunigt wird. Diese Definition ist für uns hier von geringem Nutzen und wird lediglich aus Gründen der Vollständigkeit mit angegeben. Man denke hierüber nicht zu viel nach, sondern nehme nur zur Kenntnis, dass es sich um eine Einheit zur Darstellung sehr kleiner Energien handelt, die jedoch nichtsdestoweniger auf atomaren Skalen sehr nützlich ist. Für nukleare Bindungsenergien ist sie jedoch ein wenig zu klein, daher wird häufig das Megaelektronenvolt (MeV) verwendet.
Albert Einstein beschrieb die Äquivalenz von Masse und Energie auf atomaren Skalen durch folgende Gleichung:
mit der Lichtgeschwindigkeit c
Man kann berechnen, dass einer Masse von 1 amu eine Energie von 931.48 MeV entspricht. Daher entspricht die oben gefundene Differenz zwischen der berechneten und gemessenen Masse eines 4He Atoms von 0,03038 amu einer Energie von 28 MeV. Dies entspricht ca. 7 MeV für jeden der vier Nukleonen im Kern.
Stabilität der Kerne
Bei den meisten stabilen Isotopen liegt die Bindungsenergie pro Nukleon zwischen 7 und 9 MeV. Da diese Bindungsenergie von der Anzahl der Nukleonen im Kern abhängt, also der Massenzahl A, und die elektrostatische Abstoßung vom Quadrat der Kernladungszahl Z2, kann man schließen, dass für stabile Kerne Z2 von A abhängig seien muss.
Erhöht man die Anzahl der Protonen im Kern, so erhöht sich auch die elektrostatische Abstoßung der Protonen untereinander, daher muss die Anzahl der Neutronen überproportional ansteigen um diesen Effekt durch Erhöhung der Bindungsenergie ausgleichen zu können, damit der Kern stabil gebunden bleiben kann.
Wie wir schon früher bemerkt haben gibt es eine Reihe von Isotopen für jedes Element im Periodensystem. Für jedes Element, findet man, dass das stabilste Isotop eine bestimmte Anzahl von Neutronen im Kern hat. Trägt man die Anzahl der Protonen im Kern gegen die der Neutronen für diese stabilsten Isotope auf so erhält man die Nukleare Stabilitätskurve:

Man sieht, dass die Anzahl der Protonen für kleine Kerne der Anzahl der Neutronen entspricht. Jedoch steigt die Anzahl der Neutronen mit zunehmender Größe des Kerns stärker an als die Anzahl der Protonen, so dass die Stabilität größerer Kerne gewährleistet ist. Anders ausgedrückt müssen mehr Neutronen vorhanden sein um durch ihre Bindungsenergie der elektrostatischen Abstoßung der Protonen entgegen zu wirken.
Radioaktivität
Es gibt etwa 2450 bekannte Isotope von etwa einhundert Elementen im Periodensystem. Man kann sich leicht die Größe der Liste der Isotope im Vergleich zu der des Periodensystems vorstellen. Die instabilen Isotope liegen oberhalb oder unterhalb der Stabilitätskurve. Diese instabilen Isotope entwickeln sich zur Stabilitätskurve hin, indem sie sich durch einen Prozess namens Spaltung teilen oder indem sie Teilchen und/oder Energie in Form von Strahlung aussenden. Alle diese Prozesse werden unter dem Begriff Radioaktivität zusammengefasst.
Es macht Sinn sich ein wenig näher mit dem Thema Radioaktivität zu beschäftigen. Was soll denn zum Beispiel die Stabilität von Atomkernen mit einem Radio zu tun haben? Aus historischer Sicht führe man sich vor Augen, dass man um 1900 als man diese Strahlungen entdeckte nicht genau wusste womit man es zu tun hatte. Als Leute wie Henri Becquerel und Marie Curie anfangs an seltsamen Aussendungen natürlicher Materialien arbeiteten glaubte man, dass diese Strahlungen etwas mit einem anderen damals noch nicht recht verstandenem Phänomen, dem der Radiokommunikation, zu tun hätten. Es scheint daher verständlich, dass einige Leute damals annahmen, das diese Phänomene irgendwie verwandt waren und die Materialien die Strahlung aussandten die Bezeichnung radioaktiv erhielten. (Anm. d. Ü: γ-Strahlung ist genauso wie Radiowellen elektromagnetische Strahlung, Radioaktivität umfasst jedoch noch viele weitere Strahlungen außer der elektromagnetischen.)
Heute wissen wir, dass diese Phänomene nicht direkt verwandt sind, behalten jedoch den Begriff Radioaktivität bei. Es sollte jedoch bis hierhin klar geworden sein, dass sich der Begriff Radioaktivität auf Teilchen oder Energie bezieht, die von instabilen Isotopen emittiert werden. Instabile Isotope, z.B. solche mit zu wenigen Protonen um stabil zu bleiben heißen radioaktive Isotope oder Radioisotope. Der Begriff Radionuklid wird auch gelegentlich verwendet.
Man findet nur etwa 300 der 2450 Isotope in der Natur. Alle anderen wurden von Menschen künstlich erzeugt. Die 2150 künstlichen Isotope wurden seit 1900, die meisten von ihnen sogar nach 1950 erstmalig erzeugt.
Wir werden auf die Produktion von Radioisotopen im letzten Kapitel dieses Wikibooks zurückkommen und werden uns nun die Arten der Strahlung näher anschauen, die von Radioisotopen emittiert werden.
Weiterführende Links (englisch)
- Marie and Pierre Curie and the Discovery of Polonium and Radium - an historical essay from The Nobel Foundation.
- Natural Radioactivity - an overview of radioactivity in nature - includes sections on primordial radionuclides, cosmic radiation, human produced radionuclides, as well as natural radioactivity in soil, in the ocean, in the human body and in building materials - from the University of Michigan Student Chapter of the Health Physics Society.
- The Particle Adventure - an interactive tour of the inner workings of the atom which explains the modern tools physicists use to probe nuclear and sub-nuclear matter and how physicists measure the results of their experiments using detectors - from the Particle Data Group at the Lawrence Berkeley National Lab, USA and mirrored at CERN, Geneva.
- www.t-pse.de/index-en.html - a smart, interactive Periodic Table of the Elements for offline and online use; also available in German (www.t-pse.de) and French (www.t-pse.de/index-fr.html)
- WebElements - an excellent web-based Periodic Table of the Elements which includes a vast array of data about each element - originally from Mark Winter at the University of Sheffield, England.
Radioaktiver Zerfall
Einleitung
Wir haben im letzten Kapitel gesehen, dass Radioaktivität Prozesse beschreibt, in denen instabile Atomkerne in stabile übergehen, wobei instabile Zwischenstufen auftreten können. Das bedeutet, dass solche Atomkerne, die zerfallen, entweder sofort oder nach einigen Zwischenschritten Stabilität erreichen. Ein alternativer Titel für dieses Kapitel wäre also nukleare Zerfallsprozesse.
Ebenfalls sahen wir im letzten Kapitel, dass wir die Vorgänge anhand der Stabilitätskurve der Kerne verstehen können. Somit ist ein weiterer möglicher Titel dieses Kapitels Wege zur Stabilitätskurve
Wir werden einen beschreibenden phänomenologischen Weg wählen und auf ziemlich einfache Art und Weise verstehen, was über die wichtigsten Zerfallsmechanismen bekannt ist. Wiederum wurde dieser Stoff schon einmal im Physikunterricht des Gymnasiums behandelt. Dieses Thema hier noch einmal zu bearbeiten, wird uns die Arbeit in den folgenden Kapiteln erleichtern.
Zerfallsarten
Anstatt zu fragen, was mit bestimmten Typen von Kernen passiert, ist es vielleicht einfacher einen hypothetischen Kern zu betrachten, der allen wichtigen Zerfallsprozessen unterliegen kann. Dieser hypothetische Kern ist unten gezeigt.

Zunächst sehen wir, dass zwei Neutronen zusammen mit zwei Protonen emittiert werden können. Dieser Prozess heißt Alpha-Zerfall. Als zweites sehen wir, dass ein Proton in einem Prozess namens Beta-Plus-Zerfall ein Positron freisetzen kann und dass ein Neutron ein Elektron in einem Beta-Minus-Zerfall genannten Prozess freisetzen kann. Weiterhin kann ein Elektron der Hülle von einem Proton des Kerns eingefangen werden, dies nennt man Elektroneneinfang. Drittens kann die Energie eines nuklearen Übergangs beim Gamma-Zerfall in Form eines Photons abgestrahlt werden.
Ferner kann ein Elektron aus der Elektronenhülle des Atoms direkt mit dem Kern wechselwirken und die Energie eines nuklearen Übergangs aufnehmen und somit das Atom verlassen. Als letztes kann der Kern in zwei oder mehr größere Bruchstücke zerfallen, dies bezeichnet man als spontane Spaltung.
Wir werden diese Prozesse nun nacheinander behandeln.
Spontane Spaltung
In diesem sehr destruktiven Prozess spaltet sich ein schwerer Kern in zwei bis drei Teile, wobei zusätzlich einige Neutronen emittiert werden. Die Bruchstücke sind im allgemeinen wieder radioaktiv. In Kernkraftwerken wird dieser Prozess zur Herstellung von Radioisotopen verwendet. Weiterhin findet er in der nuklearen Energieerzeugung und im Bereich der Nuklearwaffen Anwendung. Dieser Prozess ist für uns hier von geringem Interesse und wir werden darauf nicht weiter eingehen.
Alpha-Zerfall
In diesem Prozess verlassen zwei Protonen und zwei Neutronen den Kern zusammen als so genanntes Alphateilchen. Ein Alphateilchen ist tatsächlich ein 4He Kern (Helium-Kern).
Warum nennt man es daher nicht einfach 4He Kern? Warum sollte man es anders bezeichnen? Die Antwort hierauf liegt in der Geschichte der Radioaktivität. Zur Zeit ihrer Entdeckung war nicht bekannt worum es sich bei dieser Strahlung tatsächlich handelte. Man bemerkte zunächst nur die zweifach positive Ladung und erkannte erst später dass es sich um 4He Kerne handelte. In der ersten Phase ihrer Entdeckung erhielt die Strahlung den Namen Alpha-Strahlung (und die anderen beiden Strahlenarten wurden Beta- und Gamma-Strahlung genannt), wobei Alpha(α), Beta(β) und Gamma(γ) die ersten drei Buchstaben des griechischen Alphabets sind. Heute nennen wir diesen Typ Strahlung immer noch Alpha-Strahlung. Diese Bezeichnung trägt auch zur Fachsprache des Gebietes bei und führt bei Außenstehenden zum Eindruck eines stark spezialisierten Arbeitsgebiets!
Man mache sich jedoch bewusst, dass diese Strahlung wirklich aus 4He-Kernen besteht, die von einem größeren Kern emittiert werden. 4He ist ein auf der Erde recht häufig vorkommendes Element und daher eigentlich nichts besonderes. Warum also ist diese Strahlung für Menschen so gefährlich? Die Antwort hierauf liegt in der großen Energie mit der diese Teilchen emittiert werden, sowie in ihrer großen Masse und ihrer zweifach positiven Ladung. Daher können sie, wenn sie mit lebender Materie wechselwirken, einen erheblichen Schaden an den Molekülen anrichten, mit denen sie zusammentreffen, zumal sie bestrebt sind, Elektronen einzufangen und neutrales 4He zu bilden.
Ein Beispiel für den Alpha-Zerfall ist der Kern Uran-238. Die folgende Gleichung beschreibt den Zerfallsprozess:
Hier emittiert 238U einen 4He-Kern (ein Alpha-Teilchen) und der ursprüngliche Kern wandelt sich in 234 Thorium um. Man beachte, dass sich die Massenzahl des ursprünglichen Kerns um vier und seine Kernladungszahl um zwei verringert haben, was ein allgemeines Charakteristikum eines jeden Alpha-Zerfalls bei jeglichen Kernen ist.
Beta-Zerfall
Es gibt im wesentlichen drei Formen des Beta-Zerfalls:
(a) Beta-Minus-Zerfall
Einige Kerne haben einen Überschuss an Neutronen und werden stabil, indem sie ein Neutron in ein Proton umwandeln, wobei ein Elektron frei wird. Dieses Elektron heißt Beta-Minus-Teilchen, wobei das Minus die negative Ladung des Elektrons andeutet. Wir können dies durch folgende Formel ausdrücken:
wobei ein Neutron in ein Proton und ein Elektron umgewandelt wird. Man beachte, dass die Gesamtladung auf beiden Seiten der Gleichung dieselbe ist. Wir sagen, dass die Ladung erhalten bleibt.
Wir können behaupten, dass das Elektron nicht im Kern existieren kann und daher herausgeschleudert wird[1]. Wieder ist nichts sonderbares an einem Elektron. Wichtig für den Strahlenschutz ist jedoch die Energie mit der es aus dem Kern emittiert wird, sowie der chemische Schaden, den es anrichten kann, wenn es mit lebender Materie wechselwirkt.
Ein Beispiel, in dem dieser Zerfall auftritt ist der 131I Kern, welcher in 131Xe zerfällt und dabei ein Elektron emittiert:
Das entstehende Elektron wird Beta-Minus-Teilchen genannt. Man beachte, dass die Massenzahl in der obigen Gleichung konstant bleibt und sich die Kernladungszahl um eins erhöht, was ein Charakteristikum eines jeden Beta-Minus-Zerfalls ist. Man mag sich vielleicht wundern, wie ein Elektron innerhalb eines Kerns erzeugt werden kann, wenn man die vereinfachte Beschreibung des Kerns als nur aus Protonen und Neutronen bestehend, wie sie im letzten Kapitel angegeben wurde, zugrunde legt. Dies ist nur eine der Beschränkungen dieser vereinfachten Beschreibung und kann dadurch erklärt werden, dass man die zwei fundamentalen Teilchen, nämlich die Neutronen und Protonen, als wiederum aus noch kleineren Teilchen, den Quarks aufgebaut versteht. Wir werden uns hier nicht näher mit diesen Teilchen auseinandersetzen, sondern bemerken lediglich, dass gewisse Kombinationen von Quarks ein Proton und andere ein Neutron ergeben. Wir möchten am Anfang dieses einführenden Textes ein vereinfachtes Bild verwenden, obwohl der tatsächliche Sachverhalt komplizierter als der beschriebene ist. Dasselbe trifft auf die oben angegebene Behandlung des Beta-Zerfalls zu, wie wir in den folgenden Kapiteln sehen werden.
(b) Beta-Plus-Zerfall
Wenn die Anzahl der Protonen im Kern zu groß wird, so dass der Kern nicht mehr stabil ist, kann es passieren, dass er stabiler wird, indem er ein Proton in ein Neutron umwandelt und dabei ein positiv geladenes Antielektron emittiert. Dies ist kein Tippfehler. Ein Antielektron hat positive Ladung und wird auch Positron genannt. Das Positron ist das Beta-Plus-Teilchen
Die Geschichte ist hier recht interessant. Ein hervorragender Italienischer Physiker, Enrico Fermi entwickelte eine Theorie des Beta-Zerfalls, in der er vorhersagte, dass sowohl negativ als auch positiv geladene Teilchen von instabilen Kernen emittiert werden können. Die positiv geladenen wurden Antimaterie genannt und später experimentell nachgewiesen. Antielektronen leben nicht sehr lange, da sie recht schnell mit einem normalen Elektron rekombinieren. Diese Reaktion heißt Paarvernichtung und führt zur Aussendung von Gamma-Strahlen. Science-Fiction-Autoren, wie auch einige Wissenschaftler, spekulierten nach der Entdeckung der Antimaterie darüber, dass es in Teilen des Universums negativ geladene Anti-Protonen geben könnte, die Kerne bildeten, welche von positiv geladenen Elektronen umkreist wurden[2]. Aber dies führt zu weit vom eigentlichen Thema weg. Die Reaktion in unserem instabilen Kern, welcher zwei oder mehr Protonen enthält, kann wie folgt dargestellt werden.
Man beachte wiederum, dass die Ladung auf beiden Seiten der Gleichung dieselbe ist. Ein Beispiel für diesen Zerfall ist 22Na, welches in 22Ne zerfällt und dabei ein Positron abstrahlt.
Man beachte, dass die Massenzahl konstant bleibt und sich die Kernladungszahl um eins vermindert.
(c) Elektroneneinfang
Bei dieser dritten Form des Beta-Zerfalls wird das innerste Hüllenelektron vom Kern eingefangen und rekombiniert mit einem Proton zu einem Neutron. Die Reaktion kann wie folgt dargestellt werden.
Dieser Prozess heißt K-Einfang da das Elektron häufig aus der K-Schale des Atoms eingefangen wird. Wie können wir wissen, dass ein solcher Prozess auftritt, wenn doch keine Strahlung emittiert wird? Anders gefragt: Wenn ein solcher Prozess ausschließlich innerhalb eines Atoms auftritt, wird wohl keine Information darüber das Atom verlassen. Oder doch? Die Charakteristik dieses Effekts kann aus Effekten in der den Kern umgebenden Elektronenhülle gefunden werden, wenn nämlich die in der K-Schale entstandene Lücke durch ein Elektron einer äußeren Schale aufgefüllt wird. Das Auffüllen der Lücke geht mit der Aussendung eines Röntgenstrahls aus der Elektronenhülle einher. Dieser Röntgenstrahl dient als charakteristisches Merkmal dieser Form des Beta-Zerfalls. Der beim Elektroneneinfang entstehende Kern befindet sich häufig in einem angeregten Zustand und sendet bei Übergang in den Grundzustand Gammastrahlung aus, welche auch zum Nachweis des Elektroneneinfangs verwendet werden kann. Ein Beispiel für diese Art des radioaktiven Zerfalls ist 55Fe, welches durch Elektronen-Einfang in 55Mn zerfällt. Die Reaktion schreibt sich wie folgt:
Man beachte, dass die Massenzahl bei dieser Zerfallsart wiederum unverändert bleibt und sich die Kernladungszahl um eins erniedrigt.
- ↑ Physikalisch kann ein Elektron durchaus für kurze Zeit im Kern existieren, das Elektron aus dem Zerfall besitzt jedoch wegen Energie- und Impulserhaltung beim Zerfall eine hohe kinetische Energie und kann daher den Anziehungskräften des Kerns entkommen.
- ↑ Im Labor gelang es 1995 Antiwasserstoff herzustellen.
Gamma-Zerfall
Beim Gamma-Zerfall wird Energie von einem instabilen Kern in Form von elektromagnetischer Strahlung ausgesandt.
Aus der Schulphysik sollte noch bekannt sein, dass elektromagnetische Strahlung eines der wichtigsten bisher gefundenen Phänomene ist. Die Strahlung kann in Begriffen der Frequenz, Wellenlänge oder Energie charakterisiert werden. In Begriffen der Energie hat man sehr niederenergetische Strahlung namens Radiowellen, dann Infrarotstrahlung dann bei etwas höherer Energie sichtbares Licht, bei noch höherer Energie ultraviolette Strahlung und bei den höchsten Energien schließlich Röntgenstrahlen und Gammastrahlen. Wie man sich erinnert, gehören alle diese Strahlen zum elektromagnetischen Spektrum.

Bevor wir weitermachen, wollen wir einen Moment verweilen und uns den Unterschied zwischen Röntgenstrahlen und Gammastrahlen klarmachen. Diese beiden Strahlenarten sind hochenergetische Formen elektromagnetischer Strahlung und daher im Wesentlichen gleich. Der Unterschied besteht nicht darin, woraus sie bestehen, sondern wobei sie entstehen. Im allgemeinen können wir sagen, dass Strahlung, die von einem Kern emittiert wird, als Gammastrahlung und solche, die außerhalb des Kerns z. B. aus der Elektronenhülle entsteht, als Röntgenstrahlung bezeichnet wird.
Die letzte Frage, die wir noch klären müssen, bevor wir uns um die unterschiedlichen Formen der Gammastrahlen kümmern können, ist die nach der Natur der hochenergetischen Röntgenstrahlung. Es wurde experimentell gefunden, dass Gammastrahlen (sowie in diesem Zusammenhang auch Röntgenstrahlen) sich manchmal als Welle und manchmal als Teilchen manifestieren. Dieser Welle-Teilchen-Dualismus kann durch die Äquivalenz von Masse und Energie auf atomaren Skalen verstanden werden. Wenn wir einen Gammastrahl als Welle auffassen, ist es sinnvoll ihn mit Begriffen der Frequenz und Wellenlänge wie eine gewöhnliche Welle zu beschreiben. Beschreiben wir ihn jedoch als Teilchen müssen wir die Begriffe Masse und Ladung verwenden. Ferner wird der Begriff Photon für diese Teilchen verwendet. Eine interessante Eigenschaft von Photonen ist jedoch, dass sie weder Masse noch Ladung aufweisen.
Es gibt zwei wichtige Arten des Gamma-Zerfalls:
(a) Isomerieübergang
Ein Kern in einem angeregten Zustand kann seinen Grundzustand (nicht-angeregten Zustand) durch Aussendung eines Gammastrahls erreichen. Ein Beispiel für diese Art des Zerfalls ist 99mTc (Halbwertszeit 6h) - welches das wohl am häufigsten verwendete Radioisotop in der medizinischen Diagnostik ist. Die Reaktion schreibt sich wie folgt:
Hier ist der 99mTc-Kern in einem angeregten Zustand, dass heißt er besitzt überschüssige Energie. Dieser angeregte Zustand heißt hier metastabiler Zustand und der Kern daher Technetium-99m wobei das m für metastabil steht. Dieser angeregte Kern gibt seine überschüssige Energie ab, indem er einen Gammastrahl emittiert und in den Grundzustand Technetium-99 übergeht.
(b) Innere Konversion
Hierbei geht die überschüssige Energie eines angeregten Kerns direkt auf ein Elektron der Atomhülle (z.B. ein Elektron der K-Schale) über.
Zerfallsschemen
Zerfallsschemen werden häufig verwendet um radioaktive Zerfälle graphisch darzustellen. Ein Schema für einen relativ einfachen Zerfall ist unten angegeben.

Diese Abbildung zeigt das Zerfallsschema von 3H welches zu 3He mit einer Halbwertszeit von 12,3 Jahren unter Emission eines Beta-Minus-Teilchens mit einer Energie von 0,0057 MeV zerfällt.
Ein Beispiel für einen komplizierteren Zerfall ist 137Cs:

Dieses Isotop kann durch zwei Beta-Minus-Prozesse zerfallen. Der eine in 5% der Fälle auftretende Zerfall führt zu einem Beta-Minus-Teilchen mit einer Energie von 1,17 und erzeugt 137Ba. Der zweite mögliche Zerfall tritt mit einer Wahrscheinlichkeit von 95% auf und führt zu einem Beta-Minus-Teilchen der Energie 0,51 MeV und erzeugt 137mBa - also Barium in einem metastabilen Kernzustand. 137mBa zerfällt dann über einen Isomerieübergang unter Emission eines Gammastrahls mit einer Energie von 0,662 MeV.
Der generelle Aufbau eines Zerfallsschemas ist in der folgenden Abbildung gezeigt:

Die Energie wird auf der vertikalen, die Kernladungszahl auf der horizontalen Achse aufgetragen - wenngleich diese Achsen normalerweise nicht mit eingezeichnet werden. Das Isotop, für welches das Schema erzeugt wurde (X - in unserem Falle), wird zuoberst eingetragen. Dieses Isotop wird als Elternisotop bezeichnet. Es verliert Energie, wenn es zerfällt, und die entstehenden Produkte werden daher bei niedrigeren Energieniveaus eingetragen und als Tochternuklide bezeichnet.
Das Diagramm zeigt die Vorgänge für die gängigsten Formen radioaktiver Zerfälle. Der Alpha-Zerfall ist links dargestellt: Die Massenzahl wird um vier und die Kernladungszahl um 2 reduziert und es entsteht der Tochterkern A. Zu seiner rechten ist das Schema des Beta-Plus-Zerfalls dargestellt, wobei der Tochterkern B erzeugt wird. Die Situation für den Beta-Minus-Zerfall gefolgt vom Gamma-Zerfall ist auf der rechten Seite des Diagramms dargestellt, wobei die Tochterkerne C bzw. D entstehen.
Weiterführende Links (englisch)
- Basics about Radiation - overview of the different types of ionising radiation from the Radiation Effects Research Foundation - a cooperative Japan-United States Research Organization which conducts research for peaceful purposes.
- Radiation and Life - an essay by Eric J Hall, Professor of Radiology, Columbia University with sections on the unstable atom, ionising radiation, background radiation, man-made radiation and radioactive decay - from the Uranium Information Centre website.
- Radiation and Radioactivity - a self-paced lesson developed by the University of Michigan's Student Chapter of the Health Physics Society, with sections on radiation, radioactivity, the atom, alpha radiation, beta radiation and gamma radiation.
Das Zerfallsgesetz
Einleitung
Dies ist das dritte Kapitel des Wikibooks Physikalische Grundlagen der Nuklearmedizin
Wir haben den radioaktiven Zerfall von einem phänomenologischen Standpunkt aus im letzten Kapitel betrachtet. In diesem Kapitel werden wir einen allgemeineren analytischen Zugang wählen.
Der Grund hierfür ist, dass wir so eine Denkweise entwickeln können in der wir die Vorgänge quantitativ mathematisch fassen können. Wir werden uns mit den Konzepten der Zerfallskonstante und der Halbwertszeit sowie mit den für die Messung der Radioaktivität verwendeten Einheiten vertraut machen. Ferner besteht die Möglichkeit das erworbene Verständnis durch Übungen am Ende des Kapitels zu vertiefen.
Annahmen
Üblicherweise beginnt man eine physikalische Analyse mit dem Aufstellen einiger vereinfachender Annahmen über das System. Dadurch können wir unwichtige Effekte, die das Verständnis erschweren loswerden. Manchmal kann es jedoch auch vorkommen, dass wir die Situation so stark vereinfachen, dass sie zu abstrakt und damit schwer verständlich wird. Daher werden wir versuchen das Thema des radioaktiven Zerfalls mit einem aus dem Alltag bekannten Phänomen in Beziehung zu setzten welches wir als Analogie benutzen und so hoffentlich die abstrakten Probleme umschiffen können. Wir werden hier die Herstellung von Popcorn als Analogie verwenden. Man denke also an einen Topf in den man Öl gibt, anschließend Mais hinzufügt, ihn dann auf einer Herdplatte erhitzt und schaut, was passiert. Der geneigte Leser mag dies auch praktisch ausprobieren wollen. Für den radioaktiven Zerfall betrachten wir eine Probe, die eine große Zahl radioaktiver Kerne enthält, die alle von der selben Art sind. Dies entspricht den noch nicht geplatzten Maiskörnern im Topf. Als zweites nehmen wir an, dass alle radioaktiven Kerne durch den gleichen Prozess zerfallen sei es nun Alpha-, Beta- oder Gamma-Zerfall. Anders ausgedrückt platzen die intakten Maiskörner zu bestimmten Zeitpunkten während des Heizprozesses. Drittens nehmen wir uns einen Moment lang Zeit, um uns darüber klar zu werden, dass wir die Vorgänge nur in einem statistischen Sinne beschreiben können. Wenn wir ein einzelnes Maiskorn betrachten, können wir dann vorhersagen wann es platzen wird? Nicht wirklich. Wir können uns jedoch überlegen dass eine große Anzahl von ihnen nach einer bestimmten Zeit geplatzt sein wird. Aber dies ist ungleich komplizierter als die Frage bezüglich eines einzelnen Maiskorns. Anstatt uns also mit einzelnen Einheiten zu beschäftigen, betrachten wir das System auf einer größeren Skala und hier kommt die Statistik ins Spiel. Wir können den radioaktiven Zerfall statistisch als „Ein Schuss“-Prozess betrachten, das heißt, wenn ein Kern zerfallen ist, so kann er nicht noch einmal zerfallen. In anderen Worten, wenn ein Maiskorn geplatzt ist kann es nicht noch einmal platzen.
Weiterhin ist die Zerfallswahrscheinlichkeit für noch nicht zerfallene Kerne zeitlich konstant. Anders ausgedrückt ist die Wahrscheinlichkeit für ein noch nicht geplatztes Maiskorn in der nächsten Sekunde zu platzen genauso groß wie in der vorherigen Sekunde.
Lassen wir uns diese Popcorn Analogie nicht zu weit treiben. Machen wir uns bewusst, dass die Rate mit der das Popcorn platzt über die Wärme die wir dem Topf zuführen kontrollieren können. Auf die Zerfallsprozesse von Kernen haben wir jedoch keine derartigen Einflussmöglichkeiten. Die Rate mit der Kerne zerfallen kann nicht durch Heizen der Probe beeinflusst werden. Auch nicht durch Kühlung, oder Erhöhung der Drucks oder durch Änderung der Gravitation (indem man die Probe in den Weltraum bringt), auch nicht durch Änderung irgendeiner anderen Eigenschaft seiner physikalischen Umgebung. Das einzige was die Halbwertszeit eines individuellen Kerns bestimmt scheint der Kern selbst zu sein. Aber im Mittel können wir sagen, dass der Kern innerhalb einer gewissen Zeitspanne zerfallen wird.
Gesetz des radioaktiven Zerfalls
Führen wir nun einige Symbole ein um den Schreibaufwand zu reduzieren, den wir treiben müssen, um die Vorgänge zu beschreiben, und machen uns einige mathematische Methoden zu eigen, mit denen wir die Situation erheblich einfacher als zuvor beschreiben können.
Nehmen wir an wir hätten eine Probe eines radioaktiven Materials mit Kernen, welche zu einem bestimmten Zeitpunkt noch nicht zerfallen sind. Was passiert dann in einem kurzen Zeitabschnitt? Einige Kerne werden mit Sicherheit zerfallen. Aber wie viele?
Aufgrund unserer obigen Argumentation können wir sagen, dass die Anzahl der zerfallenden von der Anzahl der insgesamt vorhandenen Kerne abhängen wird und weiterhin von der Dauer der betrachteten kurzen Zeitspanne. In anderen Worten, je mehr Kerne da sind, um so mehr Kerne werden auch zerfallen. Und je länger die Zeitspanne ist, um so mehr Kerne werden zerfallen. Lassen wir uns diese Zahl der Kerne, die zerfallen mit und die Dauer des kurzen Zeitintervalls mit bezeichnen.
Somit haben wir begründet, dass die Anzahl der radioaktiven Kerne, die im Zeitintervall von bis zerfällt proportional zu und zu ist. Als Formel schreibt sich diese Tatsache wie folgt:
Das negative Vorzeichen deutet an, dass abnimmt.
Wandeln wir nun die proportionale Beziehung in eine Gleichung um, so können wir schreiben:
wobei die Proportionalitätskonstante λ Zerfallskonstante heißt.
Nach Division durch können wir diese Gleichung umschreiben zu:
Also beschreibt diese Gleichung den Vorgang für ein kurzes Zeitintervall . Um herauszufinden, was zu beliebigen Zeitpunkten los ist, können wir einfach die Vorgänge in kurzen Zeitintervallen addieren. Anders ausgedrückt müssen wir die obige Gleichung integrieren. Drücken wir dies etwas formaler aus so können wir sagen, dass in der Zeit von bis zu einem späteren Zeitpunkt die Anzahl der radioaktiven Kerne von auf gefallen sein wird, so dass:
Dieser letzte Ausdruck heißt Gesetz des radioaktiven Zerfalls. Es besagt, dass die Anzahl der radioaktiven Kerne exponentiell mit der Zeit abnimmt, wobei die Geschwindigkeit des Zerfalls durch die Zerfallskonstante λ festgelegt ist.
Bevor wir uns diese Gleichung näher anschauen betrachten wir noch einmal welche Mathematik wir oben benutzt haben. Zunächst haben wir die Integralrechnung verwendet um herauszufinden was über einen längeren Zeitraum geschieht, wobei wir wussten was über kurze Zeiträume geschieht. Zweitens verwendeten wir folgende Beziehung aus der Analysis:
wobei den natürlichen Logarithmus von x darstellt. Drittens verwendeten wir die Definition des Logarithmus also:
und damit
Kehren wir nun zum Gesetz des radioaktiven Zerfalls zurück. Das Gesetz sagt aus, dass die Anzahl der Kerne exponentiell abnimmt wobei die Rate durch die Zerfallskonstante festgelegt wird. Das Gesetz ist in der Abbildung unten als Graph dargestellt:

Aufgetragen ist die Anzahl radioaktiver Kerne gegenüber der Zeit t. Wir sehen, dass die Anzahl der radioaktiven Kerne von (der Anzahl der radioaktiven Kerne zum Zeitpunkt ) anfangs sehr schnell und später etwas langsamer abnimmt, also klassisch exponentiell verläuft.
Den Einfluss der Zerfallskonstante kann man an der folgenden Abbildung erkennen:
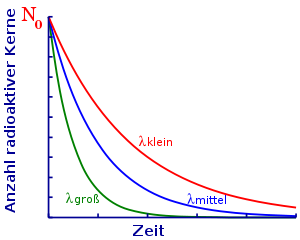
Alle drei Kurven werden durch Exponentialgesetze beschrieben, lediglich die Zerfallskonstanten sind unterschiedlich gewählt. Man beachte, dass die Kurve mit kleiner Zerfallskonstante relativ langsam und die Kurve mit großer Zerfallskonstante recht schnell abfällt.
Die Zerfallskonstante ist eine Eigenschaft des jeweiligen Radionuklids. Einige wie Uran-238 haben einen recht geringen Wert und das Material zerfällt daher langsam über einen langen Zeitraum. Andere Kerne wie Technetium-99m haben eine relativ hohe Zerfallskonstante und zerfallen daher schneller.
Es ist auch möglich das Zerfallsgesetz aus einer anderen Perspektive zu betrachten indem man den Logarithmus von Nt gegen die Zeit aufträgt. Anders ausgedrückt können wir von unserer obigen Analyse ausgehend die folgende Gleichung graphisch auftragen:
in anderer Form
Beachte, dass dieser Ausdruck eine einfache Gleichung der Form mit und ist. Die Gleichung beschreibt also eine Gerade mit der Steigung wie man in der folgenden Abbildung sieht. Eine solche Darstellung ist häufig hilfreich, wenn man einen Zusammenhang ohne die Komplikationen eines direkten exponentiellen Verhaltens verstehen möchte.

Halbwertszeit
Die meisten von uns haben nicht gelernt instinktiv in logarithmischen oder exponentiellen Skalen zu denken, wenngleich viele natürliche Phänomene exponentiell verlaufen. Die meisten Denkweisen, die wir in der Schule erlernt haben basieren auf linearen Änderungen, dies macht das intuitive Verständnis des radioaktiven Zerfalls etwas schwieriger. Aus diesem Grund gibt es eine wichtige vom Zerfallsgesetz abgeleitete Größe die es uns leichter macht zu verstehen was passiert.
Diese Größe heißt Halbwertszeit und drückt die Länge der Zeit aus die es dauert, bis sich die Radioaktivität eines Radioisotops auf die Hälfte reduziert hat. Graphisch können wir dies wie folgt ausdrücken:

die benötigte Zeit ist die Halbwertszeit, für die gilt:
Man beachte, dass die Halbwertszeit nicht beschreibt wie lange ein Material radioaktiv bleibt, sondern lediglich die Länge der Zeit die es dauert bis sich seine Radioaktivität halbiert. Beispiele für Halbwertszeiten einiger Radioisotope sind in der Tabelle unten angegeben. Man beachte, dass einige von ihnen recht kurze Halbwertszeiten haben. Diese werden gerne für Zwecke der medizinischen Diagnostik verwendet, weil so ihre Radioaktivität nach der Anwendung am Patienten nicht sehr lange im Körper verweilt, was zu relativ geringen Strahlendosen führt.
| Radioisotop | Halbwertszeit (ca.) |
|---|---|
| 13 Sekunden | |
| 6 Stunden | |
| 8 Tage | |
| 1 Monat | |
| 30 Jahre | |
| 462 Tage | |
| 1620 Jahre | |
| 4.51 · 109 Jahre |
Diese kurzlebigen Radioisotope stellen jedoch ein logistisches Problem da, wenn sie an einem Ort verwendet werden sollen, der nicht in unmittelbarer Nähe einer Herstellungsanlage für Radioisotope liegt. Wenn wir zum Beispiel 99mTc für eine Untersuchung an einem Patienten 5.000 Kilometer von der nächsten Herstellungsanlage einsetzen möchten. Die Herstellungsanlage könnte sich zum Beispiel in Sydney und der Patient in Perth befinden. Nachdem wir das Isotop in einem Kernkraftwerk erzeugt haben würde es mit einer Halbwertszeit von 6 Stunden zerfallen. Würden wir als das Material in einen Transporter packen und zum Flughafen von Sydney fahren. Dann würde das Isotop zerfallen während der Transporter im Verkehr von Sydney fest steckt, dann noch mehr während auf den Flug nach Perth gewartet wird. Dann noch mehr wenn es nach Perth geflogen wird und so weiter. Wenn es endlich bei unserem Patienten ankommt, wird sich seine Radioaktivität sehr stark reduziert haben und möglicherweise für die Untersuchung nutzlos geworden sein. Und wie wäre es, wenn wir 81mKr anstelle von 99mTc für unseren Patienten verwenden würden? Im letzten Kapitel dieses Wikibooks werden wir sehen, dass diese logistischen Herausforderungen zu recht innovativen Lösungen Anlass gegeben haben. Mehr dazu jedoch später!
Aus der Tabelle ist ersichtlich, dass andere Isotope sehr lange Halbwertszeiten haben. Zum Beispiel hat 226Ra eine Halbwertszeit von mehr als 1.500 Jahren. Dieses Isotop wurde für therapeutische Anwendungen in der Medizin verwendet. Man denke an die damit verbundenen logistischen Probleme. Offensichtlich ist das Transport vom Herstellungsort zum Anwendungsort hierbei unproblematisch. Jedoch muss man beachten wie lange das Material an seinem Bestimmungsort gelagert werden muss. Man braucht einer Lagereinheit in der das Material sicher über einen langen Zeitraum gelagert werden kann. Aber wie lange? Eine Faustregel für Größen der Radioaktivität in der Medizin besagt, dass die Radioaktivität für ca. 10 Halbwertszeiten erheblich sein wird. Somit bräuchten wir eine sichere Umgebung zur Lagerung von 226Ra über einen Zeitraum von ca. 16.000 Jahren. Diese Lagereinrichtung müsste sicher gegen nicht vorhersehbare Ereignisse, wie Erdbeben, Bombenangriffe usw. aufgebaut sein und von unseren Nachfahren als solche erkennbar sein. Eine in der Tat ausgesprochen delikate Aufgabe.
Beziehung zwischen Zerfallskonstante und Halbwertszeit
Auf Basis des oben gesagten kann man erahnen, dass es eine Beziehung zwischen Halbwertszeit und Zerfallskonstante geben müsste. Ist die Zerfallskonstante klein, so sollte die Halbwertszeit groß sein und entsprechend sollte bei großer Zerfallskonstante die Halbwertszeit klein sein. Aber wie genau sieht nun diese Beziehung aus?
Wir können diese Frage sehr leicht beantworten indem wir die Definition der Halbwertszeit in das Zerfallsgesetz einsetzen. Dieses Gesetz besagt dass zu jeder beliebigen Zeit t:
und aus der Definition der Halbwertszeit wissen wir, dass:
genau dann wenn
Wir können daher das Radioaktive Zerfallsgesetz umschreiben indem wir Nt und t wie folgt ersetzen:
Somit:
und
Diese letzten beiden Gleichungen drücken die Beziehung zwischen Halbwertszeit und Zerfallskonstante aus. Diese sind sehr nützlich zur Lösung von Rechenaufgaben im Gebiet der Radioaktivität und bilden meist den ersten Schritt zu deren Lösung.
Einheiten der Radioaktivität
Die SI (oder auch metrische) Einheit der Radioaktivität ist nach Henri Becquerel, als Ehrung für seine Entdeckung der Radioaktivität, das Becquerel mit dem Symbol Bq. Das Becquerel ist definiert als die Menge einer radioaktiven Substanz die zu einer Zerfallsrate von einem Zerfall pro Sekunde führt. In der medizinischen Diagnostik stellt ein 1 Bq eine recht geringe Menge an Radioaktivität dar. In der Tat ist es einfach sich seine Definition mit Hilfe des englischen Begriffs bugger all (zu Deutsch: rein gar nichts) zu merken. Daher werden das Kilobecquerel (kBq) sowie das Megabecquerel (MBq) häufiger verwendet. Die traditionelle (und heute veraltete) Einheit der Radioaktivität ist nach Marie Curie benannt und heißt Curie mit dem Symbol Ci. Das Curie ist definiert als die Menge einer radioaktiven Substanz die zu einer Zerfallsrate von 3.7 ·1010 Zerfällen pro Sekunde führt. In anderen Worten 37 Tausend Millionen Zerfälle pro Sekunde, was wie man sich denken kann eine erhebliche Menge an Radioaktivität darstellt. Für Zwecke der medizinischen Diagnostik werden daher das Millicurie (mCi) und das Mikrocurie (µCi) häufiger verwendet.
-
Marie Curie
-
Henri Becquerel
Warum also zwei Einheiten? Im Wesentlichen kommt es es hier wie auch sonst bei der Frage nach Maßeinheiten darauf an in welchem Teil der Welt man sich befindet. Der Kilometer wird zum Beispiel in Australien und Europa gerne als Entfernungseinheit verwendet, wohingegen man in den USA bevorzugt die Meile benutzt. So wird man in einem amerikanischen Lehrbuch häufig das Curie als Einheit der Radioaktivität und in einem australischen sehr wahrscheinlich das Becquerel und in einem europäischen häufig beide Einheiten antreffen. Daher ist es sinnvoll beide Einheiten zu kennen.
Übungen
Unten sind drei Übungsaufgaben angegeben die dabei helfen sollen das Verständnis des in diesem Kapitel behandelten Stoffs zu vertiefen. Die erste ist ziemlich einfach und übt die Anwendung des Zerfallsgesetzes sowie das Verständnis des Begriffs Halbwertszeit. Die zweite Aufgabe ist erheblich schwieriger und beschäftigt sich mit der Berechnung Anzahl der in einer Probe radioaktiven Materials pro Zeiteinheit zerfallenden Kerne und verwendet das Gesetz des radioaktiven Zerfalls. Die dritte Aufgabe ist der zweiten sehr ähnlich, fragt jedoch aus einem leicht anderen Blickwinkel.
Bevor man sich an die Fragen macht möge man sich diese Seite anschauen, die einem einige einfache Rechnungen abnehmen kann.
Aufgabe 1
(a) Die Halbwertszeit von 99mTc beträgt 6 Stunden. Nach welcher Zeit ist noch ein sechzehntel der ursprünglichen Menge des Radioisotops vorhanden?
(b) Verifiziere dein Ergebnis auf einem anderen Weg.
Lösung:
(a) Ausgehend von der ober erhaltenen Beziehung zwischen der Zerfallskonstante und der Halbwertszeit können wir nun die Zerfallskonstante wie folgt berechnen.
Wir wenden nun das Zerfallsgesetz an,
die können wir in folgende Form umschreiben:
Gefragt ist nun wann auf ein sechzehntel ihres Wertes zurückgegangen ist, das bedeutet:
Somit haben wir
was wir nach auflösen müssen. Eine Möglichkeit dies zu tun ist im folgenden angegeben:
Es wird also 24 Stunden dauern bis nur noch ein sechzehntel der ursprünglichen Radioaktivität vorhanden ist.
(b) Eine Möglichkeit die Antwort zu verifizieren benutzt die Definition der Halbwertszeit. Wir wissen aus der Aufgabenstellung, dass 99mTc eine Halbwertszeit von 6 Stunden hat. Daher ist nach sechs Stunden noch die Hälfte der Radioaktivität vorhanden. Nach 12 Stunden noch ein viertel, nach 18 Stunden noch ein achtel und nach 24 Stunden bleibt genau ein sechzehntel übrig. Und wir kommen zu selben Zahlenwert wie in (a). Also stimmt unser Ergebnis.
Man beachte dass dieser Ansatz sinnvoll ist da wir uns mit dem relativ einfachen Fall zu tun haben in dem Radioaktivität halbiert, geviertelt und so weiter wird. Aber mal angenommen die Frage wäre gewesen wie lange es dauert bis die Radioaktivität auf ein Zehntel ihres ursprünglichen Wertes gefallen ist. Die deutlich aufwendigere Ableitung im mathematischen Weg der in Teil (a) beschritten wurde, kann auch diese Frage leicht beantworten.
Aufgabe 2
Berechne die Radioaktivität von einem Gramm 226Ra, die Halbwertszeit betrage 1620 Jahre und die Avogadrozahl sei 6,023 · 1023.
Lösung:
Wir können genau wie bei Übung 1(a) ansetzen indem wir die Zerfallskonstante aus der Halbwertszeit mit Hilfe der folgenden Gleichung berechnen:
Man beachte, dass wir als Dauer eines Jahres 365,25 Tage angesetzt haben um für Schaltjahre zu kompensieren, als wir von 'pro Jahr' auf 'pro Sekunde' umrechneten. Ferner mussten wir in 'pro Sekunde' umrechnen, das die Einheit der Radioaktivität als Anzahl der pro Sekunde zerfallenden Kerne definiert ist.
Als zweites berechnen wir wie viele Kerne 1 g 226Ra enthält:
Als drittes müssen wir das Zerfallsgesetz in eine Form bringen in der wir die Anzahl der pro Zeiteinheit zerfallenden Kerne ablesen können. Wir können dies erreichen in dem wir die Gleichung wie folgt ableiten:
Der Grund dafür hier den Absolutbetrag zu verwenden ist, dass wir das Minuszeichen loswerden wollen, da wir ja wissen dass wir es mit einer zeitlich abnehmenden Größe zu tun haben. Wir können nun die Daten, die wir für λ und N oben abgeleitet haben einsetzen:
Also ist die Radioaktivität einer Probe von einem Gramm Radium-226 ungefähr 1 Ci.
Diese Antwort ist nicht verwunderlich, da die Definition des Curie ursprünglich auf der Radioaktivität von 1 g Radium-226 beruhte.
Übung 3
Was ist die minimale Masse eines 99mTc Strahlers, der eine Radioaktivität von 1 MBq hat. Nimm an, dass die Halbwertszeit 6 Stunden beträgt und die Avogadrozahl 6,023·1023 ist.
Lösung
Wir gehen von der Beziehung zwischen Halbwertszeit und Zerfallskonstante aus:
Zweitens sagt uns die Frage, dass die Radioaktivität 1 MBq beträgt. Daher haben wir wegen 1 MBq = 1 · 106 Zerfälle pro Sekunde:
Schließlich kann die Masse dieser Kerne wie folgt berechnet werden:
In anderen Worten also lediglich etwas mehr als fünf Pikogramm 99mTc werden benötigt um eine Million Gamma-Strahlen pro Sekunde ab zu strahlen. Dieses Ergebnis zeigt nochmal einen wichtigen Punkt den man über den Strahlenschutz lernen sollte. Nämlich, dass man radioaktive Materialien genauso behandeln sollte wie krankheitserregende Bakterien.
Einheiten der Strahlungsmessung
Einleitung
Dies ist das vierte Kapitel des Wikibooks Physikalische Grundlagen der Nuklearmedizin
Nach dem letzten recht langen und detaillierten Kapitel werden wir nun in etwas gemächlicherem Tempo die in diesem Gebiet wichtigen Maßeinheiten besprechen.
Bevor wir dies tun, ist es jedoch sinnvoll, sich mit einem typischen Strahlenexperiment zu beschäftigen. So werden wir eine erste Vorahnung von den vielen Größen bekommen, die gemessen werden können, bevor wir uns mit den Einheiten, in denen sie gemessen werden, beschäftigen. So werden wir als erstes nur ein typisches Strahlenexperiment betrachten und uns dann mit den Einheiten beschäftigen.
Ein typisches Strahlenexperiment
Ein typischer Aufbau eines Experiments zur Radioaktivität ist in der Abbildung unten gezeigt. Als erstes gibt es eine Strahlenquelle, als zweites einen Strahl und drittens einen Absorber, welcher Strahlung aufnimmt. Also können die zu messenden Größen mit der Quelle, dem Strahl oder dem Absorber in Zusammenhang gebracht werden.
Diese Art von Umgebung könnte eine solche sein, in der Strahlung von einer Quelle verwendet wird, um einen Patienten (der in diesem Falle den Absorber darstellt) zum Zwecke einer diagnostischen Untersuchung zu bestrahlen, wobei wir hinter dem Patienten ein Gerät anbrächten, welches ein Bild erzeugt, oder zur therapeutischen Anwendung, wobei die Strahlung dazu gedacht ist, Schaden in einem bestimmten Teil des Patienten hervorzurufen. Es ist also ein Aufbau, in dem wir mit einem Absorber und einer Strahlenquelle arbeiten.
Die Strahlenquelle
Bei einer radioaktiven Strahlenquelle ist ihre Radioaktivität eine wichtige Messgröße. Wir sahen im vorherigen Kapitel, dass die hierzu verwendeten Einheiten das Becquerel (SI Einheit) und auch das Curie (veraltete Einheit) sind.
Ionendosis
Eine messbare Eigenschaft radioaktiver Strahlung heißt Ionendosis. Diese Größe beschreibt, wie viel Ionisation ein Strahl in dem Medium, das er durchläuft erzeugt.
Im nächsten Kapitel werden wir sehen, dass einer der wichtigsten Effekte beim Durchgang von Strahlung durch Materie darin besteht, dass Ionen erzeugt werden, dies gilt natürlich auch für Luft als eine Form der Materie. Daher wird die Ionendosis, die eine radioaktive Strahlung erzeugt, in Einheiten der in der Luft erzeugten Ionisation ausgedrückt.
Der direkte Weg zur Messung dieser Ionisation besteht darin, die erzeugte Ladung zu messen. Aus der Schulphysik wird man sich erinnern, dass die SI Einheit der elektrischen Ladung das Coulomb ist.
Die SI Einheit der Ionendosis ist Coulomb pro Kilogramm und wird mit dem Symbol bezeichnet. Sie ist definiert als die Menge an radioaktiver Strahlung (Röntgen- oder Gamma-Strahlung), die beim Durchgang durch ein Kilogramm Luft unter Normalbedingungen so viele Ionenpaare erzeugt, dass die erzeugte Gesamtladung eines Vorzeichens 1 Coulomb beträgt.
Die veraltete Einheit der Ionendosis ist das Röntgen, zu Ehren von Wilhelm Röntgen (dem Entdecker der Röntgenstrahlung). Sie wird mit dem Symbol R bezeichnet. Das Röntgen ist definiert durch:
Also ist ein R im Vergleich zu einem eine kleine Strahlungsmenge – genau genommen eine 3876 mal kleinere. Man beachte, dass diese Einheit sich nur auf Röntgen- und Gamma-Strahlen bezieht. Oft ist nicht die Ionendosis, sondern die Ionisationsrate, also die Ionendosis pro Zeiteinheit, von Interesse. Die hier gebräuchlichen Einheiten sind (Coulomb pro Kilogramm und Sekunde) und (Röntgen pro Stunde).
Energiedosis
Strahlung hinterlässt beim Durchgang durch Materie Energie. Meist eine recht geringe Menge, die aber nicht zu vernachlässigen ist. Die zugehörige physikalische Messgröße heißt Energiedosis und gilt für alle Arten von Strahlen, seien es nun Röntgen- oder Gamma-Strahlen oder Alpha- oder Beta-Teilchen.
Die SI-Einheit der Energiedosis ist das Gray, nach dem berühmten Radiobiologen Louis Harold Gray und trägt das Symbol Gy. Das Gray ist definiert als Absorption von einem Joule Strahlungsenergie pro Kilogramm durchstrahlten Materials. Wenn also ein Joule Strahlungsenergie von einem Kilogramm des Absorbermaterials absorbiert wird, so beträgt die absorbierte Dosis 1 Gy.
Die veraltete Einheit der Energiedosis ist das rad, welche bezeichnenderweise für Radiation Absorbed Dose (englisch für absorbierte Strahlendosis) steht. Es ist definiert durch:
Wie man sich leicht überlegt, entspricht 1 Gy also 100 rad.
Es gibt noch weitere vom Gray oder vom rad abgeleitete Größen, die die biologischen Effekte von absorbierter Strahlung in belebter Materie, wie zum Beispiel in menschlichem Gewebe, ausdrücken. Hierunter fallen die Äquivalentdosis und die effektive Dosis .
Die Äquivalentdosis basiert auf Schätzungen der Ionisationsfähigkeit von unterschiedlichen Strahlenarten, die durch Strahlungswichtungsfaktoren , berücksichtigt werden. Man schreibt dann
wobei die Energiedosis ist. Die Effektive Dosis schließt die und Schätzungen der Anfälligkeit unterschiedlicher Gewebe so genannter Gewebewichtungsfaktoren mit ein, so dass
wobei die Summe über alle betroffenen Gewebe läuft. Sowohl die Äquivalentdosis als auch die effektive Dosis werden in SI-Einheiten namens Sievert (Sv) angegeben.
Verweilen wir hier ein wenig, um den Begriff der Dosis etwas genauer zu erläutern. Man fasst der Begriff normalerweise im medizinischen Sinne auf, indem man zum Beispiel sagt, der Arzt verschreibe eine gewisse Dosis eines Medikaments. Was hat diese Dosis mit der Energie zu tun, die ein radioaktiver Strahl in einem Absorber hinterlässt? Es könnte etwas mit den frühen Anwendungen von Strahlung Anfang des zwanzigsten Jahrhunderts zu tun haben, die damals verwendet wurde, um verschiedenste Krankheiten zu behandeln. Somit können wir spekulieren, dass der Begriff in der Umgangssprache geblieben ist. Es wäre viel sinnvoller, eine Bezeichnung wie absorbierte Strahlungsenergie zu verwenden, da wir es mit der Deposition von Strahlung in einem Absorber zu tun haben. Aber dann wäre das Fachgebiet bei weitem zu leicht verständlich!
Gammastrahlenkonstante
Abschließend wollen wir noch eine weitere Einheit einer radiologischen Messgröße kennen lernen. Es ist die Gammastrahlenkonstante eines Radioisotops. Diese Messgröße setzt sich aus Größen zusammen, die wir bereits kennen gelernt haben und beschreibt die durch die Gammastrahlung des Isotops hervorgerufene Ionisation.
Sie ist in praktischer Hinsicht ausgesprochen nützlich, wenn wir es mit einer Gammastrahlung emittierenden Quelle zu tun haben. Angenommen, man hat eine Gammastrahlenquelle (zum Beispiel 99mTc oder 137Cs) und steht, während man arbeitet, in einem gewissen Abstand von ihr. Dann wird man an der erhaltenen Ionendosis aus Gründen des Strahlenschutzes interessiert sein. Hierbei hilft die Gammastrahlenkonstante
Sie ist definiert als Ionendosisrate pro Aktivität in einem bestimmten Abstand von der Quelle. Die SI-Einheit ist daher:
;
eine veraltete Einheit ist
Diese Einheiten sind etwas unhandlich. Es wäre wohl sinnvoll gewesen, sie nach irgendwelchen berühmten Wissenschaftlern zu benennen, so das wir die SI Einheit das Smith und die veraltete Einheit das Jones hätten nennen können. Aber die Dinge sind mal wieder nicht so einfach.
Abstandsgesetz
Bevor wir dieses Kapitel abschließen können, werden wir uns damit beschäftigen, was passiert wenn wir den Absorber von der Strahlungsquelle wegbewegen. Anders ausgedrückt, werden wir uns Gedanken über den Einfluss des Abstands von der Strahlenquelle auf die Intensität der Strahlung machen. Wir werden hierbei ein sehr nützliches Ergebnis finden, das für den Strahlenschutz von großer Bedeutung ist.
Die in einer radioaktiven Quelle erzeugte Strahlung wird in alle Richtungen gleichermaßen abgestrahlt. Wir können uns dazu vorstellen, dass es Kugeln mit immer größer werdenden Radien um die Quelle gibt, auf welchen die Intensität konstant ist, und die Photonen als Teilchen, die von der Quelle im Zentrum weg fliegen.
Wir stellen uns die Oberfläche einer dieser Kugeln vor und nehmen an, dass eine bestimmte Anzahl von Photonen pro Zeiteinheit durch sie hindurch tritt. Wenn wir nun eine Kugeloberfläche in größerer Entfernung von der Quelle betrachten, so muss die gleiche Anzahl an Photonen pro Zeiteinheit durch sie hindurch treten, nur dass sie jetzt auf eine größere Fläche verteilt ist. Diesen Gedanken folgend können wir uns leicht vorstellen, dass die Strahlungsintensität mit dem Quadrat des Abstandes von der Quelle abnimmt. Als Formel schreibt man (mit der Symbolen für Intensität und für Abstand):
Dieser Effekt heißt Abstandsgesetz. Verdoppelt man demnach den Abstand von der Quelle, so reduziert sich die Intensität um einen Faktor von 22, also um 4. Wenn wir den Abstand verdreifachen, so reduziert sich die Intensität um einen Faktor 9, also 32, usw.
Dies ist eine sehr nützliche Information, wenn man sich mit einer Strahlenquelle beschäftigt und versucht, die Dosis, der man ausgesetzt ist, so klein wie möglich zu halten.
Externe Links (englisch)
- Radiation and Risk - covers the effect of radiation, how risks are determined, comparison of radiation with other risks and radiation doses.
- Radiation Effects Overview - results of studies of victims of nuclear bombs including early effects on survivors, effects on the in utero exposed, and late effects on the survivors - from the Radiation Effects Research Foundation, a cooperative Japan-United States Research Organization.
- The Radiation and Health Physics Home Page - all you ever wanted to know about radiation but were afraid to ask....with hundreds of WWW links - from the Student Chapter of the Health Physics Society, University of Michigan containing sections on general information, regulatory Information, professional organizations and societies, radiation specialties, health physics research and education.
- What You Need to Know about Radiation - to protect yourself to protect your family to make reasonable social and political choices - covers sources of radiation and radiation protection - by Lauriston S. Taylor.
Interaktion von Strahlung mit Materie
Einleitung
Dies ist das fünfte Kapitel des Wikibooks Physikalische Grundlagen der Nuklearmedizin
Im letzten Kapitel haben wir uns auf die Strahlenquellen und die unterschiedlichen Strahlenarten konzentriert. Nun können wir uns damit beschäftigen, was passiert, wenn diese Strahlung mit Materie wechselwirkt. Der Hauptgrund wozu wir dies tun, ist um zu verstehen, was genau passiert, wenn Strahlung durch Materie hindurch tritt, aber auch, um uns auf die Frage, wie man Strahlung detektieren kann, vorzubereiten. Da alle Strahlendetektoren aus irgendeiner Form von Materie bestehen, ist es nützlich, erst einmal zu verstehen, wie Strahlung mit Materie wechselwirkt, so dass wir die dabei auftretenden Effekte nutzen können um entsprechende Detektoren zu entwickeln.
Bevor wir dies im Detail angehen, wollen wir uns an die wesentlichen physikalischen Eigenschaften der wichtigsten Strahlungsarten erinnern. Wir haben dieses Thema im Detail im ersten Kapitel behandelt. Sie sind jedoch der Bequemlichkeit halber unten noch einmal zusammengefasst:
| Strahlentyp | Masse | Elektrische Ladung | Geschwindigkeit |
|---|---|---|---|
| Alphateilchen | ziemlich hoch | zweifach positiv | ziemlich gering |
| Beta-Minus-Teilchen | etwa 8000 mal leichter als Alphateilchen | einfach negativ | kleiner als Lichtgeschwindigkeit |
| Beta-Plus-Teilchen | etwa 8000 mal leichter als Alphateilchen | einfach positiv | kleiner als Lichtgeschwindigkeit |
| Gammastrahlen | Keine | Keine | Licht- geschwindigkeit |
Wir werden uns nun mit dem Durchgang jedes einzelnen Strahlentyps durch Materie beschäftigen, wobei wir das Hauptaugenmerk auf die Gammastrahlen legen werden, da sie in der Nuklearmedizin am häufigsten verwendet werden. Einer der wichtigsten Effekte die einem hierbei unabhängig vom Strahlentyp auffallen werden ist, dass Ionen entstehen, wenn Strahlung mit Materie wechselwirkt. Aus diesem Grund spricht man auch von Ionisierender Strahlung.
Bevor wir nun starten, mag es nützlich sein, sich noch kurz mit einer Analogie zu befassen. Diese Analogie basiert darauf, dass wir uns die Materie aus einer sehr großen Anzahl von Atomen (sprich Kernen mit sie umkreisenden Elektronen) aufgebaut denken und uns die Strahlung als Teilchen, die durch die Materie hindurch fliegen, vorstellen. In Analogie kann man sich ein Raumschiff vorstellen, dass durch einen Meteorsturm hindurch fliegt, wie man es von Science-Fiction-Filmen her kennt, wobei das Raumschiff die Strahlung und die Meteore die Atome des durchstrahlten Materials darstellen. Eine besondere Eigenschaft, die wir jedoch erwähnen müssen, ist die Tatsache, dass unser Raumschiff, abhängig von der Strahlenart, eine elektrische Ladung tragen kann.
Alpha-Teilchen
Wir können aus der oben abgebildeten Tabelle sehen, dass Alpha-Teilchen eine zweifach positive Ladung tragen und uns daher leicht vorstellen, dass sie eine erhebliche elektrostatische Anziehung auf die äußeren Hüllenelektronen von Atomen, an denen sie nahe vorbeifliegen, ausüben. Dies führt dazu, dass einige Elektronen von ihren Kernen weggezogen werden, sodass Ionen entstehen. Anders ausgedrückt treten Ionisationen auf.
Aus der Tabelle können wir ersehen, dass Alpha-Teilchen im Vergleich zu anderen Strahlenarten sehr schwer sind, genauso wie die Atome des Materials, das von der Strahlung durchlaufen wird. Daher durchfliegen sie die Materie, abgesehen von seltenen Zusammenstößen mit den Kernen des Materials, in gerader Linie.
Eine dritte wichtige Eigenschaft ist die hierbei emittierte Energie. Bei Alpha-Teilchen ist sie immer diskret. Zum Beispiel emittiert 221Ra Alpha-Teilchen mit einer Energie von 6,71 MeV. Jedes von diesem Radionuklid emittierte Alpha-Teilchen besitzt genau diese Energie. Ein weiteres Beispiel ist 230U, welches Alpha-Teilchen der Energien 5,66 MeV, 5,82 MeV und 5,89 MeV emittiert.
Schließlich ist es notwendig zu bemerken, dass Alpha-Teilchen große biologische Schäden anrichten, wenn sie mit lebender Materie wechselwirken. Daher werden sie bei diagnostischen in-vivo-Untersuchungen nicht verwendet. Aus diesem Grund werden wir sie in diesem Wikibook nicht näher betrachten.
Beta-Teilchen
Aus der Tabelle können wir sehen, dass Beta-Minus-Teilchen einfach negative Ladung tragen. Beachte, dass wir Positronen (Beta-Plus-Teilchen) hier nicht behandeln werden, da sie, wie wir aus Kapitel 2 wissen, nicht sehr lange in Materie überleben können, bevor sie annihiliert werden. Beta-Minus-Teilchen leben erheblich länger, weshalb wir uns hier darauf konzentrieren werden.
Wegen ihrer negativen Ladung werden sie von Kernen angezogen und von Elektronenwolken abgestoßen, wenn sie sich in Materie bewegen. Dies führt, ohne hier ins Detail zu gehen, zu Ionisationen.
Der Weg, den Beta-Teilchen zurücklegen, wird oft als gewunden beschrieben, da sie dazu tendieren, von Atom zu Atom zu prallen.
Als letzten jedoch wichtigen Punkt müssen wir bemerken, dass die Energie von Beta-Teilchen nicht diskret, wie bei Alpha-Teilchen, sondern kontinuierlich verteilt ist. Die Energien der Beta-Teilchen einer Quelle haben eine spektrale Verteilung bis zu einer maximalen Energie - siehe Abbildung unten. Beachte, dass sich die Energieverteilung über einen Bereich erstreckt und die Eigenschaften und eingezeichnet sind:

Die Frage, die wir uns hier stellen müssen ist: Warum sehen wir ein Spektrum an Energien? Sicherlich sollten Elektronen mit genau einer diskreten Energie entstehen, wenn ein Neutron im Kern in ein Proton und ein Elektron zerfällt. Die Antwort liegt in der Tatsache, dass in Wirklichkeit zwei neue Teilchen im Beta-Zerfall entstehen. Wir haben die in Kapitel 2 verschwiegen, da wir den Anfang diese Wikibooks nicht zu sehr verkomplizieren wollten. Aber wir werden es hier der Vollständigkeit halber behandeln.
Das zweite neue Teilchen, das im Beta-Zerfall entsteht heißt Neutrino und wurde von Enrico Fermi so benannt. Es ist ein etwas mysteriöses Teilchen, welches weder Masse noch Ladung besitzt und seine genauen Eigenschaften werden zur Zeit noch erforscht. Das größte Problem mit dieser Art von Teilchen ist, dass sie sehr schwer zu detektieren sind und diese Tatsache hat unser Wissen über sie bisher wesentlich beschränkt.
Das Energiespektrum der Beta-Teilchen kann man verstehen, wenn man sich klarmacht, das die Energie, die bei der Umwandlung des Neutrons in ein Proton frei wird, auf das Beta-Teilchen und das Neutrino aufgeteilt wird. Manchmal geht die gesamte Energie auf das Beta-Teilchen über, und dieses erhält somit seine maximal mögliche Energie Emax. Häufiger jedoch wird die Energie auf die beiden Teilchen verteilt, so dass das Beta-Teilchen zum Beispiel nur die mittlere Energie EMittel erhält, wobei die verbleibende Energie auf das Neutrino übergeht.
Schließlich ist es wichtig zu wissen, dass Beta-Teilchen einen recht hohen biologischen Schaden verursachen. Dies ist einer der Gründe warum sie nicht bei diagnostischen Untersuchungen am lebenden Objekt verwendet werden. Wir werden sie daher in diesem Wikibook nicht näher betrachten.
Gammastrahlung
Da wir oben schon über Energien geredet haben, wollen wir nun klarstellen, dass die Energien von Gammastrahlen die von einer radioaktiven Quelle emittiert werden immer diskret sind. Zum Beispiel emittiert 99mTc Gammastrahlung mit einer Energie von 140 keV und 51Cr emittiert Gammastrahlung bei einer Energie von 320 keV.
Gammastrahlen können auf verschieden Arten mit Materie wechselwirken. Einige von ihnen haben für die Nuklearmedizin keine Bedeutung und werden hier nicht näher behandelt.
Die für die nuklearmedizinische Bildgebung wichtigen Wechselwirkungen sind:
Wir werden sie unten beide nacheinander behandeln. Man beachte, dass die hier beschriebenen Effekte auch für die Wechselwirkung von Röntgenstrahlen mit Materie relevant sind, da wie wir bereits vorher erwähnt haben Röntgenstrahlen und Gammastrahlen im wesentlichen das selbe physikalische Phänomen darstellen (sich jedoch in ihrer Energie unterscheiden). Somit ist die unten angeführte Beschreibung auch für Röntgen-Radiographie von Bedeutung.
Photoelektrischer Effekt
Wenn ein Gamma-Strahl mit einem Hüllenelektron eines Atoms des Materials, durch das er sich hindurch bewegt, zusammen stößt, kann er dabei seine gesamte Energie an das Elektron abgeben und damit aufhören zu existieren - siehe Abbildung unten. Aufgrund des Energieerhaltungssatzes können wir ableiten, dass die kinetische Energie des aus dem Atom herausgeschlagenen Elektrons um seine Bindungsenergie (vor der Wechselwirkung) kleiner sein muss als die Energie des Gamma-Strahls. Eine solches Elektron wird auch Photoelektron genannt.
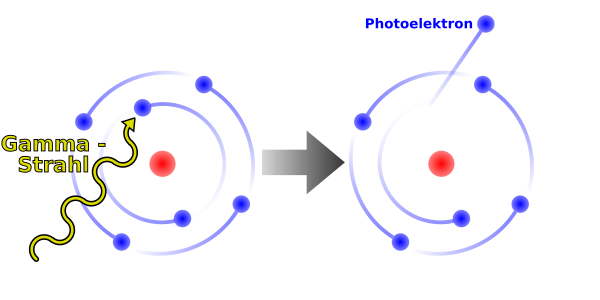
Man beachte, dass ein Ion zurückbleibt, wenn das Photoelektron das Atom verlässt und weiterhin dass der Gamma-Strahl in diesem Vorgang vollständig vernichtet wird.
Die beiden folgenden Punkte sind auch beachtenswert. Erstens kann ein Photoelektron, ähnlich einem Beta-Teilchen, Ionisationen entlang seiner Flugbahn verursachen. Weiterhin können Röntgenstrahlen emittiert werden, wenn die durch das Photoelektron entstandene Lücke in der Atomhülle durch ein Elektron einer äußeren Schale gefüllt wird. Wir erinnern uns das wir ein ähnliches Phänomen bereits in Kapitel 2 kennen gelernt haben, als wir uns mit dem Elektroneneinfang beschäftigt haben.
Compton-Effekt
Dieser Effekt ähnelt ein wenig dem Anspielen einer farbigen Kugel mit der weißen Kugel beim Billard. Hier gibt der Gammastrahl nur einen Teil seiner Energie an ein Valenzelektron, welches hier als freies Elektron betrachtet werden kann, ab - siehe Abbildung unten. Man beachte, dass das Elektron das Atom verlässt und sich wie ein Beta-Minus-Teilchen verhält und dass der Gammastrahl in eine andere Flugrichtung abgelenkt wird. Dieser abgelenkte Gammastrahl kann in weiteren Compton-Effekten mit den Elektronen des Materials wechselwirken. Wir bemerken, dass der Effekt auch als Compton-Streuung bezeichnet wird.

Dämpfung von Gamma-Strahlung
Die beiden oben beschriebenen Effekte führen zu Absorption und Streuung der radioaktiven Strahlen. Die Effekte werden unter dem Oberbegriff Dämpfung von Gamma-Strahlung zusammengefasst. Wir werden dieses Phänomen im nächsten Kapitel aus einer analytischen Perspektive untersuchen.
Strahlenbiologie
Es ist allgemein bekannt, dass ionisierende Strahlung lebende Zellen beschädigen kann. Wir haben oben die zugrundeliegenden atomaren Wechselwirkungen bereits behandelt. Für die Strahlenbiologie ist es wichtig, dass diese Wechselwirkungen komplexe Ketten biomolekularer Reaktionen auslösen können, die zu biologischen Schäden führen.
Wir haben weiter oben gesehen, dass die primären Wechselwirkungen von Strahlung und Materie zum Herausschleudern von Hüllenelektronen führen. Durch den Verlust eines oder mehrerer Hüllenelektronen bleibt das Atom positiv geladen zurück.
Andere Wechselwirkungen führen zur Anregung des Atoms und nicht zur Ionisation. Hierbei erhält ein (äußeres Valenz-) Elektron eine Energie, die ausreicht, um es in einen Anregungszustand zu heben. Ein solcher Zustand ist normalerweise nicht besetzt. Der mittlere Abstand des Elektrons vom Kern ist in diesen Zustand größer als in seinem ursprünglichen Zustand.
Dieser Effekt verändert die chemischen Kräfte, die Atome in Molekülen zusammen halten. Daher kann es zu einer Umstrukturierung der Atome zu einem neuen Molekül kommen. Daher ist die Anregung eine indirekte Methode chemische Veränderungen durch Modifikationen einzelner Atome (und damit ihrer Bindungen zu den Nachbaratomen) anzuregen.
Ionisationen und Anregungen können zu instabilen chemischen Systemen (Molekülbruchstücken) führen, welche als freie Radikale bezeichnet werden. Freie Radikale sind Atome (oder Moleküle), in denen es ungepaarte Elektronen gibt.
In Molekülen gibt es genauso wie in Atomen auch Zustände in denen sich die Elektronen des Moleküls befinden. Ein Zustand kann durch eine Gruppe von wenigen Zahlen beschrieben werden, welche man Quantenzahlen nennt. Eine von diesen heißt Spin. Alle anderen wollen wir hier als Grob-Quantenzahlen bezeichnen. Man hat experimentell gefunden, dass zwei Elektronen niemals im gleichen Zustand sind. Die Physiker Pauli und Fermi entwickelten daraufhin Theorien in denen zwei Elektronen niemals im gleichen Zustand seien dürfen. Eine Gruppe von Teilchen, zu denen auch das Elektron gehört, wurden daraufhin Fermionen genannt und die Aussage: „Zwei Fermionen befinden sich niemals im gleichen Zustand“ als Pauli-Verbot/Pauli(sches)-(Ausschließungs)-Prinzip bezeichnet. Stimmen also zwei Elektronen in allen ihren Grob-Quantenzahlen überein, so müssen Sie sich demnach in ihren Spinquantenzahlen unterscheiden. Stimmen zwei Elektronen in ihren Grobquantenzahlen überein, so bezeichnet man sie als gepaart. Gibt es in einem Atom (oder Molekül) ein Elektron, so kann es passieren, dass es kein weiteres Elektron im selben Atom (oder Molekül) gibt welches mit ihm in allen Grob-Quantenzahlen übereinstimmt. Ein solches Elektron bezeichnet man als ungepaartes Elektron und das Atom (oder Molekül) zu dem es gehört als ein Radikal.
Radikale sind chemisch sehr reaktionsfreudig und streben einen stabileren Zustand an indem sie Bindungen mit benachbarten Atomen und Molekülen eingehen. Die Entstehung freier Radikale führt daher meist zu Veränderungen der Moleküle in der Umgebung.
Aber schauen wir zuerst noch einmal die Wechselwirkungen selbst an.
Bei Wechselwirkungen mit Röntgen- und Gammastrahlen geht die Energie der Photonen (teilweise) auf die Hüllenelektronen über, zum Beispiel durch den Compton- und den Photoelektrischen Effekt. Diese Stahlen können tief in das Gewebe eindringen, da sie nur mit geringer Wahrscheinlichkeit mit Elektronen wechselwirken. In der Tat ist Nuklearmedizinische Bildgebung nur möglich, wenn die Energie der Gammastrahlen hoch genug ist, um den Körper des Patienten zu verlassen, aber zugleich klein genug ist, um mit dem Material des Detektors wechselwirken zu können und ein messbares Signal zu erzeugen.
Geladene Teilchen (z.B. Alpha- und Betateilchen) können jedoch auch durch anziehende oder abstoßende elektromagnetische Kräfte mit Atomkernen wechselwirken. Alphateilchen können auch mit Kernen kollidieren und sich oder den Kern dabei verändern. Bei der Wechselwirkung von Elektronen mit Kernen blieben beide in der Regel unverändert[1].
Die Rate, mit der ein geladenes Teilchen entlang seiner Bahn Energie verliert, hängt mit den Coulombkräften, durch die es mit den Teilchen in seiner Umgebung wechselwirkt, zusammen. Je größer die elektrische Ladung des Teilchens ist um so größer ist die Wahrscheinlichkeit Ionenpaare zu erzeugen, also soviel Energie auf (an Atome gebundene) Elektronen seiner Umgebung zu übertragen, dass sie ihre Atome verlassen. Langsamere Teilchen erzeugen ebenfalls mehr Ionenpaare, weil sie eine längere Zeit brauchen, um ihre Umgebung zu verlassen und daher länger mit dieser wechselwirken können.
Die Situation ist in der folgenden Abbildung, wo Spuren geladener Teilchen in Wasser abgebildet sind, dargestellt. Man sieht, dass die Bahn eines Alpha-Teilchens als relativ gerade Linie verläuft wie wir es bereits früher in diesem Kapitel besprochen haben. Wobei eine der große Anzahl an Wechselwirkungen (die als Kreuze entlang der Bahnkurven zu erkennen sind) pro Längeneinheit auftreten. Man sieht auch, dass die Bahnen der Elektronen stark gewunden verlaufen, wie wir bereits vorher besprochen haben, wobei die Anzahl der Wechselwirkungen pro Längeneinheit jedoch deutlich geringer ist (als bei Alpha-Teilchen).

Der Lineare Energietransfer (LET) ist definiert als die von einem ionisierenden Teilchen pro Längeneinheit an die Umgebung abgegebene Energie. Ein langsames Teilchen mit großer Ladung hat daher einen wesentlich höheren LET als ein schnelles Teilchen mit geringer Ladung. Ein Alpha-Teilchen von 5 MeV und ein Elektron von 1 MeV haben entsprechend LETs von 95 bzw. 0,25 keV/μm. Die Ionisationsdichte und damit das Muster der Wechselwirkungen, das durch die schweren stark geladenen Alpha-Teilchen hervorgerufen wird, ist viel dichter als das von den Elektronen erzeugte, wie man in der obigen Abbildung sieht.
Die Energie, die ein geladenes Teilchen auf seine Umgebung überträgt, wird sich mit der zurückgelegten Strecke ändern, da sich die Geschwindigkeit des Teilchens kontinuierlich abnimmt. Jede Wechselwirkung nimmt dem Teichen einen kleinen Teil seiner Energie, so dass der LET sich mit der von Teilchen zurückgelegten Strecke zuerst langsam und am Ende drastisch erhöht. Dieses Maximum am Ende des Weges bezeichnet man als Bragg-Peak, es tritt auf unmittelbar bevor das Teilchen zur Ruhe kommt.
Das International Commission on Radiation Units and Measurements (ICRU) schlägt vor das lineal energy ein besserer Indikator für die relative biologische Effektivität (RBE) ist. Obwohl die lineare Energie die gleichen Einheiten wie das LET hat ist sie definiert als:
Da die mikroskopische Verteilung der Energie recht anisotrop sein kann, sollte die lineare Energie ein besseres Maß für den von der Strahlung verursachten Schaden sein als der LET. Das ICRU und das ICRP haben daher vorgeschlagen, dass die biologischen Effektivität eines bestimmten Strahlentyps auf Basis der linearen Energie einer Kugel mit einem Mikrometer Durchmesser angegeben werden soll. Die lineare Energie kann für jeden gegebenen Strahlentyp und jede Energie berechnet werden und ein Strahlungswichtungsfaktor (wR) kann aus den entlang des Weges der Strahlung integrierten Werten der linearen Energie bestimmt werden.
Alles Leben auf diesem Planeten war seit Urzeiten ionisierender Strahlung ausgesetzt. Die derzeitige Situation für den Menschen ist in der folgenden Tabelle zusammengefasst:
| Quelle | Äquivalent- dosisleistung (mSv/Jahr) |
Bemerkungen |
|---|---|---|
| Kosmische Strahlung | ~0.4 | Etwa 100.000 Neutronen der kosmischen Strahlung und 400.000 kosmische Sekundärstrahlen durchdringen unseren Körper pro Stunde - und diese Dosis nimmt mit der Höhe zu! |
| Terrestrische Strahlung | ~0.5 | Über 200 Millionen Gammastrahlen durchdringen unseren Körper pro Stunde aus Quellen wie Erde und Baumaterialien. |
| Körpereigene Strahlung | ~0.3 | Ungefähr 15 Millionen 40K-Atome und ungefähr 7.000 natürliche Uranatome zerfallen stündlich in unserem Körper, hauptsächlich aus unserer Nahrung. |
| Radon und andere Gase | ~1.3 | Ungefähr 30.000 Atome, die aufgrund unserer Atmung aufgenommen werden, zerfallen stündlich in unserer Lunge |
Die Summe all dessen heißt natürliche Strahlenbelastung und beträgt etwa 2.5 mSv pro Jahr mit großen Schwankungen abhängig von der Höhe und der Nahrungsaufnahme sowie den geologischen und geographischen Gegebenheiten des Ortes.
Es wird gemeinhin angenommen, dass es in lebender Materie Reparaturmechanismen gibt, die ausgelöst werden sobald Strahlenschäden auf biomolekularer Ebene auftreten. Diese Mechanismen liegen wahrscheinlich in der Evolution begründet und stellen die Antwort auf die seit Uhrzeiten wirkende natürliche Hintergrundstrahlung dar.
Es ist bekannt, dass erhebliche Schäden im Gewebe durch höhere Strahlenflüsse verursacht werden können, sogar bei in der Medizin verwendeten Dosen. Zelltod und Übergänge von Zellen in krankhafte Zustände können auftreten und zu langen Latenzzeiten von mehreren Jahren führen bevor klinische Symptome von Krebs oder Leukämie sichtbar werden. Die weitere Behandlung des weiten Feldes der Strahlenbiologie geht jedoch hier über unsere Ziele hinaus.
- ↑ Elektronen können nur über die schwache oder elektromagnetische Kraft wechselwirken, Alphateilchen jedoch auch über die starke Kraft. Die Gravitation spielt hier keine Rolle.
Links
Folienvortrag von Dr. Manfred Krammer (Österreichische Akademie der Wissenschaften Wien). Sehr schöner Vortrag. Zielgruppe: Physikstudenten, also leider nicht so ganz einfach.
Dämpfung von Gammastrahlen
Einleitung
Dies ist das sechste Kapitel des Wikibooks Physikalische Grundlagen der Nuklearmedizin.
Wir haben die Wechselwirkung von Gammastrahlen mit Materie im letzten Kapitel von einem beschreibenden Standpunkt aus kennen gelernt und sahen, dass der Compton Effekt und der photoelektrische Effekt die beiden wesentlichen Mechanismen darstellen. Wir werden uns hier noch einmal mit diesem Thema auseinander setzen, diesmal jedoch aus einem analytischen Blickwinkel. Dies wird uns ein universelleres Verständnis dieser Vorgänge ermöglichen.
Man bemerke, dass die hier vorgeführte Behandlung des Stoffs gleichermaßen für Röntgenstrahlen gilt, da, wie wir bereits wissen, Gammastrahlen und Röntgenstrahlen unterschiedliche Erscheinungen desselben physikalischen Phänomens sind.
Unsere Behandlung beginnt mit der Beschreibung eines einfachen Strahlungsexperiments, welches leicht in einem Labor durchgeführt werden kann und welches von vielen frühen Pionieren auf diesem Gebiet durchgeführt wurde. Wir werden hierauf aufbauend eine einfache Gleichung ableiten und sie mit einigen einfachen Konzepten soweit generalisieren, dass wir sie auf beliebige Dämpfungsprobleme anwenden können.
Absorptionsexperiment
Das Experiment ist recht einfach. Es besteht darin einen dünnen Gammastrahl auf ein Material zu schießen und zu messen wie viel Strahlung hindurch kommt. Wir können sowohl die Energie der Gammastrahlen als auch die Art des Absorbermaterials ändern, wie auch seine Dicke, oder seine Dichte.
Der experimentelle Aufbau ist in der Abbildung unten gezeigt. Wir bezeichnen die Intensität die auf den Absorber auftrifft als die einfallende Intensität , und die Intensität der die durch den Absorber hindurch kommt als die transmittierte Intensität . Mit bezeichnen wir die Dicke des Absorbers:

Aus dem letzten Kapitel wissen wir, dass Gammastrahlen Wechselwirkungen wie dem photoelektrischen Effekt und dem Compton Effekt ausgesetzt sein werden während sie den Absorber passieren. Die transmittierten Strahlen werden im wesentlichen diejenigen sein, die überhaupt keine Wechselwirkung mit dem Absorbermaterial hatten.
Wir können also erwarten, dass die transmittierte Intensität geringer sein wird als die einfallende Intensität, dass heißt:
Man mag sich jedoch fragen um wie viel kleiner? Bevor wir dies klären, wollen wir erst einmal den Unterschied zwischen und als bezeichnen, formal schreiben wir:
Einfluss der Kernladungszahl
Wir wollen damit anfangen, die Änderung der Größe zu untersuchen, indem wir unterschiedliche Absorber in den Strahlengang bringen. Wir stellen dabei fest, dass sehr stark von der Kernladungszahl des Absorbermaterials abhängt. Zum Beispiel finden wir, dass im Falle eines Absorbers aus Kohlenstoff (Z=6) ziemlich klein, jedoch im Falle von Blei (Z=82) sehr groß ist.
Wir können uns dies anhand der folgenden Grafik veranschaulichen:

In dieser Graphik sind die Atome mit großer Kernladungszahl als große Kreise und solche mit kleiner Kernladungszahl als kleine Kreise dargestellt. Die von links in den jeweiligen Absorber einfallende Strahlung wird durch Pfeile angedeutet. Man beachte, dass die Atome mit größerer Kernladungszahl größere Ziele für die Strahlung darstellen und somit die Chancen für eine Wechselwirkung über den photoelektrischen und den Compton-Effekt relativ hoch sind. Die Dämpfung sollte daher recht hoch sein.
Im Falle niedriger Kernladungszahl sind jedoch die einzelnen Atome kleiner und daher sind die Chancen für Wechselwirkungen geringer. Anders ausgedrückt, hat die Strahlung eine größere Chance, durch den Absorber hindurch zu kommen und die Dämpfung ist entsprechend geringer als im Falle großer Kernladungszahl.
In der Analogie mit dem Raumschiff, die wir im letzten Kapitel hergestellt haben, kann man sich die Kernladungszahl als die Größe der einzelnen Meteore in der Meteorwolke vorstellen.
Würden wir ein präzises Experiment durchführen und die Ergebnisse detailliert untersuchen, so stellten wir fest, dass:
Wenn wir also die Kernladungszahl des Absorbers verdoppeln, erhöhen wir die Dämpfung um einen Faktor 23, also 8, wenn wir sie verdreifachen, erhöht sich die Dämpfung um den Faktor 27 usw.
Aus diesem Grunde werden Materialien mit großer Kernladungszahl, wie zum Beispiel Blei, gerne im Strahlenschutz verwendet.
Einfluss der Dichte
Als zweites untersuchen wir, wie sich die Größe ändert, wenn wir die Dichte des Absorbers verändern. Aus der Abbildung unten sehen wir, dass eine geringere Dichte, zu einer geringeren Dämpfung führt, da die Wahrscheinlichkeit einer Wechselwirkung der Strahlung mit der Materie geringer ist.

In unserer Analogie mit dem Raumschiff, können wir uns die Dichte, als Anzahl der Meteore pro Raumeinheit vorstellen. Eine geringe Dichte bedeutet hier also auch eine geringe Wahrscheinlichkeit für einen Zusammenstoß des Raumschiffs mit einem Meteor. Quantitativ erhält man, dass die Dämpfung der Dichte ρ proportional ist:
Einfluss der Dicke
Drittens können wir die Dicke des Absorbers verändern. Wie man sich leicht überlegt, bewirkt ein dickerer Absorber eine stärkere Abschwächung der Strahlung.
Einfluss der Energie der Gamma-Strahlung
Schließlich können wir in unserem Experiment die Energie der Gammastrahlung verändern. Dabei finden wir, ohne groß ins Detail zu gehen, dass Strahlung mit höherer Energie weniger stark abgeschwächt wird. Man kann sich dies auch anhand der Analogie des Raumschiffs beim Durchfliegen einer Meteorwolke überlegen, indem man die Chancen eines schnellen und eines langsamen Schiffs, die Wolke zu durchfliegen, vergleicht.
Mathematisches Modell
Wir entwickeln hier ein mathematisches Modell, das uns helfen wird unsere experimentellen Befunde zu verallgemeinern. Wir werden sehen, dass der mathematische Ansatz und die erhaltenen Ergebnisse denen aus dem Kapitel „Das Zerfallsgesetz“ sehr ähnlich sind. Also müssen wir uns hier nicht mit neuer Mathematik plagen sondern lediglich die gleiche mathematische Analyse auf ein neues Thema anwenden.
Fangen wir einfach damit an, dass wir nur die Dicke des Absorber verändern. Anders gesagt verwenden wir immer das selbe Material (also immer die gleiche Kernladungszahl) und die gleiche Dichte und benutzen immer Gammastrahlung der gleichen Energie in unserem Experiment. Nur die Dicke des Absorbers wird verändert.
Aus den obigen Betrachtungen können wir uns leicht vorstellen, dass die Größe sowohl von der Intensität der einfallenden Strahlung als auch von der Dicke des Absorbers abhängt, dass heißt für eine infinitesimal kleine Änderung der Dicke des Absorbers:
das Minuszeichen deutet an, dass die Intensität durch den Absorber verringert wird.
Wandeln wir die proportionale Beziehung in eine Gleichung um so haben wir:
wobei die Proportionalitätskonstante μ linearer Schwächungskoeffizient genannt wird.
Teilen wir dies durch , so können wir die Gleichung umschreiben zu:
Diese Gleichung beschreibt also den Effekt für kleine Änderungen in der Absorberdicke . Um herauszufinden, was sich für die gesamte Länge des Absorbers ergibt, müssen wir die Effekt für alle kleinen Teilstücke zusammenrechnen. Sprich wir müssen die Gleichung integrieren. Drücken wir dies formaler aus, so können wir sagen, dass die Intensität der Strahlung von der Dicke bis zu irgendeiner anderen Dicke von auf abnehmen wird, so dass:
Die letzte Gleichung sagt uns, dass die Intensität der Strahlung exponentiell mit der Dicke des Absorbers abnehmen wird, wobei die Abnahmerate durch den linearen Schwächungskoeffizienten gegeben ist. Diese Beziehung ist unten graphisch dargestellt. Es ist die Intensität gegenüber der Dicke des Absorbers aufgetragen. Wir sehen, dass die Intensität vom Wert , bei , zunächst sehr schnell und später immer langsamer in klassischer exponentieller Form abnimmt.
 |
 |
Der Einfluss des linearen Schwächungskoeffizienten ist in der nächsten Abbildung dargestellt. Alle drei Kurven verlaufen exponentiell, nur die linearen Schwächungskoeffizienten sind verschieden. Man sieht, dass die Kurve bei einem kleinen linearen Schwächungskoeffizienten relativ langsam und bei einem großen linearen Schwächungskoeffizienten sehr schnell abfällt.

Der lineare Schwächungskoeffizient ist eine Eigenschaft des Absorbermaterials. Einige wie zum Beispiel Kohlenstoff haben einen kleinen Wert und können leicht von Strahlung durchdrungen werden. Andere Materialien wie zum Beispiel Blei haben einen relativ großen linearen Schwächungskoeffizienten und stellen somit gute Absorber dar.
| Absorber | 100 keV | 200 keV | 500 keV |
|---|---|---|---|
| Luft | 0,000195 | 0,000159 | 0,000112 |
| Wasser | 0,167 | 0,136 | 0,097 |
| Kohlenstoff | 0,335 | 0,274 | 0,196 |
| Aluminium | 0,435 | 0,324 | 0,227 |
| Eisen | 2,72 | 1,09 | 0,655 |
| Kupfer | 3,8 | 1,309 | 0,73 |
| Blei | 59,7 | 10,15 | 1,64 |
Die Materialien in der obigen Tabelle sind Luft, Wasser, usw. und reichen von Elementen wie Kohlenstoff (Z=6) bis Blei (Z=82) und ihre Absorptionskoeffizienten sind für drei verschiedene Gamma-Energien angegeben. Als erstes bemerken wir, dass der Absorptionskoeffizient mit der Kernladungszahl zunimmt. Zum Beispiel nimmt er vom sehr kleinen Wert von 0,000195 cm-1 für Luft bei 1000 keV bis auf 60 cm-1 für Blei zu. Als zweiten Punkt stellen wir fest, dass der Absorptionskoeffizient mit zunehmender Energie der Gamma-Strahlung abnimmt. Zum Beispiel nimmt der Wert für Kupfer von 3,8 cm-1 bei 100 keV auf 0,73 cm-1 bei 500 keV ab. Drittens bemerken wir, dass der in der Tabelle erkennbare Trend mit den obigen experimentellen Erwägungen übereinstimmt.
Schließlich ist es wichtig zu bemerken, dass die obige Ableitung nur für dünne Strahlenbündel strikt gültig ist. Bei ausgedehnten Strahlen müssen weitere Faktoren berücksichtigt werden.
Halbwertsdicke
Genauso wie man die Halbwertszeit beim Zerfallsgesetz benutzt, gibt es eine vom Absorptionsgesetz abgeleitete Größe, mit der wir uns die Vorgänge veranschaulichen können. Diese Größe heißt Halbwertsdicke und beschreibt die Dicke eines Absorbermaterials, die benötigt wird, um die einfallende Strahlung um den Faktor zwei zu reduzieren. Graphisch betrachtet können wir sagen, dass wenn
gilt, die Dicke des Absorbers genau der Halbwertsdicke entspricht:

Die Halbwertsdicke für einige Absorber ist in der folgenden Tabelle für drei verschiedene Gamma-Energien angegeben:
| Absorber | 100 keV | 200 keV | 500 keV |
|---|---|---|---|
| Luft | 3555 | 4359 | 6189 |
| Wasser | 4,15 | 5,1 | 7,15 |
| Kohlenstoff | 2,07 | 2,53 | 3,54 |
| Aluminium | 1,59 | 2,14 | 3,05 |
| Eisen | 0,26 | 0,64 | 1,06 |
| Kupfer | 0,18 | 0,53 | 0,95 |
| Blei | 0,012 | 0,068 | 0,42 |
Als erstes bemerken wir, dass die Halbwertsdicke mit steigender Kernladungszahl abnimmt. Zum Beispiel beträgt der Wert für Luft bei 100 keV etwa 35 Meter, jedoch nur 0,12 mm für Blei bei der selben Energie. Anders ausgedrückt benötigt man 35 m Luft, um die Intensität eines Gamma-Strahls von 100 keV auf die Hälfte zu reduzieren, wobei man mit nur 0,12 mm Blei das selbe erreichen kann. Als zweites halten wir fest, dass die Halbwertsdicke mit zunehmender Gamma-Energie größer wird. Zum Beispiel steigt sie für Kupfer von 0,18 cm bei 100 keV auf 1 cm bei 500 keV. Drittens können wir aus den beiden obigen Tabellen sehen, dass es eine reziproke Beziehung zwischen der Halbwertsdicke und dem Absorptionskoeffizienten gibt, welche wir nun im Detail untersuchen werden.
Beziehung zwischen dem Absorptionskoeffizienten und der Halbwertsdicke
Wie schon beim Gesetz des radioaktiven Zerfalls, wo wir die Beziehung zwischen der Halbwertszeit und der Zerfallskonstante untersucht haben, kann eine Beziehung zwischen der Halbwertsdicke und dem Absorptionskoeffizienten hergeleitet werden. Wir tun dies, indem wir die Definition der Halbwertsdicke verwenden:
wobei
setzen wir dies in das Absorptionsgesetz ein, so haben wir:
dies ergibt
Somit
und
Die letzten beiden Gleichungen drücken den Zusammenhang zwischen dem Absorptionskoeffizienten und der Halbwertsdicke aus. Sie sind sehr nützlich, wenn es darum geht, Rechenaufgaben zu lösen, die etwas mit der Abschwächung von Strahlung zu tun haben und sind häufig der erste Schritt zur Lösung.
Massenabsorptionskoeffizient
Oben haben wir gesehen, dass der lineare Schwächungskoeffizient nützlich ist wenn wir es mit Absorbermaterial gleicher Dichte aber unterschiedlicher Dicke zu tun haben. Ein weiterer Koeffizient kann nützlich sein wenn wir die Dichte ρ in unsere Analyse mit einbeziehen wollen. Dieser heißt Massenabsorptionskoeffizient und ist definiert als:
Als Maßeinheit für den Absorptionskoeffizienten haben wir in der obigen Tabelle cm-1 verwendet, weiterhin ist eine übliche Einheit der Dichte. Der Leser mag sich nun selbst ausrechnen wollen, dass die entsprechende Einheit des Massenabsorptionskoeffizienten ist.
Fragen
Die beiden unten angegebenen Fragen sollen dabei helfen, das Verständnis für den Stoff dieses Kapitels zu vertiefen. Die erste ist recht einfach und übt die Anwendung der exponentiellen Schwächungsgleichung. Die zweite Frage ist erheblich anspruchsvoller und beschäftigt sich mit der Anwendung des exponentiellen Schwächungsgesetzes im Bezug auf Radioaktivität und Ionendosis.
Frage 1
Wie viel Aluminium braucht man um die Intensität eines 200 keV Gammastrahls auf 10% seiner ursprünglichen Intensität zu reduzieren. Die Halbwertsdicke von 200 keV Gammastrahlung in Al sei 2,14 cm.
Antwort
Mathematisch ausgedrückt lautet die obige Frage:
Wir wissen, dass die Halbwertsdicke 2.14 cm beträgt. Daher ist der lineare Schwächungskoeffizient:
Verbinden wir dies mit dem Absorptionsgesetz
so können wir schreiben:
Somit
Also beträgt die Dicke des Aluminiums, das man braucht, um diese Gamma-Strahlung um einen Faktor 10 zu reduzieren, etwa 7 cm. Diese relativ hohe Dicke ist der Grund dafür, dass Aluminium im allgemeinen nicht zur Abschirmung von Strahlung verwendet wird - seine Massenzahl ist nicht groß genug, um Gammastrahlung effizient schwächen zu können.
Man mag diese Frage vielleicht mit Blei als Absorber ausprobieren wollen - Die Antwort auf Frage nach der Halbwertsdicke von Blei für Gammastrahlung einer Energie von 200 keV möge der Leser selber herausfinden.
Als Hinweis möchten wir jedoch die oben aufgeführten Tabellen angeben.
Weiterhin geben wir die Lösung der Aufgabe zur Kontrolle an: 2,2 mm
In anderen Worten wird nur eine relativ dünne Bleischicht benötigt um den selben Effekt wie eine 7 cm dicke Aluminiumschicht zu erreichen.
Frage 2
Eine 105 MBq Strahlenquelle des Isotops 137Cs soll in einer Bleikiste gelagert werden, so dass die Ionisationsrate in 1 m Abstand von der Quelle 0,5 mR/Stunde beträgt. Die Halbwertsdicke für die von 137Cs emittierten Gamma-Strahlen in Blei betrage 0,6 cm. Wie dick muss die Bleikiste sein? Die spezifische Gammastrahlenkonstante von 137Cs sei 3,3 R h-1 mCi-1 bei 1 cm Abstand von der Quelle.
Antwort
Dies ist eine recht typische Frage, die auftritt, wenn man mit radioaktiven Materialien arbeitet. Wir möchten eine bestimmte Menge eines Materials benutzen und wir möchten sie aus Gründen des Strahlenschutzes so in einem Bleibehälter lagern, dass die Ionisationsrate unterhalb einer gewissen Schwelle bleibt, wenn wir in einer bestimmten Entfernung von der Quelle arbeiten. Wir kennen die Radioaktivität des benutzen Materials. Aber wir suchen eine Lösung in SI Einheiten. Wir schlagen die Ionisationsrate in einem Nachschlagewerk nach und finden, dass die Gamma-Strahlenkonstante in veralteten Einheiten angegeben ist. Genau wie in diesem Beispiel.
Fangen wir also damit an unsere Einheiten in ein Maßsystem zu bringen. Die Gamma-Strahlenkonstante ist gegeben durch:
bei 1 cm Abstand von der Quelle
Dies ist gleich:
Dies ist wiederum gleich:
nach dem Abstandsgesetz. Das Ergebnis in Becquerel ausgedrückt ist:
da . Und somit erhalten wir bei einer Radioaktivität von für die Ionisationsrate:
Die Ionisationsrate in einem Meter Abstand von der Quelle beträgt also 891,9 mR h-1.
Wir möchten die Ionisationsrate, entsprechend der Fragestellung auf weniger als 0,5 mR h-1 senken, indem wir Blei als Absorber verwenden.
Der Leser wird nun in der Lage sein, das exponentielle Dämpfungsgesetz mit der Halbwertsdicke für Gammastrahlen in Blei zu benutzen, um zu berechnen, dass die Dicke des benötigten Bleis ca. 6,5 cm beträgt.
Externe Links (englisch)
- Mucal on the Web - an online program which calculates x-ray absorption coefficients - by Pathikrit Bandyopadhyay, The Center for Synchrotron Radiation Research and Instrumentation at the Illinois Institute of Technology.
- Tables of X-Ray Mass Attenuation Coefficients - a vast amount of data for all elements from National Institute of Science & Technology, USA.
Gasgefüllte Strahlungsdetektoren
Einleitung
Dies ist das siebte Kapitel des Wikibooks Physikalische Grundlagen der Nuklearmedizin
In den letzten beiden Kapitel haben wir gelernt, wie Strahlung mit Materie wechselwirkt, und können unser Wissen nun zur Detektion von Strahlung anwenden.
Als wesentliche Folge des Wechselwirkung von Strahlung mit Materie haben wir die Entstehung von Ionen in Kapitel 5.
Dieser Effekt wird, wie wir nun sehen werden, in gasgefüllten Detektoren ausgenutzt. Der eigentliche Detektor ist in diesem Fall das Gas, in dem die Atome durch die Strahlung ionisiert werden. Wir werden im nächsten Kapitel sehen, dass auch Festkörper als Strahlungsdetektoren verwendet werden können, werden uns aber nun erst einmal mit Gasen auseinandersetzen und Detektoren wie die Ionisationskammer und den Geigerzähler kennen lernen.
Bevor wir uns mit den spezifischen Typen gasgefüllter Detektoren auseinandersetzen, werden wir den generellen Aufbau dieser Detektoren kennen lernen.
Gasgefüllte Detektoren
Wie wir oben erwähnt haben, entstehen Ionen, wenn Strahlung in diesem Detektortyp mit den Gasatomen wechselwirkt. Nach dem in Kapitel 5 gelernten, wissen wir, dass der photoelektrische Effekt und der Compton-Effekt die Ionisation verursachen, wenn wir es mit Gamma-Strahlung mit einer typischerweise in der Diagnostik verwendeten Energie zu tun haben.
Genau genommen entstehen zwei Teilchen, wenn ein Ion erzeugt wird - das positive Ion selbst und ein Elektron. Diese beiden Teilchen werden zusammen als Ionenpaar bezeichnet. Die Detektion der Erzeugung eines Ionenpaares bildet die Grundlage für die Arbeitsweise von gasgefüllten Detektoren. Diese wird erreicht, indem man ein elektrisches Feld anlegt, um die Elektronen zur positiv geladenen und die Protonen zur negativ geladenen Elektrode zu ziehen.
Schauen wir uns dazu den stark vereinfachten Aufbau in der nächsten Abbildung an:

Hier haben wir zwei Elektroden und ein Füllgas dazwischen. Dies entspricht einem Kondensator mit Dielektrikum.
Üblicherweise verwendet man ein Edelgas wie Argon oder Xenon. Man wählt ein Edelgas da man chemische Reaktionen der erzeugten Ionen vermeiden möchte, da sie die Detektoreigenschaften verändern könnten.
Eine Gleichspannung wird zwischen den Elektroden angelegt. Daher wird sich das Elektron zur positiven Elektrode und das Ion zur negativen Elektrode bewegen wenn durch die Wechselwirkung mit der Strahlung eine Ionenpaar entsteht. Werden diese Teilchen ihre Elektroden jedoch erreichen? Die Antwort hängt offenbar von der Größe der angelegten Gleichspannung ab. Zum Beispiel, könnte man im einen Extrem eine Spannung von nur einem Mikrovolt (das ist ein Millionstel von einem Volt) anlegen, so dass das entstehende elektrische Feld zu klein ist um das Ionenpaar weit genug aufzutrennen, was dazu führen kann, dass die beiden Teilchen wieder rekombinieren und ein Gasatom bilden. Im anderen Extrem könnte man eine Spannung von einer Million Volt zwischen den beiden Elektroden anlegen. In diesem Falle ist es sehr wahrscheinlich, dass Funken zwischen den beiden Elektroden fliegen - eine Blitzröhre wenn man so will - und unser Detektor verhält sich wie eine Art Neonröhre. Irgendwo zwischen diesem beiden Extremen sollten wir eine Spannung finden, die eine Kraft auf das Ion und das Elektron ausübt um eine Rekombination zu verhindern aber gleichzeitig klein genug ist um Funkenflug zu vermeiden.
Wir werden dieses Thema unten genauer unter die Lupe nehmen. Bevor wir dies jedoch tun schauen wir uns an wie das oben skizzierte Konzept eines einfachen Detektors in der Praxis angewandt wird. In realen Detektoren verwendet man üblicherweise zylindrische gasgefüllte Kammern. Da man heraus fand, dass sie effizienter arbeiten als die oben gezeigten Konstruktionen mit planparallele Elektroden.
Ein Querschnitt durch durch einen solchen Zylinder ist in der folgenden Abbildung gezeigt:

Die positive Elektrode besteht aus einem dünnen Draht im Zentrum des Zylinders und die Wand des Zylinders dient als negative Elektrode. Im Prinzip können wir einen solchen Detektor bauen indem wir ein Stück Metallrohr nehmen, einen Draht in der Mitte montieren, es mit einem Edelgas füllen und beide Enden versiegeln. Reale Detektoren sind etwas komplizierter aufgebaut, aber wir wollen uns hier noch nicht mit solchen Nebensächlichkeiten aufhalten.
Wir legen eine Gleichspannung über eine Batterie an und verbinden sie, wie in der Abbildung gezeigt, über den Widerstand R mit dem Detektor. Nehmen wir nun an, dass ein Gammastrahl in unseren Detektor einfällt. Es werden Ionenpaare im Gas entstehen, die Ionen werden nach außen zur Wand und die Elektronen zum Draht in der Mitte gezogen. Denken wir im Moment nur an die Elektronen. Wenn sie den Draht in der Mitte treffen können wir uns vorstellen, dass sie in den Draht eindringen und durch den Widerstand zum Pluspol der Spannungsquelle fließen. Diese durch den Widerstand fließenden Elektronen bilden einen elektrischen Strom, welcher nach dem Ohmschen Gesetz zu einer Spannung über dem Widerstand führt. Diese Spannung wird durch einen Verstärker verstärkt und verschiedene Geräte können benutzt werden um die verstärkte Spannung zu registrieren. Ein Lautsprecher ist ein sehr einfaches Gerät das diesen Zweck erfüllen kann und erzeugt ein Klick bei jedem Spannungspuls. Andere Geräte schließen das Ratemeter, welches die Anzahl der erzeugten Spannungspulse pro Zeiteinheit - ähnlich einem Tachometer beim Auto - misst, einen Pulszähler (oder auch Scaler), welcher die Anzahl der erzeugten Spannungspulse in einer definierten Zeitspanne zählt. Ein Spannungspuls wird in der Praxis häufig als Count bezeichnet und die Anzahl der pro Zeiteinheit erzeugten Pulse wird häufig Zählrate genannt.
Einfluss der angelegten Gleichspannung
Wenn wir einen Detektor mit der oben gezeigten Beschaltung bauen würden, so könnten wir ein Experiment durchführen welches uns erlauben würde den Einfluss der angelegten Gleichspannung auf die Größe der über den Widerstand R gemessenen Spannungspulse zu untersuchen. Man beachte, dass der Begriff Pulshöhe in diesem Gebiet häufig für die Größe des Spannungspulses verwendet wird.
Idealerweise könnten wir ein Resultat erzeugen, welches dem in der folgenden Abbildung dargestellten entspricht:

Der Graph stellt die Abhängigkeit der Pulshöhe von der angelegten Gleichspannung dar. Man beachte, dass die Pulshöhe auf der vertikalen Achse logarithmisch aufgetragen ist um einen größeren Spannungsbereich auf im Diagramm darstellen zu können.
Die Experimentellen Ergebnisse können in die fünf eingezeichneten Bereiche unterteilt werden. Wir werden nun jeden einzelnen im Detail betrachten.
- Bereich A Hier ist Vdc relativ klein so dass es zur Rekombination von Ionen und Elektronen kommt. Daher werden nicht alle Ionenpaare gesammelt und der Spannungspuls ist relativ klein. Er wird jedoch mit zunehmender Gleichspannung größer, da die Anzahl der Rekombinationen abnimmt.
- Bereich B Vdc ist so hoch, dass die Rekombinationen vernachlässigt werden können. In dieser Region arbeitet der Detektor als Ionisationskammer.
- Bereich C Vdc ist so groß, dass Elektronen die sich dem Draht in der Mitte nähern zwischen den Stößen genügend Energie aufnehmen können um weitere Ionenpaare zu erzeugen. Daher steigt die Anzahl der Elektronen und damit die über den Widerstand fließende Ladung bis zum tausendfachen des ursprünglich durch die Wechselwirkung mit der Strahlung erzeugten Ladung an. In diesem Gebiet arbeitet der Detektor als Proportionalzähler.
- Bereich D Vdc ist so groß, dass auch ein Teilchen welches minimale Ionisation verursacht zu einem sehr großen Spannungspuls führt. Die ursprüngliche von der Strahlung verursachte Ionisation startet einen Prozess bei dem es einem vollständigen Durchbruch des Detektors kommt wenn die Elektronenlawine auf den Draht in der Mitte zu rollt. Diese Region wird auch Geiger-Müller-Bereich genannt und im Geigerzähler verwendet.
- Bereich E Hier ist Vdc so groß, das es im Gas zu einem vollständigen und permanenten Durchbruch kommt, so dass das Gerät nicht mehr für den Nachweis von Strahlung verwendet werden kann.
Wir werden uns nun mit den Eigenschaften der Ionisationskammer und des Geigerzählers im Detail beschäftigen.
Ionisationskammer
Eine Ionisationskammer ist ein gasgefüllter Detektor, der mit einer relativ niedrigen Gleichspannung betrieben wird. Als erstes werden wir die Größe des von diesem Detektor erzeugten Spannungspulses abschätzen und uns anschließend mit einigen Anwendungen beschäftigen.
Wenn ein Beta-Teilchen mit dem Gas wechselwirkt braucht es eine Energie von etwas 30 eV um ein Ionenpaar zu erzeugen. Daher kann man die Anzahl der Ionenpaare die ein Beta-Teilchen einer Energie von 1MeV erzeugt wenn es vollständig absorbiert wird wie folgt berechnen:
Die erzeugte elektrische Ladung im Gas ergibt sich somit zu:
Wenn die Kapazität der Ionisationskammer (man erinnere sich, dass wir die Ionisationskammer mit dem Kondensator oben verglichen haben) mit 100 pF ansetzen, dann ergibt sich für die Amplitude des erzeugten Spannungspulses:
Da die erzeugte Spannung so klein ist, müssen wir sehr empfindliche Verstärker in der äußeren Beschaltung einer Ionisationskammer verwenden.
Wir werden nun zwei Anwendungen der Ionisationskammer kennen lernen. Als erstes dient sie zur Messung der Ionendosis. Aus Kapitel 4 wissen wir, dass die Einheit der Ionendosis (sei ein nun in SI oder traditionellem System) als erzeugte Ladung pro Kilogramm Luft definiert ist. Eine luftgefüllte Ionisationskammer ist das natürliche Instrument zur Messung solcher Größen.
Die zweite Anwendung ist die Messung der Radioaktivität. Die hier betrachtete Ionisationskammer besitzt einen so genannten reentranten Aufbau, (siehe Abbildung unten) so dass das radioaktive Material in einer Halterung in den Detektor gebracht werden kann, damit der größte Teil der emittierten Strahlung detektiert werden kann. Das Instrument wir häufig Dosiskalibrator genannt und das Tröpfeln des elektrischen Stroms, der durch Detektion von Strahlung in einem solchen entsteht wird häufig auf einer geeichten Skala so dargestellt, dass die Radioaktivität (zum Beispiel in MBq oder mCi) abgelesen werden kann. Die meisten gut geführten nuklearmedizinischen Abteilungen werden mindestens ein solches Gerät zur Verfügung haben, so dass die Radioaktivität vor der Anwendung am Patienten geprüft werden kann.

Die folgenden Abbildungen zeigen einige Ionisationskammern für verschiedene Anwendungen:
-
Ein Flächendetektor, wie er in der Radiographie verwendet wird
-
Einige Ionisationskammern mit unterschiedlichem Volumen zur Messung der Ionendosis.
-
Ein Dosimeter wie es in der Radiographie verwendet wird.
-
Ein in der Nuklearmedizin verwendeter Dosiskalibrator - der blaue Zylinder links enthält die reentrante Kammer
-
Ein Dosimeter wie es in der Radiographie verwendet wird.
-
Ein tragbarer Geigerzähler
Geigerzähler
Wir haben oben gesehen, dass Geiger-Zähler bei einer recht hohen Gleichspannung (typischerweise 300-400 Volt) betrieben werden und dass eine Elektronenlawine entsteht wenn es durch Absorption von Strahlung zu einer Ionisation im Gas kommt. Die von diesem Detektor erzeugten Spannungspulse sind relativ groß, da das Gas als ein effektiver Verstärker für die erzeugte Ladung wirkt.
Er hat vier wichtige Eigenschaften welche wir nun besprechen werden. Zunächst wird kein empfindlicher Verstärker (wie er im Falle einer Ionisationskammer notwendig war) für diesen Detektor benötigt, weil die Gasverstärkung wie erwähnt hoch genug ist.
Die zweite Eigenschaft ergibt sich aus der Tatsache, dass die Erzeugung von Elektronenlawinen gestoppt werden muss um den Detektor wiederherzustellen. Anders ausgedrückt kommt es zu einer vollständigen Durchbruch des des Gases (das gesamte Gas im Detektor wird leitend), was dazu führt, das der Detektor nicht mehr in der Lage ist das nächste eintreffende Teilchen zu detektieren. In diesem Falle haben wir im einen Moment einen Strahlungsdetektor und im nächsten Moment nicht mehr.
Man benötigt also ein Mittel um die Elektronenlawine zu stoppen - dieser Prozess wird auch als Löschen bezeichnet. Eine Möglichkeit besteht darin die Gleichspannung nach der Lawine zu senken. Häufiger verwendet man jedoch ein anderes Löschverfahren bei dem man dem Edelgas eine kleine Menge Löschgas hinzugibt. Zum Beispiel kann man Argon mit einer kleinen Menge Ethanol verwenden. Ethanoldampf besteht aus relativ großen Molekülen. Energie, welche ohne Löschgas, die Elektronenlawine aufrecht erhalten würde, wird von diesen Molekülen absorbiert. Diese großen Moleküle wirken also wie eine Bremse.
Unabhängig vom verwendeten Löschmechanismus, ist der Detektor für eine kurze Zeit nach der Absorption eines Teilchens/Photons nicht in der Lage weiter Ereignisse zu detektieren. Diese Zeit heißt Totzeit und dies ist die dritte Eigenschaft eines Detektors, mit der wir uns beschäftigen werden. Totzeiten sind relativ kurz, aber dennoch nicht vernachlässigbar, sie liegen typischerweise in der Größenordnung von 200 µs bis 400 µs. Dies führt dazu, dass die am Detektor abgelesene Zählrate kleiner ist als sie seien sollte. Die wahre Zählrate kann man, ohne hier ins Detail zu gehen, wie folgt berechnen:
Wobei T die wahre Zählrate, A die am Detektor abgelesene Zählrate und τ die Totzeit bezeichnet. Einige Instrumente führen diese Berechnung automatisch durch.
Die vierte bemerkenswerte Eigenschaft eines Detektors ist die Abhängigkeit seiner Leistung von der angelegten Gleichspannung. Der Geiger-Müller Bereich aus der obigen Abbildung ist in der Abbildung unten vergrößert dargestellt.

Man beachte, dass es ein Plateau gibt auf dem die Zählrate von der angelegten Gleichspannung unabhängig ist. Die meisten dieser Detektoren werden mit einer Gleichspannung in der Mitte dieses Plateaus betrieben. Es ist daher einsichtig, dass die Zählrate nicht von Schwankungen der Betriebspannung beeinflusst wird. Daher können relativ einfach aufgebaute Gleichspannungsquellen verwendet werden. Diese Eigenschaft führt zusammen mit der Tatsache, dass keine empfindlichen Verstärker benötigt werden zu in der Praxis recht preiswerten Strahlungsdetektoren.
Externe Links (englisch)
- Inside a smoke detector - about the ion chamber used in smoke detectors - from the How Stuff Works website.
- Ionisation Chambers - a brief description from the Triumf Safety Group.
- Radiation and Radioactivity - a self-paced lesson developed by the University of Michigan's Student Chapter of the Health Physics Society with a section on gas filled detectors.
- The Geiger Counter - a brief overview from the NASA Goddard Space Flight Center, USA.
Szintillationszähler
Einleitung
Dies ist das achte Kapitel des Wikibooks Physikalische Grundlagen der Nuklearmedizin
Die zweite Art von Strahlungsdetektoren, die wir diskutieren werden sind die Szintillationsdetektoren. Szintillationen sind kleine Lichtblitze, die in bestimmten Materialien entstehen, wenn sie Strahlung absorbieren. Diese Materialien werden Szintillatoren genannt.
Wenn wir eine radioaktive Quelle und einen Szintillator im Labor haben, können wir den Raum abdunkeln, den Szintillator nahe an die Quelle bringen und die Szintillationen mit bloßem Auge sehen. Die Blitze können grün oder blau sein oder abhängig von Szintillator eine andere Farbe haben. Wir können die Anzahl der erzeugten Blitze zählen, um so eine Abschätzung für die Radioaktivität der Quelle zu erhalten. Je mehr Blitze wir sehen, um so größer ist die vorhandene Radioaktivität.
Der Szintillationsdetektor war wahrscheinlich der erste Strahlungsdetektor, der entdeckt wurde. Man mag schon einmal die Geschichte von der Entdeckung der Röntgenstrahlung durch Wilhelm Röntgen im Jahre 1895 gehört haben. Er arbeitete an diesem Abend in seinem Labor in der deutschen Stadt Würzburg mit einem Gerät, welches einen Elektronenstrahl auf ein Target in einer evakuierten Glasröhre schoss. Während er mit den Gerät arbeitete, bemerkte er, dass einige Bariumplatinzyanürkristalle, welche zufällig in der Nähe standen, zu leuchten begannen. Er hatte also zufällig den Szintillationszähler entdeckt.
Obgleich man Szintillationen mit dem Auge sehen kann, haben wir heute um einiges besser entwickelte Methoden, um die Strahlung zu messen und zu zählen, indem wir irgendeine Art Photodetektor verwenden.
Wir werden in diesem Kapitel mehr über die Konstruktion und die Betriebsmodi dieser Art von Detektoren kennen lernen. Weiterhin werden wir sehen, wie sie benutzt werden können um nicht nur die Existenz von ionisierender Strahlung nachzuweisen sondern auch deren Energie zu messen.
Bevor wir dies jedoch tun, bemerken wir, dass Szintillatoren sehr häufig im Gebiet medizinischer Strahlungen verwendet werden. Zum Beispiel enthält eine Röntgenkassette einen Szintillator (meist als Verstärkerfolie bezeichnet) direkt vor dem photographischen Film.
Ein zweites Beispiel ist der Röntgenbildverstärker wie in der Röntgendurchleuchtung verwendet wird und ebenfalls Szintillatoren enthält. Szintillatoren werden auch in einigen Computertomographen und wie wir im nächsten Kapitel sehen werden, in der Gammakamera und im Positronenemissionstomographen verwendet. Ihre Anwendung ist nicht auf medizinisch diagnostische Strahlungen beschränkt. Szintillatoren werden auch in Fernsehern und Computermonitoren und zur Erzeugung von Licht in Leuchtstoffröhren verwendet, wobei wir nur die beiden häufigsten Anwendungen erwähnt haben. Welche anderen Anwendungen kennt man noch?
Somit sind Szintillatoren viel verbreiteter als man naiv vermutet, und man kann die hier dargestellten Informationen auch über das Studium der Nuklearmedizin hinaus verwenden.
Szintillierende Materialien
Einige szintillierende Materialien sind in der folgenden Tabelle angegeben. Thalliumaktiviertes Natriumjodid, NaI(Tl) ist kristallin, und wird zur Detektion von Gamma-Strahlen häufig verwendet. Wir werden es später genauer behandeln.
| Material | Form |
|---|---|
| NaI (Tl) | kristallin |
| CsI (Na) | kristallin |
| CaWO4 | kristallin |
| ZnS (Ag) | Pulver |
| p-Terphenyl in Toluol | flüssig |
| p-Terphenyl in Polystyrol | plastisch |
Ein anderes kristallines Material ist natriumaktiviertes Cäsiumiodid, CsI(Na), es wird häufig für die Detektion von Röntgenstrahlen verwendet, wie zum Beispiel in einem Röntgenbildverstärker. Ein weiteres ist Kalziumwolframat, CaWO4, welches häufig in Röntgenkassetten eingesetzt wurde, wenn es auch in modernen Kassetten durch andere Szintillatoren wie Lanthanoxybromid ersetzt wurde.
Man beachte, dass einige Szintillatormaterialien durch andere Elemente aktiviert werden. Das heißt, dass dem Grundmaterial eine kleine Menge des Aktivierungselements hinzugegeben wird. Der Begriff dotiert wird manchmal auch anstelle von aktiviert verwendet. Das aktivierende Element wird verwendet, um die Wellenlänge (Farbe) des vom Szintillator erzeugten Lichtes zu beeinflussen[1].
Silberaktiviertes Zinksulfid ist ein pulverförmiger Szintillator, und p-Terphenyl in Toluol ist ein flüssiger Szintillator, sein Vorteil besteht darin, dass er in engen Kontakt mit dem strahlenden Material gebracht werden kann. Haben wir zum Beispiel ein flüssiges radioaktives Material, so können wir es mit einem Flüssigszintillator mischen und so die Wahrscheinlichkeit einer Detektion erhöhen und erhalten so einen sehr empfindlichen Detektor.
Als letztes Beispiel erwähnen wir den Plastikszintillator p-Terphenyl in Polystyrol. Dieser kann, wie die meisten Plastikwerkstoffe, einfach in unterschiedliche Formen gebracht werden und ist daher nützlich, wenn eine bestimmte Form des Detektors verlangt wird.
- ↑ Die Dotierungsatome sind notwendig um Licht in einer von der Photokathode verarbeitbaren Wellenlänge (langes UV oder sichtbares blaues Licht) herzustellen. Im Bändermodell erzeugt einfallende Gammastrahlung freie Elektronen und freie Löcher. Rekombinieren Elektronen und Löcher, so entsteht ein UV-Photon (Energie größer als die Bandlücke), was nach kurzer Strecke wieder absorbiert wird. Es kann auch unvollständig absorbiert werden und ein gebundenes Elektron-Loch-Paar (Exziton) erzeugen. Dotierung erzeugt Zwischenniveaus in der Bandlücke. Diese können von Exzitonen, Elektronen, Löchern, und UV-Photonen angeregt werden. Zerfallen diese über die Zwischenniveaus, so entstehen Photonen mit Energien kleiner als die Bandlücke (langes UV oder sichtbares blau), diese werden nicht reabsorbiert, da ihre Energie nicht ausreicht um Elektronen, vom Valenzband ins Leitungsband zu heben und erreichen daher die Kathode.
Photomultiplier-Röhre
Ein mit einem Photomultiplier (PMT) gekoppelter Szintillator ist in der folgenden Abbildung dargestellt. Das Gerät hat im allgemeinen eine zylindrische Form und die Abbildung zeigt einen Querschnitt durch solch einen Zylinder:

Das Szintillatorkristall NaI(Tl) ist sehr empfindlich und dies ist einer der Gründe warum man ihn in einem Aluminiumgehäuse unterbringt. Die Innenwand des Gehäuses ist so konstruiert, dass einfallendes Licht in den Photomultiplier reflektiert wird.
Der Photomultiplier besteht aus einer Photokathode, einem fokussierenden Gitter, einer Reihe von Dynoden und einer Anode in einer evakuierten Glasröhre. Der Zweck der Photokathode besteht darin, die von Szintillatorkristall erzeugen Lichtblitze in Elektronen umzuwandeln. Das Gitter fokussiert diese Elektronen auf die erste Dynode und die Dynodenreihe dient dazu die Elektronen zu vervielfachen. Wir werden diesen Prozess unten im Detail betrachten. Schließlich werden die von der Dynodenreihe erzeugten Elektronen an der Anode gesammelt.
Die typische elektrische Beschaltung einer Photomultiplierröhre ist in der folgenden Abbildung dargestellt:

Sie besteht aus einer Hochspannungsquelle, einem Spannungsteiler und einem Lastwiderstand RL. Die Hochspannungsquelle erzeugt eine Gleichspannung Vdc, die bis zu 1000 Volt betragen kann. Sie wird an den aus gleichen Widerständen R aufgebauten Spannungsteiler angelegt. Der Zweck dieser Widerstandskette besteht darin die Spannung Vdc in gleiche Teilspannungen zu unterteilen, welche an die Dynoden angelegt werden. Somit steigt die Spannung von Dynode zu Dynode in gleichen Schritten an. Der Lastwiderstand RL wird benötigt um die Spannungspulse Vout zu erzeugen.
Die Arbeitsweise eines solchen Gerätes ist in der folgenden Abbildung dargestellt:

Die ionisierende Strahlung erzeugt Lichtblitze im Szintillatorkristall. Das Licht fällt auf die Photokathode und wird dort in Elektronen umgewandelt, welche durch ein Gitter auf die erste Dynode gelenkt werden.
Dynoden bestehen aus bestimmten Legierungen welche Elektronen emittieren, wenn ihre Oberfläche von Elektronen getroffen wird. Ihr Vorteil liegt darin, dass mehr Elektronen emittiert als absorbiert werden. Eine Dynode in einem Photomultiplier emittiert typischerweise zwischen zwei und fünf Elektronen pro einfallendem Elektron.
Wenn also ein Elektron von der Photokathode auf die erste Dynode trifft, so werden zwei bis fünf Elektronen emittiert (in der Abbildung oben sind 3 eingezeichnet) und auf die zweite Dynode geführt. Der Elektronenvervielfältigungsprozess wiederholt sich an der zweiten Dynode, so dass wir dort 9 Elektronen erhalten, die zur dritten Dynode fliegen. Es entsteht eine Elektronenlawine, die eine erhebliche Anzahl von Elektronen erzeugt und schließlich auf die Anode am Ende der Dynodenkette trifft.
Diese Elektronen fließen durch den Lastwiderstand, RL und führen zu einem elektrischen Strom, der nach dem Ohmschen Gesetz einen Spannungspuls Vout hervorruft, der von elektronischen Schaltkreisen, die wir später beschreiben werden vermessen wird.
Einige Photos von Geräten, die Szintillationszähler verwenden sind unten gezeigt:
-
Eine Röntgenkassette, wie sie in der Radiologie verwendet wird
-
Ein NaI Kristall, der mit einem Photomultiplier verbunden ist.
-
Einige identische Photomultiplierröhren von einer Gammakamera.
-
Ein Einkanalanalysator
-
Ein Einkanalanalysator mit einem Kristall-Photomultiplier-Aufbau.
-
Ein Ringdetektor.
Die wichtigste Eigenschaft eines Szintillationszählers ist, dass die Ausgangsspannung Vout zu der von der Strahlung im Kristall deponierten Energie direkt proportional ist. Wir werden gleich sehen, dass dies eine sehr nützlich Eigenschaft ist. Bevor wir dies jedoch tun wollen wir die Arbeitsweise dieser Geräte kurz quantitativ untersuchen.
Mathematisches Modell
Nun werden wir ein einfaches mathematisches Modell vorstellen, welches uns helfen wird ein besseres Verständnis für die Arbeitsweise eines Szintillationsdetektors zu entwickeln. Wir werden dies erreichen indem wir die Vorgänge im Szintillator, der Photokathode und den Dynoden quantifizieren.
Wir werden die folgenden Symbole verwenden um die einzelnen Stufen des Detektionsprozesses zu beschreiben:
- m: Anzahl der im Kristall erzeugten Photonen (Licht)
- k: Optische Durchlasseffizienz des Kristalls, die Effizienz mit der Licht durch den Kristall hindurch tritt.
- l: Quantenausbeute der Photokathode, die Effizienz mit der die Photokathode einfallende Lichtteilchen(Photonen) in Elektronen umwandelt
- n: Anzahl der Dynoden
- R: Multiplikationsfaktor der Dynoden, die Anzahl der von der Dynode pro absorbiertem Elektron emittierten Sekundärelektronen.
Somit ergibt sich für die an der Anode eingesammelte Ladung nach folgender Gleichung:
wobei e für die Elektronenladung steht. Nehmen wir zu Beispiel an, ein 100 keV Gammastrahl werde von einem Kristall absorbiert. Die Anzahl der erzeugten Lichtphotonen, liegt für einen typischen Szintillatorkristall bei etwa 1000. Ein typischer Kristall hat eine optische Effizienz k von 0.5 - anders ausgedrückt 50% des erzeugen Lichts erreicht die Photokathode, welche eine Effizienz von etwa 0.15 hat. Ein typischer Photomultiplier hat 10 Dynoden. Weiterhin nehmen wir ihren Multiplikationsfaktor mit 4.5 an. Somit berechnen wir:
Diese Ladungsmenge ist sehr klein. Obwohl wir einen so aufwendigen Photodetektor wie einen Photomultiplier verwenden, erreichen wir nur eine recht kleines elektrisches Signal.
Wir benötigen daher einen empfindlichen Verstärker um das Signal zu verstärken. Dieser Verstärkertyp wird im allgemeinen Vorverstärker genannt und wir werden ihm später wieder begegnen.
Ausgangsspannung
Oben haben wir bereits erwähnt, dass die über dem Widerstand RL abfallende Spannung, der von der Strahlung im Szintillatorkristall deponierten Energie proportional ist. Fragen wir uns nun, wie Strahlung Energie im Kristall hinterlässt.
Beschäftigen wir uns mit zunächst mit der Detektion von Gammastrahlen durch den Kristall. In Kapitel 5 sahen wir, dass zwei wesentliche Mechanismen zur Schwächung von Gammastrahlung in Materie beitragen - der Photoelektrische Effekt und der Compton-Effekt. Wir erinnern uns, dass der Photoeffekt zur vollständigen Absorption der Energie eines Gammastrahls führt, während beim Compton-Effekt nur ein Teil der Energie absorbiert wird. Da die Ausgangsspannung des Szintillationsdetektors proportional der vom Gammastrahl im Detektor deponierten Energie ist, kann man vernünftigerweise annehmen, dass der Photoelektrische Effekt im Kristall diskrete und relativ große Spannungspulse am Ausgang erzeugen wird und dass der Compton-Effekt zu kleinen Spannungspulsen am Ausgang führen wird.
Üblicherweise veranschaulicht man sich diese Situation indem man die Zählrate gegenüber der Höhe der Spannungspulse am Ausgang aufträgt. Ein solcher Graph ist in der folgenden Abbildung gezeigt:

Der Graph zeigt das Ergebnis für ein monoenergetisches gammastrahlendes Radioisotop, wie zu Beispiel 99mTc - welches, wie wir bereits wissen, nur Gammastrahlung einer Energie von 140 keV abstrahlt.
Bevor wir uns dieses im Detail anschauen, erinnern wir uns, dass die am Detektor gemessene Ausgangsspannung der von der Strahlung im Kristall deponierten Energie proportional ist. Die horizontale Achse kann daher sowohl zur Darstellung der Ausgangsspannung als auch der Energie der Gammastrahlung benutzt werden. Beide Größen sind in der Achsenbeschriftung der Graphik angegeben um diesen Zusammenhang zu verdeutlichen. Weiterhin weisen wir darauf hin, dass diese Art von Diagrammen auch als Gamma-Strahl Energiespektrum oder kurz Gammaspektrum bezeichnet wird.
Die obige Abbildung enthält zwei wichtige Bereiche. Der eine heißt Photopeak und der andere heißt Comptonkontinuum. Der Photopeak wird durch die Absorption von Gammastrahlen beim photoelektrischen Effekt verursacht - wir erinnern uns, dass wir uns in diesem Beispiel mit einem monoenergetischen Strahler zu tun haben. Wir sehen genau einen Peak. Die Position auf der x-Achse gibt uns Auskunft darüber, welche Energie die abgestrahlte Gammastrahlung hat. In unserem Beispiel also 140 keV. Wenn unser Radioisotop Gammastrahlung bei zwei unterschiedlichen Energien emittieren würde, so hätten wir zwei Photopeaks und so weiter.
Man sieht, dass der Photopeak eine statistische Streuung (die Breite des Peaks) aufweist. Diese sagt uns wie gut unser Detektor ist, wir werden jedoch hier nicht in die Details einsteigen sondern erwähnen lediglich, dass die Breite des Peaks ein Merkmal für die Qualität unseres Detektors ist. Je höher die Qualität (und je höher der Preis!) des Detektors, je kleiner wird die statistische Breite des Peaks ausfallen.
Der zweite Bestandteil des Spektrums ist das Comptonkontinuum. Es stellt einen Bereich von Ausgangsspannungen dar, in dem alle Spannungen kleiner als der Photopeak sind. Es zeigt daher die unvollständige Absorption von Gammastrahlen im Kristall an. In einigen Compton-Ereignissen geht ein großer Teil der Energie des Gammastrahls auf das Elektron über, was zu relativ großen Spannungspulsen führt. In anderen Compton-Ereignissen streift der Gammastrahl das Elektron nur leicht und überträgt ihm nur eine sehr geringe Energiemenge und daher entsteht nur ein sehr kleiner Spannungspuls. Zwischen diesen beiden Extremen gibt es ein Kontinuum an möglichen Streuereignissen, die ein Intervall von Energien abdecken und daher ein Intervall an Spannungspulshöhen. Dieses 'Kontinuum' manifestiert sich daher im Gammaenergiespektrum.
Es ist wichtig zu beachten, dass in der Abbildung ein, der besseren Verständlichkeit wegen, vereinfachtes Spektrum gezeigt ist und realistische Spektren ein wenig komplizierter aussehen. Man betrachte zum Beispiel die folgende Abbildung:

Man wird feststellen, dass man leicht ein Verständnis realer Spektren entwickeln kann, wenn man sich unser vereinfachtes Bild vor Augen hält.
Es ist auch wichtig zu erkennen, dass dieser Detektortyp im Vergleich zu gasgefüllten Detektoren zusätzliche Information erzeugt. Kurz gesagt kann ein gasgefüllter Detektor aussagen ob Strahlung vorhanden ist und wie viel Strahlung vorhanden ist. Szintillationszähler können uns auch Informationen über die Energie der gemessenen Strahlung geben. Diese Zusatzinformation kann in einer Reihe von Anwendungen, so wie zum Beispiel der Bestimmung unbekannter Radioisotope oder der Erzeugung diagnostischer Abbildungen, in der Nuklearmedizin verwendet werden. Bleiben wir jedoch einen Augenblick bei den fundamentalen Eigenschaften von Szintillationszählern und ihrer Arbeitsweise.
Der Photopeak des Gammaspektrums ist von allgemeinen Interesse für die Nuklearmedizin. Der Peak ist eine charakteristische Eigenschaft des verwendeten Radioisotops und kann durch eine so genannte Pulshöhenanalyse vom Comptonkontinuum getrennt werden.
Pulshöhenanalyse
Diese elektronische Methode erlaubt es ein Spektrum aufzunehmen, wozu zwei unterschiedliche Schaltkreise benötigt werden. Der erste wird als Lower Level Diskriminator (LLD) bezeichnet und lässt nur Spannungspulse, die größer als ein eingestellter Schwellwert sind, durch. Der zweite heißt Upper Level Diskriminator (ULD) und lässt (wie man sich denken kann) nur Spannungspulse durch, die kleiner als sein Schwellwert sind. Typischerweise werden heute Schaltkreise verwendet, die sowohl einen ULD als auch einen LLD besitzen. Sie werden schlicht als Diskriminator bezeichnet.
Verwendet ein solches Gerät oder einen LLD und einen ULD zusammen, so erhält man ein Fenster einstellbarer Breite welches man beliebig auf dem Spektrum platzieren kann. Wenn wir zum Beispiel nur an der Information aus dem Photopeak unseres vereinfachten Spektrums interessiert sind, so würde wir die Diskriminatoren wie in der folgenden Abbildung eingezeichnet einstellen:

Als letzten Punkt erwähnen wir hier noch, dass Szintillationszähler häufig verwendet werden um Informationen über die Energieverteilung der von einer radioaktiven Quelle emittierten Strahlung zu erhalten. Ein solche Aufbau wird häufig als Szintillationsspektrometer bezeichnet.
Szintillationsspektrometer
Es gibt zwei wesentliche Klassen von Szintillationsspektrometern. Der relativ simple Einkanalanalysator und der aufwendigere Mehrkanalanalysator.
In der bisherigen Diskussion haben wir nur den Einkanalanalysator beschrieben. Sein Blockdiagramm ist in der folgenden Abbildung gezeigt.

Es besteht aus einem Szintillatorkristall verbunden mit einer Photomultiplierröhre, die mit einer Hochspannung betrieben wird. Die Ausgangsspannung wird, wie wir bereits erwähnt haben, zunächst von einem empfindlichen Vorverstärker verstärkt und dann von einem weiteren Verstärker verstärkt und geformt.
Die erzeugten Spannungspulse sind dann geeignet um in einem Pulshöhenanalysator weiterverarbeitet zu werden. Dessen Ausgangssignale können in eine Scaler (Zähler) und ein Ratemeter geleitet werden um Informationen über den Teil des Spektrums, der im eingestellten Bereich des Pulshöhenanalysators liegt, darzustellen. Ein Ratemeter ist ein Anzeigegerät und misst, ähnlich wie ein Tachometer beim Auto, die Anzahl der eingehenden Pulse pro Zeiteinheit. Im Gegensatz dazu zählt ein Scaler die Anzahl der in einem definierten Zeitintervall eingehenden Spannungspulse und stellt diese meist auf einer Digitalanzeige dar.
Wir können uns die Funktionsweise dieser Geräte klarmachen, indem wir betrachten, wie sie verwendet werden können um ein Gammaenergiespektrum aufzunehmen. Wir müssen hierzu einen LLD und einen ULD verwenden um ein enges Fenster zu erzeugen und es so platzieren, dass die kleinsten von Detektor erzeugten Spannungspulse bis zum Scaler und zum Ratemeter durchkommen. Anders ausgedrückt platzieren wir ein enges Fenster ganz links im Spektrum und erhalten so Informationen über die Wechselwirkungen zwischen dem Kristall und der Strahlung bei denen am wenigsten Energie übertragen wurde. Dann passen wir die Einstellungen des LLD und ULD so an, dass wir Informationen über die Wechselwirkungen Fenster mit nächst höherem Energieübertrag aufnehmen können. Wir verfahren auf diese Art und Weise weiter, so dass wir das gesamte Spektrum abfahren und Messwerte für jedes Fenster aufnehmen.
Eine etwas komplexere Detektorschaltung ist in der folgenden Abbildung gezeigt:

Sie ähnelt sehr stark der vorhergehenden Abbildung. Es sind lediglich Pulshöhenanalysator, Zähler und Ratemeter durch einen Vielkanalanalysator und einen Computer ersetzt. Der Vielkanalanalysator (Multi Channel Analyser MCA) ist ein Bauelement, in dem viele Fenster gleichzeitig gesetzt werden können, so dass man das komplette Spektrum in einem Durchgang aufnehmen kann. Ein MCA mag zu Beispiel aus 1024 einzelnen Fenstern bestehen, und der Computer kann ein PC sein, welcher Informationen aus allen Fenstern gleichzeitig aufnehmen und das Ergebnis als Energiespektrum anzeigen kann. Auf dem Computer ist im allgemeinen eine Software installiert mit der das Spektrum in verschiedener Weise bearbeitet werden kann. Das oben gezeigte 137Cs Spektrum wurde in der Tat auf diesem Wege erstellt.
Externe Links (englisch)
- Radiation and Radioactivity - a self-paced lesson developed by the University of Michigan's Student Chapter of the Health Physics Society, with a section on sodium iodide detectors.
Nuklearmedizinische Abbildungssysteme
Einleitung
Dies ist das neunte Kapitel des Wikibooks Physikalische Grundlagen der Nuklearmedizin
In diesem Wikibook haben wir die Themen Radioaktivität, Wechselwirkung von Gammastrahlung mit Materie und Nachweis von Strahlung behandelt. Der Hauptgrund warum wir diesem Weg gefolgt sind war die Vorbereitung auf das Thema dieses Kapitels: Nuklearmedizinische Abbildungssysteme. Diese Geräte erzeugen Bilder der Verteilung eines radioaktiven Präparates welches am Patienten angewandt wurde.
Die Radioaktivität wird dem Patienten im allgemeinen in Form eines Radiopharmakons (auch der Begriff Radiotracer wird verwendet) appliziert. Diese folgt gewissen physiologischen Wegen und sammelt sich für kurze Zeit in bestimmten Teilen des Körpers an. Ein gutes Beispiel ist 99mTc-Zinn Kolloid welches sich nach intravenöser Injektion bevorzugt in der Leber des Patienten ansammelt. Die Substanz emittiert Gammastrahlen während sie sich in der Leber befindet so dass wir ein Bild ihrer Verteilung mit Hilfe nuklearmedizinischer Abbildungssysteme erzeugen können. Dieses Bild kann uns sagen, ob die Leber normal oder abnormal arbeitet oder ob Teile der Leber von irgendeiner Krankheit betroffen sind.
Unterschiedliche Radiopharmaka werden benutzt um Bilder von fast jedem beliebigen Körperteil zu erzeugen.
| Körperteil | Beispiel für Radiotracer |
|---|---|
| Hirn | 99mTc-HMPAO |
| Schilddrüse | Na99mTcO4 |
| Lunge (Atmung) | 133Xe Gas |
| Lunge (Durchblutung) | 99mTc-MAA |
| Leber | 99mTc-Zinn Kolloid |
| Milz | 99mTc-Damaged Red Blood Cells |
| Bauchspeicheldrüse | 75Se-Selenomethionine |
| Nieren | 99mTc-DMSA |
Man beachte, dass die bei diesen bildgebenden Verfahren erzeugten Informationen Auskunft über die physiologische Funktion eines Organs geben, während man in Gegensatz dazu bei Röntgenuntersuchungen hauptsächlich anatomische Information erhält. Die Nuklearmedizin stellt daher Krankheiten aus einer anderen Perspektive dar und erzeugt zusätzliche Informationen, die aus Röntgenbildern nicht erhalten werden können. Wir werden uns hier hauptsächlich mit bildgebenden Verfahren beschäftigen.
Frühe Formen bildgebender Systeme in diesem Gebiet bestanden aus einem Strahlungsdetektor (zum Beispiel einem Szintillationszähler) der langsam über einen Bereich eines Patienten gefahren wurde um die Intensität der Strahlung, die von einzelnen Punkten in diesem Bereich emittiert wurde, zu messen. Ein solches Gerät wurde Scanner genannt (siehe auch entsprechenden Abschnitt im Artikel über die Gammakamera). Solche bildgebenden Systeme wurden seit etwa 1970 durch aufwendigere Geräte, welche erheblich bessere Bilder in kürzerer Zeit erzeugen, ersetzt. Das am weitesten verbreitete, dieser modernen Geräte, ist die Gamma Kamera. Wir werden nun ihren Aufbau und ihre Arbeitsweise kennen lernen.
Gammakamera
Der grundlegende Aufbau der heute am weitesten verbreiteten Gammakamera wurde von dem amerikanischen Physiker Hal Anger entwickelt. Daher wird sie auch manchmal als Anger Kamera bezeichnet. Sie besteht aus einem großen NaI(Tl) Szintillatorkristall, welcher von einer großen Anzahl von Photomultiplierröhren beobachtet wird. Ein Blockdiagramm der wesentlichen Bestandteile einer Gammakamera ist in der folgenden Abbildung gezeigt.

Der Kristall und die Photomultiplierröhren sind einem zylindrisch geformten Gehäuse - dem Kamerakopf - untergebracht und ein Querschnitt dieses Aufbaus ist in der Abbildung gezeigt. Der Kristall hat einen Durchmesser von etwa 25 cm bis etwa 40 cm und ist etwa 1 cm dick. Der Durchmesser hängt vom Anwendungszweck des Gerätes ab. Zum Beispiel mag ein Kristalldurchmesser von 25 cm in einer Kamera für kardiologische Anwendungen ausreichend sein, wobei man zur Aufnahme der Lunge einen größeren 40 cm Kristall benötigt. Die Dicke des Kristalls ist so gewählt, dass sie eine gute Detektion von Gammastrahlung eine Energie von 140 keV, wie sie von 99mTc emittiert wird, ermöglicht. 99mTc ist das heute am weitesten verwendete Radioisotop.
Szintillationen werden im Kristall erzeugt und von einer großen Anzahl an Photomultipliern detektiert, die in einen zweidimensionalen Raster angeordnet sind. Üblicherweise besitzen moderne Gammakameras etwa 37 bis 91 Photomultiplierröhren. Die von den Photomultipliern erzeugten Ausgangsspannungen werden an eine Positionsschaltung weitergeleitet welche die vier Ausgangssignale ±X und ±Y erzeugt. Diese Signale enthalten Informationen darüber an welcher Stelle im Kristall die Szintillation erzeugt wurde. Beim allereinfachsten Aufbau einer Gammakamera werden diese Signale auf ein Oszilloskop gegeben. Wir werden die Funktionsweise eines Oszilloskops unten genauer erläutern.
Bevor wir dies jedoch tun bemerken wir, dass die Positionssignale auch Informationen über die Intensität der Szintillationen enthalten. Die Intensitätsinformation kann aus den Positionssignalen erhalten werden indem sie auf eine Summenschaltung (in der Zeichnung mit bezeichnet) gegeben werden, welche die vier Positionssignale aufaddiert und einen Spannungspuls erzeugt, der die Intensität der Szintillation darstellt. Dieser Spannungspuls wird im allgemeinen Z-Puls (sprich sieh bei Amerikanischer Betonung) genannt. Er wird über eine Pulshöhenanalyse als Unblank Signal auf das Oszilloskop gegeben und sorgt so dafür, dass zu kleine Szintillationen nicht auf dem Oszilloskop dargestellt werden.
So bekommen wir schließlich vier Positionssignale und ein Unblank Signal die wir auf ein Oszilloskop geben. Wir wollen kurz die Arbeitsweise eines Oszilloskops darstellen bevor wir fortfahren. Der Kernbestandteil eines Kathodenstrahloszillographen ist eine evakuierte Glasröhre, mit einer Elektronenkanone am einen und einem phosphorbeschichteten Schirm am anderen Ende. Die Elektronenkanone erzeugt einen Elektronenstrahl, welcher auf den Schirm geleitet wird und die Punkte in denen er auf den Schirm trifft zum leuchten anregt. Die Richtung des Elektronenstrahls kann durch vertikale und horizontale Ablenkplatten, an die entsprechende Spannungen angelegt werden, so beeinflusst werden, dass der Elektronenstrahl auf jeden beliebigen Punkt auf dem Schirm gerichtet werden kann. Im Normalbetrieb eines Oszillographen bleibt der Elektronenstrahl ständig eingeschaltet. Bei einem Oszilloskop an einer Gammakamera jedoch ist der Strahl normalerweise ausgeschaltet (im englischen bezeichnet man diesen Zustand auch als blanked, das Einschalten des Strahls somit als unblank).
Wenn der Unblankpuls vom Pulshöhenanalysator generiert wird, wird der Strahl des Oszilloskops für eine kurze Zeit eingeschaltet so dass ein Lichtblitz auf dem Schirm entsteht. Anders ausgedrückt wird der Spannungspuls des Pulshöhenanalysators verwendet um den Elektronenstrahl des Oszilloskops auf unblank zu schalten. Wo entsteht nun der Lichtblitz auf dem Oszillographenschirm? Die Position der Blitzes ist durch die, von der Positionselektronik erzeugten, Signale ±X und ±Y vorgegeben. Diese Signale werden, wie man leicht errät, an die Ablenkplatten des Oszillographen angelegt, so dass der eingeschaltete Elektronenstrahl den Schirm an einem Punkt trifft, dessen Koordinaten proportional zu den Koordinaten der ursprünglichen Szintillation im NaI(Tl) sind.
Die Gammakamera kann daher als eine aufwendige Komposition von Schaltkreisen verstanden werden, welche die Position eine Lichtblitzes im Szintillatorkristall in einen Lichtblitz an einem entsprechenden Punkt auf dem Schirm eines Oszilloskops umgewandelt. Die Verwendung eines Pulshöhenanalysators in der Schaltung erlaubt uns nur solche Szintillationen zu verarbeiten, die durch den Photoeffekt im Kristall hervorgerufen worden sind. Dies wird erreicht indem alle Spannungspulse, die nicht zum Photopeak des Gammaenergiespektrums gehören, blockiert werden.
Wir fassen zusammen was wir bislang verstanden haben bevor wir weitermachen. Ein Radiopharmakon wird dem Patienten verabreicht und es sammelt sich im zu untersuchenden Organ an. Gammastrahlen werden vom Organ in alle Richtungen emittiert, die zur die Gammakamera fallenden Strahlen dringen in den Kristall ein und erzeugen Szintillationen (man beachte, dass sich vor der Kamera ein Gerät namens Kollimator befindet, welches wir gleich erläutern werden). Die Szintillationen werden von einer Gruppe von flächenhaft angeordneten Photomultipliern, deren Ausgänge an eine Positionselektronik angeschlossen sind, detektiert. Die Positionselektronik erzeugt vier Ausgangssignale, die die Position der Szintillation im Kristall beschreiben und auf die Ablenkplatten eines Oszilloskops gegeben werden. Weiterhin werden sie auf eine Summenschaltung gegeben, dessen Ausgang (der so genannte Z-Puls) auf einen Pulshöhenanalysator gegeben wird, dessen Ausgang wiederum verwendet wird um den Elektronenstrahl im Oszilloskop einzuschalten (also als unblank-Puls benutzt wird). Somit erscheint ein Lichtblitz auf dem Schirm des Oszilloskops dessen Position, den Punkt an dem die Szintillation im NaI(Tl) Kristall aufgetreten ist anzeigt. Daher entsteht ein Bild der Verteilung des Radiopharmakons im Organ auf dem Schirm des Oszilloskops, sobald die vom Organ emittierten Gammastrahlen im Kristall detektiert werden.
Was wir oben beschrieben haben ist ein recht altertümlicher Aufbau einer Gammakamera. Moderne Konstruktionen sind um einiges aufwendiger, jedoch sind sie vom grundsätzlichen Aufbau her dem beschriebenen System sehr ähnlich. Ein Gebiet auf dem die Konstruktionen stark verbessert werden konnten ist die Bilderzeugung und Anzeige. Der einfachste Ansatz besteht darin den Schirm des Oszilloskops mit großer Belichtungszeit zu fotografieren und so die Integration zu ermöglichen und ein Bild auf einem Fotografischen Film zu erzeugen. Eine Entwicklungsstufe weiter verwendete man eine Speicherröhre, die es ermöglichte einen einmal erzeugten Lichtblitz für eine angemessene Zeit auf dem Schirm zu halten.
Der heutige Technik besteht darin, die Positionssignale im Speicher eines Computers abzulegen. Die Speicherinhalte können dann auf einem Computermonitor angezeigt und auf verschiedene Art und Weise manipuliert werden (engl. Image Processing). Zum Beispiel können verschiedene Farben verwendet werden um unterschiedliche Konzentrationen des Radiopharmakons im Organ darzustellen.
Die Verwendung dieser digitalen Bildbearbeitung ist nun in der Nuklearmedizin weit verbreitet und kann verwendet werden um die Datenaufnahme zu überwachen und Bilder oder Bildreihen darzustellen und zu analysieren, Bilder mit Namen und Befundtexten zu versehen, sie dauerhaft zu speichern und sie von Computer zu Computer über ein Netzwerk zu übertragen.
Einige Photos von Gammakameras sind unten gezeigt:
-
Gammakamera mit einem Kopf
-
Eine weitere Gammakamera mit einem Kopf
-
Der NaI Kristall einer Gammakamera.
-
Kathodenstrahloszilloskop einer Gammakamera.
-
Bildverarbeitungssystem einer Gammakamera.
-
Eine Gammakamera mit zwei Köpfen.
-
Eine weitere Ansicht der Gammakamera mit zwei Köpfen.
-
Der Bildbearbeitungsarbeitsplatz einer Gammakamera mit zwei Köpfen.
Wir werden unsere Beschreibung der Gammakamera nun fortsetzen indem wir uns den Verwendungszweck und Aufbau eines Kollimators anschauen.
Kollimation
Ein Kollimator ist ein Gerät, welches an der Vorderseite des Kopfes einer Gammakamera montiert wird. Es funktioniert ähnlich wie eine Linse in einer photographischen Kamera, jedoch ist diese Analogie nicht völlig korrekt, da es ziemlich schwierig ist Gammastrahlen zu fokussieren. Nichtsdestoweniger blockiert er, in seiner einfachsten Ausführung, alle Gammastrahlen die auf den Kristall fallen, mit Ausnahme von solchen deren Einfallswinkel zum Kristall in einem definierten Bereich liegen.

Die Abbildung zeigt eine vergrößerte Ansicht eines mit einem Kristall verbundenen Parallellochkollimators. Der Kollimator besteht einfach aus einer Bleiplatte, in die viele kleine Löchern gebohrt worden sind.
Man beachte jedoch, dass Gammastrahlen, die unter einem nicht vernachlässigbaren Winkel auf den Kristall einfallen, vom Blei absorbiert werden, und nur die Strahlen, die parallel zu den Löchern verlaufen den Kristall erreichen und dort Szintillationen auslösen. Ohne Kollimator würden die schräg einfallenden Gammastrahlen das von der Gammakamera erzeugte Bild verwischen. Anders ausgedrückt wären die erhaltenen Bilder weniger scharf.
Die meisten Gammakameras haben eine Vielzahl an Kollimatoren die entsprechend den Anforderungen der Untersuchung montiert werden können. Der grundsätzliche Aufbau ist immer gleich, sie unterscheiden sich nur bezüglich des Durchmessers eines jeden Lochs, der Länge der Löcher, und der Dicke der Bleischicht zwischen den Löchern (häufig als Septendicke bezeichnet).
Die Wahl des geeigneten Kollimators hängt davon ab wie viel Strahlung im Kristall absorbiert werden soll (was die Sensitivität der Gammakamera beeinflusst) und wie scharf die erzeugten Bilder seinen sollen (also der räumlichen Auflösung). Unglücklicherweise stehen diese beiden Faktoren in einer inversen Beziehung zu einander. Ein Kollimator, der Bilder mit guter räumlicher Auflösung erzeugt, führt im allgemeinen zu einem Instrument mit geringer Sensitivität für einfallende Gammastrahlung.
Auch andere Kollimatorkonstruktionen als der Parallellochkollimator sind in Benutzung. Zum Beispiel erzeugen Kollimatoren mit divergierenden Löchern ein verkleinertes Bild und solche mit konvergierenden Löchern ein vergrößertes. Auch Pinholekollimatoren erzeugen vergrößerte Bilder. Der Pinholekollimator ist in der folgenden Abbildung dargestellt.

Er ist typischerweise ein Kegelförmiges Gerät, dessen Wände aus Blei bestehen. Ein Querschnitt dieses Kegels ist in der obigen Abbildung gezeigt. Er funktioniert ähnlich wie eine Lochkamera und erzeugt ein gespiegeltes Abbild des Objekts - ein Bild ist in der Abbildung eingezeichnet um die Spiegelung zu verdeutlichen. Dieser Kollimator hat sich bei der Aufnahme von kleinen Objekten wie der Schilddrüse als nützlich erwiesen.
Einige nuklearmedizinische Abbildungen sind im folgenden gezeigt:
-
Ein SPECT Schnitt der Verteilung von 99m-Tc Ceretec im Hirn eines Patienten.
-
Ein SPECT Schnitt der Verteilung des Radiopharmakons in der Leber eines Patienten.
-
Vier planare Aufnahmen des Skelettes eines Patienten. (Im Uhrzeigersinn von oben links: Kopf, Brust, Knie, Becken).
-
Ein PET Schnitt durch das Hirn eines Patienten, eine die ungefähre Hautoberfläche ist als Konturlinie eingezeichnet.
-
Aufnahme der Schilddrüse, die Punkte innerhalb der eingezeichneten Konturlinie wurden für die Berechnung Radioisotopenaufnahme des Organs (Uptake) verwendet.
-
Eine Reihe von Aufnahmen der Niere (Renogrammen), wobei die rechte Niere von einem Stein blockiert ist.
-
Ausgewählte Aufnahmen einer Reihe von Nierenaufnahmen.
-
Graphische Darstellung des zeitlichen Verlaufs der Aktivität in zwei Nieren (Renogramm).
-
Ein SPECT Schnitt durch ein Herz
-
Rückseitige Aufnahme der Lunge, Atmung (links) und Durchblutung (rechts).
Emissionstomographie
Die bisher behandelten bildgebenden Verfahren werden unter dem Begriff Planare Abbildung zusammengefasst. Sie erzeugen ein zweidimensionales Bild eines dreidimensionalen Objekts. Daher enthält das Bild keine Tiefeninformation und einige Details können einander überlagern oder sich gegenseitig (teilweise oder vollständig) verdecken. Wir bemerken, dass dieses Problem auch bei herkömmlichen Röntgenuntersuchungen auftritt.
Das übliche Verfahren zur Lösung dieses Problems, besteht darin mindestens zwei Aufnahmen der Patienten aus unterschiedlichen Blickwinkeln anzufertigen. So zum Beispiel von der Seite als auch von vorne. Bei der Röntgenuntersuchung der Brust macht man meist eine posterio-anteriore (PA) (von hinten nach vorne) und eine laterale (seitliche) Aufnahme. Bei einer Aufnahme der Leber in der Nuklearmedizin, bildet man sowohl antero-posterior (AP) (von vorne nach hinten) als auch lateral (seitlich) ab.
Die Beschränkungen der planaren Röntgenaufnahme wurden durch die Entwicklung der CT um 1970 aufgehoben. CT (früher auch CAT aus dem englischen Computerized Axial Tomography / Computer Assisted Tomography) steht kurz für Computertomographie man spricht auch von CT Scans, (der Begriff Tomographie stammt vom griechischen Wort tomos, welches Scheibe bedeutet. Unabhängig von ihrer genauen Bezeichnung erlaubt diese Technik die Erstellung von Schnittbildern des Körpers, die mit Hilfe von Computern erzeugt werden. Im wesentlichen erreicht ein CT dies durch Röntgenaufnahmen des Patienten aus vielen unterschiedlichen Winkeln. Die erzeugten Schnittbilder zeigen die dritte Dimensionen, die bei planaren Aufnahmen fehlt und lösen so das Problem der Überlagerung von Details. Weiterhin können die einzelnen Schnittbilder im Computer aneinander gefügt werden und ergeben so ein dreidimensionales Bild. Mit Sicherheit ist das CT ein sehr leistungsfähiges bildgebendes Verfahren und der klassischen planaren Abbildung weit überlegen.
Das entsprechende nuklearmedizinische bildgebende Verfahren heißt Emissionstomographie. Wir werden zwei verschiedene Klassen dieser Technologie kennen lernen.
(a) Single Photon Emission Computed Tomography (SPECT)[1]
Diese SPECT Technik verwendet eine Gammakamera um Bilder aus einer Reihe von Winkeln um den Patienten aufzunehmen. Diese Bilder werden dann mit eine digitalen Bildverarbeitungsverfahren namens Bildrekonstruktion bearbeitet um Schnittbilder durch den Patienten zu erhalten.
Die gefilterte Rückprojektion als Rekonstruktionsprozess ist unten dargestellt. Nehmen wir der Einfachheit halber an, dass der Schnitt durch den Patienten tatsächlich nur aus einem 2x2 Voxel Feld besteht, wobei die Radioaktivität in den Voxeln entsprechend A1...A4 sei:
Die erste Projektion P1, ist von rechts, die zweite Projektion P2 von rechts unten, usw. aufgenommen. Als erstes werden die Projektionen wie unten gezeigt aufaddiert.
die Summierten (bzw. überlagerten) Projektionen werden nun renormiert um die Radioaktivität in jedem Voxel zu erhalten.
Ein anderes Bildrekonstruktionsverfahren heißt iterative Rekonstruktion. Diese Technik bei der sich die Werte sukzessive dem Ergebnis annähern ist im folgenden dargestellt:
Die erste Schätzung der Bildmatrix entsteht in dem man die erste Projektion P1, gleichmäßig auf die anfänglich leeren Voxel der Matrix verteilt. Die zweite Projektion, P2, wird mit einer Schätzung der Projektion in der selben Richtung die aus der ersten Schätzung der Bildmatrix ermittelt wird verglichen. Die Differenz von tatsächlicher und aus der Projektion errechneter Bildmatrix wird der ersten der Bildmatrix hinzugefügt und ergibt so die zweite Schätzung der Bildmatrix. Dieser Prozess wird für jeder Projektionsrichtung einmal durchgeführt.
Die Gammakamera wird typischerweise um den Patienten rotiert um Bilder aus unterschiedlichen Winkeln aufzunehmen. Einige Gammakameras wurden speziell für SPECT Aufnahmen entwickelt und bestehen häufig aus zwei Kameraköpfen, die gegenüberliegend, auf beiden Seiten des Patienten montiert sind. Weiterhin gibt es einige SPECT Gammakameras, die speziell für Untersuchungen des Hirns entwickelt wurden und drei Kameraköpfe in einer Dreiecksformation besitzen.
Ein Vergleich dieser Bildrekonstruktionsmethoden ist unten für einen Schnitt der Lungen (Atmungsaufnahme) eines Patienten gezeigt:
 |
|
 |
 |
(b) Positronenemissionstomographie (PET)
Wir erinnern uns aus Kapitel 2, dass Positronen von Kernen die zu viele Protonen haben emittiert werden können. Wir erinnern uns, dass Positronen nicht sehr lange in Materie überleben, da sie sehr schnell auf ein Elektron treffen werden und in einem Prozess namens Annihilation verschwinden. Bei diesem Prozess verschwinden Positron und Elektron und es entstehen zwei Gammastrahlen in entgegengesetzter Richtung[2]. Die Emission wird im englischen auch als Back-to-Back Gammastrahlung bezeichnet. Die entstehenden Gammastrahlen haben eine Energie von 0.51 MeV.
Wenn wir nun einem Patienten ein positronenemittierendes Radiopharmakon verabreichen können die Positronen mit Elektronen in ihrer Nähe annihilieren und erzeugen zwei Gammastrahlen entgegengesetzter Flugrichtung. Diese Gammastrahlen können mit einem Ring aus Strahlungsdetektoren um den Patienten detektiert werden so dass tomographische Bilder erzeugt werden können. Diese Detektoren sind im typischerweise spezielle Szintillationszähler, die auf die Detektion von Gammastrahlung einer Energie von 0.51 MeV optimiert sind. Dieser Ring von Detektoren zusammen mit den zugehörigen Gerätschaften und Computern heißt Positronen-Emissions-Tomograph

Jeder Detektor im Ring wird in Koinzidenz mit einer Reihe von gegenüberliegenden Detektoren betrieben und die durch die Annihilation der Positronen erzeugte Gammastrahlung (so genannte Vernichtungsstrahlung) wird detektiert.
Man hat auch festgestellt, dass Gammakameras mit dicken Kristallen und speziellen Kollimatoren als PET Scanner verwendet werden können.
Zu den in der Positronenemissionstomographie verwendeten Radioisotopen gehören 11C, 13N, 15O und 18F. Diese Isotope werden üblicherweise in einem Gerät namens Zyklotron hergestellt. Hinzu kommt, dass diese Isotope relativ kurze Halbwertszeiten haben. PET Scanner brauchen ein Zyklotron und angeschlossene Einrichtungen zur Herstellung der Radiopharmaka in ihrer Nähe. Wir werden Zyklotrons im nächsten Kapitel dieses Wikibooks näher kennen lernen.
Einige Fotos von Positronenemissionstomographen sind unten gezeigt:
 |
 |
 |
 |
- ↑ eine deutsche Übersetzung ist nicht üblich
- ↑ Die Strahlen sind nur dann exakt entgegengesetzt wenn die Geschwindigkeit des Schwerpunktes von Elektron und Positron vor dem Prozess genau Null war, daher ist der Winkel in der Realität immer ein bisschen von 180 Grad verschieden.
Externe Links (englisch)
- Centre for Positron Emission Tomography at the Austin & Repatriation Medical Centre, Melbourne with sections on what PET is, current facilities, projects & research and a PET image library.
- Online Learning Tools - an advanced treatment from the Department of Radiology, Brigham and Women's Hospital, USA containing nuclear medicine teaching files, an atlas of myocardial perfusion SPECT, an atlas of brain perfusion SPECT and the physical characteristics of nuclear medicine images.
- The Power of Molecular Imaging - a brochure all about Positron Emission Tomography (PET) from the Department of Molecular & Medical Pharmacology, University of California LA, USA.
Produktion von Radionukliden
Einleitung
Dies ist das zehnte Kapitel des Wikibooks Physikalische Grundlagen der Nuklearmedizin
Die meisten der in der Natur vorkommenden Radioisotope haben relativ lange Halbwertszeiten. Auch gehören sie zu Elementen die vom menschlichen Körper nicht verarbeitet werden. Daher benötigen medizinische Anwendungen Radioisotope welche künstlich hergestellt werden müssen.
Wir haben uns in den vergangenen Kapiteln dieses Wikibooks mit dem Thema Radioaktivität beschäftigt und sind dann zur Interaktion von Strahlung mit Materie fortgeschritten und haben uns mit Strahlungsdetektoren und Bildgebenden Systemen beschäftigt. In diesem Kapitel kommen wir auf die Strahlenquellen zurück und lernen Methoden kennen die verwendet werden, um Radioisotope zu erzeugen.
Ein Radioisotop, das in der nuklearmedizinischen Bildgebung sinnvoll verwendet werden kann sollte so beschaffen sein, dass die vom Patienten aufgenommene Dosis möglichst klein bleibt. Aus diesem Grund haben solche Isotope im allgemeinen eine sehr kurze Halbwertszeit und emittieren ausschließlich Gamma-Strahlung, also keine Beta-, oder Alpha-Teilchen. Die Energie der Gammastrahlung sollte nicht so gering sein, dass sie vollständig innerhalb des Körpers des Patienten absorbiert wird und nicht zu hoch um noch detektiert werden zu können. Aus diesem Grunde werden meist Radioisotope mittlerer Energien verwendet, dass heißt von ca. 100keV bis ca. 200keV. Schließlich sollte das Radioisotop, da es in irgendeine Form von Radiopharmakon eingebracht werden muss auch in einer Form herstellbar sein die der chemischen, pharmazeutischen und sterilen Verarbeitung zugänglich ist.
Als Produktionsmechanismen werden wir Spaltung, Kernreaktionen und Radioisotopengeneratoren betrachten.
Kernspaltung
In Kapitel Kapitel 2 haben wir spontane Kernspaltung eingeführt, wobei wir sahen, dass schwere Kerne in eine Anzahl von Fragmenten zerbrechen können. Dieser Spaltungsprozess kann bei einigen schweren Kernen durch Absorption von Neutronen induziert werden. Nach der Absorption eines Neutrons können solche Kerne in kleinere Fragmente mit Kernladungszahlen zwischen etwa 30 und 65 zerfallen. Einige dieser neuen Kerne sind in der Nuklearmedizin verwendbar und können von anderen Spaltungsfragmenten durch chemische Prozesse getrennt werden.
Der Spaltungsprozess kann in einem Gerät namens Kernreaktor kontrolliert ablaufen. Ein solcher Reaktor existiert in Australien bei Lucas Heights in New South Wales und viele weiter existieren an verschiedenen Orten der Welt.
Kernreaktionen
Bei diesem Herstellungsverfahren für Radioisotope werden geladene Teilchen bis zu sehr hohen Energien beschleunigt und dann auf ein Target geschossen. Beispiele solcher Teilchen sind Protonen, Alpha-Teilchen und Deuteronen. Neue Kerne können hierbei erzeugt werden, wenn diese Teilchen mit Kernen der Targets kollidieren. Einige dieser Kerne sind für die Nuklearmedizin von Nutzen.
Ein Beispiel für diese Methode ist die Herstellung von 22Na wobei ein Target aus 24Mg mit Deuteronen beschossen wird. Das heißt:
Ein Deuteron ist, wie man aus dem ersten Kapitel weiß, das zweit häufigste Wasserstoffisotop 2H. Wenn es mit 24Mg kollidiert entsteht ein 22Na Kern und ein Alpha-Teilchen. Ein solches Target wird einige Zeit einem Deuteronenstrahl ausgesetzt und anschließend chemisch weiterverarbeitet um das 22Na ab zu separieren.
Das üblicherweise für diese Art der Isotopenproduktion verwendete Gerät heißt Zyklotron. Es besteht aus einer Ionenkanone die geladene Teilchen herstellt, und einigen Elektroden die diese zu hohen Energien beschleunigen sowie einem Magneten um sie im Zyklotron zu halten und schließlich auf das Target zu lenken und besitzt einen kreisförmigen Aufbau.
Isotopengenerator
Dieses Verfahren wird häufig angewandt um gewisse kurzlebige Radioisotope in einem Krankenhaus oder einer Klinik herzustellen. Es besteht darin ein relativ langlebiges Isotop zu verwenden, welches in das gewünschte kurzlebige Isotop zerfällt.
Ein gutes Beispiel ist 99mTc welches, wie wir bereits wissen eines der in der Nuklearmedizin am häufigsten verwendeten Radioisotope ist. Dieses Isotop hat eine Halbwertszeit von sechs Stunden, was sehr kurz ist wenn wir es unmittelbar von einer nuklearen Herstellungsanlage heranschaffen müssen. Statt dessen versorgt uns die Herstellungsanlage mit dem Isotop 99Mo welches zu 99mTc mit einer Halbwertszeit von ca. 2.75 Tagen zerfällt. Das 99Mo wird Mutterisotop und das 99mTc wird Tochterisotop genannt.
Also wird in der Kernanlage das Mutterisotop hergestellt, welches relativ langsam in das Tochterisotop zerfällt, welches im Krankenhaus/Klinik chemisch vom Mutterisotop getrennt wird. Das Gerät zur Trennung heißt in unserem Beispiel 99mTc Generator:

Er besteht aus einer Keramiksäule an deren Oberfläche 99Mo angelagert ist. Eine Lösung, auch Eluent genannt, wird durch die Säule laufen gelassen und reagiert chemisch mit dem entstandenen 99mTc und verlässt den Generator in einer chemischen Form, die geeignet ist zusammen mit einem Pharmakon zu einem Radiopharmakon verarbeitet zu werden. Der in der obigen Abbildung gezeigte Aufbau und heißt Überdrucksystem, wobei das Eluent mit Druck, etwas höher als der atmosphärische Druck, durch die Keramiksäule in das Auffanggefäß gepresst wird.
Die Keramiksäule und das Auffanggefäß müssen, aus Gründen des Strahlenschutzes, durch eine Bleiabschirmung geschützt werden. Weiterhin müssen alle erzeugten Produkte in sterilem Zustand gehalten werden, da die gesammelte Lösung Patienten verabreicht werden wird.
Schließlich wird bei einem 99mTc Generator eine Ionisationskammer benötigt um die Radioaktivität einer dem Patienten zu verabreichenden Dosis während deren Herstellung zu bestimmen und zu überprüfen ob Reste von 99Mo in der gesammelten Lösung vorhanden sind.
Einige Fotos, die in den heißen Zellen nuklearmedizinischer Laboratorien aufgenommen wurden, sind unter gezeigt:
-
Fünf 99m-Tc Generatoren.
-
Bleiabschirmung um eine Flowbox in der Radiopharmaka hergestellt werden.
-
Die Blei-Abschirmung um die Flowbox aus einer anderen Perspektive.
Betrieb eines 99m-Tc Generators
Nehmen wir an wir haben eine Probe von 99Mo und nehmen wir weiterhin an, dass wir zur Zeit genau Kerne in unserer Probe haben. Die Anzahl der 99Mo Kerne nimmt mit der Zeit entsprechend dem radioaktiven Zerfallsgesetz welches wir in Kapitel 3 behandelt haben ab:
wobei die Zerfallskonstante von 99Mo bezeichnet.
Daher ist die Anzahl der 99Mo Kerne die in einem kurzen Zeitintervall zerfallen durch folgende Gleichung gegeben:
Da 99Mo in 99mTc zerfällt, entsteht die gleiche Anzahl an 99mTc Kernen während des Zeitintervalls . Zu einer Zeit ist nur noch der Bruchteil von diesen Kernen vorhanden, da 99mTc selbst auch zerfällt. Die Zeit in der 99mTc zerfallen kann ist gegeben durch . Setzen wir dies in das radioaktive Zerfallsgesetz ein, so erhalten wir:
Nun summieren wir die kleinen Beiträge . Anders ausgedrückt integrieren wir über um die Zahl der 99mTc Kerne, die zum Zeitpunkt vorhanden sind, zu erhalten.
Lösen wir schließlich dieses Integral, so erhalten wir:
Die unten gezeigt Abbildung stellt das Ergebnis unserer Rechnung graphisch dar. Auf der horizontalen Achse ist die Zeit in Tagen und auf der vertikalen die Anzahl der Kerne (in beliebigen Einheiten) dargestellt. Die Grüne Kurve stellt den exponentiellen Zerfall von reinem 99mTc dar. Die rote Kurve zeigt die Anzahl der 99mTc Kerne in einem 99mTc Generator, der niemals eluiert wird. Die blaue Kurve zeigt schließlich den Verlauf für einen 99mTc Generator, der alle 12 Stunden eluiert wird

Weiterführende Links (englisch)
- Cyclotron Java Applet - a Java-based interactive demostration of the operation of a cyclotron from GFu-Kwun Hwang, Dept. of Physics, National Taiwan Normal University, Virtual Physics Laboratory.
- Nuclear Power Plant Demonstration - a Java-based interactive demonstration of controlling a nuclear reactor. Also contains nuclear power Information links.
- ANSTO's HIFAR Reactor - details about the nuclear reactor at Lucas Heights, NSW.
Medical Valley - contains information on what nuclear medicine is, production of nuclear pharmaceuticals, molybdenum and technetium - from The Netherlands Energy Research Foundation Petten.
Computer in der Nuklearmedizin
Einleitung
Dies ist das elfte Kapitel des Wikibooks Physikalische Grundlagen der Nuklearmedizin
Computer werden heute in fast allen Bereichen der Nuklearmedizin eingesetzt. Hier liegt die Hauptanwendung in der Aufnahme und Verarbeitung von Bilddaten. Dieses Kapitel beschreibt den allgemeinen Aufbau eines Bildverarbeitungssystems und gibt eine kurze Einführung in die digitale Bildgebung sowie einige Beispiele bekannter nuklearmedizinischer Datenverarbeitungsverfahren und schließt mit einem Überblick über Bildarchivierungs- und Übertragungssysteme. Bevor wir uns diesen Themen zuwenden, müssen wir jedoch einige Anmerkungen über die Art und Weise, wie Daten in Computern verarbeitet werden, sowie über Technologie die der Entwicklung der Computer zugrunde liegt machen, so dass wir die Diskussion in einen Kontext einbetten können.
Binäre Darstellung
Nahezu alle heute verwendeten Computer basieren auf der Manipulation von Daten, die in Form von binären Zahlen kodiert sind. Eine Binärziffer kann nur einen von zwei möglichen Werten annehmen, nämlich 0 oder 1. Diese Stellen werden nach dem englischen binary digits bits genannt. Wird eine Information als eine Sequenz von Bits dargestellt, so wird diese häufig als Word bezeichnet. Wenn die Sequenz genau 8 Bits enthält, nennt man sie ein Byte. Das Byte wird heute als Basiseinheit für digital codierte Information verwendet. Entsprechend werden größere Mengen binär kodierter Information in Einheiten von Kilobyte, Megabyte, etc. angegeben. Es ist wichtig zu beachten, dass Bedeutungen dieser Einheiten geringfügig von ihren traditionellen Bedeutungen abweichen. Dies liegt in der Natur der binären Kodierung begründet. Im Computerjargon versteht man unter einem Kilo eine Menge von 1024 (entsprechend 210) Einheiten. 1024 ist diejenige Zweierpotenz, die am nächsten bei 1000 liegt. Daher entspricht 1 Kilobyte 1024 Byte und ein 1 MegaByte 1024 mal 1024 Byte.
Binäre Kodierung von Bildinformation wird benötigt, um Bilder in einem Computer zu speichern. Die meisten bildgebenden Geräte in der Medizin erzeugen kontinuierliche Ausgabewerte in einem vorgegebenen Intervall, also analoge Information. Es ist daher notwendig diese analoge Information in eine diskrete Form zu wandeln, um die Bilder binär zu kodieren und in einem Computer zu verarbeiten. Die geschieht im Allgemeinen mit einem Gerät namens Analog-Digital-Konverter (ADC). Weiterhin verarbeiten die meisten photographischen Geräte, die in der Medizin zur Anzeige der Bilder verwendet werden, analoge Signale. Es ist daher notwendig die digitalen Bilddaten bei der Ausgabe aus dem Computer in analoge Formate zurück zu wandeln, wobei ein Digital-Analog-Konverter (DAC) Verwendung findet.
Entwicklung moderner Computer
Die Entwicklung moderner Computer hing beinahe vollständig von den wichtigen Entwicklungen in den Materialwissenschaften und der digitalen Elektronik ab, die in den letzten dreißig Jahren stattgefunden haben. Diese haben dazu geführt, dass komplexe elektronische Schaltkreise in kleine Plastikpakete komprimiert werden konnten, welche als integrierte Schaltkreise (ICs) bezeichnet werden. Diese Pakete enthalten winzige Stückchen Silizium (oder ein anderes Halbleitermaterial) welches speziell bearbeitet wurde, um komplexe elektronische Prozesse ausführen zu können. Diese Siliziumstückchen werden im allgemeinen als Silizium-Chips bezeichnet. Innerhalb eines Chips kann eine höhere elektrische Spannung zur Darstellung der (binär-) Ziffer 1 und eine niedrige Spannung zur Darstellung der Ziffer 0 verwendet werden. So kann die die Schaltung verwendet werden, um Informationen zu manipulieren, welche in Form von Binärzahlen kodiert sind.
Eine wichtige Eigenschaft dieser elektronischen Komponenten ist die sehr hohe Geschwindigkeit, mit der die Spannungsstufen in unterschiedlichen Teilen der Schaltung umgeschaltet werden können. Dies führt dazu, dass Computer binäre Information sehr schnell verarbeiten können. Weiterhin erlaubt die geringe Größe moderner ICs die Herstellung von winzigen Computern, die nicht mehr so große Mengen an Hitze produzieren - vorherige Generationen von Computern nahmen ganze Räume in Anspruch und mussten gekühlt werden, da sie aus größeren elektronischen Bauelementen, wie Transistoren und Elektronenröhren aufgebaut waren. Daher können moderne Computer auf einem Schreibtisch aufgebaut werden und benötigen keine besondere Umgebung oder Klimaanlage. Dazu kam, dass die Massenproduktion von integrierten Schaltkreisen zu einem enormen Rückgang der Kosten geführt hat - was zu der phänomenalen Explosion dieser Technologie in den letzten Jahren beigetragen hat.
Bevor wir anfangen, ist es wichtig zu bemerken, dass sich die Informationen in diesem Kapitel mit der Zeit ändern wird, da es noch weiterhin rasante Weiterentwicklungen in diesem Gebiet gibt. Dieses Kapitel beschränkt sich daher im wesentlichen auf allgemeine Konzepte - und man muss sich darüber im klaren sein, dass heutige Techniken von den hier beschriebenen stark abweichen können. Schließlich bemerken wir, dass jegliche Erwähnung von Hardware- und Softwareprodukten nicht darauf abzielt, diese Produkte zu bewerben, sondern nur zur Illustration in der Diskussion dient.
Hardware
Die untere Abbildung zeigt das Blockdiagramm der wichtigsten Hardwarekomponenten eines allgemeinen Computers. Das Diagramm zeigt deutlich, dass ein Computer aus einem zentralen Verbindungssystem dem Bus besteht mit dem die elektronischen Komponenten verbunden sind. Jede dieser Komponenten ist unten kurz beschrieben.

Hauptprozessor (CPU)
Diese Komponente basiert in vielen modernen Computern auf einem integrierten Schaltkreis namens Mikroprozessor. Dessen Zweck besteht darin, als Hirn des Computers zu funktionieren, wo Befehle interpretiert und ausgeführt werden und Daten manipuliert werden. Die CPU besteht üblicherweise aus zwei Unterkomponenten - der Kontrolleinheit (CU) und der arithmetisch-logischen Einheit (ALU).
Die Kontrolleinheit wird verwendet um die in den Computerprogrammen enthaltenen Befehle zu dekodieren und auszuführen. Diese Befehle können zum Beispiel verwendet werden, um Informationen zu anderen Komponenten zu senden oder die Arbeitsweise solcher anderen Komponenten zu steuern. Die ALU wird hauptsächlich verwendet, um Daten mit mathematischen Methoden zu manipulieren, wie zum Beispiel bei der Multiplikation und Addition von Zahlen.
Wichtige Eigenschaften einzelner Mikroprozessoren sind die Wortlänge, die Architektur, die Flexibilität der Programmierung und die Geschwindigkeit. Ein Indikator für die Geschwindigkeit ist die Taktrate, deren Werte für gebräuchliche Mikroprozessoren angegeben ist. Man beachte dass die Taktrate allein nicht ausreicht um über die Geschwindigkeit eines Computers zu entscheiden, da die Spezifikationen der anderen Komponenten ebenfalls berücksichtigt werden müssen.
| Mikroprozessor | Hersteller | Taktrate (MHz) | Beispielcomputer |
|---|---|---|---|
| Pentium | Intel | 60-200 | IBM-PC |
| PowerPC 604e | Motorola | 160-350 | Power Macintosh |
| Turbo SPARC | Sun | 170 | SPARC Station 5 |
| STP1031LGA | Sun | 250 | Ultra SPARC II |
| Pentium II | Intel | 233-450 | IBM-PC |
| PowerPC 750 | Motorola | 233-500 | Power Macintosh |
| Alpha 21164 | DEC | 300-625 | DEC Alpha |
| Pentium 4 | Intel | 1'300-1'700 | IBM-PC |
Hauptspeicher
Diese Komponente besteht üblicherweise aus einer großen Anzahl integrierter Schaltkreise, welche verwendet werden, um Informationen zu speichern, die der Benutzer des Computers zur Zeit benötigt. Diese Schaltkreise gibt es im allgemeinen in zwei Arten - Random Access Memory (RAM) (Wahlfrei zugreifbarer Speicher) und Read only Memory (ROM) (Nur lesbarer Speicher). RAM wird verwendet um Informationen kurzfristig zu speichern. Es handelt sich um einen flüchtigen Speicher, weil der Inhalt des Speichers verloren geht, wenn die Stromversorgung des Computers abgeschaltet wird. Sein Inhalt kann auch sehr schnell gelöscht und mit neuen Informationen beschrieben werden. ROM, auf der anderen Seite, ist nicht flüchtig und wird verwendet, um die für die grundlegenden Funktionen des Computers notwendigen Informationen zu speichern.
Sekundärspeicher Diese Komponente wird verwendet, um Informationen permanent und löschbar für einen längeren Zeitraum zu speichern, z.B. für Informationen die zur Zeit nicht vom Benutzer benötigt werden, jedoch zu einem späteren Zeitpunkt vom Benutzer benötigt werden könnten. Die unterschiedlichen Gerätearten, die als Sekundärspeicher Verwendung finden, sind in der folgenden Tabelle zusammengefasst. RAM ist zu Vergleichszwecken mit in die Tabelle aufgenommen worden.
| Gerät | Kapazität (Mbyte) | Zugriffszeit | Löschbar? |
|---|---|---|---|
| Magnetband | 500-16000 | Minuten | Ja |
| Disketten | 0.3-1.5 | 200-500 ms | Ja |
| Festplatten | 1000-300000 | 20-80 ms | Ja |
| Wechselfestplatte | 100-100000 | 100-200 ms | Ja |
| Optische Disk | 250-4700 | 100-500 ms | Ja/Nein |
| RAM | 256-4000 | 10-100 ns | Ja |
Üblicherweise wird Technologie auf Basis von magnetischen Materialien verwendet, ähnlich denen für die Audioaufzeichnung in HiFi System verwendet werden. Hier wird die Information gespeichert, indem der lokale Magnetismus in Material ortsabhängig geändert wird. Informationen werden gelesen, indem der Magnetismus detektiert wird. Der lokale Magnetismus kann wegen der binären Natur der zu speichernden Daten immer nur einen von zwei möglichen Werten annehmen. Materialien wie Plastikbänder oder -scheiben, die mit einer metallischen Schicht überzogen sind, werden verwendet. Magnetische Bänder gibt es sowohl in Form von offenen Rollen als auch als geschlossene Kassetten, während magnetische Scheiben im allgemeinen aus flexiblen (Floppy) Scheiben oder Scheiben aus einem härteren Plastik bestehen. Floppy-Disks (Disketten), wie auch magnetische Bänder können aus dem Computer entfernt und als Backup Speicher verwendet werden. Diese Tatsache ermöglicht es auch, Informationen zwischen Computern aus zu tauschen. Hard-Disks (Festplatten) auf der anderen Seite sind fest im Computer verbaut und können nicht leicht entfernt werden. Obwohl auch austauschbare Versionen in der Größe vergleichbar mit Floppydisks Verwendung finden.
Moderne Forschungen über magnetische und optische Merkmale von Materialien führten zu der Produktion der sogenannten optischen Disk, die der Compact Disk (CD) ähnelt, die in HiFi Anlagen Verwendung findet. Es gibt drei grundlegende Typen von optischen Disks: diejenigen, die Programme von Software-Firmen beinhalten (CD-ROM), die, die von Nutzer einmal beschrieben werden können (CD-R) und die löschbaren (CD-RW oder magnetisch-optische Disk). Die DVD ist sozusagen der Nachfolger der CD-ROM - die erste Generation hatte eine Speicherkapazität von 4.700 MByte (4,7 GByte) und die zweite Generation von 17.000 MByte (17GByte).
Es gibt einen allgemeiner Unterschied zwischen einer Kassette und einer Disk als sekundäres Speichermedium: Der Zugang zu Informationen auf einer Kassette ist sequentiell, im Gegensatz zum wahlfreien (in beliebiger Reihenfolge möglichen) Zugang, den eine Disk bietet. Daher sind diskbasierte Medien normalerweise schneller bei der Speicherung oder Bereitstellung von Daten als Kassetten. Viele moderne Designs von Sekundärspeichern basieren daher auf harten magnetischen Disks für regelmäßige Datenspeicherung, mit Disketten für ein Backup mit kleinen Informationsinhalten und optische Disks für Backup von größeren Datenmengen.
Ein-/Ausgabe Geräte Diese Komponenten sind für die Benutzereingabe zuständig und bestehen normalerweise aus einer Tastatur, einem Darstellungsgerät (z.B. Bildschirm) und einem Drucker. Hierbei ist eine große Menge an Technologien im Einsatz, die Details würden den Rahmen dieses Kapitels sprengen. Diese Komponenten umfassen auch Geräte wie die Maus, der Joystick oder das TrackPad (auch Touchpad genannt), die für eine verbesserte Benutzerinteraktion mit dem Computer sorgen.
Computer BUS Dies ist das Medium zur Kommunikation zwischen den Komponenten des Computers - seine Funktion ist ähnlich der des zentralen Nervensystems. Die Arten der über den BUS kommunizierten Informationen beinhaltet spezielle Daten, Kontrollangaben sowie die Speicheradressen, an denen Informationen gespeichert bzw. abgerufen werden. Wie sich erahnen lässt, ist das Tempo, mit dem ein Computer arbeitet, abhängig von der Geschwindigkeit dieser Kommunikationsbrücke. Diese Geschwindigkeit muss kompatibel zu den anderen Komponenten sein, wie der CPU oder dem Arbeitsspeicher.
Software
Computertechnologie braucht mehr als nur elektronische Hardware. Um zu funktionieren, benötigen die elektronischen Komponenten Informationen in Form von Daten und Computerbefehlen. Diese Informationen werden generell als Software bezeichnet. Computerbefehle sind in der Regel in Computerprogrammen enthalten.
Kategorien von Computerprogrammen beinhalten:
- Betriebssysteme - welche für das Funktionieren des Computers und das Verwalten verschiedener Ressourcen des Computers notwendig sind;
- Anwendungen - welche für die Benutzung von routinierten Benutzern auf dem Computer benötigt werden. Diese Anwendungen beinhalten Programme, welche für Textverarbeitung (z.B. MS Word), Kalkulationstabellen (z.B. MS Excel), Datenbanken (z.B. FileMaker Pro), Grafikbearbeitung (Adobe Illustrator) und digitale Bildverarbeitung (beinhaltet Software, die für den Betrieb von bestimmten medizinischen Abbildungssystemen verwendet werden) benutzt werden;
- Programmiersoftware - welche für das Schreiben von neuen Programmen verwendet werden. Beispiele von bekannten Programmiersprachen sind C (und die vielen Variationen davon) und Java. Eine Anzahl von zusätzlichen Softwarebausteinen werden für das Schreiben solcher Programme benötigt. Diese Beinhalten:
- Einen Editor um den Programmcode in den Computer zu schreiben (ähnlich einem Textbearbeitungsprogramm);
- Eine Bibliothek von Unterprogrammen - welche kleine Programme für das Ausführen von bestimmten bekannten Funktionen darstellen;
- Einen Linker welcher das vom Benutzer geschriebene Programm mit der Unterprogramm-Bibliothek verbindet;
- Einen Compiler oder Übersetzer um das selbstgeschriebene Programm in eine Version zu übersetzen, welche vom Computer direkt verstanden wird. Der Compiler codiert die Befehle in ein maschinenspezifisches digitales Format.
Digitale Bildverarbeitung
Neben solchen, welche in einem gewöhnlichen Computer vorhanden sind, bestehen Computer für digitale Bildverarbeitung normalerweise aus einer weiteren Anzahl von speziellen Bauteilen. Diese spezialisierten Komponenten sind wegen der sehr großen Datenmengen notwendig, welche in Bildern enthalten sind, und erfordern folglich viel Speicherplatz, einen sehr schnellen Datenaustausch sowie große Kapazitäten zur Datenverarbeitung.
Digitale Bildverarbeitung beinhaltet die Bearbeitung von Bildmaterial und die Bildanalyse. Ein Beispiel von Bildbearbeitung ist die künstliche Verbesserung von Bildern, sodass weitere Details mit verbesserter Brillanz angezeigt werden. Ein Beispiel von Bildanalyse ist das Herausheben von Anzeichen, welche einen funktionellen Aspekt einer anatomischen Region in einer Untersuchung ausdrücken. Die meisten medizinischen Bildsysteme ermöglichen extensive Kapazitäten zur Bildbearbeitung mit einer limitierten Auswahl an Bildanalyseverfahren. Systeme für die Verarbeitung von Röntgenbildern (inklusive SPECT und PET) stellen auch Einsatzmöglichkeiten zur extensiven Datenanalyse bereit. Diese Situation bewirkt aufgrund der Funktionalität eine Verschiebung des Schwergewichtes von der anatomischen Medizin hin zur Radiologie.
Die folgende Abbildung zeigt einen verallgemeinerten digitalen Bildverarbeitungsrechner. Die schattierten Komponenten im unteren Teil der Zeichnung entsprechen denen eines allgemeinen Computers, wie er oben beschrieben wurde. Die digitalen Bildverarbeitungskomponenten sind jene, welche mit dem Bild Daten BUS verbunden sind. Jede dieser zusätzlichen Komponenten werden unten kurz beschrieben. Die schattierten Komponenten oben im Diagramm sind die externen Geräte, welche in medizinischen Bildsystemen weit verbreitet sind.

Abbildungssystem Dies ist das Gerät, welches die primäre Bildinformation produziert. Beispiele von solchen Geräten sind CT-Scanner, Ultraschallgeräte, Röntgen-Fluorographie, MRI-Systeme, Gamma-Kameras, PET-Scanner und Computer-gesteuerte Radiographiesysteme. Das Gerät ist häufig physisch von den anderen Komponenten abgegrenzt wie beim CT-Scanner, aber sie können auch in dasselbe Gehäuse wie die anderen Komponenten eingebaut sein (wie z.B. in Ultraschallgeräten). Die vom System produzierte Bildinformation wird in die Bildverarbeitung des digitalen Bildprozessors eingespeist.
Es gibt im allgemeinen auch Verbindungen vom digitalen Bildprozessor zum Abbildungssystem. Sie werden benutzt, um spezifische Aspekte der Operation des Abbildungssystems zu kontrollieren, z.B. die Steuerung einer beweglichen SPECT-Kamera. Diese zusätzlichen Verbindungen werden zur besseren Übersicht in der Grafik nicht dargestellt.
Bildaufnahme
Diese Komponente wird verwendet, um die analoge, vom Abbildungssystem produzierte Information in einen Binärcode zu konvertieren. Hierzu dient ein Analog-zu-Digital Konverter (ADC). Die Bildaufnahmekomponente kann auch Funktionen zur Bearbeitung der digitalisierten Daten beinhalten, um beispielsweise allfällige Fehler in den Bilddaten zu korrigieren. Hierzu werden die Daten mit Hilfe einer "Input Look-Up Table" vorverarbeitet. Beispiele für diese Art von Datenbearbeitung sind vorverarbeitende Funktionen in Ultraschallgeräten und logarithmische Bildtransformation in digitalen Fluorographiesystemen.
Bildschirm
Diese Komponente wird benutzt, um digitale Bilder in ein analoges Format zu konvertieren, damit sie sich in einer Form befinden, welche von einem Display, zum Beispiel einem Videomonitor angezeigt werden kann. Zu diesem Zwecke wird ein Digital-zu-Analog Konverter (DAC) benötigt. Die Bildanzeige kann auch eine Vorrichtung zur Bearbeitung der angezeigten Bilder enthalten, damit man beispielsweise ihre Brillianz verbessern kann. Hierbei kommt eine "Output Look-Up Table" zur Anwendung. Beispiele dieser Art von Datenmanipulation beinhalten nachverarbeitende Funktionen an Ultraschallgeräten und "Windowing" in Nuklearmedizinischen Systemen. Andere Formen von Bildverarbeitung, welche vom Bildanzeigegerät zur Verfügung gestellt werden können, sind Bildvergrößerung und die Möglichkeit, mehrere Bilder auf einem Bildschirm anzuzeigen. In diesem Zusammenhang können auch Bemerkungen zu den Bildern hinzugefügt werden, wie z.B. der Name und gegebenenfalls weitere Daten des Patienten, welche für seine Untersuchung von Bedeutung sind.
Arbeitsspeicher
Diese Komponente besteht normalerweise aus einer RAM-Einheit, welche das Speichern aller Bilder erlaubt, welche für den Benutzer momentan von Bedeutung sind.
Bildspeicher
Diese Komponente besteht generell aus magnetischen Laufwerken (HDD) mit hinreichend großer Kapazität, um eine riesige Anzahl an Bildern zu speichern, welche momentan nicht von Interesse für den Benutzer sind, jedoch bei Bedarf in den Arbeitsspeicher übertragen werden können.
Bild ALU
Diese Komponente besteht aus einem gezielt zur Handhabung von Bilddaten entworfenen ALU. Sie wird generell für relativ rechenintensive Berechnungen benutzt, wie die Bildsubtraktion in DSA und die Reduktion von Bildrauschen durch das Mitteln von Bildsequenzen.
Matrix-Prozessor
Diese Komponente besteht aus einer Schaltung, welche für komplexere Bildbearbeitung bei höheren Verarbeitungsgeschwindigkeiten, als mit dem Bild ALU, entworfen wurde. Sie enthält typischerweise eine zusätzliche CPU, sowie ein spezielles Modul für Hochgeschwindigkeits-datenkommunikation und -speicherung. Sie kann als separater Computer für Sonderzwecke angesehen werden, dessen Design einen gewisser Verlust an Anwendungsmöglichkeiten und Flexibilität, im Austausch gegen größere Rechengeschwindigkeit bedeutet. Diese Geschwindigkeit wird von der Möglichkeit zur parallelen Datenmanipulation ermöglicht, im Gegensatz zu einer sequenziellen Manipulation (wie es in allgemeinen Computern der Fall ist). Diese Komponente wird beispielsweise benutzt, um schnelle Fourier-Transformationen zu berechnen und für die Rekonstruktionsberechnungen in Querschnitt-Abbildungen, wie CT, SPECT und MRI.
Bilddaten-BUS
Diese Komponente besteht aus einer speziell für Bilddaten entwickelte Hochgeschwindigkeits-kommunikationsverbindung.
Digitale Abbildung
Die Digitalisierung von Bildern besteht generell aus zwei gegensätzlichen Prozessen - Sampling (Abtasten) und Quantisierung. Diese zwei Prozesse werden unten kurz beschrieben, gefolgt von einer Abhandlung der Speicheranforderungen für digitale Bilder.
Bild-Sampling
Dieser Prozess wird verwendet, um die räumliche Information in einem Bild zu digitalisieren. Dies wird normalerweise durch die Aufsplittung eines Bildes in quadratische oder rechteckige Anordnung von Samplingpunkten erreicht. Jeder dieser Samplingpunkte wird als Bildelement bezeichnet (oder Pixel, um Computerjargon zu verwenden).

Der Prozess kann als Digitalisierung eines analogen Bildes in ein N x N Pixel-Format zusammengefasst werden. Beispiele von Werten für N sind 128 für ein Röntgenbild, 512 für CT und MRI-Scans, 1024 für ein DSA Bild und 2048 für ein Computer-Radiographiebild und digitale Radiographie. Man beachte, dass wegen der binären Natur von modernen Computertechniken, N eine Zweierpotenz seien muss. Dies ist zum Beispiel Voraussetzung zur Anwendung der Fast-Fourier-Transformation auf ein Bild.
Je größer die Anzahl der Pixel, um so höher ist natürlich die räumliche Auflösung des digitalisierten Bildes. Entsprechend bedeutet eine größere Pixelzahl eine bessere Näherung an das analoge Originalbild. Dieser Sachverhalt ist weiter unten in einer Abbildung dargestellt.
Bild-Quantisierung
Dieser Prozess bezieht sich auf die Digitalisierung der Helligkeitsinformation eines Bildes. Er wird normalerweise durch die Wiedergabe der Helligkeit eines Pixels durch eine ganze Zahl erreicht, deren Wert proportional zur Helligkeit ist. Diese Zahl wird 'Pixelwert' bezeichnet, und die Bandbreite von möglichen Pixelwerten, welche ein System haben kann, wird als 'Graustufen' bezeichnet. Je größer die Skala für Graustufen, desto näher befindet sich natürlich die Helligkeitsinformation im digitalen Bild an der des analogen Originalbildes (siehe Bild weiter unten).
Der Prozess kann als Digitalisierung der Bildhelligkeit in G Graustufen angesehen werden. Der Wert von G hängt von der binären Natur der Informationscodierung ab. Folglich ist G generell ein Wert einer Potenz, deren Grundzahl 2 ist, d.h. G=2 m, wobei m eine ganze Zahl ist, welche die Anzahl für die Speicherung benötigter Bits beschreibt. Beispiele für Werte von G sind 256 (m=8) in Ultraschalltechnologie, 1024 (m=10) in DSA und 4096 (m=12) in Nuklearmedizin.
Digitale Bildauflösung Die Anzahl Bits, b, die benötigt wird, um ein Bild in einem digitalen Format darzustellen wird durch
vorgegeben.
Die folgende Tabelle zeigt die Anzahl Bits, welche notwendig sind um digitalisierte Bilder darzustellen, welche verschiedene räumliche Auflösungen und Graustufenzahlen haben. Man sieht, dass sehr große Datenmengen benötigt werden, um eine Auflösung zu erreichen, wie sie in medizinischen Bereichen typischerweise eingesetzt wird (man erkennt als größten Wert in der Tabelle: 6 Mbytes). Die resultierenden Mengen an benötigter Computerkapazität, um solche Bilder zu speichern sind folglich ziemlich groß und die Bearbeitungszeit kann relativ hoch sein, wenn man solche große Datenmengen bearbeitet. Diese Eigenschaft digitaler Bilder erhöht der Bedarf an entsprechender spezieller Hardware für die Verarbeitung der Bilddaten, welche nicht zu den gewöhnlichen Komponenten eines Computers gehören, wie wir ihn oben beschrieben haben (obwohl dieser Unterschied mit der fortlaufenden technischen Entwicklung abnimmt).
| N x N | m = 8 | m = 10 | m = 12 |
|---|---|---|---|
| 128 x 128 | 131,072 | 163,840 | 196,608 |
| 256 x 256 | 524,288 | 655,360 | 786,432 |
| 512 x 512 | 2,097,152* | 2,621,440 | 3,145,728 |
| 1024 x 1024 | 8,388,608 | 10,485,760 | 12,582,912 |
| 2048 x 2048 | 33,554,432 | 41,943,040 | 50,331,648 |
Digitale Bildbearbeitung
Kontraststeigerung Diese Form digitaler Bildverarbeitung (gewöhnlich als Windowing bezeichnet) wird unten beschrieben und ist ein Beispiel der vielen Arten von Datenbearbeitungsprozessen, welche auf modernen Systemen verfügbar sind. Kontraststeigerung ist eine Form von Graustufen-Transformation, wo für die Anzeige der reelle Pixelwert durch einen neuen Pixelwert ersetzt wird.
Der Prozess wird generell mit einer "Output Look-Up Table" in der Bildanzeigekomponente des digitalen Bildprozessors ausgeführt. Folglich werden die ursprünglichen Originaldaten im Arbeitsspeicher nicht durch den Prozess beeinflusst, sodass die originalen Bilddaten jederzeit wieder hervorgeholt werden können, falls das bearbeitete Bild nicht zufriedenstellend ist. Zusätzlich kann der Prozess durch das Benutzen moderner Elektronik bei sehr hohen Geschwindigkeiten implementiert werden, so dass Benutzerinteraktivität möglich ist.
Ein Beispiel einer Look-Up Table (LUT), welche für Kontraststeigerung verwendet werden kann, wird in der folgenden Darstellung illustriert. Diese Information wird gewöhnlich mit Hilfe eines Graphen der wirklichen Pixelwerte, welche im Arbeitsspeicher abgelegt sind, parallel zu den Pixelwerten, welche zur Anzeige verwendet werden, dargestellt. Der Prozess wird normalerweise von zwei Controllern an der Konsole des digitalen Bildprozessors gesteuert, dem LEVEL-Controller und dem WINDOW-Controller. Es sollte beachtet werden, dass Variationen der Namen dieser Controller und ihrer exakten Aufgabe zwischen unterschiedlichen Systemen existieren, aber der hier beschriebene Ansatz genügt für unsere Zwecke. In der Abbildung sieht man, dass der LEVEL den Grenzwert bestimmt unterhalb dessen alle Pixel schwarz dargestellt werden und der WINDOW den entsprechenden Wert für eine weiße Anzeige bestimmt. Die gleichzeitige Verwendung der zwei Controller erlaubt die Anwendung eines Graustufen-Fensters variabler Größe, welches irgendwo in der Graustufenskala eingesetzt werden kann. Feine Graustufenwechsel innerhalb von Bildern können hierdurch verbessert werden, so dass diese klarer angezeigt werden. Eine gewöhnliche Anwendung dieser Form von digitaler Bildbearbeitung in der Nuklearmedizin ist die Entfernung von Hintergründen aus Bildern.

Eine andere Form von Kontrasterhöhung, welche in der Nuklearmedizin verwendet wird, stellt die Anwendung von LUTs mit logarithmischem, exponentiellem oder einem anderen nichtlinearen Input/Output-Verhältnis dar (Das logarithmische LUT wird momentan für die Umrechnung einer großen Bandbreite von Graustufen eingesetzt). Farb-LUTs sind auch bekannt, wo die digitale Kontrastauflösung eines Bildes durch verschiedene Farben dargestellt wird (Beispielsweise ein Regenbogenschema wie in der folgenden Darstellung) oder durch verschiedene Farbtöne einer oder weniger Farben.
 |
 |
 | |
Der Rot-, Grün- und Blaukanal werden auf verschiedenen Ebenen angezeigt.
Andere Beispiele digitaler Bildbearbeitung werden in folgender Darstellung gezeigt.
-
Unbearbeitetes Bild
-
Kontrasterhöhung
-
Graustufenumkehrung
-
Schärfungsfilter
-
Weichzeichnen
-
Flankenerkennung
-
Schemenfilter
-
Glättung
-
Medianfilter
-
Leichter Gaußscher Filter
-
Starker Gaußscher Filter
-
Schwellenwert
Eine Detaillierte Abhandlung über die Bildverarbeitungsmöglichkeiten moderner Personalcomputer findet man unter folgendem
externen Link.
Zur den weiteren üblichen Formen der digitalen Bildbearbeitung gehört es, geometrische Transformationen auf die Bilder anzuwenden, um sie z.B. zu vergrößern oder um Geometriefehler zu korrigieren, die sich aus der Bildaufnahme ergeben. Das Vergrößern kann durch Replikation der Pixel erfolgen, wobei jedes Pixel N2 mal dargestellt wird, wobei N der Vergrößerungsfaktor ist. Dieser Prozess ist in der folgenden Abbildung dargestellt.

Ein Nachteil dieses Ansatzes besteht jedoch darin, das die vergrößerten Bilder pixelig wirkten. Dies ergibt sich aus den effektiv größeren Pixeln. Obwohl man diesen Effekt durch Anwendung eines Glättungsfilters verringern kann (siehe auch Pixelation), lässt sich ein visuell ansprechenderes Ergebnis durch räumliche Interpolation erreichen. Hierbei werden die Helligkeitswerte unbekannter Pixel durch die Helligkeitswerte bekannter benachbarter Pixel geschätzt. Angenommen das obere Bild werde wiederum vergrößert und die bekannten Pixel werde auf die Ecken des vergrößerten Bildes verteilt. Dann ergibt sich sich die in der folgenden Abbildung dargestellte Situation:

Die Aufgabe des Interpolationsprozesses besteht darin, die Helligkeitswerte unbekannter Pixel aus den Helligkeitswerten bekannter Pixel an den Ecken zu berechnen. Der einfachste Ansatz ist die lineare Interpolation, wobei ein linearer Verlauf der Helligkeitswerte zwischen den bekannten Pixeln angenommen wird. Angenommen wir wollten den Helligkeitswert des in der folgenden Abbildung rot markierten Pixels bestimmen. Im Falle einer zweidimensionalen linearen Interpolation, auch bilineare Interpolation genannt, besteht der erste Schritt in der Berechnung des Helligkeitswertes an der Position welche in der Abbildung gelb markiert ist. Die Berechnung gestaltet sich wie folgt.
wobei den normierten Abstand entlang der horizontalen Achse bezeichnet.
Entsprechend berechnet sich der Helligkeitswert des in der untersten Zeile gelb markierten Pixels an der Position nach der folgenden Gleichung:
Schließlich kann der Helligkeitswert des unbekannten in der Abbildung rot markierten Pixels durch lineare Interpolation zwischen diesen beiden in der Abbildung gelb markierten Pixeln wie folgt berechnet werden.
wobei für den normierten Abstand entlang der vertikalen Achse steht.
Dieses Verfahren wird auf alle unbekannten Pixel des Bildes angewandt. Unten ist dies beispielhaft gezeigt.

Auch nichtlineare Verfahren können verwendet werden, um ein ansehnlicheres Ergebnis zu erhalten. Als Beispiele sind die zweidimensionale polynomielle sowie kubische Spline Interpolation zu nennen. Man muss sich jedoch vergegenwärtigen, dass jede Art von Interpolierten der Daten keine neuen realen Messwerte erzeugt (wie man sie erhalten würde wenn man ein Abbildungssystem höherer Auflösung verwenden würde), es handelt sich viel mehr um einen Verfahren um das pixelige Aussehen der vergrößerten Bildes zu vermeiden und visuell ansprechendere Bilder zu erhalten. Die Helligkeitswerte der Zwischenpixel werden lediglich geraten. Wir werden weitere Anwendungen des Verfahren im Kapitel Röntgen Computertomographie kennen lernen.
Die Fourier-Transformation - Eine bildliche Abhandlung
In vielen Lehrbüchern wird für die Abhandlung der Fourier-Transformation (FT) auf ein Niveau der Mathematik zurückgegriffen, welches selbst vielen Medizinstudenten ziemlich fremd ist. Diese Abhandlung hier wird einen anderen Zugang zum Thema suchen, basierend auf einer bildlichen Abhandlung, einem Versuch das Konzept, auf welchem die Transformation basiert, effektiver mitzuteilen. Es kann keinesfalls eine detaillierte mathematische Behandlung des Themas ersetzen, und zielt einzig darauf ab, das Verständnis für die Bildfilterung zu unterstützen.
Diese Präsentation wird demonstrieren, dass Bilder in zwei Darstellungen betrachtet werden können, der Ortsdarstellung und der Raumfrequenzdarstellung. Die Ortsdarstellung ist die konventionelle Art, Bilddaten zu präsentieren und bezieht sich auf wirkliche Parameter, wie Zeit und Raum. Ein Bild kann aber auch als eine große Anzahl räumlicher Frequenzen angesehen werden, welche miteinander zusammenwirken um das Gesamtbild zu ergeben. Dieser Aspekt wird zu Beginn anhand eines relativ einfachen Bildes behandelt, und danach an einem komplizierteren, nämlich einer Radiographie der Brustkorbes. Die FT transformiert die Bilddaten aus der Ortsdarstellung in die Raumfrequenzdarstellung und die inverse FT führt die umgekehrte Operation aus (siehe folgende Abbildung).

Die folgende Abbildung (a) zeigt sinusförmige Helligkeitsschwankungen, die in einem Winkel von 45 Grad zur Horizontalen verlaufen. Eine Graphik von Pixelwerten entlang einer Gerade zwischen den Punkten A und B zeigt diesen sinusförmige Verlauf in einer Dimension, wie sie in Abbildung (b) gezeigt ist. Man kann dies auch auf eine andere Art darstellen, indem man die Amplitude der Sinuswellen in Abbildung (b) gegen ihre räumliche Frequenz aufträgt. Dies ist in Abbildung (c) gezeigt. Hier erkennt man, das es nur eine dominante räumliche Frequenz gibt. Man erwartet diesen Sachverhalt auch intuitiv, wenn man Abbildung (b) betrachtet. Die Darstellung in Abbildung (c) bezeichnet man als 1D Fourier-Spektrum, sie ergibt sich durch eindimensionale Fourier-Transformation der Daten aus Abbildung (b). Man beachte, dass in den Abbildungen (b) und (c) nur eindimensionale Informationen dargestellt sind.
Wenn die Frequenzinformation wie in Feld (d) zweidimensional dargestellt wird, so nennt man dies ein 2D Fourier-Spektrum, dieses wird durch eine 2D-Fourier-Transformation der Bilddaten berechnet. Räumliche Frequenzen der vertikalen und horizontalen Bilddimensionen werden auf die vertikalen und horizontalen Achsen übertragen, mit dem Ursprung im Zentrum (durch einen kleinen schwarzen Punkt dargestellt). In Feld (d) können aber noch zwei weitere Punkte (an die sich dünne horizontale Strukturen anschließen) erkannt werden (Ein Punkt befindet sich leicht links oberhalb der Zentrums und der andere leicht rechts unterhalb des Zentrums). Ihre Position im Bild (d) entspricht der Frequenz der Sinuskurve in Bild (a). Da die FT positive und negative Werte für die Frequenz generiert, ergeben sich zwei Frequenzen, welche symmetrisch zum Ursprung liegen.
Ein komplizierteres 2D Fourier-Spektrum erhält man, wenn eine Brustkorbradiographie in eine räumliche Frequenzdarstellung transformiert wird, wie im folgenden Bild. Die transformierten Daten zeigen eine große Bandbreite räumlicher Frequenzen mit signifikanten vertikalen und horizontalen Merkmalen, wie man vielleicht von den horizontalen Rippen und der vertikalen Wirbelsäule in einer Radiographie erwartet.

Eine potenzielle Anwendung der FT und ihrer Umkehrung ist die Entfernung unerwünschter oder beschädigter Daten von einem digitalen Bild, wie man es im letzten Bild unten sieht. Ein extremes Beispiel eines beschädigten Bildes erhält man durch das Übereinanderlegen zweier Bilder wie in Feld (a). Das Fourierspektrum in Feld (b) zeigt die Frequenzeigenschaften der überlegten Bilder. Die unerwünschten Eigenschaften, welche man der sinusförmigen Anordnung zuordnet, kann durch das Bearbeiten der Bilddaten in Frequenzdarstellung wie in Feld (c) entfernt werden, bevor die umgekehrte FT ausgeführt wird um ein Bild zu erhalten, das frei von Störungen ist, wie in Feld (d).
Aus diesen drei Beispielen kann man den Schluss ziehen, dass die Ortsdarstellung und die Raumfrequenzdarstellung der Bilddaten völlig gleichwertig sind. Die Frequenzdarstellung hat zahlreiche Vorteile bezüglich Datenbearbeitung. Generell stellen uns die FT und ihre Umkehrung die Werkzeuge für eine Transformation der Daten aus der echten Welt in eine von räumlichen Frequenzen und umgekehrt zu Verfügung.
Vielen herzlichen Dank an Alle, die sich an der Übersetzung dieser Seite beteiligt haben. Mitwirkende an dieser Übersetzung sind in der Seitenhistorie dieser Seite vermerkt. Falls Sie Spaß daran gefunden haben und weitere Seiten übersetzen wollen, finden Sie hier weitere.
Fourier-Methoden
Einleitung
Fourier-Methoden werden unten in recht allgemeiner Form beschrieben. Wir werden sehen, dass jede beliebige Wellenform mathematisch in mehrere Sinuswellen unterschiedlicher Frequenz und Amplitude zerlegt werden kann. Hierzu führt man häufig eine sogenannte Fouriertransformation durch. Wir werden sehen, dass das resultierende Fourier-Spektrum modifiziert werden kann um bestimmte Frequenzen zu verstärken oder zu unterdrücken. Der Zweck der Übungsaufgaben ist es, die Modulationsübertragungsfunktion (MTF) und die Filterstufe eines tomographischen Rekonstruktionsprozesses im Detail zu behandeln.
Man beachte dass hier eine Tabelle heruntergeladen werden kann, mit der man die verschiedenen unten angegeben Prozesse simultan untersuchen kann.
Periodische Funktionen
Eine periodische Funktion ist eine Funktion, die sich (nach einem bestimmten Raum- oder Zeitintervall regelmäßig) wiederholt. Einfache Beispiele sind die Sinusfunktion oder die Rechteckfunktion. Die Geschwindigkeit der zeitlichen Wiederholung einer periodischen Funktion wird durch ihre Frequenz beschrieben. Die Frequenz ist die Anzahl der Perioden, die einen festen Punkt pro Zeiteinheit passieren. Die Frequenz wird üblicherweise in Perioden pro Sekunde angegeben. Ihre Si-Einheit ist Hertz mit dem Formelzeichen Hz. Es gilt:
Ein medizinisches Beispiel einer periodischen Funktion ist der Herzschlag, wie er im Elektrokardiogramm dargestellt wird.
Die folgende Abbildung zeigt den Graphen einer Sinusfunktion. Eine Periode ist beispielhaft eingezeichnet.

Wenn eine periodische Funktion nicht zeitlich, sondern räumlich veränderlich ist, spricht man auch von einer Raumfrequenz. Diese ist entsprechend als die Anzahl der Perioden pro Raumeinheit definiert. Also zum Beispiel als Perioden pro mm, mit der Einheit:

Ein Beispiel aus der medizinisches Bildgebung für eine solchen Fluktuation ist das Bleibalkenmuster, welches häufig verwendet wird, um die räumliche Auflösung eines Abbildungssystems zu bestimmen (siehe folgende Abbildung). In diesem Fall wird die räumliche Auflösung in Linienpaare pro mm angegeben, wobei jeder Bleibalken mit seine angrenzenden Leerstelle als Linienpaar bezeichnet wird.
 |

Räumliche Auflösung
Eine Frage, die häufig im Rahmen der medizinischen Bildgebung auftritt, lautet: "Was ist die kleinste Struktur, die man mit einem gegebenen abbildenden System auflösen kann?" Die technische Größe, die diese Frage beantwortet, heißt räumliche Auflösung des abbildenden Systems. Man definiert sie je nach Zweck etwas unterschiedlich. Hier beschränken wir uns auf folgende einfache Definition: Die räumliche Auflösung ist der kürzeste Abstand, den zwei Linien haben dürfen, um noch als zwei getrennte und nicht als eine große verschmierte Linie gesehen werden zu können. Die Einheit der räumlichen Auflösung ist mm. Schauen wir uns zunächst ein Beispiel an. Die folgenden beiden Graphiken zeigen das gleiche Bild. Es besteht aus vertikalen Linien. Ihr Abstand und ihre Dicke nehmen nach rechts ab. Das Bild auf der linken Seite zeigt das Bild wie es von einem nahezu perfekten abbildenden System (mit sehr hoher räumlicher Auflösung) aufgenommen wurde. Man erkennt klar die einzelnen Linien, insbesondere auch am rechten Rand des Bildes. Das rechte Bild wurde mit einem qualitativ schlechteren abbildenden Verfahren aufgenommen. Man kann offenbar zum rechten Rand hin keine einzelnen Linien mehr ausmachen. In der Realität hat jedoch jedes abbildende System eine begrenzte räumliche Auflösung. Somit zeigt das rechte Bild einen realistischeren Fall.
 |
 |
Man erkennt weiterhin, dass es ziemlich schwierig ist, einen exakten Wert für die räumliche Auflösung eines abbildenden Systems anzugeben. Man muss hierzu den Bereich in der rechten Abbildung betrachten, in dem zwei benachbarte Linien sich gerade so weit überlappen, dass man sie nicht mehr als zwei getrennte Linien erkennen kann. Man erkennt sofort, dass dieser Effekt nicht bei einer bestimmten Linie auftritt, sondern über mehrere Linien allmählich zunimmt. Aber man sieht auch, dass man am linken Rand klar getrennte Linien und auf am rechten Rand überhaupt keine Linien mehr erkennen kann.
Schauen wir uns diese beiden Abbildungen nun in einer anderen Darstellung an. Die folgende Abbildung zeigt zwei Graphen. Der grüne Graph entspricht dem rechten und der rote dem linken Bild. Der obere Rand entspricht einem weißen Pixel und der untere Rand einem schwarzen Pixel. Zwischenwerte stehen entsprechend für graue Pixel. Der rote Graph würde normalerweise vertikale Linien enthalten, welche die horizontalen mit einander verbinden. Diese wurden jedoch, der Übersichtlichkeit wegen, nicht dargestellt. Die x Achse in dieser Abbildung entspricht den x Achsen in den beiden oberen Abbildungen. Somit enthalten beide Darstellungen dieselbe Information. Sie ist lediglich etwas anders aufgetragen.

Wir erkennen hier zwei Tatsachen wieder, die wir oben bereits bemerkt haben. Wir sehen jedoch auch, dass die Amplitude (der Abstand zwischen Minimum und Maximum in y Richtung) des Signals linear nach rechts abnimmt, bis die Funktion schließlich nicht mehr periodisch ist. Somit müssen wir zugeben, dass offensichtlich im rechten Teil fast alle Information verloren gegangen ist. Jedoch können wir die Information im periodischen Teil zurückgewinnen. Wir können die Amplituden entsprechend skalieren um die volle Amplitude wiederherzustellen. Leider skalieren wir jedoch auch das Rauschen. Somit funktioniert dieses Verfahren nur so lange, wie das Signal deutlich stärker ist als das Rauschen. Unten sieht man dieselbe Funktion mit einer in blau eingetragenen Einhüllenden.

Nun skalieren wir die Funktion und erhalten ein Bild mit höherer Auflösung. Wir halten den Kontrast auf der rechten Seite des Bildes konstant, aber wir erhöhen ihn um den Faktor 10 für die Pixel am rechten Rand und verwenden eine monotone Funktion für die dazwischenliegenden Pixel. Um die Berechnung technisch durchzuführen, benutzen wir die blaue einhüllende Funktion und verwenden den Skalierungsfaktor , welcher von der (Pixel-) Position abhängt. Unten sieht man zwei Bilder. Das rechte wurde mit der hier beschriebenen Methode verbessert.
 |
 |
Wir können auf dem rechten Bild deutlich mehr Linien erkennen als auf dem linken. Dennoch sehen wir am rechten Rand keine Linien mehr. Aber wir erkennen das wir durch die Skalierung des Kontrastes eine Verbesserung der räumlichen Auflösung erreichen konnten. Wir haben also die räumliche Auflösung durch ein rein rechnerisches Verfahren erhöht und dabei die Gerätschaften zur Bildaufnahme nicht verändert. Wir haben den Kontrast im rechten Teil des Bildes erhöht, jedoch war das Bild so beschaffen, dass die Raumfrequenz nach rechts zunimmt. Die bedeutet, dass wir tatsächlich die hochfrequenten Anteile des Bildes verstärkt haben. Und genau das ist die Idee bei der Bildoptimierung mit Hilfe von Fouriermethoden. Fouriermethoden erlauben es uns, selektiv bestimmte Raumfrequenzen zu verstärken und somit die räumliche Auflösung zu verbessern. Man muss jedoch aufpassen, nicht zu stark zu verstärken, weil man immer auch das Rauschen mit verstärkt und somit Gefahr läuft, ein stark verrauschtes Bild zu erhalten. Es ist wichtig, sich zu vergegenwärtigen, dass wir in diesem Beispiel noch keine Fouriermethoden verwendet haben. Wir haben lediglich ein Bild verwendet, was geschickt für unsere Zwecke konstruiert war, so das wir den Effekt der Verstärkung hoher Raumfrequenzen studieren konnten, ohne Fouriermethoden anwenden zu müssen. Das Schöne an wirklichen Fouriermethoden ist, dass man sie auf jedes Bild anwenden kann und sie meist viel besser funktionieren als der hier vorgeführte mathematische Taschenspielertrick.
Fourier-Reihen
Fast alle periodischen Funktionen, die man in der medizinischen Bildgebung braucht, können als Fourierreihe dargestellt werden. Dieser Ansatz basiert auf der Tatsache, dass jede Wellenform (mathematisch: jede periodische Funktion, die abschnittsweise stetig und monoton ist) als eine Reihe aus Sinus- und Kosinusfunktionen angesehen werden kann. Man kann sie dann wie folgt aufschreiben.
Wobei wir hier die Reihe nur bis zu dem Glied bzw. aufgeschrieben haben. Häufig hat man damit aber noch nicht genau die Funktion erreicht, die man erreichen wollte. Man hat lediglich eine sehr ähnliche Funktion. Selbst wenn man es nicht schafft, die exakte Funktion durch eine endliche Reihe darzustellen, so kann man immerhin eine Regel angeben, nach der man beliebig viele Glieder einer unendlichen Reihe berechnen kann. Mit jedem weiteren Glied nähert man sich immer besser an die gesuchte Funktion an. Ferner kann man sich beliebig genau an die gesuchte Funktion annähern, wenn man nur genügend viele Glieder berechnet. Man sagt dann auch, die unendliche Reihe ist die gesuchte Funktion. Diese Aussage ist mathematisch korrekt, allerdings kann man eine unendliche Reihe numerisch nicht genau berechnen, denn dazu müsste man ja unendliche lange rechnen. Wichtig ist nur, dass man eine Funktion durch ihre Fourierreihe beliebig genau berechnen kann, wenn man die Regel kennt, nach der die einzelnen Glieder der Reihe zu berechnen sind, und lange genug rechnet.
Eine Rechteckfunktion besitzt folgende Fourierreihe.
(1)
Wobei die Amplitude der Rechteckfunktion bezeichnet.
Auch die Gegenrichtung ist mathematisch möglich. z. B. kann eine Rechteckfunktion konstruiert werden indem, man eine große Zahl von Sinusschwingungen unterschiedlicher Amplitude aufaddiert. Die Summation der ersten 4 Terme ist in der folgenden Abbildung dargestellt. Der erste Term ist in Abbildung (a) gezeigt die Addition des zweiten Terms in Abbildung (b) und so weiter. Man beachte, dass die Fundamentale, (auch erste Harmonische bezeichnet, Abbildung (a)) dieselbe Frequenz wie die Rechteckfunktion hat, und höhere Frequenzen die Form der Rechteckwelle nacheinander aufbauen (Abbildungen (b) bis (d)). Wir schließen daraus, dass höhere Frequenzen zur Schärfe der Flanken der Rechteckwelle beitragen.
 |
 |
 |
 |
Fourier-Spektrum
Die Fourierreihe kann auch als Frequenzspektrum dargestellt werden. Als Beispiel sind in der folgenden Abbildung die Amplituden der Frequenzkomponenten aus der Gleichung der Rechteckwelle (1) gegen die Raumfrequenz dargestellt. Man beachte, dass das Fourierspektrum dazu verwendet werden kann, diejenigen Frequenzen und Amplituden zu identifizieren, die zu einer gegebenen Wellenform beitragen. Man beachte weiterhin, dass Graphen, in denen die Amplitude gegen die Strecke aufgetragen wird, im allgemeinen als Darstellung im Ortsraum und Graphen, in denen die Amplitude gegen die Raumfrequenz aufgetragen ist, als Darstellung im Frequenzraum bezeichnet werden.

Fourier-Transformation
Die Fourier-Transformation ist eine elegante mathematische Methode, um Daten vom Ortsraum in den Frequenzraum zu konvertieren (siehe folgende Abbildung). Anders ausgedrückt, kann man die Frequenzen und Amplituden, aus denen eine beliebige Wellenform aufgebaut ist, leicht bestimmen, indem man die Fouriertransformierte dieser Wellenform berechnet.

Die Fouriertransformation wird im Bereich der medizinischen Bildgebung weithin verwendet. Einige ihre Anwendungen sind:
- Bestimmung der räumlichen Auflösung von abbildenden Systemen.
- räumliche Lokalisierung in NMR (Kernspin) Bildgebung.
- Analyse von Doppler-Ultraschall-Signalen.
- Filterung von Bildern in der Transmissions- und Emissions-Tomographie.
Die Inverse Fourier-Transformation ist eine mathematische Methode um Daten in der umgekehrten Richtung zu konvertieren. Also vom Frequenzraum in den Ortsraum, wie in der folgenden Abbildung zu sehen ist:

Zusammenfassend stellen wir fest, dass die Fouriertransformation FT uns erlaubt, die Sinuswellen zu bestimmen, aus denen eine Wellenform aufgebaut ist und dass wir mit der inversen Fouriertransformation IFT eine Wellenform aus einzelnen Sinuswellen zusammen bauen können.
Schließlich sollte noch erwähnt werden, dass die Berechnung von Fouriertransformationen mittels digitaler Computer meist mit einem speziellen Algorithmus namens Fast Fourier Transformation (FFT) durchgeführt wird.
Die Dirac-Delta Funktion
Ein für die medizinische Bildgebung wichtiger und interessanter Fall ist die Diracsche Delta-Funktion . (Mathematisch korrekt müsste man sie eigentlich Delta- Distribution nennen, weil sie die mathematischen Eigenschaften, die es braucht, um sich Funktion nennen zu dürfen, nicht ganz erfüllt, aber außerhalb der Mathematik nimmt man es damit meist nicht so genau.) Sie hat überall den Wert 0, außer an der Stelle . Dort kennt man ihren Wert nicht wirklich. Ferner gilt die Normierungsbedingung:
.
Ihre Fourier-Transformierte ist in der folgenden Abbildung gezeigt:

Die Fouriertransformation der Delta-Funktion ist eine konstante Funktion. Die Fourierreihe der Delta-Funktion ist also die Summe aus unendlich vielen Sinus-Funktionen, die alle die gleiche Amplitude haben. Wenn wir nun anfangen, die Delta Funktion zu verbreitern (also etwa durch eine schmale Gauß-Funktion, die der Normalbedingung genügt, ersetzen), sehen wir, dass die Sinusfunktionen mit niedrigeren Frequenzen hohe Amplituden haben und dass die Amplituden mit zunehmender Raumfrequenz abnehmen.

Modulationsübertragungsfunktion
Diese Verbreiterung ist ein Phänomen sehr ähnlich denen, die in der medizinischen Bildgebung auftreten. Wir können annehmen, dass die vorhergehende Grafik in der Amplitude gegen Strecke folgenden Effekten ähnlich ist:
- Dichtprofil einer Abbildung eines kleinen Lochs in einer Bleiplatte.
- Zählratenprofil durch ein Bild einer radioaktiven Punktquelle.
Die in dieser Grafik dargestellte Funktion wird als Point Spread Function (PSF, auf Deutsch Punktantwortfunktion, jedoch meist zugunsten des englischen Begriffs nicht verwendet) bezeichnet. Ihre Fouriertransformierte wird Modulationsübertragungsfunktion MTF genannt.

Einen Vergleich von allgemeinen Begriffen und Begriffen der Bildgebung, die in diesem Themenkreis verwendet werden, ist in der folgenden Tabelle gegeben.
| Gebiet | Allgemeiner Begriff | Begriff in der Bildgebung |
|---|---|---|
| Ortsraum | Ausgangsfunktion | Punktantwortfunktion (PSF) |
| Frequenzraum | Fourierspektrum | Modulationsübertragungsfunktion (MTF) |
Weiterhin kann man die MTF bestimmen aus:
- Linienantwortfunktion (Line-Spread-Function LSF)
- der differenzierten Eckenantwortfunktion (Edge-Response-Function ERF).
Symbolisch können wir schreiben:
wobei die mathematische Faltungsoperation bezeichnet. Anders ausgedrückt erhält man das reale Bild indem man das ideale Bild mit der PSF des Abbildungssystems faltet.
Um das ideale Bild zurückzuerhalten, muss man den Effekt der PSF auf rechnerische Weise rückgängig machen. Dies kann man leicht erreichen, indem man Fouriertransformation verwendet, weil der Faltungsprozess zu einer Multiplikation im Frequenzraum äquivalent ist. Also:
wobei die Fouriertransformierte der Ortsraumfunktion bezeichnet. Damit hat man:
.
Der vollständige Rekonstruktionsprozess, der auch als Entfaltung bezeichnet wird, ist durch die folgende Gleichung gegeben:
wobei die inverse Fouriertransformation der Frequenzraumfunktion bezeichnet.
Filterung des Fourierspektrums
Die oben vorgestellte Methode zur Rückgewinnung des idealen Bildes aus dem realen Bild ist ein Beispiel für die Filterung des Fourierspektrums. Anders ausgedrückt kann das Fourierspektrum, sobald es einmal für ein Bild erzeugt worden ist, gefiltert werden, so dass bestimmte Raumfrequenzen modifiziert, d.h. verstärkt oder unterdrückt werden. Das gefilterte Spektrum kann dann zurücktransformiert werden um daraus das gefilterte Bild zu gewinnen, und es so zu schärfen oder zu glätten. Dieser Prozess ist in der folgenden Abbildung schematisch dargestellt.

Eine Sache müssen wir noch im Detail klären, bevor wir uns näher mit den Bilddaten im Frequenzraum beschäftigen. Wir erinnern uns, dass Bilder im allgemeinen digital in einer rechteckigen Punktmatrix aufgenommen werden. Wobei die Größe dieser Punkte bestimmt, wie genau das digitale Bild seinem analogen Gegenstück entspricht. Die sich hieraus ergebende digitale räumliche Auflösung führt zu einer Grenze für die maximale Raumfrequenz die noch aufgenommen werden kann. Das üblicherweise in der digitalen Bildgebung verwendete Kriterium basiert auf dem Nyquist-Shannon-Abtasttheorem welches besagt, dass:
Wenn ein Bild Raumfrequenzkomponenten bis zu einer maximalen Raumfrequenz f enthält, dann sollten die Bilddaten mit einer Abtastfrequenz die mindestens doppelt so hoch wie f ist abgetastet werden um eine treue Wiedergabe zu erreichen.
Diese Abtastfrequenz wird üblicherweise als Nyquist-Frequenz bezeichnet. Bei geringeren Abtastfrequenzen, können die entstehenden digitalen Bilder Artefakte enthalten, die als Moiré-Effekt bezeichnet werden. Man bezeichnet dies gelegentlich auch als Alias-Effekt.
Gefilterte Rückprojektion
Der einfacheste Rückprojektionsprozess führt zu einer Unschärfe die das Bild so aussehen lässt als wäre es mit einer Funktion verschmiert worden. In der gefilterten Rückprojektion werden Fourierfilter benutzt um den Effekt der Verwischung zu entfernen.
In Formeln, kann man die gemessene Projektion als einer Faltung mit der Schmierfunktion wir folgt aufschreiben:
Die erste Stufe des Filterungsprozesses besteht in der Fouriertransformation der gemessenen projizierten Daten. D.h.
.
Die korrigierte Projektion, , erhält man dann indem man die gemessene Projektion
durch teilt und die inverse Fouriertransformation berechnet:
.
Der Ausdruck ist einfach eine steigende Ursprungsgerade (Diese wird im Englisch als Ramp bezeichnet).
Weiterhin kann man, wenn man die Funktion variiert, gleichzeitig die Unschärfe korrigieren und bestimmte Eigenschaften des rückprojizierten Bildes unterdrücken oder verstärken. Zum Beispiel kann man das Bild schärfen und gleichzeitig:
- feine Details hervorheben (wie im sogenannten Knochenalgorithmus in der Röntgencomputertomographie)
- das Bildrauschen unterdrücken (wie im sogenannten Weichgewebealgorithmus in der Röntgencomputertomographie)
Man kann die Ramp-Funktion variieren in dem man sie mit einer zweiten Funktion multipliziert, z.B. mit einer Butterworth Funktion wie sie beim SPECT verwendet wird:
wobei:
- die Cutoff Frequenz bezeichnet, welche die Frequenz definiert, bei welcher der Filter nur noch 50% des Signals durchlässt.
- : die Ordnung des Filters definiert (je höher die Ordnung, um so steiler fällt die Durchlasskurve des Filters im Bereich der Cutoff-Frequenz ab).
 |
 |
 |
Die Eigenschaften einer Anzahl von Filtern, die in der SPECT-Bildgebung verwendet werden, sind in der folgenden Tabelle angegeben:
| Amplitude = 1 für f < fc; Amplitude = 0 für f > fc |
||
| für ; |
||
| für f < fc; |
||
| für ; |
||
| für f < fc; |
||
| für f < fc; |
||
| für ; |
Bei der Auswahl des Filters für eine gegeben Rekonstruktionsaufgabe muss man im allgemeinen einen Kompromiss zwischen der Rauschunterdrückung und der Verstärkung feiner Details finden. Wobei man das Raumfrequenzspektrum der interessierenden Bilddaten berücksichtigen muss. In einigen Fällen ist ferner eine Erhöhung des Kontrastes notwendig und muss somit zusätzlich zu den oben genannten Anforderungen berücksichtigt werden.
Entfaltung
Einleitung
In der Nuklearmedizin versteht man unter einem Renogramm die Messung der Radioaktivität in der Niere, nach Injektion eines Radiotracers in die Außenvene. Die Ankunft des Tracers in der der Niere ist zeitlich verschmiert, und die unmittelbare Reaktion kann nicht direkt gemessen werden. Die Entfaltungsanalyse ist, wie wir unten sehen werden, eine Methode um die Antwortfunktion aus dem Renogramm zu bestimmen. So dass die Stoffwechselfunktion beider Nieren eines Patienten oder der Nieren zweier unterschiedlicher Patienten zuverlässig verglichen werden können.
Der Tracer enthält ein radioaktives Isotop, daher nimmt seine Aktivität zeitlich ab. Dieser Effekt überlagert sich mit der zeitlich veränderlichen Verteilung des Tracers im Körper. In diesem Kapitel lassen wir jedoch Effekte durch die zeitliche Veränderung der Radioaktivität des im Tracer enthaltenen Radioisotops außer Acht. Dieses Vorgehen ist berechtigt solange wir Untersuchungen durchführen deren Dauer erheblich kürzer ist als die Halbwertszeit des verwendeten Radioisotops. Bei einem Faktor 15 (entsprechend einer Untersuchungsdauer von 25 Minuten bei 99mTc) beträgt der Fehler etwa 5%.
Renographie
In der Renographie, zeigen hintergrundkorrigierte Kurven an wie sich die Menge eines Tracers in jeder Niere mit der Zeit verändert. Weiterhin hängt die Form jeder der beiden Kurven von der Rate ab, mit der der Tracer:
- über das renale arterielle System in die Nieren eintritt.
- die Nieren über den Harnleiter verlässt.
Die Rate mit der der Tracer in die Nieren eintritt wird Eingangsrate genannt und hängt ab von
- der Plasmakonzentration der Tracers in der renalen Arterie
- der Rate mit der der Tracer aus dem Plasma durch die Nieren extrahiert wird.
In Falle eines Tracers der schnell durch die Nieren extrahiert wird (wie z.B. OIH, MAG3) hängt die Extraktionsrate vom effektiven renalen Plasma-Fluss () ab, so dass:
Im Falle eines Tracers der durch Filterung durch die Glomeruli[1] extrahiert wird (z.B. DTPA) hängt die Rate der Extraktion von der glomerulären Filterungsrate ab (), so dass:
Der Verlauf der Plasmakonzentration enthält zu Anfang ein ausgeprägtes Maximum, dessen Amplitude und Dauer abhängt von:
- der Injektionsgeschwindigkeit
- der Körperstelle an der die Injektion durchgeführt wurde
- der Mischungsrate zwischen Tracer und Blut.
Nach diesem anfänglichen Maximum nimmt die Plasmakonzentration biexponentiell mit der Zeit ab. Dieser Abfall ist abhängig von:
- Der Austauschrate mit extravaskulären Regionen
- Dem Uptake[2] des Tracers durch die Niere
Die Plasmakonzentration , ist dementsprechend abhängig von Faktoren die in keiner direkten Beziehung zur Nierenfunktion stehen. Es ist somit schwer, falls nicht sogar unmöglich, die Renogramme verschiedener Patienten oder des selben Patienten zu unterschiedlichen Zeiten zu vergleichen.
- ↑ Ein Glomerulus ist Teil eines Nierenkörperchens. Ein Nierenkörperchen ist Teil eines Nephrons. Eine Niere besitzt ca. eine Million Nephronen. Das Nierenkörperchen filtert Primärharn aus dem Blut.
- ↑ Der Begriff Uptake wurde unverändert ins Deutsche übernommen. Er bezeichnet Aufnahme eines Stoffes in einem Organ.
Ein ideales Renogramm
Ein ideales Renogramm würde man erhalten wenn man den Tracer direkt in die Niere injizieren könnte. Idealerweise sollte eine solche Injektion zu einer Eingangsrate führen die durch eine Deltafunktion beschrieben werden kann. Eine solche würde man als Impulseingangsfunktion bezeichnen.
Das sich ergebende ideale Renogramm wird als Impulsantwort der Niere bezeichnet.
In der Praxis, misst man jedoch die Antwortfunktion der Niere für eine nicht ideale Eingangsrate. Diese reale Antwortfunktion , kann man sich als eine Faltung der tatsächlichen Eingangsrate mit der Impulsantwortfunktion der Niere vorstellen:
Der Prozess der Bestimmung von aus der Messung von und wird als Entfaltung bezeichnet. Anders ausgedrückt erlaubt die Entfaltung von Renogramm-Kurven die Antwortfunktion der Niere auf für eine ideale Injektion zu bestimmen. Als Ergebnis daraus kann man genauere Vergleiche von mehreren Untersuchungen eines Patienten oder zwischen unterschiedlichen Patienten anstellen. Zumindest in der Theorie!
Faltung
Bevor wir uns mit dem Thema Entfaltung beschäftigen, werden wir zunächst den Faltungsprozess behandeln.
Man betrachte das in der folgenden Abbildung dargestellte grob vereinfachte Modell einer Niere. Das Modell nimmt an, dass die Niere aus vier Durchgangswegen besteht, durch die der Tracer in gleicher Weise fließt. Nehmen wir an der Tracer brauche 3 Minuten um den kürzesten Weg zu passieren und 6 Minuten für den längsten, sowie 4 und 5 Minuten für die verbleibenden beiden Wege.

Gibt man eine Deltafunktion auf den Eingang des Modells, so wird die Antwort des Systems durch die Impulsantwortfunktion gegeben sein, wie dies in der obigen Abbildung dargestellt ist. Die Form der Impulsantwortfunktion kann man verstehen indem man die zeitliche Bewegung des Tracers durch das Modell betrachtet:
- Die Impulsantwortfunktion, , wird in den ersten drei Minuten nach der Injektion gleich eins sein, da die Ausgangsmenge des Tracers während dieser Zeit vollständig im Sichtfeld der Gamma Kamera verbleibt.
- In der vierten Minute wird die Menge des Tracers sich um 25% verringert haben. Denn der Anteil, der den kürzesten Weg genommen hat, wird das Sichtfeld der Kamera verlassen haben. Somit wird auf 0,75 abgenommen haben.
- Ähnlich wird in der fünften Minute auf 0,5 abfallen.
- Und schließlich auf 0.25 in der sechsten Minute und auf 0 in der siebenten Minute.
Der wichtige Punkt, den wir uns hier merken sollten ist, dass die Art und Weise wie die Antwortfunktion abfällt, Informationen über die Durchgangszeit der Wege enthält. Man kann das Abfallen der Antwortfunktion durch eine mittlere und eine maximale Durchgangszeit charakterisieren.
Man beachte das man dieses einfache Modell durch Hinzunahme weiterer Durchgangswege erweitert werden kann und dann auch Durchgangszeiten beschreibt, die realen Nieren sehr ähnlich sind. Man beachte weiterhin das diese Modellierungsverfahren einzeln auf das renale Parenchym[1], sowie auf das Nierenbecken[2] oder auf die Niere als ganzes angewandt werden können.
Leider ist es jedoch in der Praxis quasi unmöglich ideale Eingangsimpulse zu erzeugen. Eine Ausnahme bildet vielleicht der Fall einer Bolusinjektion[3] in die renale Arterie. Nichtsdestoweniger kann man den oben vorgestellten Gedankengang so abwandeln, dass er die Effekte bei einer nicht idealen Injektion entsprechend berücksichtigt.

Hier haben wir keinen idealen Eingangsimpuls (manchmal Bolus genannt) auf unser extrem vereinfachtes Modell der Niere gegeben. Wir haben vielmehr eine zeitlich ausgedehnte Eingangsfunktion verwendet in der die eingehende Tracermenge exponentiell abfällt. Wenn wir nun annehmen , dass die Antwort der Niere auf die Folge der Eingangsimpulse sich als Summe der Antworten der Einzelimpulse ergibt, so kann man die Gesamtantwortfunktion wie folgt berechnen.
wobei das Zeitintervall ist welches für die Messung der Menge des Tracers verwendet wird.
Daher gilt im allgemein:
wobei
Gehen wir nun von der oben vorgestellten diskreten Formulierung auf die kontinuierliche Schreibweise über, so erhalten wir eine Funktion die Faltungsintegral genannt wird.
welches man üblicherweise folgendermaßen aufschreibt:
Anders ausgedrückt kann man die reale Renogrammkurve als Ergebnis der Faltung der idealen Renogrammkurve mit der realen Eingangsfunktion begreifen.
Das gerade beschriebene Modell ist ein Beispiel für ein sogenanntes lineares System also ein System bei dem die Antwort auf eine Folge von Eingangsimpulsen sich als Summe der Antworten auf die einzelnen Impulse ergibt. Bei einem solchen System wird weiterhin angenommen, dass der Fluss des Tracers durch das System über die Messzeit konstant ist, es sich also um ein stationäres System handelt.
Anders ausgedrückt wird, für die Renographie, angenommen, dass die renale Clearance[4] und der Urinfluss über die Dauer der Untersuchung konstant sind.
Die renale Clearance nach der Injektion kann, nach der Anfangsphase des Renogramms, als zeitlich konstant angesehen werden, da die verwendete Tracermenge (sei es nun O123IH, 99mTc-MAG3 oder 99mTc-DTPA) so klein ist, dass sie die Funktion der Niere nicht beeinflusst. Das selbe trifft auf die den Urinfluss zu, jedoch tritt die Ausscheidung aus dem Nierenbecken häufig schubweise auf und nicht als kontinuierlicher Fluss. Dieses Fehlen eines stationären Zustandes führt zu großen Problemen bei der Anwendung von Entfaltungsverfahren.
- ↑ renal: die Niere betreffend. Parenchym: Grundgewebe welches eine bestimmte Funktion ausübt. renales Parenchym: Gewebe in der Niere welches die Funktion der Reinigung des Blutes ausübt
- ↑ trichterförmiges oberes Ende des Harnleiters
- ↑ einmalige Injektion einer hohen Dosis
- ↑ das Volumen an Plasma das die Nieren pro Zeiteinheit vom Tracer befreien können
Entfaltung
Die Entfaltung ist ein mathematisches Verfahren das verwendet wird um aus Messungen von und bestimmen. Man verwendet in der Renographie unter anderem folgende Entfaltungstechniken:
- Matrix Inversion - wobei das Faltungsintegral in Form einer Matrix ausgedrückt wird als:
- Wobei für die Matrixmultiplikation steht. Die lässt sich auflösen zu:
- wobei die inverse Matrix der Matrix bezeichnet.
- Fourier Transformation - wobei die Fouriertransformierte () des Faltungsintegrals berechnet wird. Also:
- kann bestimmt werden aus:
d.h. indem man die Fouriertransformierte von durch die Fouriertransformierte von , teilt und die inverse Fouriertransformation () des Ergebnisses berechnet.
Diese beiden Techniken sind sehr anfällig gegen statistische Fluktuationen der gemessenen Daten und der gemessenen Verläufe von und . Daher werden sie üblicherweise geglättet bevor die Fouriertransformation auf sie angewandt wird.
In der Klinischen Praxis verwendet man ein hintergrundkorrigiertes Renogramm als R(t), und wählt eine vaskuläre Region[1] (ROI[2]), z.B. das Hertz, in dem man misst. Die Impulsantwortfunktion erhält man entsprechend durch Entfaltung. Sie hat ungefähr die in der folgenden Abbildung gezeigt Form.

ist die Impulsantwort zur Zeit und man kann zeigen, dass sie gleich der Nieren Uptake Konstante ist. Man misst verschiedene Zeiten für den Durchgang des Tracers durch die Nieren, wie z.B. die minimale die mittlere oder die maximale Durchgangszeit. Man kann auch ein Durchgangszeitspektrum angeben indem man differenziert.
Schließlich bleibt zu bemerken dass ein hintergrundkorrigiertes Renogramm nicht strikt notwendig ist um eine Entfaltung durchzuführen und man somit auch das gemessene Renogramm unmittelbar verwenden kann. Der Grund hierfür wird klar sobald man sich vergegenwärtigt, dass die Gesamtantwortfunktion, welche sich aus den gemessenen Rohdaten ergibt, die Summe der Nierenantwortfunktion und der Gewebeantwortfunktion darstellt wie die folgende Abbildung zeigt.

Die Durchgangszeiten der Niere können auch noch aus der kombinierten Antwortfunktion ermittelt werden. Weiterhin erkennt man, dass die Uptake Konstante durch Extrapolation der Daten bestimmt werden kann.
- ↑ eine für die Blutgefäße repräsentative Region
- ↑ Der Begriff Region of Interest wurde aus dem Englischen unverändert in deutsche übernommen, übersetzt bedeutet er etwa Bereich von Interesse
Sonographie
Einleitung
Sonographie ist eine Anwendung des Sonars in der medizinischen Bildgebung, mit der die Oberfläche innerer Organe und ihre innere Struktur dargestellt werden können (siehe Bild unten). Diese Art der Bildgebung hat den Vorteil, dass ausschließlich nicht ionisierende Strahlung verwendet wird, daher setzt man sie häufig ein, um anatomische Zusatzinformationen zu nuklearmedizinischen Bildern zu erhalten. Dieses Kapitel bietet eine Übersicht über die wesentlichen Eigenschaften sonographischer Bildgebung.
Wir beginnen mit einer Übersicht über die relevanten Eigenschaften von Schallwellen und wenden uns später den einzelnen Verfahren im Detail zu.
Schallwellen
Schallwellen wie sie sich z. B. in Luft ausbreiten, stellen periodische Änderungen des Luftdrucks dar, also veränderliche Regionen hoher und niedriger Dichte der Luftteilchen.

Diese Longitudinalwellen bewegen sich mit einer Geschwindigkeit von etwa in Luft bei Normalbedingungen und mit höheren Geschwindigkeiten in dichteren Medien, wie z. B. Wasser oder weichem Gewebe. In der Tat benötigen mechanische Wellen ein Medium, in dem sie sich ausbreiten können. Der Satz Im Weltraum hört Dich niemand schreien, aus der Werbung zum Kinofilm Alien ist daher physikalisch korrekt. Eine Folge von einer Region hoher und einer Region niedriger Dichte wird auch eine Periode der Welle genannt (siehe Abbildung oben). Die Wellenlänge ist definiert als die Länge einer Periode und die Frequenz als die Anzahl der Perioden, die einen raumfesten Ort pro Sekunde passieren. Man verwendet für die Schallgeschwindigkeit gemeinhin den Buchstaben , gelegentlich jedoch auch (kleiner Deutscher Buchstabe v, innerhalb von Formeln häufig kursiv gesetzt). Dieser ist nicht zu verwechseln mit (kleiner griechischer Buchstabe ny). Dieser steht nämlich für die Frequenz. Diese Größen stehen der folgenden bedeutenden Beziehung zu einander:
Das menschliche Ohr kann Schallwellen bis zu einer Frequenz von ca. 20 kHz wahrnehmen. Wellen mit hören Frequenzen werden als Ultraschall bezeichnet. In der diagnostischen Sonographie werden jedoch viel höhere Frequenzen, im Bericht von etwa 1MHz bis 15MHz verwendet. Die unteren Frequenzen in diesem Bereich können verwendet werden um große tief liegende Strukturen abzubilden. Hohe Frequenzen können bei kleinen Strukturen nahe an der Oberfläche betrachtet werden.
Die Geschwindigkeit von Ultraschallwellen entspricht der von Schallwellen im selben Medium. Sie ist in der folgenden Tabelle für einige innere Organe angegeben. Man beachte, dass im Allgemeinen eine Geschwindigkeit von 1540 m/s für weiches Gewebe in der Sonographischen Bildgebung angenommen werden kann. Diese Zahl ist ein Mittelwert der entsprechenden Werte für einzelne Arten von Gewebe Muskeln und Organen.
| Medium | Geschwindigkeit (m/s) |
|---|---|
| Luft | 331 |
| Hirn | 1541 |
| Niere | 1561 |
| Leber | 1549 |
| Muskelgewebe | 1585 |
| Fettgewebe | 1450 |
| Weiches Gewebe (Mittelwert) |
1540 |
Ultraschallwellen für die sonographische Bildgebung werden meist in einzelnen Pulsen erzeugt. Die Zeit zwischen den Pulsen wird verwendet, um die Echos der Ultraschallwellen aus dem Körper zu messen. Diese Technik verwendet das sogenannte Echo-Puls Prinzip, wie es im Diagramm unten dargestellt ist. Die obere Hälfte des Diagramms zeigt einen Ultraschallsender, der einen Ultraschallpuls in einen hypothetischen Körper sendet, welcher der Einfachheit halber nur aus zwei Gewebesorten bestehen soll. Die untere Hälfte des Diagramms zeigt die Situation nachdem der Ultraschallpuls die Grenze zwischen den beiden Gewebesorten passiert hat. Man erkennt einen reflektierten Puls (bzw. ein Echo), das sich wieder zurück auf den Sender zu bewegt, sowie den transmittierten ursprünglichen Puls, der sich im zweiten Medium weiter ausbreitet.
Die Zeitdauer die der Puls braucht, nachdem er im Sender erzeugt worden ist, um zur Grenze der beiden Gewebe zu gelangen plus der Zeit die der reflektierte Puls braucht um zum Sender zurückzukehren nennt man Puls-Echo Zeit . Sie erlaubt die Messung der Tiefe der Gewebegrenze d nach der folgenden Formel.
Man beachte,
- Es wird die mittlere Geschwindigkeit von Ultraschallwellen in Gewebe verwendet.
- Der Faktor tritt auf weil der Puls und das Echo dieselbe Strecke zurücklegen müssen. Der gesendete Puls vom Sender zur Schnittstelle und der Echopuls von der Schnittstelle zurück zum Sender
Ultraschallsender verwenden das piezoelektrische Prinzip und regen dadurch einen Kristall zu Schwingungen im Ultraschall Frequenzbereich an. Diese Schwingungen übertragen sich auf das umgebende Medium (Gewebe) und erzeugen dort Regionen höhere und niedriger Dichte die sich als Wellen durch Gewebe ausbreiten. Echos aus dem Gewebe werden dann im selben Kristall detektiert in dem der piezoelektrische Effekt in Umgekehrter Richtung ausgenutzt wird.

Die Ultraschallpulse werden gedämpft, während sie sich durch das Gewebe ausbreiten. Es kommt zu vier wichtigen Effekten, wenn eine Ultraschallwelle auf eine Grenzfläche zwischen zwei Geweben trifft. Diese sind in der folgenden Abbildung dargestellt.

| Schnittstelle | Reflektions Koeffizient (%) |
|---|---|
| Weiches Gewebe -Luft | 99.9 |
| Fett - Muskel | 1.08 |
| Fett - Niere | 0.64 |
| Muskel - Leber | 1.5 |
Ein Teil der Energie des Pulses wird ungerichtet gestreut. Ein weiterer Teil erzeugt ein Echo durch gerichtete Reflexion. Ein weiterer Teil wird durch die Grenzfläche hindurch transmittiert und kann an weiteren Grenzflächen erneute Reflektionen hervorrufen. Ein kleiner Teil der Energie wird an der Grenzfläche absorbiert. Die Reflektivität einer Grenzfläche hängt von den Schallkennimpedanzen der beiden beteiligten Gewebe ab. Repräsentative Werte sind in der Tabelle aufgeführt.
Man erkennt aus der Tabelle, dass es zu einer starken Reflektion an der Grenzfläche von Luft und weichem Gewebe kommen kann. Daher wird ein Koppelmedium zwischen dem Sender und der Haut des Patienten verwendet. Körperinterne Reflektionen weisen, wie man aus der Tabelle sieht, einen Reflektionsgrad in der Größenordnung von 1% auf, was eine hinreichende Transparenz für die Bildgebung bedeutet.
Ultraschall Scanner
In der Ultraschalltechnik ist es üblich, die reflektierten Schallwellen mit den selben Bauteil zu empfangen, mit dem sie erzeugt werden. Als Bezeichnung hat sich daher neben Sender/Empfänger die Bezeichnung Transducer (Englisch für Umformer) eingebürgert, die wir im folgenden verwenden werden. Ein vereinfachtes Blockbild eines Ultraschallsystems ist in der Abbildung unten gezeigt. Der gezeigte Scanner arbeitet mit einem Parallelschallkopf, den wir in Kürze im Detail kennen lernen werden. Wir sehen den zentralen Zeitgeber oben rechts im Bild. Dieser Schaltkreis legt die Anzahl der Ultraschallpulse fest, die der Transducer pro Sekunde erzeugt. Dieser Faktor wird als Pulswiederholrate (PWR) bezeichnet. Man sieht ferner, dass die von Transducer empfangenen Echopulse durch einen Empfangsverstärker verstärkt werden, an dessen Ausgang sich ein Demodulator befindet der seine Signale an einen Scan Konverter weitergibt, so dass die Amplitude der detektierten Echos angezeigt werden kann.

Ein Zeit-Verstärkungs-Kompensationskreis (TGC) führt zur selektiven Verstärkung der Echos. Entfernte Echos werden stärker verstärkt als nahe, um die Dämpfung über die längere Signallaufstrecke zu kompensieren. Der Demultiplexer wird verwendet, um die einzelnen Kristalle im Transducer nacheinander anzuregen.

Im einfachsten Aufbau werden die Kristalle hintereinander mit jeweils einem Spannungspuls angeregt. Diese emittieren daraufhin einer nach dem anderen jeweils einen Ultraschallpuls. So dass das Gewebe Zeilenweise beschallt wird. Üblicherweise geschieht dies in schneller Folge mehrere Male hintereinander. Das dabei entstehende Ultraschallbild wird auch als B-Mode Scan bezeichnet. Es besteht aus einer zweidimensionalen Darstellung des Echo-Puls-Musters, in einem Querschnitt durch das Gewebe, wobei sich die Transducerposition am oberen Bildrand befindet. Die Orte mit hoher Echointensität werden meist als helle Punkte auf dunklem Hintergrund dargestellt, wobei die Amplitude der Echopulse durch Zwischenwerte als Helligkeit der Pixel dargestellt wird. Die folgende Abbildung wurde mit einem ähnlichen Verfahren erzeugt.

Genaugenommen wurde für das Bild ein aufwändigerer Empfänger verwendet, ein sogenannter Sektorscanner. Ein Sektorscanner nimmt wie der Name sagt ein sektorförmiges Bild auf. Im Englischen wird der Sektorscanner als Phased Array Transducer bezeichnet. Der Begriff Phased Array wird häufig unverändert ins Deutsche übernommen und findet als Funktionsprinzip nicht nur im Ultraschallbereich sondern z.B. auch in der Radartechnik Verwendung. Ein Phased Array- bzw. Sektor- Scanner besteht aus einigen kleinen Kristallen die auf einer Linie angeordnet sind. Sie werden nun in geschickter Weise zeitversetzt angesteuert, wie im Bild unten andeutungsweise gezeigt wird. Die Richtung und Fokussierung des Ultraschallstrahls kann allein durch diese Ansteuerung der Kristalle modifiziert werden.

Es gibt viele weitere Transducer Anordnungen, die jeweils in bestimmten klinischen Anwendungen ihre besonderen Vorzüge haben. Zwei Bauformen mechanischer Transducer sind unten als Beispiele gezeigt. Links ist ein Transducer dargestellt, der während der Aufnahme vor und zurück gezogen wird. Rechts hingegen sieht man einen Aufbau aus mehreren rotierenden Einzelkristallen.
 |
 |
Das Blockschaltbild der Umwandlungselektronik ist in der folgenden Abbildung dargestellt.

Die Abbildung zeigt den Prozess der Digitalisierung des Echo Signals mit Hilfe eines Analog-Digital Konverters (ADC) und die Vorverarbeitung des Signals mit einer Eingangskonversionstabelle (Input look up table ILUT), vor der Speicherung in einem wahlfrei zugreifbaren Speicher (random access memory RAM). Das RAM wird der Reihe nach mit den Daten gefüllt, die beim Scannen des Patienten entstehen, und in einer für das Anzeigegerät geeigneten Weise ausgelesen. Vor der Anzeige können die Bilddaten nachbearbeitet werden, indem eine Ausgangskonversionstabelle (Output look up table OLUT) verwendet wird, so dass Kontrastverstärkung oder andere Nachbearbeitungen vorgenommen werden können.
Wir erinnern uns, dass wir diese Art der Bildverarbeitung bereits in einer allgemeineren Form im einem vorhergehenden Kapitel dieses Wikibooks behandelt haben. Der Kasten mit der Bezeichnung Prozessor stellt einen Mikroprozessor dar welcher verwendet wird um den Scan und Konversionsprozess, sowie viele weitere Funktionen des Gerätes (wie zum Beispiel die zeitliche Abfolge des Sendens und Empfangens der Pulse beim Phased-Array-Transducer), zu steuern.
Eine häufig in der Sonographie benutzte Auflösung ist 512 x 512 x 8 Bits. Ein vergrößerter Ausschnitt des oben bereits gezeigten B-Mode Scans der Leber eines Patienten ist unten gezeigt um die digitale Natur des Bilder zu verdeutlichen.

Wir beschließen diesen Abschnitt mit Photos eines Sonographischen Systems und einiger typischer Transducer.
 |
 |
 |
 |
Doppler Ultraschall
Der Doppler Effekt wird häufig verwendet um die Bewegung entfernter Gegenstände zu vermessen. Er wird in der medizinischen Sonographie verwendet um Bilder (und Töne) von den Bewegungen strömenden Blutes zu erhalten. Der Dopplereffekt tritt bei allen Wellen und wellenähnlichen Vorgängen auf, seien sie nun longitudinale oder transversale Wellen, oder gar Licht. Beim Licht wurde er zum Beispiel verwendet um nachzuweisen, dass wir in einem Expandierenden Universum leben. Er wird auch bei Radiowellen zur Geschwindigkeitskontrollen im Straßenverkehr in sogenannten Radarfallen verwendet. Er kann auf intuitiv als Änderung der Tonhöhe der Sirene eine vorbeirauschenden Krankenwagens erfahren werden.
Betrachten wir als Beispiel den von einer Lokomotive erzeugten Lärm, wie er im Diagramm unten dargestellt ist.

Wenn der Zug steht, und der Wind nicht bläst, wird sich der Ton in alle Richtungen gleichermaßen ausbreiten. Bewegt sich jedoch der Zug, so werden die Frequenzen in Vorderrichtung erhöht sowie die in in Rückrichtung entsprechend erniedrigt sein. Dies ist in der obigen Abbildung anschaulich dargestellt. Die Stärke des Effekts hängt offenbar von der Geschwindigkeit des Zuges ab. Diese von einem ruhenden Beobachter wahrgenommene Veränderung der Frequenz bezeichnet man als Doppler-Verschiebung. Eine Anwendung des Doppler-Effekts zur Bestimmung des Blutflusses ist in der folgenden Abbildung dargestellt.

wobei die Schallgeschwindigkeit im Medium bezeichnet.
Man verwendet in der Medizin üblicherweise Ultraschallpulse mit einer Frequenz von 2 bis 10 MHz um Blut in den Arterien (welches typischerweise mit 0 bis 5 m/s fließt) zu untersuchen. Die obere Gleichung ergibt, dass die Frequenzunterscheide in dem hörbaren Bereich des akustischen Spektrums von 0 bis 15 kHz liegt. Diese Signale können daher unmittelbar auf Lautsprecher ausgegeben und als Ton gehört werden. Man klicke Hier um die den Blutfluss der Halsschlagader des Autors des englischen Originaltextes als Beispiel zu hören.
Es ist auch möglich das Frequenzspektrum der Dopplerverschiebung zu untersuchen um feine Details der Verteilung der Flussgeschwindigkeiten des Blutes während eines Pumpzyklus des Herzens zu untersuchen indem man Fourier Transformierte des Signals berechnet.
Es ist jedoch gebräuchlicher Bilder der Verteilung der Frequenzverschiebung innerhalb von Blutgefäßen darzustellen indem man Techniken wie Farbdoppler- oder Powerdoppler-Sonographie verwendet. Diese Techniken verschmelzen automatisch Doppler Signale mit B-Mode Ultraschallbilder wie in die Beispielen unten gezeigt wird:
 |
 |
Farbdopplersonographie zeigt die Richtung des Blutflusses an. Sie kann daher sowohl positive als auch negative Dopplerverschiebungen detektieren und verwendet eine Farbnachschlagtabelle (Colour look up table CLUT) so dass Dopplerverschiebungen in der einen Richtung (meist auf die Sonde zu) in verschiedenen Rottönen und die in der anderen Richtung (meist von der Sonde weg) in Blautönen dargestellt werden wie es im obigen linken Bild am Beispiel an der Jugularvene (Halsader) und der Karotide (Halsschlagader) dargestellt wird. Ein vereinfachtes Blockdiagramm für diese Art der Bildgebung ist in der Abbildung unten dargestellt.

Das System verwendet einen Strahlformungsschaltkreis um die Piezokristalle in eine Phased Array Transducer zur B-Mode Bildgebung und zur Detektion der Dopplerverschiebung im schnellen Wechsel. Wobei die Echo Signale in den B-Mode Scanschaltkreis und die Dopplersignale zur Analyse in einen Autokorrelationsdetektor geführt werden. Ausgangsdaten von diesen beiden Schaltkreisen werden dann im Scan Konvertierungs und Bildaufbereitungsschaltkreis überblendet und zu einem Bild verschmolzen welches dargestellt wird.
Als letzten Punkt bleibt zu beachten dass das Amplitudencodierte Dopplersonogramm (Powerdoppler, rechte Abbildung) keine Information über die Flussrichtung des Blutes enthält da mit dieser Technik nur die Leistung der Reflektierten Dopplerpulse nicht jedoch deren Frequenzverteilung gemessen wird.
Literatur
Wikipedia Artikel : Sonografie
Kapitelzusammenfassungen
Dies ist das letzte Kapitel des Wikibooks Physikalische Grundlagen der Nuklearmedizin
Atom- und Kernstruktur
- Ein Atom besteht aus zwei Komponenten - einem (positiv geladenen) Kern und einer (negativ geladenen) Elektronenhülle
- Der Radius des Kerns ist etwa 10000 mal kleiner als der des Atoms
- Ein Kern kann aus zwei verschieden Teilchensorten bestehen - (ungeladenen) Neutronen und (positiv geladenen) Protonen, die man beide zusammen mit dem Überbegriff Nukleonen bezeichnet
- Die Masse eines Protons entspricht etwa der eines Neutrons, sowie der Masse von 1840 Elektronen
- Die Anzahl der Protonen entspricht bei einem isolierten neutralen Atom der Anzahl der Neutronen
- Die Kernladungszahl gibt die Anzahl der Protonen im Kern an.
- Die Massenzahl gibt die Anzahl der Nukleonen im Kern an
- Isotope eines Elements haben die gleiche Kernladungszahl, jedoch unterschiedliche Massenzahlen
- Isotope werden durch ihr chemische Elementsymbol mit ihrer Massenzahl hochgestellt und ihrer Kernladungszahl tiefgestellt vor dem Elementsymbol bezeichnet
- Die Atomare Masseneinheit wird definiert als 1/12 der Masse eines Atoms des stabilen und häufigsten Kohlenstoffisotops 12C.
- Die Bindungsenergie ist die Energie, welche die Nukleonen im Kern zusammenhält und wird in Elektronenvolt (eV) gemessen.
- Um dem Effekt der mit steigender Protonenzahl zunehmender elektrostatischen Abstoßung zu kompensieren, steigt die Anzahl der Neutronen schneller und ergibt so den Verlauf der Stabilitätskurve
- Es gibt etwa 2450 Isotope von etwa 100 Elementen und die instabilen Isotope liegen oberhalb oder unterhalb der Stabilitätskurve
- Instabile Isotope zerfallen zur Stabilitätskurve hin, indem sie in größere Teile zerbrechen (Spaltung) oder Teichen/Energie aussenden (Radioaktivität)
- Instabile Isotope = radioaktive Isotope = Radioisotope = Radionuklide
- ca. 300 der 2450 Isotope werden in der Natur gefunden - der Rest wird künstlich hergestellt
Radioaktiver Zerfall
- Spaltung: Einige schwere Kerne zerfallen indem sie in zwei oder drei Fragmente und einige Neutronen zerbrechen. Diese Fragmente bilden neue Kerne, welche im allgemeinen wiederum radioaktiv sind
- Alpha Zerfall: Zwei Protonen und zwei Neutronen verlassen den Kern zusammen in als ein Teilchen namens Alpha-Teilchen
- Ein Alpha-Teilchen ist ein 4He Kern
- Beta Zerfall - Elektronen-Emission: Einige Kerne mit einem Überschuss an Neutronen werden stabiler indem ein Neutron in ein Proton umwandelt und dabei ein Beta-Minus-Teilchen abstrahlt.
- Ein Beta-Minus-Teilchen ist ein Elektron
- Beta Zerfall - Positronen-Emission: Wenn die Zahl der Protonen in einem Kern einen Überschuss bildet, kann der Kern stabiler werden indem sich ein Proton in ein Neutron umwandelt und dabei ein Beta-Plus-Teilchen emittiert.
- Ein Beta-Plus-Teilchen ist ein Positron
- Positronen annihilieren sich mit Elektronen und ergeben zwei Gamma Strahlen die sich (im Schwerpunktsystem) entgegengesetzt auseinander fliegen.
- Beta Zerfall - Elektronen-Einfang: Ein Elektron einer inneren Schale wechselwirkt direkt mit einem Proton des Kerns und verbindet sich mit diesem einem Neutron
- Elektronen-Einfang wird auch K-Einfang (eigentlich nur falls das Elektron aus der K-Schale kommt) genannt.
- Nach einem Elektronen-Einfang, kann der angeregte Kern Gamma-Strahlen aussenden. Weiterhin wird Röntgenstrahlung emittiert wenn die Leerstelle in einer inneren Schale durch ein Elektron einer höheren Schale aufgefüllt wird.
- Gamma Zerfall – Isomerübergang: Ein Kern in einem angeregten Zustand kann seinen Grundzustand durch Abstrahlung eines Gamma-Strahl erreichen.
- Ein Gamma-Strahl ist ein Photon (Austauschteilchen der elektromagnetischen Wechselwirkung) von hoher Energie
- Gamma Zerfall- Innere Konversion: Die Anregungsenergie eines angeregten Kerns kann direkt auf ein Elektron aus der Elektronenhülle übergehen.
Das Zerfallsgesetz
- Das Zerfallsgesetz als Gleichung:
- Radioaktivität ist die Anzahl der radioaktiven Zerfälle pro Zeiteinheit
- Die Zerfallskonstante ist definiert als der Anteil an der ursprünglich vorhandenen Anzahl radioaktiver Kerne, der in einer Zeiteinheit zerfällt
- Halbwertszeit: Die Zeit die es dauert bis sich die Anzahl der radioaktiven Kerne in einer Probe auf die Hälfte reduziert hat
- Die SI Einheit der Radioaktivität ist das Becquerel (Bq)
- 1 Bq = ein radioaktiver Zerfall pro Sekunde
- Die traditionelle (veraltete) Einheit der Radioaktivität ist das Curie (Ci)
- 1 Ci = 3.7 · 1010 Zerfälle pro Sekunde
Einheiten der Strahlungsmessung
- Die Ionendosis beschreibt die Intensität von Röntgen- oder Gamma-Strahlung;
- Die SI Einheit der Ionendosis ist Coulomb pro Kilogramm ;
- = die Menge an Röntgen- oder Gamma-Strahlung, die beim Durchgang durch ein Kilogramm Luft (T=0°C; p=1013 hPa) Elektronen einer Ladung von 1 Coulomb freisetzt.
- Eine veraltete Einheit der Ionendosis ist das Röntgen (R);
- 1 R = 2.58·10-4C
- Die Ionisationsrate ist die Ionendosis per Zeiteinheit, also:
- Die Energiedosis ist die pro Kilogramm durchstrahlten Materials aufgenommene Energiemenge
- Die SI Einheit der Energiedosis ist das Gray (Gy)
- 1 Gy = Eine Absorption von 1 Joule pro Kilogramm bestrahlten Materials
- Eine veraltete Einheit der Energiedosis ist das rad
- 1 rad = Eine Absorption 10-2 Joule pro Kilogramm bestrahlten Materials
- Die Gammastrahlenkonstante beschreibt die Ionisationsrate die durch Gamma-Strahlung eines Radioisotops hervorgerufen wird
- Die SI Einheit der Gammastrahlenkonstante ist ausgedrückt in SI Einheiten ;
- Die von einem Röntgen- oder Gamma-Strahler empfangene Strahlung nimmt mit dem Quadrat der Entfernung von der Quelle ab.
Interaktion von Strahlung mit Materie
- Alpha-Teilchen
- üben eine erhebliche Anziehungskraft auf Elektronen der äußeren Hüllenelektronen der Atome an denen sie vorbei fliegen aus und lösen dadurch Ionisationen aus.
- bewegen sich geradlinig, bis auf selten auftretende direkte Zusammenstöße mit Atomkernen, die ihnen im Weg liegen.
- haben immer eine diskrete Energie
- Beta-Minus-Teilchen
- werden von Kernen angezogen und von Elektronen der Hüllen abgestoßen und können auf ihrem Weg Ionisationen auslösen.
- beschreiben eine gekrümmete Bahn
- haben kontinuierlich verteile Energien, da immer zwei Teilchen emittiert werden - ein Beta-Teilchen und ein Neutrino
- Gammastrahlen:
- haben immer eine diskrete Energie;
- haben viele verschiedene Wechselwirkungen mit Materie;
- wichtig für die nuklearmedizinische Bildgebung (und Radiographie) sind der photoelektrische Effekt und der Compton-Effekt.
- photoelektrischer Effekt:
- Wenn ein Gammastrahl mit einem Hüllenelektron zusammen stößt, kann er seine gesamte Energie an das Elektron abgeben und damit aufhören zu existieren.
- Das Elektron kann das Atom mit einer kinetischen Energie verlassen, die der Energie des Gammastrahls abzüglich der Bindungsenergie entspricht.
- Es entsteht ein positives Ion, wenn das Elektron das Atom verlässt.
- Das Elektron wird auch Photoelektron genannt.
- Das Photoelektron kann weitere Ionisationen auslösen.
- Röntgenstrahlung entsteht wenn das Loch in der Elektronenhülle durch eine Elektron einer höheren Schale gefüllt wird.
- Compton Effekt:
- Ein Gammastrahl kann auch nur einen Teil seiner Energie auf auf eine Valenzelektron (welches im wesentlichen als frei angesehen werden kann) übertragen.
- Führt zu einem gestreuten Gamma-Strahl
- wird auch Compton-Streuung genannt
- erzeugt ein positives Ion
- der Begriff Dämpfung wird sowohl bei Absorption als auch bei Streuung von Strahlung verwendet.
Dämpfung von Gamma-Strahlen
- Dämpfung steigt mit größer werdender Dicke, Dichte und Kernladungszahl des Absorbers an.
- Dämpfung nimmt mit steigender Energie der Gamma-Strahlung ab.
- Dämpfung wird durch die Gleichung beschrieben.
- Der lineare Schwächungskoeffizient ist definiert als Anteil der einfallenden Intensität die beim Durchgang durch eine Längeneinheit des Absorbermaterials absorbiert wird.
- Der lineare Schwächungskoeffizient wird meist in cm-1 angegeben.
- Die Halbwertsdicke ist die Dicke an Absorbermaterial die benötigt wird um die Intensität einfallender Strahlung um einen Faktor 2 zu reduzieren.
- Der Massenabsorptionskoeffizient ist definiert als der lineare Schwächungskoeffizient geteilt durch die Dichte des Absorbers.
- Der Massenabsorptionskoeffizient wird meist in der Einheit angegeben.
Gasgefüllte Strahlungsdetektoren
- Zu den gasgefüllten Strahlungsdetektoren gehören die Ionisationskammer , der Proportionalzähler und der Geiger-Zähler
- Sie arbeiten auf Basis der von der einfallenden Strahlung erzeugten Ionisation der Gasatome, wobei die entstehenden positiven Ionen und negativen Elektronen an den Elektroden gesammelt werden
- Der Begriff Ionenpaar bezeichnet ein positives Ion zusammen mit einem Elektron
- Die Betriebseigenschaften eines gasgefüllten Detektors hängen entscheidend von der angelegten Gleichspannung ab.
- Die Ausgangsspannung einer Ionisationskammer kann auf Basis ihrer Kapazität berechnet werden.
- Man benötigt einen sehr präzisen Verstärker um die Spannungspulse eine Ionisationskammer zu messen.
- Als Füllgas für eine Ionisationskammer benutzt man im allgemeinen Luft.
- Ionisationskammern werden üblicherweise verwendet um die Strahlenbelastung (in einem Gerät namens Dosimeter) oder die Radioaktivität (in einem Gerät namens Dosiskalibrator) zu messen.
- Die gesamte in einem Proportionalzähler gesammelte Ladung kann bis zu 1000 mal so groß wie die ursprünglich durch die Strahlung erzeugte Ladung sein.
- Die ursprüngliche Ionisation durch Strahlung führt zu einem vollständigen Durchschlag in einem Geigerzähler
- Das Gas in einem Geigerzähler ist üblicherweise ein Edelgas
- Der Durchschlag des Geigerzählers muss gestoppt werden um den Geigerzähler für das nächste Ereignis scharf zu machen. Dies bezeichnet man auch als Löschen des Geigerzählers
- Geigerzähler haben eine Totzeit, eine kleine Zeitspanne unmittelbar nach dem Durchbruch des Gases ist der Zähler inaktiv.
- Die wahre Zählrate kann aus der abgelesenen Zählrate mittels der Totzeitgleichung bestimmt werden.
- Die anzulegende Gleichspannung muss sorgfältig gewählt werden, jedoch sind die Anforderungen an die Stabilität der Spannungsquelle gering.
Szintillationszähler
- NiI(Tl) is ein Szintillatorkristall, der häufig in der Nuklearmedizin verwendet wird.
- Der Kristall ist an eine Photomultiplier Röhre gekoppelt, die einen der von der Strahlung im Kristall deponierten Energie proportionalen Spannungspuls erzeugt
- Man benötigt einen sehr empfindlichen Verstärker um diese Spannungspulse zu messen
- Die Amplitude der Spannungspulse hängt davon ab, wie die Strahlung mit dem Kristall wechselwirkt. Die Pulshöhen bilden also ein Spektrum dessen Verlauf von den beteiligten Wechselwirkungsmechanismen abhängt. Für Gammastrahlung mittlerer Energie wie sie in der nuklearmedizinischen Diagnostik am Patienten angewandt wird, sind dies zum Beispiel der Compton Effekt und der photoelektrische Effekt.
- Ein Energiespektrum eines monoenergetischen Gammastrahlers mittlerer Energie besteht aus einem Photopeak und einem Compton Kontinuum.
- Pulshöhen Analyse wird verwendet um nur Spannungspulse, deren Amplitude innerhalb eines definierten Intervalls liegt, zu selektieren.
- Ein Pulshöhenanalysator besteht aus einem Lower-Level-Diskriminator (durch den nur Pulse größer als sein eingestellter Schwellwert hindurch kommen) und einem Upper-Level-Diskriminator (durch den nur Pulse kleiner als sein eingestellter Schwellwert hindurch kommen)
- Man erhält so ein variables Fenster welches man beliebig auf dem Spektrum platzieren kann, wenn man es zum Beispiel Schrittweise abtasten möchte.
- Ein Einkanalanalysator (engl. Single Channel Analyser SCA) besteht aus einem Pulshöhenanalysator und einem Zähler (engl. Scaler) oder einem Ratemeter.
- Ein Mehrkanalanalysator ist ein computergesteuertes Gerät welches Daten in mehreren Fenstern gleichzeitig aufnehmen kann.
Nuklearmedizinische Abbildungssysteme
- Eine Gammakamera besitzt einen NI(Tl Kristall) mit großen (25-40 cm) Durchmesser und einer Dicke von etwa 1 cm.
- Der Kristall wir meist von 37 bis 91 Photomultipliern beobachtet.
- Die von den Photomultiplierröhren erzeugten Signale werden von einer Positionselektronik verarbeitet, welche +/- X und +/- Y Signale erzeugt.
- Diese Signale werden summiert und ergeben das Z Signal welches an einem Pulshöhenanalysator weitergeleitet wird.
- Die +/- X, +/- Y und das diskriminierte (vom Pulshöhenanalysator verarbeitete) Z Signal werden im Computer digital zu einem Bild verrechnet
- Ein Kollimator wird verwendet um die räumliche Auflösung der Gammakamera zu erhöhen.
- Kollimatoren bestehen im allgemeinen aus einer Bleiplatte mit vielen kleinen Löchern
- Am weitesten verwendet wird der Parallellochkollimator
- Das am besten auflösbare Gebiet liegt unmittelbar vor dem Kollimator
- Parallellochkollimatoren gibt es in unterschiedlichen Durchmessern, Lochlängen, Lochdurchmessern und Wandstärken. Die Kombination dieser Eigenschaften bestimmt die Sensitivität und räumliche Auflösung der bildgebenden Systeme.
- An weitere Kollimatortypen gibt es solche mit divergierenden Löchern (welche verkleinerte Abbildungen erzeugen), solche mit konvergierenden Löchern (welche vergrößerte Abbildungen erzeugen) und Pinhole Kollimatoren (welche vergrößerte gespiegelte Bilder erzeugen).
- Konventionelle Bildgebende Verfahren mit einer Gammakamera werden auch als planare Bildgebung bezeichnet, das heißt man erhält beim zweidimensionalen abbilden eines dreidimensionalen Objekts eine Überlagerung der dreidimensionalen Details und damit keine Tiefeninformation.
- Single Photon Emission Computed Tomography (SPECT) erzeugt Schnittbilder des Körpers
- SPECT verwendet eine Gammakamera um Bilder aus einer Reihe von Winkeln um den Patienten aufzunehmen.
- Die erhaltenen Daten können durch gefilterte Rückprojektion und interaktive Rekonstruktion weiterverarbeitet werden.
- SPECT-Gammakameras haben ein, zwei oder drei Kamera Köpfe
- Positronen Emissionstomographie (PET) erzeugt ebenfalls Schnittbilder des Körpers
- PET nutzt die Tatsache aus, dass bei der Annihilation von Positronen mit Elektronen zwei Gammastrahlen zu je 511 keV mit entgegengesetzter Ausbreitungsrichtung erzeugt werden.
- Wenn die beiden entstehenden Gammastrahlen von zwei der in einem Ring um den Patienten angeordneten Detektoren detektiert werden liegt muss ihr Ursprungsort auf der direkten Verbindungslinie dieser beiden Detektoren liegen.
- Eine Flugzeit Berechnung kann benutzt werden um den Ursprungsort der Strahlung zu lokalisieren.
- PET Systeme benötigen ein nahe gelegenes Zyklotron um kurzlebige Radioisotope, wie C-11, N-13, O-15 und F-18 zu erzeugen.
Produktion von Radionukliden
- Natürlich vorkommende Radioisotope haben im allgemeinen lange Halbwertszeiten, gehören zu relativ schweren Elementen, und sind daher für die medizinische Diagnostik unbrauchbar.
- Radioisotope für die medizinische Diagnostik werden im allgemeinen künstlich hergestellt.
- Spaltungsprozesse können so verwendet werden. dass die interessanten Radioisotope chemisch von den Spaltprodukten getrennt werden können.
- Ein Zyklotron kann benutzt werden um geladene Teilchen auf so hohe Energien zu beschleunigen, dass das Material des Target mit dem sie zu Kollision gebracht werden aktiviert wird.
- Ein Radioisotopengenerator wird im allgemeinen im Krankenhaus verwendet um kurzlebige Radioisotope herzustellen.
- Ein Technetium-99m Generator besteht aus einer Aluminiumsäule, die 99Mo enthält welches in 99mTc zerfällt.
- Eine Salzlösung wird durch den Generator gepresst um das entstandene 99mTc zu eluieren. Die entstehende Lösung heißt Natriumpertechnetrat
- Sowohl Überdruck- als auch Unterdruck-Generatoren werden verwendet
- Ein Dosiskalibrator wird benötigt, wenn ein Technetium-99m Generator verwendet wird. Zum einen um die Radioaktivität bei der Herstellung der am Patienten anzuwendenden Dosis zu messen und um zu prüfen ob Reste von 99Mo in der gesamten Lösung vorhanden sind.
Übungsfragen
- Diskutiere den Prozess des Radioaktiven Zerfalls und argumentiere dabei anhand der nuklearen Stabilitätskurve!
- Beschreibe vier häufige Formen des radioaktiven Zerfalls!
- Gib das Gesetz des radioaktiven Zerfalls als Formel an und erkläre die Bedeutung der einzelnen Variablen !
- Definiere die folgenden Größen
- Halbwertszeit
- Zerfallskonstante
- Becquerel
- Eine Probe radioaktiven Materials wird mit einer Radioaktivität von 100 kBq gemessen. 82 Tage später findet man bei einer erneuten Messung eine Radioaktivität von 15 kBq. Berechne:
- die Halbwertszeit
- die Zerfallskonstante
- Definiere jeder der folgenden Einheiten radioaktiver Strahlung
- Röntgen
- Becquerel
- Gray
- Sievert
- Schätze die Ionendosisrate in einem Meter Entfernung von einer Quelle mit einer Radioaktivität von 100 MBq und einer spezifischen Gammastrahlenkonstante von 50mR pro Stunde pro MBq bei 1 cm Abstand ab.
- Erkläre kurz das Funktionsprinzip eines gasgefüllten Strahlungsdetektors
- Skizzierte die Abhängigkeit der in gasgefüllten Detektoren erzeugten Spannungspulse von der angelegten Gleichspannung. Erkläre in welchen Bereichen Geigerzähler und Ionisationskammern betrieben werden.
- Beschreibe den grundsätzlichen Aufbau und die Funktionsweise ein Szintillationsspektrometers.
- Erkläre die Komponenten des Energiespektrums einer monoenergetischen, Gammastrahlenquelle mittlerer Energie, welches man mit einem Szintillationsspektrometer erhält. Begründe deine Erklärung jeder einzelnen Komponente, aus der Wechselwirkung der Strahlung mit den Szintillatorkristall.
- Beschreibe den Aufbau und das Funktionsprinzip einer Gammakamera
- Vergleiche die Eigenschaften sowie die Vor und Nachteile dreier unterschiedlicher Kollimatortypen die mit einer Gammakamera verwendet werden können.
Multiple Choice (englisch)
Click HERE to access over one hundred online multiple choice questions covering this wikibook.
Lizenz
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 published by the Free Software Foundation; with no Invariant Sections, with no Front-Cover Texts, and with no Back-Cover Texts. In order to receive a copy of the GFDL GNU Free Documentation License write to the Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA 02110-1301, USA or see http://www.gnu.org/copyleft/fdl.html.