Teilchenphysik/ Druckversion
Vorwort
[Bearbeiten]Die Teilchenphysik (oder Elementarteilchenphysik) behandelt den elementaren Aufbau der Materie und beschreibt die Wechselwirkungen ihrer fundamentalen Bausteine. Diese Bausteine gelten im Rahmen des Standardmodells als nicht weiter teilbare Einheiten der Materie. Aus diesen setzt sich die beobachtbare Materie zusammen.
Wenn wir "Teilchen" sagen, meinen wir eigentlich etwas, das sich - infolge der Dualität zwischen Teilchen und Welle - manchmal wie ein Teilchen, manchmal aber auch wie eine Welle verhält.
Wie wir im weiteren Verlauf des Buches sehen werden, gibt es noch weitere, in unserer normalen Umwelt nicht vorkommende, elementare oder aber auch zusammengesetzte Teilchen. Das heutige Wissen über die Elementarteilchen und ihre Wechselwirkungen wird im so genannten Standardmodell zusammengefasst. In diesem ersten Teil soll es hauptsächlich um das Standardmodell gehen. Neuere, darüber hinausgehende Theorien werden im zweiten Teil dieses Buches kurz angeschnitten.
Wie wir sehen werden, benutzen die Teilchenphysiker manche dieser Eigenschaften zur Einteilung der inzwischen relativ groß gewordenen Anzahl an Teilchen in Gruppen. Im letzten Teil dieses Buches wird es schließlich um die experimentelle Teilchenphysik gehen, also darum, wie man die Eigenschaften eines Teilchens bestimmt und wie man überhaupt die, in unserer gewohnten Umgebung nicht vorkommenden, Teilchen erzeugen kann.
Quantenmechanik
[Bearbeiten]Die Quantenmechanik ist eine der beiden Säulen, auf welchen die heutige Physik basiert. Auch in diesem Buch werden wir nicht ganz ohne die Quantenmechanik auskommen. Da die Quantenmechanik eines der komplexesten Gebiete der Physik ist und eine genaue Beschreibung dieser den Rahmen dieses Buches sprengen würde, sollen im folgenden Exkurs nur die wichtigsten Grundlagen der Quantenmechanik zusammengefasst werden. Wenn sie sich genauer zu diesem Thema informieren wollen, so finden sie dazu jede Menge eigene Literatur, von welcher ich im Anhang D einige nennen will. Wenn Sie die Grundlagen der Quantenmechanik bereits kennen, so können sie dieses Kapitel problemlos überspringen.
Sie sollten nicht versuchen die Quantenmechanik zu "verstehen" - der menschliche Geist ist von der uns umgebenden Welt so geprägt, dass wir uns die mikroskopische Welt der Quantenmechanik nicht vorstellen können - wir müssen uns damit abfinden.
Welle-Teilchen-Dualismus
[Bearbeiten]In der klassischen Physik kennt man zwei Arten, auf welche sich Energie und "Informationen" bewegen können. Entweder als Strom aus Teilchen oder als Welle. Diese haben fundamental unterschiedliche Eigenschaften. Dies soll mit dem Doppelspalt symbolisiert werden.
Wir haben ein Hindernis mit zwei Spalten. Nun schießen wir mit kleinen Kügelchen (Beispielsweise Erbsen) auf das Hindernis. Ein Teil der Erbsen fliegt durch den einen Spalt - ein Teil durch den anderen - wieder andere prallen am Hindernis ab. Wenn wir hinter dem Hindernis anschauen, wo die Erbsen ankommen, so stellen wir wie erwartet fest, dass nur direkt hinter den beiden Spalten Erbsen ankommen. Wenn wir die ankommenden Teilchen auf ein Papier auftragen, so bekommen wir also zwei Streifen an welchen die Teilchen ankommen.
Nun führen wir dasselbe Experiment anstatt mit Erbsen mit Wasserwellen durch. Wellen haben die Eigenschaft, dass sie interferieren können. Das heißt, wenn man zwei Wellen überlagert können sie sich entweder verstärken oder auslöschen oder wie in unserem Versuch: sie löschen sich an manchen Orten aus und verstärken sich an anderen Orten. Bringen wir hinter dem Doppelspalt einen Schirm an, so können wir nun mehrere Maxima sehen, wobei der Mittlere zwischen den beiden Spalten liegt.

Nun führen wir den Versuch mit Licht durch. Wenn wir die Spalten genügend klein machen (Größenordnung einige hundert Nanometer), so erhalten wir auch hier ein Interferenzmuster auf dem Schirm. Dies ist ein Beweis dafür, dass Licht eine Welle ist. Wenn wir die Lichtquelle nun jedoch sehr schwach machen, so erkennen wir auf dem Schirm einzelne Punkte - was ein Beweis für die Teilcheneigenschaft des Lichtes ist. Diese Dualität des Lichtes - dass also Licht sowohl Teilchen als auch Welleneigenschaften besitzt - widerspricht sowohl der klassischen Physik als auch dem menschlichen Vorstellungsvermögen. In der modernen Physik deutet man dies so, dass das Licht aus Teilchen besteht, welche sich jedoch nicht auf bestimmten berechenbaren Bahnen, wie unsere Erbsen von oben, bewegen, sondern dass die Wellennatur des Lichtes die Wahrscheinlichkeit dafür angibt, dass ein Teilchen an einer bestimmten Position ist. In der Quantenmechanik lassen sich keine präzisen Vorhersagen machen, sondern immer nur Wahrscheinlichkeitsaussagen. Dies ist kein Fehler unserer Theorien, sondern eine universelle Eigenschaft der Natur des Mikrokosmos. Im Jahre 1924 postulierte Louis de Broglie, dass dieser Welle-Teilchen-Dualismus nicht nur für das Licht, sondern für alle Teilchen gilt. Im Jahre 1961 gelang es Claus Jönsson schließlich bei einem Doppelspaltexperiment auch eine Interferenz von Elektronen zu zeigen. Jedes Teilchen hat also auch Welleneigenschaften, die Wellenlänge hängt dabei von der Masse des Teilchens ab: Desto größer die Masse desto kleiner die Wellenlänge. Da Interferenz nur auftritt wenn die Spaltbreite kleiner ist als die Wellenlänge, erklärt dies auch warum wir im alltäglichem Leben nicht von der Wellennatur der Teilchen mitbekommen - die Wellenlängen sind so extrem klein, dass es keine Spalten gibt, bei welchen Interferenzen auftreten.
Heisenbergsche Unschärferelation
[Bearbeiten]Wir sehen also, dass in der Quantenmechanik der Ort eines Teilchens nicht genau festgelegt ist, sondern nur mit einer Wahrscheinlichkeitsfunktion (Welle) angegeben werden kann. Eine weitere Aussage, bei welcher dies deutlich wird, ist die 1927 von Werner Heisenberg formulierte Heisenbergsche Unschärferelation. Sie sagt aus, dass es unmöglich ist, zwei gekoppelte Größen eines Teilchens gleichzeitig beliebig genau zu bestimmen. Diese beiden gekoppelten Größen können entweder Ort und Impuls oder aber Zeit und Energie sein. Es ist also unmöglich von einem Teilchen den Aufenthaltsort und den Impuls gleichzeitig exakt messen. Man hat immer Ungenauigkeiten von:
Dies liegt nicht daran, dass unsere Experimente zu schlecht sind (in Wahrheit sind unsere Messmethoden noch wesentlich ungenauer als diese Differenz), sondern es ist eine fundamentale Eigenschaft der Natur. Gleichermaßen gilt für die Energie zu einen bestimmten Zeitpunkt eines Teilchens:
Da das Plancksche Wirkungsquantum h=6,6*10-34Js extrem klein ist, spielt diese Grenze in unserem Alltag keine Rolle - wohl aber in der modernen Physik.
Das Standardmodell
[Bearbeiten]Von den Atomen zu den Elementarteilchen
[Bearbeiten]Das Atom
[Bearbeiten]Bereits 400 vor Christus, im antiken Griechenland, vermutete der Philosoph Demokrit, dass die Welt aus unteilbaren Teilchen besteht - er bezeichnete sie, nach dem griechischen a-tomos für unteilbar, als Atome. In einem wörtlich erhaltenen Fragment des Demokrit heißt es:
"Nur der Meinung nach", sagt Demokrit, "gibt es süß, nur der Meinung nach bitter, warm, kalt, nur der Meinung nach Farbe, in Wahrheit gibt es nur Atome und den leeren Raum".
Es ist erstaunlich, dass ein Philosoph durch Denken allein zu so einer tiefen Aussage kam. Es ist allerdings wahrscheinlich, dass er ein Experiment zur Gewinnung von Süßwasser aus dem Meerwasser mittels Dialyse kannte, das von Aristoteles beschrieben wird. Im weiteren historischen Verlauf setzte sich jedoch Aristoteles' Auffassung der 5 Elemente durch, die die Naturwissenschaft der folgenden 2 Jahrtausende prägte.
Nachdem die Atom-Idee bis ins 18. Jahrhundert in Vergessenheit geraten war, wurde sie von John Dalton, dem Schöpfer der modernen Chemie, wieder aufgegriffen. Aber noch um 1900 war Ernst Mach, der berühmte österreichische Physiker und Philosoph, ein eifriger Gegner der Atomhypothese. Zu Anfang des zwanzigsten Jahrhunderts konnte man aber erstmals experimentell zeigen, dass die Welt wirklich aus Atomen aufgebaut ist, beispielsweise durch Beobachtung der Brownschen Bewegung und ihrer quantitativen Erklärung durch Einstein.
Sichtbarmachung der Atome
[Bearbeiten]Der schottische Botaniker Robert Brown entdeckte 1827 unter dem Mikroskop, dass Pollenkörner in einem Wassertropfen unregelmäßig zuckende Bewegungen machen. Er nahm zunächst an, dass dies ein Hinweis auf die "Lebenskraft" sei, deren Wirken lange Zeit vermutet wurde; Brown fand den Effekt aber später auch bei eindeutig unbelebten Staubkörnern. Das Video links zeigt die "Brownsche Bewegung" von Fetttröpfchen in Milch.
Die Brownsche Bewegung wird hier dadurch bewirkt, dass die bewegten Wassermoleküle der Umgebung unregelmäßig gegen die Fetttröpfchen stoßen, so dass sich manchmal eine etwas größere Kraft in der einen, manchmal in einer anderen Richtung ergibt. Die durchschnittliche Geschwindigkeit der Bewegungen hängt von der Temperatur des Mediums ab - je schneller sich die Moleküle bewegen, desto wärmer ist das Medium. Im Jahre 1905 gelang Albert Einstein die quantitative Beschreibung dieser Bewegung, wobei sich aus der Beobachtung der Bewegung die Größe der sogenannten Avogadro-Konstanten, der Anzahl der atomaren Teilchen in einem Mol einer Substanz, bestimmen lässt. Es war also nicht nur möglich geworden, die Bewegung der Moleküle infolge ihrer thermischen Energie indirekt zu beobachten, sondern auch ihre Zahl pro Masseneinheit zu bestimmen.

1951 wurde erstmals ein Mikroskop entwickelt, mit welchem man einzelne Atome "sehen" konnte. Seit den Achtzigerjahren des 20. Jahrhunderts ist es aber auch möglich, mit Hilfe des Rastertunnelmikroskops (oder dem verwandten Rasterkraftmikroskop) die atomare Struktur einer Festkörperoberfläche unmittelbar abzubilden.1 In dem Bild links wurde eine Graphit-Oberfläche bei Raumtemperatur, an Luft, mit Hilfe eines Rastertunnelmikroskops gemessen. Die Vergrößerung lässt sich an dem Maßstab rechts unten ablesen, der eine Länge von 0,5 nm = 0,5 × 10-9 m hat. Die regelmäßige Anordnung der Graphitatome ist offenkundig, und zwar sieht man diejenigen Oberflächenatome, die kein unmittelbares Nachbaratom in der nächst unteren Graphitschicht besitzen.
Einschub: Wie untersucht man kleinste Strukturen?
[Bearbeiten]Auch wenn wir uns der Thematik der experimentellen Teilchenphysik erst im dritten Teil des Buches widmen wollen, so ist es doch zum problemlosen Verständnis der folgenden Abschnitte nötig zu wissen, wie man zu dieser Erkenntnis kam. Wir wollen also hier erklären, wieso in der Teilchenphysik keine Mikroskope verwendet werden und woher die Teilchenphysik ihre Kenntnisse nimmt.
Wenn man beispielsweise die Struktur einer pflanzlichen oder tierischen Zelle untersuchen will, verwendet man bekanntlich ein Mikroskop. Die Auflösung (d.h. seine Fähigkeit, kleinste Objekte getrennt darzustellen) ist durch die Wellennatur des Lichtes begrenzt. Das heißt, man kann zwei Körnchen, die näher beisammen liegen als die Wellenlänge des Lichtes (etwa 500 nm = 5 × 10-7 m)2 nicht mehr unterscheiden. Benötigt man höhere Auflösung, so kann man z.B. ein Elektronenmikroskop verwenden. Die de Broglie-Wellenlänge des (als Materiewelle betrachteten) Elektronenstrahls ist über die Energie der Elektronen wesentlich kleiner wählbar, dadurch ist eine wesentlich bessere Auflösung möglich. Die Auflösungen solcher Mikroskope sind zwar bereits - wie wir oben gesehen haben - hoch genug um Atome darzustellen, um jedoch zu testen ob Atome wirklich elementar sind reichen solche Mikroskope nicht aus.
Eine andere Möglichkeit, kleinste Strukturen zu untersuchen, besteht darin, atomare Teilchen auf das Objekt zu schießen und damit deren Oberfläche bzw. Bestandteile abzutasten. Gemessen wird die Streuung dieser Teilchen - deshalb spricht man hier von Streuexperimenten. Jedoch haben nach der Quantenmechanik auch Teilchen Wellencharakter, somit gelten auch für diese Methode die obengenannten Einschränkungen der klassischen Licht-Mikroskopie. Um also immer kleinere Stukturen zu untersuchen, benötigt man Teilchenstrahlen mit möglichst kleiner Wellenlänge, dies läßt sich dadurch realisieren, dass man Teilchen mit hoher Energie, also sehr schnelle Teilchen verwendet. Hier kommen die Teilchenbeschleuniger mit denen wir uns im dritten Teil noch ausführlich beschäftigen werden zum Zuge. Auf diese Weise war es möglich, zunächst die Größe und Form der Atomkerne zu messen, dann die Größe und Form der Protonen, und schließlich hat man Strukturen innerhalb der Protonen entdeckt - aber dazu kommen wir noch.
Atomhülle und Atomkern
[Bearbeiten]
Joseph Thomson entdeckte 1897 die negativ geladenen Elektronen als Bestandteile des Atoms. Er nahm jedoch an, dass diese Elektronen in die (positive) Masse des Atoms eingebettet seien wie Rosinen in einen Kuchen. In den Jahren 1911 beschossen Hans Geiger und Ernest Marsden im Labor von Ernest Rutherford eine nur wenige tausend Atome dicke Goldfolie mit sogenannten Alphateilchen aus einer radioaktiven Quelle (Radium) und zählten die unter verschiedenen Winkeln gestreuten Teilchen. Alphateilchen sind Teilchen welche von einigen radioaktiven Teilchen ausgesendet werden. Es zeigte sich, dass die meisten Teilchen die Folie geradlinig durchsetzten; einige, wenige aber wurden um Winkel von über 140 Grad zurückgestreut. Das war, wie Rutherford sagte, "beinahe so unglaublich, als wenn man mit einer 15-Zoll-Granate auf ein Stück Seidenpapier schießt und die Granate zurückkommt und einen selber trifft". Aus diesem Messresultat schloss Rutherford, dass sich irgendwo im Inneren ein kleiner Körper hoher Dichte befinden musste, der in der Lage war, ein schnell fliegendes Teilchen nicht nur abzulenken, sondern zurückprallen zu lassen. Die Masse des Atoms befand sich also hauptsächlich in einem kleinen, zentralen Teil - dem Atomkern. Erstaunlich war auch, dass der größte Teil des Atoms weitgehend leer sein musste, denn die meisten Alphateilchen flogen durch die Goldschicht nahezu ungehindert hindurch. Besonders dieses Ergebnis war nur schwer zu verstehen, widersprach es doch augenscheinlich der üblichen Vorstellung von der Festigkeit der Materie.
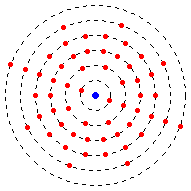
Aus dem Rutherfordschen Atommodell entwickelte der dänische Physiker Niels Bohr ein planetenartiges Atommodell. Danach bewegen sich die Elektronen auf bestimmten Bahnen um den Kern, wie Planeten die Sonne umkreisen. Die Bahnen werden auch als Schalen bezeichnet. Der Kern in der Mitte ist massiv und viel, viel kleiner als die Elektronenhülle (Faktor 104 also 10.000).
Das Bild links stellt die schalenmäßige Anordnung der 56 Hüllenelektronen im Bariumatom (Kernladungszahl Z = 56), gemäß dem bohrschen Atommodell, dar - wobei die Größenverhältnisse natürlich nicht korrekt sind.
Seit 1928 wissen wir, dass das Bohrsche Atommodell nicht korrekt ist, da die Elektronen gemäß der Quantenmechanik keine genaue Bahn besitzen. Der Atomkern ist von Orbitalen umgeben, welche die Aufenthaltswahrscheinlichkeit der Elektronen angibt. Da sich die Teilchenphysik jedoch nur am Rande mit den Orbitalen beschäftigt und ein Verständnis des Orbitalmodells Kenntnisse der Quantenmechanik erfordern würde, will ich hier nicht weiter darauf eingehen und mich lieber dem Atomkern widmen.
Der Aufbau des Atomkerns
[Bearbeiten]Der Atomkern ist kein elementares punktförmiges Teilchen, sondern hat eine endliche Größe. Beispielsweise hat der Kern des Bariumatoms einen Radius von etwa 6 fm (1 fm = 10-15 m). Der Atomkern ist aus sogenannten Nukleonen aufgebaut. Es gibt zwei verschiedene Nukleonen:
- Proton: Elektrische Ladung +1 e, Masse etwa 1836 Elektronenmassen
- Neutron: Elektrische Ladung 0 e, Masse etwas größer als beim Proton (1839 Elektronenmassen)
Protonen und Elektronen tragen die gleiche Ladung e = 1.6 x 10-19 C (Coulomb), nur mit entgegengesetztem Vorzeichen. Bei dieser Ladung handelt es sich um die Elementarladung, sie ist die kleinste Ladung, welche ein frei vorkommendes Teilchen besitzen kann. Wenn man in der Teilchenphysik von elektrischen Ladungen spricht, so gibt man diese immer in Vielfachen der Elementarladung an (Das gilt natürlich auch für dieses Buch).
In einem Atom ist normalerweise die Zahl der Protonen gleich der Zahl der Elektronen, daher ist das Atom normalerweise elektrisch neutral, weil sich die Ladungen, nach außen hin, aufheben. Die Elektronen bestimmen die chemischen Eigenschaften. Daher bestimmt die Anzahl der Protonen indirekt, um welches chemische Element es sich handelt - die Anzahl der Neutronen bestimmt, um welches Isotop des Elements es sich handelt. Die Zahl der Protonen heißt Kernladungszahl Z, die Zahl der Neutronen heißt N, die Gesamtzahl der Nukleonen heißt Kernmassenzahl A. Es ist Z + N = A.
Sie werden sich jetzt vielleicht fragen, wieso ein Atomkern stabil sein kann, da gleich geladene Teilchen (wie die Protonen) sich gegenseitig abstoßen. Tatsächlich würde ein Kern sofort zerfallen, wenn er nur aus Protonen bestünde. Es muss also eine weitere Kraft geben, welche die Nukleonen zusammenhält und dadurch den Atomkern stabilisiert. Diese Kraft heißt Starke Kraft - wir werden uns weiter unten noch mit ihr beschäftigen. Sie wirkt zwischen allen Nukleonen, also zwischen Neutronen und Neutronen, zwischen Protonen und Neutronen, und auch (zusätzlich zur elektrischen Kraft) zwischen Protonen und Protonen. Nur wenn ein genügend hoher Anteil an Neutronen im Kern vorhanden ist, ist diese Kraft stark genug, die Teilchen zusammenzuhalten. Dies erklärt auch, warum sehr große Atomkerne einen hohen Anteil an Neutronen haben. So besitzt das häufigste Sauerstoff-Isotop 8 Protonen und 8 Neutronen - das langlebigste Uran-Isotop besitzt hingegen 92 Protonen und 146 Neutronen. Damit ist die Materie um uns herum aus drei Teilchen: dem Elektron, dem Proton und dem Neutron, aufgebaut.


Das Nukleon
[Bearbeiten]Auch die Nukleonen sind ebenfalls nicht punktförmig, sondern haben eine endliche Größe (ungefähr 1 fm). In den 1960er-Jahren hat sich in Streuexperimenten gezeigt, dass die Nukleonen aus Quarks bestehen, die von Gluonen zusammengehalten werden. Die Gluonen sind dabei masselose Teilchen.
Der Name Quark geht auf Murray Gell-Mann zurück, der diesen Ausdruck im Buch "Finnegan's Wake" von James Joyce fand. Das ist das erste Beispiel der blumigen Sprache, wie sie Physiker bei der Beschreibung kleinster Teilchen verwenden. Während in der normalen makroskopischen Physik alle elektrischen Ladungen Vielfache der Elementarladung e sind, haben die Quarks nur Bruchteile dieser Ladung. In der normalen Materie, wie wir sie kennen, kommen nur zwei Arten von Quarks vor (später werden wir noch weitere kennen lernen): Das Up-Quark mit einer elektrischen Ladung von +2/3 und das Down-Quark mit einer Ladung von -1/3. Ein Proton besteht aus 2 Up- und einem 1 Down-Quark, das Neutron hingegen besteht aus 1 Up- und 2 Down-Quarks; die Ladungen sind daher 2/3 + 2/3 - 1/3 = 1, bzw. 2/3 - 1/3 - 1/3 = 0 (immer in Einheiten der Elementarladung e).
Freie Quarks (mit Bruchteilen der Elementarladung) hat man trotz eifriger Suche noch nie gefunden; die Quarks kommen nur in Gruppen von drei, zwei - oder ganz selten auch fünf - Quarks vor.
Auch die Quarks haben hübsche blumige Namen, wie wir noch sehen werden; die Bezeichnungen "Up" und "Down" haben jedenfalls nichts mit einer Richtung im Raum zu tun.
1) Es sei angemerkt, dass es heute etliche Mikroskope gibt, mit welchen man Atome sichtbar machen kann.
2) Zur Erklärung der Schreibweise der Zahlen und zu den Präfixen der Einheiten siehe den Anhang A.
Die Grundkräfte
[Bearbeiten]Die Grundkräfte der Physik sind die Kräfte, die allen physikalischen und chemischen Phänomenen in der Natur zugrunde liegen. In der klassischen Physik gibt es z.B. die Schwerkraft, die im Gravitationsfeld der Erde wirkt oder die elektrische Kraft in der Umgebung einer geladenen Kugel. Der moderne Ausdruck Wechselwirkung betont die Symmetrie: die Wechselwirkung wirkt immer zwischen zwei Teilchen. Wechselwirkungen werden durch virtuelle Wechselwirkungsteilchen – sogenannte Bosonen – übertragen. Man kann sich als Bild zwei Kinder auf Rollschuhen vorstellen, die miteinander Ball spielen. Das Ballwerfen und -fangen erzeugt eine abstoßende Kraft. Aber wenn sie einander den Ball aus der Hand reißen, dann ist die Kraft anziehend.
Die Physik kennt vier Grundkräfte:
Elektromagnetische Kraft
[Bearbeiten]Bis ins 19. Jahrhundert hinein waren Elektrizität (z.B. der elektrische Strom) und Magnetismus (z.B. die Ausrichtung einer Kompassnadel nach Norden) zwei unterschiedliche Bereiche von Phänomenen. Erst die Arbeit von James Clerk Maxwell zeigte, dass all diese Phänomene durch einen einzigen Satz von 4 Gleichungen, die Maxwellschen Gleichungen, beschrieben werden. Seither spricht man von Elektromagnetismus.
Für unser tägliches Leben ist die elektromagnetische Kraft die wichtigste, denn ohne sie wäre unsere Welt ziemlich düster: es gäbe weder Licht, noch Strom, noch Funk oder Elektronik! Und es gäbe auch uns nicht, denn die Atome, aus denen wir bestehen, werden durch die elektrische Kraft zusammengehalten. Auch die Chemie basiert auf dieser Kraft, denn schließlich betrifft eine Reaktion zwischen Atomen nur die Atom-Hülle, und damit die elektrische Kraft.
Es gibt positive und negative elektrische Ladung. Ladungen, die das gleiche Vorzeichen haben, stoßen sich ab – Ladungen mit unterschiedlichem Vorzeichen ziehen sich an. Je größer die Ladungen, desto größer die Anziehung oder Abstoßung. Das Austauschteilchen, welches die Elektromagnetische Kraft überträgt, ist das Photon . Die elektromagnetische Kraft hat eine unendliche Reichweite und ist die zweitstärkste der vier Kräfte. Die Kraft F sinkt jedoch mit dem Quadrat der Entfernung r – es gilt: F~1/r². Das heißt, wenn zwei geladene Teilchen doppelt soweit auseinander sind, ist die elektrische Kraft, die zwischen ihnen wirkt, nur noch 1/4 der ursprünglichen Kraft. Magnetfelder werden durch bewegte elektrische Ladungen erzeugt.
Im heutigen Standardmodell wird der Elektromagnetismus durch die sogenannte Quanten-Elektrodynamik (QED) beschrieben. Diese fasst die klassische Elektrodynamik als Grenzfall ein. Eines ihrer besten Ergebnisse ist die Berechnung des anomalen magnetischen Moments des Elektrons, die auf 11 Dezimalstellen mit dem experimentell bestimmten Wert übereinstimmt. Damit ist die QED heute die am genauesten experimentell überprüfte Theorie.
Starke Kraft
[Bearbeiten]Wir haben weiter oben schon bemerkt, dass die Protonen im Atomkern elektrisch positiv geladen sind und sich aufgrund der Elektromagnetischen Kraft abstoßen und auseinander fliegen müssten. In der Realität gibt es jedoch viele stabile Atomkerne – es muss also etwas geben, was die Nukleonen im Kern zusammen hält. Dies ist die Starke Wechselwirkung, welche deswegen oft auch Kernkraft genannt wird. Auch elektrisch gleich geladene Quarks, wie die beiden positiv geladenen Up-Quarks des Protons, werden durch die Starke Kraft zusammengehalten. Die Überwindung der elektromagnetischen Abstoßung gelingt ihr, da sie etwa 100-mal stärker als der Elektromagnetismus ist. Dies erklärt auch, warum große Atomkerne einen deutlich höheren Anteil an Neutronen haben, während die leichten Atomkerne meist gleich viele Protonen und Neutronen besitzen: Neutronen üben zwar die Starke Kraft aus, nicht jedoch die elektromagnetische. Deshalb braucht es bei großen Atomkernen mit vielen positiven Ladungen mehr Neutronen, um die hohe elektrische Abstoßung auszugleichen.
Die Starke Kraft wird von Gluonen – von denen es acht gibt – übertragen. (Das Wort „Gluon“ erinnert an das englische „Glue“, d.h. Leim). Ähnlich wie die Elektromagnetische Kraft, ist auch die Starke Kraft an eine Ladung gekoppelt, diese nennt man Farbladung („Farbe“ hat hier nichts mit Farben zu tun, wie wir sie im Alltag kennen). Der Aufbau des Protons und des Neutrons aus drei verschiedenfarbigen Quarks ist oben im Abschnitt „Nukleonen“ symbolisch dargestellt. Im Gegensatz zum Photon, welches keine elektrische Ladung trägt, haben die Gluonen selbst eine komplizierte Farbladung. Daher können Gluonen mit sich selbst stark wechselwirken. Daraus folgt die paradoxe Eigenschaft der Starken Kraft, dass sie bei größeren Entfernungen stärker als bei kleinen Entfernungen ist, da bei kleinen Entfernungen die Gluonen häufiger mit sich selbst, anstatt mit den betroffenen Teilchen, wechselwirken. Jedoch besitzt die Starke Kraft eine maximale Reichweite von 2,5·10−15 Metern. Die Starke Kraft wird heute durch die Quanten-Chromo-Dynamik (QCD) beschrieben („Chromos“ heißt Farbe im Griechischen). Teilchen, die der Starken Wechselwirkung unterliegen, heißen Hadronen. Darauf werden wir im Kapitel „Klassifizierung“ noch zu sprechen kommen.
Schwache Kraft
[Bearbeiten]Beim Betazerfall können Elektronen oder Positronen entstehen; wir betrachten hier als Beispiel den ersten Fall: der Atomkern emittiert ein Elektron, dadurch erhöht sich die Kernladungszahl um eins, während die Kernmassenzahl gleich bleibt. Folglich muss also ein Neutron in ein Proton und ein Elektron zerfallen sein. Während man früher dachte, dies sei ein Beweis dafür, dass es sich bei Neutronen um einen gebundenen Zustand eines Elektrons und eines Protons handelt, wissen wir heute, dass die Nukleonen aus Quarks aufgebaut sind. Folglich muss es möglich sein, dass ein Down-Quark sich in ein Up-Quark umwandelt, indem es ein Elektron emittiert. (Es sei angemerkt, dass dabei noch ein anderes Teilchen, ein Neutrino, entsteht, womit wir uns jedoch erst weiter unten beschäftigen werden.) Das Interessante daran ist, dass man seitdem weiß, dass Teilchen sich ineinander umwandeln können. Man stellte schnell fest, dass es dafür eine neue Wechselwirkung braucht. Diese Kraft ist sehr schwach, und wird deswegen Schwache Wechselwirkung genannt. Die schwache Kraft wird durch die , - und die Bosonen übertragen. Die W-Bosonen sind elektrisch geladen, können also selbst wechselwirken; die Z-Teilchen sind ungeladen. Die W- und Z-Bosonen sind die einzigen Wechselwirkungsüberträger, welche eine Masse haben – und diese ist sogar ziemlich groß. Ihre große Masse ist schuld daran, dass die Schwache Kraft nur über eine Entfernung von maximal 10-18 Meter wirkt.
Gravitation
[Bearbeiten]Die Gravitation oder Schwerkraft ist in der Öffentlichkeit wohl die bekannteste der Wechselwirkungen. Denn sie sorgt dafür, dass ein Apfel von Baum fällt, dass wir auf dem Boden und nicht an der Decke gehen und dass die Planeten um die Sonnen kreisen. Trotzdem ist die Gravitation die einzige Kraft, über welche die Teilchenphysik nichts aussagen kann. Die Gravitation, welche wir heute durch die allgemeine Relativitätstheorie beschreiben, spielt in der bisherigen Teilchenphysik keine Rolle, da bisher alle Bemühungen scheiterten, diese Kraft mittels einer geeigneten Theorie mit den dominierenden Kräften der Elementarteilchen zu vereinheitlichen. Allerdings kann die allgemeine Relativitätstheorie nur auf makroskopische Objekte angewandt werden, unter anderem deshalb wird es eine der zukünftigen Aufgaben der Teilchenphysik sein, diese mit einzubeziehen.
Ebenfalls wird es Sie vermutlich überraschen, wenn ich Ihnen erzähle, dass die Gravitation mit Abstand die schwächste der Wechselwirkungen ist. Sie werden sich nun vielleicht überlegen, warum wir dann die Gravitation so stark zu spüren bekommen? Das liegt ganz einfach daran, dass die betroffenen Massen – wie die Erde oder die Sonne – so riesig groß sind, und dass sie elektrisch ungeladen sind. Die Gravitation wirkt immer nur anziehend – niemals abstoßend, da die einzige „Ladung“, welche für die Gravitation verantwortlich ist, die immer positive Masse des Teilchens ist.
Woher kommt die Energie der Teilchen?
[Bearbeiten]Wir haben oben schon festgehalten, dass beispielsweise die elektrische Kraft durch den Austausch von Photonen erfolgt. Aber Photonen haben Energie: wo kommt also die Energie zur Erzeugung dieser Photonen her? Man könnte sagen, die Natur bedient sich eines Tricks: Energie ist zwar eine Erhaltungsgröße, aber anderseits gilt die Heisenbergsche Unschärferelation für Energie und Zeit:
- ,
wobei = 6,6 × 10-34 Js das Plancksche Wirkungsquantum ist, und bzw. die Ungenauigkeit bezeichnen, mit der die Messung von Energie und Zeit grundsätzlich, d.h. unabhängig von der Messapparatur, behaftet ist (Natürlich können bei einer schlechten Messapparatur die Messfehler auch größer sein). Daraus folgt
- .
Das heißt (durch Umkehrung dieser Ungleichung): die Erzeugung eines Photons der Energie ist möglich (weil nicht beobachtbar) für eine Zeit, die kleiner ist als . Anders gesagt: während dieser Zeit ist die Verletzung der Energieerhaltung erlaubt, weil unmessbar. Man nennt ein solches Photon ein virtuelles Photon. Da beliebig klein sein kann, kann die Zeit (und damit der vom Photon zurückgelegte Weg) beliebig groß sein. Das heißt: die Reichweite der Coulombkraft ist unendlich.
| relative Stärke | Reichweite | Überträgerteilchen | Masse der Überträgerteilchen (GeV/c2) |
Wirkungsbereich | |
|---|---|---|---|---|---|
| Gravitation | 10-39 | unendlich | Graviton (?) | 0 (?) | Himmelskörper |
| Schwache Kraft | 10-13 | 10-17 m | W+, W-, Z0 | 80, 80, 91 | Betazerfall |
| Elektromagnetische Kraft | 10-2 | unendlich | Photon | 0 | z.B. zwischen Kern und Hüllenelektronen |
| Starke Kraft | 1 | 10-15 m | Gluon | 0 | Nukleonen im Kern |
Die Weltformel
[Bearbeiten]Seit James Clerk Maxwell in den 1860er Jahren Elektrizität und Magnetismus zur elektromagnetischen Wechselwirkung vereint hat, bemühen sich die Physiker, auch andere Wechselwirkungen zu vereinen. Die Vereinigung ist eines der größten Ziele der modernen Physik (wenn nicht sogar das größte), eine Theorie, welches dieses leistet, nennt man Weltformel oder Theory of Everything (TOE). Eine Theorie, die 3 der 4 Kräfte beschreibt, nennt man Grand Unification Theory (GUT).
Den Theoretikern Abdus Salam, Sheldon Glashow und Steven Weinberg ist es gelungen, die elektromagnetische und die schwache Kraft zu vereinen. So betrachtet man die elektromagnetische und die schwache Kraft heute nicht mehr als unterschiedliche Kräfte, sondern als unterschiedliche Betrachtungsweisen einer elektroschwachen Kraft; bei sehr hohen Energien werden beide Kräfte identisch, auch in ihrer Stärke. Auch bei der Suche nach einer GUT gibt es inzwischen Fortschritte, allerdings gibt es noch keine abgeschlossene und allgemein anerkannte Theorie dieser Art. Für eine Weltformel gibt es zwar schon einige Versuche, allerdings sind diese noch Jahrzehnte von der „Fertigstellung“ entfernt und natürlich nicht Teil des Standardmodells. Wir werden im dritten Teil dieses Buches („BSM – Erweiternde Theorien“) kurz auf diese Theorien eingehen. Eine ausführliche Auseinandersetzung mit diesen Theorien würde jedoch den Rahmen dieses Buchs sprengen, deswegen werden wir dort auf andere empfehlenswerte Bücher verweisen.
| Elektrizität | Magnetismus | Schwache Wechselwirkung |
Starke Wechselwirkung |
Gravitation |
| Elektromagnetische Wechselwirkung | ||||
| Quantenelektrodynamik | Quantenchromodynamik | Allgemeine Relativitätstheorie | ||
| Elektroschwache Wechselwirkung | ||||
| „Große vereinheitlichte Theorie“ oder „Grand Unification Theory“ (GUT) | ||||
| „Weltformel“ oder „Theory of Everything“ (TOE)" | ||||
Spontane Symmetriebrechung
[Bearbeiten]Sie werden sich vielleicht fragen, wie es möglich sein soll, diese so grundsätzlich unterschiedlichen Wechselwirkungen, zu einer Kraft zu vereinheitlichen? Möglich wird dies durch die spontane Symmetriebrechung. Ein klassisches Beispiel für spontane Symmetriebrechung ist Wasser. In flüssigem Wasser können sich die H2O-Moleküle frei in jede Richtung bewegen. Hier liegt also eine Kugelsymmetrie vor, denn das Wasser sieht, von jeder Richtung aus, gleich aus. Die Symmetrie ist also nur sichtbar, wenn das Wasser genügend Energie (Temperatur) besitzt. Gefriert das Wasser jedoch zu Eis, so bilden die Moleküle eine starre Gitter-Struktur. Somit geht die Symmetrie verloren – sie wird gebrochen. In den 1960er Jahren übertrugen mehrere Physiker dies auf die Teilchenphysik. Hier kann sie erklären, warum eine gewisse Theorie Symmetrien aufweist, obwohl diese für uns nicht erkennbar sind. So basiert die elektroschwache Theorie auf einer Symmetrie zwischen dem Photon und den W- und Z-Teilchen. Für uns ist diese Symmetrie nicht sichtbar, da die W- und Z-Teilchen Masse haben; das Photon jedoch nicht. Bei hohen Energien wie sie kurz nach dem Urknall herrschten, waren die beiden Wechselwirkungen tatsächlich identisch und wurden von vier masselosen Teilchen übertragen. Erst durch die Abkühlung des Universums wurde diese Symmetrie gebrochen und erst seitdem sind diese beiden Wechselwirkungen unterscheidbar.
Antimaterie
[Bearbeiten]1928 stellte P.A.M. Dirac (1902-1984) seine relativistische Theorie des Elektrons auf und schloss aus dieser Theorie, dass es ein anderes Teilchen geben müsse, welches dieselben Eigenschaften wie das Elektron, jedoch die entgegengesetzte elektrische Ladung - also +1 - habe. Carl David Anderson (1905-1991) entdeckte 1932 in einer Nebelkammeraufnahme dieses Teilchen und nannte es Positron. Das Bild ist in horizontaler Richtung mit Hilfe einer Wilsonkammer aufgenommen und zeigt in der Mitte eine Bleiplatte von 6 mm Wandstärke. Ein horizontales Magnetfeld bewirkt eine Ablenkung der Teilchen von der Geraden. Aus der Richtung der Ablenkung im Magnetfeld ergibt sich, dass es ein positives Teilchen sein muss. Da die Krümmung oben stärker ist, muss das Teilchen von unten gekommen sein. Aus der Länge und der Bahnkrümmung schloss Anderson, dass es sich nicht um ein Proton handeln kann, sondern dass es ein leichteres Teilchen sein muss.
Heute wissen wir, dass es zu fast jedem Teilchen ein Antiteilchen gibt, welches dieselbe Masse wie das "normale" Teilchen, aber die entgegengesetzte elektrische Ladung hat. Eine Ausnahme davon sind einige neutrale Teilchen (z.B. das Photon), die mit ihrem Antiteilchen identisch sind. Wenn Sie jetzt jedoch denken, dass das Neutron kein Antiteilchen hätte, so muss ich Sie enttäuschen, denn wie wir gesehen haben, sind Neutronen aus drei geladenen Quarks aufgebaut. Ein Antineutron besteht also aus drei Antiquarks (1 Anti-Up- und 2 Anti-Down-Quarks), und ist so ebenfalls elektrisch neutral.
Da Antiteilchen - die Ladung ausgenommen - dieselben Eigenschaften wie normale Materie besitzen, können sich Antiteilchen ebenfalls zu Antimaterie zusammensetzen. So ist es bereits 1995 gelungen, ein Anti-Wasserstoff-Atom zu erzeugen, das aus einem Antiproton und einem Positron besteht.
Trifft ein Teilchen auf sein entsprechendes Antiteilchen, so vernichten sie sich beide vollständig und werden zu Energie - also zu Photonen. Diesen Prozess nennt man Annihilation. Die Annihilation von Positronen verwendet man bei dem medizinischen Bildgebungsverfahren der Positronen-Emissions-Tomographie. Dabei kann ein dreidimensionales Bild von metabolischen Prozessen, die im Körper ablaufen, gewonnen werden. Die zwei Gammastrahlen, die bei der Annihilation auftreten und in entgegengesetzte Richtung fliegen, ermöglichen eine genaue Feststellung des Ortes der Annihilation.
Die bei der Annihilation auftretenden Energien sind enorm, denn schließlich wird die komplette Masse nach Einsteins Formel E = mc² umgewandelt. So hat 1 kg Antimaterie ein Energieäquivalent von 9 · 1016 Joule; bei der Annihilation mit 1 kg Materie entstünden etwa 50 Milliarden kWh. Dies hat dazu geführt, dass man über die Möglichkeit der Nutzung der Antimaterie als Energiequelle - aber auch als Massenvernichtungswaffe - nachgedacht hat. Da in der Natur jedoch praktisch keine Antimaterie vorkommt (was ja nur logisch ist, sonst hätte sie sich ja schon annihiliert) und die Erzeugung von Antimaterie weit mehr Energie braucht, als man durch sie wieder gewinnen kann, ist dies unrealistisch.1
Andersherum, kann sich ein Photon, wenn es genügend Energie hat, in der Nähe eines Atomkerns in ein Teilchen-Antiteilchen-Paar verwandeln - hier spricht man von Paarbildung.
Bei teilchenphysikalischen Formeln stellt man Antiteilchen immer mit dem Zeichen ihres "normalen" Partners und mit einem Querstrich darüber dar. Das Antiteilchen des Protons ist also das . Eine Ausnahme davon ist das Positron, welches man schreibt - es ist das Antiteilchen des Elektrons.
| Teilchen | Ladung des Teilchens | Antiteilchen | Ladung des Antiteilchens |
|---|---|---|---|
| + 1 | - 1 | ||
| 0 | 0 | ||
| + 2/3 | - 2/3 | ||
| - 1/3 | + 1/3 | ||
| - 1 | + 1 |
1) Es sei angemerkt, dass spekuliert wird, Albert Einstein hätte kurz vor seinem Lebensende eine Möglichkeit dazu entdeckt und diese Entdeckung nicht veröffentlicht, um zu verhindern, dass Sie als Waffe verwendet wird.
Die Elementarteilchen
[Bearbeiten]Eigentlich wäre die Liste der Elementarteilchen ziemlich knapp und übersichtlich, denn wie wir gesehen haben, sind für den Aufbau der Materie - wie wir sie kennen - nur drei Teilchen nötig:
- das Elektron,
- das Up-Quark
- und das Down-Quark
Dazu kämen dann nur noch die in der Tabelle ganz unten genannten Wechselwirkungsteilchen (Eichbosonen). Allerdings kennt man noch eine ganze Reihe weiterer Teilchen, welche im Folgenden beschrieben werden sollen.
Bei den fundamentalen Bestandteilen unterscheidet man zwischen Quarks und Leptonen, die beide zu den Fermionen, das heißt Teilchen mit dem Spin ½, gehören. Die Tabellen weiter unten geben einen kurzen Überblick über die Teilchen beider Gruppen.
Der Betazerfall und die Erfindung des Neutrinos
[Bearbeiten]Der Betazerfall ist das am längsten bekannte Phänomen, das durch die Schwache Wechselwirkung bewirkt wird. Zu Beginn des zwanzigsten Jahrhunderts hatten Ernest Rutherford und Frederic Soddy entdeckt, dass sich bei manchen radioaktiven Zerfällen (und zwar beim Alpha- und beim Betazerfall) die chemische Natur des Elements ändert, es tritt also eine spontane Elementumwandlung ein.
Beim Betazerfall zerfällt der Atomkern eines chemischen Elements (der "Mutterkern") in einen Kern des Nachbarelements (den "Tochterkern"). Dabei wird ein Betateilchen emittiert. Zum Beispiel zerfällt 90Sr (Strontium-90) (Kernladungszahl 38) mit einer Halbwertszeit von 29 Jahren in 90Y (Yttrium-90) (Kernladungszahl 39). Die Kernladung steigt also um 1, das emittierte Elektron hat die Ladung -1: Ladung ist also erhalten, wie es sein muss.

Die negativen Betateilchen sind identisch mit den Elektronen der Atomhülle. Die Bezeichnungen β-, e und e- bezeichnen dasselbe Teilchen. Man verwendet aber im Zusammenhang mit der Atomhülle nur die Bezeichnung e; die Bezeichnung β- wird anderseits nur im Zusammenhang mit dem Betazerfall verwendet.
Mit Hilfe eines Teilchenspektrometers kann man die Energien der emittierten Betateilchen messen. Dabei zeigt sich, wie im Bild rechts zu sehen, dass alle Energien von Null bis zu einer Energie Emax auftreten, mit verschiedener Intensität (Häufigkeit). Dies bedeutete für die Physiker in der Zeit vor 1930 ein großes Problem: die für den Betazerfall zur Verfügung stehende Energie ergibt sich eindeutig aus der Differenz der Massen von Mutter- und Tochterkern. Daher müssten die Betateilchen eigentlich eine wohldefinierte Energie haben und nicht ein breites Energiespektrum, wie im Bild zu sehen. Man dachte damals sogar daran, den Satz von der Erhaltung der Energie in Zweifel zu ziehen.
Eine kühne Lösung dieses Problems schlug Wolfgang Pauli im Jahre 1930 in einem offenen Brief an Lise Meitner und die "lieben radioaktiven Damen und Herren" auf einer Tagung in Tübingen vor. (Er selbst sei nämlich wegen eines Balles in Zürich leider verhindert, zu der Tagung zu kommen). Pauli schlug die Existenz eines noch unbekannten, masselosen, ungeladenen Teilchens vor, das die fehlende Energie (und auch den fehlenden Impuls) beim Betazerfall übernimmt, so dass die Gültigkeit von Energie- und Impulserhaltung wieder gewährleistet ist, dass aber das Teilchen infolge seiner Eigenschaften praktisch kaum nachweisbar ist (tatsächlich wurde es aber Jahrzehnte später nachgewiesen). Wenn das Elektron die Energie Ee hat, so muss das neue Teilchen die Energie Emax - Ee haben, so dass die Summe beider Energien jeweils Emax ergibt.
Pauli schlug den Namen "Neutron" für dieses Teilchen vor. Dieser Name wurde aber für das Teilchen gebraucht, das wir als Neutron kennen, als dieses 1932 von Chadwick entdeckt wurde. Daher änderte der Italiener Enrico Fermi den Namen auf Neutrino, als er 1934 seine Theorie des Betazerfalls vorlegte. ('Neutrone' ist im Italienischen "das große Neutrale", während '-ino' die Verkleinerungsform ist).
Die Gleichung für den Zerfall eines Kernes X in einen Kern Y lautet allgemein:
Das letzte Teilchen in der Gleichung ist das neu eingeführte Neutrino. Wir haben hier einen Querstrich über das ν gesetzt, um anzudeuten, dass es sich um ein Antineutrino handelt. Dadurch wird Leptonenerhaltung möglich (siehe unten). Speziell für den oben erwähnten Strontiumzerfall würde diese Gleichung lauten:
Da beim Betazerfall die Kernladungszahl steigt, die Nukleonenzahl jedoch gleich bleibt, bedeutet das auf der Ebene der Nukleonen den Zerfall eines Neutrons in ein Proton:

Als Fermi seine Theorie des Betazerfalls erstellte, nahm er an, das die Wechselwirkung punktförmig ist, d.h., die Umwandlung bzw. Erzeugung der Teilchen findet an einem Punkt statt. So haben wir es auch in den Gleichungen oben dargestellt. Seit der Entdeckung der W-Teilchen wissen wir aber, dass zunächst ein W-Boson als Zwischenteilchen auftritt. Das ist in dem Feynman-Diagramm rechts symbolisch dargestellt. In diesem Diagramm verläuft die Zeit von unten nach oben. Ein Neutrino, das in verkehrter Zeitrichtung (von oben nach unten) fliegt, bedeutet ein Antineutrino.
Da wir bereits wissen, dass Neutronen aus 1 Up- und 2 Down-Quarks; Protonen aber aus 2 Up- und 1 Down-Quark bestehen, werden Sie jetzt annehmen, dass ein Down-Quark in ein Up-Quark, ein Elektron und ein Neutrino zerfallen kann. Das stimmt zwar, doch es geschieht über das Zwischenstadium eines W-Bosons: also das down-Quark emittiert zuerst ein W-Boson, welches dann in einem zweiten Schritt zerfällt:
Wir haben die Überlegungen alle für den Fall eines β--Zerfalls durchgeführt. Es gibt aber auch den dazu spiegelbildlichen β+-Zerfall, bei dem Positronen emittiert werden:
- ,
zum Beispiel
- .
Wenn nicht genug Energie vorhanden ist, um ein Positron zu erzeugen, so findet meist trotzdem ein Zerfall statt, der sogenannte Elektroneneinfang, zum Beispiel:
Dabei verschluckt der Atomkern ein Elektron der eigenen Atomhülle (meist aus der K-Schale) und emittiert ein Neutrino. Die Existenz dieser Zerfallsart beweist, dass β--Teilchen mit den Hüllenelektronen identisch sind, denn sonst könnte der Kern nicht ein Hüllenelektron in sich aufnehmen.
Kraftvermittlung durch Teilchenaustausch: Mesonen
[Bearbeiten]Wie wir heute wissen, wirkt eine Kraft zwischen zwei Teilchen nicht direkt, sondern durch den Austausch von Teilchen. Wir haben das oben am Beispiel des Photonenaustauschs für die elektrische Kraft erläutert. Dort folgte aus der Masselosigkeit des Photons die unendliche Reichweite der elektromagnetischen Kraft.
Nun wollen wir diese Überlegungen auf die kurzreichweitige Kernkraft erweitern und werden dabei auf ein Austauschteilchen endlicher Masse stoßen. Man kann sich als Bild zwei Kinder auf Rollschuhen vorstellen, die miteinander Ball spielen. Das Ballwerfen und -fangen erzeugt eine abstoßende Kraft. Aber wenn sie versuchen, einander den Ball aus der Hand zu reißen, dann ist es eine anziehende Kraft.
Wir folgen dabei ungefähr den Überlegungen, die Hideki Yukawa 1935 angestellt hat. Wir beginnen wieder mit der Heisenbergschen Unschärferelation für Energie und Zeit:
- ,
wobei = 6,6 × 10-34 Js das Plancksche Wirkungsquantum ist, und bzw. die Ungenauigkeit bezeichnen, mit der die Messung von Energie bzw. Zeit grundsätzlich, d.h. unabhängig von der Güte der Messapparatur, behaftet ist. Daraus folgt
- ,
also je genauer die Energiemessung sein soll, desto länger muss sie dauern.
Damit aber eine Verletzung der Energieerhaltung nicht gemessen werden kann, ist die Ungleichung umzukehren:
- ,
das heißt, die Messung darf höchstens eine Zeit dauern. Zur Erzeugung eines Teilchens der Masse M ist die Energie = Mc2 nötig. Das Teilchen kann höchstens mit Lichtgeschwindigkeit c fliegen, daher ist die Reichweite der vermittelten Kraft höchstens
- .
Setzt man hier Zahlen ein und nimmt eine Masse M von 200 Elektronenmassen an, so erhält man eine Reichweite von etwa 1 fm, wie es der Kernkraft entspricht.
Diese Überlegungen Yukawas setzen zwar eine Stufe zu hoch an weil, wie wir heute wissen, die starke Kraft von den Gluonen vermittelt wird, aber hier wird erstmals aus der endlichen Reichweite auf ein massives Austauschteilchen geschlossen, und tatsächlich sind Mesonen für die Kernkraft verantwortlich.
Das Myon und die Klassifikation der Elementarteilchen
[Bearbeiten]Im Jahr 1936 entdeckte Carl Anderson beim Studium der kosmischen Strahlung ein Teilchen mit einer Masse von etwa 200 Elektronenmassen, das er Mesotron nannte, weil seine Masse zwischen der des Elektrons und der des Protons liegt (meso- im Griechischen bedeutet mittel-). Kurz vorher hatte Yukawa, wie oben erläutert, die Theorie aufgestellt, dass die Kraft zwischen Proton und Neutron durch den Austausch eines Teilchens vermittelt wird, das er 'Meson' nannte. Dessen Masse sollte etwa 200 Elektronenmassen betragen, um die geringe Reichweite der Kernkraft zu erklären.

Es war nun naheliegend zu vermuten, dass das neu gefundene Mesotron mit dem von Yukawa postulierten Meson identisch ist. Weil später noch andere Mesonen gefunden wurden, wurde das Mesotron zur Unterscheidung in μ-Meson umbenannt. Dann stellte sich aber heraus, dass dieses μ-Meson gar nicht das Yukawa-Teilchen sein kann, weil es eine viel zu geringe Wechselwirkung mit den Nukleonen hat. (Das richtige Yukawa-Meson wurde erst 1947 gefunden und Pi-Meson oder Pion genannt).
Nun war es klar, dass die ursprüngliche Einteilung der Elementarteilchen nach ihrer Masse keine glückliche Einteilung ist. Die Teilchen wurden daraufhin nach ihrer Wechselwirkung eingeteilt, und diese Einteilung gilt bis heute. Danach sind Mesonen Teilchen, die der Starken Wechselwirkung unterliegen, also Hadronen (s.o.), wie das Pion. Dem μ-Meson musste der Name "Meson" aberkannt werden, und seither heißt es Myon (ausgesprochen Müon). Während das Pion aus zwei Quarks besteht, ist das Myon ein elementares Teilchen, ein 'Lepton'. Die mittlere Lebensdauer eines freien Myons beträgt 2,2 × 10−6 Sekunden, dann zerfällt es in ein Myonneutrino, ein Antielektronneutrino und ein Elektron. (Zu diesen Teilchen kommen wir gleich.)
Negative Myonen haben dieselben Eigenschaften wie Elektronen mit Ausnahme der Masse. Sie können daher in gewisser Weise Elektronen in der Atomhülle ersetzen - da sie jedoch 200 mal schwerer als Elektronen sind, liegen ihre Bohrschen Umlaufbahnen deutlich näher am Atomkern. Bei schweren Atomen kann die Bahn des Myons sogar innerhalb des Atomkerns liegen, dann kann das Myon vom Kern absorbiert werden und ein Proton in ein Neutron umwandeln. Natürlich sind auch leichte Myonische Atome nicht stabil, da die Myonen selbst ja zerfallen.
Leptonen
[Bearbeiten]In der alten Einteilung der Elementarteilchen waren die Leptonen die leichten Teilchen, d.h. leichter als Mesonen (leptos = leicht im Griechischen). In der jetzt gültigen Einteilung sind Leptonen Teilchen, die nur der schwachen Wechselwirkung unterliegen und (sofern sie geladen sind) auch der elektromagnetischen.
Es gibt insgesamt 6 Leptonen:
| Name | Symbol | Elektrische Ladung in e | (Ruhemasse × c²) in MeV | Mittl. Lebensdauer in [s] | Generation | Antiteilchen |
|---|---|---|---|---|---|---|
| Elektron | - | −1 | 0,511 | (stabil) | 1 | + |
| Elektron-Neutrino | 0 | < 0,2 · 10−3 (: < 3 · 10−6) | (stabil) | 1 | ||
| Myon | - | −1 | 105,66 | 2,197 · 10−6 | 2 | + |
| Myon-Neutrino | 0 | < 0,19 | (stabil) | 2 | ||
| Tau-Lepton | - | −1 | 1777 | 2,9 · 10−13 | 3 | + |
| Tauon-Neutrino | 0 | < 18,2 | (stabil) | 3 |
Jedes dieser Leptonen hat auch ein Antiteilchen, das durch einen Querstrich über dem Symbol bzw. durch das Pluszeichen vom Teilchen unterschieden wird, siehe Teilchenphysik: Antimaterie. Man schreibt den Teilchen die Leptonenzahl +1 zu, den Antiteilchen die Leptonenzahl -1.
Das Myon und das Tau-Teilchen (Tauon) können Sie sich wie ein schweres Elektron vorstellen, denn sie gleichen diesem stark - nur dass sie 200- beziehungsweise 3.500-mal so schwer wie Elektronen sind, und bereits nach kurzer Zeit zerfallen.
Jedes der geladenen Leptonen hat sein eigenes Neutrino, das von den anderen Neutrinos verschieden ist. Man kann das zeigen: ein Kernreaktor ist eine starke Quelle von Elektron-Antineutrinos, die bei den zahlreichen β--Zerfällen entstehen. Stellt man einen großen Neutrinodetektor in die Nähe eines Kernreaktors, so werden dort von den Antineutrinos Elektronen erzeugt, aber keine Myonen.
Beim Betazerfall, den wir oben besprochen haben, entstehen Elektronen (Leptonenzahl +1) und Antineutrinos (Leptonenzahl -1): die Leptonenzahl ist bei der schwachen Wechselwirkung eine Erhaltungsgröße. Die Leptonen werden in drei Generationen (englisch: Flavors) eingeteilt; jede Generation hat ihre eigene Leptonenzahl als Erhaltungsgröße. (Der Ausdruck "Flavor" = "Geschmack" ist wieder einmal ein Hinweis auf die blumige Sprache der Physiker; Flavor hat natürlich nichts mit menschlichem Geschmack zu tun).
Es wundert Sie vielleicht, dass in der obigen Tabelle die Teilchen negativ sind und die Antiteilchen positiv. Das hat eine historische Erklärung: nach der Entdeckung der statischen Elektrizität hat man zufällig die Elektrizität, auf die sich ein geriebener Glasstab auflädt, positiv genannt. Erst viel später hat sich herausgestellt, dass der Grund dafür ein Mangel an Elektronen ist; daher sind die wichtigsten Ladungsträger, die Elektronen, definitionsgemäß negativ.
Tau
[Bearbeiten]1975 entdeckten Martin L. Perl und seine Mitarbeiter bei einer Elektron-Positron-Kollision im SPEAR-Ring ein weiteres Lepton, welches man Tau-Teilchen (auch Tauon; kurz: τ) nannte. Insbesondere für diese Entdeckung erhielt Perl im Jahre 1995 den Nobelpreis für Physik. Die Masse des Tau ist mit 1,777 GeV das 3477,5-fache von der des Elektrons. Seine Lebenszeit beträgt etwa . Der Name Tauon, bzw. der Buchstabe tau, stammt von dem griechischen Wort für "Drittes" triton, weil das Tauon das dritte geladene Lepton ist.
Neutrinos
[Bearbeiten]
Die Neutrinos sind Teilchen, welche zwar in großer Anzahl in der Natur vorkommen, von denen wir jedoch nichts mitbekommen, da sie extrem selten mit Materie reagieren. Der experimentelle Nachweis der Existenz des Neutrinos gelang erst 1956 durch Clyde L. Cowan und Frederick Reines in der Nähe eines Kernreaktors, der (nebenbei) als Neutrinoquelle diente. Die Suche nach Neutrinos war so lange erfolglos gewesen, da Neutrinos so selten mit Materie wechselwirken. So durchqueren in jeder Sekunde über 50 Billionen von der Sonne kommende Neutrinos jeden menschlichen Körper, ohne mit ihm zu reagieren! Und ein starker Strom von Sonnenneutrinos durchsetzt unsere Erde und wird dabei fast gar nicht geschwächt.
Dass geladene Teilchen von ihren - entgegengesetzt geladenen - Antiteilchen verschieden sind, ist leicht einsehbar. Aber wie soll man sich den Unterschied zwischen einem Neutrino und seinem Antiteilchen vorstellen? Da hilft unserer Vorstellung eine Tatsache, die wir seit der Entdeckung der Paritätsverletzung im Betazerfall (1956) wissen: Neutrino und Antineutrino sind durch ihre Helizität, d.h. ihren Schraubensinn unterscheidbar.
Das ist in dem Bild links symbolisch dargestellt. Da sehen die Neutrinos wie Kugeln aus - in Wirklichkeit sind sie natürlich punktförmig. Oben ist ein Neutrino dargestellt, darunter ein Antineutrino. Beide fliegen mit (nahezu) Lichtgeschwindigkeit von links hinten nach rechts vorne; sowohl die Geschwindigkeit wie der Impuls ist nach rechts vorne gerichtet. Das Antineutrino unten bewegt sich ähnlich wie eine Rechtsschraube, das heißt, es rotiert im Uhrzeigersinn, wenn man in Flugrichtung, also von links hinten, schaut. Diese Rotation stellt man üblicherweise durch einen Spinvektor dar, der ebenfalls von hinten nach vorne zeigt. Das Neutrino oben dagegen bewegt sich wie eine Linksschraube, das heißt, es rotiert im Gegenzeigersinn, wenn man in Flugrichtung blickt; der Spinvektor zeigt daher nach hinten.
Neutrino-Masse
[Bearbeiten]Da bisher für keines der Neutrinos eine Ruhemasse gemessen werden konnte, wird die Neutrinomasse in vielen Theorien - das Standardmodell eingeschlossen - Null gesetzt. (Das bedeutet auch, dass Neutrinos mit Lichtgeschwindigkeit fliegen). Allerdings spricht nichts dagegen, dass Neutrinos doch eine Masse (ungleich Null) haben, und tatsächlich ergibt sich das aus der Entdeckung der Neutrino-Oszillationen (siehe???). Alle direkten Messungen konnten bisher lediglich Obergrenzen für die Masse liefern. Die Obergrenze für die Masse des Elektron-Neutrino, durch sorgfältige Messung der Form eines Betaspektrums bestimmt, liegt derzeit bei etwa 2,3 eV (Beachten sie: ein Elektron hat eine Ruheenergie von 510.000 eV!). Für die beiden anderen Neutrinos liegen die Obergrenzen aufgrund der schwierigen Experimente höher (siehe Tabelle oben).
Quarks
[Bearbeiten]Die Quarks sind die fundamentalen Bestandteile der Nukleonen und der Mesonen. Sie sind Hadronen, d.h., sie unterliegen der Starken Wechselwirkung. Die Quantenchromodynamik (QCD), eine Eichtheorie der starken Wechselwirkung, beschreibt die Interaktion von Quarks und Gluonen und von ihren Antiteilchen. Die elektrische Ladung der Quarks ist –1/3 oder +2/3 in Einheiten der Elementarladung e (das ist der Betrag der Ladung des Elektrons, 1,6 × 10-19C). Die QCD beinhaltet unter anderem, dass Quarks nicht isoliert auftreten können, sondern sich immer derart vereinen, dass nach außen nur ganzzahlige elektrische Ladungen sichtbar sind. Dies wird in der QCD mittels der nur bei den Quarks (bzw. Antiquarks und Gluonen) zusätzlich wirkenden Farbladung formuliert: diese Ladungen heißen rot, grün und blau (so wie die Farbkomponenten am Fernsehschirm).
Man postuliert nun, dass farbige Quarks niemals einzeln auftreten können. Stattdessen müssen sie sich stets zu farblosen Teilchen, wie zum Beispiel den Nukleonen, gruppieren. Man sieht das oben am Beispiel der Nukleonen bildlich dargestellt (siehe: Das Nukleon), und man stellt sich vor, dass rot+grün+blau farblos ergibt. Dieses Verhalten heißt im Englischen Confinement (deutsch etwa: "Einsperrung"), und es bedeutet: in der Natur kommen nur farbneutrale Objekte vor. Damit im Zusammenhang steht die Asymptotische Freiheit: Quarks sind im Grenzfall kleinster Abstände bzw. höchster Energien frei beweglich. Das Gegenteil der asymptotischen Freiheit tritt bei niedrigeren Energien oder größeren Abständen auf und führt zum Confinement. Die Quarks sind sozusagen in einem idealen Gefängnis: sie sind völlig frei, können aber nicht hinaus.
Eine rigorose Ableitung des "Nur-weiße-Teilchen"-Postulats aus den Grundlagen der QCD ist bisher nicht möglich. Dies zählt zu den größten ungelösten Problemen der Theoretischen Physik. (Die Farbladung wird im übernächsten Kapitel genauer beschreiben). Quarks sind die einzigen Elementarteilchen, die allen vier Grundkräften der Physik unterliegen. In der folgenden Tabelle sind nur die ersten zwei Quarks, Up und Down, Bausteine der Materie, so wie wir sie kennen. Die übrigen vier benötigen die großen Energien von Teilchenbeschleunigern zu ihrer Erzeugung.
| Masse [MeV/c2] | Spin | elektrische Ladung [e] | |
|---|---|---|---|
| up (u) | 1,5 bis 4 | 1/2 | + 2/3 |
| down (d) | 4 bis 8 | 1/2 | - 1/3 |
| strange (s) | 80 bis 150 | 1/2 | - 1/3 |
| charme (c) | 1.150 bis 1.500 | 1/2 | + 2/3 |
| bottom (b) | 4.100 bis 4.400 | 1/2 | - 1/3 |
| top (t) | 171.400 ± 2100 | 1/2 | + 2/3 |
Wechselwirkungsteilchen: Eichbosonen
[Bearbeiten]Bosonen nennt man alle Teilchen mit ganzzahligem Spin, in Einheiten von . Neben zusammengesetzten Teilchen - wie zum Beispiel Deuteriumkernen (ein Neutron und ein Proton) - gibt es auch elementare Bosonen - die Eichbosonen. Eichbosonen sind Wechselwirkungsteilchen, das heißt sie übertragen eine der oben bereits angesprochenen Grundkräfte.
| Masse [GeV/c2] | Ladung [e] | Spin | Verantwortlich für Kraft | |
|---|---|---|---|---|
| Photon | 0 | 0 | 1 | Elektromagnetische |
| Gluon | 0 | 0 | 1 | Starke |
| W+ | 80 | +1 | 1 | Schwache |
| W- | 80 | -1 | 1 | Schwache |
| Z | 91 | 0 | 1 | Schwache |
| Graviton (hypothetisch) | 0 | 0 | 2 | Gravitation |
Zitate
[Bearbeiten]Weitere Teilchen
[Bearbeiten]Weitere Teilchen
[Bearbeiten]Nun haben wir alle wirklich elementaren Teilchen kennen gelernt. Doch vielleicht ist ihnen schon etwas aufgefallen: Wir haben zwar gesagt, dass Quarks nie frei in der Natur vorkommen können - allerdings behauptete ich weiter oben auch, dass die Nukleonen nur aus Up- und Down-Quarks aufgebaut sind. Wo kommen also die anderen vier Quark-Arten vor? Nun auf die Notwendigkeit der Existenz dieser Quarks ist man dadurch gekommen, dass man weitere Teilchen gefunden hat, welche genau wie die Nukleonen aus Quarks aufgebaut sind. Da man die Eigenschaften einiger dieser Teilchen nicht mit den zwei schon bekannten Quarks erklären konnte, kam man auf die Idee, weitere Quarks müssten existieren.
Baryonen
[Bearbeiten]Baryonen sind Teilchen, welche aus drei Quarks bestehen, zu ihnen gehören also auch die Nukleonen. Das Proton, ist das einzige Baryon, welches ungebunden stabil ist. Das Neutron ist zwar stabil, wenn es mit anderen Nukleonen in einem Atomkern gebunden ist - in freier Form zerfällt es jedoch nach einer mittleren Lebensdauer von etwa 15 Minuten. Alle anderen Baryonen haben Lebensdauern von unter 10-9 Sekunden, abgesehen vom "ewigen" Proton mit einer Lebenszeit von über 1032 Jahren.
Eine Liste von Baryonen mit ihren Eigenschaften finden Sie hier: Liste der Baryonen
Mesonen
[Bearbeiten]Mesonen sind aus einem Quark und einem Antiquark aufgebaut. Es gibt kein stabiles Meson, sie zerfallen alle in weniger als 10-7 Sekunden. Sie werden nun vermutlich glauben, es könnte maximal 36 (zwei Stück aus möglichen 6 Quarks und 6 Antiquarks) Mesonen geben. Man weiß jedoch heute, dass es jedoch deutlich mehr als 36 Möglichkeiten gibt.
Wir wissen bereits, dass Quarks - wie alle Teilchen - einen Spin besitzen. Die Spins der beiden Quarks in einem Meson, können also zueinander parallel oder antiparallel sein, je nachdem unterscheidet man zwischen Vektormesonen und pseudoskalaren Mesonen. Mesonen, welche zwar aus den gleichen Quarks aufgebaut sind, von denen jedoch das eine ein Vektormeson und das andere ein pseudoskalares Meson ist, haben unterschiedliche Eigenschaften und sind deshalb als komplett unterschiedliche Teilchen zu betrachten.
Eine Liste von Mesonen mit ihren Eigenschaften finden Sie hier: Liste der Mesonen
Pentaquarks
[Bearbeiten]1997 sagten Dmitri Diakonov, V. Petrov und M. Polyakov die Existenz von Pentaquarks voraus. Dies sind Teilchen, welche aus fünf Quarks (griech. penta, dt. fünf) bestehen. Von Anfang an war die Vorhersage umstritten, da die vorhergesagten Teilchen leicht aufzuspüren sein sollten. Im Juli 2003 beobachtete Takashi Nakano an der Universität von Osaka, Japan ein solches Pentaquark (genannt Θ+), Ken Hicks am Jefferson Laboratory, Virginia, USA bestätigte dieses Ergebnis. Dies war eine große Überraschung und führte dazu, dass viele andere Wissenschaftler bereits existierender Daten nach Signalen für das Pentaquark durchsuchten. Innerhalb von wenigen Monaten meldeten etwa ein Dutzend verschiedene Gruppen ebenfalls Evidenz für das Θ+ entdeckt zu haben. Einige Gruppen behaupteten sogar, weitere Pentaquarks nachweisen zu können. Ähnlich viele Forschergruppen fanden jedoch keinerlei Spuren auf ein solches Teilchen, weshalb Zweifel an den Entdeckungsberichten aufkam. Am Jefferson Laboratory führte die CLAS Collaboration schließlich die größte Studie zur Pentaquark-Hypothese durch - und konnte dabei keine Hinweise von Pentaquarks finden. Sie gehen davon aus, dass die bisherigen Nachweise von Pentaquarks auf falsch interpretierten Daten beruhen. Es ist jedoch bis heute nicht bekannt warum einige Gruppen Hinweise auf Pentaquarks fanden, andere jedoch nicht. Da es auch keinen eindeutigen Widerleg für die Existenz von Pentaquarks gibt, kann es als offen betrachtet werden, ob diese existieren oder nicht. Neue Erkenntnisse könnten entweder Hilfe von Computersimulationen der Quantenchromodynamik (so genannten Gittereichtheorien) gewonnen werden - hierfür benötigt man jedoch extrem komplexe Algorithmen sowie viel Rechenzeit auf einem Supercomputer - oder durch neue Experimente.
Teilcheneigenschaften
[Bearbeiten]Nun haben wir die verschiedenen Arten von Teilchen kennen gelernt, doch welche Eigenschaften haben diese Teilchen? Was unterscheidet sie und was haben manche Teilchen gemeinsam? Die wichtigsten Eigenschaften von Teilchen haben wir bereits in der Einleitung kennen gelernt: Masse, Spin, Lebensdauer & Ladungen der Teilchen. Nun wollen wir uns noch ein paar weitere Eigenschaften und Beschreibungskriterien von Teilchen anschauen. Die Eigenschaften werden also sogenannten Quantenzahlen festgehalten.
Masse und Energie eines Teilchens
[Bearbeiten]Die wohl wichtigste Eigenschaft eines Teilchens ist seine Masse - also die Angabe, wie schwer das Teilchen ist. Laut der 1905 von Albert Einstein veröffentlichten Speziellen Relativitätstheorie scheinen Masse und Energie nur wie zwei unterschiedliche Seiten einer Münze zu sein. Masse und Energie lassen sich beliebig ineinander umwandeln - hierbei gilt E = mc2. Also ist es gleichwertig, statt von der Masse eines Teilchens von dessen Energie zu reden. Aus Gründen der Einfachheit geben Teilchenphysiker oft nicht die Masse, sondern die Energie eines Teilchens an.
Aus der Relativitätstheorie folgt noch eine weitere Besonderheit, welche die Energie eines Teilchens betrifft. Sie besagt, dass die Energie eines Teilchens um so größer ist, je schneller es sich bewegt. Das heißt, dass ein Teilchen, das sich mit annähernd Lichtgeschwindigkeit bewegt, eine sehr viel größere Energie hat als ein sich in Ruhe befindendes Teilchen. Die Energie lässt sich mit der Formel berechnen. Dabei ist c die Lichtgeschwindigkeit, v die Geschwindigkeit des Teilchens und m0 die Masse, welche es besitzt, wenn es sich nicht bewegt. Um Energien und Massen trotzdem als vergleichbare Eigenschaft von Teilchen verwenden zu können, verwendet man die Begriffe Ruheenergie und Ruhemasse. Hierbei handelt es sich um die Energie bzw. die Masse, welche ein Teilchen besitzt, wenn es komplett still steht. Die oben berechnete Energie Erel bezeichnet man als relativistische Energie - die damit verbundene Masse wird folglich als relativistische Masse bezeichnet. Wird in der Teilchenphysik von der Masse oder Energie einer Art von Teilchen geredet, so ist damit fast immer die Ruhemasse/energie gemeint.
Energien geben Teilchenphysiker meist mit der Einheit Elektronen-Volt - kurz eV - an. Diese Einheit ist so definiert, dass 1 eV die Energie ist, welche ein Elektron gewinnt, wenn man es mit einem Volt Spannung beschleunigt - 1 eV ist somit 1,602176487*10-19 Joule. Da m=E/c2, ist die Einheit für Massen folglich eV/c2 - dies entspricht 1,8·10−36 kg. Ein Teilchen mit der Ruhemasse von 1 eV/c2 hat die Energie 1 eV - folglich werden die beiden Einheiten oft fälschlich vermischt oder gleichgesetzt.
Der Radius von Teilchen
[Bearbeiten]Vermutlich stellen Sie sich unter den Teilchen kleine Kügelchen vor. Für die Nukleonen, Mesonen und Barionen - also für alle nicht elementaren Teilchen - haben Sie Recht. Sie haben Durchmesser von um die 10-15 m. Bei Teilchen wie dem Photon, welches weder Masse noch Ladung besitzt, kann man davon ausgehen, dass seine Energie, solange es als Welle in Erscheinung tritt, innerhalb einer Wellenlänge lokalisiert werden kann. Tritt das Photon jedoch als Punktteilchen auf, so ist seine Energie in einem infinitesimalen Punkt konzentriert. Bei den anderen Teilchen ist es jedoch etwas komplizierter. In den 1930er Jahren beschäftigten sich viele Physiker intensiv mit der Größe des Elektrons. Sie versuchten eine theoretische Formel für den Radius des Elektrons zu entwickeln und kamen zu der Formel , wonach das Elektron einen Radius von 3 · 10-13 cm hätte. Zunächst schien dieser Wert mit den Beobachtungen einiger Erscheinungen gut übereinzustimmen, aber neuere Experimente sowie die Gleichungen der QED zeigen, dass das Elektron punktförmig zu sein scheint. Wir nehmen also an, dass alle elementaren Teilchen keine räumliche Ausdehnung haben. Ihr Radius ist Null, sie sind Punktteilchen ohne jede Ausdehnung. Das wird Sie vermutlich irritieren, denn wie kann ein Teilchen ohne Radius eine Masse besitzen? Auch wenn dies nicht vorstellbar ist, so ist es durchaus kein Widerspruch - denn Masse und räumliche Ausdehnung sind voneinander unabhängige Größen.
Ladungen
[Bearbeiten]Unter Ladung versteht man in der Physik die Eigenschaft eines Objektes, mit einem Feld wechselzuwirken. Für die verschiedenen Wechselwirkungen gibt es jeweils eine eigene unabhängige Ladung. Die Ladung bestimmt sowohl, welches Feld in welcher Stärke vom Teilchen erzeugt wird, als auch, wie das Teilchen vom Feld beeinflusst wird. Für jedes Elementarteilchen besitzt jede Ladung einen genau festgelegten, nicht veränderbaren Wert.
Eine solche "Ladung" haben wir gerade schon beschrieben. Die Masse kann gewissermaßen als die Ladung der Gravitation betrachtet werden. Masse kann jedoch nicht wie die elektrische Ladung positive und negative Werte annehmen. deshalb wirkt die Gravitation immer anziehend und nie abstoßend.
Elektrische Ladung
[Bearbeiten]Die elektrische Ladung (Q) eines Teilchens gibt an, wie stark dieses der elektromagnetischen Kraft ausgesetzt ist. Die elektrische Ladung kann positiv oder negativ sein. Gleichnamig geladene Teilchen stoßen sich ab, und entgegengesetzt geladene Teilchen ziehen sich an. Dass die elektrische Ladung gequantelt ist, stellte der amerikanische Physiker Robert Andrews Millikan (1868-1953) im Jahr 1909 fest - dafür erhielt er später den Nobelpreis. Jedes Teilchen hat eine elektrische Ladung, welche man in vielfachen der Elementarladung (e) angibt. Die Elementarladung ist die Ladung des Elektrons und sie ist die kleinste frei vorkommende elektrische Ladung. Zwar haben die Quarks Ladungen von 1/3 beziehungsweise 2/3 e, allerdings können diese Teilchen, wie wir gesehen haben, nie frei vorkommen. Alle anderen Teilchen haben eine Ladung, welche ein ganzzahliges Vielfaches von e darstellt. Die Elementarladung gibt man mit etwa 1,602 · 10-19 Coulomb an.
Farbladung
[Bearbeiten]Die Farbladung ist die zur starken Kraft gehörende Ladung. Dabei ist zu betonen, dass es sich lediglich um ein Konzept zur Unterscheidung der elementaren Bausteine handelt und dies nichts mit der Farbe des Lichtes oder Objekten zu tun hat. Gewählt hat man diesen Begriff, da es bei der Starken Kraft nicht - wie bei der Elektromagnetischen Kraft - zwei entgegengesetzte Ladungen gibt, welche sich aufheben (Plus und Minus). Hier gibt es drei Ladungen, welche man rot, grün und blau nennt. Antiteilchen haben im Gegensatz zu Teilchen Antifarben - es gibt also zu jeder der drei Farben auch noch ein Gegenstück. Alle drei unterschiedlichen Farben oder alle drei Anti-Farben zusammen neutralisieren sich. Eine Farbe und die dazugehörige Antifarbe neutralisieren sich ebenfalls. Analog zur Lichtfarbenmischung bezeichnet man den neutralen Zustand auch als weiß (denn rotes, grünes & blaues Licht gemischt ergibt weißes Licht). Im Gegensatz zur elektrischen Ladung ist es nicht so, dass man jeder Teilchenart eine Farbe zuordnen kann, sondern es gibt rote, grüne und blaue Quarks jeder Art, sowie acht verschiedene Gluonen, welche immer eine Farbe und eine Antifarbe besitzen - alle anderen Teilchen besitzen keine Farbladung, sie sind weiß.
Schwache Ladung
[Bearbeiten]Auch zur schwachen Wechselwirkung gehört eine Ladung - diese nennt man Schwache Ladung. Die schwache Ladung ähnelt der elektrischen Ladung in mehreren Eigenschaften. Beide kommen immer nur als ganzzahlige Vielfache einer Elementarladung vor: im Falle der elektrischen Ladung ist dies e (für die nicht frei existierenden Quarks sind hier ausnahmsweise drittelzahlige Werte erlaubt), und im Falle der schwachen Ladung ist dies g. Nur die linkshändigen elementaren Fermionen tragen eine schwache Ladung. In der Theorie der Elektroschwachen Wechselwirkung hängen die elektrische und die schwache Elementarladung miteinander über eine Konstante namens Weinbergwinkel zusammen:
Lebensdauer & Halbwertszeit
[Bearbeiten]Schaut man sich ein instabiles Teilchen an, so ist es, genauso wie beim radioaktiven Zerfall, nicht möglich zu sagen, wann das Teilchen zerfallen wird. Zeichnet man jedoch die Lebensdauer einer großen Menge an gleichen Teilchen in ein Koordinatensystem ein, so erkennt man eine Wahrscheinlichkeitsverteilung der Lebensdauern. Differenziert man diese, so erhält man eine neue Wahrscheinlichkeitsverteilung, welche die Wahrscheinlichkeit eines Zerfalls zu einem bestimmten Zeitpunkt angibt. Der Mittelwert dieser Kurve ist als die Lebensdauer () definiert. Vor allem in der Kernphysik verwendet man oft auch die Halbwertszeit () zur Angabe der Lebensdauer von Teilchen. Sie ist die Dauer nach der nur noch die Hälfte der Teilchen vorhanden ist. Sie lässt sich berechnen über:
Der Spin
[Bearbeiten]Ähnlich wie die Planeten im Sonnensystem, so scheinen auch die Elementarteilchen um ihre eigene Achse zu rotieren. Dies bezeichnet man als den Spin der Teilchen. Ähnlich, wie auch die Rotationsachse der Planeten geneigt ist, so ist auch die Rotationsachse der Elementarteilchen geneigt. In Gegensatz zum Drehimpuls von Planeten ist der Spin von Teilchen jedoch auf Grund der Quantenmechanik gequantelt - er kann nur ganz- oder halbzahlige vielfache des Planckschen Wirkungsquantums ( ) annehmen, also zum Beispiel: , , , , ... (Bei der Angabe des Spins eines Teilchens lässt man das meist weg.) Eine weitere Eigenschaft eines Elementarteilchens ist seine Ausrichtung, im Modell mit den Planeten würde sie die Richtung darstellen, in welcher das Teilchen rotiert (linksherum oder rechtsherum). Während der Betrag des Spins einer gewissen Art von Teilchen (beispielsweise eines Elektrons) immer der selbe ist (in diesen Fall 1/2), ist die Richtung variierbar. Zwischen wie vielen Richtungen ein Teilchen "entscheiden" kann, hängt vom Betrag des Spins ab - Teilchen mit einem Spin von 1/2 können zwei verschiedene Richtungen einnehmen - Teilchen mit Spin 0 können nur einen, Teilchen mit Spin 1 hingegen drei Zustände einnehmen. Bei den Spin 1/2 Teilchen, gibt man die Richtung mit dem Vorzeichen des Spins an, Ein Elektron kann Beispielsweise einen Spin von -1/2 oder +1/2 haben. Teilchen mit gleichem Ausrichtung können sich niemals in derselben "Raumregion" aufhalten. Dies ist der Grund, weshalb sich nur maximal zwei Elektronen in einem Orbital aufhalten dürfen. Die Größe 2S+1, wobei bei 'S' der Spin ist, nennt man Multiplizität, sie gibt an, in wie viele verschiedene Raumrichtungen sich der Spin-Vector ausrichten kann. Die Multiplizität spielt vor allem in der Spektroskopie und der Chemie eine wichtige Rolle. (Richtungsquantelung).
Warum sich die Teilchen doch nicht drehen
[Bearbeiten]Wir nahmen bislang immer an, dass sich die Teilchen wirklich um ihre Achse drehen - doch heute wissen wir, dass dies nicht der Fall ist. Um zu verstehen, warum dies nicht der Fall ist, müssen wir uns zunächst überlegen, was eine "Rotation" überhaupt ist. Die logische Antwort darauf ist, dass man von einer Rotation spricht, wenn sich etwas um eine Achse dreht. Man erkennt eine Rotation also daran, dass sich mindestens ein Punkt um einen anderen Punkt bewegt. Wie wir jedoch weiter oben festgestellt haben, sind alle Fermionen und Eichbosonen - nach unseren derzeitigen Vorstellungen - Punktteilchen. Sie bestehen also nur aus einem einzigen Punkt ohne räumliche Ausdehnung. Für eine Rotation um eine Achse sind jedoch immer zwei Punkte nötig. Auch wenn man annimmt, dass die Teilchen keine Punkte, sondern kleine Kugeln wären, so kann es sich beim Spin nicht um das Resultat einer Rotation handeln. Betrachten wir den Spin des Elektrons: um die beobachtete Stärke des Drehimpuls zu erreichen, müsste das Elektron so schnell rotieren, dass sich die Oberfläche des Teilchen zwangsläufig mit Überlicht-Geschwindigkeiten bewegte; die Spezielle Relativitätstheorie verbietet dies. Vermutlich fragen Sie sich jetzt, was der Spin dann ist - eine Antwort darauf kann ich Ihnen jedoch nicht geben. Sie sollten sich den Spin auch weiterhin als "eine Art Rotation" vorstellen - denn eine bessere Verbildlichung gibt es nicht - dabei sollten Sie jedoch immer im Kopf behalten, dass dies nur eine Verbildlichung ist und sich beispielsweise nicht darüber den Kopf zerbrechen, wie sich ein Teilchen in mehr als zwei verschiedene Richtungen drehen kann.

Der Spin der Nukleonen
[Bearbeiten]Der Gesamtspin eines zusammengesetzten Teilchens ist die Summe aller Teilspine - unter Beachtung der Spinrichtung. So haben zwei Teilchen gleichen Spinbetrags zusammen entweder den doppelten Spinbetrag oder den Spin null. Da der Spin der Nukleonen 1/2 ist, und sie aus drei Quarks bestehen, liegt die Vermutung nahe, dass der Spin zwei dieser drei Teilchen sich auf heben und der dritte die Richtung des Spins bestimmt. Dies erscheint zwar zunächst plausibel, ist jedoch ein sehr stark vereinfachtes Modell - man nennt es daher das "naive Quarkmodell". Zum einen wird das ganze dadurch verkompliziert, dass, wie wir gesehen haben, die Quarks in den Nukleonen von Gluonen zusammen gehalten werden, welche selbst einen Spin - nämlich den Spin 1 - haben. Was jedoch noch hinzukommt, ist ein gewisser Quantenmechanischer Effekt, den man Quantenfluktuation oder Vakuumfluktuation nennt. Stellen Sie sich dazu einen sehr armen Mann vor, welcher rein gar nichts hat. Nun erfährt dieser, dass er einen schwerreichen Onkel im Amerika hatte, welcher verstarb, und da es sonst keine anderen Verwandten mehr gibt, fällt dem äußerst armen Hinterbliebenen das gesamte Millionen-Erbe zu. Sein Onkel hat jedoch in seinem Testament verfügt, dass das Erbe persönlich in der USA abgeholt werden muss. Da der arme Schlucker jedoch bei weitem zuwenig Geld hat, um den Flug dorthin zu bezahlen, leiht er sich das Geld kurzfristig von einem Freund, fliegt in die USA und löst dort das Erbe ein. Von dem geerbten Geld kann er seine Schulden problemlos wieder begleichen. Nach der Heisenbergschen Unschärferelation, können sich Teilchen ebenso für kurze Zeit Energie aus dem Nichts "leihen", vorausgesetzt, dass sie diese innerhalb kurzer Zeit wieder "zurückzahlen". Da aus Energie Teilchen-Antiteilchen-Paare entstehen können, können somit auf submikroskopischer Ebene virtuelle Teilchen sozusagen aus dem Nichts entstehen. Dies geschieht auch im Inneren von Nukleonen "zwischen" den reellen Quarks. Dort entstehen somit ständig Up-, Down- und sogar Strange-Quarks - und ihre Antiteilchen - in großer Anzahl und vernichten sich nach wenigen Augenblicken wieder. Im Gegensatz zu den virtuellen Quarks, bezeichnet man die eigentlichen, "echten" Bestandteile des Nukleons als Konstituenten-Quarks. Es ist gegenwärtig nicht möglich, zu berechnen, wie sich die vielen Teilspins zu dem Gesamtspin von 1/2 summieren. Während man früher dachte, dass diese virtuellen Teilchen nur einen relativ kleinen Anteil am Gesamtspin haben, so hat man in Experimenten in den 1980er Jahren herausgefunden, das diese nur minimal zum Spin des Nukleons beitragen, während die virtuellen Quarks - vor allem die Strange-Quarks einen unerwartet großen Beitrag zum Nukleonen-Spin beitragen. Da dies den Vermutungen widersprach, befand man sich zwischenzeitlich in der "Spinkrise". Man nimmt heute an, dass nur etwa 30 Prozent des Spins eines Protons durch seine Konstituentenquarkbestandteile entsteht und dass etwa 10 Prozent des Spins durch virtuelle Strange-Quarks entstehen. Es gibt heute Modelle, welche dies erklären, indem man annimmt, dass die Gluonen einen relativ hohen Anteil am Spin haben - daher spricht man kaum noch von einer "Spinkrise".
Die Seltsamkeit von Teilchen
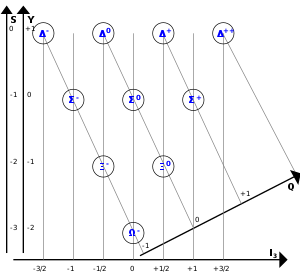
[Bearbeiten]Um anzugeben, welche Quarks in einem Teilchen enthalten sind, benützt man oft eine Reihe von Quantenzahlen. Der am häufigsten verwendete davon ist die Strangeness (S) - manchmal im Deutschen auch Seltsamkeit genannt - sie gibt an, wie viele Strange-Quarks in einem Teilchen enthalten sind. Der Charm (C), die Bottomness (B) und die Topness (T) geben entsprechend an, wie viele der anderen entsprechenden Quarks enthalten sind. Für das Up- und das Downquark werden keine solchen Begriffe verwendet.
Um sowohl mit Quarks als auch mit Antiquarks umgehen zu können, wurden diese Quantenzahlen als die Differenz zwischen der Anzahl der Antiquarks und der Anzahl der Quarks definiert. Die Strangeness S wird berechnet durch:
Das b-Quark ist ebenfalls ein Quark vom Down-Typ, entsprechend gilt für die Bottomness B':
Für die Quarks von Up-Typ ist die Vorzeichenwahl dagegen umgekehrt:
und
Das soll an zwei Beispielen veranschaulicht werden:
- Das Xi-null-Baryon (Ξ0) besteht aus einem Up-Quark und zwei Strange-Quarks. Daraus folgend gilt: S = 0 - 2. Es hat also eine Strangeness von -2.
- Das Phi-Meson (Φ0) besteht aus einem Strange-Quark und einem Anti-Strange-Quark. Daraus folgend gilt: S = 1 - 1. Es hat also eine Strangeness von 0.
Materie, die seltsame Teilchen enthält, wird Seltsame Materie oder auch Strangelet genannt - sie kommt auf der Erde nicht natürlich vor, man vermutet jedoch, dass es stabile Seltsame Materie in besonders schweren Neutronensternen geben könnte.
Die Leptonenzahlen
[Bearbeiten]Die Leptonenzahlen sind die Entsprechungen zu den letztgenannten Quantenzahlen. Zu jeder der drei Gruppen (Familien) von Leptonen gibt es eine Familien-Leptonenzahl, also eine elektronische Leptonenzahl Le, eine myonische Leptonenzahl Lμ und eine tauonische Leptonenzahl Lτ. Sie werden genauso wie die obigen Quantenzahlen berechnet, wobei auch die Neutrinos mitgerechnet werden. Die Leptonenzahl L ist die Summe dieser Familien-Leptonenzahlen.
Baryonenzahl
[Bearbeiten]Die Baryonenzahl (B) ist für alle Baryonen (Proton, Neutron, Lambda, etc.) 1, für die Antiteilchen (Antiproton, Antilambda etc.) entsprechend -1. Da die Baryonen aus 3 Quarks bestehen tragen die einzelnen Quarks die Baryonenzahl 1/3, bzw. -1/3 für die Antiquarks. Tatsächlich nimmt die Baryonenzahl für alle nur denkbaren farbneutralen Quark-Kombinationen, die nicht der QCD widersprechen, einen ganzen Wert an. Die Baryonenzahl ist also eine einfache Möglichkeit, zu bestimmen, ob ein hypothetisches Teilchen in der Natur überhaupt vorkommen kann. Hat ein Teilchen eine gebrochene Baryonenzahl (1/3, 2/3, -1/3, -4/3) so kann es laut QCD nie ungebunden auftreten.
Eigenparität
[Bearbeiten]Die Parität kann man sich wie eine "Rechts-Links-Symmetrie" vorstellen. Genauso, wie viele Gebäude, oder das menschliche Gesicht symmetrisch sind, so sind es auch die meisten Reaktionen in der Teilchenphysik. Um zu überprüfen, ob eine Reaktion die Parität einhält, muss man die Produkte der Eigenparitäten, auf beiden Seiten der Reaktion miteinander vergleichen. Die Eigenparität ist eine weitere Quantenzahl. Grob gesagt, kann jedes Teilchen als eine mathematische Wellenfunktion dargestellt werden. Sind die Funktionen zum Ursprung symmetrisch, so spricht man von einer geraden Eigenparität (geschrieben als +1); ist sie hingegen antisymmetrisch, so spricht man von einer ungeraden Eigenparität (geschrieben als -1). Die Nukleonen und die so genannten Hyperonen - das sind Baryonen mit einem Strange-Quark - haben eine gerade Eigenparität; die Mesonen und das Photon haben eine ungerade Eigenparität.
Der Isospin
[Bearbeiten]Der Isospin hat nichts mit dem Spin zutun - es ist eine völlig andere Größe. Das Proton und das Neutron sind einander sehr ähnlich: Außer der elektrischen Ladung unterscheiden sie sich in keiner der bisher genannten Quantenzahlen und auch ihre Massen sind fast gleich. Als man in Streuprozessen feststellte, dass sie auch gleich stark wechselwirken, kam Werner Heisenberg im Jahr 1932 auf die Idee, dass das Proton und das Neutron zwei verschiedene Ladungszustände ein und desselben Teilchens, des Nukleons, sind. Um dies zu beschreiben, führte er die Quantenzahl Isospin ein. Ähnlich wie der Spin, so besteht auch der Isospin aus zwei Teilen: dem Isospin selbst (I) und der so genannten dritten Komponente des Isospins (I3), auch z-Komponente des Isospins (Iz) genannt. Die dritte Komponente des Isospins wird oft auch als Projektion des Isospins bezeichnet. Bei diesem Vergleich entspricht I dem Betrag des Spins und I3 der Ausrichtung des Spins. Die Neutronen haben einen Isospin von 1/2.
Hyperladung
[Bearbeiten]Die Hyperladung ist eine weitere Quantenzahl, sie hat das Formelzeichen Y. Sie ist über die Gell-Mann-Nishijima-Relation fest mit der elektrischen Ladung und der Projektion des Isospins verknüpft. Sie lässt sich jedoch auch auf Grund der Baryonenzahl und der Strangeness berechnen. Es gilt:
Die Nukleonen haben beide eine Hyperladung von 1.
Erhaltungssätze
[Bearbeiten]Die Erhaltungssätze
[Bearbeiten]Wir haben jetzt die Größen zur Beschreibung der Teilchen kennen gelernt - doch welche von diesen sind Erhaltungsgrößen? Erhaltungsgrößen sind Eigenschaften, welche sich grundsätzlich nie ändern dürfen - auch nicht bei Zerfällen oder Wechselwirkungen - dort müssen die Gesamtgrößen links und rechts des Reaktionspfeils gleich bleiben. Bei den meisten Erhaltungsgrößen ist die Gesamtgröße die Summe aller Einzelgrößen, bei manchen ist Sie jedoch das Produkt aller Einzelgrößen.
Die bekannteste Erhaltungsgröße ist mit Sicherheit die Energieerhaltung, sie ist schon in der klassischen Physik bestens bekannt. Und auch in der modernen Teilchenphysik ist die Energieerhaltung weiterhin genauso gültig - jedoch mit einer Ausnahme: man muss die Masse als eine Art von Energie betrachten, denn sie können sich ineinander umwandeln. Die Summe von Energie und Masse muss jedoch immer erhalten bleiben. Lassen sie uns ein Beispiel ansehen. Beim Beta-Zerfall findet im Atomkern folgende Reaktion statt: . Lasst uns nun die Energien betrachten - da wir die Ruheenergien der Quarks nicht exakt wissen, nehmen wir einfach Mittelwerte von 3 MeV für das Up-Quark und 6 MeV für das Down-Quark an. Auf der linken Seite des Zerfalls existiert nur ein Down-Quark - die gesamte Energie auf der linken Seite ist also 6 MeV + Ekd, wobei Ekd die kinetische Energie des Down-Quarks ist. Auf der rechten Seite finden wir drei Teilchen: ihre gemeinsame Ruheenergie ist 3 MeV + 0,51 MeV + 0 MeV = 3,51 MeV. Wenn wir annehmen, dass die komplette Bewegungsenergie des Down-Quarks auf das Up-Quark übergeht (was nahe liegt, da beide in einem Nukleon gebunden sind), so sind immer noch 2.49 MeV "übrig". Sie müssen sich also folglich auf das Elektron und das Neutrino, in Form von Bewegungsenergie, aufteilen. Also ist Eke + Ekυ = 2.49 MeV.
Der Spin ist nach der Masse wohl die wichtigste Eigenschaft eines Teilchens und auch er ist eine Erhaltungsgröße. Genauer gesagt ist sein Betrag eine Erhaltungsgröße nicht jedoch seine Ausrichtung, diese kann sich nämlich beliebig ändern. Wir wollen die Spinerhaltung wieder an obiger Reaktion nachvollziehen. Alle in ihr beteiligten Reaktionen haben einen Spinbetrag von 1/2. Um die Spinerhaltung zu erfüllen, müssen die Spinausrichtungen der Produkte so sein, dass sich auf der rechten Seite zwei der Spinbeträge aufheben. So müssen zwei der Produkte die Spins -1/2, +1/2 haben, denn (-1/2) + (+1/2) + (±1/2) = ±1/2.
Eine weitere Erhaltungsgröße ist die elektrische Ladung. Die Gesamtladung vor und nach einer Wechselwirkung muss immer identisch sein. Auch die Baryonenzahl und die Leptonenzahlen bleiben immer erhalten. Im Normalfall bleibt jede Leptonenzahl einzeln für sich erhalten. Eine inzwischen beobachtete Ausnahme ist die Neutrino-Oszillation. Genaugenommen wird also nur die Summe aller Leptonenzahlen erhalten - aus praktischen Gründen werden wir jedoch weiterhin alle Leptonenzahlen einzeln als Erhaltungsgrößen betrachten. Auch diese drei Erhaltungsgrößen wollen wir im Folgenden mit obigem Zerfall demonstrieren.
| Ladung: | |||
|---|---|---|---|
| Baryonenzahl: | |||
| Leptonenzahl: |
Die Erhaltung der Baryonenzahl hat eine wichtige Folge. Denn wenn die Baryonenzahl immer erhalten bleiben muss, so folgt daraus, dass ein Baryon immer nur in genau ein anderes Baryon und beliebige Leptonen zerfallen kann. Betrachten wir nun das Proton, wie könnte es denn theoretisch zerfallen? Die Antwort des Standardmodells: gar nicht! Denn das Proton ist das leichteste aller Baryonen und da die Energieerhaltung vorschreibt, dass das die entstandenen Produkte alle zusammen dieselbe Masse wie das Proton haben, gibt es folglich keinen einzigen möglichen Zerfall. Somit ist das Proton stabil.
Auch bei vielen der anderen Größen war man sich bis vor kurzem sicher, sie würden erhalten bleiben. Jedoch hat man festgestellt, dass diese Größen nur bei ein oder zwei der drei Wechselwirkungen erhalten bleiben.
| Erhaltungsgröße | Starke WW | Elektromagnetische WW | Schwache WW |
|---|---|---|---|
| Energie | Ja | Ja | Ja |
| Gesamtdrehimpuls | Ja | Ja | Ja |
| Ladung | Ja | Ja | Ja |
| Baryonenzahl | Ja | Ja | Ja |
| Leptonenzahl | Ja | Ja | Ja |
| Isospin | Ja | Nein | Nein |
| Dritte Komponente des Isospins | Ja | Ja | Nein |
| Strangeness, Charm, Topness, Bottomness | Ja | Ja | Nein |
| Parität | Ja | Ja | Nein |
| CP | Ja | Ja | Nein |
| CPT | Ja | Ja | Ja |
Wie man in der Tabelle sieht, wird die Strangeness bei der schwachen Wechselwirkung nicht erhalten. Dies hat den folgenden Grund: die Strangeness ist keine eigentliche Erhaltungsgröße, vielmehr wird die Erhaltung der Strangeness durch die Erhaltung der Farbladung bedingt. Diese verbietet alle physikalischen Vorgänge, welche die Strangeness verletzen würden. Dies bedeutet, die Erhaltung der Strangeness ist kein unabänderliches Grundprinzip der Physik - wie etwa die Erhaltungssätze der Energie oder des Spins - sondern eine Konsequenz der Theorie der starken Wechselwirkung und der dazugehörenden Farberhaltung. Da die Farbladung jedoch nur der Überträger der starken Wechselwirkung ist, gilt dies nur für diese Kraft.
Die Spiegel der Teilchenphysik
[Bearbeiten]Es ist davon auszugehen, dass von jedem in der Natur auftretendem Objekt auch das dazugehörende Spiegelbild vorkommen kann und dass auch das Spiegelbild eines Experiments oder einer Wechselwirkung hervorrufbar ist. Die Natur unterscheidet nicht zwischen links und rechts – dies nennt man die Raumspieglungssymmetrie oder Parität (P). Im Gegensatz zu einem gewöhnlichen Spiegel, dreht die Raumspiegelung der Teilchenphysik nicht nur eine, sondern alle drei Raumachsen um. Seit 1956 wissen wir jedoch, dass dies bei der schwachen Wechselwirkung nicht der Fall ist: Die Natur unterscheidet durchaus zwischen links und rechts. Vorgeschlagen wurde dies von T.D. Lee und C.N. Yang, um sonst unerklärliche Eigenschaften von K-Mesonen zu erklären; beide bekamen dafür den Physiknobelpreis. C.S. Wu bewies dies endgültig: Der Kern von Kobalt-60 (60Co) zerfällt bekannterweise gemäß dem β--Zerfall zu 60Ni. Dabei entsendet es ein Neutrino und ein Elektron. Da auch Atomkerne sich also um ihre virtuelle Achse drehen, können wir ihn uns als eine rotierende Kugel vorstellen. Wu richtete die Drehrichtung einer großen Menge an Kobaltkernen mit einem Magnetfeld bei sehr tiefen Temperaturen alle in dieselbe Richtung aus. Wu stellte damit fest, dass die Elektronen immer in die Richtung wegfliegen, in die gesehen die Drehrichtung linksherum ist. Würden wir dieses Experiment im Spiegel ansehen, so würden die Elektronen jedoch in die Richtung fliegen, in die die Kerne rechtsherum rotieren. Dies kann jedoch in der Natur nicht auftreten, da die Gesetze der schwachen Wechselwirkung dies verbieten. Somit war klar, dass die Raumspieglungssymmetrie gebrochen werden kann. Neben dieser räumlichen Vertauschung gibt es in der Physik noch zwei weitere wichtige Vertauschungen: Die Zeit- (T) und die Ladungskonjugation (C). Hinter dem zweiten Begriff versteht man den Austausch sämtlicher Teilchen durch Antiteilchen und umgekehrt. Aus diesen drei Spiegelungen lassen sich insgesamt sieben Kombinationen dieser Vertauschung zusammensetzten: C, P, T, CP, CT, PT und CPT.
Zur Überprüfung der C-Symmetrie schaute man sich das μ- an. Auf den ersten Blick scheint die C-Symmetrie hier zu stimmen, denn das Myon zerfällt in ein Elektron und zwei Neutrinos – das Antimyon zerfällt hingegen in ein Positron (und zwei entsprechende Neutrinos):
- .
Doch auch beim Myon gilt ähnliches wie bei den Kaonen aus Wus Experiment: Die Drehrichtung des (Anti-)Myons steht in Korrelation zur Flugrichtung des Elektrons bzw. Positrons. Jedoch die Korrelation beim μ+ entspricht nicht der des μ-, sondern stimmt mit dessen Spiegelbild überein. Somit ist der Myonen-Zerfall nicht C-, sondern CP-symmetrisch. Die Entdeckung, dass die C- und P-Symmetrien gebrochen werden können, hat die meisten Physiker geschockt. Da jedoch alle Naturgesetze CP-symmetrisch zu sein schienen, kamen viele Physiker zu dem Schluss, die CP sei die „wahre“ Raumspiegelung. Diese Interpretation wurde haltlos, als 1956 entdeckt wurde, dass auch die CP nicht allgemeingültig ist, sondern gebrochen werden kann. Nun zur T-Symmetrie, der Zeitvertauschung. Sie kehrt die Reihenfolge aller Ereignisse um und damit auch die Bewegungsrichtung. In makroskopischen Verhältnissen verbietet der zweite Hauptsatz der Thermodynamik eine Zeitumkehr, da dieser festlegt, dass die Entropie stetig ansteigen muss. Für mikroskopische Phänomene, wie sie in der Teilchenphysik interessant sind, ist die Frage nach der T-Symmetrie nicht so einfach zu beantworten. Aus Gründen, welche wir gleich erörtern werden, geht man davon aus, dass sie genauso wie die CP-Symmetrie zwar existiert, jedoch von bestimmten schwachen Wechselwirkungen gebrochen werden kann. So bleibt schließlich noch die CPT-Symmetrie. Die heutige Teilchenphysik ist sich sicher, dass sie eine grundsätzliche Symmetrie der Natur ist, welche allgemein gültig ist. Um das noch einmal zu verdeutlichen: Eine CPT-Spiegelung bedeutet, dass in einer Wechselwirkung jedes Teilchen durch sein Antiteilchen getauscht wird, der Umkehrung aller drei Raumachsen und der Umkehrung der Zeit. Sie ist also auch das Resultat aus CP- und T-Spiegelung. Da wir wissen, dass die CP verletzt werden kann, die CPT jedoch nicht, folgt daraus, dass die T-Symmetrie ebenfalls verletzt werden kann – denn nur dadurch lässt sich die Verletzung der CP aufheben. Würde man feststellen, dass auch die CPT-Symmetrie verletzt werden kann, so würden die lokalen Feldtheorien – welche experimentell sehr gut bestätigt sind – zusammenbrechen.
Einteilungen und Klassifizierung der Teilchen
[Bearbeiten]Einteilungen und Klassifizierung der Teilchen
[Bearbeiten]Eine der Aufgaben der Teilchenphysik ist es auch, die Teilchen zu klassifizieren und in Gruppen einzuteilen. Im bisherigen Verlauf des Buches haben wir bereits einige Gruppen genannt (Zum Beispiel den Begriff "Leptonen"), nun wollen wir sie in einen Gesamtzusammenhang bringen und ihre allgemeinen Eigenschaften erklären. Im Laufe der Geschichte wurden hier immer wieder neue Ansätze entwickelt - und nach Entdeckung von neuen Teilchen wieder verworfen. Im Folgenden wollen wir die verschiedenen Klassifizierungen erläutern.
Historisch (I): Einteilung aufgrund der Massen
[Bearbeiten]Die Einteilung der Teilchen nach ihrer Masse ist heute nicht mehr aktuell. Wir wollen jedoch trotzdem darauf hinweisen, da von ihr einige der Namen von Teilchenfamilien übriggeblieben sind.
In den 1930er Jahren geprägt, als die Erkenntnisse in der Teilchenphysik noch nicht sehr umfangreich waren, klassifizierte man die damals bekannten Teilchen in drei Kategorien:
- Leptonen vom griechischen leptos = leicht, für Teilchen besonders geringer Masse
- Mesonen vom griechischen mesos = mittleres, für Teilchen mittlerer Masse
- Baryonen vom griechischen barys = schwer, für Teilchen mit großer Masse
Als man ein weiteres Teilchen mittlerer Masse fand, nannte man es µ-Meson und gliederte es als Meson ein, siehe Myon. Jedoch stellte man nach einiger Zeit fest, dass eine Einteilung auf Grund der Massen ungeeignet ist und wählte stattdessen eine Einteilung nach den Wechselwirkungen, denen die Teilchen unterliegen. Also benannte man das µ-Meson in Myon um und stufte es als Lepton ein.
Die Klassifizierung auf Grund der Masse wurde verworfen; die Namen Lepton, Meson und Baryon blieben jedoch bis heute erhalten.
Einteilung auf Grund der Wechselwirkung
[Bearbeiten]Die aktuelle Einteilung basiert auf der Wechselwirkung, welcher die Teilchen unterliegen. Eine Auswahl:
- Hadronen unterliegen der starken, der elektromagnetischen und der schwachen Wechselwirkung;
- Leptonen unterliegen der schwachen und (sofern elektrisch geladen) der elektromagnetischen Wechselwirkung;
- Photonen unterliegen nur der elektromagnetischen Wechselwirkung.
Alle Teilchen unterliegen außerdem der Gravitation, sofern ihre Masse nicht Null ist.
Damit ergibt sich etwa folgende Übersicht (eine viel vollständigere Teilchenliste findet man in der graphischen Übersicht weiter unten):
| Familie | Teilchen | Symbol | Ruhemasse × c² in MeV | Mittlere Lebensdauer (s) |
| Photon | photon | 0 | stabil | |
| Leptonen | Elektron | , | 0,511 | stabil |
| Myon | , | 105,7 | ||
| Tauon | , | 1777 | ||
| Elektronneutrino | ~0 | stabil | ||
| Myonneutrino | ~0 | stabil | ||
| Tauonneutrino | ~0 | stabil | ||
| Hadronen | Pion | , | 139,6 | |
| Pion | 135,0 | |||
| Kaon | , | 493,7 | ||
| Kaon | 497,6 | |||
| Kaon | 497,6 | |||
| Etameson | 547,5 | |||
| Proton | 938,3 | stabil | ||
| Neutron | 939,6 | 886 | ||
| Lambda | 1116 | |||
| Sigma | 1189 | |||
| Sigma | 1193 | |||
| Sigma | 1197 | |||
| Xi | 1315 | |||
| Xi | 1322 | |||
| Omega | 1672 |
Zu den Hadronen gehören Mesonen, Baryonen und Pentaquarks:
- Mesonen (Pion, Kaon...) bestehen aus zwei Quarks, sind daher Bosonen;
- Baryonen (Proton, Neutron,...) bestehen aus drei Quarks, sind daher Fermionen;
- Pentaquarks bestehen (wie der Name sagt) aus fünf Quarks, sind daher Fermionen; ihre Existenz ist erst seit wenigen Jahren bekannt (sie sind in der Liste oben nicht enthalten).
Die Hadronen sind daher keine Elementarteilchen im Sinne der in der Einleitung genannten Definition, da sie aus kleineren Bestandteilen aufgebaut sind. Man kann allerdings Hadronen nicht in ihre Bestandteile zerlegen, da freie Quarks nicht vorkommen.
Die Rolle des Spins und der Ladung
[Bearbeiten]Wir haben bereits gehört, dass alle Teilchen einen Spin haben - sie scheinen sich zu drehen. Dieser Spin wird als rationale Zahl angegeben. Diese Zahl kann entweder ganzzahlig (1, 2, 3) oder halbzahlig sein (1/2, 3/2, 5/2). Die Aussage: "Das Teilchen hat Spin ½" bedeutet: in Bezug auf jede beliebige Achse im Raum kann der Eigendrehimpuls des Teilchens nur den Wert +½ oder -½ annehmen, wobei ist, und das plancksche Wirkungsquantum.
Dieses elementare Unterscheidungsmerkmal nutzt man, um die Teilchen in zwei Gruppen einzuteilen:
- Fermionen sind Teilchen mit halbzahligen Spin
- Bosonen sind Teilchen mit ganzzahligen Spin
Zu den Fermionen gehören die Quarks und die Leptonen. Von den Bosonen haben wir bereits die Eichbosonen kennen gelernt. Hadronen können zu beiden Gruppen von Teilchen gehören. Genauer gesagt, gehören alle Baryonen zu den Fermionen - die Mesonen hingegen zu den Bosonen.
Jedoch kann man nicht nur bei diesen Teilchen den Spin messen, grundsätzlich haben auch alle Atomkerne einen Spin, mit welchem man sie in eine dieser beiden Gruppen einteilen kann. Wenn wir in diesem Buch (und generell in der Teilchenphysik) von Bosonen und Fermionen sprechen, so sind damit - soweit nicht anders vermerkt - subatomare Teilchen gemeint.

Ob der Spin halb- oder ganzzahlig ist, wirkt sich entscheidend auf das Verhalten der Teilchen aus. Bosonen gehorchen der Bose-Einstein-Statistik, Fermionen hingegen gehorchen der Fermi-Dirac-Statistik. Der Begriff "Statistik" bezieht sich in diesem Zusammenhang auf das Verhalten mehrerer Teilchen mit identischen Eigenschaften. Die Fermi-Dirac-Statistik schreibt vor, dass sich in einem räumlichen Bereich niemals zwei oder mehrere Fermionen befinden dürfen, welche in ihren Quantenzahlen übereinstimmen - man spricht bei diesem Quantenmechanischen Phänomen von dem paulischen Ausschließungsprinzip. Die Fermionen können sich also nicht beliebig nahe kommen. Eine Folge davon ist, dass normale Materie nicht beliebig komprimierbar ist. Die Bosonen können sich jedoch, nach der Bose-Einstein-Statistik, auf einem beliebig kleinen Volumen aufhalten. Ein Beispiel dazu ist ein starker Laserstrahl. Dort kommen sehr viele Photonen in einem kleinen Raum - dem Lichtstrahl - vor.
Die Fermionen lassen sich wiederum nach ihrer Ladung aufteilen. Die Quarks haben alle drittelzahlige - die Leptonen hingegen immer ganzzahlige Ladungen.
Das Generationenmodell
[Bearbeiten]| Familie 1 | Familie 2 | Familie 3 |
|---|---|---|
| Quarks | ||
| up (u) | charm (c) | top (t) |
| down (d) | strange (s) | bottom (b) |
| Leptonen | ||
| Elektron (e-) | Myon () | Tauon () |
| Elektron-Neutrino () | Myon-Neutrino () | Tauon-Neutrino () |
Wie wir bereits weiter oben festgestellt haben, sind zum Aufbau unserer Welt und zur Erklärung aller physikalischen Phänomene nur die folgenden elementaren Fermionen nötig:
- Das Up-Quark
- Das Down-Quark
- Das Elektron
- Das Elektron-Neutrino
Nun haben wir jedoch gesehen, dass jedoch noch 8 andere elementare Fermionen existieren. Dem aufmerksamen Leser wird - wie einst den Physikern - aufgefallen sein, dass die Fermionen sich immer in Dreiergruppen einteilen lassen: Zwei Dreiergruppen mit Quarks; eine Dreiergruppe mit geladenen Leptonen und eine Dreiergruppe mit Neutrinos. Die oben gelisteten, in der Natur vorkommenden Teilchen, sind jeweils das leichteste Teilchen aus jeder dieser Gruppen.
Man ist also auf die Idee gekommen, die Fermionen in drei "Familien" oder "Generationen" einzuteilen. Die erste Familie enthält die Teilchen aus denen wir bestehen; die beiden anderen Familien enthalten Teilchen, welche zwar ähnliche Eigenschaften wie die der ersten Familie haben - jedoch deutlich schwerer sind. Ebenso, wie die Teilchen der zweiten Familie deutlich schwerer sind, als die der ersten, so sind auch die der dritten Familie deutlich schwerer als die der zweiten. Eine Ausnahme des hier gesagten stellen die Neutrinos dar, da diese laut Standardmodell keine Massen haben.
Ladungs-Multipletts
[Bearbeiten]Beim Isospin haben wir es schon einmal angesprochen - die starke Ähnlichkeit zwischen Teilchen, wie dem Neutron und dem Proton. In der obigen Grafik können sie weitere solche Teilchen erkennen. So gibt es je drei Pionen, Kaonen, D-Mesonen und Sigma-Baryonen sowie zwei Xi- und vier Delta-Baryonen. Die Teilchen dieser Teilchengruppen haben alle die gleichen Eigenschaften wie ihre Gruppenmitglieder - mit einer Ausnahme: Der elektrischen Ladung. Aus diesem Grund nennt man solche Teilchengruppen Ladungsmultipletts. Ladungsmultipletts, die nur aus zwei Teilchen bestehen, werden oft Ladungsdupletts genannt. Neben den bereits genannten, gibt es noch eine Vielzahl anderer Ladungsmultipletts, auf welche wir jedoch nicht weiter einzugehen brauchen. Der winzige Massenunterschied zwischen den Teilchen eines Ladungsmultipletts folgt aus ihrer elektrischen Ladung, welche sie "abbremst" und dadurch träge macht. So ist es auch nicht verwunderlich, dass das Verhältnis der Massendifferenz zur Gesamtmasse des leichtesten Teilchens, gleich dem Verhältnis zwischen der elektromagnetischen und der starken Kraft ist.
Wenn wir uns zunächst auf die Seltsamkeit (Strangeness) beschränken, so haben alle Teilchen eines solchen Ladungs-Multipletts dieselbe Strangeness. Damit lässt diese sich wie folgt berechnen: S = 2Q - B, wobei Q (auch QØ ) die durchschnittliche Ladung aller Teilchen des Multipletts und B die Baryonenzahl ist.
Allgemein benutzt man die Hyperladung Y = B + S + C + B' + T. Alle Teilchen eines Ladungs-Multipletts stimmen nicht nur in der Stangeness S, sondern auch in den anderen Flavour-Quantenzahlen Charm C, Bottomness B' und Topness T, und damit in ihrer Hyperladung überein. Wegen der Gell-Mann-Nishijima-Relation Y = 2(Q-Iz), wobei Iz die z-Komponente des Isospins bezeichnet, sind daher Ladungs-Multipletts auch Isospin-Multipletts. Für ein solches Ladungs- oder Isospin-Multiplett von Baryonen bzw. Mesonen gilt daher verallgemeinert: Y = 2Q, bzw. S + C + B' + T = 2Q - B, wobei Q wieder die mittlere Ladung der Teilchen des Multipletts bezeichnet.
Historisch (II): Das Sakata-Modell
[Bearbeiten]Wie schon öfters angesprochen gibt es eine Vielzahl an Hadronen, das war der Grund, warum bereits in den 40er Jahren die Teilchenphysiker versuchten diese Teilchen zu ordnen. Einen ersten Ansatz dazu schlug der japanische Physiker S. Sakata im Jahre 1956 vor. Er vermutete, dass alle 17 bis dahin bekannten Hadronen sich aus Kombinationen von zwei aus sechs andern Teilchen zusammensetzen. Diese sechs nach Sakata elementaren Teilchen wären das Proton, das Neutron das neutrale Lambda und deren Antiteilchen. Alle anderen Hadronen sind demnach Teilchen-Antiteilchen-Paare dieser sechs Teilchen. Das π- wäre demnach aus einem Neutron und einem Antiproton zusammengesetzt; das K+ wäre hingegen eine Kombination aus Proton und dem neutralem Anti-Lambda.
Ein scheinbares Problem des Sakata-Modells war, dass die Masse eines zusammengesetzten Teilchens viel kleiner ist, als die Summe aller Teilchen, aus denen es besteht. So addieren sich die Massen von Proton und Antiproton zu 1877 MeV, während das neutrale Pion - welches laut Sakata aus diesen beiden Teilchen zusammengesetzt ist - eine Masse von lediglich 135 MeV. Dies sollte jedoch nicht unbedingt als ein Fehler im Modell angesehen werden, denn laut der Speziellen Relativitätstheorie sind Masse und Energie ineinander umwandelbar. So ist auch ein Atomkern leichter als seine Bestandteile, die Differenz liegt als Bindungsenergie vor. Das Sakata-Modell wurde von den Physikern sehr unterschiedlich aufgenommen, schließlich aber verworfen, da weitere Hadronen gefunden wurden.
Supermultipletts
[Bearbeiten]Es gibt eine einfache, aber faszinierende Methode um die Hadronen in Gruppen einzuteilen und - sortiert nach ihren Eigenschaften - in ein "Koordinatensystem" einzuzeichnen.
Zunächst lassen sich die drei Spins der Quarks zu einem Gesamtspin von 1/2 oder einem Gesamtspin von 3/2 koppeln. Aus dem Pauli-Prinzip folgt, wie viele mögliche Kombinationen von Baryonen es in dieser Gruppe gibt: So gibt es acht Baryonen mit einem Gesamtspin von 1/2 und 10 Baryonen mit einem Spin von 3/2. Die Baryonen mit dem Spin 1/2 ergeben also ein Baryonoktett - während die anderen ein Baryondekuplett ergeben. Wir zeichnen also zwei getrennte Koordinatensysteme. Bei beiden wählen wir die dritte Komponente des Isospins als waagerechte x-Achse und die Strangeness des Teilchens als senkrechte y-Achse.
Zeichnen wir nun die Baryonen nach ihrem Spin getrennt in die beiden Koordinatensysteme, so ordnen sich die Teilchen in den beiden Koordinatensystemen nach je einem symmetrischen, geometrischen Muster. Und in diesen Mustern, erkennt man noch weitere Regelmäßigkeiten. So steigt die elektrische Ladung von unten links nach oben rechts. Und die Hyperladung steigt parallel zur Strangeness - jedoch um eins verschoben. Die Masse hingegen steigt von oben nach unten und sehr schwach auch von rechts nach links. Wenn sie sich die Teilchen, welche auf demselben waagerechten Niveau liegen, betrachten, so fällt ihnen vielleicht auf, dass es sich hier um die oben vorgestellten Ladungs-Multipletts handelt. Wenn wir uns den Quark-Aufbau der Teilchen anschauen, erkennen wir noch eine weitere Auffälligkeit: Die Teilchen sind nach ihren Quarks geordnet. In den Ecken befinden sich jeweils Teilchen, welche nur aus eine Sorte von Quarks aufgebaut sind. In den Mitte hingegen befinden sich die Teilchen, welche alle drei Arten von Quarks enthalten. Die Tatsache, dass in der Mitte des Baryonoktetts zwei Teilchen eingezeichnet sind (Sigma-null und Lambda-null) heißt nicht, dass dies nur zwei unterschiedliche Namen für dasselbe Teilchen sind. Die Teilchen unterscheiden sehr wohl. So hat das neutrale Sigma eine Masse von 1,192.5 GeV, das neutrale Lambda hat hingegen nur 1,115.6 GeV. Sehr deutlich unterscheiden sie sich in ihrer Lebensdauer: Das Lambda-null-Meson lebt 5 Milliarden mal länger (allerdings ist das immer noch weniger als ein Milliardstel einer Sekunde).
-
Das Baryondekuplett
-
Dieselbe Grafik wie links, jedoch sind hier die Quarks eingezeichnet
-
Das Baryonoktett
-
Dieselbe Grafik wie links, jedoch sind hier die Quarks eingezeichnet
Zum Zeitpunkt der Entdeckung dieser Symmetrie, war beispielsweise das Omega-Teilchen noch nicht bekannt. Mit Hilfe der gerade genannten Symmetrien, konnte man jedoch seine Eigenschaften problemlos vorhersehen.
Auch Mesonen bilden solche Multipletts wenn man sie in ein Koordinatensystem einzeichnet. Auch die Mesonen teilt man dafür in zwei Gruppen ein. Mesonen bestehen aus zwei Quarks, deren Spinausrichtungen entweder parallel oder antiparallel sein können. Der Spin ist dementsprechend entweder null oder eins. Die ersteren nennt man pseudoskalare Mesonen, die Mesonen mit Spin 1 hingegen Vektormesonen.
Sowohl die pseudoskalaren Mesonen, als auch die Vektormesonen bilden ein Nontet - also ein Gebilde aus neun Teilchen. In der Mitte dieser Nontets - welche in der Form dem Baryondekuplett ähneln - sitzen jeweils drei Teilchen. Des Weiteren findet man in den Mesonen-Nontets das Antiteilchen eines bestimmten Teilchens immer genau gegenüber. Den Quarkaufbau der Teilchen einzuzeichnen sparen wir uns hier, da dies bei Mesonen etwas komplizierter ist. So ist der exakte Quarkaufbau des ρ0-Mesons .
-
Das Mesonennonet für pseudoskalare Mesonen
-
Das Mesonennonet für Vektormesonen
Dreidimensionale Supermultipletts
[Bearbeiten]
Vielleicht ist ihnen schon aufgefallen, dass wir in diesen Grafiken nur Teilchen betrachten, welche aus den drei leichtesten Quarks - nämlich den Up-, Down- und Strange-Quark - aufgebaut sind. Das liegt daran, dass man damals nur diese Teilchen kannte. Heute ist jedoch bekannt, dass es außer diesen drei leichten Quarks noch drei weitere sog. schwere Quarks (charm, bottom und top) gibt. Mit diesen schweren Quarks können weitere Hadronen erzeugt werden. Indem man beispielsweise beim Lambda-Baryon (uds) das Strange-Quark durch ein Charm-Quark ersetzt, erhält man das mit einer etwa 1200 MeV größeren Masse. Auch die Hadronen, welche ein oder mehrere Charm-Quarks enthalten, lassen sich gut in Supermultipletts wie die obigen einzeichnen, indem am eine dritte räumliche Achse verwendet. Auch hier ergeben sich wieder verblüffend symmetrische Objekte. So ergeben die Baryonen mit Spin 3/2 eine dreikantige Pyramide, deren Grundfläche das Baryondekuplett von oben ist.
Aus diesen Supermultipletts kann man acht Quantenzahlen ablesen: Baryonenzahl, Ladung, Hyperladung, Strangeness, Spin, Isospin, dritte Komponente des Isospins und Multiplizität. In Anlehnung an den Edlen Achtfachen Pfad - welcher im Buddhismus den Weg zur Aufhebung des Leidens darstellt - nannte man diese gruppentheoretischen Überlegungen den Achtfachen Weg (engl.: Eightfold Way). Dieser Weg wurde in den 1960er Jahren von Murray Gell-Mann und Yuav Ne'eman entwickelt. Die mathematische Grundlage greift auf ein Konzept zurück, welches Sophus Lie schon im 19. Jahrhundert entwickelte: Die Lie-Gruppen. Die Lie-Grupe in diesem Fall bezeichnet man als SU(3). Dies ist die Schreibform für eine spezielle unitäre Gruppe der 3x3 Matrizen. Was dies wiederum konkret ist, können wir aufgrund der Komplexität in diesem Buch nicht erläutern. Wichtig ist nur, dass Sie den Ausdruck SU(N) kennen. Der Achtfache Weg führte unmittelbar zur Quark-Hypothese.
Referenzen
[Bearbeiten]
Der Higgs-Mechanismus
[Bearbeiten]In der 1970er Jahren schrieb der Brite Peter Higgs (* 29. Mai 1929) an einen Studenten: "Ich habe etwas völlig Nutzloses entdeckt". Heute halten wir diese Entdeckung jedoch nicht mehr für ganz so nutzlos - ganz im Gegenteil: gegenwärtig geben wir Milliarden von Dollar aus, um diese Entdeckung zu überprüfen.
Das Ganze hat damit begonnen, dass man in Experimenten bei den Eichbosonen der schwachen Kraft eine Masse feststellte. Den Theorien des Standardmodells der Teilchenphysik zufolge dürften Eichbosonen jedoch keine Masse besitzen. Peter Higgs fragte sich deshalb, warum Teilchen überhaupt eine Masse besitzen. Er überlegte sich - wie schon viele andere - wie es sein kann, dass das leichte Elektron betragsmäßig exakt die gleiche elektrische Ladung hat wie das fast 2000 mal schwerere Proton. Oder warum das Neutron fast die gleiche Masse wie das Proton hat - jedoch ein kleines bisschen schwerer ist als das Proton (was eine grundlegende Voraussetzung für unser Dasein ist, denn schließlich ist das Neutron instabil und zerfällt zu einem Proton; wäre es andersherum, hätten sich keine Atome bilden können). Das gipfelt darin, dass das Standardmodell überhaupt keine Massen für Teilchen vorsieht - die Existenz von massiven Teilchen steht im direkten Widerspruch mit dem Standardmodell. Eine Lösung für dieses Problem bietet das Higgs-Feld.
Als ein Vergleich zum Higgs-Mechanismus, kann man sich eine politische Veranstaltung vorstellen. Zunächst stehen die Leute gleichmäßig im Raum verteilt. Betritt zum Beispiel ein hohes Regierungsmitglied den Saal, so wird es sofort von einer Menschenmenge umgeben - man will Autogramme oder man will mit ihm reden. Will diese Person nun an das andere Ende des Saales gelangen, so wird sie sich durch die Menschenmenge durchkämpfen müssen. Betritt jedoch der Oppositionsführer den Raum, so wird man sich demonstrativ von ihm abwenden und er hätte keinerlei Problem den Saal zu durchqueren.
Ähnlich funktioniert der Mechanismus. Peter Higgs stellte die Hypothese auf, nach der im gesamten Universum ein überall gleichmäßiges Feld - heute Higgs-Feld genannt - existiert. Dieses Feld übernimmt die Aufgabe der Menschen im obigen Vergleich. Manche Teilchen bremst es mehr ab, andere weniger. So entsteht die Trägheit - und da die Trägheit mit der Masse des Teilchens verknüpft ist, erhält jedes Materieteilchen so seine Masse.
Da wir wissen, dass ein Feld grundsätzlich immer mit einem Teilchen verbunden sein muss, folgt aus dem Higgs-Feld die Notwendigkeit eines neuen, unentdeckten Teilchens – genauer gesagt eines Bosons, dieses Teilchen nennen wir Higgs-Boson.
Über dieses Teilchen weiß man, dass es einen Spin von 0 haben muss und dass es elektrisch ungeladen sein muss. Es selbst hat eine Masse ungleich null. Aus dem Standardmodell ergibt sich eine obere Grenze der Masse des Higgs-Teilchens von etwa 1.000 GeV/c². Durch experimentell gemessene Daten kann die Masse auf zwischen 114 GeV/c² und 600 GeV/c² eingeschränkt werden. Durch neuere Berechnungen wird die Masse auf zwischen 117 GeV/c² und 153 GeV/c² geschätzt. Es gibt jedoch auch Theorien, welche ein Higgs-Multiplett mit Energien von über 200 GeV/c² ermöglichen. Zum Vergleich: ein Nukleon hat eine Masse von knapp 1 GeV/c². Da die Masse des Higgsteilchens so hoch ist, widersetzte es sich der Entdeckung, bis sein Nachweis im Jahre 2012 bekannt gegeben wurde und drei seiner Entdecker im Folgejahr den Physik-Nobelpreis erhielten.
Weitere Informationen:
- Erklärung des Higgs-Mechanismus von der Uni Wuppertal mit einer erklärenden Animation.
- Alpha Centauri: Was ist ein Higgs-Teilchen? (Video)
- Suche nach dem Higgs-Boson; erfordert mathematische Vorkenntnisse (PDF)
BSM - Erweiternde Theorien
[Bearbeiten]Auch wenn das jetzige Standardmodell eine sehr lange Zeit als ein fast „perfektes Modell“ galt, so häufen sich heute die Vermutungen, dass einige grundlegende Aspekte möglicherweise falsch sind. Denn zum einen scheinen viele Phänomene nicht erklärbar und zum anderen stoßen die Teilchenphysiker immer häufiger auf unüberwindbare Probleme beim Versuch zwei Theorien zu vereinigen. Dabei handelt es sich beispielsweise häufig um unsinnige Unendlichkeitswerte. Für etliche dieser Probleme existieren bereits (meist unfertige) Lösungen, für andere nicht. Solche Theorien nennt man Beyond the Standard Model-Theorien.
Im Folgenden wollen wir die wichtigsten Probleme kurz erklären und - soweit vorhanden - auch auf mögliche Lösungen eingehen. Wir werden sie jedoch nicht ausführlich erklären können (das würde den Rahmen diese Buches sprengen) - dafür werden wir Hinweise auf Bücher (sowohl Wikibooks-Bücher als auch gedruckte) und Links zu Internet-Seiten listen.
Der Protonenzerfall
[Bearbeiten]Wie wir schon im Kapitel zu den Erhaltungssätzen gesehen haben, ist das Proton aufgrund der Baryonenzahlerhaltung stabil. Viele Physiker sind heute jedoch der Ansicht, dass die Baryonenzahl veränderlich ist, was zur Folge hat, dass das Proton nicht stabil ist, sondern nur eine sehr hohe Lebensdauer besitzt.
Lassen sie uns die Gründe zu dieser Annahme erörtern. Die anderen Erhaltungsgrößen wie Energie oder Ladung haben alle eine unmittelbare, beobachtbare physikalische Bedeutung. So erzeugen beispielsweise elektrische Ladungen ein magnetisches Feld, welches selbst wieder auf andere elektrische Ladungen wirkt. Die Baryonenzahl wurde jedoch nur dafür eingeführt, um das scheinbare Nichtauftreten von Reaktionen wie dem Protonenzerfall zu erklären. Es gibt kein uns bekanntes Phänomen, welches die Baryonenzahl benötigt. Auch die Erhaltung der Ladung ist nicht grundlos, denn auf ihr beruhen die Theorien zur Beschreibung des Elektromagnetismus, ohne die Ladungserhaltung würden diese Theorien ihren Sinn verlieren. Für die Erhaltung der Baryonenzahl gibt es jedoch keine vergleichbare Begründung. Man könnte jetzt annehmen, dass es ein weiteres uns noch unbekanntes Feld gibt - wir nennen es im Folgenden barytropisches Feld. Mit einem solchem Feld wäre natürlich auch eine Kraft verbunden - es gäbe also zu den vier uns bekannten Kräften noch eine weitere noch nicht entdeckte. Doch die Erde zum Beispiel besteht aus Milliarden von Baryonen - ihre Baryonenzahl ist also extrem stark positiv und würde alles ihn ihrer Nähe - also auch uns - anziehen oder abstoßen. Der Unterschied zur Gravitation wäre jedoch, dass die Schwerkraft proportional zur Masse - die barytropische Kraft jedoch proportional zur Baryonenzahl ist. Man kann also durch Untersuchung von Objekten, welche unterschiedliche Baryonenzahl aber gleiche Masse haben, bestimmen, wie stark eine solche Kraft maximal sein dürfte. Durch Untersuchungen wissen wir heute, dass die Anziehung nahezu exakt proportional zur Masse ist, die barytropische Kraft muss also um viele Größenordnungen schwächer sein, als die Gravitation es ist. Und wenn Sie sich zurückerinnern: Wir haben gesagt, dass die Gravitation schon - für teilchenphysikalische Verhältnisse - sehr schwach ist. Die Existenz einer solchen Kraft ist daher eher unwahrscheinlich.
In der Geschichte der Teilchenphysik ist man bereits einigen Größen begegnet, welche keine unmittelbare physikalische Bedeutung haben, jedoch trotzdem - zumindest unter bestimmten Bedingungen - einen Erhaltungssatz erfüllen. Ein Beispiel, welches wir bereits kennen gelernt haben, ist die Strangness, welche durch die Farbladung bei starken Wechselwirkungen erhalten wird. Alle diese Erhaltungsgrößen kann man jedoch mit einer Kraft in Verbindung bringen - nur die Baryonenzahl nicht.
Ein weiterer Hinweis darauf, dass die Baryonenzahl nicht exakt gleich bleibt, liefert die Kosmologie. Man könnte eigentlich annehmen, dass am Anfang des Universums, also beim Urknall, dieses gleich viel Materie wie Antimaterie enthielt. Aber dann würden sich die Materieteilchen mit den Antimaterieteilchen immer wieder vernichten und dann wieder entstehen. Die uns umgebene Welt ist jedoch äußerst stabil und besteht so weit wir wissen nur aus Materie. Wäre dies nicht so, könnten wir nicht existieren und darüber nachdenken, warum dies so ist. Dieses Phänomen bezeichnet man als die Baryonenasymmetrie. Frühere Erklärungsversuche, dass das Universum in einigen Bereichen mit Materie, in anderen mit Antimaterie gefüllt sei, gelten heute als unwahrscheinlich. Denn in den Grenzgebieten müsste Annihilationsstrahlung entstehen, welche jedoch nicht nachgewiesen werden konnte. Man geht deshalb heute davon aus, dass von Anfang an eine winzige Differenz zwischen Materie und Antimaterie bestand und dadurch etwas an Materie übrig geblieben ist, während die andern Teilchen sich vernichteten. Eine alternative Erklärung ergibt sich wenn man die Baryonenzahl als nicht konstant ansieht. Wenn man annimmt, dass es am Anfang des Universums gleich viel Materie und Antimaterie gab, so war damals die gesamte Baryonenzahl des kompletten Universums genau null - während sie heute stark positiv ist. Das wäre ein Verstoß gegen die Baryonenzahlerhaltung - wenn die Baryonenzahl jedoch nicht unveränderlich ist, so wären Reaktionen vorstellbar, in denen mehr Materie als Antimaterie entsteht. Einen weiteren Hinweis auf Protonenzerfälle geben die Beobachtungen von Neutrino-Oszillationen. Auch sagen einige der Entwürfe für GUTs einen Protonenzerfall unmittelbar voraus.
Aber was würde es bedeuten wenn die Baryonenzahl keine Erhaltungsgröße ist? Nun, wie schon gesagt, würde ein Zerfall des Protons dadurch möglich. Ein möglicher Zerfall wäre: p → e+ + π0. Aber auch in Atomkernen gebundene Neutronen könnten zerfallen, unter der Annahme, dass die Baryonenzahl sich verändern kann. Das heißt wiederum, dass alle Atome - also alle Isotope aller chemischen Elemente - radioaktiv wären und mit der Zeit zerfallen würden. Doch wie lang ist dann die Lebensdauer des Protons und der gebunden Neutronen? Sie muss auf jeden Fall größer als 1016 Jahre sein, denn sonst würden von den in unserem Körper enthaltenen Protonen so viele zerfallen, dass wir durch unsere eigene Strahlung eine Gefahr für unsere Gesundheit wären. Neuere Experimente, bei denen viele Tonnen schwere Materialproben überwacht wurden, konnten diese Grenze weiter auf 1035 Jahre heben. Bisher wurde noch kein Protonenzerfall beobachtet, man sucht jedoch weiter danach.
Die Supersymmetrie
[Bearbeiten]Wie wir bereits erfahren haben, gibt es zwei unterschiedliche grundlegende Arten von Elementarteilchen: Fermionen und Bosonen. Fermionen haben einen halbzahligen Spin - Bosonen einen ganzzahligen. Die Supersymmetrie geht davon aus, dass man jedem Fermion einen Bosonen-Partner und jedem Boson einen Fermionen-Partner zuordnen kann. Die Elementarteilchen kommen also paarweise vor, bei denen eins einen ganzzahligen und eins einen halbzahligen Spin besitzt. Den Partner eines Teilchens nennt man Superpartner.
Als die Physiker Mitte der siebziger Jahre versuchten, die Supersymmetrie in das Standardmodell einzugliedern, mussten sie feststellen, dass anders als bisher vermutet, keines der bekannten Teilchen der Superpartner eines anderen bekannten Teilchens ist. Laut der Supersymmetrie verdoppelt sich die Anzahl der Elementarteilchen auf mindestens 38. Bis jetzt konnte man noch keines der Superteilchen finden, weshalb man annimmt, sie hätten deutlich höhere Massen.
Dunkle Materie
[Bearbeiten]Als Astrophysiker die Umlaufgeschwindigkeiten von Sternen in Spiralgalaxien maßen, stellten sie fest, dass diese den mit Hilfe von Newtons Gravitationsgesetz berechneten Voraussagen widersprachen. Während man annahm, dass in den äußeren Regionen die Umlaufgeschwindigkeit abnimmt, beobachtete man dort eine Zunahme der Geschwindigkeiten. Um diesen Unterschied zwischen Berechnung und Wirklichkeit zu erklären, gibt es zwei Möglichkeiten: Entweder man erklärt das Newtonsche Gesetz für ungültig, oder man nimmt an, dass es noch eine große Menge an Materie gibt, welche wir mit unseren Teleskopen nicht beobachten können. Da die meisten Physiker der Meinung sind, dass das Newtonsche Gesetz richtig ist, gehen die meisten Wissenschaftler von letzterem Fall aus. Auch wenn gewöhnliche Materie, welche einfach für unsere Teleskope zu schwach leuchtet (zum Beispiel Braune Zwerge, Schwarze Löcher, Neutronensterne oder kaltes Gas), einen Anteil der dunklen Materie ausmacht, so sind sich die meisten Forscher einig, dass dies nur ein relativ kleiner Anteil ist und es noch eine weitere Form von Materie gibt, welche wir noch überhaupt nicht kennen und welche nicht mit elektromagnetischen Wellen wechselwirkt. Diese Kalte Dunkle Materie besteht also aus Teilchen, welche die Teilchenphysik noch nicht kennt. Hier kommt die Supersymmetrie ins Spiel, denn sie sagt eine ganze Menge neuer Teilchen, mit größtenteils unbekannten Eigenschaften, voraus, von denen unter anderem der Superpartner des Photons, das Photino, in Frage kommen würde. Teilchen, welche nur der Gravitation und der schwachen Wechselwirkung unterliegen, nennt man WIMPS (Weakly Interacting Massive Particles, zu deutsch: Schwach wechselwirkende massive Teilchen).

Weitere Informationen zur Dunklen Materie finden Sie hier.
Das Hierarchieproblem
[Bearbeiten]Wie wir bereits gesehen haben, gehen wir davon aus, dass sich spätestens im Bereich der Planck-Energie die elektroschwache und die starke Kraft vereinigen und es zu einer GUT kommt. Dies würde bei ca. 1016 GeV (EGUT) - also weit jenseits jedes messbaren Bereichs - auftreten. Zu Zeiten kurz nach dem Urknall war das Universum jedoch noch so heiß, dass diese Energien herrschten und alle drei Kräfte ununterscheidbar waren. Erst als sich das Universum auf eine bestimmte Temperatur abgekühlt hatte, wurden sie zu unterschiedlichen Kräften. An diesem Punkt liegt somit ein spontaner Symmetriebruch vor. Als das Universum noch weiter abkühlte, kam es bei deutlich tieferen Energien (100 GeV) zu einem weiteren spontanen Symmetriebruch und die elektrische und die schwache Kraft trennten sich. Die Quantenfeldtheorie kann jedoch die Stabilität einer GUT nicht bewahren, wenn sie zwei spontane Symmetriebrüche bei unterschiedlicher Energie enthält. In solchen Fällen verschiebt ein Mechanismus der Quantenfeldtheorie die untere Brechung zu den Energien der oberen Brechung - was, wie wir gerade erläutert haben, nicht der Wirklichkeit entspricht.
Um dem Problem auszuweichen, kann man jedem Teilchen einen Partner zuordnen, der (bei größeren Energien) genau die gleichen Eigenschaften hat. Eine Lösung wäre damit die Supersymmetrie die jedem Fermion einen Bosonischen Partner zuordnet. Eine andere Möglichkeit wäre, dass es zwei Higgsbosonen gibt und mindestens eines davon ein zusammengesetztes Teilchen ist. Dieses Higgs-Teilchen, wäre aus uns unbekannten Bausteinen - welche Techniteilchen genannt werden - zusammengesetzt und sie würden durch die Technifarbe zusammengehalten.
Der Weg zur Weltformel
[Bearbeiten]Bereits oben haben wir den Weg zur Weltformel beschrieben - hier wollen wir lediglich die wichtigsten Kandidaten für eine GUT oder TOE vorstellen.
Die Große Vereinheitlichte Theorie
[Bearbeiten]Es gibt bereits eine große Anzahl von Kandidaten für eine große Vereinheitlichung. Diese GUTs sagen verschiedene Erscheinungen voraus, nach denen man experimentell suchen kann. So sagen etliche der GUTs die Instabilität des Protons, und seine Lebensdauer, voraus. Die einfachste GUT, die als „minimale SU(5)“ bezeichnet wird, wurde bereits vor längerem verworfen, da sie eine Lebensdauer von 2,5 · 1031 Jahren für das Proton voraussagt - was, wie oben erklärt, nicht zutreffen kann. Es gibt andere GUTs, welche sehr viel längere Protonen-Lebensdauern vorhersagen, diese werden schwer zu überprüfen sein. GUTs, welche die Supersymmetrie miteinbeziehen, nennt man Super-GUTs oder SUSY-GUTs. So gibt es beispielsweise eine SUSY-GUT, die als „minimales supersymmetrisches großvereinheitlichtes Modell“ (kurz: MSGM) bezeichnet wird und bisher jeder theoretischen Prüfung standhielt. Für die experimentelle Bestätigung einer solcher SUSY-GUT werden wir voraussichtlich auf Beschleuniger warten müssen, welche genügend hohe Energie aufbringen können, um s-Teilchen zu erzeugen.
Einer der vielversprechendsten Kandidaten ist SO(10) (SO: Spezielle Orthogonale Gruppe). Sie enthält im Gegensatz zu anderen GUTs keine exotischen, unbekannten Fermionen. Eine Reihe von weiteren GUTs basieren auf Untergruppen der SO(10): minimales Links-Rechts Modell, SU(5), Flipped SU(5) und das Pati-Salam-Modell; auch die GUT mit dem Namen „E6“ basiert auf SO(10). Daneben gibt es noch etliche andere Kandidaten einer GUT.
Die Weltformel
[Bearbeiten]Im Moment gibt es zwei potentielle Kandidaten zur einheitlichen Beschreibung der vier Grundkräfte: Die Stringtheorie und die Loop-Quantengravitation. Wobei Vertreter beider Theorien betonen, dass die bestehenden Theorien unvollständig sind, und dass zur Formulierung einer endgültigen Theorie noch wesentliche Probleme gelöst werden müssen. Auf die Stringtheorie werden wir weiter unten eingehen, da sie es vermag noch weitere Fragen zu beantworten.
Schleifenquantengravitation
[Bearbeiten]Die Schleifenquantengravitation - oft auch Loop-Quantengravitation genannt - ist ein Ansatz um die Probleme, welche auftreten, wenn man die allgemeine Relativitätstheorie mit der Quantengravitation zusammen anwendet, lösen kann. Sie geht davon aus, dass die Raumzeit kein teilnahmsloser Behälter für das in ihm eingebettete Geschehen, sondern selbst ein den Gesetzen der Quantenmechanik gehorchendes, dynamisches Objekt ist. Die Raumzeit wird in ihr als ein Netzwerk von Knoten beschrieben, welche mit Linien verbunden sind. Die Knotenabstände entsprechen der Planck-Länge (10-35 m) beziehungsweise der Planck-Zeit (10-43 s). Somit quantisieren sie die Raumzeit. Das heißt Längen unterhalb der Planck-Länge und Zeitdauern unterhalb der Planck-Zeit sind nicht möglich! Damit enthält ein Kubikzentimeter ganze 1099 Knoten. Ein Elementarteilchen entspricht in dieser Theorie einem Netzknoten mit bestimmten Eigenschaften. Die Bewegung von Teilchen entspricht dabei einer Verschiebung entsprechender Knotentypen im Netz. Wichtig ist hierbei, dass man sich dieses Netz nicht in oder auf einem Raum während eines Zeitpunktes vorstellen darf, dieses Netz ist selbst Raum und Zeit. Ein Raum als Behälter für das Netz existiert nicht. Zwischen den Netzknoten befindet sich also kein Raum. Ihren Namen hat die Theorie daher, da in ihr schleifenförmige Strukturen (engl. loop = Schleife) in der Raumzeit eine wichtige Rolle spielen.
Zwar hat es die Loop-Quantengravitation bisher noch nicht geschafft alle vier Grundkräfte zu vereinigen, jedoch sind ihre Anhänger zuversichtlich, dass dies früher oder später möglich sein wird. Ein weiteres Problem ist, dass es noch nicht gelang die allgemeine Relativitätstheorie direkt aus der Schleifenquantengravitation abzuleiten.
Weitere Informationen zur Schleifenquantengravitation finden Sie hier.
Das Graviton
[Bearbeiten]Vielleicht ist Ihnen schon aufgefallen, dass wir von der Gravitation nicht einmal das zugehörige Eichboson kennen - und das obwohl sie die am längsten bekannte der Grundkräfte ist.
Für dieses noch unentdeckte Teilchen hat man sich schon einen Namen ausgedacht: Graviton. Auch einige der Eigenschaften des Gravitons hat man bereits vorhersagen können - Sie finden diese in Tabelle 5.
Die Superstringtheorie & M-Theorie
[Bearbeiten]
Viele Physiker (und vielleicht auch Sie?) fragen sich, warum es genau drei Teilchen-Generationen gibt. Warum nicht nur eine oder zwei - oder aber auch vier oder mehr? Und warum haben die Teilchen genau die Eigenschaften, welche wir messen können? Welchen Grund hat es, dass Neutronen und Protonen fast gleich schwer sind - aber nicht ganz? Viele (Teilchen-)Physiker fragen sich, ob man wirklich all diese Daten nur durch Messen herausfinden kann. Wäre es nicht denkbar, dass man diese Daten ebenfalls aus einer Theorie ableiten kann? Ist es möglich, eine Theorie zu erschaffen, welche gänzlich ohne „Input“, also ohne Messdaten, auskommt?
Die Anhänger der Superstringtheorie (oft auch nur Stringtheorie) sagen ja! Die Stringtheorie soll nicht nur in der Lage sein, diese Fragen zu beantworten, sie soll auch eine Weltformel (TOE) sein, denn sie löst die Konflikte zwischen der Allgemeinen Relativitätstheorie und der Quantenmechanik. Diese beiden Theorien beschreiben ihr jeweiliges Gebiet, den Makro- bzw. den Mikrokosmos zwar sehr genau, sie lassen sich jedoch nicht auf Bereiche anwenden, die eine Beschreibung beider Theorien verlangen. Solche Punkte im Universum, die z.B. im Zentrum Schwarzer Löcher oder zu Beginn des Universums vorkommen, nennt man Singularitäten.
Die Superstringtheorie basiert auf der Annahme, dass die Elementarteilchen nicht wie bisher angenommen Punktteilchen ohne Ausdehnung sind, sondern dass sie extrem kleine schwingende eindimensionale Fäden - welche man Strings nennt - sind. Die Schwingungsmuster die ein String ausführt, bestimmen die Eigenschaften des durch ihn verkörperten Teilchens. So bedeutet z.B. eine höhere Anzahl von Wellenbergen und -tälern eine höhere Energie (ähnlich wie bei einer Gitarrensaite) und somit nach Einsteins berühmter Formel E=mc² auch eine höhere Masse des Strings. Aus etwas komplizierteren Überlegungen folgen die anderen Eigenschaften des Teilchens. Das „Super“ in Superstringtheorie deutet darauf hin, dass die Superstringtheorie die Supersymmetrie fast mit einschließt.

Aus der Stringtheorie folgen viele interessante neue Kenntnisse und Annahmen. So benötigt die Stringtheorie z.B. ein elfdimensionales (zehn Raumdimensionen und eine Zeitdimension) statt dem gewohnten vierdimensionalen (drei Raumdimensionen und eine Zeitdimension) Universum. Die sieben Zusatzdimensionen sind zu extrem kleinen Gebilden - Calabi-Yau-Räume - „zusammengeknüllt“, so dass wir sie nicht wahrnehmen, die Strings, die in etwa die gleiche Größe besitzen jedoch schon, was ihre Eigenschaften maßgeblich beeinflusst. Des Weiteren erlaubt die Stringtheorie die Existenz von exotischen Phänomenen, wie z.B. Elementarteilchen mit elektrischen Ladungen von beispielsweise 1/5, 1/11 oder 1/53 - um nur einige zu nennen – oder der Variation von Naturkonstanten, was in der klassischen Physik ausgeschlossen ist.
Bis vor einiger Zeit gab es fünf unterschiedliche, miteinander konkurrierende Stringtheorien, welche scheinbar sehr unterschiedlich waren. In den letzten Jahren hat sich herausgestellt, dass diese Theorien nur Teile einer viel umfassenderen sind: der M-Theorie. In ihr kommen neben den klassischen eindimensionalen Strings auch Objekte mit bis zu neun Dimensionen vor, die als „Branen“ bezeichnet werden. Wie die theoretische Existenz dieser Objekte zu deuten ist, ist noch umstritten. So gibt es auch theoretische Modelle, die davon ausgehen, dass das bekannte vierdimensionale Universum, welches wir wahrnehmen, in Wirklichkeit eine riesige dreidimensionale Bran ist, die in die elfdimensionale Raumzeit eingebettet ist. Davon bekommen wir deshalb nichts mit, weil sich alle Teilchen bis auf das Graviton (das Teilchen, welches die Gravitation vermittelt) nur innerhalb sogenannter D-Branen bewegen können. Andere Modelle gehen hingegen davon aus, dass es sich bei den Elementarteilchen um Branen handelt.
Die Superstring- bzw. die M-Theorie schafft es zwar, einige der ungelösten Probleme des Standardmodells zu bewältigen, es gibt jedoch noch viele offenstehende Fragen, die sie nicht beantworten kann. Auch die mathematischen Gleichungen, die sie beschreiben, sind so komplex, dass sie bisher nur näherungsweise gelöst werden können. Ob die Superstringtheorie es also schafft eine Weltformel zu werden bleibt abzuwarten.
Weitere Informationen über die Stringtheorie finden Sie hier
Sind Quarks und Leptonen wirklich elementar?
[Bearbeiten]In der Vergangenheit hat man immer wieder festgestellt, dass die Gebilde, von denen man annahm sie seien elementar, doch nicht elementar sind. So war es mit den Molekülen, den Atomen, den Atomkernen und schließlich den Nukleonen. Eine der einfachsten Ideen auf welche man kommen kann, wenn man nach neuen Theorien sucht, ist die Frage ob wir mit dem Prozess des „Zwiebelschälens“ am Ende sind, oder ob wir nach den Bestandteilen der Quarks und Leptonen suchen sollen. Nach unseren derzeitigen experimentellen Erkenntnissen sind diese Teilchen wirklich elementar, doch es ist nicht ausgeschlossen, dass es noch tiefere Strukturen gibt. Es wurden bereits einige Modelle vorgeschlagen, nach denen Quarks und Leptonen nicht elementar sind.
Eines dieser Modelle ist das 1979 vorgeschlagene Modell der Rischonen. Dabei gibt es nur zwei elementare Teilchen - Rischonen genannt - sowie deren Antiteilchen. Die beiden Rischonen wurden Tohu und Vohu (hebrä. „formlos“ bzw. „wüst“/„leer“; die Beschreibung des Universums in seinem Urzustand in der Schöpfungsgeschichte) genannt. Das T trägt die elektrische Ladung von +1/3, während das V elektrisch neutral ist. In diesem Modell können immer entweder drei Rischonen oder drei Antirischonen ein Teilchen bilden - Rischonen und Antirischonen können jedoch nicht miteinander kombiniert werden. Somit bauen sich die acht Quarks und Leptonen wie in der nebenstehenden Tabelle auf. Indem man den Rischonen Farben zuordnet, kann man erklären, warum Quarks eine Farbe haben - Leptonen jedoch nicht.
Experimentelle Teilchenphysik
[Bearbeiten]

Kosmische Strahlung
[Bearbeiten]Die Erde wird ununterbrochen aus dem Weltall mit verschiedensten Teilchen beschossen, insgesamt treffen auf die äußere Erdatmosphäre ca. 1000 Teilchen pro Quadratmeter und Sekunde. Durch die hohen Energien, welche sie haben, wechselwirken sie sowohl mit anderen kosmischen Teilchen als auch mit der Materie in der Atmosphäre. In folge dessen zerfallen sie in der Erdatmosphäre zu neuen Teilchen und bieten so den Teilchenphysikern eine praktische Teilchenquelle. Da die Teilchen - wie in der speziellen Relativitätstheorie gefordert - durch ihre hohen Geschwindigkeiten langsamer altern, können manche von ihnen noch bis zum Erdboden fliegen, bevor sie - in für die Forscher uninteressante Teilchen - zerfallen. Da jedoch andere Teilchen bereits weit über dem Meeresspiegel zerfallen, musste man die Detektoren möglichst weit nach oben bringen. Dafür gibt es zwei grundsätzliche Möglichkeiten: entweder baut man die Observatorien möglichst hoch in den Bergen oder man baut die Detektoren möglichst kompakt und lässt sie mit einem Ballon (sowohl "Wetterballone" als auch "Heißluftballone" sind möglich) in die Höhe steigen.
Durch die Kosmische Strahlung wurden folgende Teilchen entdeckt:
- 1932: Entdeckung des Positrons
- 1936: Entdeckung des Myons
- 1947: Entdeckung des geladenen Pions (π-)
Teilchenbeschleuniger
[Bearbeiten]Wenn man nicht nur warten will, bis interessante Teilchen ankommen, dann muss man sich selber welche produzieren. Auch sind die Teilchen, welche in der Kosmischen Strahlung oder anderen natürlichen Prozessen zu beobachten sind beschränkt. Dabei arbeitet man mit der Einsteinschen Energie-Masse-Äquivalenz. Wenn man leichte Teilchen mit großer kinetischer Energie - also mit hohen Geschwindigkeiten - kollidieren lässt, kann man durch die große Energie Teilchen mit großer Masse erzeugen. Auf diese Weise kann man neue schwerere Teilchen finden. Grundsätzlich lassen sich nur Teilchen mit elektrischer Ladung beschleunigen, denn alle Teilchenbeschleuniger basieren auf dem selben Prinzip: eine Spannung zwischen zwei Elektroden zieht ein geladenes Teilchen zu der, der Teilchenladung entgegengesetzt geladenen, Elektrode. Wobei sich die Beschleunigungsenergie wie folgt berechnet:
[Kinetische Energie] = [geleistete Arbeit] = [Kraft] x [Abstand] = [Teilchenladung] x [elektrisches Feld] x [Abstand] = [Teilchenladung] x [Spannung]/[Abstand] x [Abstand] = [Teilchenladung] x [Spannung]
Somit hängt die Beschleunigung nur von der Teilchenladung und der angelegten Spannung ab.
Linearbeschleuniger
[Bearbeiten]Beim Linearbeschleuniger wird das Teilchen durch linear hintereinander angeordnete elektrische Felder geschickt. Durch die Ladung erhält es in jedem der Felder eine geradlinige Beschleunigung.
Die elektrischen Felder werden durch Anlegen von Wechselspannung an Spulen in Röhren, welche um den Teilchenstrahl gewundenen sind, erzeugt - Gleichspannung erwies sich als ungeeignet, da sie bei höheren Energien einen Lichtbogen erzeugt. Die elektrischen Felder sind der Stärke nach aufsteigend sortiert, wodurch die kinetische Energie der Teilchen in relativ kleinen Schritten zunimmt. Die Wechselspannung wird so synchronisiert, dass das Potenzial der folgenden Röhre immer entgegengesetzt zur Ladung des Teilchens ist, während die Röhre in der das Teilchen sich momentan befindet die gleiche Ladung wie das Teilchen hat. Das komplette System wird - wie bei allen Teilchenbeschleunigern - in ein Vakuumrohr eingeschlossen, um zu verhindern, dass die Teichen ihre Energie in Kollisionen mit Luftmolekülen verlieren. Durch die Verwendung von vielen einzelnen Spulen, kann man mit relativ geringen Spannungen sehr hohe Beschleunigungsenergien erreichen. So beträgt der kinetische Energie Zuwachs eines Teilchens, in einem Linearbeschleuniger mit 25 Spulen von je 100.000 Volt, 2,5 MeV. Dabei sollte erwähnt werden, dass Linearbeschleuniger oft hunderte oder tausende Rohre enthalten. Das Problem bei solchen Linearbeschleunigern ist, dass man um höhere Energien zu erreichen, die Linearbeschleuniger immer länger bauen muss. Der Platz limitiert also die erreichbaren Energien. Auch ist der Bau großer Linearbeschleuniger äußerst kostspielig, da eine Vielzahl an Spulen und Stromwandlern benötigt wird.

Aus diesen Gründen haben Linearbeschleuniger in der modernen Teilchenphysik nur noch eine geringe Bedeutung. Sie werden jedoch noch sehr häufig als Vorbeschleuniger für andere Beschleuniger verwendet. Es gibt jedoch noch wenige große und wichtige Linearbeschleuniger, von welchen der 3,2 km lange SLAC in Kalifornien der längste ist - er beschleunigt Elektronen und Positronen auf Energien von 50 GeV. Es gibt Planungen für einen neuen Linearbeschleuniger den International Linear Collider, dieser soll 40 km lang sein, und damit bisher unerreichte Energien von 500-1000 GeV ermöglichen. Des Weiteren werden Linearbeschleuniger heute häufig für Medizinische Zwecke verwendet.
Van-de-Graaff-Beschleuniger
[Bearbeiten]Van-de-Graaff-Beschleuniger sind spezielle Beschleuniger die im Gegensatz zu normalen Linearbeschleunigern mit Gleichspannung arbeiten. Sie arbeiten dafür mit einem Van-de-Graaff-Generator. Das Endlosband des Generators lädt dabei ein sogenanntes Hochspannungsterminal positiv auf. Mit der Ladung werden dann - wie bei Linearbeschleuniger - mehrere elektrische Felder aufgebaut, durch welche das Teilchen beschleunigt wird.
Tandem-Beschleuniger
[Bearbeiten]Beim Tandem-Beschleuniger werden negativ geladene Ionen über mehrere Meter auf von einer positiv geladenen Folie angezogen. Wenn sie auf die Folie treffen haben sie genug Energie um diese zu durchdringen, beim durchdringen geben sie jedoch einen Teil der Elektronen ab. Dadurch werden sie von der Folie abgestoßen, und ein zweites mal beschleunigt.
Tandembeschleuniger werden u.A. zur Radiokarbon-Methode verwendet.
Kreisbeschleuniger
[Bearbeiten]Da der Bau von immer längeren Linearbeschleuniger sehr kostspielig wurde, kam man auf die Idee, eine Beschleunigungsstrecke mehrfach zu nutzen, indem man das Teilchen auf einer Kreisbahn wieder zurück leitet, und es so immer und immer wieder beschleunigen zu können.
Zyklotron
[Bearbeiten]Im Jahre 1929 erfand der amerikanische Physiker E.O. Lawrence eine neue Art von Beschleunigern, das Zyklotron. Sie kennen vermutlich aus dem Physik-Schulunterricht den Begriff der Lorenzkraft. Diese wirkt zum einen, wenn ein elektrischer Strom senkrecht zu einem Magnetfeld fließt, zum anderen jedoch auch wenn sich eine Ladung in einem solchem bewegt. Bewegt sich also ein geladenes so wird dieses gemäß der rechten-Hand-Regel auf eine Kreisbahn gezwungen. Desto größer die Energie der Teilchen ist, desto größer ist der Radius der Kreisbahn. Die Dauer die ein Teilchen für einen Umlauf benötigt, bleibt jedoch gleich groß - solange die Geschwindigkeit relativ klein im Vergleich zur Lichtgeschwindigkeit ist. Wird ein Teilchen also in einem homogenen Magnetfeld beschleunigt, so bewegt es sich also auf einer Sprialbahn nach außen.
Bei einem Zyklotron verwendet man zwei D-förmige Halbkreise, zwischen welchen man eine Wechselspannung, mit einer Amplitude von zwischen einigen Tausend bis zu über einer Million Volt, anlegt. Diese Halbkreise, welche man D's, Dees oder auch Duanden nennt, befinden sich in einem homogenen Magnetfeld, welchen durch einen Elektromagneten erzeugt werden. Das Teilchen beginnt in der Nähe der Mitte des Kreises welchen die beiden D's bilden. Immer wenn es den Spalt zwischen den beiden D's überquert, wird es durch die anliegende Spannung beschleunigt und das Magnetfeld sorgt dafür, das das Teilchen sich auf eine Spiralbahn bewegt und nicht etwa gleich den Beschleuniger verlässt. Die Wechselspannung dient dazu, damit die Ladung der D's bei beiden Beschleunigungsstrecken eine positive Beschleunigung auf das Teilchen ausübt, und es nicht wieder bremst. Da das Teilchen pro Umlauf zweimal beschleunigt wird und mit einem genügend starkem Magnetfeld die Bahn es Teilchens eng gehalten werden kann, sind damit hohe Energien erreichbar. Wird allerdings die Geschwindigkeit es Teilchen sehr hoch, so kommt die allgemein Relativitätstheorie mit ins Spiel. Dann bleibt die Umlaufdauer nicht mehr konstant, was dazu führt, dass man die Frequenz der Wechselspannung synchronisieren muss. Die nötige Anpassung der Frequenz von der Geschwindigkeit abhängt, für die Herstellung neuer Teilchen jedoch nicht die Geschwindigkeit, sondern vielmehr die Energie es Teilchens von Interesse ist, verwendet man hauptsächlich Teilchen mit hoher Ruhe Energie. Es sei noch anzumerken, dass heutige Zyklotrone nicht mehr aus nur zwei, sondern mehreren Dees bestehen.

Synchrotron
[Bearbeiten]Beim Zyklotron ist das Magnetfeld konstant und der Radius der Teilchenbahn nimmt mit zunehmender Geschwindigkeit zu. Der Durchmesser des Magneten muss jedoch immer so groß sein, wie der der größten Teilchenbahn am Ende der Bechleunigung. Das führt jedoch dazu, dass man immer größere Magnete benötigt, dabei stieß man jedoch bald an technische Grenzen. Deshalb ersann man sich ein neues Konzept, bei dem der Radius der Teilchenbahn konstant bleibt und dafür die Stärke des Magnetfeldes angepasst wird. Einen solchen Beschleuniger nennt man Synchrotron. Sie sind das Prinzip, nach dem heute die meisten großen Teilchenbeschleuniger gebaut werden. Der Begriff Kreisbeschleuniger wird oft als Synonym für Synchrotron verwendet, allerdings ist ein Synchrotron nur eine - wenn auch sicherlich die wichtigste - von mehreren Arten von Kreisbeschleunigern (eine zweite haben wir ja bereits kennen gelernt). In einem Synchrotron fliegen die Teilchen in einem evakuierten Ring auf einer Kreisbahn, worauf sie durch Magnete auf der Bahn gehalten werden. Um mit wachsender Geschwindigkeit der Teilchen diese weiterhin auf der exakten Kreisbahn zu halten, muss die Stärke der Magnete ständig angepasst werden. In der Kreisbahn befinden sich ein oder mehrerer Beschleunigungsbereiche, in denen die Teilchen bei jedem Durchflug - wie in einem Linearbeschleuniger - beschleunigt werden. Da der Radius der Teilchen gleich bleibt, kann man sehr viele Umläufe machen und so die Teilchen auf sehr hohe Energien bringen. Meist verwendet man einen Linearbeschleuniger als Vorbeschleuniger, er beschleunigt die Teilchen auf Energien von der Größenordnung von 1 MeV, bevor sie in den Ringbeschleuniger eingespeist werden. Längs des Ringes sind zwei Arten von Magneten angebracht: Die Fokusierungsmagneten lenken gestreute Teilchen zum Strahl zurück, so dass man einen dünnen, gebündelten Teilchenstrahl erhält. Die Krümmungsmagneten sorgen hingegen dafür, dass die Teilchen eine Kreisbahn fliegen. Haben die Teilchen die gewünschte Energie erreicht, wird ein Elektromagnet am Röhrenausgang so geschaltet, dass die Teilchen aus ihrer Kreisbahn abgelenkt und sie somit aus dem Ring ausgestoßen werden. Der Teilchenstrahl kann nun zum gewünschten Experiment geleitet werden. Bis in die 1950er Jahre konnte man keine Energien von mehr als etwa 10 GeV erreichen, da immer zu leichten Schwingungen des Teilchenstrahls kommt, was eine Destabilisierung des Strahles zur Folge hat. 1952 wurde jedoch das Prinzip der starken Fokussierung erfunden, hierbei werden Quadrupolmagneten so angeordnet, dass sie den Strahl abwechseln horizontal und vertikal fokussieren. Durch diese Vermeidung der Schwingungen, stabilisiert man den Strahl und ist in der Lage den Querschnitt des Beschleunigerrohrs stark zu verringern. Dies bringt den Vorteil, dass man die Magneten - und auch andere Bauteile - wesentlich kleiner machen kann als bei einem Synchrotron der alten Bauweise.
Sie könnten jetzt denken, man könnte beliebig große Energien erreichen, indem man die Teilchen einfach immer mehr Umrundungen machen lässt, dem ist jedoch leider nicht so. Denn wenn die Teilchen durch die Magnetfelder auf ihre Kreisbahn gelenkt werden, verlieren sie durch diese Felder wieder einiges ihrer Energie in Form von Synchrotronstrahlung. Um diesen Verlust zu minimieren, muss man die Krümmung der Teilchenbahn möglichst stark minimieren - anders ausgerückt, muss man einen immer größeren Radius für den Kreisbeschleuniger verwenden. (Die Emission von Synchrotronstrahlung ist proportional zu E4/M4R2, wobei E die Energie, M die Masse des Teilchens und R der Radius des Beschleunigers ist.) Eine Vergrößerung des Bahnradius hat des Weiteren zur Folge, dass man weniger starke Magnetfelder braucht, um die Teilchen in ihrer Bahn zu halten.
Bedeutende Synchrotrone sind heute HERA am DESY in Hamburg, der LEP in CERN oder Tevatron. Im Moment baut man im Europäischen Forschungszentrum CERN einen noch deutlich größeren Beschleuniger, den Large Hadron Collider (LHC). Der LHC hat einen Kreisumfang von 27 Kilometern, und wird Protonen auf 17 TeV und Bleiionen auf 1148 TeV beschleunigen. Damit wollen die Teilchenphysiker unter anderem das Higgs-Teilchen finden.
Teilchenquellen
[Bearbeiten]Doch natürlich braucht man erst einmal Teilchen, um diese in einem Teilchenbeschleuniger mit hohen Energien aufeinander prallen zu lassen. Meist verwendet man dafür stabile, in der Natur vorkommende Teilchen. Beliebte Teilchen sind unter anderem:
- Protonen
- Gold- und Bleiionen
- Heliumkerne
- Elektronen
Doch auch wenn diese Teilchen auf der Erde in Maßen existieren, so treten sie meist gebunden auf. Die Protonen findet man in jedem Atomkern und die Atomkerne sind meist nur als Bestandteil kompletter Atome zu finden, welche wiederum meist in Molekülen oder Atomgittern gebunden sind. Dazu kommt noch, dass man für Experimente in Beschleunigern einen Teilchenstrahl braucht, der sehr viele der gewünschten Teilchen enthalten soll, jedoch kaum andere Teilchen enthalten darf. Man braucht also Teilchenquellen, welche einen sauberen, reinen Teilchenstrahl erzeugen.

Elektronenquelle
[Bearbeiten]Ich bin mir fast sicher, dass auch Sie eine "Teilchenquelle" für Elektronen zuhause haben - vermutlich sitzen sie genau in diesem Moment davor! Denn ein Röhrenmonitor basiert auf dem selben Prinzip, wie die in Teilchenbeschleunigern eingesetzten Elektronenquellen: der Kathodenstrahlröhre. Die Kathodenstrahlröhre besteht aus einem abgeschlossenen evakuierten Glaskolben mit einer Glühkathode. Wird an der beheizten Kathode eine hohe elektrische Spannung angelegt, so werden die aus der Kathode ausgetretenen Elektronen beschleunigt und durchfliegen das Beschleunigungsfeld der Kathodenstrahlröhre. Durch ein, meist aus Magneten bestehendes, Fokussiersystem werden die Elektronen dort zu einem Strahl gebündelt, so dass sie - beim Einsatz in Teilchenbeschleunigern - dann mit elektromagnetischen Feldern in Richtung Beschleunigungsstrecke abgelenkt werden können.
Alphastrahler
[Bearbeiten]Heliumkerne (He2+) sind ebenfalls sehr einfach zu "erzeugen". Sie entstehen natürlich beim Alphazerfall von Atomen. Um einen relativ reinen Alphastrahl zu erzeugen, legt man einen reinen Alphastrahler in eine Box mit einem kleinen Loch, durch welchen die Heliumkerne entweichen können. Um den entstehenden Strahl von Betastrahlung (Elektronen) und anderen Teilchen zu "reinigen", lenkt man ihn durch ein Magnetfeld auf eine Platte mit einem Spalt. Der Spalt ist so angebracht, dass er nur Teilchen mit einer elektrischen Ladung von +2 hindurch gelangen - Teilchen mit anderer Ladung werden entweder stärker oder schwächer abgelenkt.
Detektoren
[Bearbeiten]Jetzt wissen wir, woher die Teilchenphysiker ihre Teilchen bekommen - doch wie untersuchen sie diese? Dafür haben die Teilchenphysiker einige verschiedene Techniken erfunden - die wichtigsten davon will ich im folgenden beschreiben.
Fotoemulsionen
[Bearbeiten]Die älterste Methode zum Nachweiß ist die Fotographische Platte - auch Kernspurplatten genannt. (Als Fotoemulsionen bezeichnet man die lichtempfindliche Schicht auf der Platte). Dabei handelt es im Grunde um die Gleichen Lichtempfindlichen Platten welche in jeder analogen Kamera eingesetzt werden. Fliegt ein geladenes Teilchen hindurch, so kommt es durch Ionisation zu der gleichen Chemischen Reaktion, als wenn Licht auf die Platte fällt. Somit lassen sich Teilchenbahn auf der Photografischen Platte als schwarzer Strich verfolgen. Vor allem in den frühen Jahren der Teilchenphysik wurden viele wichtige Entdeckungen mithilfe dieser Methode gemacht. Die wohl bekannteste Entdeckung die damit gemacht wurde, war als Becquerel 1896 damit die Radioaktivität entdeckte. Die Methode wurde vor allem in Wien weiterentwickelt, und fand ihren Höhepunkt mit der Entwicklung der Kernemulsion, mit welcher unter anderem 1947 das Pion entdeckt wurde.

Ionisationskammer
[Bearbeiten]Tritt ein ionisierendes Teilchen in eine mit einem Gas gefüllte Kammer ein, so werden entlang seiner Bahn die Teilchen ionisiert. Das heißt, dass einige der Elektronen einiger der Atome des Gases von der Atomkernen getrennt werden. Durch einen Kondensator wird in der Kammer nun ein Elektrisches Feld erzeugt. Dadurch werden die Elektronen zu positiven- und die - nun positiv geladenen - Atome zur negativen-Platte gezogen. Treffen Sie darauf, so fließt ein Strom der gemessen werden kann. Früher maß man die Ladung mit einem Elektroskop, heute kann man ihn elektrisch verstärken und messen. Mit der Ionisationskammer wurde unter anderem das Neutron entdeckt.
Geiger-Müller-Zähler
[Bearbeiten]Ein naher Verwandter der Ionisationskammer ist das Zählrohr. Wird mit einer Spannung im sogenannten Plateau- oder Auslösebereich betrieben, nennt man es Geiger-Müller-Zähler. Der Hauptunterschied zur Ionisationskammer ist, dass das elektrische Feld stärker ist. Dadurch werden die Elektronen auf eine Geschwindigkeit beschleunigt, mit der sie selbst andere Atome ionisieren können. Dadurch entsteht eine Kettenreaktion, welche die Anzahl der messbaren Ladungen erhört. Geigerzähler sind zylinderförmig aufgebaut: Ein Metallrohr dient als Kathode und ein in dessen Mitte befindender Metalldraht als Anode. Die angelegte Spannung beträgt mehrere hundert Volt. Damit die Kettenreaktion nicht zu stark wird, gibt man dem Füllgas kleine Mengen eines mehratomigen Gases - beispielsweise Alkoholdampf - hinzu. Der entstehende Stromfluss wird über einen Widerstand in ein Spannungssignal umgewandelt. Dieses wird elektronisch verstärkt und entweder als Blinken einer Lampe oder als Knacken eines Lautsprechers ausgegeben. Um die Intensität genauer abschätzen zu können, werden die Signale mit einem Zähler gezählt.

Indem der Widerstand ausreichend hoch gewählt wird wird gewährleistet, dass der Stromfluss nach kurzer Zeit zusammenbricht und dann die Spannung wieder am Zählrohr anliegt. Nach dieser sogenannten Totzeit ist der Geiger-Müller-Zähler wieder für neue Teilchen empfindlich. Da Teilchen, die während der Totzeit in das Zählrohr kommen, nicht registriert werden, ist es wichtig durch geschickte Bauweise die Totzeit zu minimieren. Der Effekt der Totzeit lässt sich jedoch auch rechnerisch ausgleichen.
Funkenkammer
[Bearbeiten]Bei einer Funkenkammer befinden sich viele Platten parallel in einer durchsichtigen Kammer. Der Raum zwischen den Platten ist wieder mit einem Edelgas gefüllt. Jede zweite Platte ist geerdet, die anderen sind mit einer Hochspannungsquelle (~20 kV) verbunden - diese wird immer wieder für einige Millisekunden angeschaltet, danach jedoch gleich wieder abgeschaltet. Die Spannung wird so angelegt, dass es gerade nicht zu einem Funken-Durchschlag kommt. Fliegt nun ein Teilchen durch die Platten, so kommt es wieder zu der oben schon beschriebenen Ionisation zwischen den Platten und es entstehen Funken entlang der Bahn. Die Funken wiederum regen das Gas an, wodurch sie eine - vom Gas abhängige - Farbe annehmen. Die Funken bleiben so lange sichtbar, bis man die Spannung abschaltet - dies ist der Grund, warum man die Spannungsquelle immer nur für wenige Millisekunden anschaltet. Um die Bahnkurve nicht zu verfälschen, schaltet man - bei besseren Funkenkammern - die Spannung genau dann ein, wenn das Teilchen die Kammer verlässt. Um diesen Zeitpunkt zu erfahren, verwendet man am Anfang und am Ende der Kammer einen weiteren Teilchendetektor (meist einen Geiger-Zähler oder einen Szintillationszähler). Die Funkenkammer wurde Anfang der 1960er Jahre entwickelt, sie spielt heute in der Wissenschaft keine Rolle mehr.
Nebelkammer
[Bearbeiten]
Ist ein verschlossenes Gefäß zu einem Teil mit Wasser (oder einer anderen Flüssigkeit) gefüllt, so herrscht ein Gleichgewicht zwischen den Wassermolekülen im Wasser und denen in der darüber liegenden Luft: durch die thermischen Bewegungen der Moleküle im Wasser entweichen immer wieder Moleküle in die Luft; dagegen wirkt die Anziehungskraft der Moleküle aufeinander. Sehr kleine Tröpfchen einer Flüssigkeit verdampfen jedoch viel leichter, da die einzelnen Wassermoleküle von weniger anderen Molekülen angezogen werden - sie verdampfen auch wenn das Gleichgewicht bereits eingestellt ist. Dadurch ist es also unter gewissen Bedingungen möglich eine Gas zu übersättigen, so dass mehr Wasser in der Luft ist, als es eigentlich möglich. Denn damit ein solches System sich normalisiert, müssten sich kleine Wassertröpfchen bilden - diese würden jedoch sofort wieder verdampfen. Damit also das Wasser kondensieren kann braucht es einen Kondensationskeim an welchem sich größere Tropfen bilden, welche nicht gleich wieder verdampfen. Eine Nebelkammer ist ein meist mit einem übersättigten Luft-Alkohol-Gemisch gefüllter Behälter. Wenn ein elektrisch geladenes Teilchen das Gas durchquert, ionisiert es einzelne Atome des Gases. Die so entstandenen Ionen wirken als Kondensationskeime und dadurch entstehen auf dem Weg des Teilchens durch die Nebelkammer sichtbare Kondensationen, welche Kernspuren genannt werden. Die sichtbaren Kondensationen werden mit einer geeigneten Kamera fotografiert. Dabei entstehen die so genannten Kernspuraufnahmen. Doch was sagen diese Spuren aus?
Während die Teilchen das übersättigte Gemisch durchqueren, verlieren sie Bewegungsenergie, wie viel hängt von der Masse des Teilchens ab. Man kann also aus der Reichweite der Teilchen in dem Gemisch auf ihre Anfangsgeschwindigkeit und ihre Masse schlissen. Sollten sie zu schnell sein, und nicht innerhalb der Detektors abgebremst werden, so behilft man sich einer Bleiplatte, denn Blei "bremst" die Teilchen sehr viel mehr aus. Um noch mehr über das Teilchen zu erfahren, erzeugt man im Detektor ein Magnetfeld. Durchläuft es dieses, so wird es je nach Ladung abgelenkt. Ein positives Teilchen wird ihn die eine Richtung, ein negatives Teilchen in die entgegengesetzte Richtung abgelenkt - ein neutral geladenes Teilchen wird jedoch von dem Magnetfeld nicht beeinflusst. Die Stärke der Ablenkung hängt von der Masse, der Ladung und der Geschwindigkeit des Teilchens ab.
Technisch lässt sich eine Nebelkammer auf zwei verschiedene Arten bauen. Sehr einfach aufgebaut ist die Wilson'sche Nebelkammer (auch Expansionsnebelkammer), dabei handelt es sich um eine luftdicht abgeschlossene Dose mit einem Kolben, der wie eine Luftpumpe wirkt, daran. Zieht man ruckartig an dem Kolben, so verringert sich der Druck und die Temperatur kurzfristig und es können für wenige Augenblicke Teilchenspuren gesehen werden. Wesentlich beeindruckender aber auch teurer ist eine kontinuierliche Nebelkammer. In dieser wird ein Temperaturgefälle aufgebaut, indem oben in der Kammer warmer Dampf aus Verdampfer ausströmt und nach unten sinkt, wo er beispielsweise durch Trockeneis gekühlt wird. In dem Temperaturgefälle gibt es ein empfindliches Gebiet, in der nun durchgehend Teilchenspuren beobachtet werden können.
Blasenkammer
[Bearbeiten]Eine wichtige Weiterentwicklung der Nebelkammer ist die Blasenkammer, in ihr wird eine Flüssigkeit, wie zum Beispiel flüssiger Wasserstoff, durch plötzliche Druckabsenkung überhitzt. Durchquert ein elektrisch geladenes Teilchen die Kammer, so ionisiert es Atome darin. Die Ionen wirken als Kondensationskeime, so dass sich entlang der Teilchenbahn Dampfbläschen bilden, welche man mit geeigneter Beleuchtung fotografieren kann. Durch die höhere Dichte der Flüssigkeit - im Vergleich zu dem Gas in der Nebelkammer - kommt es zu sehr viel mehr Reaktionen als in einer Nebelkammer. Auch sind dadurch die Teilchenspuren kürzer, wodurch sich oft auch die Folgereaktionen beobachten lassen.
Der amerikanische Physiker Donald A. Glaser erhielt 1960 den Physik-Nobelpreis für die Erfindung der Blasenkammer. Von den 1960ern bis in die 1980ern spielte die Blasenkammer eine bedeutende Rolle in der Teilchenphysik. Heute spielen sie an den modernden Teilchenbeschleunigern keine Rolle mehr, sie werden jedoch noch verwendet, um nach Teilchen der Dunklen Materie zu suchen.
Szintillationszähler
[Bearbeiten]Alle bisher genannten Detektoren sind nur zum Auffinden von Teilchen im klassischen Sinn, also nur Teilchen, die eine Masse ungleich null haben. Wie jedoch weist man Eichbosonen nach? Wir wollen uns also der Frage stellen: Wie misst man elektromagnetische Strahlung im Gammabereich?
Im Bereich des sichtbaren Lichts ist die Messung sehr einfach, schließlich macht das menschliche Auge nichts anderes, die analoge Fotografie existiert seit dem 19. Jahrhundert und 1970 konstruierte Bell den ersten CCD-Sensor, wie man ihn heute noch in Digitalkammeras verwendet. Es währe also einfach, γ-Strahlung zu messen, wenn man diese in sichtbares Licht umwandeln könnte. Dies geht zwar nicht direkt, jedoch behilft man sich mit einem sogenannten Szintillator. Gerät ein geeignetes Teilchen, wie beispielsweise ein γ-Quant, in den Szintillator, regt es diesen an und es entsteht ein Lichtblitz, bei dem mehrere Photonen mit niedriger Energie entstehen. Doch diese Lichtblitze sind meist sehr schwach - teilweise handelt es sich nur um wenige einzelne Photonen. Da ein gewöhnliches Display oder Fotodioden meist bei weitem nicht so empfindlich ist, benützt man einen sogenannten Photomultiplier.

Die Photonen treffen auf eine Photokathode und schlagen dabei durch den Photoeffekt Elektronen aus deren Oberfläche. Diese Elektroden werden beschleunigt und auf eine Elektroden - Dynoden genannt - geleitet. Dort schlagen sie weitere Elektronen - Sekundärelektronen genannt - aus der Elektrodenoberfläche heraus. Der Elektronenstrahl wird erneut beschleunigt und trift, dann wieder auf eine Dynode - dies wiederholt sich etliche Male, wobei sich die Anzahl der Elektronen bei jeder der Dyonen vermehrfacht. Damit dies funktioniert, muss die an den Dynoden anliegende Spannung von Dynode zu Dynode immer größer werden. Meist wird das realisiert, indem die ursprüngliche Hochspannung über eine Spannungsteilerkette heruntergeteilt wird. Zum Schluss treffen die Elektronen auf eine Anode, wo sie als Stromfluss gemessen werden können. Da die Anzahl der Elektronen in solchen Photomultiplier oft vermillionenfacht werden, lassen sich damit sogar einzelne Photonen messen. So kann ein Photomultiplier mit zehn Dynoden je nach Spannung dei Photonenanzahl um einen Faktor von 106 bis 1010 vervielfachen.
Nun wissen wir, wie ein Szintillationszähler Gammastrahlung misst. Je nach Szintillator eignet sich ein Szintillationszähler zur Messung von Alpha-, Beta-, Gamma- oder Neutronenstrahlung. Die zeitliche Auflösung eines Szintillationszähler beträgt zwischen 10-6 und 10-8 Sekunden.
Zahlen und SI-Präfixe
[Bearbeiten]Natürlich spielen in der Teilchenphysik - wie auch in den meisten anderen Naturwissenschaften - die Zahlen eine große Rolle. Da es hier oft zu sehr großen oder sehr kleinen Zahlen kommt, haben die Wissenschaftler spezielle Schreibweisen dafür eingeführt. Denjenigen unter den Lesern, welche mit diesen Schreibweisen noch nicht vertraut sind, soll dieser Anhang Aufschluss geben.
Große Zahlen ausgeschrieben
[Bearbeiten]Wissen Sie wie man eine "1" mit fünfzehn Nullen nennt? Hier die wichtigeren der großen Zahlennamen:
| Zahl | Zahlenname | Exponentialschreibweise |
|---|---|---|
| 1 | Eins | = 100 |
| 10 | Zehn | = 101 |
| 100 | Hundert | = 102 |
| 1.000 | Tausend | = 103 |
| 1.000.000 | Million | = 106 |
| 1.000.000.000 | Milliarde | = 109 |
| 1.000.000.000.000 | Billion | = 1012 |
| 1.000.000.000.000.000 | Billiarde | = 1015 |
| 1.000.000.000.000.000.000 | Trillion | = 1018 |
| 1.000.000.000.000.000.000.000 | Trilliarde | = 1021 |
| 1.000.000.000.000.000.000.000.000 | Quadrillion | = 1024 |
| 1.000.000.000.000.000.000.000.000.000 | Quadrilliarde | = 1027 |
| 1.000.000.000.000.000.000.000.000.000.000 | Quintillion2 | = 1030 |
| 1.000.000.000.000.000.000.000.000.000.000.000 | Quintilliarde2 | = 1033 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000 | Sextillion | = 1036 |
| 1.000.000.000.000.000.000.000.000.000.000.000.000.000 | Sextilliarde | = 1039 |
Um die Zahlen numerisch zu schreiben, ohne zu viel Platz zu brauchen - und ohne die Nullen zählen zu müssen - verwendet man die Exponentialschreibweise. Dabei wird die Zahl als Potenz der Zahl 10 dargestellt. Dabei ist der Exponent (die Zahl die hochgestellt steht) also die Anzahl der Stellen der Zahl (das gilt allerdings nur für Potenzen von 10!). Um auch Zahlen darzustellen, die nicht eine Potenz von 10 sind, multipliziert man sie mit einem Faktor. Dabei wählt man den 10-Exponenten meist so, dass der Faktor genau eine Vorkommastelle hat.
Beispiele:
| 100.000 | 1,0 * 105 |
| 10.000.000.000 | 1,0 * 1010 |
| 1.230.000 | 1,23 * 106 |
| 12.300.000 | 1,23 * 107 |
Kleine Zahlen
[Bearbeiten]Sehr kleine Zahlen werden fast auf die gleiche Art geschrieben, wie man es mit großen Zahlen tut. Will man sie ausschreiben, so verwendet man dieselben Zahlwörter, streicht eventuell das "e" am Ende, fügt ihnen jedoch noch ein "stel" hinzu: Hundertstel, Tausendstel; Millionstel; Milliardstel...
Um sie in Exponentialschreibweise darzustellen, verwendet man dieselbe Methode, aber mit einem negativen Exponenten.
Beispiele:
| 0,00001 | 1,0 * 10-5 |
| 0,0000000001 | 1,0 * 10-10 |
| 0,000123 | 1,23 * 10-4 |
SI-Präfixe
[Bearbeiten]Sehr beliebt sind die Präfixe, die man jeder Einheit voranstellen kann. Sie sind im internationalen Einheitensystem (SI) festgelegt:
| Symbol | Name | Ursprung | Wert | ||
|---|---|---|---|---|---|
| Y | Yotta | ital. otto = acht | (103)8 = 1024 | 1 000 000 000 000 000 000 000 000 | Quadrillion |
| Z | Zetta | ital. sette = sieben | (103)7 = 1021 | 1 000 000 000 000 000 000 000 | Trilliarde |
| E | Exa | gr. exa: über alles / gr. εξάκις, hexákis = sechsmal | (103)6 = 1018 | 1 000 000 000 000 000 000 | Trillion |
| P | Peta | gr. petanünnein: alles umfassen / gr. πεντάκις, pentákis = fünfmal | (103)5 = 1015 | 1 000 000 000 000 000 | Billiarde |
| T | Tera | gr. τέρας, téras = Ungeheuer / τετράκις, tetrákis = viermal | (103)4 = 1012 | 1 000 000 000 000 | Billion |
| G | Giga | gr. γίγας, gígas = Riese | (103)3 = 109 | 1 000 000 000 | Milliarde |
| M | Mega | gr. μέγας, mégas = groß | (103)2 = 106 | 1 000 000 | Million |
| k | Kilo | gr. χίλιοι, chílioi = tausend | (103)1 = 103 | 1 000 | Tausend |
| h | Hekto | gr. εκατόν, hekatón = hundert | 102 | 100 | Hundert |
| da | Deka | gr. δέκα, déka = zehn | 101 | 10 | Zehn |
| Einheit | 100 | 1 | Eins | ||
| d | Dezi | lat. decimus = zehnter | 10−1 | 0,1 | Zehntel |
| c | Zenti | lat. centesimus = hundertster | 10−2 | 0,01 | Hundertstel |
| m | Milli | lat. millesimus = tausendster | (10−3)1 = 10−3 | 0,001 | Tausendstel |
| μ | Mikro | gr. μικρός, mikrós = klein | (10−3)2 = 10−6 | 0,000 001 | Millionstel |
| n | Nano | gr. νάνος, nános und ital. nano = Zwerg | (10−3)3 = 10−9 | 0,000 000 001 | Milliardstel |
| p | Piko | ital. piccolo = klein | (10−3)4 = 10−12 | 0,000 000 000 001 | Billionstel |
| f | Femto | skand. femton/femten = fünfzehn | (10−3)5 = 10−15 | 0,000 000 000 000 001 | Billiardstel |
| a | Atto | skand. atten = achtzehn | (10−3)6 = 10−18 | 0,000 000 000 000 000 001 | Trillionstel |
| z | Zepto | lat. septem = sieben | (10−3)7 = 10−21 | 0,000 000 000 000 000 000 001 | Trilliardstel |
| y | Yokto | lat. octo = acht | (10−3)8 = 10−24 | 0,000 000 000 000 000 000 000 001 | Quadrillionstel |
Beispiele:
| 1 MHz | 1×106 Hertz |
| 1 nm | 1×10-9 Meter |
Vorsicht: im englischen Sprachgebrauch bedeutet "billion" eine Milliarde! So hieß z.B. der Beschleuniger in Kalifornien, mit dem das Antiproton entdeckt wurde, Bevatron, weil er Teilchen mit einigen BeV (d.h., einigen Milliarden eV) produzierte!
Tabelle der Teilchen und deren Eigenschaften
[Bearbeiten]Kräfte, Eichbosonen & das Higgs-Boson
[Bearbeiten]| Kraft | Teilchen (Symbol) | Masse [GeV/c2] | Elektr. Ladung [e] | Spin | relative Stärke |
Reichweite [m] |
Abstands- Wirkung |
|---|---|---|---|---|---|---|---|
| Elektro-Magnetische | Photon (γ) | 0 | 0 | 1 | 10−2 | ∞ | 1/r2 |
| Starke | Gluon (g) | 0 | 0 | 1 | 1 | 2,5·10−15 | |
| Schwache | W+ | 80 | +1 | 1 | 10−13 | 10−18 | 1/r5 bis 1/r7[A 1] |
| W- | -1 | ||||||
| Z | 91 | 0 | |||||
| Gravitation | Graviton [A 2] | 0 | 0 | 2 | 10−38 | ∞ | 1/r2 |
| Higgs-Boson[A 2] | >114 | 0 | 0 |
Fermionen
[Bearbeiten]Quarks
[Bearbeiten]Alle Quarks haben den Spin 1/2.
| Generation | Quark | kurz | Masse [MeV/c2] | el. Ladung | Lebensdauer [s] |
|---|---|---|---|---|---|
| 1 | Up | u | 1-3 | +2/3 | stabil |
| Down | d | 3-7 | -1/3 | stabil/einige hundert Sekunden | |
| 2 | Charm | c | 1250 ± 90 | +2/3 | 10-12 |
| Strange | s | 95 ± 25 | -1/3 | 5x10-8 | |
| 3 | Top | t | 171.000 ± 2100 | +2/3 | 10-25 |
| Bottom | b | 4200 ± 70 | -1/3 | 2x10-12 |
Leptonen
[Bearbeiten]| Generation | Teilchen | Symbol | Masse (MeV) | Mittlere Lebensdauer (s) |
|---|---|---|---|---|
| 1 | Elektron | , | 0,511 | stabil |
| 2 | Myon | , | 105,7 | |
| 3 | Tau | , | 1777 | |
| 1 | Elektronneutrino | stabil | ||
| 2 | Myonneutrino | stabil | ||
| 3 | Tauneutrino | stabil |
- Quelle
Hadronen
[Bearbeiten]Baryonen
[Bearbeiten]Laut Particle Data Group (Datensammlung von 2007) sind derzeit 36 Baryonen zweifelsfrei nachgewiesen (existence is certain) und weitere 18 mit an Sicherheit grenzender Wahrscheinlichkeit (existence ranges from very likely to certain).
Auf weitere 21 gibt es deutliche Hinweise (evidence of existence is only fair) und 25
sind nur schwach belegt (evidence of existence is poor).
Die folgende Tabelle ist eine Auswahl der wichtigsten Baryonen mit Quark-Zusammensetzung, Massen und Lebensdauern.
| Name | Zeichen | Quarks | Q | Y | S | I | ν | Masse (GeV·c-2) | Lebensdauer (s) | Hauptzerfälle |
|---|---|---|---|---|---|---|---|---|---|---|
| Proton | p | uud | +1 | 1/2 | 0 | 1/2 | 2 | 0,938.3 | > 1032 a | - |
| Neutron | n | udd | 0 | -1/2 | 0 | 1/2 | 2 | 0,939.6 | 885,7(8) (als freies Neutron]]) | |
| Lambda | uds | 0 | 0 | -1 | 1/2 | 2 | 1,115.6 | 2,6·10-10 | ||
| Sigma-plus | uus | +1 | 1 | -1 | 1/2 | 2 | 1,189.4 | 0,8·10-10 | ||
| Sigma-null | uds | 0 | 0 | -1 | 1/2 | 2 | 1,192.5 | 5,8·10-20 | ||
| Sigma-minus | dds | -1 | -1 | -1 | 1/2 | 2 | 1,197.3 | 1,48·10-10 | ||
| Xi-null | uss | 0 | 1/2 | -2 | 1/2 | 2 | 1,314.9 | 2,9·10-10 | ||
| Xi-minus | dss | -1 | -1/2 | -2 | 1/2 | 2 | 1,321.3 | 1,64·10-10 | ||
| charmed Lambda | udc | +1 | 0 | 0 | 1/2 | 2 | 2,281 | 2·10-13 | verschiedene schwache Prozesse | |
| bottom Lambda | udb | 0 | 0 | 0 | 1/2 | 2 | 5,624 | 1,2·10-12 | ||
| Delta | uuu | +2 | 3/2 | 0 | 3/2 | 4 | 1,232 | 0,6·10-23 | ||
| Delta | uud | +1 | 1/2 | 0 | 3/2 | 4 | 1,232 | 0,6·10-23 | ||
| Delta | udd | 0 | -1/2 | 0 | 3/2 | 4 | 1,232 | 0,6·10-23 | ||
| Delta | ddd | -1 | -3/2 | 0 | 3/2 | 4 | 1,232 | 0,6·10-23 | ||
| Omega-Minus | sss | -1 | 0 | -3 | 3/2 | 4 | 1,672 | 0,82·10-10 | ||
| Cascade b]] | dsb | -1 | -1/2 | -1 | 3/2 | 4 | 5,774(26) | 1,42·10-12 |
Y: Hyperladung
S: Strangeness
I: Isospin
ν: Multiplizität
A: Baryonenzahl
Mesonen
[Bearbeiten]| Name | Symbol | Quarks | Masse/MeV | S | C | B | I | Lebensdauer/s |
|---|---|---|---|---|---|---|---|---|
| Pseudoskalare Mesonen | ||||||||
| Pion | π+, π− | ud, ud | 139,6 | 0 | 0 | 0 | 1 | 2,6 · 10−8 |
| Pion | π0 | (uu − dd) | 135,0 | 0 | 0 | 0 | 1 | 8,3 · 10−17 |
| Kaon | K+, K− | us, su | 493,7 | -/+1 | 0 | 0 | 1⁄2 | 1,2 · 10−8 |
| Kaon | KS0 | (ds − sd) | 497,6 | 0 | 0 | 1⁄2 | 9 · 10−11 | |
| Kaon | KL0 | (ds + sd) | 497,6 | 0 | 0 | 1⁄2 | 5,1 · 10−8 | |
| Eta | η0 | (uu + dd) | 547,8 | 0 | 0 | 0 | 0 | 5 · 10−19 |
| Eta' | η'0 | ss | 958,8 | 0 | 0 | 0 | 0 | 3 · 10−21 |
| D-Meson | D+, D− | cd, cd | 1869,4 | 0 | -/+1 | 0 | 1⁄2 | 10,4 · 10−13 |
| D-Meson | D0, D0 | cu, cu | 1864,6 | 0 | -/+1 | 0 | 1⁄2 | 4,1 · 10−13 |
| Ds-Meson | Ds+, Ds− | cs, cs | 1968,3 | -/+1 | -/+1 | 0 | 0 | 4,9 · 10−13 |
| B-Meson | B+, B− | ub, ub | 5270,8 | 0 | 0 | -/+1 | 1⁄2 | 1,4 · 10−12 |
| B-Meson | B0, B0 | bd, bd | 5274,2 | 0 | 0 | -/+1 | 1⁄2 | 1,4 · 10−12 |
| Vektormesonen | ||||||||
| Rho | ρ+, ρ− | ud, ud | 770 | 0 | 0 | 0 | 1 | 4 · 10−24 |
| Rho | ρ0 | (uu − dd) | 770 | 0 | 0 | 0 | 1 | 4 · 10−24 |
| Kaon | K*+, K*− | us, su | 891,7 | -/+1 | ? | ? | 1,3 · 10−23 | |
| Kaon | K*0 | (ds + sd) | 896,0 | ? | ? | 1,3 · 10−23 | ||
| Omega | ω0 | (uu + dd) | 782,6 | 0 | 0 | 0 | 7 · 10−22 | |
| Phi | Φ'0 | ss | 1020 | 0 | 0 | 0 | 0 | 2 · 10−22 |
| J/Psi | J/Ψ | cc | 3096,9 | 0 | 0 | 0 | 0 | 8 · 10−19 |
| Ypsilon | Y | bb | 9460,4 | 0 | 0 | 0 | 0 | 1,3 · 10−20 |
Das griechische Alphabet
[Bearbeiten]Es sei angemerkt, das in der Physik die griechischen Buchstaben nicht griechisch ausgesprochen werden, sondern bei ihrem Namen genannt werden. Ein α-Teilchen wird also "Alpha-Teilchen" ausgesprochen nicht "a-Teilchen"!
| Zeichen | Name (altgr. Schreibung) | Transkription | Grichische Aussprache |
| Α, α | Alpha (ἄλφα) | a | [a], [aː] |
| Β, β | Beta (βῆτα) | b | [b] |
| Γ, γ | Gamma (γάμμα) | g | [g] |
| Δ, δ | Delta (δέλτα) | d | [d] |
| Ε, ε | Epsilon (ἔ ψιλόν) | e | [e] |
| Ζ, ζ | Zeta (ζῆτα) | z | [zd], [dz] |
| Η, η | Eta (ἦτα) | ē | [ɛː] |
| Θ, θ | Theta (θῆτα) | th | [tʰ] |
| Ι, ι | Iota (ἰῶτα) | i | [i], [iː] |
| Κ, κ | Kappa (κάππα) | k | [k] |
| Λ, λ | Lambda (λάμβδα) | l | [l] |
| Μ, μ | My (μῦ) | m | [m] |
| Ν, ν | Ny (νῦ) | n | [n] |
| Ξ, ξ | Xi (ξῖ) | x | [ks] |
| Ο, ο | Omikron (ὄ μικρόν) | o | [o] |
| Π, π | Pi (πῖ) | p | [p] |
| Ρ, ρ | Rho (ῥῶ) | r(h) | [r], [rʰ] |
| Σ, σ | Sigma (σίγμα) | s | [s], [z] |
| Τ, τ | Tau (ταῦ) | t | [t] |
| Υ, υ | Ypsilon (ὔ ψιλόν) | y bei αυ, ευ, ου: u | [y], [yː] |
| Φ, φ | Phi (φῖ) | ph | [pʰ] |
| Χ, χ | Chi (χῖ) | ch | [kʰ] |
| Ψ, ψ | Psi (ψῖ) | ps | [ps] |
| Ω, ω | Omega (ὦ μέγα) | ō | [ɔː] |
Empfehlenswerte Bücher und Internetseiten
[Bearbeiten]Im Folgenden listen wir einige populärwissenschaftliche Bücher und Webseiten auf, welche für Leser dieses Buches ebenfalls interessant sein könnten.
Allgemein
[Bearbeiten]- Yuval Neeman & Yoram Kirsh, Die Teilchenjäger, Springer Verlag, 1995, ISBN 3-540-53206-4
- Hans Günter Dosch, Jenseits der Nanowelt, Leptonen Quarks Eichbosonen, Springer Verlager, 2005, ISBN 3-540-22889-6
- Das Unteilbare - Quanten, Quarks und die subnukleare Struktur der Materie
Online Buch über Teilchenphysik - Teilchenphysik.org
- Elementarteilchen auf Quantenwelt.de
- Grundlagen der Teilchenphysik von der Universität Erlangen
- DESYs KworkQuark - Teilchenphysik für Kinder
- Quarks, Grundbausteine der Materie von Volkard Linke; Institut für Theoretische Physik, FU Berlin
- Hyperphysics Strukturierte Darstellung der gesamten Physik von Carl Rod Nave, Georgie State University
- Ein kleiner Aufsatz über Nutzen und Gefahr von Antimaterie:
Dunkle Materie
[Bearbeiten]- Dunkle Materie. Weshalb? Wieviel? Wo? (Uni Bonn)
- Sendungen aus der Fernsehsendung Alpha Centauri:
- David B. Cline: Die Suche nach Dunkler Materie. In: Spektrum der Wissenschaft. Heidelberg, Spektrumverlag 2003, 10/05 (Okt.), S.44-51. ISSN 0170-2971
- Wolfgang Rau: Auf der Suche nach der Dunklen Materie. in: Sterne und Weltraum. Heidelberg, Spektrumverlag 44.2005,1, S.32-42. ISSN 0039-1263
- James Trefil: Fünf Gründe, warum es die Welt nicht geben kann. Rowohlt Verlag GmbH, ISBN 3499193132
- Douglas Clowe et al.: A direct empirical proof to the existence of dark matter. ApJ Letters in press (2006) pdf
- Alexander Unzicker: Why do we Still Believe in Newton's Law ? Facts, Myths and Methods in Gravitational Physics. Preprint
Stringtheorie
[Bearbeiten] Die Stringtheorie – eine populärwissenschaftliche Einführung
Die Stringtheorie – eine populärwissenschaftliche Einführung- Brian Greene; Das elegante Universum - Superstrings, verborgene Dimensionen und die Suche nach der Weltformel, 2006
- Brian Greene: Der Stoff, aus dem der Kosmos ist - Raum, Zeit und die Beschaffenheit der Wirklichkeit, 2004
- Lisa Randall: Verborgene Universen - Eine Reise in den extradimensionalen Raum, 2005��
- Stringtheorie
Schleifenquantengravitation
[Bearbeiten]- Webmuster des Raums: Spin-Netzwerke
- Vaas, Rüdiger: "Tunnel durch Raum und Zeit", Franckh-Kosmos, 2006