Stetige Inhalte auf Sigma-Ringen – Serlo „Mathe für Nicht-Freaks“
In diesem Artikel leiten wir die Definition für Stetigkeit von Inhalten her. Wir untersuchen, wie die Begriffe Stetigkeit von unten und von oben zusammenhängen und lernen -Ringe als Definitionsbereiche von stetigen Inhalten kennen.
Motivation der Stetigkeit von Inhalten
[Bearbeiten]Im letzten Kapitel haben wir auf Ringen definierte Inhalte als Formalisierung des Messens extensiver Größen kennengelernt. Beim Messen solcher Größen erwarten wir oft, dass kleine Änderungen des gemessenen Objekts nur kleine Änderungen des Messergebnisses zur Folge haben. Beispiele hierfür sind
- das Wiegen einer Zutat: Nimmt man nur wenig dazu, dann ändert sich auch das Gewicht nicht viel.
- das Zählen von Objekten: Bestimmt man die Anzahl einer höchstens abzählbar unendlichen Menge von Objekten, so verändert sich diese nur wenig, wenn nur wenige Objekte hinzugetan oder weggenommen werden.
- der Flächeninhalt/Umfang eines Kreises: Er ändert sich nur wenig, wenn der Radius nur wenig verändert wird.
Es bietet sich die Formulierung an, dass solche Größen sich stetig verhalten. Allerdings werden wir noch definieren müssen, was unter der Stetigkeit eines Inhalts genau zu verstehen ist, sodass wir diesen Begriff vorerst nur intuitiv benutzen können.
Tatsächlich ist es schwierig, extensive Größen in der Natur zu finden, die sich nicht stetig verhalten. Es ist also eine natürliche und wichtige Frage, ob und wann Inhaltsfunktionen stetig sind. Darüber hinaus hat Stetigkeit eine sehr nützliche Eigenschaft zur Folge: Sie erlaubt die Approximation von zu messenden Mengen. Da geringe Abweichungen der Mengen voneinander nur geringe Abweichungen der Messwerte bewirken, kann der Fehler der Approximation über die Genauigkeit der approximierenden Mengen kontrolliert werden. Damit können auch "komplizierte" Mengen gemessen werden, indem man sie mit (möglicherweise einfacher zu messenden) Mengen approximiert. Ein Beispiel ist die Approximation des Flächeninhalts eines Kreises durch Rechteckfiguren, deren Flächeninhalt einfacher zu bestimmen ist.

Stetigkeit scheint deshalb eine wünschenswerte Eigenschaft eines Inhalts zu sein. Bevor wir diesen Begriff genauer untersuchen: Gibt es überhaupt Inhalte, die sich (in unserem intuitiven Sinne) unstetig verhalten?
Beispiel (Ein unstetiger Inhalt)
Wir betrachten die Grundmenge und den Inhalt , der von einer beliebigen Teilmenge der natürlichen Zahlen bestimmt, ob sie endlich oder unendlich ist:
Im Artikel Inhalte auf Ringen haben wir gesehen, dass wirklich ein auf dem Ring definierter Inhalt ist. Betrachten wir nun für die Mengen . Für approximieren diese offenbar die Grundmenge . Da aber jedes einzelne der endlich ist, ist für jedes . Durch Approximation von lässt sich nicht der Funktionswert approximieren, der Übergang von endlich zu unendlich ist "unstetig".
Es ist also nicht jeder Inhalt stetig. Wie können wir die Stetigkeit eines Inhalts mathematisch formalisieren? In Anlehnung an die Folgenstetigkeit reeller Funktionen versuchen wir die folgende Definition:
Definition (Stetiger Inhalt, erster Versuch)
Ein Inhalt auf einem Ring heißt stetig, wenn für eine Folge mit gilt, dass ist.
Aber hier müssen wir vorsichtig sein: Was ist unter zu verstehen, wenn die Mengen sind? Wir brauchen zuerst einen Konvergenzbegriff für Mengenfolgen.
Mengenfolgen
[Bearbeiten]Es ist schwer zu sagen, wogegen die Folge , konvergiert. Dagegen kann man vermuten, dass die Folge der gegen die Menge konvergiert: Da die fallend ineinander enthalten sind, kann man die Mengenfolge als Approximation der Menge "von Außen" auffassen. Ebenso kann man Folgen aufsteigend ineinander enthaltener Mengen als Approximation einer Menge "von Innen" auffassen (zum Beispiel die Folge der , welche ausschöpfen). Naheliegend ist dann, den Schnitt bzw. die Vereinigung der als Grenzwert der Folge zu setzen.
-
Die Mengenfolge läuft "unendlich weit nach rechts" und konvergiert daher nicht.
-
Die Mengenfolge schrumpft zusammen auf (blauer Bereich) und konvergiert damit.
Definition (Monotone Mengenfolge)
Sei eine Menge und eine Folge von Teilmengen.
Die Folge heißt aufsteigend oder monoton wachsend, falls für alle gilt. In diesem Fall setzen wir
und schreiben .
Die Folge heißt absteigend oder monoton fallend, falls für alle gilt. In diesem Fall setzen wir
und schreiben .
Hinweis
Mit unserer Definition können wir nur dann vom Grenzwert einer Mengenfolge sprechen, wenn diese monoton ist. Uns reicht das an dieser Stelle. Man kann aber für beliebige Mengenfolgen und definieren, die wie bei reellen Zahlenfolgen immer existieren.
Schauen wir uns ein paar Beispiele an:
Beispiel (Monotone Mengenfolgen)
Die Folge der ist monoton fallend mit Grenzwert
Die Inklusion "" gilt, da für alle ist. Andererseits kann der Grenzwert nicht mehr Elemente enthalten, da keines der negative Zahlen enthält und jede Zahl echt größer als Eins für einen Index nicht mehr in , also auch nicht im Schnitt liegt.
Ein weiteres Beispiel für eine monoton fallende Mengenfolge ist die Folge der . Man zeigt mit ähnlichen Argumenten, dass für diese Folge gilt.
Die Folge der ist ein Beispiel für eine monoton wachsende Mengenfolge. Ihr Grenzwert ist
Die Inklusion "" gilt, da jedes für einen Index in der Menge liegt. Andererseits kann der Grenzwert kein größeres Intervall sein, da keines der negative Zahlen oder die Eins enthält.
Ebenfalls monoton wachsend ist die Folge der . Der Grenzwert ist , wie man auf ähnliche Weise begründen kann.
Wie vertragen sich Grenzwerte monotoner Mengenfolgen mit Mengenringen? Schauen wir uns den Ring der Quaderfiguren im und zwei Beispiele von monoton wachsenden Mengenfolgen in diesem Ring an. Im linken Bild wird ein Rechteck durch eine Folge von Quaderfiguren approximiert. Der Grenzwert ist selbst eine Quaderfigur und liegt wieder in . Rechts sehen wir, wie ein Kreis durch Quaderfiguren approximiert wird. Der Grenzwert ist aber keine Quaderfigur mehr und liegt damit nicht in .
Offenbar muss also der Grenzwert einer monotonen Folge von Mengen aus einem Ring nicht unbedingt wieder im Ring liegen. Unsere Begründung dafür war mit den Quaderfiguren eher intuitiv, aber wir können auch ein ganz konkretes Beispiel angeben:
Beispiel (Grenzwert liegt nicht im Ring)
Betrachten wir den Ring aller endlichen Teilmengen von (diesen Ring haben wir hier kennengelernt). Die Folge mit ist monoton wachsend und liegt in . Ihr Grenzwert ist aber ganz und liegt damit nicht mehr im Ring aller endlichen Teilmengen von .
Stetigkeit von unten und von oben
[Bearbeiten]Definition der Stetigkeit
[Bearbeiten]Ausgestattet mit dieser Definition von Grenzwerten von Mengenfolgen können wir nun einen weiteren Versuch machen, die Stetigkeit eines Inhalts auf einem Ring zu definieren. Wir haben eben gesehen, dass für eine monotone Mengenfolge in einem Ring ihr Grenzwert nicht unbedingt wieder im Ring liegt. Beachte, dass wir deshalb die einschränkende Bedingung stellen müssen, dass der Grenzwert der Mengenfolge wieder im Ring liegt, damit die Definition sinnvoll ist.
Definition (Stetiger Inhalt, zweiter Versuch)
Ein Inhalt auf einem Ring heißt stetig von unten (von oben), falls für jede aufsteigende (absteigende) Mengenfolge mit Grenzwert
gilt. Ein Inhalt heißt stetig, falls er stetig von unten und von oben ist.
Schauen wir an einem Beispiel, ob diese verbesserte Definition den Begriff der Stetigkeit schon zu unserer Zufriedenheit beschreibt.
Beispiel (Ein Problem in der Definition)
In der Einleitung haben wir das Zählen der in einer Menge enthaltenen Elemente als Beispiel eines (intuitiv) stetigen Inhalts kennengelernt. Schauen wir das Mengensystem
aller endlichen Teilmengen von an. Im Artikel Inhalte auf Ringen haben wir gesehen, dass das Zählen der Elemente endlicher Teilmengen von
wirklich ein auf einem Ring definierter Inhalt ist. Wir erwarten nun, dass stetig von unten und von oben im Sinne der neuen Definition ist. Sei also eine monoton wachsende Folge, deren Grenzwert ebenfalls in liegt. Da die gegen konvergieren, muss die Anzahl der Elemente in der Grenzwert der Anzahl der Elemente der sein. Mit anderen Worten, es gilt
Damit ist stetig von unten im Sinne unserer Definition. Sei nun eine monoton fallende Folge, deren Grenzwert ebenfalls in liegt. Auch hier muss aus denselben Gründen die Bedingung für die Stetigkeit erfüllt sein. Damit ist auf dem Ring stetig im Sinne der Definition.
Man kann den Inhalt auch auf der ganzen Potenzmenge betrachten. Intuitiv sollte das Zählen von Elementen bei beliebigen Teilmengen von genauso stetig sein wie bei endlichen Teilmengen. Bei der Argumentation sollten wir aber sicherheitshalber zwischen Endlich und Unendlich eine Unterscheidung treffen. Sei also wieder eine monoton wachsende Folge von Teilmengen mit Grenzwert . Enthält nur endlich viele Elemente, dann wegen der Monotonie auch jedes der und wir können wie oben argumentieren. Da aber der Grenzwert der ist, funktioniert das Argument auch, wenn unendlich viele Elemente enthält: Wäre , dann würde die Anzahl der Elemente in den ab einem Index nicht mehr wachsen. Damit wäre die Folge der ab einem Index konstant und könnte insbesondere nicht gegen eine unendliche Menge konvergieren. Also muss sein und es gilt auch für unendliches
Bilden die nun eine monoton fallende Folge und sind alle Mengen der Folge endlich, dann ist wegen der Monotonie auch der Grenzwert eine endliche Menge und wir können wie oben argumentieren. Genauso funktioniert es, wenn nur endlich viele der unendlich sind: Wir können ohne Einschränkung alle unendlichen Folgenglieder weglassen, da das Weglassen endlich vieler Glieder einer Folge ihren Grenzwert nicht ändert, und bekommen wieder eine Folge nur aus endlichen Mengen. Anders sieht es aus, wenn alle der Folge unendliche Mengen sind. Um die Bedingung der Stetigkeit zu erfüllen, müsste
gelten, der Grenzwert der Folge also ebenfalls unendlich viele Elemente enthalten. Da die Folge aber monoton fallend ist, ist das nicht garantiert. Es ist nicht ausgeschlossen, dass eine absteigende Folge unendlicher Mengen gegen eine endliche Menge konvergiert. Versuche, eine solche Folge zu finden, bevor du weiterliest!
Nehmen wir die Folge mit . Die konvergieren absteigend gegen die leere Menge. Gleichzeitig gilt aber für alle . Wir haben also
Der Inhalt , der intuitiv stetig sein sollte, ist also nicht stetig von oben im Sinne unserer Definition.
Es gibt also Inhalte, die intuitiv stetig, aber unstetig im Sinne unserer Definition sind. Offenbar gibt es ein Problem bei der Definition der Stetigkeit von oben. Beachte: Bei der Stetigkeit von unten können auch solche "unvernünftigen" Fälle auftreten. Es kann etwa die monotone Folge der beschränkt sein, also gegen einen endlichen Wert konvergieren, während für den Grenzwert der Mengenfolge gilt. Einen solchen Inhalt als unstetig zu bezeichnen widerspricht aber nicht unserer Intuition, im Gegenteil. Ein Beispiel dafür haben wir am Anfang des Artikels gesehen.
Was ist nun das Problem bei der Stetigkeit von oben? Es liegt offenbar am Auftreten des Werts Unendlich: Zwar ist jedes der etwas "weniger" unendlich als seine Vorgänger, es gilt aber trotzdem . Diesen Fall muss man in der Definition der Stetigkeit von oben ausschließen. Dafür fordern wir Endlichkeit der absteigenden Folge ab einem Index.

Definition (Stetiger Inhalt (finale Version))
Ein Inhalt auf einem Ring heißt stetig von unten, falls für jede aufsteigende Mengenfolge mit Grenzwert
gilt.
Er heißt stetig von oben, falls für jede absteigende Mengenfolge mit für ein (und damit für alle darauffolgenden) und mit Grenzwert
gilt.
Ein Inhalt heißt stetig, falls er stetig von unten und von oben ist.
Hinweis
Die Stetigkeit von Inhalten oder allgemeiner von Mengenfunktionen wird manchmal auch als -Stetigkeit ("Sigma-Stetigkeit") bezeichnet. Der Präfix soll an "Summe" erinnern und bedeutet in diesem Zusammenhang so viel wie "abzählbar": -stetige Inhalte verhalten sich stetig beim Übergang von endlichen zu abzählbaren Vereinigungen bzw. Schnitten.
Beachte: Es ist nicht nötig, die Endlichkeit ab einem Index bei der Stetigkeit von unten zu fordern: Gilt für einen Index , dann gilt auch für alle darauffolgenden wegen der Monotonie des Inhalts . Aus demselben Grund gilt es dann auch für den Grenzwert .
Aus der Stetigkeit von unten folgt die Stetigkeit von oben
[Bearbeiten]Stetigkeit von oben und Stetigkeit von unten scheinen nicht ganz äquivalent zu sein: Zumindest muss man bei der Stetigkeit von oben Einschränkungen treffen, die bei der Stetigkeit von unten nicht nötig sind. Wie hängen die beiden Begriffe genau zusammen? Wir versuchen eine Analogie zu Folgen reeller Zahlen zu finden.
Sei eine monoton fallende Folge nichtnegativer reeller Zahlen. Man kann daraus eine monoton steigende Folge nichtnegativer reeller Zahlen machen, indem man die Folge betrachtet. Wenn diese Folge gegen einen Wert konvergiert, können wir daraus schließen, dass die ursprüngliche Folge gegen konvergiert.
Angenommen, wir wissen nun von einem Inhalt, dass er stetig von unten ist. Dann können wir daraus die Stetigkeit von oben folgern, indem wir auf dieselbe Art aus einer monoton fallenden Mengenfolge die monoton steigende Folge machen. Für diese können wir dann die Stetigkeit von unten ausnutzen. Entscheidend dabei ist, dass wir nur fallende Mengenfolgen mit Mengen endlichen Inhalts betrachten zu brauchen, sodass wir keine Probleme bei der Subtraktion bekommen.
Satz (Stetigkeit von unten impliziert Stetigkeit von oben)
Sei ein Inhalt auf einem Ring . Ist stetig von unten, so ist auch stetig von oben. Insbesondere ist Stetigkeit eines Inhalts von unten äquivalent zur Stetigkeit.
Beweis (Stetigkeit von unten impliziert Stetigkeit von oben)
Sei eine monoton fallende Mengenfolge mit ab einem Index . Da das Weglassen endlich vieler Folgenglieder den Grenzwert nicht ändert, können wir ohne Einschränkung annehmen. Der Grenzwert liege ebenfalls in . Wir wollen zeigen.
Die Folge ist monoton steigend und liegt ebenfalls im Ring . Auch der Grenzwert liegt in . Ferner haben aufgrund der Monotonie alle diese Mengen ebenfalls endlichen Inhalt. Aus der Stetigkeit von unten wissen wir, dass gilt. Da außerdem für alle gilt, ist . Mit der Additivität des Inhalts folgt damit
also . (Alternativ kann man direkt mit der Subtraktivität von Inhalten auf Ringen argumentieren.) Genauso gilt . Da die Inhalte aller beteiligten Mengen endlich sind, sind diese Differenzen sinnvoll und wir haben wegen der Stetigkeit von unten
Aus der Stetigkeit von oben folgt nicht die Stetigkeit von unten
[Bearbeiten]Genauso müsste es funktionieren, wenn wir wissen, dass ein Inhalt stetig von oben ist: Wir machen aus einer aufsteigenden Folge eine absteigende und nutzen die Stetigkeit von oben aus. Aber hier müssen wir vorsichtig sein! Wir haben die Stetigkeit von oben nur für Folgen von Mengen, die ab einem Index endlichen Inhalt haben. Es ist nicht garantiert, dass diese Bedingung erfüllt ist, wenn wir ausgehend von einer beliebigen aufsteigenden Mengenfolge eine absteigende Folge konstruieren. Dieses Problem kann auch bei reellen Zahlenfolgen auftreten: Aus einer gegen ein konvergenten, monoton steigenden Folge nichtnegativer reeller Zahlen kann man die monoton fallende Folge machen. Wenn aber nicht nach oben beschränkt ist, sondern gegen Unendlich strebt, ist das nicht mehr möglich.
Bei Mengenfolgen ist zwar für jede monoton wachsende Folge mit Grenzwert die Folge monoton fallend. Aber dasselbe Problem wie bei den reellen Zahlenfolgen kann auch hier auftreten, denn es kann für alle sein. Bei einer solchen Folge können wir nicht die Stetigkeit von oben benutzen. Wir können also nicht erwarten, dass aus der Stetigkeit von oben immer die Stetigkeit von unten folgt. Das zeigt das folgende Beispiel, das wir schon im ersten Abschnitt als Beispiel eines unstetigen Inhalts kennengelernt haben:
Beispiel (Stetigkeit von oben impliziert nicht die Stetigkeit von unten)
Die Mengenfolge mit ist aufsteigend mit . Damit ist die Folge der eine absteigende Folge mit . Während alle endliche Mengen sind, sind die alle unendlich. Betrachten wir nun den Inhalt, der von einer Teilmenge der natürlichen Zahlen bestimmt, ob sie endlich oder unendlich ist:
Offenbar ist stetig von oben: Die einzigen absteigenden Mengenfolgen, die die Endlichkeitsbedingung erfüllen, sind ab einem Index endlich, und da ist ihr Inhalt konstant .
Nun erfüllt die Folge der aber nicht die Bedingung der Endlichkeit ab einem Index, sodass wir sie nicht benutzen können, um die Stetigkeit von unten von für die Folge der zu folgern. Und in der Tat gilt
ist nicht stetig von unten. Insbesondere folgt aus der Stetigkeit eines Inhalts von oben im Allgemeinen nicht die Stetigkeit von unten!
Wir haben diesen Inhalt schon in der Einleitung als Beispiel für einen (intuitiv) unstetigen Inhalt kennengelernt. Das Beispiel zeigt, dass auch im Sinne unserer Definition nicht stetig ist.
Wir halten diese Erkenntnis fest:
Warnung
Aus der Stetigkeit eines Inhalts von oben folgt im Allgemeinen nicht die Stetigkeit von unten.
Äquivalenz von "unten" und "oben" für endliche Inhalte
[Bearbeiten]Intuitiv ist die Stetigkeit von oben schwächer, weil man die Bedingung der Endlichkeit des Inhalts der Mengen der Folge ab einem Index stellen muss und auf diese Weise ein paar Folgen "verliert", wenn der Inhalt nicht nur endliche Werte annimmt. In der Tat sind "von oben" und "von unten" für endliche Inhalte äquivalent:
Satz (Stetigkeit von oben und von unten bei endlichen Inhalten)
Sei ein endlicher Inhalt auf einem Ring , d.h. für alle . Dann gilt
Beweis (Stetigkeit von oben und von unten bei endlichen Inhalten)
Wir haben bereits gezeigt, dass Stetigkeit von unten immer Stetigkeit von oben impliziert. Folglich reicht es nun für den endlichen Fall, die andere Richtung zu zeigen.
Sei also stetig von oben und eine von unten gegen ein konvergente Folge von Mengen in , also .
Wir halten fest, dass stets wieder im Ring liegt. (Differenzstabilität).
Wir konstruieren aus der aufsteigenden eine absteigende Mengenfolge , um danach die Stetigkeit von oben auszunutzen.
Dazu definieren wir: für alle . Da aufsteigend war, ist absteigend.
Daraus folgt, dass .
Also ist eine gegen konvergente Mengenfolge in . Wegen der angenommenen Stetigkeit von oben gilt dann
Hier benutzten wir zudem die Endlichkeit von um die Stetigkeit von oben anwenden zu dürfen ( ist immer endlich).
Für jedes ist wegen der Additivität .
Damit ist
Äquivalente Charakterisierung der Stetigkeit von oben
[Bearbeiten]Zuletzt geben wir noch eine einfachere Charakterisierung der Stetigkeit von oben. Sie kann nützlich sein, um die Stetigkeit endlicher Inhalte nachzuweisen:
Satz (Stetigkeit von oben und Stetigkeit in )
Für einen Inhalt auf einem Ring sind äquivalent:
- ist stetig von oben.
- ist stetig in , d.h. für alle monoton fallenden Folgen mit ab einem und gilt .
Beweis (Stetigkeit von oben und Stetigkeit in )
: Dies ist einfach die Definition von "Stetigkeit von oben" auf angewandt.
: Sei nun stetig in , und sei mit ab einem und .
Dann ist monoton fallend, und mit der Monotonie-Eigenschaft von Inhalten gilt ab einem .
Da zudem gilt, dass , konvergiert von oben gegen .
Nach unserer Annahme ist dann .
Da für hinreichend große endlich ist, und da immer gilt, folgt .
Wir können also folgern:
Beispiele für stetige Inhalte
[Bearbeiten]Jetzt wo wir so viel über stetige Inhalte wissen, können wir uns ein paar konkrete Beispiele angucken.
Beispiel
Sei ein Ring. Ein Inhalt der Form
ist immer stetig. Konvergiert von unten gegen ein , so gibt es zwei Möglichkeiten:
: Dann folgt wegen , dass für alle . Also gilt .
: Dann folgt wegen , dass es ein gibt mit . Folglich gilt wegen der Monotonie der Mengenfolge, dass für alle . Daher gilt .
Damit ist stetig von unten und somit auch stetig.
Beispiel (Inhalte auf Ringen endlicher Kardinalität)
Ist ein Inhalt auf , mit , dann sind die in konvergenten Folgen gerade die Mengenfolgen, die ab einem Index konstant die gleiche Menge (ihrem Grenzwert) sind. Die Stetigkeit von folgt dann direkt.
Beispiel (Der elementargeometrische Inhalt)
Wir kennen schon den Ring der Quaderfiguren (oder elementargeometrischen Mengen): Es ist die Menge aller endlichen Vereinigungen von achsenparallelen Quadern im . (Ein achsenparalleler Quader im ist ein Produkt von Intervallen (jeweils offen, halboffen oder abgeschlossen).)
Den elementargeometrischen Inhalt auf diesem Ring haben wir wie folgt definiert:
Für einen einzelnen Quader ist das Produkt der Seitenlängen.
Für eine Quaderfigur (wobei die achsenparallele Quader sind, ohne Einschränkung paarweise disjunkt) definiere .
Man kann zeigen, dass der elementargeometrische Inhalt stetig ist.
Zeige, das \lambda stetig (von unten) ist / skizziere den Beweis. dies geht genauso wie man auch zeigt, dass \lambda ein Prämaß ist, mit etwas epsilontik...
Weiterhin kann man leicht zeigen, dass endliche Linearkombinationen von stetigen Inhalten wieder stetig sind.
Sigma-Ringe
[Bearbeiten]-
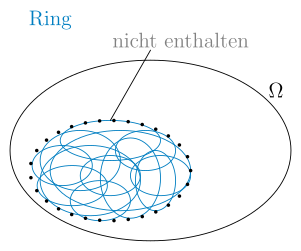
Ein Ring muss nicht unbedingt alle Grenzwerte von Mengen enthalten.
-
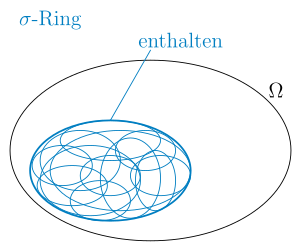
In einem -Ring müssen hingegen alle Grenz-Mengen enthalten sein.
Wir wissen nun, was Stetigkeit eines Inhalts auf einem Ring bedeutet. In der Einleitung haben wir festgestellt, dass Stetigkeit ermöglicht, Mengen durch Approximation zu messen, da kleine Abweichungen der Mengen voneinander nur kleine Abweichungen der Messwerte zur Folge haben. Ist also ein Inhalt auf einem Ring stetig, so sollten nicht nur die Mengen aus gemessen werden können, sondern auch alle mit Mengen aus approximierbaren Mengen. Die approximierbaren Mengen sind gerade die Grenzwerte monoton steigender bzw. fallender Mengenfolgen. Es ist bei stetigen Inhalten also sinnvoll, einen Ring als Definitionsbereich zu benutzen, welcher auch die Grenzwerte solcher Folgen enthält:

Definition (-Ring)
Ein Ring über einer Grundmenge heißt -Ring, falls gilt:
- Grenzwerte aufsteigender Mengenfolgen aus liegen in ,
- Grenzwerte absteigender Mengenfolgen aus liegen in .
Für die Stetigkeit eines Inhalts reichte die Stetigkeit von unten, weil man aus jeder fallenden eine aufsteigende Mengenfolge machen kann. Genauso reicht es, die Abgeschlossenheit von nur für Grenzwerte aufsteigender Mengenfolgen zu formulieren: Ist eine monoton fallende Mengenfolge mit Grenzwert , dann ist die Folge der eine monoton wachsende Folge mit Grenzwert . Da ein Ring, also insbesondere stabil unter Differenzen ist, gilt
für alle und
Bei den Gleichheiten auf der linken Seite haben wir bzw. ausgenutzt. Es reicht also zu fordern, dass Grenzwerte monoton steigender Mengenfolgen wieder im Mengensystem liegen, und wir haben die äquivalente Definition:
Definition (-Ring (äquivalente Definition))
Ein Ring über einer Grundmenge heißt -Ring, falls für jede aufsteigende Mengenfolge in auch ihr Grenzwert in liegt.
In der Literatur werden -Ringe oft anders definiert. Wir beweisen diese äquivalente Charakterisierung.
Satz (Alternative Charakterisierung von -Ringen)
Ein Mengensystem über einer Grundmenge ist genau dann ein -Ring, falls gilt:
Beweis (Alternative Charakterisierung von -Ringen)
Sei ein -Ring. Dann sind, da ein Ring ist, die Eigenschaften 1) und 3) dieses Satzes direkt erfüllt. Sei nun eine Folge in . Da ein Ring ist, sind endliche Vereinigungen der Form . Da ein -Ring ist, und da eine aufsteigende Mengenfolge in ist, folgt . Damit ist auch Eigenschaft 2) gezeigt.
Sei nun ein Mengensystem mit den Eigenschaften 1), 2) und 3). Wegen 1) und 3) gilt . Denn es gibt und daraus folgt . Damit folgt aus der Vereinigungsstabilität bezüglich abzählbar unendlichen Vereinigungen auch die Vereinigungsstabilität bezüglich endlicher Vereinigungen, weshalb ein Ring ist. Um zu zeigen, dass ein -Ring ist, sei eine aufsteigende Mengenfolge in . Dann ist wegen Eigenschaft 2) direkt . Das heißt ist abgeschlossen im Bezug auf Grenzwertbildung von aufsteigenden Mengenfolgen und damit ist ein -Ring.
Beispiele für sigma-Ringe
[Bearbeiten]Beispiel (Potenzmenge und endliche Ringe)
Für jede Grundmenge ist die Potenzmenge ein -Ring.
Jeder endliche Ring (d.h. enthält nur endlich viele Mengen) ist ein -Ring: Die zweite Eigenschaft in der Definition ist trivialerweise erfüllt, da es nur endlich viele Mengen gibt, die vereinigt werden können, und als Ring abgeschlossen unter endlichen Vereinigungen ist.
Beispiel (abzählbare Teilmengen)
Wir haben schon den Ring der abzählbaren Teilmengen von kennengelernt. Es ist sogar ein -Ring:
- Da die leere Menge abzählbar ist, ist nichtleer.
- Ist eine Folge von abzählbaren Mengen, dann ist auch ihre Vereinigung abzählbar, also gilt .
- Sind abzählbar, dann ist wegen auch ihre Differenz abzählbar und es gilt .
Beispiel (endliche Teilmengen)
Im Gegensatz dazu ist das Mengensystem der endlichen Teilmengen von zwar ein Ring, aber kein -Ring: Für die Mengen gilt
Beispiel (Von den Quaderfiguren erzeugter -Ring)
Betrachte das Mengensystem
der achsenparallelen Quader im . (Die Intervalle im Produkt können offen, halboffen oder abgeschlossen sein.) Wir kennen schon den Ring der Quaderfiguren in . Er ist definiert als der von erzeugte Ring, das heißt der kleinste Ring, der enthält. Genauso kann man den von erzeugten -Ring betrachten. Wie der Ring der Quaderfiguren, so kann auch als Durchschnitt aller -Ringe über definiert werden, welche die Quader enthalten. (Vergleiche auch den Artikel zu erzeugten -Algebren.)

Während der von den Quadern erzeugte Ring nur Quaderfiguren enthält, liegen im -Ring zusätzlich alle Mengen, die sich durch Quaderfiguren approximieren lassen, wie etwa der Kreis.






![{\displaystyle \mu :{\mathcal {P}}(\mathbb {N} )\to [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04bf67a86a1f985d753df0b07345dfb4f9d258b4)










![{\displaystyle \mu :{\mathcal {R}}\to [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad7b11383d04db361504135058e7751dc669c823)






![{\displaystyle A_{n}=[n,n+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bce753f2080392eccb922c4ebf2f042404a0345)
![{\displaystyle A_{n}=[0,1+1/n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0495d848763b2e501afeb21507ff20d9306ff7e5)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle A_{n}=[0,1-1/n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c00c61d68f0237db9790cfcc986675bc2e5e42ca)














![{\displaystyle A_{n}=[0,1+1/n]\subseteq \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/78e440df5cae54033e86412be2f3b46ba9808d8c)
![{\displaystyle \lim _{n\to \infty }A_{n}=\bigcap _{n=1}^{\infty }[0,1+1/n]=[0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d20641afe067aa107c02a6e60bfd9b1e22f47a77)

![{\displaystyle [0,1]\subseteq A_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b71d3ee38fe8d28ade53fcc0fb4fadb34054b91)


![{\displaystyle A_{n}=[0,1-1/n]\subseteq \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/16603a74058e046939e0abfc78df001d431198d7)
![{\displaystyle \lim _{n\to \infty }A_{n}=\bigcup _{n=1}^{\infty }[0,1-1/n]=[0,1).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3015b0056348c3bcfb13b09187070bdcc9f02f5b)









![{\displaystyle \mu :{\mathcal {R}}\to [0,\infty ],\quad \mu (A)=|A|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a746022f7b19160393c36e7b0e5e3eb9b2387fa6)












































![{\displaystyle \mu :{\mathcal {P}}(\mathbb {N} )\to [0,\infty ],\quad \mu (A)={\begin{cases}0,{\text{ falls }}|A|<\infty ,\\\infty {\text{ sonst.}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bebb5b3d97a6c51ae772173f00f0bc5cf4ab169f)