MathemaTriX ⋅ Aufgabenheft

Grundniveau 1

G1.1 Grundrechenartenvorrang

Typ 1

1. 1. $\ 11+96:(23-3\cdot 5)-(20-13)+(17-91:7)\cdot 2\$
   2. $\ 63:(2\cdot 11-30:2)-(90:5-3\cdot 6)\cdot 4$
2. 1. $\ 54:(4\cdot 5-14)-34+(105:7-5)\cdot 3-(11+3)\$
   2. $\ 65:(2\cdot 13-125:5)-(90:6-2\cdot 7)\cdot 65$
3. 1. $\ 33-55:(26-3\cdot 5)-(73-14)-(182:13-11)\cdot 10+34\$
   2. $\ 66:(2\cdot 11-48:3)-(156:12-3\cdot 4)\cdot 4$
4. 1. $\ 99:(32-3\cdot 7)-(65-41)+46+(48:12+5)\cdot (7-5)\$
   2. $\ 120:(2\cdot 7-36:9)-(35:5-3\cdot 2)\cdot 4$
5. 1. $\ 99:(4\cdot 8-21)+53-(5+54:9)\cdot 3-(14+5)\$
   2. $\ (42:3-2\cdot 7)\cdot 5+210:(2\cdot 7-36:9)$
6. 1. $\ 23+56:(23-3\cdot 7)-(7+2)+(3+48:12)\cdot 8\$
   2. $\ 105:(2\cdot 11-45:3)-(1-9:9)\cdot 5$
7. 1. $\ 84:(3\cdot 7-18)-(41-27)+22-(2+60:12)\cdot 9\$
   2. $\ 13:(2\cdot 12-69:3)-(70:5-2\cdot 7)\cdot 23$
8. 1. $\ 33+56:(3\cdot 7-13)-(11+3)-(3+36:18)\cdot 8\$
   2. $\ (112:7-4\cdot 4)\cdot 14-17:(2\cdot 11-30:6)$

G1.2 Strich und Punkt Bruchrechnungen

$\ {\frac {5}{13}}-{\frac {2}{13}}\qquad \qquad$ $\ {\frac {5}{4}}+{\frac {2}{3}}\$ ${\frac {5}{4}}\cdot {\frac {3}{7}}\qquad \qquad \quad$ $\ {\frac {5}{4}}:{\frac {3}{7}}\$	$\ {\frac {5}{11}}-{\frac {7}{4}}\qquad \quad$ $\ {\frac {5}{11}}\cdot {\frac {7}{4}}$ $\ -{\frac {5}{11}}-{\frac {7}{11}}\qquad$ $\ {\frac {5}{11}}:{\frac {7}{4}}\$	$\ {\frac {7}{5}}:{\frac {11}{9}}\qquad$ $\ -{\frac {7}{5}}+{\frac {11}{9}}\$ $\ {\frac {7}{5}}\cdot {\frac {11}{9}}\qquad$ $\ {\frac {7}{9}}+{\frac {11}{9}}\$
$\ {\frac {11}{3}}:{\frac {8}{13}}\qquad \quad$ $\ {\frac {11}{3}}-{\frac {8}{13}}\$ $\ -{\frac {11}{13}}-{\frac {2}{13}}\qquad$ ${\frac {11}{3}}\cdot {\frac {8}{13}}$	$\ {\frac {15}{7}}-{\frac {11}{7}}\qquad$ $\ {\frac {15}{7}}:{\frac {11}{4}}$ $\ {\frac {15}{7}}+{\frac {11}{4}}\ \qquad \quad$ ${\frac {15}{7}}\cdot {\frac {11}{4}}$	$\ {\frac {11}{13}}+{\frac {15}{13}}\qquad$ ${\frac {11}{8}}\cdot {\frac {15}{13}}$ $\ {\frac {11}{8}}:{\frac {15}{13}}\qquad \quad$ $\ {\frac {11}{8}}-{\frac {15}{13}}\$
$\ {\frac {7}{13}}-{\frac {4}{13}}\qquad$ $\ {\frac {3}{4}}+{\frac {2}{5}}\$ ${\frac {4}{5}}\cdot {\frac {7}{3}}\qquad \quad$ $\ {\frac {4}{5}}:{\frac {7}{3}}\$	$\ {\frac {4}{11}}-{\frac {7}{5}}\qquad \quad$ $\ {\frac {11}{5}}\cdot {\frac {4}{7}}$ $\ -{\frac {3}{11}}-{\frac {9}{11}}\qquad$ $\ {\frac {11}{5}}:{\frac {4}{7}}\$

G1.3 Direkte Proportionalität

1. Ein Baum setzt durchschnittlich jede 25 min 0,8 Liter Sauerstoff frei.
   1. Wie viel Sauerstoff setzt er in 0,7 min frei?
   2. Wie lang braucht er, um 459 Liter freizusetzen?
2. 3,5 Liter eines Stoffes wiegen 14,7 kg.
   1. Wie viel wiegen 0,0175 Liter?
   2. Wie viel Liter sind 3850kg?
3. Ein Supermarktketteneigentümer macht 0,09 € Gewinn pro Zwölfflaschenkiste eines Biers.
   1. Wie viel ist sein tägliches Gewinn aus diesem Bier, wenn im ganzen Land täglich 264000 Flaschen Bier verkauft werden?
   2. Wie viele Flaschen Bier müssen verkauft werden, damit sein Gewinn 990 € ist?
4. In EU produzierte im Jahr (365 Tage) 2016 eine Person durchschnittlich 6,5 Tonnen CO₂.
   1. Wie viel war die Produktion pro Woche (7 Tage)?
   2. Wie viele Tage hätte sie gebraucht, um 0,13 Tonnen zu produzieren?
5. Nach einer Finanzkrise verbraucht jede Person durchschnittlich 6234 Liter Benzin weniger pro Woche. Wie viel ist die Reduktion pro Monat (30 Tage)?
6. Für 12 Kühe braucht man 73,8 Tonnen Futter bis sie geschlachtet werden.
   1. Wie viel Tonnen Futter braucht man für 15 Kühe?
   2. Für wie viele Kühe braucht man 123 Tonnen?
7. 0,7 km² Ackerland reichen für die Ernährung von 23 vegetarische Menschen.
   1. Für wie viele Menschen reichen 3,5 km²?
   2. Wie viel Ackerland brauchen 575 vegetarische Menschen?
8. Wenn eine Person mit dem Fahrrad zur Arbeit fährt, ist ihr CO2 Ausstoß 11,2g. Der Abstand zur Arbeit ist 8 km.
   1. Wie weit fährt man. wenn der CO2 Ausstoß 0,448 g ist?
   2. Wie viel ist der CO2 Ausstoß, wenn eine Person mit dem Fahrrad 20 km fährt?

G1.4 Grundaufgaben der Prozentrechnung

Wie viel % von 23 kg sind 5329 kg? Wie viel ist 23% von 5329 kg? Von wie vielen kg sind 23 kg 5329%? Von wie vielen Volt sind 346 Volt 0,56%? Wie viel % von 346 Volt sind 0,56 Volt? Wie viel ist 346% von 0,56 Volt? Wie viel % von 17 h sind 10 h? Von wie vielen h sind 17 h 10%? Wie viel ist 17% von 10 h? Von wie vielen h sind 0,17 h 6510%? Wie viel % von 0,17 h sind 6510 h? Wie viel ist 0,17% von 6510 h?

Wie viel ist 0,8% von 5000 h? Wie viel % von 0,8 h sind 5000 h? Von wie vielen h sind 0,8 h 5000%? Wie viel ist 3000% von 6000 h? Von wie vielen h sind 3000 h 6000%? Wie viel % von 3000 h sind 6000 h? Von wie vielen Volt sind 350 Volt 0,28%? Wie viel % von 350 Volt sind 0,28 Volt? Wie viel ist 350% von 0,28 Volt? Wie viel % von 17 h sind 42,5 h? Von wie vielen h sind 17 h 42,5%? Wie viel ist 17% von 42,5 h?

G1.5 Ausmultiplizieren mit einer oder zwei Klammer

Lösen Sie die Klammer auf und fassen Sie die daraus entstandenen Termen ggf. zusammen!
$\ 2x^{2}(3x^{5}-7+5x)\ \quad$ $\ (2m^{2}-5)(3m^{2}-4)$	$\ 2b^{7}(7b^{2}+4b-7)\ \quad$ $(2w^{5}-5w^{3})(5w^{2}-4)$	$\ 4s^{5}(2s^{3}+5s^{4}-7)\ \quad$ $(3w^{5}+w^{3})(5w^{3}-4w)$
$\ 4v^{7}(7v^{4}+3v^{5}-2v)\ \quad$ $(2g^{5}-3g^{3})(5g^{2}+4g)$	$\ 7n^{2}(2n^{12}-2n^{7}+5n^{5})\ \quad$ $\ (5c^{2}-6)(3-4c^{2})$	$\ 3z^{4}(2z^{2}+4z^{3}-7z)\ \quad$ $(2p^{5}-3p^{3})(4-5p^{2})$
$\ 4s^{4}(2s^{4}+5s-7s^{3})\ \quad$ $(2w^{5}+w^{3})(5w^{2}-4w)$	$\ 4v(v^{4}+3v^{5}-2v)\ \quad$ $(2a^{5}-3a^{3})(5a^{2}+4a)$

G1.6 Textaufgaben zu den Grundrechenarten

Typ 1

1. 1. Dividieren Sie die Zahl 34 um 5 erhöht durch die Differenz von 17 und 4!
   2. Berechnen Sie die Summe von 4 und 3 und multiplizieren Sie das Ergebnis mit der Zahl 31 um 25 reduziert!
   3. Addieren Sie zum Produkt aus 3 und 7 das 5-fache von 4!
   4. Teilen Sie die Zahl 63 auf 7 und subtrahieren Sie aus dem Ergebnis den Quotient von 39 und 3!
2. 1. Dividieren Sie die Summe von 26 und 4 durch die Zahl 33 um 27 reduziert!
   2. Erhöhen sie die Zahl 2 um 5 und multiplizieren Sie das Ergebnis mit der Differenz von 17 und 14!
   3. Berechnen Sie den Quotient aus 105 und 7 und addieren Sie das Ergebnis zur Zahl 44 auf 11 geteilt!
   4. Subtrahieren Sie aus dem Produkt aus 3 und 4 das 9-fache von 6!
3. 1. Dividieren Sie die Zahl 23 um 5 erhöht durch die Differenz von 19 und 12!
   2. Berechnen Sie den Quotient aus 49 und 7, teilen Sie die Zahl 52 auf 13 und multiplizieren Sie die zwei Ergebnisse.!
   3. Addieren Sie die Summe von 7 und 1 zur Zahl 29 um 25 reduziert!
   4. Berechnen Sie das Produkt aus 6 und 7 und subtrahieren Sie aus dem Ergebnis das 8-fache von 11!
4. 1. Berechnen Sie das Produkt aus 6 und 7, reduzieren Sie die Zahl 39 um 48 und addieren Sie die zwei Ergebnisse!
   2. Dividieren Sie die Summe von 7 und 33 durch die Differenz von 19 und 15!
   3. Berechnen Sie das 8-fache von 7 und Subtrahieren Sie das Ergebnis aus der Zahl 23 um 15 erhöht!
   4. Multiplizieren Sie den Quotient aus 91 und 7 mit der Zahl 26 auf 13 geteilt!
5. 1. Dividieren Sie die Zahl 7 um 5 erhöht durch die Differenz von 17 und 13!
   2. Berechnen Sie die Summe von 1 und 6 und multiplizieren Sie das Ergebnis mit der Zahl 23 um 17 reduziert!
   3. Addieren Sie zum Produkt aus 5 und 4 das 7-fache von 3!
   4. Teilen Sie die Zahl 45 auf 5 und subtrahieren Sie aus dem Ergebnis den Quotient von 52 und 4!
6. 1. Dividieren Sie die Summe von 17 und 13 durch die Zahl 15 um 9 reduziert!
   2. Erhöhen sie die Zahl 3 um 4 und multiplizieren Sie das Ergebnis mit der Differenz von 20 und 17!
   3. Berechnen Sie den Quotient aus 60 und 4 und addieren Sie das Ergebnis zur Zahl 16 auf 4 geteilt!
   4. Subtrahieren Sie aus dem Produkt aus 6 und 9 das 3-fache von 4!
7. 1. Dividieren Sie die Zahl 20 um 8 erhöht durch die Differenz von 21 und 14!
   2. Berechnen Sie den Quotient aus 70 und 10, teilen Sie die Zahl 64 auf 16 und multiplizieren Sie die zwei Ergebnisse.!
   3. Addieren Sie die Summe von 3 und 1 zur Zahl 33 um 25 reduziert!
   4. Berechnen Sie das Produkt aus 2 und 21 und subtrahieren Sie aus dem Ergebnis das 22-fache von 4!
8. 1. Berechnen Sie das Produkt aus 3 und 14, reduzieren Sie die Zahl 43 um 52 und addieren Sie die zwei Ergebnisse!
   2. Dividieren Sie die Summe von 8 und 32 durch die Differenz von 21 und 17!
   3. Berechnen Sie das 7-fache von 8 und Subtrahieren Sie das Ergebnis aus der Zahl 17 um 21 erhöht!
   4. Multiplizieren Sie den Quotient aus 78 und 6 mit der Zahl 28 auf 14 geteilt!

Typ 2

1. Welche Angabe passt zu welcher Berechnung? Verbinden Sie die Kästchen miteinander:

   1	Die Differenz der Zahlen 35 und 5 wird um den Quotient dieser Zahlen reduziert.	$\qquad$	$\qquad$	A	$(35-5)\cdot (35+5)=$
   2	Die Differenz der Zahlen 35 und 5 wird mit der Summe dieser Zahlen multipliziert.			B	$(35\cdot 5):(35+5)=$
   3	Teilen Sie das Produkt der Zahlen 35 und 5 durch die Zahl 35 um 5 erhöht.			C	$(35-5)-(35:5)=$

2. Welche Angabe passt zu welcher Berechnung? Verbinden Sie die Kästchen miteinander:

   1	Die Summe der Zahlen 7 und 12 wird um den Quotient dieser Zahlen reduziert.	$\qquad$	$\qquad$	A	$(7-12)\cdot (7:12)=$
   2	Das Produkt der Zahlen 7 und 12 wird durch die Differenz dieser Zahlen dividiert.			B	$(7\cdot 12):(7-12)=$
   3	Multiplizieren Sie die Differenz der Zahlen 7 und 12 mit der Zahl 7 auf 12 geteilt.			C	$(7+12)-(7:12)=$

3. Welche Angabe passt zu welcher Berechnung? Verbinden Sie die Kästchen miteinander:

   1	Die Summe der Zahlen 26 und 13 wird um den Quotient dieser Zahlen reduziert.	$\qquad$	$\qquad$	A	$(26+13)-(26:13)=$
   2	Das Produkt der Zahlen 26 und 13 wird durch die Differenz dieser Zahlen dividiert.			B	$(26\cdot 13):(26-13)=$
   3	Multiplizieren Sie die Differenz der Zahlen 26 und 13 mit der Zahl 26 auf 13 geteilt.			C	$(26-13)\cdot (26:13)=$

4. Welche Angabe passt zu welcher Berechnung? Verbinden Sie die Kästchen miteinander:

   1	Subtrahieren sie aus dem 15-fachen von 6 die Summe dieser Zahlen	$\qquad$	$\qquad$	A	$(15\cdot 6):(15-6)$
   2	Dividieren Sie das Produkt aus 15 und 6 durch die Differenz dieser Zahlen			B	$(15\cdot 6)-(15+6)$
   3	Multiplizieren Sie den Quotient aus 15 und 6 mit der Zahl 15 um 6 erhöht.			C	$(15:6)\cdot (15+6)$

5. Welche Angabe passt zu welcher Berechnung? Verbinden Sie die Kästchen miteinander:

   1	Die Summe der Zahlen 3 und 5 wird um das Produkt dieser Zahlen reduziert.	$\qquad$	$\qquad$	A	$(3+5):(3-5)=$
   2	Die Summe der Zahlen 3 und 5 wird durch die Differenz dieser Zahlen dividiert.			B	$(3\cdot 5):(3+5)=$
   3	Teilen Sie das Produkt der Zahlen 3 und 5 durch die Zahl 3 um 5 erhöht.			C	$(3+5)-(35\cdot 5)=$

6. Welche Angabe passt zu welcher Berechnung? Verbinden Sie die Kästchen miteinander:

   1	Das Produkt der Zahlen 7 und 2 wird um den Quotient dieser Zahlen reduziert.	$\qquad$	$\qquad$	A	$(7-2)\cdot (7:2)=$
   2	Das Produkt der Zahlen 7 und 2 wird durch die Differenz dieser Zahlen dividiert.			B	$(7\cdot 2):(7-2)=$
   3	Multiplizieren Sie die Differenz der Zahlen 7 und 2 mit der Zahl 7 auf 2 geteilt.			C	$(7\cdot 2)-(7:2)=$

7. Welche Angabe passt zu welcher Berechnung? Verbinden Sie die Kästchen miteinander:

   1	Die Summe der Zahlen 6 und 3 wird um den Quotient dieser Zahlen reduziert.	$\qquad$	$\qquad$	A	$(6+3)-(6:3)=$
   2	Das Produkt der Zahlen 6 und 3 wird durch die Differenz dieser Zahlen dividiert.			B	$(6\cdot 3):(6-3)=$
   3	Multiplizieren Sie die die Zahl 6 um 3 erhöht mit der Zahl 6 auf 3 geteilt.			C	$(6+3)\cdot (6:3)=$

8. Welche Angabe passt zu welcher Berechnung? Verbinden Sie die Kästchen miteinander:

   1	Addieren Sie zum 15-fachen von 6 die Summe dieser Zahlen	$\qquad$	$\qquad$	A	$(15\cdot 6):(15:6)$
   2	Dividieren Sie das Produkt aus 15 und 6 durch denQuotient dieser Zahlen			B	$(15\cdot 6)+(15+6)$
   3	Multiplizieren Sie die Differenz von 15 und 6 mit der Zahl 15 um 6 erhöht.			C	$(15-6)\cdot (15+6)$

G1.1 Grundrechenartenvorrang mit Plus-Minus Regel

Typ 2

$\ 96:(3\cdot 5-23)+(-13)-(91:7-17)\cdot 2\$ $\ 34+54:(4\cdot 5-14)-(105:7-5)\cdot (-3)\$ $\ 55:(3\cdot 5-26)-(-14)-(182:13-17)\cdot 10\$ $\ (-41)+99:(3\cdot 7-32)-(48:12+5)\cdot (-5)\$

$\ (-99):(21-4\cdot 8)+53+(54:9+5)\cdot (-3)\$ $\ 23-56:(19-3\cdot 7)-(48:12-11)\cdot (-8)\$ $\ 84:(3\cdot 7-18)-(11-33)+(48:12+3)\cdot (-9)\$ $\ 33+56:(3\cdot 7-13)-(36:18-7)\cdot (-8)\$

Typ 3

$\ 63:(2\cdot 11-30:2)-(90:5-3\cdot 6)\cdot 4$ $\ (-65):(2\cdot 13-125:5)-(90:6-4\cdot 4)\cdot 65$ $\ 66:(5\cdot 2-48:3)-(156:12-2\cdot 7)\cdot (-4)$ $\ (+120):(2\cdot 7-36:9)-(35:5-3\cdot 2)\cdot (-4)$

$\ (42:3-2\cdot 7)\cdot (5)+210:(2\cdot 7-36:9)$ $\ 105:(2\cdot 11-45:3)-(9:9+2\cdot 1)\cdot 5$ $\ 13:(2\cdot 11-69:3)-(70:5-2\cdot 7)\cdot 23$ $\ (112:7-4\cdot 4)\cdot 14-17:(2\cdot 11-30:6)$

Typ 4

$\ (4\cdot 11-54:6):(39:3-2\cdot 9)$ $\ (4\cdot 3-84:7):(78:3-4\cdot 7)$ $\ (54:6-8\cdot 3):(64:4-3\cdot 7)$ $\ (7\cdot 3-56:2):(45:3-4\cdot 2)$

$\ (4\cdot 7-26:2):(45:3-4\cdot 3)$ $\ (5\cdot 3+39:3):(24:3+4\cdot 5)$ $\ (44:11-54:6):(39:3-2\cdot 9)$ $\ (5\cdot 2-54:6):(65:13-2\cdot 2)$

Typ 5

An der Tafel steht folgende Rechnung. Leider gibt es einen Fehler. Wo liegt er? $21+56:7-(79-2\cdot 5):3=$ $77:7-(79-10):3=$ $11-69:3=11-23=$ $-12$ Berechnen Sie jetzt richtig: $21+56:7-(79-2\cdot 5):3...$ An der Tafel steht folgende Rechnung. Leider gibt es einen Fehler. Wo liegt er? $43+56:8-(30-2\cdot 5):4=$ $43+7-(28\cdot 5):4=$ $50-140:4=$ $50-35=$ $15$ Berechnen Sie jetzt richtig: $43+56:8-(30-2\cdot 5):4=...$ An der Tafel steht folgende Rechnung. Leider gibt es einen Fehler. Wo liegt er? $43+72:8-(56-2\cdot 20):4=$ $43+9-(56-2\cdot 5)=$ $52-(56-10)=$ $52-46=$ $6$ Berechnen Sie jetzt richtig: $43+72:8-(56-2\cdot 20):4=...$ An der Tafel steht folgende Rechnung. Leider gibt es einen Fehler. Wo liegt er? $63-(56:7-2)\cdot 9+72:3=$ $63-(8-2)\cdot 81:3=$ $63-6\cdot 81:3=$ $63-486:3=$ $-99$ Berechnen Sie jetzt richtig: $63-(56:7-2)\cdot 9+72:3=$

An der Tafel steht folgende Rechnung. Leider gibt es einen Fehler. Wo liegt er? $21+56:7-(77-2\cdot 4):3=$ $21+8-(75\cdot 4):3=$ $29-300:3=29-100=$ $-71$ Berechnen Sie jetzt richtig: $21+56:7-(77-2\cdot 4):3=...$ An der Tafel steht folgende Rechnung. Leider gibt es einen Fehler. Wo liegt er? $40+56:8-(30-2\cdot 5):4=$ $96:8-(30-10):4=$ $12-20:4=$ $12-5=$ $7$ Berechnen Sie jetzt richtig: $43+56:8-(30-2\cdot 5):4=...$ An der Tafel steht folgende Rechnung. Leider gibt es einen Fehler. Wo liegt er? $33+72:8-(56-2\cdot 20):4=$ $33+9-(56-40):4=$ $42-(56-10)=$ $42-46=$ $-4$ Berechnen Sie jetzt richtig: $33+72:8-(56-2\cdot 20):4=...$ An der Tafel steht folgende Rechnung. Leider gibt es einen Fehler. Wo liegt er? $63-(56:7-2):3+72:6=$ $63-(8-2):3+72:6=$ $63-6:3+72:6=$ $57:3-12=$ $7$ Berechnen Sie jetzt richtig: $63-(56:7-2)\cdot 9+72:3=$

Grundniveau 2

G2.1 Gemischte Zahlen

Gemischte Zahl in unechten Bruch

Rechnen Sie folgende gemischten Zahlen in unechten Brüchen um!
$4{\frac {4}{9}}\ \qquad \ 9{\frac {3}{13}}\ \qquad \ 1{\frac {5}{7}}\ \$	$7{\frac {4}{7}}\ \qquad \ 1{\frac {4}{5}}\ \qquad \ 11{\frac {2}{3}}\ \$	$3{\frac {2}{3}}\ \qquad \ 6{\frac {10}{11}}\ \qquad \ 1{\frac {8}{9}}\ \$
$5{\frac {2}{7}}\ \qquad \ 1{\frac {1}{6}}\ \qquad \ 9{\frac {8}{9}}\ \$	$4{\frac {1}{9}}\ \qquad \ 8{\frac {3}{13}}\ \qquad \ 5{\frac {1}{7}}\ \$	$8{\frac {4}{7}}\ \qquad \ 3{\frac {4}{5}}\ \qquad \ 10{\frac {2}{3}}\ \$
$1{\frac {2}{3}}\ \qquad \ 6{\frac {6}{11}}\ \qquad \ 1{\frac {12}{13}}\ \$	$6{\frac {5}{7}}\ \qquad \ 1{\frac {1}{12}}\ \qquad \ 9{\frac {1}{9}}\ \$

Unechten Bruch in gemischte Zahl

Rechnen Sie folgende unechten Brüchen in gemischten Zahlen um!
${\frac {392}{11}}\ \qquad \ {\frac {56}{8}}\ \qquad \ {\frac {133}{12}}\ \$	${\frac {447}{12}}\ \qquad \ {\frac {33}{5}}\ \qquad \ {\frac {99}{9}}\ \$	${\frac {442}{13}}\ \qquad \ {\frac {9}{5}}\ \qquad \ {\frac {97}{8}}\ \$
${\frac {447}{11}}\ \qquad \ {\frac {9}{7}}\ \qquad \ {\frac {35}{5}}\ \$	${\frac {389}{11}}\ \qquad \ {\frac {72}{8}}\ \qquad \ {\frac {135}{12}}\ \$	${\frac {451}{12}}\ \qquad \ {\frac {39}{5}}\ \qquad \ {\frac {88}{8}}\ \$
${\frac {455}{13}}\ \qquad \ {\frac {11}{5}}\ \qquad \ {\frac {95}{8}}\ \$	${\frac {407}{11}}\ \qquad \ {\frac {8}{7}}\ \qquad \ {\frac {38}{5}}\ \$

Substraktion

Führen Sie folgende Subtraktionen mit natürlichen Zahlen aus!
$4-{\frac {25}{9}}\ \quad \ 9-{\frac {3}{13}}\ \quad \ {\frac {13}{7}}-3\ \quad \ {\frac {23}{5}}-1\$	$7-{\frac {24}{7}}\ \qquad \ 1-{\frac {4}{5}}\ \qquad \ {\frac {44}{3}}-11\ \quad \ {\frac {19}{4}}-7\$	$3-{\frac {25}{3}}\ \qquad \ 6-{\frac {10}{11}}\ \qquad \ {\frac {10}{9}}-1\ \quad \ {\frac {5}{13}}-5\$
$5-{\frac {52}{7}}\ \qquad \ 1-{\frac {1}{6}}\ \qquad \ {\frac {143}{9}}-10\ \quad \ {\frac {16}{17}}-1\$	$1-{\frac {11}{9}}\ \qquad \ 8-{\frac {105}{13}}\ \qquad \ {\frac {69}{7}}-5\ \quad \ {\frac {1}{7}}-1\$	$8-{\frac {4}{7}}\ \qquad \ 3-{\frac {24}{5}}\ \qquad \ {\frac {20}{11}}-1\ \quad \ {\frac {9}{14}}-4\$
$1-{\frac {2}{7}}\ \qquad \ 6-{\frac {67}{11}}\ \qquad \ {\frac {79}{13}}-2\ \quad \ {\frac {8}{9}}-2\$	$6-{\frac {59}{7}}\ \qquad \ 1-{\frac {1}{12}}\ \qquad \ {\frac {100}{9}}-3\ \quad \ {\frac {26}{3}}-9\$

G2.2 Bruchkürzen

Kürzen Sie folgende Brüche!
$\ {\frac {6}{15}}=\qquad$ $\ {\frac {15}{35}}=\qquad$ $\ {\frac {21}{14}}=\qquad$ $\ {\frac {35}{14}}=\qquad$ $\ {\frac {42}{24}}=\qquad$ $\ {\frac {10}{15}}=\qquad$ $\ {\frac {21}{35}}=\qquad$ $\ {\frac {33}{44}}=\qquad$ $\ {\frac {10}{12}}=\qquad$ $\ {\frac {30}{45}}=\qquad$	$\ {\frac {6}{9}}=\qquad$ $\ {\frac {20}{22}}=\qquad$ $\ {\frac {45}{55}}=\qquad$ $\ {\frac {55}{66}}=\qquad$ $\ {\frac {42}{28}}=\qquad$ $\ {\frac {21}{14}}=\qquad$ $\ {\frac {21}{12}}=\qquad$ $\ {\frac {12}{39}}=\qquad$ $\ {\frac {39}{52}}=\qquad$ $\ {\frac {33}{99}}=\qquad$

G2.3 Umformen Grundwissen Gegenrechnungen

Berechnen Sie jeweils die unbekannte Variable!

$\ c+4452=341\qquad$ $\ {\tfrac {k}{5}}=11\qquad$ $\ 3f=114\qquad$ $\ x-867=341\qquad$ $\ 23m=214\qquad$ $\ 11w=214\qquad$ $\ c+587=2579\qquad$ $\ {\tfrac {k}{2}}=26\qquad$ $\ 10f=450\qquad$ $\ x-3559=424\qquad$ $\ 22m=484\qquad$ $\ 26w=428\qquad$ $\ c+4752=741\qquad$ $\ {\tfrac {k}{12}}=5\qquad$ $\ 3f=168\qquad$ $\ x-687=-4341\qquad$ $\ 33m=216\qquad$ $\ 17w=214\qquad$ $\ c+5347=2744\qquad$ $\ {\tfrac {k}{7}}=13\qquad$ $\ 6f=168\qquad$ $\ x-592=-5426\qquad$ $\ 58m=986\qquad$ $\ 51w=900\qquad$

$\ c+4653=542\qquad$ $\ {\tfrac {k}{10}}=5{,}5\qquad$ $\ 6f=228\qquad$ $\ x-907=301\qquad$ $\ 46m=428\qquad$ $\ 22w=428\qquad$ $\ c+367=2359\qquad$ $\ {\tfrac {k}{4}}=13\qquad$ $\ 5f=225\qquad$ $\ x-3759=224\qquad$ $\ 11m=242\qquad$ $\ 13w=214\qquad$ $\ c+3752=-259\qquad$ $\ {\tfrac {k}{6}}=10\qquad$ $\ 6f=336\qquad$ $\ x-387=-4641\qquad$ $\ 11m=72\qquad$ $\ 34w=428\qquad$ $\ c+3344=741\qquad$ $\ {\tfrac {k}{13}}=7\qquad$ $\ 3f=84\qquad$ $\ x-452=-5566\qquad$ $\ 29m=493\qquad$ $\ 17w=300\qquad$

G2.4 Einheiten und physikalische Größen

Typ 1

Ordnen Sie die passenden Einheiten zu den entsprechenden physikalischen Größen richtig zu: Länge einer Zunge $\qquad$ $\$cm³ Dauer eines Filmes $\$km Dauer eines Herzschlags $\$m Länge eines Zuges $\$h Abstand zwischen Paris und Rom$\quad$ $\quad$ $\$s Volumen einer Spritze $\$cm Ordnen Sie die passenden Einheiten zu den entsprechenden physikalischen Größen richtig zu: Höhe eines Fernsehturms $\qquad$ $\$cm³ Volumen eines Ölkanisters $\$km Dauer einer Unterrichtspause $\$m Volumen eines LKWs $\$m3 Abstand Mogadischu-Kambala$\quad$ $\quad$ $\$min Volumen einer Spritze $\ \ell$

Ordnen Sie die passenden Einheiten zu den entsprechenden physikalischen Größen richtig zu: Fläche eines Fingernagels $\qquad$ $\$m2 Dauer einer Flugreise $\$km2 Höhe eines Hauses $\$h Fläche eines Zimmers $\$m Abstand zwischen den Augen$\quad$ $\quad$ $\$mm2 Fläche eines Staates $\$cm Ordnen Sie die passenden Einheiten zu den entsprechenden physikalischen Größen richtig zu: Fläche eines Staates $\qquad$ $\$m2 Dauer einer Flugreise $\$km2 Dauer einer Schulpause $\$h Fläche eines Zimmers min$\quad$ Abstand zwischen den Augen$\quad$ $\quad$ $\$s Dauer eines Atemzugs cm$\$

Typ 2

Es wurde vergessen, die richtigen Maßeinheiten anzugeben. Ergänzen Sie diese: Das Klassenzimmer hat eine Fläche von 35 __________ . Der Turm von Pisa ist 55,8 __________ hoch. Der Film dauert 1,5 ______. Der Abstand zwischen Paris und Berlin 870 __________. Ein Becher Joghurt wiegt 450 _________. Der Umfang des Fensters beträgt 2,4 _________. Es wurde vergessen, die richtigen Maßeinheiten anzugeben. Ergänzen Sie diese: Ein Mal atmen dauert 8,4 ______. Die Fläche eines Laptop-Bildschirms ist ca. 2,7 __________. Ein Glas Marmelade wiegt 0,62 _________. Eine Stadt hat eine Fläche von 345 __________ . Die dicke einer Fingernagel ist 0,8 __________ . Eine Kuh wiegt 1,3 _________. Es wurde vergessen, die richtigen Maßeinheiten anzugeben. Ergänzen Sie diese: Die Fläche eines Fensters ist ca. 0,78 __________. Eine Zugreise dauert 211 ______. Das Volumen eines Kuhschranks ist 0,62 _________. Die Dicke eines Fensters ist 8 __________ . Eine Katze wiegt 4395 _________. Das Volumen eines Kugelschreibers ist 21,6 __________ . Es wurde vergessen, die richtigen Maßeinheiten anzugeben. Ergänzen Sie diese: Die Fläche einer Bettdecke ist ca. 195 __________. Das Volumen einer Flasche Bier ist 524 ______. Eine Katze wiegt 0,0037 _________. Die Dicke eines Bleistifts ist 7,2 __________ . Das Volumen eines Zimmer ist 40,6 _________. Ein Tag dauert 1440 __________ .

Es wurde vergessen, die richtigen Maßeinheiten anzugeben. Ergänzen Sie diese: Der Deckel eines Marmeladenglases hat eine Fläche von 27,3 __________ . Der Eiffelturm von Paris ist 0,324 __________ groß. Der Orgasmus einer Frau dauert durchschnittlich 0,4 ______. Die Länge eines Busses ist 83,4 __________. Eine Kübel Farbe wiegt 0,01 _________. Der Umfang eines Doppelbettes beträgt 735 _________. Es wurde vergessen, die richtigen Maßeinheiten anzugeben. Ergänzen Sie diese: Ein Herzschlag dauert 0,01 ______. Die Fläche der Seite eines Buches ist ca. 2,3 __________. Die Fläche einer Fingernagel ist 0,73 _________. Ein Tempel hat eine Fläche von 345 __________ . Der Taille einer Frau ist 62 __________ . Ein Elephant wiegt 5680 _________. Es wurde vergessen, die richtigen Maßeinheiten anzugeben. Ergänzen Sie diese: Die Fläche einer Badewanne ist ca. 0,88 __________. Eine Busfahrt in einer Stadt dauert 911 ______. Das Volumen eines Schlafzimmers ist 32,5 _________. Die Dicke einer Schlüssel ist 8 __________ . Ein Hund wiegt 8,34 _________. Das Volumen eines Honigglases ist 632 __________ . Es wurde vergessen, die richtigen Maßeinheiten anzugeben. Ergänzen Sie diese: Die Fläche eines Schachspielbrettes ist ca. 6,25 __________. Das Volumen eines Kochtopfes ist 2524 ______. Eine Ziege wiegt 15300 _________. Die Dicke eines Kugelschreibers ist 3,2 __________ . Das Volumen eines Zahns ist 1,06 _________. Ein Atemzug dauert ca. 9,5 __________ .

G2.5 Einheiten ohne Hochzahl

Rechnen Sie um: 537 km in cm 537 mm in m 837 min in h 0,00047 t in g 0,032 Tage in s	Rechnen Sie um: 445 m in cm 445 mm in dm 4536 min in Tage 0,000445 t in g 0,0495 h in s	Rechnen Sie um: 793 mg in kg 793 m in cm 0,793 dm in km 0,000793 kg in g 0,0783 Tage in h	Rechnen Sie um: 0,577 mm in m 577 km in dm 0,793 kg in mg 0,000783 s in min 0,0773 Tage in min
Rechnen Sie um: 53700 m in mm 537 m in km 837 s in min 0,00047 kg in mg 0,032 Tage in s	Rechnen Sie um: 445 dm in mm 445 cm in m 4536 min in Tage 0,000445 kg in mg 0,0495 h in s	Rechnen Sie um: 793 g in t 793 dm in mm 0,0793 mm in m 0,000793 g in mg 0,0783 Tage in h	Rechnen Sie um: 0,577 m in km 5770 m in mm 0,793 t in g 0,000783 min in h 0,0773 Tage in min

G2.6 Lageparameter

Die Familien eines kleinen Dorfes haben Kirschen geerntet. Die Ernte für die verschiedenen Familien war: 54kg, 65kg, 48kg, 76kg, 52kg, 65kg, 45kg. Sie haben allerdings vereinbart, dass jede Familie doch gleich so viele Kirschen bekommt. Wie viel bekommt jede Familie? Wie viel ist der Median und der Modus in diesem Fall? Das Gewicht der Schüler in einer Klasse ist: 52kg, 65kg, 48kg, 76kg, 52kg, 65kg, 45kg, 65kg, 45 kg, 45kg, 78kg, 69kg. Berechnen Sie die Mittelwerte! Gegeben sind folgende Zahlen: 4, 7, -2, 2, 2, −309, 4, 0, 2, 7, 9, 10, 19, 11, 419, 7, -2, 12. Berechnen Sie die Mittelwerte. Gegeben sind die folgenden zwei Wertegruppen, die Daten aus einer Studie der EU über die Vermögensverteilung um das Jahr 2010 ähneln: Das Modell DE, das die Verteilung des Vermögens in Deutschland ähnelt: 16 10 10 1 1 300 10 1 1 10 Das Modell GR, das die Verteilung des Vermögens in Griechenland ähnelt: 11 9 1 1 1 100 1 14 11 11 Berechnen Sie jeweils die Mittelwerte.

Gegeben sind die folgenden zwei Wertegruppen: 1 0 1 3 0 1 101 0 3 3 0 1 3 0 0 0 3 0 0 0 und 3 0 1 101 0 Berechnen Sie jeweils die Mittelwerte. Gegeben sind die folgenden Zahlen: 5, 8, 2, −6, 2, 0, 5, 7 Berechnen Sie jeweils die Mittelwerte. Gegeben sind die folgenden zwei Wertegruppen, die Daten aus einer Studie der EU über die Vermögensverteilung um das Jahr 2010 ähneln: Das Modell AT, das die Verteilung des Vermögens in Österreich ähnelt: 10 8 10 2 2 300 10 2 2 10 Das Modell PO, das die Verteilung des Vermögens in Portugal ähnelt: 100 11 1 11 1 11 11 12 1 1 Berechnen Sie jeweils die Mittelwerte. Gegeben sind die folgenden zwei Wertegruppen: 0 0 0 0 0 0 202 0 0 0 6 2 6 2 6 2 6 2 6 0 und 2 0 0 202 6 Berechnen Sie jeweils die Mittelwerte.

G2.7 Säulendiagramm

Lesen Sie vom Diagramm ab, wie viele Packungen: genau 4 Bananen genau 3 Bananen keine Banane höchstens 3 Bananen mindestens 3 haben mindestens 2 und höchstens 4 Bananen haben! Lesen Sie vom Diagramm ab, in wie vielen Häusern: genau 3 Autos genau 5 Autos kein Auto höchstens 3 Autos mindestens 3 Autos mindestens 2 und höchstens 4 Autos haben!

Lesen Sie vom Diagramm ab, wie viele Tische: genau 3 Stühle genau 5 Stühle keinen Stuhl höchstens 3 Stühle mindestens 3 Stühle haben mindestens 2 und höchstens 4 Stühle haben! Lesen Sie vom Diagramm ab, wie viele Töpfe: genau 3 Blumen genau 5 Blumen keine Blume höchstens 3 Blumen mindestens 3 Blumen haben mindestens 2 und höchstens 4 Blumen haben! Lesen Sie vom Diagramm ab, wie viele SchülerInnen: genau 3 Punkte genau 5 Punkte keine Punkte höchstens 3 Punkte mindestens 3 Punkte haben mindestens 2 und höchstens 4 Punkte haben!

Lesen Sie vom Diagramm ab, wie viele SchülerInnen: genau 4 Bücher genau 3 Bücher kein Buch höchstens 3 Bücher mindestens 3 Bücher mindestens 2 und höchstens 4 Bücher lesen! Lesen Sie vom Diagramm ab, wie viele Klassen: genau 3 Schüler*innen genau 5 Schüler*innen keine Schüler*innen höchstens 3 Schüler*innen mindestens 3 Schüler*innen mindestens 2 und höchstens 4 Schüler*innen haben! Lesen Sie vom Diagramm ab, wie viele Häuser: genau 3 Schlafzimmer genau 5 Schlafzimmer keine Schlafzimmer höchstens 3 Schlafzimmer mindestens 3 Schlafzimmer mindestens 2 und höchstens 4 Schlafzimmer haben!

G2.8 Kürzen mit Primfaktorzerlegung

$\ {\frac {6664}{8820}}=\qquad$ $\ {\frac {15288}{16632}}=\qquad$ $\ {\frac {53361}{47124}}=\qquad$ $\ {\frac {3920}{3528}}=\qquad$ $\ {\frac {5929}{11025}}=\qquad$ $\ {\frac {25480}{25025}}=\qquad$ $\ {\frac {68796}{72072}}=\qquad$ $\ {\frac {25025}{29645}}=\qquad$ $\ {\frac {2448}{4914}}=\qquad$ $\ {\frac {6552}{4410}}=\qquad$ $\ {\frac {2184}{5544}}=\qquad$ $\ {\frac {56056}{32760}}=\qquad$

$\ {\frac {6664}{3528}}=\qquad$ $\ {\frac {25480}{16632}}=\qquad$ $\ {\frac {59290}{47124}}=\qquad$ $\ {\frac {3920}{8820}}=\qquad$ $\ {\frac {53361}{11025}}=\qquad$ $\ {\frac {15288}{25025}}=\qquad$ $\ {\frac {68796}{56056}}=\qquad$ $\ {\frac {25025}{29645}}=\qquad$ $\ {\frac {6552}{4914}}=\qquad$ $\ {\frac {2448}{4410}}=\qquad$ $\ {\frac {2184}{5544}}=\qquad$ $\ {\frac {72072}{32760}}=\qquad$

G2.9 Prozentrechnung bei Wachstum und Abnahme

Das Gehalt eines Beamten war 1800€ und wurde um 2,5% gekürzt. Berechnen sie das neue Gehalt! Um wie viel € wurde das Gehalt gekürzt? Eine Pflanze ist 60 cm hoch. Wie lang ist sie danach, wenn sie 60% kleiner wird? Wie viel cm kleiner wird sie? Ein Gummiband ist 24 cm und wird um 150% verlängert. Wie viel ist die neue Länge? Wie viel cm länger wird es? Das Gehalt einer Managerin war 650000€ und wurde nach eine Massenentlassung von Angestellten um 5,4% erhöht. Berechnen sie das neue Gehalt! Um wie viel € wurde das Gehalt erhöht?

Eine Person wiegt 68 kg und nimmt 5% zu. Wie viel ist ihr neues Gewicht? Wie viel kg hat sie zugenommen? Eine Person wiegt 72 kg und nimmt 5% ab. Wie viel ist ihr neues Gewicht? Wie viel kg hat sie abgenommen? Ein Lied dauert 3,4 min. Eine verlängerte Version dauert 15% länger. Wie lang dauert die verlängerte Version? Wie viel Minuten mehr dauert sie? Die Ölreserven der Erde reichen für 20 Jahre noch. Wenn wir etwas sparen, dann werden sie um 150% länger ausreichen. Wie lang werden sie dann ausreichen? Wie viele Jahre mehr sind es?

G2.10 Einheiten mit Hochzahl

Rechnen Sie um: 537 km² in dm² 537 mm³ in dm³ 537 dm² in km² 0,000537 km³ in dm³ 0,032 dm² in m²	Rechnen Sie um: 374 dm³ in m³ 374 dm³ in mm³ 374 mm² in m² 0,000374 m³ in cm³ 0,0374 cm² in m²	Rechnen Sie um: 257 dm² in mm² 257 m³ in km³ 257 dm² in km² 0,000257 cm³ in mm³ 0,0257 cm² in dm²	Rechnen Sie um: 447 dm³ in cm³ 257 dm² in km² 311 mm² in m² 0,00335 cm³ in mm³ 0,0257 dm³ in mm³
Rechnen Sie um: 53700 m² in mm² 537 cm³ in m³ 5,37 mm² in m² 0,537 m³ in mm³ 0,032 mm² in cm²	Rechnen Sie um: 374 mm³ in cm³ 374 m³ in cm³ 374 m² in km² 0,000374 dm³ in mm³ 0,0374 mm² in dm²	Rechnen Sie um: 257 m² in cm² 257 mm³ in m³ 2,57 mm² in m² 0,000257 m³ in dm³ 0,0257 mm² in cm²	Rechnen Sie um: 447 cm³ in mm³ 2,57 mm² in m² 311 m² in km² 0,00335 dm³ in cm³ 0,0257 m³ in cm³

G2.11 Formel Einsetzen in der ebenen Geometrie

Berechnen Sie in den folgenden Aufgaben jeweils den Umfang und die Fläche! Der Radius eines Autorads ist 28 cm. Die Breite eines Fensters ist 32 cm und seine Höhe 5 dm. Die Seiten des Verkehrszeichens sind alle gleich 3,2 cm. Berechnen Sie in den folgenden Aufgaben jeweils den Umfang und die Fläche! Die Seite eines Quadrats ist 28 cm. Die Breite eines Bildschirms ist 32 cm und die Länge 5 dm. Der Durchmesser des Bodens einer Tasse ist 3,2 cm. Berechnen Sie in den folgenden Aufgaben jeweils den Umfang und die Fläche! Der Boden einer Flasche ist 8 cm "lang". Die Seite einer Raute ist 2,5 dm, die Diagonalen 40 cm bzw. 0,3 m. Ein Zimmer ist 3,2 m mal 42 dm groß. Berechnen Sie in den folgenden Aufgaben jeweils den Umfang und die Fläche! Eine Tür ist 21,5 dm hoch und 77 cm breit. Der größte Abstand zwischen den Punkten eines Tellerrands ist 2,8 dm. Die Länge eines Parallelogramms ist 0,34 m, die entsprechende Höhe 9 cm und die kürzere Seite 2,3 dm.

Berechnen Sie in den folgenden Aufgaben jeweils den Umfang und die Fläche! Der Radius eines Autorads ist 14 cm. Die Breite eines Fensters ist 16 cm und seine Höhe 2,5 dm. Die Seiten des Verkehrszeichens sind alle gleich 6,4 cm. Berechnen Sie in den folgenden Aufgaben jeweils den Umfang und die Fläche! Die Seite eines Quadrats ist 14 cm. Die Breite eines Bildschirms ist 16 cm und die Länge 2,5 dm. Der Durchmesser des Bodens einer Tasse ist 1,6 cm. Berechnen Sie in den folgenden Aufgaben jeweils den Umfang und die Fläche! Der Boden einer Flasche passt genau in einem Quadrat mit 4 cm Seite. Die Seite einer Raute ist 1,25 dm, die Diagonalen 20 cm bzw. 0,15 m. Ein Zimmer ist 1,6 m mal 21 dm groß. Berechnen Sie in den folgenden Aufgaben jeweils den Umfang und die Fläche! Eine Tür ist 10,75 dm hoch und 38,5 cm breit. Der größte Abstand zwischen den Punkten eines Tellerrands ist 1,4 dm. Die Länge eines Parallelogramms ist 0,17 m, die entsprechende Höhe 4,5 cm und die kürzere Seite 1,15 dm.

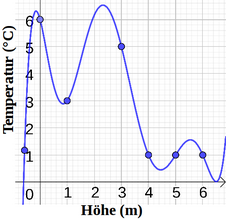
G2.12 Liniendiagramm

Lesen Sie vom Diagramm ab: Wie viel war die Temperatur um 2, um 12, um 15 Uhr und um 16:15? Um wie viel Uhr war die Temperatur 36,2°C? Um wie viel Uhr war die Temperatur 36,3°C? Um wie viel Uhr war die Temperatur 36,4°C? Das Diagramm stellt die Temperatur in einem Wassertank in Bezug auf seine Höhe dar. Lesen Sie vom Diagramm ab: Wie viel ist die Temperatur bei 3, 4, 6 und 0 m Höhe? Bei welcher Höhe ist die Temperatur 1°C? Bei welcher Höhe ist die Temperatur 3°C? Bei welcher Höhe ist die Temperatur 6°C? Bei welcher Höhe ist die Temperatur 0°C? Das Diagramm stellt dar, wie viele FußgängerInnen eine Ampel pro Minute überqueren (y-Achse) in Bezug auf die Zeit (x-Achse). Lesen Sie vom Diagramm ab: Wie viele FußgängerInnen pro Minute überqueren die Ampel um 02:00, um 03:00, um 06:30 und um 11:00? Wann überqueren die Ampel 8 FußgängerInnen pro Minute? Wann überqueren die Ampel 1 FußgängerIn pro Minute? Wann überqueren die Ampel 5 FußgängerInnen pro Minute? Wann überqueren die Ampel 9 FußgängerInnen pro Minute? Das Diagramm stellt die Konzentration von CO2 (y-Achse) in Bezug auf die Zeit (x-Achse, Tausende Jahre in der Vergangenheit) dar. Lesen Sie vom Diagramm ab: Wie viel die Konzentration vor 50, 100 und 400 Tausende Jahre war. Wann die Konzentration 280 ppmv war. Wann die Konzentration 190 ppmv war. Lesen Sie vom Diagramm ab: Wie viel war das Volumen am Anfang und nach 1, nach 2, nach 4 und nach 5,5 s? Nach wie vielen s war das Volumen 2 m3? Nach wie vielen s war das Volumen 4 m3? Nach wie vielen s war das Volumen 7 m3 Nach wie vielen s war das Volumen 0 m3 Das Diagramm stellt die Temperatur in einem Keller in Bezug auf seine Tiefe dar. Lesen Sie vom Diagramm ab: Wie viel ist die Temperatur bei 3, 4, 6 und 0 m Tiefe? Bei welcher Tiefe ist die Temperatur 1°C? Bei welcher Tiefe ist die Temperatur 3°C? Bei welcher Tiefe ist die Temperatur 6°C? Bei welcher Tiefe ist die Temperatur 0°C? Lesen Sie vom Diagramm ab: Wie viel war der Druck bei 2m, 5,5m, 0m und 3m? Bei welcher Tiefe ist der Druck 0,5 Pa(Pascal)? Bei welcher Tiefe ist der Druck 2 Pa(Pascal)? Bei welcher Tiefe ist der Druck 4 Pa(Pascal)? Das Diagramm stellt die Konzentration von CO2 (y-Achse) in Bezug auf die Zeit (zwischen 2017-2019) dar. Lesen Sie vom Diagramm ab: Wie viel die Konzentration am Anfang jedes Jahres war. Wann die Konzentration 408 ppmv war. Wann die Konzentration 410 ppmv war.

G2.13 Textaufgaben zu den Bruchrechnungen

Die Ernte einer Bäuerin war 1260 t. $\textstyle \ {\frac {2}{7}}\$davon waren Kartoffeln, $\textstyle \ {\frac {2}{9}}\$Tomaten, $\textstyle \ {\frac {3}{20}}\$Gurken, 11 t Karotten und der Rest Getreide. Wie viel t von jeder Sorte hat sie geenrtet? Welcher Anteil der Ernte war Getreide? (als gekürzter Bruch) Eine Schule hat 924 SchülerInnen. $\textstyle \ {\frac {2}{11}}\$ sind aus Serbien, $\textstyle \ {\frac {1}{7}}\$ aus der Türkei, $\textstyle \ {\frac {1}{2}}\$ aus Österreich und der Rest aus anderen Staaten. Wie viele SchülerInnen kommen aus Österreich, Serbien, Türkei bzw. anderen Staaten? Welcher Anteil der SchülerInnen kommt aus anderen Staaten? (als gekürzter Bruch) In einem Staat mit ca. 9,702 Millionen EinwohnerInnen und 1,32 Milliarden € Vermögen haben 99 Menschen $\textstyle \ {\frac {4}{15}}\$des Vermögens ("Multimillionäre"), noch 2640 Menschen $\textstyle \ {\frac {10}{33}}\$ des Vermögens ("Millionäre"), noch 3,528 Millionen Menschen $\textstyle \ {\frac {4}{11}}\$ des Vermögens (Mittelschicht), und die restlichen Menschen den Rest des Vermögens ("der Rest"). Wie viel Geld besitzt jede Gruppe? Fleißaufgabe: Welcher Anteil der Bevölkerung (als gekürzte Bruch) gehört zu jeder Gruppe Vergleichen Sie diese Daten mit Daten aus ihrem eigenen Staat!

Manche Parteien behaupten, dass Leistung (allein?) belohnt werden soll und gleichzeitig, dass Vermögen nicht versteuert werden soll. Hier eine Aufgabe, die den Widerspruch zwischen den Behauptungen zeigen kann. In einem Staat mit 8,46 Millionen Einwohner trinkt jeder Einwohner durchschnittlich vier Neuntel Liter Milch täglich. Wie viel Liter werden dann täglich konsumiert? Der Gewinn für die Eigentümer ist 0,8¢/Liter Milch. Wie viel ist der tägliche Gewinn? Finden Sie ihn gerechtfertigt? $\quad$In einem anderen Staat gibt es 4 Supermarktketten. $\quad$Zusammen gewinnen die Eigentümer 105000€ täglich. $\quad$Eigentümer A bekommt zwei Fünftel des Gewinns, $\quad$Eigentümer B ein Drittel und den Rest teilen die anderen$\quad$ $\quad$zwei Eigentümer C und D. Wie viel gewinnt täglich jeder $\quad$Eigentümer? Finden Sie den Gewinn gerechtfertigt? Susanne hat 616 kg Obst geerntet. ${\tfrac {3}{7}}\$davon waren Orangen, ${\tfrac {4}{11}}\$Äpfel und der Rest Birnen. Was wiegt mehr, die Orangen oder die Äpfel? Wie viel wiegen die Birnen? Ein Test hat 63 Punkte. Saskia hat ${\tfrac {7}{9}}\$ und Kosta ${\tfrac {5}{7}}\$der Punkte erreicht. Wer hat mehrere Punkte erreicht? Für ein "Sehr Gut" sind ${\tfrac {6}{7}}\$der Punkte notwendig. Wie viele Punkte hätte Saskia noch gebraucht, um ein "Sehr Gut" zu erreichen? In einem Schrank gibt es 660 Kleiderstücke. ${\tfrac {3}{11}}\$davon sind Unterwäsche, ${\tfrac {11}{30}}\$ T-shirts, ${\tfrac {7}{22}}\$ Hosen und der Rest sonstiges. Was ist mehr, die Unterwäsche oder die Hosen? Wie viel Stücke ist der "Rest"? In einem Elektronik-Geschäft gibt es einen Fach mit 924 Kondensatoren. ${\tfrac {21}{44}}\$davon sind Kunststoff-Folienkondensator, ${\tfrac {7}{66}}\$ Elektrolytkondensatoren, ${\tfrac {6}{77}}\$ variable Kondensatoren und der Rest Keramikkondensatoren. Was ist mehr, die Elektrolytkondensatoren oder die variablen Kondensatoren? Wie viele Keramikkondensatoren gibt es?

G2.14 Indirekte Proportionalität

Typ 1

3 Arbeiter brauchen 15 Stunden, um ein Haus mit Fliesen zu verlegen. Wie viel Zeit brauchen dann 5 Arbeiter? Eine Torte wird auf 13 Personen geteilt und jede Person kriegt 55 g. Wie viel kriegt jede Person, wenn 2 Personen doch keine Torte essen wollen? In einer WG bezahlt jede der 7 Personen 265 € pro Monat. Wie viel bezahlt jede Person, wenn 2 Personen die WG ohne Ersatz verlassen? Nach heutigem Stand der Wissenschaft gibt es eine bestimmte Grenze am Energieverbrauch auf der Erde. Nehmen wir an, dass bei 7 Milliarden Menschen dies einen durchschnittlichen Energieverbrauch von 3 kWh pro Stunde ist. Wie viel wäre er bei 15 Milliarden Menschen? In einer Klasse wird FAIRTRADE-Schokolade ausgeteilt, jedes der 21 Kinder bekommt 2 Stücke. 7 Kinder sagen, dass sie keine Schokolade mehr haben wollen. Wie viel Schokolade bekommt jedes der restlichen Kinder?

An der Elfenbeinküste müssen 26 Kinder 6 Tagen arbeiten, um die bestellte Menge Kakaobohnen für eine europäische Firma zu produzieren. Die Arbeitsbedingungen (genauso wie der Lohn) sind nicht besonders gut. Ein Kind stirbt und 5 dazu erkranken so schwer, dass sie für mehr als zwei Wochen nicht arbeiten können. Wie lang wird die Arbeit nun wahrscheinlich dauern? In einem Dorf in Indien mit 24 Bewohnern reicht das vorhandene Wasser für noch 14 Tage aus. Eine Familie mit 8 Glieder verlässt das Dorf, um ihr Glück irgendwo anders zu finden. Für wie viele Tage insgesamt reicht dann das vorhandene Wasser aus? Jede der 11 reichsten Personen eines Staates mit 22 Millionen EinwohnerInnen besitzen ein Vermögen von 200 Milliarden €. Wie viel € Vermögen würde jede EinwohnerIn bekommen, wenn dieses Geld auf alle EinwohnerInnen gleich verteilt wäre?

Typ 2

An der Elfenbeinküste müssen 26 Kinder 9 Tagen arbeiten, um die bestellte Menge Kakaobohnen für eine europäische Firma zu produzieren. Die Arbeitsbedingungen (genauso wie der Lohn) sind nicht besonders gut. Nach 4 Tagen stirbt daher ein Kind und 5 dazu erkranken so schwer, dass sie für mehr als zwei Wochen nicht arbeiten können. Um wie viele Tage später wird die Arbeit nun wahrscheinlich beendet? In einem Dorf in Indien mit 24 Bewohnern reicht das vorhandene Wasser für noch 27 Tage aus. Nach 13 Tagen verlässt eine Familie mit 8 Glieder das Dorf, um ihr Glück irgendwo anders zu finden. Für wie viele Tage insgesamt reicht dann das am Anfang vorhandene Wasser aus? Die Erdölreserven eines Staates mit 10 Millionen Einwohnern reichen für 26 Jahre aus. Nach 5 Jahren wandern 4 Millionen Personen in den Staat ein. Für wie viele Jahre insgesamt reicht der anfängliche Vorrat in diesem Fall? In einer Klasse wird FAIRTRADE-Schokolade ausgeteilt, jedes der 21 Kinder bekommt 5 Stücke. Nachdem alle Kinder 3 Stücke schon bekommen haben, sagen 7 Kinder, dass sie keine Schokolade mehr haben wollen. Wie viel Schokolade bekommt jedes Kind?

Von einer Baufirma wird kalkuliert, dass 25 Arbeiter 9 Tage benötigen. Nach 3 Tagen müssen jedoch 5 Arbeiter von der Baustelle abgezogen werden. Um wie viele Tage später wird die Arbeit nun wahrscheinlich beendet? Zwei Staaten befinden sich im Krieg. Viele Kinder verlieren dadurch ihre Eltern. In einem Waisenhaus mit 27 Kindern reicht das vorhandene Geld für noch 25 Tage aus. Nach 7 Tagen werden 9 Kinder in Ausland adoptiert und verlassen sie das Waisenhaus. Für wie viele Tage insgesamt wird dann das am Anfang vorhandene Geld ausreichen? Der Futtervorrat in einem Bauernhof mit 19 Kühe reicht für 22 Tage aus. Nach 6 Tagen werden 13 Kühe dazu gekauft. Für wie viele Tage insgesamt reicht der anfängliche Vorrat in diesem Fall? Jede der 5 reichsten Personen eines Staates mit 8 Millionen EinwohnerInnen besitzen ein Vermögen von 180 Milliarden €. Sie besitzen dadurch neun Zehntel des gesamten Vermögens des Staates. Wie viel € würde jede EinwohnerIn des Staates besitzen, wenn das ganze Vermögen des Staates auf alle EinwohnerInnen gleich verteilt wäre?

G2.15 Sachaufgaben zu den Grundrechenarten

In einer Klasse gibt es 21 Kinder und sie wollen gemeinsam Schokoladen kaufen. 3 davon wollen die billigste Variante der Firma H, sie kostet 1,2 €. Doppelt so viele Kinder wollen nicht, dass Kinderarbeit und Chemikalien in ihrer Schokolade stecken. Denen ist allerdings egal, ob die Firma, wo sie Schokolade kaufen, auch Schokoladen produziert, die doch mit Kinderarbeit verbunden sind. Diese Schokoladen (der Firma N) kosten das 1,5-Fache der billigsten. Der Rest der Klasse hat sich für Schokoladen entschieden, die von Firmen produziert werden, die Kinderarbeit und Chemikalien in ihrer Produktionskette völlig ausschließen. Diese Schokoladen (der Firma G) kosten das 2,5-Fache der billigsten. Wie viel kosten alle Schokoladen zusammen? Das wie-viel-Fache der Kinder, die Schokolade der Firma H gekauft haben, sind die Kinder, die Schokoladen aus der Firma G gekauft haben?

Bei einem Spiel hat Anja 6, Nikole 5, Boris 8 und Gregor 1 Stein. Gregor bekommt von Nikole doppelt so viel Steine wie seine eigene, von Anja ein Drittel ihre Steine und die Hälfte der Steine von Boris. Wie viele Steine hat Gregor am Ende? Wie viele Steine hat Nikole am Ende? Vivian hat 12 Kirschen, Fabian 7 und Lili 15. Vivian isst drei ihre Kirschen und gibt Fabian von den restlichen ein drittel. Lili gibt ihr dann das doppelt so viel, wie Vivian gegessen hat. Danach isst Fabian vier von seinen Kirschen und Lili 5 von ihren Kirschen. Wie viele Kirschen hat Vivian am Ende? Wie viele Kirschen hat Fabian am Ende? An einem Dorf in Somalia arbeiten die Einwohner für eine chinesische Firma. An einem Monat bekommt Fatima 6 €, Milou 5, Hassan 8 und Hamed 1 €. Hamed bedroht die anderen und bekommt von Milou doppelt so viel € wie seine eigene, von Fatima ein Drittel ihres Gehaltes und die Hälfte des Gehaltes von Hassan. Wie viele € hat Hamed am Ende? Wie viele € hat Milou am Ende?

Vertiefendes Niveau 1

V1.1 Umkehraufgaben der Prozentrechnung

1. Der pro Kopf Energieverbrauch in Deutschland ist zwischen den Jahren 2000 und 2011 um 20% auf 5,4 kW gestiegen. Wie viel war er im Jahr 2000?
2. Ein Tisch wurde um 10% geschnitten. Die neue Länge ist 2,7m. Berechnen Sie die ursprüngliche Länge!
3. Ein Baby wächst in einem Jahr um 20% auf 42 cm. Wie viel war die ursprüngliche Größe?
4. Der pro Kopf Energieverbrauch in EU sei 3,6 kW und damit 1400% mehr als in Kongo. Wie viel ist er im Kongo?

V1.2 Bruchstrichrechnungen mit Primfaktorzerlegung

Vereinfachen Sie mit Hilfe der Primfaktorzerlegung!
${\frac {41}{120}}-3{\frac {11}{36}}+2{\frac {237}{300}}$	$2{\frac {9}{20}}-{\frac {11}{15}}+3{\frac {13}{60}}$	$2{\frac {9}{28}}+{\frac {11}{63}}-3{\frac {5}{12}}$	$2{\frac {9}{28}}+{\frac {11}{63}}-1{\frac {5}{24}}$
$2{\frac {9}{20}}+{\frac {11}{50}}-3{\frac {13}{25}}$	${\frac {35}{36}}+5{\frac {5}{12}}-7{\frac {5}{18}}$	${\frac {9}{20}}-3{\frac {11}{25}}+2{\frac {13}{15}}$	$2{\frac {9}{20}}-{\frac {11}{36}}+3{\frac {13}{15}}$

V1.3 Umformen einfache Kombinationen

Lösen Sie folgende Gleichung, also formen Sie auf die unbekannte Variable um, um sie zu berechen!
$5(2x-7)=2x+5$ $61-4\cdot (b-5)=7\cdot (2\cdot b-9)$	$3(7-2b)=4b+41$ $7-4\cdot (2k+5)=4\cdot (3k-2)+55$	$7(2m+5)=9m+37$ $8+3\cdot (5g+3)=4\cdot (3g-2)+22$
$7(3z+2)=9z-10$ $4-3\cdot (5m+3)=3\cdot (3m-2)+25$	$3(4b-5)=2b+10$ $23-4\cdot (2b-5)=9\cdot (2\cdot b-1)$	$7(3z+2)=9z+10$ $7-4\cdot (2k+5)=4\cdot (3k-2)+15$
$3(4z-17)=54-9z$ $9+3\cdot (5g+3)=3\cdot (3g-5)+21$	$7(3z+2)=9z+2$ $4-3\cdot (5m+3)=3\cdot (3m-2)-23$

V1.4 Vergleich direkter und indirekter Proportionalität

1. Nach heutigem Stand der Wissenschaft gibt es eine bestimmte Grenze am Energieverbrauch auf der Erde. Nehmen wir an, dass bei 7 Milliarden Menschen dies einen durchschnittlichen Stundenenergieverbrauch von 3 kWh pro Person ist.
   
   1. Wie viel wäre er in 33 Minuten?
   2. Wie viel wäre der durchschnittliche Stundenenergieverbrauch bei 5,4 Milliarden Menschen, wenn der gesamte Energieverbrauch gleich bleiben würde?
   3. Bei welcher Bevölkerung wäre der durchschnittliche Stundenenergieverbrauch 16,8 kWh, wenn der gesamte Energieverbrauch gleich bleiben würde?
   4. Wie viel wäre der durchschnittliche Energieverbrauch pro Person bei 5,4 Milliarden Menschen und in 570 Minuten, wenn der gesamte Energieverbrauch gleich bleiben würde?
2. In einer WG bezahlt jede der 7 Personen 375 € pro Monat.
   
   1. Wie viel bezahlt jede Person, wenn 2 Personen die WG ohne Ersatz verlassen?
   2. Wie viel bezahlt jede der 7 Personen pro Woche?
      (1 Monat=30 Tage)
   3. Wie viel bezahlt jede Person pro Jahr, wenn doch 8 Personen in der WG wohnen? (1 Jahr=360 Tage)
3. Mit 3000€ kann jedes von 15 Kindern 5 Mal ein Spiel spielen.
   
   1. 7 Kinder haben keinen Bock drauf. Wie oft darf dann jedes der anderen Kinder Spielen?
   2. Wie oft darf jedes der 15 Kinder spielen wenn 4200 € vorhanden sind?
   3. Wie oft darf jedes von 12 Kindern spielen, wenn 3450 € vorhanden sind?
4. In Prato in Italien produzierten ChinesInnen (oft unter Druck) im Jahr 2018 billige Kleidung (oft um weniger als 1 € Stundenlohn und für mehr als 14 Stunden Arbeit pro Tag). In 21 Stunden produzieren 6 ArbeiterInnen Kleidung im Wert von 1400€.
   
   1. Wie lang brauchen diese ArbeiterInnen um 210€ Wert Kleidung zu produzieren?
   2. Wie lang brauchen 9 ArbeiterInnen um diese 1400€ Wert Kleidung zu produzieren?
   3. Wie lang brauchen 8 ArbeiterInnen um 1750€ Wert Kleidung zu produzieren?
5. An der Elfenbeinküste müssen 26 Kinder 9 Tagen arbeiten, um die 585 t Kakaobohnen für eine europäische Firma zu ernten.
   
   1. Wie viel können sie in 5 Tagen ernten?
   2. Wie lang müssen 20 Kinder arbeiten, um die 585 t zu ernten?
   3. In wie vielen Tagen können 30 Kinder 450 t ernten?
6. In einem Dorf in Jemen mit 24 Bewohnern reichen die vorhandenen 7,7 t Wasser für noch 27 Tage aus.
   
   1. Für wie viele Tage reicht das Wasser aus, wenn 8 Personen das Dorf verlassen?
   2. Für wie viele Tage reichen für die 24 Bewohnern 3,3 t Wasser aus?
   3. Wie viele Tonnen Wasser brauchen 16 Bewohner für 20 Tage?
7. In einer Klasse mit 21 Kindern wird jeden Tag FAIRTRADE-Schokolade ausgeteilt, 105 Schokoladen reichen für 12 Tage aus.
   
   1. Für wie viele Kinder reichen dann 70 Schokoladen aus?
   2. Für wie viele Kinder reichen die 105 Schokoladen für 28 Tage aus?
   3. Für wie viele Tage reichen für 6 Kinder 50 Schokoladen aus?
8. Von einer Baufirma wird kalkuliert, dass 25 Arbeiter:innen 9 Tage benötigen, um 4500 m² Boden mit Fliesen zu verlegen.
   
   1. Wie lang brauchen diese Arbeiter:innen um 2100 m² Boden mit Fliesen zu verlegen?
   2. Wie lang brauchen 9 Arbeiter:innen um diese 4500 m² Boden mit Fliesen zu verlegen?
   3. Wie viele Arbeiter:innen sind notwendig, um in 50 Tagen 27000 m² Boden mit Fliesen zu verlegen?

V1.5 Punktrechnungen von zwei Potenzen mit der gleichen Basis

Schreiben Sie folgende Terme als eine Potenzzahl auf!
$\quad {a^{-7}}\cdot {a^{5}}\quad \qquad$ $\quad {4^{3}}\cdot {4^{b}}$ $\quad {\frac {c^{5}}{c^{9}}}\qquad \qquad$ $\quad {\frac {w^{-8}}{w^{-5}}}$	$\quad {a^{b}}\cdot {a^{-x}}\qquad \quad$ $\quad {4^{-3}}\cdot {4^{7}}$ $\quad {\frac {c^{-5}}{c^{9}}}\qquad \qquad$ $\quad {\frac {w^{7}}{w^{-5}}}$	$\quad {7^{-7}}\cdot {7^{7}}\quad \qquad$ $\quad {t^{2b}}\cdot {t^{-5b}}$ $\quad {\frac {c^{3}}{c^{b}}}\qquad \qquad$ $\quad {\frac {w^{-b}}{w^{12}}}$
$\quad {3^{-5}}\cdot {3^{6}}\qquad \quad$ $\quad {b^{-2t}}\cdot {b^{-5t}}$ $\quad {\frac {b^{-3}}{b^{-5}}}\qquad \qquad$ $\quad {\frac {w^{-b}}{w^{-12}}}$	$\quad {c^{-5}}\cdot {c^{-2}}\qquad \quad$ $\quad {3^{2t}}\cdot {3^{-7}}$ $\quad {\frac {5^{3}}{5^{-3}}}\qquad \qquad$ $\quad {\frac {w^{-2b}}{w^{3b}}}$	$\quad {3^{7}}\cdot {3^{-7}}\qquad \quad$ $\quad {a^{-2t}}\cdot {a^{z}}$ $\quad {\frac {b^{3}}{b^{5}}}\qquad \qquad$ $\quad {\frac {3^{-w}}{3^{3w}}}$
$\quad {7^{-b}}\cdot {7^{2b}}\qquad \quad$ $\quad {t^{-3}}\cdot {t^{t}}$ $\quad {\frac {20^{7}}{20^{5}}}\qquad \qquad$ $\quad {\frac {u^{b}}{u^{-12}}}$	$\quad {7^{-19}}\cdot {7^{20}}\qquad \quad$ $\quad {j^{-3w}}\cdot {j^{5w}}$ $\quad {\frac {3^{-3b}}{3^{-7b}}}\qquad \qquad$ $\quad {\frac {b^{-w}}{b^{5}}}$

V1.6 Textaufgaben linearer Gleichungssysteme mit 2 Variablen

1. Ein Balkon hat 33 Blumentöpfe, manche mit 3 und der Rest mit 8 Blumen. Insgesamt sind die Blumen 209. Wie viele Töpfe mit 3 bzw. 8 Blumen gibt es?
2. Ein Zug hat 13 Wagons, manche mit 40 und der Rest mit 65 Sitzplätze. Insgesamt haben die Wagons 720 Sitzplätze. Wie viele Wagons mit 40 bzw. 65 Sitzplätze gibt es?
3. In einem Dorf mit 51 Müttern haben manche Mütter 3 und die restlichen 2 Kinder. Insgesamt haben alle Mutter 116 Kinder. Wie viele Mutter haben 2 bzw. 3 Kinder?
4. An einem Wohnblock gibt es 18 Wohnungen, manche haben 20 und der Rest 15 Steckdosen. Insgesamt haben sie 315 Steckdosen. Wie viele Wohnungen mit 15 bzw 20 Steckdosen gibt es?
5. In einem Café gibt es 8 Tische. Manche sind für 3 Personen und der Rest für 5 Personen. Insgesamt kann das Café 36 Personen bedienen. Wie viele 3 bzw. 5 Personen-Tische gibt es im Café?
6. An einem Balkon gibt es 23 Blumentöpfe, manche mit 4 und der Rest mit 7 Blumen. Zusammen sind die Blumen 146. Wie viele Töpfe mit 4 bzw. 7 Blumen gibt es am Balkon?
7. Eine Flugzeugfirma hat 26 Flugzeuge, manche für 130 und der Rest für 150 Passagiere. Insgesamt kann die Firma 3680 Passagiere gleichzeitig bedienen. Wie viele Flugzeuge für 130 bzw. 150 Passagiere hat die Firma?
8. Eine Klasse mit 24 Personen war bei der Aufforstung eines Waldes. Durchschnittlich hat jedes Mädchen 9 Bäume eingepflanzt und jeder Knabe 7, insgesamt hat die Klasse 194 Bäume eingepflanzt. Wie viele Mädchen bzw. Knaben hat die Klasse?

V1.7 Kombinationsaufgaben der Prozentrechnung

1. Die Produzenten eines Filmes hatten vor dem Schnitt zu viel Material. Beim ersten Schnitt haben Sie 80% geschnitten. Das war ihnen aber doch zu kurz, daher haben sie eine neue um 15% längere (als der geschnittene Film) Version gemacht. Die letzte Version dauert 1,61 Stunden.
   1. Berechnen Sie die ursprüngliche Dauer, also die Dauer des ungeschnittenen Films!
   2. Ist der Film insgesamt länger oder kürzer geworden und um wie viel Prozent?
2. Die Nase von Pinocchio ist nach einer Lüge um 50% gewachsen, danach ist sie um 35% auf 2,34 cm zurückgegangen.
   1. Wie groß war sie ursprünglich?
   2. Ist sie insgesamt größer oder kleiner geworden und um wie viel Prozent?
3. Das Gehalt einer Arbeiterin wurde anfangs um 12% erhöht, dann aber um 10% auf 1764 € wieder gekürzt.
   1. Wie groß war es ursprünglich?
   2. Wurde es insgesamt erhöht oder reduziert und um wie viel Prozent?
4. Frankreich bezieht mehr als 70% seiner elektrischen Energie aus Kernkraftwerken. Ein (riesiges) Problem dabei ist der radioaktiver Müll, der für Hunderte bis Tausende Jahre gefährlich bleibt. Nehmen wir an, dass die Menge eines solchen Stoffes zwischen 1993 und 1994 um 4% gestiegen und zwischen 1994 und 1995 um weiter 5% auf 16,38 t gestiegen ist.
   1. Wie viele t wäre sie ursprünglich?
   2. Um wie viel Prozent wäre sie insgesamt gestiegen?
5. Katia ist um 20% größer als Manina. Vladimir ist 176,7 cm groß und 5% kleiner als Katia.
   1. Wie groß ist Manina?
   2. Wie viel Prozent kleiner oder Größer als Vladimir ist Manina
6. Die Nase von Pinocchio wächst nach einer Luge um 150% und dann geht sie um 60% auf 2,5 cm zurück.
   1. Wie lang war sie ursprünglich?
   2. Ist sie insgesamt größer oder kleiner geworden und um wie viel Prozent?
7. Das Volumen des Magens einer Person wächst nach dem Essen um 120% und dann geht es um 35% auf 500,5 ml zurück.
   1. Wie groß war er ursprünglich?
   2. Wurde er insgesamt größer oder kleiner und um wie viel Prozent?
8. Das Volumen des Herzens einer Person wächst bei einem Puls um 150% und dann geht es um 60% auf 440 ml zurück.
   1. Wie viele war es ursprünglich?
   2. Wurde er insgesamt größer oder kleiner und um wie viel Prozent?

V1.8 Vorrang und Bruchrechnungen

Vorrang mit Klammern in Klammern

$\ -(+13)-[96:(3\cdot 5-23)+4]:(-4)-(+15-43)+(91:7-4\cdot 3{,}5)\cdot 2+(+11)\$ $\ -(-13+7)-[(-3\cdot 5-33):(+12)-(+4)]\cdot (-8)+(+37)-(132:11-3\cdot 4)\cdot (-2)-(-11)\$ $\ -(+11-22)+(72:9-9)\cdot 2-(+22)-[99:(3\cdot 7-60:5)+4]\cdot (-2)+(+20)\$ $\ -(-41+37)-[(-3\cdot 8-11):(+7)-(+4)]:(-9)+(+37)-(91:7-13)\cdot (-2)-(-11)\$ $\ -(+44)+(96:12-9)\cdot 7+(+11)-[63:(4\cdot 5-29)+2]\cdot (-0{,}2)-(+33-37)\$ $\ -[(-3\cdot 7-3\cdot 9):(+12)+(-4)]:(-2)-(-13-7)-(132:12-11)\cdot (-5)+(+39)\$ $\ -(+22)-[56:(-3\cdot 5+2\cdot 4)+1]:(-7)-(+11-22)+(88:8-9)\cdot 5+(+33)\$ $\ -(-41+33)-[(-3\cdot 8-48:4):(+9)-(+4)]\cdot (-1)+(+37)-(-14+105:7)\cdot (-2+14:7)-(-11)\$

Bruchrechnungen und Vorrang

${\frac {2}{3}}+\left({\frac {6}{7}}-{\frac {9}{7}}\right)\cdot \left({\frac {2}{5}}-{\frac {16}{21}}:{\frac {4}{7}}\right)$ $1{\frac {1}{22}}:\left({\frac {2}{3}}+{\frac {8}{11}}\right)-3\cdot \left(2{\frac {1}{3}}:3{\frac {3}{6}}-{\frac {1}{3}}\right)$ ${\frac {28}{39}}\cdot \left({\frac {6}{7}}-{\frac {35}{4}}:{\frac {21}{8}}\right)-{\frac {3}{8}}\cdot {\frac {14}{15}}$ ${\frac {16}{77}}:\left({\frac {3}{5}}-{\frac {45}{28}}:2{\frac {1}{4}}\right)-1{\frac {1}{11}}\cdot {\frac {5}{4}}$

$\left({\frac {5}{6}}-{\frac {1}{2}}\right)-2{\frac {1}{3}}\cdot \left({\frac {1}{7}}\cdot 3{\frac {1}{2}}-{\frac {1}{4}}:{\frac {7}{8}}\right)$ $1{\frac {2}{5}}\cdot {\frac {2}{7}}-\left({\frac {1}{9}}:{\frac {2}{15}}-{\frac {1}{2}}\right)$ ${\frac {28}{39}}\cdot \left({\frac {3}{7}}+{\frac {5}{28}}:{\frac {5}{14}}\right)-1{\frac {3}{25}}:{\frac {14}{5}}$ ${\frac {28}{39}}\cdot \left({\frac {3}{7}}+{\frac {9}{28}}:{\frac {9}{14}}\right)-\left({\frac {1}{2}}+{\frac {1}{6}}\right)$

V1.9 Umformen in der ebenen Geometrie konkret

Der Umfang eines Quadrats ist 12cm. Berechnen Sie die Fläche! Die Fläche eines Kreises ist 12cm². Berechnen Sie den Umfang! Der Umfang eines Rechtecks ist 3,8 dm, seine Breite 9 cm. Berechnen Sie seine Fläche! Der Umfang eines Kreises ist 12cm. Berechnen Sie die Fläche! Die Fläche eines Quadrats ist 576 cm². Berechnen Sie den Umfang!

Die Fläche eines Parallelogramms ist 12 dm², die zur längsten Seite entsprechende Höhe 20cm und die kürzere Seite 0,3 m. Berechnen Sie den Umfang! Die Fläche eines Rechtecks ist 3,8 dm², seine Breite 16 cm. Berechnen Sie seinen Umfang! Der Umfang eines gleichseitigen Dreiecks ist 12cm. Berechnen Sie die Fläche!

V1.10 Mittelwerte bei einem Säulendiagramm

Berechnen Sie die Mittelwerte in jedem Diagramm aus der Aufgabe "Säulendiagramm" (Grundniveau 2)

Vertiefendes Niveau 2

V2.1 Prozentrechnung und Brüche

1. Ein viertel der Bevölkerung in Deutschland sind armutsgefährdet. Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie!

   	richtig	falsch
   4% sind gefährdet.
   Das 0,25-fache der Bevölkerung sind armutsgefährdet.
   Das Verhältnis „nicht gefährdet“ zu „gefährdet“ beträgt 3 : 1.

2. Die 20 reichsten Personen eines Staates besitzen vier fünftel des gesamten Vermögens. Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie!

   	richtig	falsch
   Die reichsten 20 besitzen 20% des Vermögens.
   Das Verhältnis des Vermögens der reichsten zum Rest ist 5 : 2.
   Die reichsten haben das 5-Fache Vermögen wie der Rest der Bevölkerung

3. Zwei fünftel der Bevölkerung eines Staates sind für eine Diktatur. Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie!

   	richtig	falsch
   Das Verhältnis der Anhänger einer Diktatur zum Rest ist 2 : 5.
   60% der Bevölkerung ist nicht für eine Diktatur
   Die Personen, die nicht für eine Diktatur sind, sind das 1,5-Fache der Personen, die dafür sind

4. Zwei drittel der Bevölkerung kauft jedes Jahr ein neues Handy. Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie!

   	richtig	falsch
   Diejenigen, die jedes Jahr ein neues Handy kaufen, sind doppelt so viel, wie diejenigen, die es nicht tun.
   Das Verhältnis derjenigen, die ein neues Handy jedes Jahr kaufen, zur ganzen Bevölkerung ist 2 : 1.
   $33{,}{\dot {3}}\%\$kaufen nicht ein neues Handy jedes Jahr

5. Zwei fünftel einer Ernte sind faul. Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie!

   	richtig	falsch
   20% ist faul.
   Das 0,6-fache der Ernts ist nicht faul.
   Das Verhältnis „faul“ zu „nicht faul“ beträgt 2 : 3.

6. Drei fünftel der Zuschauer eines Fußballspiels sind für "Milano". Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie!

   	richtig	falsch
   30% der Zuschauer sind für "Milano".
   Das 0,6-fache der Zuschauer sind nicht für "Milano".
   Das Verhältnis der "Milano" Anhänger zu den restlichen beträgt 3 : 5.

7. Zwei siebtel des Gewichts eines Kuchens ist Zucker. Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie!

   	richtig	falsch
   20% des Gewichts ist Zucker.
   Das $0{,}{\overline {285714}}{\text{-fache}}\$ des Gewichts ist Zucker.
   Das Verhältnis Zucker zu den restlichen Inhalten beträgt 2 : 5.

8. Zwei fünftel der Kinder einer Klasse sind Buben. Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie!

   	richtig	falsch
   40% der Kinder sind Buben.
   Das $0{,}4{\text{-fache}}\$ der Kinder sind nicht Buben.
   Das Verhältnis der restlichen Kindern zu den Buben beträgt 3 : 2.

V2.2 Umformen in der ebenen Geometrie abstrakt

1. Begründen Sie, ob in einem Kreis mit Flächeninhalt A der Radius R mit der Formel:$\ R={\tfrac {\sqrt {A}}{\pi }}$ berechnet werden kann.
2. Begründen Sie, ob in einem Rechteck mit Umfang u und Breite b die Länge a mit der Formel: $a={\tfrac {2u-b}{2}}\$berechnet werden kann.
3. Begründen Sie, ob in einem Rechteck mit Umfang u und Diagonale d und Länge a die Breite b mit der Formel: $b={\sqrt {a^{2}+d^{2}}}\$berechnet werden kann.
4. Begründen Sie, ob in einem gleichseitigen Dreieck mit Fläche A die Seite a mit der Formel: $\textstyle {a={\sqrt {A\cdot {\tfrac {4}{\sqrt {3}}}\ }}}$ berechnet werden kann.
5. Begründen Sie, ob in einem Rechteck mit Umfang u und Länge a die Breite b mit der Formel: $b={\tfrac {u-2a}{2}}\$berechnet werden kann.
6. Begründen Sie, ob in einem Kreis mit Umfang u der Durchmesser d mit der Formel: $d={\tfrac {u\cdot 2}{\pi }}$ berechnet werden kann.
7. Begründen Sie, ob in einem rechtwinkeligem Dreieck mit Hypotenuse c und Katheten a und b die Kathete b mit der Formel: $b={\sqrt {a^{2}-c^{2}}}\$berechnet werden kann.
8. Begründen Sie, ob in einem Kreis mit Flächeninhalt A der Durchmesser d mit der Formel:$\ d={\sqrt {\tfrac {4\,A}{\pi }}}$ berechnet werden kann.

V2.3 Lineare Funktion Tabelle und Diagramm

Tabelle für eine lineare Funktion erstellen

1. 1. Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=-2x+1$ und für die folgenden x-Werte: $-2,\ -1,\ 0,\ 1,\ 2.$
   2. Für die gleiche Funktion sind folgende y-Werte gegeben: $-4,\ -2,\ 0,\ 2,\ 4.$ Finden Sie die entsprechenden x-Werte.
2. 1. Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=-2x+1$ und für die folgenden x-Werte: $-4,\ -2,\ 0,\ 2,\ 4.$
   2. Für die gleiche Funktion sind folgende y-Werte gegeben: $-2,\ -1,\ 0,\ 1,\ 2.$ Finden Sie die entsprechenden x-Werte.
3. 1. Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=3x-1$ und für die folgenden x-Werte: $-2,\ -1,\ 0,\ 1,\ 2.$
   2. Für die gleiche Funktion sind folgende y-Werte gegeben: $-4,\ -2,\ 0,\ 2,\ 4.$ Finden Sie die entsprechenden x-Werte.
4. 1. Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=3x-1$ und für die folgenden x-Werte: $-4,\ -2,\ 0,\ 2,\ 4.$
   2. Für die gleiche Funktion sind folgende y-Werte gegeben: $-2,\ -1,\ 0,\ 1,\ 2.$ Finden Sie die entsprechenden x-Werte.
5. 1. Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=-0,5x+2$ und für die folgenden x-Werte: $-2,\ -1,\ 0,\ 1,\ 2.$
   2. Für die gleiche Funktion sind folgende y-Werte gegeben: $-4,\ -2,\ 0,\ 2,\ 4.$ Finden Sie die entsprechenden x-Werte.
6. 1. Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=-0,5x+2$ und für die folgenden x-Werte: $-4,\ -2,\ 0,\ 2,\ 4.$
   2. Für die gleiche Funktion sind folgende y-Werte gegeben: $-2,\ -1,\ 0,\ 1,\ 2.$ Finden Sie die entsprechenden x-Werte.
7. 1. Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=1,5x-3$ und für die folgenden x-Werte: $-2,\ -1,\ 0,\ 1,\ 2.$
   2. Für die gleiche Funktion sind folgende y-Werte gegeben: $-4,\ -2,\ 0,\ 2,\ 4.$ Finden Sie die entsprechenden x-Werte.
8. 1. Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=1,5x-3$ und für die folgenden x-Werte: $-4,\ -2,\ 0,\ 2,\ 4.$
   2. Für die gleiche Funktion sind folgende y-Werte gegeben: $-2,\ -1,\ 0,\ 1,\ 2.$ Finden Sie die entsprechenden x-Werte.

Diagramm ablesen

Das Diagramm stellt den Gewinn bei der Produktion von Mehl dar. Lesen Sie vom Diagramm ab: Wie viel war der Gewinn bei der Produktion von 3, 4, 0,5 und 0 Tonnen? Ab welcher Menge macht die Produktion Gewinn und wie viel sind die Grundkosten? Bei welcher Menge ist der Gewinn 2000, 3400 bzw. 6000 €? Das Diagramm stellt ein Modell der Abhängigkeit der Lebenserwartung vom Rauchen dar. Lesen Sie vom Diagramm ab: Wie viel die Lebenserwartung ist, wenn eine Person 25 Zigaretten am Tag raucht. Wie viel die Lebenserwartung ist, wenn eine Person 14 Zigaretten am Tag raucht. Wie viele Zigaretten täglich geraucht werden, wenn die Lebenserwartung 68 Jahre ist. Wie viele Zigaretten täglich geraucht werden, wenn die Lebenserwartung 65 Jahre ist. Wie viel die Lebenserwartung für nicht-rauchende Personen ist. Das Diagramm gibt den wöchentlichen CO2 Ausstoß (in Liter) in Abhängigkeit vom wöchentlichen Fleischkonsum (in Kg) an. Lesen Sie vom Diagramm ab: Wie viele Liter der Ausstoß bei einem Konsum von 1, 2, 2,5 bzw. 2,8 kg ist! Wie viel der Konsum bei einem Ausstoß von 36, 28, 24 bzw. 16 Liter ist! Wie viel ist nach diesem Modell der Ausstoß, wenn man kein Fleisch ist? Wie viel ist nach diesem Modell der Fleischkonsum, wenn der Ausstoß 40 Liter ist? Das Diagramm stellt ein Modell der Abhängigkeit der Lebenserwartung vom Rauchen dar. Lesen Sie vom Diagramm ab: Wie viel die Lebenserwartung ist, wenn eine Person 3 Zigaretten am Tag raucht. Wie viel die Lebenserwartung ist, wenn eine Person 10 Zigaretten am Tag raucht. Wie viele Zigaretten täglich geraucht werden, wenn die Lebenserwartung 63 Jahre ist. Wie viele Zigaretten täglich geraucht werden, wenn die Lebenserwartung 72 Jahre ist. Wie viel die Lebenserwartung für nicht-rauchende Personen ist.

Das Diagramm gibt den wöchentlichen CO2 Ausstoß (in Liter) in Abhängigkeit vom wöchentlichen Fleischkonsum (in Kg) an. Lesen Sie vom Diagramm ab: Wie viele Liter der Ausstoß bei einem Konsum von 1, 2, 2,5 bzw. 2,8 kg ist! Wie viel der Konsum bei einem Ausstoß von 40, 28, 24 bzw. 20 Liter ist! Wie viel ist nach diesem Modell der Ausstoß, wenn man kein Fleisch ist? Wie viel ist nach diesem Modell der Fleischkonsum, wenn der Ausstoß 44 Liter ist? Das Diagramm gibt die Änderung des Volumens einer Flüssigkeit in Bezug auf ihre Temperatur in einem bestimmten physikalischen Prozess an. Lesen Sie vom Diagramm ab: Wie viel ist das Volumen bei 40, 60, 70 und 90°C? Wie viel ist das Volumen bei 0°C und wie viel wäre die Temperatur bei 2 Liter Volumen? Wie viel ist die Temperatur bei 4, 5, 6 und 6,5 Liter Volumen? Das Diagramm gibt die Frequenz einer Welle in Bezug auf ihre Länge an. Lesen Sie vom Diagramm ab: Wie viel ist die Frequenz bei 20, 40, 70 und 120 cm Länge? Wie viel wäre die Frequenz bei 0 cm Läng und wie viel die Länge bei 0 Hz Frequenz Wie viel ist die Länge bei20, 40, 50 und 10 Hz Frequenz Das Diagramm gibt die Änderung des Drucks (in Pascal: Pa) einer Flüssigkeit in Bezug auf ihre Temperatur in einem bestimmten physikalischen Prozess an. Lesen Sie vom Diagramm ab: Wie viel ist der Druck bei 30, 45, 70 und 90°C? Wie viel ist der Druck bei 0°C und wie viel wäre die Temperatur bei 9 Pa Druck? Wie viel ist die Temperatur bei 4, 5, 6 und 7,4 Pa Druck?

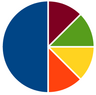
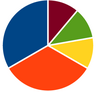
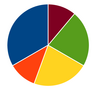
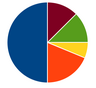
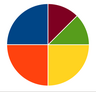
V2.4 Kreisdiagramm

Zu welchen der folgenden Aussagen passen die folgenden Diagrammen? Ein Stall hat 2 Ziegen, 3 Schafe, 8 Kühe, 2 Schweine und 1 Pferd. Ein Kind hat 3 Kartenspiele, 2 Brettspiele, 2 Bälle, 1 Puppe und 1 Spielschwert. In einer Schule gibt es 2 Lehrer für Mathematik, 2 für Englisch, 2 für Deutsch, 1 für Geographie und 1 für Musik. Ein Bauernhof hat 18 Hühner, 1 Hahn, 3 Gänsen, 3 Kanarinen, 2 Katzen und 9 Enten. In einem Tierheim gibt es 8 schwarze Katzen, 4 roten, 2 weißen, 1 dreifarbige und 1 schwarz-rot. In einer Klasse sind 8 Personen aus Österreich, 2 aus Deutschland, 2 aus der Türkei, 2 aus Serbien und 2 aus Tschechien. In einer Klasse wählen 6 Personen die Partei "Bild", 6 Personen die Partei "Welt", 2 die Partei "Nature", 2 die Partei "Grob" und 2 keine Partei. Ein Haus hat 6 Schlafzimmer, 3 WCs, 1 Küche, 1 Wohnraum und 1 Badezimmer.
W X Y Z	P Q R S
K L M N	N M L K

Zu welchen der folgenden Aussagen passen die folgenden Diagrammen? Ein Stall hat 2 Ziegen, 3 Schafe, 8 Kühe, 2 Schweine und 1 Pferd. Ein Kind hat 1 Kartenspiele, 2 Brettspiele, 2 Bälle, 3 Puppe und 1 Spielschwert. In einer Schule gibt es 2 Lehrer für Mathematik, 1 für Englisch, 2 für Deutsch, 2 für Geographie und 1 für Musik. Ein Bauernhof hat 18 Hühner, 1 Hahn, 3 Gänsen, 3 Kanarinen, 2 Katzen und 9 Enten. In einem Tierheim gibt es 2 schwarze Katzen, 4 roten, 1 weißen, 8 dreifarbige und 1 schwarz-rot. In einer Klasse sind 2 Personen aus Österreich, 2 aus Deutschland, 8 aus der Türkei, 2 aus Serbien und 2 aus Tschechien. In einer Klasse wählen 3 Personen die Partei "Bild", 3 Personen die Partei "Welt", 3 die Partei "Nature", 6 die Partei "Grob" und 3 keine Partei. Ein Haus hat 6 Schlafzimmer, 1 WCs, 1 Küche, 1 Wohnraum und 3 Badezimmer.

W X Y Z

X R L O

Zu welchen der folgenden Aussagen passen die folgenden Diagrammen? Ein Stall hat 2 Ziegen, 3 Schafe, 8 Kühe, 2 Schweine und 1 Pferd. Ein Kind hat 1 Kartenspiele, 2 Brettspiele, 1 Bälle, 3 Puppe und 2 Spielschwert. In einer Schule gibt es 3 Lehrer für Mathematik, 6 für Englisch, 3 für Deutsch, 3 für Geographie und 3 für Musik. Ein Bauernhof hat 18 Hühner, 1 Hahn, 3 Gänsen, 3 Kanarinen, 2 Katzen und 9 Enten. In einem Tierheim gibt es 8 schwarze Katzen, 4 roten, 2 weißen, 1 dreifarbige und 1 schwarz-rot. In einer Klasse sind 8 Personen aus Österreich, 2 aus Deutschland, 2 aus der Türkei, 2 aus Serbien und 2 aus Tschechien. In einer Klasse wählen 6 Personen die Partei "Bild", 6 Personen die Partei "Welt", 2 die Partei "Nature", 2 die Partei "Grob" und 2 keine Partei. Ein Haus hat 6 Schlafzimmer, 3 WCs, 1 Küche, 1 Wohnraum und 1 Badezimmer.

P Q R S

Q M L V

V2.5 Vergleichen von Mittelwerten

1. Die Familien eines kleinen Dorfes haben Kirschen geerntet. Die Ernte für die verschiedenen Familien war: 54kg, 65kg, 48kg, 76kg, 52kg, 65kg, 45kg. Sie haben allerdings vereinbart, dass jede Familie doch gleich so viele Kirschen bekommt.
   1. Wie viel bekommt jede Familie? Wie viel ist der Median und der Modus in diesem Fall?
   2. Vergleichen Sie Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
2. Das Gewicht der Schüler in einer Klasse ist: 52kg, 65kg, 48kg,
   76kg, 52kg, 65kg, 45kg, 65kg, 45 kg, 45kg, 78kg, 69kg.
   
   1. Berechnen Sie die Mittelwerte!
   2. Vergleichen Sie Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
3. Gegeben sind folgende Zahlen:
   4, 7, -2, 2, 2, −309, 4, 0, 2, 7, 9, 10, 19, 11, 419, 7, -2, 12.
   1. Berechnen Sie die Mittelwerte.
   2. Vergleichen Sie Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
4. Gegeben sind die folgenden zwei Wertegruppen, die Daten aus einer Studie der EU über die Vermögensverteilung um das Jahr 2010 ähneln:
   • Das Modell DE, das die Verteilung des Vermögens in Deutschland ähnelt:

   16

   10

   10

   1

   1

   300

   10

   1

   1

   10

   • Das Modell GR, das die Verteilung des Vermögens in Griechenland ähnelt:

   11

   9

   1

   1

   1

   100

   1

   14

   11

   11

   1. Berechnen Sie jeweils die Mittelwerte.
   2. Vergleichen Sie Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
5. Gegeben sind die folgenden zwei Wertegruppen:

   1

   0

   1

   3

   0

   1

   101

   0

   3

   3

   0

   1

   3

   0

   0

   0

   3

   0

   0

   0

   und

   3

   0

   1

   101

   0

   1. Berechnen Sie jeweils die Mittelwerte.
   2. Vergleichen Sie Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
6. Gegeben sind die folgenden Zahlen:
   5, 8, 2, −6, 2, 0, 5, 7
   1. Berechnen Sie jeweils die Mittelwerte.
   2. Vergleichen Sie Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
7. Gegeben sind die folgenden zwei Wertegruppen, die Daten aus einer Studie der EU über die Vermögensverteilung um das Jahr 2010 ähneln:

   Das Modell AT, das die Verteilung des Vermögens in Österreich ähnelt:

   10

   8

   10

   2

   2

   300

   10

   2

   2

   10

   Das Modell PO, das die Verteilung des Vermögens in Portugal ähnelt:

   100

   11

   1

   11

   1

   11

   11

   12

   1

   1

   1. Berechnen Sie jeweils die Mittelwerte.
   2. Vergleichen Sie Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
8. Gegeben sind die folgenden zwei Wertegruppen:
   

   0

   0

   0

   0

   0

   0

   202

   0

   0

   0

   6

   2

   6

   2

   6

   2

   6

   2

   6

   0

   und

   2

   0

   0

   202

   6

   1. Berechnen Sie jeweils die Mittelwerte.
   2. Vergleichen Sie Durchschnitt mit Median. Was können Sie über die Verteilung sagen?

V2.6 Wachstum und Abnahme

1. 1. China hatte im Jahr 1966 eine Bevölkerungsgröße von circa 750 Millionen Menschen. Das jährliche Wachstum lag bei circa 2,5%. Wie groß wäre die Bevölkerung im Jahr 2466, wenn das Wachstum gleich bliebe?
   2. Das Iod-Isotop ¹³¹I (wird in nuklear-medizinischen Therapie benutzt) wird täglich um 8,3% weniger. Wie viele Atome des Isotops bleiben nach 3 Wochen, wenn wir am Anfang 250000 Atome haben?
2. 1. Im Jahr 2018 war die Bevölkerung Deutschlands 83 Millionen. Ohne Einwanderung schrumpft sie um 0,5% pro Jahr. Wie groß wäre sie im Jahr 2600 ohne Einwanderung?
   2. Ein altes Problem lautet: Wenn ich einen Weizenkorn auf das erste Feld eines Schachbretts lege, auf das zweite Feld das Doppelte, also zwei, auf das dritte wiederum die doppelte Menge, also vier und so weiter, wie viele Körner wird es am letzten Feld geben?
3. 1. Die Stromstärke in einem Stromkreis ist 3,2 A und fällt um 77,4% pro Minute. Wie viel wird sei nach 674 ms sein?
   2. Eine Bakterienkultur mit einem Bakterium wächst um 2,1% pro Minute. Wie viele Bakterien wird es nach 3,47 Stunden geben?
4. 1. In Nigeria, ein Land in dem großen Armut, Hunger und Krieg herrschen, war die Bevölkerung im Jahr 2018 circa 200 Millionen Menschen. Das jährliche Wachstum lag trotzdem bei circa 2,44%. Wie groß wird die Bevölkerung im Jahr 2040 bzw. 2400 sein, wenn das Wachstum gleich bleibt (genauer gesagt: bleiben könnte)?
   2. Das Caesium-Isotop ¹³⁷Cs (radioaktiver Abfall) wird jährlich um 2,267% weniger. Wie viele Atome des Isotops bleiben nach 23 Monaten, wenn wir am Anfang 50000 Atome haben?
5. 1. Von 307640 Bakterien sterben pro Stunde 13% aus. Wie viele bleiben nach 414 min?
   2. Eine Bakterienkultur mit einem Bakterium wächst um 243% pro Stunde. Wie viele Bakterien wird es nach 282 Minuten geben?
6. 1. Die Temperatur des heißen Kaffees in einer Tasse ist 98°C und nimmt um 4% pro Minute ab. Wie heiß ist der Kaffee nach 0,43 Stunden?
   2. In einer Bevölkerung werden pro Woche 107% mehr Menschen von einem Virus infiziert. Am Anfang sind 31 Menschen infiziert. Wie viele werden nach 22,4 Tagen infiziert sein?
7. 1. Die Geburtsrate in einem Staat ist ziemlich niedriger als 2 Kinder pro Frau, die Bevölkerung ist 30,8 Millionen und nimmt um 0,8% pro Jahr ab. Wie viel ist sie nach 4,37 Jahrzehnten?
   2. Eine Bakterienkultur mit 13 Bakterien wächst um 0,08% pro Sekunde. Wie viele Bakterien wird es nach 2,56 Stunden geben?
8. 1. In Österreich leben im Jahr 2020 ca. 8,9 Millionen Menschen. Das jährliche Bevölkerungswachstum liegt bei ca. 0,5%. Wie groß wird die Bevölkerung im Jahr 2040 bzw. 2400 sein, wenn das Wachstum gleich bleibt?
   2. In Österreich leben im Jahr 2020 ca. 8,9 Millionen Menschen. Das jährliche Bevölkerungswachstum liegt bei ca. 0,5%. Wie groß wird die Bevölkerung im Jahr 2040 bzw. 2400 sein, wenn das Wachstum gleich bleibt?

V2.7 Satz von Pythagoras

Typ 1

Die zwei Katheten eines rechtwinkeligen Dreiecks sind 1dm bzw. 105mm. Wie lang ist die Hypotenuse? In der Figur seien a=135m und b=12709cm. Wie viel ist dann c?

Die eine Kathete und die Hypotenuse eines rechtwinkeligen Dreiecks sind 15dm bzw. 11,3m. Wie lang ist die andere Kathete? In der Figur seien a=12cm und c=169mm. Wie viel ist dann b?

Typ 2

1. Die Diagonale eines Rechtecks ist 145 mm, seine Breite 1dm. Wie viel ist seine Fläche?
2. Ein quadratisches Fenster wird an eine Wand angelehnt. Der Abstand seiner unteren Seite von der Wand ist 9cm, seiner oberen Seite vom Boden 4dm. Wie lang ist die Diagonale des Fensters (genau und mit zwei Nachkommastellen)?
3. Die Diagonale eines Quadrats ist 45mm. Wie viel ist sein Umfang (genau und mit zwei Nachkommastellen)?
4. Ein Schiff wird mit dem Dock über eine 229cm lange Rampe verbunden, der Hohenunterschied der beiden Enden der Rampe ist 6dm. Wie viel ist die horizontale Entfernung der beiden Enden der Rampe?
5. Die Diagonale eines Quadrats ist 45mm. Wie viel ist sein Umfang (genau und mit zwei Nachkommastellen)?
6. Ein quadratisches Fenster wird an eine Wand angelehnt. Der Abstand seiner unteren Seite von der Wand ist 9cm, seiner oberen Seite vom Boden 4dm. Wie lang ist die Diagonale des Fensters (genau und mit zwei Nachkommastellen)?
7. Die Diagonale eines Rechtecks ist 145 mm, seine Breite 1dm. Wie viel ist seine Fläche?
8. Ein Schiff wird mit dem Dock über eine 229cm lange Rampe verbunden, der Hohenunterschied der beiden Enden der Rampe ist 6dm. Wie viel ist die horizontale Entfernung der beiden Enden der Rampe?

V2.8 Umsatzsteuer und Rabatt

Umsatzsteuer (USt.)

1. Der Nettoverkaufspreis einer Ware ist 50 €, die USt. 12%. Berechnen Sie den Bruttoverkaufspreis und die USt..
2. Der Bruttoverkaufspreis einer Ware ist 69€. Berechnen Sie den Nettoverkaufspreis, wenn die USt. 15% ist.
3. Der Netto- bzw. Bruttoverkaufspreis einer Ware ist 40 bzw. 45 €. Wie viel Prozent ist die USt.?
4. Der Bruttoverkaufspreis einer Ware ist 93€. Berechnen Sie den Nettoverkaufspreis, wenn die USt. 24% ist.

Rabatt

1. Der Verkaufspreis einer Ware nach 15% Rabatt ist 56,1€. Berechnen Sie den Bruttoverkaufspreis.
2. Der Bruttoverkaufspreis einer Ware ist 650 €. Wie viel ist der Preis nach 12% Rabatt?
3. Der Verkaufspreis einer Ware nach einem Rabatt ist 748 €. Der Bruttoverkaufspreis war 850 €. Wie viel Prozent ist der Rabatt?
4. Der Verkaufspreis einer Ware nach einem Rabatt ist 836,6 €. Der Bruttoverkaufspreis war 890 €. Wie viel Prozent ist der Rabatt?

USt. und Rabatt Gegebener Endwert

1. Der Verkaufspreis einer Ware nach 15% Rabatt ist 56,1€. Berechnen Sie den Nettoverkaufspreis , wenn die USt. 10% ist. Wie viel € ist der Rabatt bzw. die USt.?
2. Der Bruttoverkaufspreis einer Ware ist 96,9 €. Der Preis nach einem Rabatt ist 77,52 €. Wie viel ist der Nettoverkaufspreis, wenn die USt. 14% ist? Wie viel Prozent ist der Rabatt?
3. Der Verkaufspreis einer Ware nach 25% Rabatt ist 395,85 €. Berechnen Sie den Netto- und Bruttoverkaufspreis , wenn die USt. 16% ist. Wie viel € ist der Rabatt bzw. die USt.?
4. Der Verkaufspreis einer Ware nach 20% Rabatt ist 88 €. Berechnen Sie den Netto- und Bruttoverkaufspreis , wenn die USt. 25% ist. Wie viel € ist der Rabatt bzw. die USt.?

USt. und Rabatt Kombinationsaufgaben

$\$Berechnen Sie die fehlenden Werte in der Tabelle:$\$ $\$Bsp. 1$\$ $\$Bsp. 2$\$ Nettoverkaufspreis € $\$$\qquad$$\$ $\$$\qquad$$\$ Umsatzsteuer % 60% Umsatzsteuer € 195€ Bruttoverkaufspreis € 88€ Rabatt % 37,5% Rabatt € 195€ Preis nach dem Rabatt € 780€ $\$Berechnen Sie die fehlenden Werte in der Tabelle:$\$ $\$Bsp. 1$\$ $\$Bsp. 2$\$ Nettoverkaufspreis € $\$336000€$\$ $\$$\qquad$$\$ Umsatzsteuer % 20% Umsatzsteuer € Bruttoverkaufspreis € 369600€ Rabatt % 3% 5% Rabatt € Preis nach dem Rabatt € 478,8€ $\$Berechnen Sie die fehlenden Werte in der Tabelle:$\$ $\$Bsp. 1$\$ $\$Bsp. 2$\$ Nettoverkaufspreis € $\$$\qquad$$\$ $\$$\qquad$$\$ Umsatzsteuer % 50% Umsatzsteuer € 129€ Bruttoverkaufspreis € Rabatt % 10% Rabatt € 195€ Preis nach dem Rabatt € 939,55€ 780€ $\$Berechnen Sie die fehlenden Werte in der Tabelle:$\$ $\$Bsp. 1$\$ $\$Bsp. 2$\$ Nettoverkaufspreis € $\$$\qquad$$\$ $\$$\qquad$$\$ Umsatzsteuer % 14% Umsatzsteuer € 8,4€ Bruttoverkaufspreis € 3990€ Rabatt % 10% Rabatt € 9,24€ Preis nach dem Rabatt € 83,16€

$\$Berechnen Sie die fehlenden Werte in der Tabelle:$\$ $\$Bsp. 1$\$ $\$Bsp. 2$\$ Nettoverkaufspreis € $\$$\qquad$$\$ $\$$\qquad$$\$ Umsatzsteuer % 14% Umsatzsteuer € 33€ Bruttoverkaufspreis € Rabatt % 37,5% Rabatt € 399€ Preis nach dem Rabatt € 55€ 3591€ $\$Berechnen Sie die fehlenden Werte in der Tabelle:$\$ $\$Bsp. 1$\$ $\$Bsp. 2$\$ Nettoverkaufspreis € $\$420%€$\$ $\$$\qquad$$\$ Umsatzsteuer % 60% Umsatzsteuer € Bruttoverkaufspreis € 504€ Rabatt % 5% 37,5% Rabatt € Preis nach dem Rabatt € 55€ $\$Berechnen Sie die fehlenden Werte in der Tabelle:$\$ $\$Bsp. 1$\$ $\$Bsp. 2$\$ Nettoverkaufspreis € $\$$\qquad$$\$ $\$$\qquad$$\$ Umsatzsteuer % 14% Umsatzsteuer € 6€ Bruttoverkaufspreis € Rabatt % 15% Rabatt € 19,38€ Preis nach dem Rabatt € 56,1€ 77,52€ $\$Berechnen Sie die fehlenden Werte in der Tabelle:$\$ $\$Bsp. 1$\$ $\$Bsp. 2$\$ Nettoverkaufspreis € $\$$\qquad$$\$ $\$$\qquad$$\$ Umsatzsteuer % 16% Umsatzsteuer € 4,2€ Bruttoverkaufspreis € 527,8€ Rabatt % 25% Rabatt € 2,21€ Preis nach dem Rabatt € 41,99€

V2.9 Eine lineare Funktion mit Hilfe von zwei Punkten ermitteln

Benutzen Sie die Diagramme aus der Aufgabe Lineare Funktion Diagramm (Vertiefendes Niveau 2). Berechnen Sie mit Hilfe jedes Diagramms die entsprechende lineare Funktion! Welche sind die Einheiten von y, x und der Steigung?

V2.10 Geometrie Beweise

Mit Hilfe der Figur beweisen Sie den Satz von Pythagoras. Mit Hilfe der Figur und von Formeln der Geometrie zeigen Sie, dass $(a+b)^{2}=a^{2}+2\ a\ b+b^{2}$ Zeigen Sie, dass bei einem Rechteck mit Länge 2 cm und Breite 3 cm die Fläche 6 cm² sein wird! Zeigen Sie geometrisch, dass ${\frac {2}{5}}+{\frac {3}{7}}={\frac {29}{35}}\$ ist!

Mit Hilfe der Figur und von Formeln der Geometrie zeigen Sie, dass $(a-b)^{2}=a^{2}-2\ a\ b+b^{2}$ Mit Hilfe der Figur beweisen Sie den Satz von Pythagoras. Zeigen Sie mit Hilfe der Formel der Fläche eines Rechtecks, dass bei einem Parallelogramm mit Seiten a und b (wobei b die Basis ist) und Höhe h, die Fläche A=b⋅h sein wird! Zeigen Sie geometrisch, dass ${\frac {3}{5}}-{\frac {3}{7}}={\frac {6}{35}}\$ ist!

V2.11 Zinsrechnung

Im Jahr 2013 war das Guthaben in einem Konto 6368,53€, der Zinssatz 0,6%. Wie viel war das Guthaben, die Zinsen, die effektiven Zinsen und die KESt. im Jahr 2014? Wie viel war das Guthaben im Jahr 2012? Wie viel wäre das Guthaben im Jahr 2058? Im Jahr 1993 war das Guthaben in einem Konto 7459,48€, der effektiver Zinssatz 2,7%. Wie viel war das Guthaben, die Zinsen, die effektiven Zinsen und die KESt. im Jahr 1994? Wie viel war das Guthaben im Jahr 1992? Wie viel war das Guthaben im Jahr 2008? Im Jahr 1999 war das Guthaben in einem Konto 6368,53€, der Zinssatz 1,8%. Wie viel war das Guthaben, die Zinsen, die effektiven Zinsen und die KESt. im Jahr 2000? Wie viel war das Guthaben im Jahr 1998? Wie viel war das Guthaben im Jahr 2157? Im Jahr 2001 war das Guthaben in einem Konto 80000€, der effektiver Zinssatz 1,05%. Wie viel war das Guthaben, die Zinsen, die effektiven Zinsen und die KESt. im Jahr 2002? Wie viel war das Guthaben im Jahr 2000? Wie viel war das Guthaben im Jahr 2107?

Im Jahr 2013 war das Guthaben in einem Konto 6368,53€, der effektiver Zinssatz 0,45%. Wie viel war das Guthaben, die Zinsen, die effektiven Zinsen und die KESt. im Jahr 2014? Wie viel war das Guthaben im Jahr 2012? Wie viel wäre das Guthaben im Jahr 2058? Im Jahr 1993 war das Guthaben in einem Konto 7459,48 €, der Zinssatz 3,6%. Wie viel war das Guthaben, die Zinsen, die effektiven Zinsen und die KESt. im Jahr 1994? Wie viel war das Guthaben im Jahr 1992? Wie viel war das Guthaben im Jahr 2008? Im Jahr 1999 war das Guthaben in einem Konto 6368,53€, der effektiver Zinssatz 1,35%. Wie viel war das Guthaben, die Zinsen, die effektiven Zinsen und die KESt. im Jahr 2000? Wie viel war das Guthaben im Jahr 1998? Wie viel war das Guthaben im Jahr 2157? Im Jahr 2001 war das Guthaben in einem Konto 80000€, der Zinssatz 1,4%. Wie viel war das Guthaben, die Zinsen, die effektiven Zinsen und die KESt. im Jahr 2002? Wie viel war das Guthaben im Jahr 2000? Wie viel war das Guthaben im Jahr 2107?

V2.12 Potenzen Erklärung

Warum ist$\ a^{0}=1$? Warum ist$\textstyle \ {\frac {z^{7}}{z^{4}}}=z^{3}$?

Warum ist$\textstyle \ {w^{7}}\cdot {w^{4}}=z^{11}$? Warum ist$\textstyle \ s^{-1}={\frac {1}{s}}$?

V2.13 Säulendiagramm erstellen

1. Die ans Rauchen zuzuschreibenden gemeldeten Todesfälle in den Dörfern einer Region in einer Woche waren:
   7, 6, 3, 4, 3, 8, 7, 7, 8, 6, 7, 6, 3, 8, 8, 7, 6, 6.
   1. Zeichnen Sie ein Säulendiagramm, aus dem man ablesen kann, wie viele Dörfer welche Anzahl von Todesfälle hat
   2. Geben Sie den Durchschnitt, den Modalwert, den Median und die Spannweite der Todesfälle an!
2. Im folgenden wird die Anzahl der Betten in den verschiedenen Räumen einer Jugendherberge angegeben:
   8, 4, 0, 2, 4, 4, 2, 4, 2, 2, 4, 2, 1, 8, 8, 1.
   1. Zeichnen Sie ein Säulendiagramm, aus dem man ablesen kann, welche Anzahl von Räumen die jeweilige Anzahl an Betten hat.
   2. Geben Sie den Durchschnitt, den Modalwert, den Median und die Spannweite des angegebenen Zusammenhangs an.
3. Im folgenden wird die Anzahl der Personen an den verschiedenen Tischen in einem Restaurant angegeben:
   1, 3, 0, 1, 2, 9, 0, 3, 3, 1, 1, 1, 0, 3, 0.
   1. Zeichnen Sie ein Säulendiagramm, aus dem man ablesen kann, welche Anzahl von Tischen die jeweilige Anzahl an Personen hat.
   2. Geben Sie den Durchschnitt, den Modalwert, den Median und die Spannweite des angegebenen Zusammenhangs an.
4. In einer Umfrage wurden Personen gefragt, mit wie vielen PartnerInnen sie im letzten Jahr geschlafen hatten. Im folgenden sehen wir die Antworten:
   1, 3, 0, 1, 3, 14, 0, 3, 3, 1, 1, 1, 0, 3, 2.
   1. Zeichnen Sie ein Säulendiagramm, aus dem man ablesen kann, welche Anzahl von Personen mit der jeweiligen Anzahl an PartnerInnen geschlafen hat.
   2. Geben Sie den Durchschnitt, den Modalwert, den Median und die Spannweite des angegebenen Zusammenhangs an.
5. Im Folgenden wird angegeben, wie viele Tonnen Bananen die ("arbeitenden") Kinder in einer Plantage in Südamerika an einem Tag geliefert haben: 7, 5, 4, 7, 4, 4, 8, 6, 6, 8, 7, 7, 4, 4, 5, 6.
   1. Zeichnen Sie ein Säulendiagramm, aus dem man ablesen kann, welche Anzahl von Kindern das jeweilige Gewicht an Tonnen geliefert hat.
   2. Geben Sie den Durchschnitt, den Modalwert, den Median und die Spannweite des angegebenen Zusammenhangs an.
6. Die Blumentöpfe an einem Balkon haben folgende Anzahl von Blumen:
   7, 5, 0, 3, 0, 8, 7, 7, 8, 7, 5, 3, 0, 8, 8, 7.
   1. Zeichnen Sie ein Säulendiagramm, aus dem man ablesen kann, wie viele Töpfe welche Anzahl von Blumen hat.
   2. Geben Sie den Durchschnitt, den Modalwert, den Median und die Spannweite der Blumenanzahl an.
7. Im folgenden wird die Anzahl der Kinder der Mütter eines Dorfes angegeben:
   2, 3, 1, 1, 2, 7, 2, 3, 3, 1, 1, 1, 2, 3, 2, 6, 2, 1, 3.
   1. Zeichnen Sie ein Säulendiagramm, aus dem man ablesen kann, welche Anzahl von Müttern die jeweilige Anzahl an Kinder hat.
   2. Geben Sie den Durchschnitt, den Modalwert, den Median und die Spannweite des angegebenen Zusammenhangs an.
8. Im folgenden wird die Anzahl der Bücher, die verschiedener Kinder in einer Klasse im letzten Jahr gelesen haben:
   1, 3, 0, 1, 3, 14, 0, 3, 3, 1, 1, 1, 0, 3, 2.
   1. Zeichnen Sie ein Säulendiagramm, aus dem man ablesen kann, welche Anzahl von Kindern die jeweilige Anzahl an Bücher gelesen hat.
   2. Geben Sie den Durchschnitt, den Modalwert, den Median und die Spannweite des angegebenen Zusammenhangs an.

Expertenniveau 1

X1.1 Herausheben

Faktorisieren Sie, so weit es mit natürlichen Zahlen geht:
$45\ b^{4}y^{2}n^{7}-30\ y^{5}n^{9}-75\ b^{8}y^{8}n^{8}+105\ b\ y\ n^{7}$	$35\ x^{4}c^{2}m^{4}-14\ x^{9}c^{4}m^{3}-7\ x^{4}c\ m^{3}+63\ b\ x^{7}c^{9}m^{13}$
$3\ x^{4}c^{2}m^{4}-33\ x^{9}c^{4}m^{7}-27\ x^{4}c^{2}m^{5}+63\ b\ x^{7}c^{9}m^{13}$	$18\ b^{4}\ y^{3}\ n^{4}-12\ y^{7}n^{6}-30\ b^{8}y^{1}0n^{5}+6\ y^{3}\ n^{4}$
$45\ x\ c^{5}m^{3}-18\ x^{6}c^{6}m^{2}-9\ x\ c^{4}\ m^{2}+81\ b\ x^{4}c^{12}m^{12}$	$20\ x^{4}c^{4}m^{2}-8\ x^{9}c^{5}m-4\ x^{4}\ c^{3}\ m+36\ b\ x^{7}c^{11}m^{11}$
$33\ y^{3}n\ b^{4}-22\ y^{7}n^{3}-55\ b^{8}y^{10}n^{2}+11\ y^{3}\ n$	$15\ y^{3}b^{8}-10\ y^{7}n^{2}b^{4}-25\ b^{12}y^{10}n+5\ y^{3}\ b^{4}$

X1.2 Zusammengesetzte Figuren

Formel

Drücken Sie den dunklen Flächeninhalt durch die Länge a der Seite des (großen) dunklen Quadrats aus!
Drücken Sie den dunklen Flächeninhalt durch die Länge a der Seite des gleichseitigen Dreiecks aus! Drücken Sie den dunklen Flächeninhalt durch die Länge r des Radius des kleinen (dunklen) Kreises aus! Drücken Sie den dunklen Flächeninhalt durch die Seite a des kleinen (weißen) Quadrats aus!
Drücken Sie den grünen Flächeninhalt durch die Längen a, b, c, und r aus! Drücken Sie den schwarzen Flächeninhalt durch die Längen a, b, c, und r aus! Drücken Sie den dunklen Flächeninhalt durch die Länge a der Seite des (großen) dunklen Quadrats aus!

Einheiten

Berechnen Sie die dunklen Flächen in der folgenden Figur! Ein kleines Quadrat gilt als eine Einheit. In der folgenden Figur ist die Seite a des kleinen (weißen) Quadrats 2,5 Einheiten. Berechnen Sie die dunklen Flächen! Berechnen Sie die dunklen Flächen in der folgenden Figur! Ein kleines Quadrat gilt als eine Einheit. In der folgenden Figur ist die Länge des Rechtecks 7,5 Einheiten. Berechnen Sie die dunklen Flächen!

Berechnen Sie die dunklen Flächen in der folgenden Figur! Ein kleines Quadrat gilt als eine Einheit. Berechnen Sie die dunklen Flächen in der folgenden Figur! Ein kleines Quadrat gilt als eine Einheit. In der folgenden Figur ist der Radius des großen (weißen) Kreises 6 Einheiten. Berechnen Sie die dunklen Flächen! Berechnen Sie die dunklen Flächen in der folgenden Figur! Ein kleines Quadrat gilt als eine Einheit.

X1.3 Doppelbrüche

$\quad$ ${\dfrac {\ {\frac {2}{3}}-{\frac {3}{4}}\ }{{\frac {3}{5}}-{\frac {3}{4}}}}$ $\quad$	$\quad$ ${\dfrac {\ {3}-2{\frac {3}{4}}\ }{{5}-4{\frac {5}{6}}}}$ $\quad$	$\quad$ ${\dfrac {\ {\frac {2}{3}}-{1}\ }{{\frac {5}{3}}+1}}$ $\quad$	$\quad$ ${\dfrac {\ {\frac {4}{3}}-{1}\ }{{\frac {5}{4}}-1}}$ $\quad$
$\quad$ ${\dfrac {\ 2{\frac {2}{3}}-3\ }{5{\frac {3}{5}}-6}}$ $\quad$	$\quad$ ${\dfrac {\ {2}-3{\frac {3}{4}}\ }{{5}-3{\frac {5}{6}}}}$ $\quad$	$\quad$ ${\dfrac {{\frac {5}{3}}+1}{\ {\frac {2}{3}}-{2}\ }}$ $\quad$	$\quad$ ${\dfrac {2{\frac {1}{4}}-1}{\ 1{\frac {1}{3}}-{3}\ }}$ $\quad$

X1.4 Mittelwerte Argumentationsaufgaben

1. Die Familien eines kleinen Dorfes haben Kirschen geerntet. Die Ernte für die verschiedenen Familien war: 54kg, 65kg, 48kg, 76kg, 52kg, 65kg, 45kg. Sie haben allerdings vereinbart, dass jede Familie doch gleich so viele Kirschen bekommt.
   1. Wie viel bekommt jede Familie? Wie viel ist der Median und der Modus in diesem Fall?
   2. Vergleichen Sie Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
   3. • Wird die Verteilung durch diese Maßnahme gleichmäßiger? Wird sie dadurch gerechter?
      • Es wird oft erwähnt, dass China im Jahr 2018 den größten CO₂ Ausstoß hat. Was hat unseres Beispiel mit diesem Vergleich von China mit anderen Staaten zu tun? Was sollte man eigentlich vergleichen?
2. Das Gewicht der Schüler in einer Klasse ist: 52kg, 65kg, 48kg,
   76kg, 52kg, 65kg, 45kg, 65kg, 45 kg, 45kg, 78kg, 69kg.
   
   1. Berechnen Sie die Mittelwerte!
   2. Vergleichen Sie Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
   3. Ist ein Schüler über- bzw untergewichtig?
3. Gegeben sind folgende Zahlen:
   4, 7, -2, 2, 2, −309, 4, 0, 2, 7, 9, 10, 19, 11, 419, 7, -2, 12.
   1. Berechnen Sie die Mittelwerte.
   2. Vergleichen Sie Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
   3. Welchen Einfluss haben negative Werte auf den Vergleich der Mittelwerte?
4. Gegeben sind die folgenden zwei Wertegruppen, die Daten aus einer Studie der EU über die Vermögensverteilung um das Jahr 2010 ähneln:
   • Das Modell DE, das die Verteilung des Vermögens in Deutschland ähnelt:

   16

   10

   10

   1

   1

   300

   10

   1

   1

   10

   • Das Modell GR, das die Verteilung des Vermögens in Griechenland ähnelt:

   11

   9

   1

   1

   1

   100

   1

   14

   11

   11

   1. Berechnen Sie jeweils die Mittelwerte.
   2. Vergleichen Sie jeweils Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
   3. • Sind die Verteilungen gleich- oder ungleichmäßig? Was ist ihrer Unterschied?
      • Es wurde damals oft in Zeitungen geschrieben, dass der "deutsche Steuerzahler" den Griechen "Geld gibt", obwohl Griechen "reicher sind". Welcher Lagerparameter wird in dieser Aussage verglichen? Ist dieser Vergleich wirklich aussagekräftig? Wo ist das Geld wirklich gelangen also wem hat tatsächlich der "Steuerzahler" das Geld gegeben? (Dazu kann man insbesondere dieses Unterkapitel in Wikipedia lesen)
5. Gegeben sind die folgenden zwei Wertegruppen:

   1

   0

   1

   3

   0

   1

   101

   0

   3

   3

   0

   1

   3

   0

   0

   0

   3

   0

   0

   0

   und

   3

   0

   1

   101

   0

   1. Berechnen Sie jeweils die Mittelwerte.
   2. Vergleichen Sie jeweils Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
   3. Welcher Unterschied zwischen den beiden Verteilungen ist entscheidend?
6. Gegeben sind die folgenden Zahlen:
   5, 8, 2, −6, 2, 0, 5, 7
   1. Berechnen Sie jeweils die Mittelwerte.
   2. Vergleichen Sie Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
   3. Welchen Einfluss haben negative Werte auf den Vergleich der Mittelwerte?
7. Gegeben sind die folgenden zwei Wertegruppen, die Daten aus einer Studie der EU über die Vermögensverteilung um das Jahr 2010 ähneln:

   Das Modell AT, das die Verteilung des Vermögens in Österreich ähnelt:

   10

   8

   10

   2

   2

   300

   10

   2

   2

   10

   Das Modell PO, das die Verteilung des Vermögens in Portugal ähnelt:

   100

   11

   1

   11

   1

   11

   11

   12

   1

   1

   1. Berechnen Sie jeweils die Mittelwerte.
   2. Vergleichen Sie jeweils Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
   3. • Sind die Verteilungen gleich- oder ungleichmäßig? Was ist ihrer Unterschied?
      • Es wurde oft in Zeitungen geschrieben, dass der "österreichische Steuerzahler" den Portugiesen "Geld gibt", obwohl Portugiesen "reicher sind". Welcher Lagerparameter wird in dieser Aussage verglichen? Ist dieser Vergleich wirklich aussagekräftig? Wo ist das Geld wirklich gelangen also wem hat tatsächlich der "Steuerzahler" das Geld gegeben? (Dazu kann man insbesondere dieses Unterkapitel in Wikipedia lesen)
8. Gegeben sind die folgenden zwei Wertegruppen:
   

   0

   0

   0

   0

   0

   0

   202

   0

   0

   0

   6

   2

   6

   2

   6

   2

   6

   2

   6

   0

   und

   2

   0

   0

   202

   6

   1. Berechnen Sie jeweils die Mittelwerte.
   2. Vergleichen Sie jeweils Durchschnitt mit Median. Was können Sie über die Verteilung sagen?
   3. Welcher Unterschied zwischen den beiden Verteilungen ist entscheidend?

X1.5 Textaufgaben zu den linearen Funktionen

1. Der 69 Liter Tank eines Generators ist zu zwei drittel voll und verbraucht jede 10 Minuten halbes Liter Brennstoff.
   1. Geben Sie zuerst den Zusammenhang zwischen Zeit und Volumen des Brennstoffes als lineare Funktion an!
   2. Wie lang dauert es, bis der Tank leer wird?
   3. Nach wie viel Zeit hat der Tank noch 25 Liter?
2. Eine Rakete wird aus einem Flugzeug, dass sich auf 500m befindet, abgeschossen und fliegt jede 4 Minuten 14 km höher.
   
   1. Geben Sie zuerst den Zusammenhang zwischen Höhe und Zeit als lineare Funktion an!
   2. Wie hoch befindet sie sich nach 25s?
   3. Wie lang braucht sie (in s und in min),
      bis sie eine Höhe von 4km erreicht?
3. Eine Kerze ist 1,8 dm hoch und brennt um 1,4 cm pro Stunde.
   
   1. Geben Sie zuerst den Zusammenhang zwischen Zeit und Höhe als lineare Funktion an!
   2. Nach wie vielen Minuten brennt sie aus?
   3. Wie viel ist ihr Höhe nach 99s?
4. Ein Auto fährt von Paris nach der 311 km entfernten Stadt Brüssels mit 72 km/h durchschnittlicher Geschwindigkeit.
   
   1. Geben Sie zuerst den Zusammenhang zwischen Zeit und Abstand von Brüssels als lineare Funktion an!
   2. Wie lang dauert die Fahrt?
   3. Wie weit von Brüssels und wie weit von Paris entfernt
      befindet sich das Auto nach 24 min?
   4. Wie viel kg ist der CO₂ Ausstoß nach 24 min,
      wenn 7 kg nach 40 km ausgestoßen werden?
5. Ein Hotelschwimmbad mit 74 m³ Wasser wird mit Hilfe von zwei Pumpen ausgeleert. Die eine Pumpe leert 17 Liter pro Minute, die andere 13 Liter pro Minute.
   1. Geben Sie zuerst den Zusammenhang zwischen Volumen des verbliebenen Wassers und Zeit als lineare Funktionen an!
   2. Wie lang dauert es, bis das Schwimmbad leer wird?
   3. Nach wie viel Zeit hat das Schwimmbad noch 14 m³ Wasser?
6. Ein Fallschirmspringer springt aus einem Flugzeug. Ab eine Höhe von 2,3 km fällt er mit einer konstanten Geschwindigkeit von 44 m/s weiter.
   1. Geben Sie zuerst den Zusammenhang zwischen Höhe und Zeit als lineare Funktion an, ab den Zeitpunkt, wo die Geschwindigkeit konstant wird!
   2. Wie hoch befindet sie sich nach 45s?
   3. Wie lang braucht sie (in s und in min), bis sie eine Höhe von 1,3 km erreicht?
   4. Nach wie viel Zeit wird sie den Boden erreichen, wenn der Fallschirm nicht aufgeht?
7. Ein Schwimmbecken wird mit Wasser gefüllt. In 4 min laufen 13 m³ hinein.
   
   1. Stellen Sie zuerst den Zusammenhang zwischen Zeit und Volumen des Wassers als lineare Funktion dar!
   2. Nach wie vielen Minuten ist das Volumen 66 m³?
   3. Wie viel ist das Volumen nach 14 min?
8. Ein Auto fährt von Wien nach der 287 km entfernten Stadt Salzburg. Durchschnittlich fährt das Auto 138 km in 2 Stunden.
   
   1. Stellen Sie zuerst den Zusammenhang zwischen Zeit und Abstand von Salzburg als lineare Funktion dar!
   2. Wie lang dauert die Fahrt?
   3. Wie weit von Wien und wie weit von Salzburg entfernt befindet sich das Auto nach 15 min?
   4. Wie viel kg ist der CO₂ Ausstoß nach 15 min, wenn 7 kg nach 33 km ausgestoßen werden?

X1.6 Binomische Formeln

Ausmultiplizieren

Multiplizieren Sie folgende binomische Formeln aus:
$\ \left(a^{3}-4\right)^{2}\qquad$ $\ \left(5\ x^{2}+4\ z^{2{,}5}\right)^{2}\quad$	$\ \left(7\ w^{3{,}5}+6\ w^{6{,}5}\right)^{2}\qquad$ $(5\ a^{3}+11\ a^{1{,}5})(5\ a^{3}-11\ a^{1{,}5})\quad$
$\ \left(2\ g^{4}-13\ g^{6{,}5}\right)^{2}\qquad$ $(4\ a^{4}+11\ a^{6})(11\ a^{6}-4\ a^{4})\quad$	$\ \left(12\ g^{2{,}5}+7\ g^{6{,}5}\right)^{2}\qquad$ $(4\ a^{4}-11\ a^{6})^{2}\quad$

Faktorisieren

Faktorisieren Sie folgende Terme:
$\ 169\ a^{8}-52\ a^{4}+4\qquad$ $\ 81\ x^{4}+180\ x^{2}\ z^{4{,}5}+100\ z^{9}\quad$	$\ 49\ w^{7}+70\ w^{10}+25\ w^{13}$ $9\ c^{4}-49\ b^{10}$
$\ 121\ v^{5}-66\ v^{12}+9\ v^{19}$ $4\ n^{4}-9\ n^{10}$	$\ 225\ v^{7}+360\ v^{12}+144\ v^{17}$ $4\ n^{4}-10\ n^{10}+6{,}25\ n^{16}$

Erkennen

Können folgende Ausdrücke als binomische Formeln faktorisiert werden? Wenn nicht, welches Element (wenn möglich nur eines) könnte geändert werden?
$\ 169\ a^{8}-52\ a^{4}+16$ $\ 81\ x^{4}+180\ x^{2}\ z^{4{,}5}+100\ z^{9}$	$\ 49\ w^{7}+70\ w^{11}+25\ w^{13}$ $\ 5\ a-2\ a^{7}$
$\ 36\ w^{7}+12\ w^{11}+4\ w^{15}$ $\ 5\ a^{4}-144\ a^{12}$	$\ 121\ r^{7}+330\ r^{12}+225\ r^{17}$ $\ 49\ c^{7}+14\ c^{11}+4\ c^{17}$

X1.7 Bruchterme kürzen

Kürzen Sie folgende Bruchterme:
${\frac {6x^{2}-5x+3x^{2}+2x}{18x^{3}-12x^{2}+2x}}$	${\frac {48b^{2}-60b+27b^{2}+12}{25c\ b^{3}-4c\ b}}$	${\frac {27x^{3}-18x^{2}+3x}{7x^{2}-4x+4x^{2}+1x}}$	${\frac {25c\ b^{3}+4c\ b-8c\ b}{c(148b^{2}-100b-23b^{2}+20)}}$
${\frac {3y^{2}c^{2}+7c^{2}\ y+2y^{2}c^{2}+11y^{3}c^{2}-56y\ c^{2}-2c^{2}\ y^{3}-5c^{2}\ y^{2}}{84c\ y+98c+18y^{2}c}}$ ${\frac {4y^{2}c^{3}-2c^{3}\ y+3y^{2}c^{3}+11y^{3}c^{3}-47y\ c^{3}-2c^{3}\ y^{3}-7c^{3}\ y^{2}}{126c\ y+147c+27y^{2}c}}$

X1.8 Ähnlichkeit von Figuren

Die Seiten eines Dreiecks sind: b=52 mm, c=0,8 dm und k=5,8 cm. Die entsprechende zu c Seite c' eines ähnlichen Dreiecks ist 4,9 cm. Wie lang sind die anderen Seiten k' und b'? In den Figuren werden zwei ähnliche Dreiecke dargestellt. Gegeben sind die Längen der folgenden Seiten: c=78 mm, b=4,4 cm, d=1,12 dm und f=9 cm. Wie lang sind die restlichen Seiten? Die Seiten eines Dreiecks sind: g=48 dm, d=3400 mm und k=5,8 m. Die entsprechende zu d Seite d' eines ähnlichen Dreiecks ist 490 cm. Wie lang sind die anderen Seiten k' und g'? In den Figuren werden zwei ähnliche Dreiecke dargestellt. Gegeben sind die Längen der folgenden Seiten: c=95 mm, b=7,4 cm, d=1,86 dm und f=14 cm. Wie lang sind die restlichen Seiten?

Die Seiten eines Dreiecks sind: b=0,044 m, c=0,11 dm und k=5,5 cm. Die entsprechende zu c Seite c' eines ähnlichen Dreiecks ist 2,75cm. Wie lang sind die anderen Seiten k' und b'? In den Figuren werden zwei ähnliche Dreiecke dargestellt. Gegeben sind die Längen der folgenden Seiten: c=80 mm, b=7 cm, d=1,05 dm und f=9 cm. Wie lang sind die restlichen Seiten? Die Seiten eines Dreiecks sind: g=48 dm, d=3400 mm, die dritte Seite wird durch k dargestellt. Die entsprechende zu d Seite d' eines ähnlichen Dreiecks ist 8,5 m, die entsprechende zu k Seite k' 375 cm. Wie lang sind die anderen Seiten k und g'? In den Figuren werden zwei ähnliche Dreiecke dargestellt. Gegeben sind die Längen der folgenden Seiten: c=96 mm, b=7,5 cm, d=0,5 dm und f=3 cm. Wie lang sind die restlichen Seiten?

X1.9 Direkte und indirekte Beweise

1. 1. Zeigen Sie den Zusammenhang zwischen Steigung einer linearen Funktion, Ähnlichkeit von ebenen Figuren und direkter Proportionalität!
   2. Zeigen Sie, dass die Steigung s einer linearen Funktion $\textstyle s={\frac {\Delta y}{\Delta x}}\$ist!
2. Mit Hilfe des Satzes von Pythagoras beweisen Sie die Formel für die Fläche eines gleichseitigen Dreiecks:
   $A={\frac {{\sqrt {3}}\ a^{2}}{4}}$
3. Beweisen Sie folgenden Zusammenhang für alle natürliche Zahlen n:
   $\sum _{k=1}^{n}k^{2}={\frac {n\cdot (n+1)\cdot (2n+1)}{6}}$
4. Zeigen Sie, dass die ${\sqrt {3}}$ eine irrationale Zahl ist! Hinweis: Anstatt gerade und ungerade Zahlen, benutzen Sie Fallunterscheidung mit 3n, 3n+1 und 3n+2!
5. 1. Zeigen Sie den Zusammenhang zwischen Steigung einer linearen Funktion, Ähnlichkeit von ebenen Figuren und direkter Proportionalität!
   2. Zeigen Sie, dass die Steigung s einer linearen Funktion $\textstyle s={\frac {\Delta y}{\Delta x}}\$ist!
6. Wenn wir eine Strecke so teilen, dass das Verhältnis der ganzen Strecke zum größten Teil so viel wie das Verhältnis des größten zum kleineren Teil ist, wird dieses Verhältnis  Goldener Schnitt genannt und mit $\Phi$ bezeichnet. Zeigen Sie, dass:
   $\Phi ={\frac {1+{\sqrt {5}}}{2}}$
   ist.
7. Beweisen Sie folgenden Zusammenhang für alle natürliche Zahlen n:
   $\sum _{k=1}^{n}(2k-1)^{2}={\frac {n\cdot (2n-1)\cdot (2n+1)}{3}}$
8. Mit Hilfe eines Beispiels zeigen Sie, dass minus mal minus plus sein soll!

X1.10 Zahlenmengen

Zur welchen Zahlenmengen gehören folgende Zahlen? $\quad$ $\mathbb {N}$ $\mathbb {Z}$ $\mathbb {Q}$ $\mathbb {I}$ $\mathbb {R}$ $\textstyle {\frac {5}{13}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle {\frac {26}{13}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle -{\frac {\sqrt {5}}{13}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {7}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $-{\sqrt {196}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {-4}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {169}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle -{\frac {26}{13}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ Zur welchen Zahlenmengen gehören folgende Zahlen? $\quad$ $\mathbb {N}$ $\mathbb {Z}$ $\mathbb {Q}$ $\mathbb {I}$ $\mathbb {R}$ $\textstyle +{\frac {\sqrt {0{,}25}}{13}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {33}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $-{\sqrt {441}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {-9}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $6$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle {\frac {\sqrt {11}}{13}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle {\frac {65}{13}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle -{\frac {8}{4}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ Zur welchen Zahlenmengen gehören folgende Zahlen? $\quad$ $\mathbb {N}$ $\mathbb {Z}$ $\mathbb {Q}$ $\mathbb {I}$ $\mathbb {R}$ ${\sqrt {144}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle +{\frac {39}{3}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle {\frac {13}{6{,}5}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle -{\frac {\sqrt {81}}{13}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle {\frac {\sqrt {8}}{13}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {289}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $-{\sqrt {-6}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {4}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ Zur welchen Zahlenmengen gehören folgende Zahlen? $\quad$ $\mathbb {N}$ $\mathbb {Z}$ $\mathbb {Q}$ $\mathbb {I}$ $\mathbb {R}$ $\textstyle {\frac {0{,}5}{\sqrt {0{,}0625}}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle -{\frac {38}{3}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle -{\frac {52}{1{,}3}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle {\frac {\sqrt {169}}{13}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle {\frac {\sqrt {-9}}{13}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${28}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $-{\sqrt {(-25)(-4)}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {18}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$

Zur welchen Zahlenmengen gehören folgende Zahlen? $\quad$ $\mathbb {N}$ $\mathbb {Z}$ $\mathbb {Q}$ $\mathbb {I}$ $\mathbb {R}$ $\textstyle {\frac {11}{7}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle {\frac {28}{7}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle -{\frac {\sqrt {7}}{15}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {15}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $-{\sqrt {625}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {-121}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {256}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle -{\frac {45}{15}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ Zur welchen Zahlenmengen gehören folgende Zahlen? $\quad$ $\mathbb {N}$ $\mathbb {Z}$ $\mathbb {Q}$ $\mathbb {I}$ $\mathbb {R}$ ${\sqrt {81}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle +{\frac {70}{5}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle {\frac {23}{11{,}5}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle -{\frac {\sqrt {144}}{12}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle {\frac {\sqrt {27}}{9}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {324}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $-{\sqrt {-35}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {49}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ Zur welchen Zahlenmengen gehören folgende Zahlen? $\quad$ $\mathbb {N}$ $\mathbb {Z}$ $\mathbb {Q}$ $\mathbb {I}$ $\mathbb {R}$ $\textstyle +{\frac {\sqrt {0{,}09}}{11}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {70}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $-{\sqrt {1600}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {-25}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $6$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle {\frac {\sqrt {33}}{33}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle {\frac {60}{12}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle -{\frac {33}{11}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ Zur welchen Zahlenmengen gehören folgende Zahlen? $\quad$ $\mathbb {N}$ $\mathbb {Z}$ $\mathbb {Q}$ $\mathbb {I}$ $\mathbb {R}$ $\textstyle -{\frac {0{,}2}{\sqrt {0{,}01}}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle -{\frac {45}{6}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle -{\frac {42}{1{,}4}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle {\frac {\sqrt {289}}{17}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\textstyle {\frac {\sqrt {-16}}{4}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${41}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $-{\sqrt {(-16)(-9)}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ ${\sqrt {12}}$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$

Expertenniveau 2

X2.1 Potenzen mit negativer Hochzahl

Schreiben Sie folgende Terme ohne Bruch auf!
$\ \ {\frac {1}{6^{x-4}}}=\quad$ $\ \ {\frac {3\cdot 7^{3u+4}}{7^{5u-8}}}=\quad$ $\ \ {\frac {5}{z^{-d}}}=\quad$	$\ \ {\frac {1}{6^{x-1}}}=\quad$ $\ \ {\frac {3\cdot 11^{2-x}}{11^{3x-4}}}=\quad$ $\ \ {\frac {5}{z^{-r}}}=\quad$	$\ \ {\frac {5}{r^{x-4}}}=\quad$ $\ \ {\frac {3\ b^{4z-5}}{b^{8}}}=\quad$ $\ \ 5\cdot {\frac {1}{z^{z}}}=\quad$	$\ \ {\frac {3}{r^{2r-4}}}=\quad$ $\ \ {\frac {11\ b^{4-5w}}{b^{3w}}}=\quad$ $\ \ 5\cdot {\frac {1}{5^{z}}}=\quad$

X2.2 Raumgeometrie Formelanwendung

Formel Einsetzen in der Raumgeometrie

1. Die Länge eines Lineals ist 3,1 dm, seine Breite 2,5 cm, seine Dicke 2 mm. Berechnen Sie die Gesamtlänge seine Kanten, seine Oberfläche und sein Volumen!
2. Der Radius einer Christbaumkugel ist 32mm. Wie viel ist der Umfang eines Großkreises, die Oberfläche und das Volumen?
3. Der Radius der Basis eines zylinderförmigen Glases ist 19 mm, seine Höhe 0,8 dm. Wie viel ist der Umfang der Basis, die (äußere) Oberfläche und das Volumen des Glases?
4. Der Abstand vom Mittelpunkt bis am Rand der Basis eines Tipis (indianisches Zelt) ist 39 dm, seine Höhe 2,8 m. Wie viel ist der Umfang der Basis, der Mantel, der Boden und das Volumen des Zeltes?
5. Die Länge einer Schuhschachtel ist 2,5 dm, ihre Breite 20 cm, ihre Höhe 0,1 m. Berechnen Sie die Gesamtlänge ihre Kanten, ihre Oberfläche und ihr Volumen!
6. Der Radius eines Balles ist 16 cm. Wie viel ist der Umfang eines Großkreises, die Oberfläche und das Volumen?
7. Die Seite der Basis einer quadratischen Pyramide ist 0,3 km, ihre Höhe 200 m. Wie viel ist der Umfang der Basis, die Oberfläche und das Volumen der Pyramide?
8. Der Abstand vom Mittelpunkt bis am Rand der Basis eines Tipis (indianisches Zelt) ist 78 dm, seine Höhe 1,4 m. Wie viel ist der Umfang der Basis, der Mantel, der Boden und das Volumen des Zeltes?

Umformen in der Raumgeometrie konkret

1. Das Volumen eines Zylinders ist 12 π dm³, seine Höhe 30 cm. Wie viel ist seine Oberfläche?
2. Die Oberfläche eines Quaders ist 180 cm², zwei seiner Kanten 90 mm bzw. 0,4 dm. Wie viel ist sein Volumen?
3. Das Volumen eines Kegels ist 54π cm², der Durchmesser der Basis 1,8 dm. Wie viel ist seine Oberfläche?
4. Die Oberfläche eines Balles ist 1256,64 cm². Wie viel ist sein Volumen?
5. Die Oberfläche eines Zylinders ist 18 π dm², sein Radius 20 cm. Wie viel ist sein Volumen?
6. Die Oberfläche eines Tetraders ist 180 mm². Wie viel ist sein Volumen?
7. Das Volumen eines Prismas mit einem regelmäßigen Sechseck als BAsis ist 5,4 dm³, die Höhe 8 cm. Wie viel ist seine Oberfläche?
8. Die Oberfläche eines Wurfels ist 294 cm². Wie viel ist sein Volumen?

Umformen in der Raumgeometrie abstrakt

Grundaufgaben

1. Natascha gibt für die Berechnung des Radius R einer Kugel mit Volumen V folgende Formel an:
   
   $\qquad R={\sqrt {\frac {3\ V}{4\ \pi }}}$
   
   Überprüfen Sie, ob die Formel richtig ist und, falls
   nicht, geben Sie die richtige Formel an!
2. Bill gibt für die Berechnung der Kante a eines Würfels mit Oberfläche O folgende Formel an:
   
   $\qquad a={\frac {\sqrt {O}}{6}}$
   
   Überprüfen Sie, ob die Formel richtig ist und, falls
   nicht, geben Sie die richtige Formel an!
3. Margarita gibt für die Berechnung der Fläche A der Basis eines Zylinders mit Oberfläche O, Radius der Basis r und Höhe h folgende Formel an:
   
   $\qquad A=O-\pi \ r\ h$
   
   Überprüfen Sie, ob die Formel richtig ist und, falls
   nicht, geben Sie die richtige Formel an!
4. Leo gibt für die Berechnung der Seite a der Basis einer quadratischen Pyramide mit Volumen V, deren Höhe h so viel wie diese Seite der Basis ist, folgende Formel an:
   
   $\qquad a={\sqrt[{3}]{3V}}$
   
   Überprüfen Sie, ob die Formel richtig ist und, falls nicht, geben Sie die richtige Formel an!
5. Shanti gibt für die Berechnung der Höhe h eines Kegels mit Volumen V, dessen Basisradius r ist, folgende Formel an:
   
   $\qquad h={\sqrt[{3}]{\frac {V}{r}}}$
   
   Überprüfen Sie, ob die Formel richtig ist und, falls nicht, geben Sie die richtige Formel an!
6. Pristina gibt für die Berechnung des Radius R einer Kugel mit Oberfläche O folgende Formel an:
   
   $\qquad R={\sqrt {\frac {O}{2\ \pi }}}$
   
   Überprüfen Sie, ob die Formel richtig ist und, falls nicht, geben Sie die richtige Formel an!
7. Pristina gibt für die Berechnung der Oberfläche O eines Zylinders mit Volumen V, deren Basisradius und Höhe gleich sind, folgende Formel an:
   
   $\qquad O=4{\sqrt[{3}]{\pi \cdot V^{2}}}$
   
   Überprüfen Sie, ob die Formel richtig ist und, falls nicht, geben Sie die richtige Formel an!
8. Alaah gibt für die Berechnung der Oberfläche O eines Quaders mit Volumen V und quadratischer Basis mit Seite a folgende Formel an:
   
   $\qquad O=4a^{2}+2{\frac {V}{a}}$
   
   Überprüfen Sie, ob die Formel richtig ist und, falls nicht, geben Sie die richtige Formel an!

Faktoraufgaben

2. Was passiert mit dem Volumen einer Kugel und was mit ihrer Oberfläche, wenn sich ihre Radius verdreifacht?
4. Was passiert mit dem Volumen eines Quaders, wenn sich eine seiner Kanten verdreifacht und eine andere halbiert, während die dritte gleich bleibt?
6. Was passiert mit dem Volumen eines Zylinders, wenn der Basisdurchmesser ein drittel wird und die Höhe das 4,5-fache?
8. Was passiert mit dem Volumen einer Quadratischen Pyramide, wenn die Seite der Basis das 1,5-fache wird und die Höhe gleich bleibt?
10. Was passiert mit dem Volumen eines Kegels, wenn sich der Radius seiner Basis verdoppelt und seine Höhe verdreifacht?
12. Was passiert mit der Oberfläche eines Würfels, wenn seine Kante das 1,2-fache wird?
14. Was passiert mit der Oberfläche eines Zylinders, dessen Höhe dem Radius der Basis gleich ist, wenn sich der Radius seiner Basis verdoppelt und seine Höhe halbiert?
16. Was passiert mit der Oberfläche einer Kugel, wenn ihre Volumen das 125-fache wird?

X2.3 Bruchtermegleichungen

Finden Sie die Definitions- und die Lösungsmenge der folgenden Bruchtermegleichungen:
${\frac {2x-4}{x^{2}-4}}-{\frac {3x}{x^{2}-x}}={\frac {3x-13{,}5}{x^{2}-1}}$	${\frac {2}{w+1}}-{\frac {3}{w^{2}+w}}={\frac {1}{w}}$	${\frac {9y^{2}-7y+34}{3y^{2}-6y}}+{\frac {5y^{2}+30y+45}{3y^{2}+9y}}={\frac {3y^{2}+6y}{y^{2}-4}}$
${\frac {2x+3}{x-2}}-{\frac {2x-5}{x+2}}={\frac {11x+6}{x^{2}-4}}$	${\frac {7b^{2}+14b}{b^{2}-4}}-{\frac {5b^{2}+10b}{b^{2}+4b+4}}={\frac {2b^{2}+6}{b^{2}-4}}$	${\frac {4x^{2}-5x-2x^{2}+4x}{x^{2}+x}}-{\frac {2x}{x-1}}={\frac {2x+15}{x^{2}-1}}$
${\frac {2a^{2}-a}{a^{2}+a}}-{\frac {2a}{a-1}}={\frac {2(a+4)}{a^{2}-1}}$	${\frac {2m-4}{m^{2}-3m+2}}-{\frac {3m}{m^{2}+m}}={\frac {3m-13}{m^{2}-1}}$

X2.4 Lineare Gleichungssysteme mit 2 Variablen

Sind folgende Gleichungsysteme Lösbar? Finden Sie die jeweilige Lösungsmenge. Finden Sie die Lösung, falls diese nur eine ist.
$\ \left|\ {\begin{matrix}2x+3y=11\\7x+2y=-4\end{matrix}}\ \right|$ $\ \left|\ {\begin{matrix}x+y=8\\4x+4y=32\end{matrix}}\ \right|$	$\ \left|\ {\begin{matrix}2x+8y=-6\\6y+1{,}5x=28\end{matrix}}\ \right|$ $\ \left|\ {\begin{matrix}2x-5y=-9\\3x+4y=-2\end{matrix}}\ \right|$	$\ \left|\ {\begin{matrix}9x+4y=5\\2y+4{,}5x=5\end{matrix}}\ \right|$ $\ \left|\ {\begin{matrix}9x+4y=5\\6x+3y=4\end{matrix}}\ \right|$	$\ \left|\ {\begin{matrix}12x+5y=24\\2{,}5y+6x=12\end{matrix}}\ \right|$ $\ \left|\ {\begin{matrix}8x+4y=4\\6x+5y=7\end{matrix}}\ \right|$
$\ \left|\ {\begin{matrix}x+y=8\\3x+5y=36\end{matrix}}\ \right|$ $\ \left|\ {\begin{matrix}2x+3y=11\\4x+6y=-4\end{matrix}}\ \right|$	$\ \left|\ {\begin{matrix}2x+8y=-6\\6y-5x=28\end{matrix}}\ \right|$ $\ \left|\ {\begin{matrix}2x-5y=-10\\-7y+2{,}8x=-14\end{matrix}}\ \right|$	$\ \left|\ {\begin{matrix}9x+4y=5\\2y-3x=5\end{matrix}}\ \right|$ $\ \left|\ {\begin{matrix}9x+4y=2\\6x+{\frac {8}{3}}y={\frac {5}{3}}\end{matrix}}\ \right|$	$\ \left|\ {\begin{matrix}12x+5y=23\\2y-3x=1\end{matrix}}\ \right|$ $\ \left|\ {\begin{matrix}8x+4y=4\\6x+3y=3\end{matrix}}\ \right|$

X2.5 Prozentrechnung abstrakt

1. In den folgenden Beispielen gehen wir davon aus, dass es in der Bevölkerung so viele Männer gibt wie Frauen.
   1. Der Anteil der Raucher unter der Bevölkerung ist 27,5%. Der Anteil der Raucher unter den Männern ist 35%. Wie viel ist der Anteil der Raucherinnen unter den Frauen?
   2. Die Lebenserwartung der Bevölkerung ist 80 Jahre. Die Lebenserwartung der nicht-Raucher ist 82,4 Jahre. Wie viele Jahre weniger ist die Lebenserwartung der Rauchenden in Vergleich zu den nicht-Rauchenden Personen?
   3. Wäre das Rauchen die einzige Erklärung für den Unterschied der Lebenserwartung zwischen den beiden Geschlechtern, wie viel Jahre wäre diese für Männer und für Frauen?
   4. Welche Information ist noch notwendig, um den Einfluss des Rauchens auf den Lebenserwartungsunterschied zwischen den Geschlechtern genauer zu bestimmen?
   5. Wenn wir letztere Information haben, was ist noch notwendig, um zu entscheiden, ob das Rauchen bei dieser Frage tatsächlich der einzige bestimmende Faktor ist? Vergleichen Sie ihre Ergebnisse mit tatsächlichen offiziellen Statistiken!
2. Die Seite einer Figur F ist das 1,5-fache der Seite einer ähnlichen Figur G.
   1. Um wie viel Prozent größer ist der Umfang von F als der von G?
   2. Um wie viel Prozent kleiner ist der Umfang von G als der von F?
   3. Um wie viel Prozent größer ist die Fläche von F als die Fläche von G?
   4. Um wie viel Prozent kleiner ist die Fläche von G als die von F?
3. Der Radius einer Kugel A ist um 150% größer als der Radius einer Kugel B.
   1. Um wie viel Prozent größer ist die Oberfläche von A in Bezug auf B?
   2. Um wie viel Prozent größer ist das Volumen von A in Bezug auf B?
   3. Um wie viel Prozent kleiner ist der Durchmesser von B in Bezug auf A?
   4. Um wie viel Prozent kleiner ist die Oberfläche von B in Bezug auf A?
4. In den folgenden Beispielen gehen wir davon aus, dass es in der Bevölkerung so viele Männer gibt wie Frauen.
   1. Der Anteil der Raucher unter der Bevölkerung ist 45%. Der Anteil der Raucher unter den Männern ist 60%. Wie viel ist der Anteil der Raucherinnen unter den Frauen?
   2. Die Lebenserwartung der Bevölkerung ist 79 Jahre. Die Lebenserwartung der nicht-Raucher ist 82,6 Jahre. Wie viele Jahre weniger ist die Lebenserwartung der Rauchenden in Vergleich zu den nicht-Rauchenden Personen?
   3. Wäre das Rauchen die einzige Erklärung für den Unterschied der Lebenserwartung zwischen den beiden Geschlechtern, wie viel Jahre wäre diese für Männer und für Frauen?
   4. Welche Information ist noch notwendig, um den Einfluss des Rauchens auf den Lebenserwartungsunterschied zwischen den Geschlechtern genauer zu bestimmen?
   5. Wenn wir letztere Information haben, was ist noch notwendig, um zu entscheiden, ob das Rauchen bei dieser Frage tatsächlich der einzige bestimmende Faktor ist? Vergleichen Sie ihre Ergebnisse mit tatsächlichen offiziellen Statistiken!
5. Bei den Wahlen in einer Gemeinde hat 60% der Wählerschaft tatsächlich gewählt. Die Partei D (Die Partei) hat 5% der Stimmen bekommen, die Partei U (Partei nur für Uns) 65%, die Partie K (Partei der Keuschheit) 1,5%, die Partei V (Partei für die Vergangenheit) 15%, die Partei Z (Partei für die Zukunft) 7,5% und der Rest der Stimmen war nicht gültig.
   1. Zeigen Sie, dass die am stärksten vertretene Gruppe die nicht-WählerInnen war! Wie viel Prozent mehr waren sie als die Wählerschaft der stärksten Partei?
   2. Wie viel Prozent mehr als die ungültigen Stimmen waren die Stimmen der Partei für die Keuschheit?
   3. Wie viel Prozent der Stimmen weniger als die Partei V hat die Partei K bekommen?
   4. Wie viel Prozent der Stimmen mehr als die Partei K hat die Partei V bekommen?
   5. Wie viel Prozent der gesamten Wählerschaft hat die Partei D gewählt?
   6. Wie viel Prozent der gültigen Stimmen hat jede Partei durchschnittlich bekommen?
6. Die Seite einer Figur F ist das doppelte der Seite einer ähnlichen Figur G.
   1. Um wie viel Prozent größer ist der Umfang von F als der von G?
   2. Um wie viel Prozent kleiner ist der Umfang von G als der von F?
   3. Um wie viel Prozent größer ist die Fläche von F als die Fläche von G?
   4. Um wie viel Prozent kleiner ist die Fläche von G als die von F?
7. Der Radius einer Kugel A ist um 200% größer als der Radius einer Kugel B.
   1. Um wie viel Prozent größer ist die Oberfläche von A in Bezug auf B?
   2. Um wie viel Prozent größer ist das Volumen von A in Bezug auf B?
   3. Um wie viel Prozent kleiner ist der Durchmesser von B in Bezug auf A?
   4. Um wie viel Prozent kleiner ist die Oberfläche von B in Bezug auf A?
8. Bei den Wahlen in einer Gemeinde hat 70% der Wählerschaft tatsächlich gewählt. Die Partei D (Die Partei) hat 19% der Stimmen bekommen, die Partei U (Partei nur für Uns) 22%, die Partie K (Partei der Keuschheit) 1,5%, die Partei V (Partei für die Vergangenheit) 42%, die Partei Z (Partei für die Zukunft) 15% und der Rest der Stimmen war nicht gültig.
   1. Zeigen Sie, dass die am stärksten vertretene Gruppe die nicht-WählerInnen war! Wie viel Prozent mehr waren sie als die Wählerschaft der stärksten Partei?
   2. Wie viel Prozent mehr als die ungültigen Stimmen waren die Stimmen der Partei für die Keuschheit?
   3. Wie viel Prozent der Stimmen weniger als die Partei V hat die Partei K bekommen?
   4. Wie viel Prozent der Stimmen mehr als die Partei K hat die Partei V bekommen?
   5. Wie viel Prozent der gesamten Wählerschaft hat die Partei D gewählt?
   6. Wie viel Prozent der gültigen Stimmen hat jede Partei durchschnittlich bekommen?

X2.6 Raumgeometrie Textaufgaben

1. Das Volumen einer Getränkedose aus Aluminium ist 0,45 Liter, die Höhe 15cm. Berechnen die Kosten für die Produktion von 20 Dosen, wenn die Kosten des Aluminiums 0,7¢/dm² sind.
2. Mit Hilfe welches geometrischen Körpers würden sie versuchen, das Volumen und die Oberfläche eines 2500 m hohen Berges, dessen Fuß einen Umfang von 15 km umfasst, annähernd zu berechnen? Wie viel ist dieser Annäherung nach das Volumen und die Oberfläche?
3. Sie wollen in einem Schrank mit 8 dm Breite, 1,2 m Länge und 50 cm Höhe würfelförmige Boxen mit einer Kante von 45 mm lagern. Wie viele Boxen passen im Schrank hinein?
4. Kann man einen 1,5m langen Besenstiel in einem Schrank mit 8 dm Breite, 1,2 m Länge und 50 cm Höhe lagern?
5. Die Cheops-Pyramide ist eine quadratische Pyramide mit ursprüngliche Höhe von 280 Cubits (Arme, also ca. 147 m) und Seite der Basis von 440 Cubits (ca. 231 m). Sie bestand aus ca. 2,3 Millionen Steinblöcke. Nehmen wir an, dass alle diese Steinblöcke gleiche Breite und Höhe hatten, und dass die Länge das 1,5-fache der Breite war. Berechnen Sie die Dimensionen der Steinblöcke in Cubits!
6. Ein Zimmer ist 6 m Lang, 35 dm Breit und 250 cm hoch. Wie viele Eimer Farbe sind notwendig, um seine Wände und seine Decke zu streichen, wenn ein Eimer für 12 m² ausreicht?
7. Wie viel kostet das Holz für den Bau eines Schrankes mit 6 dm Breite, 1 m Länge und 2,3 m Höhe, wenn das Holz 59,9€/m² kostet?
8. Der Abstand vom Mittelpunkt bis am Rand der Basis eines Tipis (indianisches Zelt) ist 78 dm, seine Höhe 1,4 m. Für den Mantel wurden rechteckige Lederstücke mit 2 m Länge und 150 cm Breite zusammengenäht. Wie viele solche Stücke zumindest waren dafür notwendig? Was muss man in dieser Berechnung berücksichtigen?

X2.7 Das pascalsche Dreieck Binompotenzen

Multiplizieren Sie mit Hilfe des pascalschen Dreiecks folgende Binome aus:
$\ (5x^{3}-7z^{2})^{4}\quad$	$\ (3a^{4}-7a)^{5}\quad$	$\ (2m^{4}-7n^{5})^{3}\quad$	$\ (5b^{2}-7e)^{4}\quad$
$\ (4x^{2}-5z^{3})^{4}\quad$	$\ (3a^{2}-2a^{3})^{5}\quad$	$\ (7m^{3}-3n^{4})^{3}\quad$	$\ (4b-5e^{2})^{4}\quad$

X2.8 Textaufgaben Primfaktorzerlegung

1. Die Formel für den Gesamtwiderstand R 4 parallel angeschlossener elektrischer Widerstände ist:
   ${\frac {1}{R}}={\frac {1}{R}}_{1}+{\frac {1}{R}}_{2}+{\frac {1}{R}}_{3}+{\frac {1}{R}}_{4}$
   Wie viel ist R, wenn $R_{1}=10,\ R_{2}=20,\ R_{3}=12,\ R_{4}=9\ \Omega \$ sind.
2. Zwei Buslinien fahren jeden Tag ab 5 Uhr in der früh. Die letzte Fahrt der Linie, die früher aufhört, ist um 21 Uhr. Eine Linie fährt jede 11, die andere jede 10,5 Minuten.
   • Wie oft während des Tages werden Sie gleichzeitig losfahren?
   • Nach wie viel Zeit fahren sie wieder gleichzeitig los?
   • Wie oft fährt jeder Bus, bis sie wieder gleichzeitig losfahren?
3. Kathrin will ihren rechteckigen Fenster (0,63 m x 6,6 dm) komplett mit den großmöglichsten quadratischen Mustern decken. Wie lang wird die Seite jedes Quadrats sein und wie viele wird sie benötigen?
4. Zwei Planeten und ihre Sonne befinden sich auf einer Gerade. Die Laufbahn der Planeten um ihrer Sonne dauert 11088 bzw. 56056 (von unseren) Tage. Wie lang dauert es bis die zwei Planeten und ihre Sonne sich wieder auf einer Gerade befinden?
5. Fifi will ihren rechteckigen Tisch (77 cm x 0,56 m) komplett mit den großmöglichsten quadratischen Mustern decken. Wie lang wird die Seite jedes Quadrats sein und wie viele wird sie benötigen?
6. Zwei Buslinien fahren jeden Tag ab 5 Uhr in der früh. Die letzte Fahrt der Linie, die früher aufhört, ist um 21:10. Eine Linie fährt jede 14, die andere jede 10,5 Minuten.
   • Wie oft während des Tages werden Sie gleichzeitig losfahren?
   • Nach wie viel Zeit fahren sie wieder gleichzeitig los?
   • Wie oft fährt jeder Bus, bis sie wieder gleichzeitig losfahren?
7. Die Formel für den Gesamtwiderstand R 4 parallel angeschlossener elektrischer Widerstände ist:
   ${\frac {1}{R}}={\frac {1}{R}}_{1}+{\frac {1}{R}}_{2}+{\frac {1}{R}}_{3}+{\frac {1}{R}}_{4}$
   Wie viel ist R, wenn $R_{1}=10,\ R_{2}=15,\ R_{3}=12,\ R_{4}=8\ \Omega \$ sind.
8. Zwei Planeten und ihre Sonne befinden sich auf einer Gerade. Die Laufbahn der Planeten um ihrer Sonne dauert 32340 bzw. 19110 (von unseren) Tage. Wie viele Drehungen muss die Planeten mindestens machen, damit die Planeten und ihre Sonne sich auf eine Gerade noch ein mal befinden?

X2.9 Ähnlichkeit von Körpern

1. Der Radius der Basis eines Kegels ist 4 dm, seine Höhe 60 cm. Die Fläche der Basis eines ähnlichen Kegels ist $144\ \pi \ dm^{2}.$ Wie hoch ist dieser Kegel?
2. Die Seiten eines Quaders sind 2,5 cm, 60 mm bzw. 0,4 dm. Das Volumen eines ähnlichen Quaders ist 7,5 cm³. Wie lang sind seine Seiten?
3. Der Radius der Basis eines Zylinders ist 3 dm, seine Höhe 60 cm. Der Mantel eines ähnlichen Zylinders ist $4\ \pi \ dm^{2}.$ Wie hoch ist dieser Kegel?
4. Die Basis einer quadratischen Pyramide ist 225 dm², ihr Volumen 0,9 m³. Das Volumen einer ähnlichen Pyramide ist 112,5 m³. Wie lang ist die Seite ihrer Basis?
5. Die Seiten eines Quaders sind 2 dm, 25 cm bzw. 0,45 m. Das Volumen eines ähnlichen Quaders ist 1,44 m³. Wie lang sind seine Seiten?
6. Der Radius der Basis eines Kegels ist 5 dm, seine Höhe 40 cm. Die Fläche der Basis eines ähnlichen Kegels ist $25\ \pi \ dm^{2}.$ Wie hoch ist dieser Kegel?
7. Die Basis einer quadratischen Pyramide ist 16 dm², ihr Volumen 0,08 m³. Das Volumen einer ähnlichen Pyramide ist 10 dm³. Wie lang ist die Seite ihrer Basis?
8. Der Radius der Basis eines Zylinders ist 12,5 cm, seine Höhe 10 mm. Der Mantel eines ähnlichen Zylinders ist $\pi \ dm^{2}.$ Wie hoch ist dieser Kegel?