MathemaTriX ⋅ Diagramme 3

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

LINKS

 ACHTUNG! 
Zumindest Aufgabe 1 bis 4 probieren,
sie sind unterschiedlich!

	lle	Gaben
	uf-

Aufgaben

1. 
   

   Im Bild sehen wir die durch ein Graph angenäherte Form einer Rutsche. Die Funktion 3. Grades f führt knickfrei zur Gerade g am Punkt (2|1). Der untere Rand der Rutsche befindet sich am Punkt (0,5|0,5), wo sie eine horizontale Tangente hat. Jemand behauptet, dass die Steigung sowohl der Gerade als auch der Funktion am Punkt (2|1) 50% ist. Warum stimmt diese Aussage? Wie lautet die Funktion f? Die Gerade g führt ebenfalls knickfrei zur quadratischen Funktion h am Punkt (6|3). An der Stelle 6,5 bildet die Tangente der Funktion h zur Waagerechte einen 5° Winkel (siehe Bild). Erstellen Sie ein Gleichungssystem zur Berechnung der Koeffizienten der Funktion h! In einem Tierheim gibt es 8 schwarze Katzen, 4 roten, 2 weißen, 1 dreifarbige und 1 schwarz-rot. Zu welchen der folgenden Diagramme passt diese Aussage? W X Y Z Sei S1 die Menge aller Katzen des Tierheims, die (ggf. auch) weiß sind, S2 die Menge deren, die (ggf. auch) schwarz und die Menge S3 deren, die (ggf. auch) rot sind. Stellen Sie das entsprechende Venn-Diagramm auf! Veranschaulichen Sie in diesem Diagramm den Ausdruck $\left(S1\cap S2\right)\cup S3$ und drücken Sie diese Menge in diesem Zusammenhang aus! Die (senkrechte) Fassade eines modernen Gebäudes hat die Form der dargestellten Figur. Die Länge ihrer Dachlinie ist $780\ cm$, ihre Höhe $190\ dm$, ihre Fläche $210m^{2}.$ Berechnen Sie die Länge der Bodenlinie! Der Verlauf einer Epidemie wird durch zwei Modelle beschrieben. Im ersten Modell gibt es am Anfang 800 Angesteckten (allerdings nur 5,5% sind krank) und die Anzahl der Angesteckten wächst jeden Tag um 3%. Im zweiten Modell gibt es am Anfang 600 Angesteckten und die Anzahl wächst jede Woche um 700 Personen. Erstellen Sie die entsprechenden Gleichungen für beide Modelle so, dass man sie im gleichen Koordinatensystem darstellen kann und zeichnen Sie sie im gleichen Koordinatensystem! Im welchem Intervall weist das zweite Modell mehr Infizierte als das erste auf? Warum dürfen beide Modelle bei der Darstellung einer Epidemie (auf langer Sicht aber nicht nur) nicht benutzt werden? Laut einer Definition der Meile sind 5 Meilen gleich 8 Kilometer. Rechnen Sie 69 Meilen/min in km/h um. Rechnen Sie 15 m/s in Meilen/h um.

2. 
   

   Temperatur (°C): $4$ $5$ $1$ Höhe (dm): $\ \ 3\ \$ $\ \ 3{,}4\ \$ $\ \ 0\ \$ In einem Diagramm wird die Temperatur in Abhängigkeit von der Höhe in einem kleineren Kühlschrank gezeigt. Aus dem Diagramm werden die Werte in der angezeigte Tabelle entnommen. Überprüfen Sie, ob diese Punkte zu einer exponentielle Funktion gehören! Überprüfen Sie mit Hilfe von Differenzenquotienten, ob diese Punkte zu einer linearen Funktion gehören! 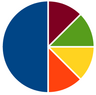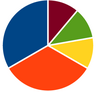Geben Sie die Winkel und die Prozentsätze für das dargestellte Kreisdiagramm auf zwei Nachkommastellen gerundet an! Das Diagramm zeigt die erreichten Punkte bei zwei Wettbewerben des gleichen Sports. In beiden Fällen haben die gleichen 95 Personen teilgenommen. 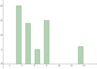Geben Sie das arithmetische Mittel, den Zentralwert, die Quartile, den Quartilabstand, die Spannweite, die Ausreißer, das Maximum und das Minimum des 1. Didagramms an! Was bedeutet es, wenn das 1. Quartil keiner der nicht dargestellten gemessenen Werte ist? Welche der folgenden Ausdrücken stimmt? (mehrere richtige Antworten möglich) Der Median ist gleich in beiden Diagrammen Der Quartilabstand ist im ersten Diagramm größer Eine Person mit 40 Punkte gehört in Diagramm A zu den 25% schlechtesten Eine Person mit 40 Punkte gehört in Diagramm B zu den 25% schlechtesten 25% der Personen haben in beiden Diagrammen zumindest 46 Punkte gehabt Es gibt mit Sicherheit zumindest eine Persone, die 98 Punkte hatte Zumindest 75% der Personen haben in beiden Diagrammen 37 oder mehr Punkte gehabt Die rechte "Antenne" im ersten Diagramm ist das 1,5-fache des IQR Wenn wir im ersten Diagramm bei einer Person 44 statt 43 Punkte eintragen, ändert sich das Diagramm nicht Drücken Sie die grau markierte Fläche mit Hilfe der Länge a, der Funktion $f$ und des Winkels $\gamma$ aus! Drücken Sie den Winkel $\beta$ mit Hilfe der Höhe h und der Länge $\ell$ der Basis aus! Welche der Ausdrücke in der Tabelle A sind zueinander gleich? A ${\sqrt[{2a}]{625}}$ A ${\tfrac {1}{a^{25}}}$ B $5^{\frac {2}{a}}$ C ${\sqrt[{a}]{25}}$ D $25^{\frac {1}{-a}}$ E ${\sqrt[{a}]{2500\%}}$ F $a^{2{,}5}$ G $\qquad$ B $850\cdot 10^{6}$ $85\cdot 10^{7}$ $8{,}50\cdot 10^{9}$ $8500\cdot 10^{-7}$ $Billionen$ $0{,}850\cdot 10^{9}$ Schreiben Sie 0,85 Milliarden in Gleitkommadarstellung auf! Welche der Möglichkeiten in der Tabelle B entsprechen dieser Zahl nicht? Der Luftdruck auf der Oberfläche eines Planeten ist 2,4 Atm und wird jede 50 km Höhe um 8% weniger. Erstellen Sie eine Funktion für diesen Zusammenhang und geben Sie an, was die x- bzw. die y-Achse darstellt (samt Einheiten)! Was ist die Bedeutung des y-Achsenabschnittes und der Steigung in diesem Sachzusammenhang?

3. 
   

   Es gilt ${\vec {a}}={\tbinom {-6}{-4}},\quad {\vec {c}}={\tbinom {b}{4}}$ Vom Punkt (0|4) ausgehend zeichnen Sie ${\tfrac {1}{2}}{\vec {a}}.\$Spiegeln Sie das Ergebnis auf der y-Achse! Welche Stadt befindet sich am Endpunkt des letzten Vektors? Das Skalarprodukt der beiden Vektoren ist 2. Wie viel ist die Zahl b? Es werden Metallteile für Küchengeräte produziert. Ihre Länge und die entsprechende Anzahl werden in der nachstehenden Tabelle erfasst. Länge in cm Anzahl $\quad$ Länge in cm Anzahl rot grün 6,5 32 3,5 20 schwarz 5 14 5,5 14 6,5 5 6 10 8 15 10 19 13,5 6 14 5 Stellen Sie ein Kreisdiagramm für die Länge der grünen Teile auf und geben sie die entsprechenden Prozentsätze an! Stellen Sie ein Säulendiagramm für die Länge der grünen Teile auf! Wie viel ist das arithmetische Mittel, die Standardabweichung, der Zentralwert und die Spannweite der Länge der schwarzen Teile und wie viel der roten Teile? Welche der folgenden Ausdrücken gibt die Standardabweichung der grünen Teile an? (1 von 5 Möglichkeiten) ${\sqrt {\tfrac {20\cdot (3{,}5-6{,}225)^{2}+14\cdot (5-6{,}225)^{2}+5\cdot (6{,}5-6{,}225)^{2}+15\cdot (8-6{,}225)^{2}+6\cdot (13{,}5-6{,}225)^{2}}{3}}}$ ${\sqrt {\tfrac {3{,}5\cdot (20-6{,}225)^{2}+5\cdot (14-6{,}225)^{2}+6{,}5\cdot (5-6{,}225)^{2}+8\cdot (15-6{,}225)^{2}+13{,}5\cdot (6-6{,}225)^{2}}{60}}}$ ${\sqrt {\tfrac {(3{,}5-6{,}225)^{2}+(5-6{,}225)^{2}+(6{,}5-6{,}225)^{2}+(8-6{,}225)^{2}+(13{,}5-6{,}225)^{2}}{60}}}$ ${\sqrt {\tfrac {20\cdot (3{,}5-6{,}225)^{2}+14\cdot (5-6{,}225)^{2}+5\cdot (6{,}5-6{,}225)^{2}+15\cdot (8-6{,}225)^{2}+6\cdot (13{,}5-6{,}225)^{2}}{60}}}$ ${\tfrac {\sqrt {20\cdot (3{,}5-6{,}225)^{2}+14\cdot (5-6{,}225)^{2}+5\cdot (6{,}5-6{,}225)^{2}+15\cdot (8-6{,}225)^{2}+6\cdot (13{,}5-6{,}225)^{2}}}{60}}$ Eine Person wählt von allen diesen Teilen zufällig einen ohne ihn wegzunehmen. Das macht sie 12 Mal. Wie viel ist die Wahrscheinlichkeit, dass sie in weniger als die Hälfte der Fälle einen nicht grünen Teil wählt? Was sollten in diesem Zusammenhang die Ausdrücke ${\sqrt {12\cdot {\tfrac {6}{14}}\cdot {\tfrac {8}{14}}\ }}$ bzw. $P(E)=\sum _{i=6}^{12}{\tbinom {12}{i}}\cdot \left({\tfrac {6}{14}}\right)^{i}\cdot \left({\tfrac {8}{14}}\right)^{12-i}\$ bedeuten? Die Daten der Rauchengewohnheiten in einer kleinen Gruppe von Menschen wurden in der angezeigten Tabelle zusammengefasst. Zigar. pro Tag 14 0 33 11 0 0 36 1 Todes- alter 68 86 56 48 75 92 39 82 Geben Sie die Gleichung der entsprechenden Regressionsgerade an! Wie viel ist die Steigung und wie viel der y.Achsenabschnitt? Geben Sie ihre Bedeutung in diesem Zusammenhang an! Die Steigung einer Strasse ist 15%. Wie viel ist der Höhenwinkel?

4. 
   

   In einer Blasmusikkapelle mit 25 Musiker gibt es 5, die Trompete spielen können und 6, die Gitarre spielen. Von denen können 2 beide Instrumente spielen. Füllen Sie das Diagramm mit den entsprechenden Zahlen aus! Das Diagramm zeigt die Funktion $v(t)=0{,}1t^{3}-0{,}5t^{2}+0.1t+3$ der Geschwindigkeit in km/h eines Fußgängers in Abhängigkeit von der Zeit t in h. An welchem Zeitpunk ungefähr ist die Beschleunigung null? Berechnen Sie die zurückgelegte Strecke zwischen 1. und 4. Stunde! Jemand behauptet, dass nach 2 Stunden die Geschwindigkeit ${\tfrac {1}{1{,}8}}(=0{,}{\dot {5}})\ m/s$ ist. Weisen Sie nach, dass diese Behauptung stimmt! In einer Jugendheberge gibt es 4- und 8-Betten-Zimmer. In den 4-Betten-Zimmern gibt es jeweils 2, in den 8-Betten-Zimmern jeweils 3 Spiegel. Insgesamt haben die Zimmer 31 Spiegel und 76 Betten. Wie viele Zimmer mit 4 und wie viele mit 8 Betten gibt es? Die Anzahl der Bakterien (in Millionen) in zwei Petrischalen wird in der folgenden Tabelle angegeben. Die erste Zeile gibt Stunden an, die zweite ist die Petrischale A (ohne Antibiotikum) und die dritte die Petrischale O (mit Antibiotikum). 1 2 3 4 N 2,4 6 15 $\qquad$ M 4 3,6 3,2 Überprüfen Sie nachweislich, welche der beiden Folgen eine arithmetische und welche eine geometrishe ist! Berechnen Sie das jeweilige 4. Glied! Erstellen Sie für die Petrischale N ein rekursives und für die Petrischale M ein explizites Bildungsgesetz! Wenn die Erde ein Teller mit 5 cm langen Radius wäre, wäre die Sonne ein Kreisverkehr mit 11 m Durchmesser. Das wievielfache der Erdoberfläche ist dann die Oberfläche der Sonne? (mit Rechenweg) Der Blutdruck einer Person ist 125 mmHg und fällt nach einer Verletzung um 3 mmHg pro 50 ml Blutverlust. Erstellen Sie eine Funktion für diesen Zusammenhang und geben Sie an, was die x- bzw. die y-Achse darstellt (samt Einheiten)! Was ist die Bedeutung der Nullstellen und der Steigung in diesem Sachzusammenhang?