MathemaTriX ⋅ ExponentialfunktionS

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

LINKS

Zumindest eine Aufgabe probieren

	lle	Gaben
	uf-

Theorie in Kürze (mit Geogebra)

$N(t)=N_{0}\cdot a^{t}$

N(t) ist die y-Achse (das y), t die x-Achse (das x). $N_{0}\$ist der "Anfangswert", also der Wert der Funktion (y-Wert) da, wo x Null ist (y-Achsenabschnitt). Die Basis der Potenzzahl (das ist ein "Änderungsfaktor") kann man auch als "Prozentsatz" interpretieren, z.B. $N(t)=N_{0}\cdot 0{,}964^{t}$ bedeutet, dass bei jeder Änderung der x-Achse (z.B. t Zeit in Jahren) um 1 (z.B. jährlich) bleiben (0,964=) 96,4% des vorherigen Wertes, also 3,6% (100%−96,4%) weniger.

Extra Merkmal der Exponentialfunktion: Halbwertszeit: Nach der gleichen Änderung des x-Wertes wird der Wert der Funktion (y-Wert) immer halbiert. Im Bild: Am Anfang (also an der Stelle 0) ist der Wert der Funktion $N(0)=N_{0}\cdot a^{t}=8000\cdot a^{0}=8000\cdot 1=8000$, nach 3,5 auf der x-Achse (also an der Stelle 3,5) ist N(t) =N(3,5)=4000 (also die Hälfte), nach noch 3,5 auf der x-Achse (also an der Stelle 7) ist N(t) 2000 (also die Hälfte der Hälfte) usw.
Die Halbwertszeit kann man berechnen, indem man am Wert Funktion die Hälfte des Anfangswerts einsetzt, z.B. $2350=4700\cdot 0{,}9^{t}$ (2350 ist die Hälfte von 4700) oder $0{,}5=0{,}6^{t}$ (hier "fehlt" der Anfangswert, er ist also 1, und die Hälfte von 1 ist ja 0,5). Entsprechend für eine "Verdoppelungszeit" oder ähnliches: $2=0{,}7^{t}$, $7{,}6=3{,}8\cdot 0{,}9^{t}$ usw.

Noch dazu: die Exponentialfunktion hat keine "Nullstellen": sie kommt immer näher zur x-Achse aber trifft diese nie!

Vergleich linearer und exponentieller Funktion:

	Lineare Funktion	Exponentialfunktion
Formel	$f(x)=s\cdot x+A_{y}$	$N(t)=N_{0}\cdot a^{t}$
Im Text erkennen durch	Steigung der Gerade (in der Formel: s) Änderungsrate y-Einheiten PRO eine x-Einheit	Basis der Hochzahl (in der Formel: a) Relative Änderung ("Prozent"-Änderung) des y-Wertes bei Änderung des x-Wertes um 1
Änderungsrate	Absolut (genauer Wert)	Relativ (Anteil, Prozent, -fach)
steigend ("nach oben") Wachstum	s>0 (positiv)	a>1
fallend ("nach unten") Abnahme	s<0 (negativ)	0<a<1
y-Achsenabschnitt (i.d.R. "Anfangswert")	$A_{y}$	$N_{0}$
Diagramme

Aufgaben

1. 
   

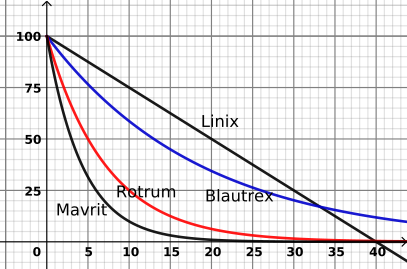
   4 verschiedene Waschmittel wurden auf ihre Effektivität geprüft. Das Diagramm zeigt welcher Anteil (in Prozent) des Schmutzes geblieben ist in Bezug auf die Zeit (in Minuten) Zeichnen Sie in Diagramm einen linearen Zusammenhang, der genau nach 10 Minuten wirksamer als Mavrit wird.(Wird es dann immer wirksamer sein?) Folgende Gleichung über ein bestimmtes Waschmittel wird gelöst: $0{,}5=0{,}791^{t}.\$Was bedeutet die Lösung dieser Gleichung in diesem Zusammenhang? Folgende Gleichung über ein bestimmtes Waschmittel wird gelöst: $0{,}3=0{,}791^{t}.\$Was bedeutet die Lösung dieser Gleichung in diesem Zusammenhang? Nach wie viel Zeit bleibt 20% des Schmutzes, wenn man Rotrum benutzt? Mit Hilfe des Diagramms erstellen Sie die Funktion für Mavrit! Ein weiteres Waschmittel eliminiert 60% des Schmutzes nach 9 Minuten. Nach 5 weiteren Minuten eliminiert es insgesamt 75% des Schmutzes. Mit Hilfe der zwei Werte am Anfang und nach 9 Minuten erstellen Sie ein exponentielles Wachstumsmodell. Nach wie viel Zeit in Sekunden wird nach diesem Modell der Schmutz halbiert? Beurteilen Sie, ob nach diesem Modell der Wert nach 14 Minuten akzeptiert werden kann, wenn eine Abweichung von 3 Prozenteinheiten toleriert wird. Was soll man ändern, wenn der Wert außerhalb der hinnehmbaren Abweichung steht, das Modell oder den Wert? Argumentieren Sie, ob der Schmutz nach diesem Modell irgendwann völlig verschwindet! Sei $T_{H}\$die Halbwertszeit. Kreuzen Sie die zutreffende(n) Aussage(n) an! Nach 3 $T_{H}\$wird ${\tfrac {1}{6}}\$des Schmutzes übrig bleiben Nach 2 $T_{H}\$wird ${\tfrac {1}{2}}\$des Schmutzes übrig bleiben Nach 5 $T_{H}\$wird der Schmutz $10\%\$des Ausgangswertes sein Nach 2 $T_{H}\$nimmt der Schmutz um $75\%\$ab Nach 3 $T_{H}\$wird ${\tfrac {1}{4}}\$des Schmutzes übrig bleiben Für noch ein weiteres Waschmittel gilt für den Prozentsatz des verbliebenen Schmutzes in Abhängigkeit von der Zeit in Minuten folgende Gleichung: $T(t)=14+86\cdot e^{-b\cdot t}$ Wie viel ist der Wert am Anfang? Was bedeutet die Zahl 14 in dieser Gleichung? Wie schnell nimmt der Schmutz nach 0,2 Stunden ab, wenn $b=0{,}3?$ Wie viel ist dann die mittlere Schmutzabnahme zwischen 2 und 12 Minuten? Nehmen wir an, dass nach 18 Minuten 45% des Schmutzes eliminiert wird. Wie viel Prozent des Schmutzes wäre in diesem Fall nach 24 Minuten übrig geblieben?

2. 
   

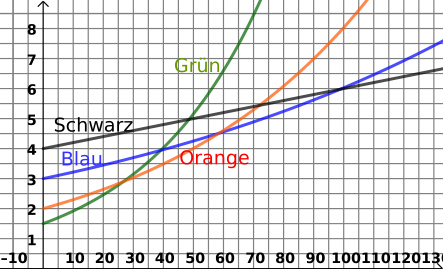
   Das Wachstum der Bevölkerung (in Millionen) in 4 verschiedenen (imaginären) Städten in Abhängigkeit von der Zeit in Jahren wurde im Diagramm zusammengefasst. Zeichnen Sie in Diagramm einen linearen Zusammenhang einer Stadt, die am Anfang 500000 Einwohner hat und ab 20 Jahren später mehr Einwohner als die blaue Stadt hat. (wird sie dann immer eine größere Bevölkerung haben?) Folgende Gleichung über eine bestimmte Stadt wird gelöst: $2=1{,}64^{t}.\$Was bedeutet die Lösung dieser Gleichung in diesem Zusammenhang? Folgende Gleichung über eine bestimmte Stadt wird gelöst: $7=1{,}64^{t}.\$Was bedeutet die Lösung dieser Gleichung in diesem Zusammenhang? Nach wie viel Zeit hat die grüne Stadt das dreifache ihrer Anfangsbevölkerung erreicht? Mit Hilfe des Diagramms erstellen Sie die Funktion für die grüne Stadt! Die Bevölkerung einer weiteren Stadt ist am Anfang 800000 und wächst um 40% nach 17 Jahren. Nach 4 weiteren Jahren wächst sie insgesamt um 45%. Mit Hilfe der zwei Werte am Anfang und nach 21 Jahren erstellen Sie ein exponentielles Wachstumsmodell. Nach wie viel Zeit in Jahrzehnten wird sich nach diesem Modell die Bevölkerung verdoppeln? Beurteilen Sie, ob nach diesem Modell der Wert nach 17 Jahren akzeptiert werden kann, wenn eine Abweichung von 200000 toleriert wird. Was soll man ändern, wenn der Wert außerhalb der hinnehmbaren Abweichung steht, das Modell oder den Wert? Argumentieren Sie, warum ein exponentielles Modell für den Bevölkerungswachstum auf lange Sicht nicht realistisch sein kann! Sei $T_{D}\$die Verdoppelungszeit. Kreuzen Sie die zutreffende(n) Aussage(n) an! Nach 4 $T_{D}\$wird die Bevölkerung das 8-fache sein. Nach 5 $T_{D}\$wird die Bevölkerung das 32-fache sein. Nach 2 $T_{D}\$wird die Bevölkerung das 3-fache sein. Nach 3 $T_{D}\$nimmt die Bevölkerung um $800\%\$zu. Nach 3 $T_{D}\$wird die Bevölkerung das 8-fache sein. Für noch eine weitere Stadt gilt für die Bevölkerung in Millionen in Abhängigkeit von der Zeit in Jahren folgende Gleichung: $T(t)=5{,}7+2{,}3\cdot e^{-b\cdot t}$ Wie viel ist der Wert am Anfang? Was bedeutet die Zahl 5,7 in dieser Gleichung? Wie schnell nimmt die Bevölkerung nach 276 Monaten ab, wenn $b=0{,}18?$ Wie viel ist dann die mittlere Abnahme zwischen 6 und 17 Jahren? Nehmen wir an, dass nach 13 Jahren die Bevölkerung um 35% abnimmt. Wie viel Prozent der Bevölkerung wäre in diesem Fall nach 21 Jahren übrig geblieben?

3. 
   

   4 verschiedene Antibiotika wurden in Petrischalen getestet. Im folgendem Diagramm ist der Prozentsatz der gebliebenen Bakterien in Abhängigkeit von der Zeit in Stunden dargestellt, sie nehmen Exponentiell ab (mit der Ausnahme von Baktrex). Zeichnen Sie in Diagramm einen linearen Zusammenhang eines Antibiotikums, das nach 6 Stunden wirksamer als Antibiox sein wird. Folgende Gleichung über ein bestimmtes Antibiotikum wird gelöst: $0{,}5=0{,}87^{t}.\$Was bedeutet die Lösung dieser Gleichung in diesem Zusammenhang? Folgende Gleichung über ein bestimmtes Antibiotikum wird gelöst: $0{,}3=0{,}87^{t}.\$Was bedeutet die Lösung dieser Gleichung in diesem Zusammenhang? Nach wie viel Zeit bleibt 15% der Bakterien, wenn man Antibiox benutzt? Mit Hilfe des Diagramms erstellen Sie die Funktion für Antibiox! Ein weiteres Antibiotikum eliminiert 20% der Bakterien nach 2,5 Stunden. Nach 30 weiteren Minuten eliminiert es insgesamt 25% der Bakterien. Mit Hilfe der zwei Werte am Anfang und nach 2,5 Stunden erstellen Sie ein exponentielles Wachstumsmodell! Nach wie viel Zeit in Minuten werden nach diesem Modell die Bakterien halbiert? Beurteilen Sie, ob nach diesem Modell der gegebene Wert nach 180 Minuten akzeptiert werden kann, wenn eine Abweichung von 5 Prozenteinheiten toleriert wird. Was soll man ändern, wenn der Wert außerhalb der hinnehmbaren Abweichung steht, das Modell oder den Wert? Argumentieren Sie, ob die Bakterien nach diesem Modell irgendwann völlig verschwinden! Sei $T_{H}\$die Halbwertszeit. Kreuzen Sie die zutreffende(n) Aussage(n) an! Nach 3 $T_{H}\$wird ${\tfrac {1}{27}}\$der Bakterien übrig bleiben Nach 2 $T_{H}\$wird ${\tfrac {1}{4}}\$der Bakterien übrig bleiben Nach 4 $T_{H}\$werden die Bakterien $6{,}25\%\$des Ausgangswertes sein Nach 3 $T_{H}\$nehmen die Bakterien um $87{,}5\%\$ab Nach 4 $T_{H}\$werden ${\tfrac {1}{4}}\$der Bakterien übrig bleiben Für noch ein weiteres Antibiotikum gilt für den Prozentsatz der verbliebenen Bakterien in Abhängigkeit von der Zeit in Stunden folgende Gleichung: $T(t)=31+69\cdot e^{-b\cdot t}$ Wie viel ist der Wert am Anfang? Was bedeutet die Zahl 31 in dieser Gleichung? Wie schnell nehmen die Bakterien nach 300 Minuten ab, wenn $b=0{,}07?$ Wie viel ist dann die mittlere Abnahme zwischen 2 und 3 Stunden? Nehmen wir an, dass nach 5 Stunden 69% der Bakterien eliminiert wird. Wie viel Prozent der Bakterien wäre in diesem Fall nach 8 Stunden übrig geblieben?

4. 
   

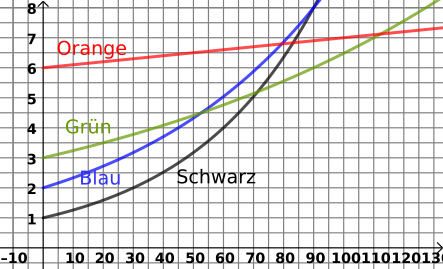
   Das Wachstum der Bevölkerung (in Millionen) in 4 verschiedenen (imaginären) Städten in Abhängigkeit von der Zeit in Jahren wurde im Diagramm zusammengefasst. Zeichnen Sie in Diagramm einen linearen Zusammenhang einer Stadt, die am Anfang 800000 Einwohner hat und ab 20 Jahren später mehr Einwohner als die grüne Stadt hat. (Wird sie dann immer eine größere Bevölkerung haben?) Folgende Gleichung über eine bestimmte Stadt wird gelöst: $2=1{,}791^{t}.\$Was bedeutet die Lösung dieser Gleichung in diesem Zusammenhang? Folgende Gleichung über eine bestimmte Stadt wird gelöst: $5=1{,}791^{t}.\$Was bedeutet die Lösung dieser Gleichung in diesem Zusammenhang? Nach wie viel Zeit hat die blaue Stadt das 1,5-fache ihrer Anfangsbevölkerung erreicht? Mit Hilfe des Diagramms erstellen Sie die Funktion für die schwarze Stadt! Die Bevölkerung einer weiteren Stadt ist am Anfang 1,5 Millionen und wächst um 60% nach 25 Jahren. Nach 4 weiteren Jahren wächst sie insgesamt um 75%. Mit Hilfe der zwei Werte am Anfang und nach 29 Jahren erstellen Sie ein exponentielles Wachstumsmodell. Nach wie viel Zeit in Jahrzehnten wird sich nach diesem Modell die Bevölkerung verdoppeln? Beurteilen Sie, ob nach diesem Modell der Wert nach 25 Jahren akzeptiert werden kann, wenn eine Abweichung von 700000 toleriert wird. Was soll man ändern, wenn der Wert außerhalb der hinnehmbaren Abweichung steht, das Modell oder den Wert? Argumentieren Sie, warum ein exponentielles Modell für den Bevölkerungswachstum auf lange Sicht nicht realistisch sein kann! Sei $T_{D}\$die Verdoppelungszeit. Kreuzen Sie die zutreffende(n) Aussage(n) an! Nach 3 $T_{D}\$wird die Bevölkerung das 8-fache sein. Nach 2 $T_{D}\$wird die Bevölkerung das 6-fache sein. Nach 5 $T_{D}\$wird die Bevölkerung das 16-fache sein. Nach 2 $T_{D}\$nimmt die Bevölkerung um $300\%\$zu. Nach 3 $T_{D}\$wird die Bevölkerung das 12-fache sein. Für noch eine weitere Stadt gilt für die Bevölkerung in Millionen in Abhängigkeit von der Zeit in Jahren folgende Gleichung: $T(t)=4{,}3+2{,}7\cdot e^{-b\cdot t}$ Wie viel ist der Wert am Anfang? Was bedeutet die Zahl 4,3 in dieser Gleichung? Wie schnell nimmt die Bevölkerung nach 0,36 Jahrzehnten ab, wenn $b=0{,}2?$ Wie viel ist dann die mittlere Abnahme zwischen 8 und 13 Jahren? Nehmen wir an, dass nach 17 Jahren die Bevölkerung um 45% abnimmt. Wie viel Prozent der Bevölkerung wäre in diesem Fall nach 21 Jahren übrig geblieben?