MathemaTriX ⋅ Lineare Funktion

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

LINKS

 ACHTUNG! 
Zumindest Aufgabe 1 von jedem Aufgabentyp probieren,
sie sind unterschiedlich!

	lle	Gaben
	uf-

Aufgaben

Lineare Funktion Alltagsbeispiel

1. 
   

   Die Talstation einer Seilbahn befindet sich auf 346 m Höhe, die erste Station auf dem Berg auf 930 m Höhe und in einer horizontalen Abstand von 2,84 km. Nehmen wir an, dass das Seil gerade ist. Fertigen Sie eine Skizze dieses Zusammenhangs in einem Koordinatensystem an. Wie lautet die entsprechende lineare Funktion? Auf welcher Höhe befindet sich das Seil in einem horizontalen Abstand von 490 m von der Talstation entfernt? Bei welchem horizontalen Abstand ist die Höhe 560 m?

2. 
   

   Ein Swimmingpool ist nach unten geneigt. An einem Rand ist die Tiefe 1,4 m, am anderen 2 m, der Abstand dazwischen ist 50 m. Fertigen Sie eine Skizze dieses Zusammenhangs in einem Koordinatensystem an. Wie lautet die entsprechende lineare Funktion? Wie viel ist die Tiefe genau in der Mitte? Bei welchem horizontalen Abstand (vom weniger tiefen Rand gemessen) ist die Tiefe 1,6 m?

3. 
   

   Nehmen wir an, dass die Menge des erzeugten Plastikmülls eines Haushalts vom Gehalt abhängig ist. Bei keinem Gehalt ist der Müll 0,8 kg pro Monat, bei 2000 € Gehalt 8,9 kg pro Monat. Fertigen Sie eine Skizze dieses Zusammenhangs in einem Koordinatensystem an. Wie lautet die entsprechende lineare Funktion? Wie viel wäre nach diesem Modell der Müll bei einem Gehalt von 280000 €? Bei welchem Gehalt wäre der Müll 3,8 kg?

4. 
   

   Nehmen wir an, dass es einen linearen Zusammenhang zwischen täglichem Obstkonsum und ökologischen Fußabdruck besteht: je größer der Konsum ist, desto kleiner der Fußabdruck. Wenn kein Obst gegessen wird, ist der Fußabdruck 4 t $CO_{2}$ pro Monat, bei 300 g täglichen Konsum 2,8 t $CO_{2}$ pro Monat. Fertigen Sie eine Skizze dieses Zusammenhangs in einem Koordinatensystem an. Wie lautet die entsprechende lineare Funktion? Wie viel ist der Fußabdruck nach diesem Modell bei einem Konsum von 880 g? Bei welchem Konsum verschwindet der Fußabdruck nach diesem Modell?

Eine lineare Funktion mit Hilfe von zwei Punkten ermitteln

1. 
   

   Das Diagramm stellt den Gewinn bei der Produktion von Mehl dar. Berechnen Sie mit Hilfe des Diagramms die entsprechende lineare Funktion! Welche sind die Einheiten von y, x und der Steigung?

2. 
   

   Das Diagramm gibt die Frequenz einer Welle in Bezug auf ihre Länge an. Berechnen Sie mit Hilfe des Diagramms die entsprechende lineare Funktion! Welche sind die Einheiten von y, x und der Steigung?

3. 
   

   Das Diagramm gibt die Dichte einer Flüssigkeit in Bezug auf ihre Temperatur an. Berechnen Sie mit Hilfe des Diagramms die entsprechende lineare Funktion! Welche sind die Einheiten von y, x und der Steigung?

4. 
   

   Das Diagramm stellt ein Modell der Abhängigkeit der Lebenserwartung vom Rauchen dar. Berechnen Sie mit Hilfe des Diagramms die entsprechende lineare Funktion! Welche sind die Einheiten von y, x und der Steigung?

5. 
   

   Das Diagramm gibt die Höhe des Seils einer Bergbahn in Abhängigkeit von der horizontalen Abstand von der Talstation her an. Berechnen Sie mit Hilfe des Diagramms die entsprechende lineare Funktion! Welche sind die Einheiten von y, x und der Steigung?

6. 
   

   Das Diagramm gibt die sogenannten ökologischen Fußabdruck (in Tonnen CO2) in Abhängigkeit vom Obstkonsum (in g) an. Berechnen Sie mit Hilfe des Diagramms die entsprechende lineare Funktion! Welche sind die Einheiten von y, x und der Steigung?

7. 
   

   Das Diagramm gibt den Wasserpegel (in m) eines Wassertanks in Abhängigkeit von der Zeit (in h) an. Berechnen Sie mit Hilfe des Diagramms die entsprechende lineare Funktion! Welche sind die Einheiten von y, x und der Steigung?

8. 
   

   Das Diagramm stellt ein Modell der Abhängigkeit der Lebenserwartung vom Rauchen dar. Berechnen Sie mit Hilfe des Diagramms die entsprechende lineare Funktion! Welche sind die Einheiten von y, x und der Steigung?

Textaufgaben zu den linearen Funktionen

1. 
   

   Der 69 Liter Tank eines Generators ist zu zwei drittel voll und verbraucht jede 10 Minuten halbes Liter Brennstoff. Geben Sie zuerst den Zusammenhang zwischen Zeit und Volumen des Brennstoffes als lineare Funktion an! Wie lang dauert es, bis der Tank leer wird? Nach wie viel Zeit hat der Tank noch 25 Liter?

2. 
   

   Eine Rakete wird aus einem Flugzeug, dass sich auf 500m befindet, abgeschossen und fliegt jede 4 Minuten 14 km höher. Geben Sie zuerst den Zusammenhang zwischen Höhe und Zeit als lineare Funktion an! Wie hoch befindet sie sich nach 25s? Wie lang braucht sie (in s und in min), bis sie eine Höhe von 4km erreicht?

3. 
   

   Eine Kerze ist 1,8 dm hoch und brennt um 1,4 cm pro Stunde. Geben Sie zuerst den Zusammenhang zwischen Zeit und Höhe als lineare Funktion an! Nach wie vielen Minuten brennt sie aus? Wie viel ist ihr Höhe nach 99s?

4. 
   

   Ein Auto fährt von Paris nach der 311 km entfernten Stadt Brüssels mit 72 km/h durchschnittlicher Geschwindigkeit. Geben Sie zuerst den Zusammenhang zwischen Zeit und Abstand von Brüssels als lineare Funktion an! Wie lang dauert die Fahrt? Wie weit von Brüssels und wie weit von Paris entfernt befindet sich das Auto nach 24 min? Wie viel kg ist der CO2 Ausstoß nach 24 min, wenn 7 kg nach 40 km ausgestoßen werden?

5. 
   

   Ein Hotelschwimmbad mit 74 m3 Wasser wird mit Hilfe von zwei Pumpen ausgeleert. Die eine Pumpe leert 17 Liter pro Minute, die andere 13 Liter pro Minute. Geben Sie zuerst den Zusammenhang zwischen Volumen des verbliebenen Wassers und Zeit als lineare Funktionen an! Wie lang dauert es, bis das Schwimmbad leer wird? Nach wie viel Zeit hat das Schwimmbad noch 14 m3 Wasser?

6. 
   

   Ein Fallschirmspringer springt aus einem Flugzeug. Ab eine Höhe von 2,3 km fällt er mit einer konstanten Geschwindigkeit von 44 m/s weiter. Geben Sie zuerst den Zusammenhang zwischen Höhe und Zeit als lineare Funktion an, ab den Zeitpunkt, wo die Geschwindigkeit konstant wird! Wie hoch befindet sie sich nach 45s? Wie lang braucht sie (in s und in min), bis sie eine Höhe von 1,3 km erreicht? Nach wie viel Zeit wird sie den Boden erreichen, wenn der Fallschirm nicht aufgeht?

7. 
   

   Ein Schwimmbecken wird mit Wasser gefüllt. In 4 min laufen 13 m3 hinein. Stellen Sie zuerst den Zusammenhang zwischen Zeit und Volumen des Wassers als lineare Funktion dar! Nach wie vielen Minuten ist das Volumen 66 m3? Wie viel ist das Volumen nach 14 min?

8. 
   

   Ein Auto fährt von Wien nach der 287 km entfernten Stadt Salzburg. Durchschnittlich fährt das Auto 138 km in 2 Stunden. Stellen Sie zuerst den Zusammenhang zwischen Zeit und Abstand von Salzburg als lineare Funktion dar! Wie lang dauert die Fahrt? Wie weit von Wien und wie weit von Salzburg entfernt befindet sich das Auto nach 15 min? Wie viel kg ist der CO2 Ausstoß nach 15 min, wenn 7 kg nach 33 km ausgestoßen werden?

Mittlere Änderungsrate

1. 
   

   Das Diagramm zeigt die Temperatur eines Patienten im Verlauf des Tages. Wie viel war die absolute Temperaturänderung zwischen 20 und 22 Uhr? Wie viel war die mittlere Temperaturänderung zwischen 6 und 22 Uhr (mit Einheit)? Wie viel war die mittlere Temperaturänderung zwischen 4 und 14 Uhr? Interpretieren Sie das Ergebnis!

2. 
   

   4 verschiedene Waschmittel wurden auf ihre Effektivität geprüft. Das Diagramm zeigt welcher Anteil (in Prozent) des Schmutzes geblieben ist in Bezug auf die Zeit (in Minuten). Wie viel war die absolute prozentuale Änderung für Blautrex zwischen 3. und 15. Minute? Wie viel war die mittlere prozentuale Änderung für Mavrit zwischen 3 und 23 Minute (mit Einheit)? Wie viel war die mittlere prozentuale Änderung für Linix zwischen 8 und 16 Minute? Interpretieren Sie das Ergebnis!

3. 
   

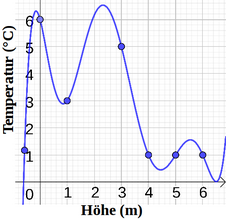
   Das Diagramm stellt die Temperatur in einem Wassertank in Bezug auf seine Höhe dar. Wie viel ist die absolute Temperaturänderung zwischen 3 und 5,5 m? Wie viel ist die mittlere Temperaturänderung zwischen 1 und 4 m (mit Einheit)? Wie viel ist die mittlere Temperaturänderung zwischen 4 und 5 m? Interpretieren Sie das Ergebnis!

4. 
   

   Das Wachstum der Bevölkerung (in Millionen) in 4 verschiedenen (imaginären) Städten in Abhängigkeit von der Zeit in Jahren wurde im Diagramm zusammengefasst. Wie viel ist das absolute Bevölkerungswachstum für die grüne Stadt für die ersten 20 Jahren? Wie viel ist das mittlere Bevölkerungswachstum für die schwarze Stadt für die ersten 60 Jahren? (mit Einheit)? Wie viel ist das mittlere Bevölkerungswachstum für die schwarze Stadt zwischen 60 und 90 Jahr? Interpretieren Sie das Ergebnis!

Die Steigung und ihre Zusammenhänge

1. 
   

   Zeigen Sie, dass die Steigung s einer linearen Funktion $\textstyle s={\frac {\Delta y}{\Delta x}}\$ist!

2. 
   

   Welcher Zusammenhang besteht zwischen Steigung und direkter Proportionalität?

3. 
   

   Welcher Zusammenhang besteht zwischen Steigung und Ähnlichkeit von Figuren?

Darstellungen der linearen Funktion

1. 
   

   Wie lautet die implizite und die Vektorform der linearen Funktion $y={\tfrac {2}{3}}x-5$? Wie lautet die explizite und die Vektorform der linearen Funktion $5x+2y=13$? Wie lautet die explizite und die implizite Form der linearen Funktion ${\tbinom {x}{y}}={\tbinom {3}{4}}t+{\tbinom {0}{3}}$? Berechnen Sie den Winkel zwischen den Geraden der zweiten und der dritten Funktion!

2. 
   

   Wie lautet die implizite und die Vektorform der linearen Funktion $y=-{\tfrac {4}{7}}x--{\tfrac {3}{7}}$? Wie lautet die explizite und die Vektorform der linearen Funktion $-mx+y=n$? Wie lautet die explizite und die implizite Form der linearen Funktion ${\tbinom {x}{y}}={\tbinom {-m}{1}}t+{\tbinom {0}{n}}$? Berechnen Sie den Winkel zwischen den Geraden der zweiten und der dritten Funktion!

3. 
   

   Wie lautet die implizite und die Vektorform der linearen Funktion $y={\tfrac {n}{m}}x-c$? Wie lautet die explizite und die Vektorform der linearen Funktion $-5x-c\ y=13$? Wie lautet die explizite und die implizite Form der linearen Funktion ${\tbinom {x}{y}}={\tbinom {m}{n}}t+{\tbinom {0}{n}}$? Berechnen Sie den Winkel zwischen den Geraden der ersten und der dritten Funktion!

4. 
   

   Wie lautet die implizite und die Vektorform der linearen Funktion $y=bx-5$? Wie lautet die explizite und die Vektorform der linearen Funktion $2\ x-q\ y=w$? Wie lautet die explizite und die implizite Form der linearen Funktion ${\tbinom {x}{y}}={\tbinom {2}{-q}}t+{\tbinom {3}{4}}$? Berechnen Sie den Winkel zwischen den Geraden der zweiten und der dritten Funktion!

5. 
   

   Wie lautet die implizite und die Vektorform der linearen Funktion $y=0{,}3x-5$? Wie lautet die explizite und die Vektorform der linearen Funktion $3y-2{,}5x=13$? Wie lautet die explizite und die implizite Form der linearen Funktion ${\tbinom {x}{y}}={\tbinom {2}{-4}}t+{\tbinom {3}{3}}$? Berechnen Sie den Winkel zwischen den Geraden der zweiten und der dritten Funktion!

6. 
   

   Wie lautet die implizite und die Vektorform der linearen Funktion $y={\sqrt {5}}\ x+3$? Wie lautet die explizite und die Vektorform der linearen Funktion $x-y=13$? Wie lautet die explizite und die implizite Form der linearen Funktion ${\tbinom {x}{y}}={\tbinom {-2}{1}}t+{\tbinom {3}{-5}}$? Berechnen Sie den Winkel zwischen den Geraden der zweiten und der dritten Funktion!