MathemaTriX ⋅ Prozentrechnung

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

 ACHTUNG! 
Zumindest Aufgabe 1 von jedem Aufgabentyp probieren,
sie sind unterschiedlich!

	lle	Gaben
	uf-

Theorie in Kürze (mit Geogebra)

• Der Wert am Anfang (Grundwert) ist 100%. Das ist der Wert, mit dem verglichen wird ("als", Genitiv oder "von"). Bei zeitlicher Reihenfolge ist das der erste Wert (außer wenn der zweite Wert der Vergleichswert ist).
• Prozentberechnungen gehen notfalls (und am Einfachsten) mit Hilfe der Schlussrechnung. Am besten allerdings mit der Umrechnung arbeiten (siehe weiter: "Komma verschieben")
• Prozent ist eine Zahl. Prozent bedeutet "Hundertstel".
• Daher ist 100%=1
• Also: von % zur Zahl Komma zwei mal links, von Zahl zu % zwei mal rechts verschieben.
• Bei Wachstum addiert man den "Wachstumsprozent" zu 100%, bei Abnahme wird subtrahiert.

Beispiele: 0,02%=0,0002; 230=23000%; 230%=2,3 also 130% mehr als der Anfangswert; 0,8=80% also 20% weniger als der Anfangswert.

Bei einer Reihenfolge von Prozentänderungen ist das Ergebnis nicht die Summe der Prozentänderungen: Der Grundwert ist nicht der Gleiche!

Beispiel: Eine Pflanze wird 20% größer und dann noch 50% größer. Das Endergebnis ist nicht 70% größer!
Der Grundwert ist nicht der Gleiche!
Um die tatsächliche Gesamtänderung zu berechnen gehen wir so vor:
$100\%+20\%=120\%=1{,}2.\$
$100\%+50\%=150\%=1{,}5.\$
$1{,}2\cdot 1{,}5=1{,}8=180\%.\$
Also 80% Wachstum. Klarer wird es mit konkreten Zahlen.

Grundaufgaben der Prozentrechnung

1. 
   

   Ein Supermarktketteneigentümer macht 0,09 € Gewinn pro Zwölfflaschenkiste eines Biers. Wie viel ist sein tägliches Gewinn aus diesem Bier, wenn im ganzen Land täglich 264000 Flaschen Bier verkauft werden? Wie viele Flaschen Bier müssen verkauft werden, damit sein Gewinn 990 € ist?

2. 
   

   Ein Baum setzt durchschnittlich jede 25 min 0,8 Liter Sauerstoff frei. Wie viel Sauerstoff setzt er in 0,7 min frei? Wie lang braucht er, um 459 Liter freizusetzen?

3. 
   

   3,5 Liter eines Stoffes wiegen 14,7 kg. Wie viel wiegen 0,0175 Liter? Wie viel Liter sind 3850kg?

4. 
   

   In EU produzierte im Jahr (365 Tage) 2016 eine Person durchschnittlich 6,5 Tonnen CO2. Wie viel war die Produktion pro Woche (7 Tage)? Wie viele Tage hätte sie gebraucht, um 0,13 Tonnen zu produzieren?

5. 
   

   Nach einer Finanzkrise verbraucht jede Person durchschnittlich 6234 Liter Benzin weniger pro Woche. Wie viel ist die Reduktion pro Monat (30 Tage)?

6. 
   

   Für 12 Kühe braucht man 73,8 Tonnen Futter bis sie geschlachtet werden. Wie viel Tonnen Futter braucht man für 15 Kühe? Für wie viele Kühe braucht man 123 Tonnen?

7. 
   

   0,7 km² Ackerland reichen für die Ernährung von 23 vegetarische Menschen. Für wie viele Menschen reichen 3,5 km²? Wie viel Ackerland brauchen 575 vegetarische Menschen?

8. 
   

   Wenn eine Person mit dem Fahrrad zur Arbeit fährt, ist ihr CO2 Ausstoß 11,2g. Der Abstand zur Arbeit ist 8 km. Wie weit fährt man. wenn der CO2 Ausstoß 0,448 g ist? Wie viel ist der CO2 Ausstoß, wenn eine Person mit dem Fahrrad 20 km fährt?

Prozentrechnung bei Wachstum und Abnahme

1. 
   

   Das Gehalt eines Beamten war 1800€ und wurde um 2,5% gekürzt. Berechnen sie das neue Gehalt! Um wie viel € wurde das Gehalt gekürzt?

2. 
   

   Eine Pflanze ist 60 cm hoch. Wie lang ist sie danach, wenn sie 60% kleiner wird? Wie viel cm kleiner wird sie?

3. 
   

   Ein Gummiband ist 24 cm und wird um 150% verlängert. Wie viel ist die neue Länge? Wie viel cm länger wird es?

4. 
   

   Das Gehalt einer Managerin war 650000€ und wurde nach eine Massenentlassung von Angestellten um 5,4% erhöht. Berechnen sie das neue Gehalt! Um wie viel € wurde das Gehalt erhöht?

5. 
   

   Eine Person wiegt 68 kg und nimmt 5% zu. Wie viel ist ihr neues Gewicht? Wie viel kg hat sie zugenommen?

6. 
   

   Eine Person wiegt 72 kg und nimmt 5% ab. Wie viel ist ihr neues Gewicht? Wie viel kg hat sie abgenommen?

7. 
   

   Ein Lied dauert 3,4 min. Eine verlängerte Version dauert 15% länger. Wie lang dauert die verlängerte Version? Wie viel Minuten mehr dauert sie?

8. 
   

   Die Ölreserven der Erde reichen für 20 Jahre noch. Wenn wir etwas sparen, dann werden sie um 150% länger ausreichen. Wie lang werden sie dann ausreichen? Wie viele Jahre mehr sind es?

Umkehraufgaben der Prozentrechnung

1. 
   

   Der pro Kopf Energieverbrauch in Deutschland ist zwischen den Jahren 2000 und 2011 um 20% auf 5,4 kW gestiegen. Wie viel war er im Jahr 2000?

2. 
   

   Ein Tisch wurde um 10% geschnitten. Die neue Länge ist 2,7m. Berechnen Sie die ursprüngliche Länge!

3. 
   

   Ein Baby wächst in einem Jahr um 20% auf 42 cm. Wie viel war die ursprüngliche Größe?

4. 
   

   Der pro Kopf Energieverbrauch in EU sei 3,6 kW und damit 1400% mehr als in Kongo. Wie viel ist er im Kongo?

Relative Änderung

1. 
   

   Das Diagramm zeigt die Funktion T(t) der Temperatur eines Patienten im Verlauf des Tages. Wie viel war die absolute Temperaturänderung zwischen 2 und 12 Uhr? Wie viel war die relative Temperaturänderung zwischen 6 und 22 Uhr Wie viel war die relative Temperaturänderung zwischen 4 und 14 Uhr? Interpretieren Sie das Ergebnis! Was bedeutet ${\tfrac {T(t_{1})-T(t_{2})}{T(t_{1})}}=0{,}032\$in diesem Zusammenhang? Was bedeutet ${\tfrac {T(t_{1})-T(t_{2})}{T(t_{2})}}=-0{,}024\$in diesem Zusammenhang?

2. 
   

   4 verschiedene Waschmittel wurden auf ihre Effektivität geprüft. Das Diagramm zeigt welcher Anteil (in Prozent) des Schmutzes geblieben ist in Bezug auf die Zeit (in Minuten). Die entsprechenden Funktionen sind L(t) für Linix, B(t) für Blautrex, R(t) für Rotrum und M(t) für Mavrit. Wie viel war die absolute prozentuale Änderung für Rotrum zwischen 5 und 17 Minute? Wie viel war die relative prozentuale Änderung für Mavrit zwischen 3 und 23 Minute Wie viel war die relative prozentuale Änderung für Linix zwischen 8 und 16 Minute? Interpretieren Sie das Ergebnis! Was bedeutet ${\tfrac {B(t_{2})-B(t_{1})}{B(t_{1})}}=-0{,}032\$in diesem Zusammenhang? Was bedeutet ${\tfrac {L(t_{1})-L(t_{2})}{L(t_{2})}}=2{,}024\$in diesem Zusammenhang?

3. 
   

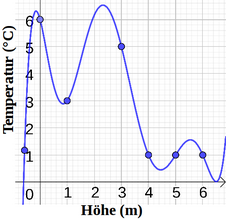
   Das Diagramm stellt die die Funktion T(h) der Temperatur in einem Wassertank in Bezug auf seine Höhe in m dar. Wie viel ist die absolute Temperaturänderung zwischen 2 und 3 m? Wie viel ist die relative Temperaturänderung zwischen 1 und 4 m Wie viel ist die relative Temperaturänderung zwischen 4 und 5 m? Interpretieren Sie das Ergebnis! Was bedeutet ${\tfrac {T(h_{1})-T(h_{2})}{T(h_{1})}}=-3{,}032\$in diesem Zusammenhang? Was bedeutet ${\tfrac {T(h_{1})-T(h_{2})}{T(h_{2})}}=1{,}024\$in diesem Zusammenhang?

4. 
   

   Das Wachstum der Bevölkerung (in Millionen) in 4 verschiedenen (imaginären) Städten in Abhängigkeit von der Zeit in Jahren wurde im Diagramm zusammengefasst. Die entsprechenden Funktionen sind R(t) für Orange, G(t) für Grün, B(t) für Blau und S(t) für Schwarz. Wie viel ist das absolute Bevölkerungswachstum für die blaue Stadt für die ersten 45 Jahren? Wie viel ist das relative Bevölkerungswachstum für die schwarze Stadt für die ersten 60 Jahren? Wie viel ist das relative Bevölkerungswachstum für die schwarze Stadt zwischen 60 und 90 Jahr? Interpretieren Sie das Ergebnis! Was bedeutet ${\tfrac {G(t_{1})-G(t_{2})}{G(t_{1})}}=-0{,}032\$in diesem Zusammenhang? Was bedeutet ${\tfrac {S(t_{2})-S(t_{1})}{S(t_{2})}}=0{,}024\$in diesem Zusammenhang?

Kombinationsaufgaben der Prozentrechnung

1. 
   

   Die Produzenten eines Filmes hatten vor dem Schnitt zu viel Material. Beim ersten Schnitt haben Sie 80% geschnitten. Das war ihnen aber doch zu kurz, daher haben sie eine neue um 15% längere (als der geschnittene Film) Version gemacht. Die letzte Version dauert 1,61 Stunden. Berechnen Sie die ursprüngliche Dauer, also die Dauer des ungeschnittenen Films! Ist der Film insgesamt länger oder kürzer geworden und um wie viel Prozent?

2. 
   

   Die Nase von Pinocchio ist nach einer Lüge um 50% gewachsen, danach ist sie um 35% auf 2,34 cm zurückgegangen. Wie groß war sie ursprünglich? Ist sie insgesamt größer oder kleiner geworden und um wie viel Prozent?

3. 
   

   Das Gehalt einer Arbeiterin wurde anfangs um 12% erhöht, dann aber um 10% auf 1764 € wieder gekürzt. Wie groß war es ursprünglich? Wurde es insgesamt erhöht oder reduziert und um wie viel Prozent?

4. 
   

   Frankreich bezieht mehr als 70% seiner elektrischen Energie aus Kernkraftwerken. Ein (riesiges) Problem dabei ist der radioaktiver Müll, der für Hunderte bis Tausende Jahre gefährlich bleibt. Nehmen wir an, dass die Menge eines solchen Stoffes zwischen 1993 und 1994 um 4% gestiegen und zwischen 1994 und 1995 um weiter 5% auf 16,38 t gestiegen ist. Wie viele t wäre sie ursprünglich? Um wie viel Prozent wäre sie insgesamt gestiegen?

5. 
   

   Katia ist um 20% größer als Manina. Vladimir ist 176,7 cm groß und 5% kleiner als Katia. Wie groß ist Manina? Wie viel Prozent kleiner oder Größer als Vladimir ist Manina

6. 
   

   Die Nase von Pinocchio wächst nach einer Luge um 150% und dann geht sie um 60% auf 2,5 cm zurück. Wie lang war sie ursprünglich? Ist sie insgesamt größer oder kleiner geworden und um wie viel Prozent?

7. 
   

   Das Volumen des Magens einer Person wächst nach dem Essen um 120% und dann geht es um 35% auf 500,5 ml zurück. Wie groß war er ursprünglich? Wurde er insgesamt größer oder kleiner und um wie viel Prozent?

8. 
   

   Das Volumen des Herzens einer Person wächst bei einem Puls um 150% und dann geht es um 60% auf 440 ml zurück. Wie viele war es ursprünglich? Wurde er insgesamt größer oder kleiner und um wie viel Prozent?

Prozentrechnung und Brüche

1. 
   

   Ein viertel der Bevölkerung in Deutschland sind armutsgefährdet. Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie! richtig falsch 4% sind gefährdet. Das 0,25-fache der Bevölkerung sind armutsgefährdet. Das Verhältnis „nicht gefährdet“ zu „gefährdet“ beträgt 3 : 1.

2. 
   

   Die 20 reichsten Personen eines Staates besitzen vier fünftel des gesamten Vermögens. Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie! richtig falsch Die reichsten 20 besitzen 20% des Vermögens. Das Verhältnis des Vermögens der reichsten zum Rest ist 5 : 2. Die reichsten haben das 5-Fache Vermögen wie der Rest der Bevölkerung

3. 
   

   Zwei fünftel der Bevölkerung eines Staates sind für eine Diktatur. Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie! richtig falsch Das Verhältnis der Anhänger einer Diktatur zum Rest ist 2 : 5. 60% der Bevölkerung ist nicht für eine Diktatur Die Personen, die nicht für eine Diktatur sind, sind das 1,5-Fache der Personen, die dafür sind

4. 
   

   Zwei drittel der Bevölkerung kauft jedes Jahr ein neues Handy. Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie! richtig falsch Diejenigen, die jedes Jahr ein neues Handy kaufen, sind doppelt so viel, wie diejenigen, die es nicht tun. Das Verhältnis derjenigen, die ein neues Handy jedes Jahr kaufen, zur ganzen Bevölkerung ist 2 : 1. $33{,}{\dot {3}}\%\$kaufen nicht ein neues Handy jedes Jahr

5. 
   

   Zwei fünftel einer Ernte sind faul. Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie! richtig falsch 20% ist faul. Das 0,6-fache der Ernts ist nicht faul. Das Verhältnis „faul“ zu „nicht faul“ beträgt 2 : 3.

6. 
   

   Drei fünftel der Zuschauer eines Fußballspiels sind für "Milano". Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie! richtig falsch 30% der Zuschauer sind für "Milano". Das 0,6-fache der Zuschauer sind nicht für "Milano". Das Verhältnis der "Milano" Anhänger zu den restlichen beträgt 3 : 5.

7. 
   

   Zwei siebtel des Gewichts eines Kuchens ist Zucker. Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie! richtig falsch 20% des Gewichts ist Zucker. Das $0{,}{\overline {285714}}{\text{-fache}}\$ des Gewichts ist Zucker. Das Verhältnis Zucker zu den restlichen Inhalten beträgt 2 : 5.

8. 
   

   Zwei fünftel der Kinder einer Klasse sind Buben. Welche der folgenden Aussagen stimmen mit dieser Aussage überein? Kreuze jeweils an, ob die Aussage richtig oder falsch ist. Begründen Sie! richtig falsch 40% der Kinder sind Buben. Das $0{,}4{\text{-fache}}\$ der Kinder sind nicht Buben. Das Verhältnis der restlichen Kindern zu den Buben beträgt 3 : 2.

Prozentrechnung abstrakt

1. 
   

   In den folgenden Beispielen gehen wir davon aus, dass es in der Bevölkerung so viele Männer gibt wie Frauen. Der Anteil der Raucher unter der Bevölkerung ist 27,5%. Der Anteil der Raucher unter den Männern ist 35%. Wie viel ist der Anteil der Raucherinnen unter den Frauen? Die Lebenserwartung der Bevölkerung ist 80 Jahre. Die Lebenserwartung der nicht-Raucher ist 82,4 Jahre. Wie viele Jahre weniger ist die Lebenserwartung der Rauchenden in Vergleich zu den nicht-Rauchenden Personen? Wäre das Rauchen die einzige Erklärung für den Unterschied der Lebenserwartung zwischen den beiden Geschlechtern, wie viel Jahre wäre diese für Männer und für Frauen? Welche Information ist noch notwendig, um den Einfluss des Rauchens auf den Lebenserwartungsunterschied zwischen den Geschlechtern genauer zu bestimmen? Wenn wir letztere Information haben, was ist noch notwendig, um zu entscheiden, ob das Rauchen bei dieser Frage tatsächlich der einzige bestimmende Faktor ist? Vergleichen Sie ihre Ergebnisse mit tatsächlichen offiziellen Statistiken!

2. 
   

   Die Seite einer Figur F ist das 1,5-fache der Seite einer ähnlichen Figur G. Um wie viel Prozent größer ist der Umfang von F als der von G? Um wie viel Prozent kleiner ist der Umfang von G als der von F? Um wie viel Prozent größer ist die Fläche von F als die Fläche von G? Um wie viel Prozent kleiner ist die Fläche von G als die von F?

3. 
   

   Der Radius einer Kugel A ist um 150% größer als der Radius einer Kugel B. Um wie viel Prozent größer ist die Oberfläche von A in Bezug auf B? Um wie viel Prozent größer ist das Volumen von A in Bezug auf B? Um wie viel Prozent kleiner ist der Durchmesser von B in Bezug auf A? Um wie viel Prozent kleiner ist die Oberfläche von B in Bezug auf A?

4. 
   

   In den folgenden Beispielen gehen wir davon aus, dass es in der Bevölkerung so viele Männer gibt wie Frauen. Der Anteil der Raucher unter der Bevölkerung ist 45%. Der Anteil der Raucher unter den Männern ist 60%. Wie viel ist der Anteil der Raucherinnen unter den Frauen? Die Lebenserwartung der Bevölkerung ist 79 Jahre. Die Lebenserwartung der nicht-Raucher ist 82,6 Jahre. Wie viele Jahre weniger ist die Lebenserwartung der Rauchenden in Vergleich zu den nicht-Rauchenden Personen? Wäre das Rauchen die einzige Erklärung für den Unterschied der Lebenserwartung zwischen den beiden Geschlechtern, wie viel Jahre wäre diese für Männer und für Frauen? Welche Information ist noch notwendig, um den Einfluss des Rauchens auf den Lebenserwartungsunterschied zwischen den Geschlechtern genauer zu bestimmen? Wenn wir letztere Information haben, was ist noch notwendig, um zu entscheiden, ob das Rauchen bei dieser Frage tatsächlich der einzige bestimmende Faktor ist? Vergleichen Sie ihre Ergebnisse mit tatsächlichen offiziellen Statistiken!

5. 
   

   Bei den Wahlen in einer Gemeinde hat 60% der Wählerschaft tatsächlich gewählt. Die Partei D (Die Partei) hat 5% der Stimmen bekommen, die Partei U (Partei nur für Uns) 65%, die Partie K (Partei der Keuschheit) 1,5%, die Partei V (Partei für die Vergangenheit) 15%, die Partei Z (Partei für die Zukunft) 7,5% und der Rest der Stimmen war nicht gültig. Zeigen Sie, dass die am stärksten vertretene Gruppe die nicht-WählerInnen war! Wie viel Prozent mehr waren sie als die Wählerschaft der stärksten Partei? Wie viel Prozent mehr als die ungültigen Stimmen waren die Stimmen der Partei für die Keuschheit? Wie viel Prozent der Stimmen weniger als die Partei V hat die Partei K bekommen? Wie viel Prozent der Stimmen mehr als die Partei K hat die Partei V bekommen? Wie viel Prozent der gesamten Wählerschaft hat die Partei D gewählt? Wie viel Prozent der gültigen Stimmen hat jede Partei durchschnittlich bekommen?

6. 
   

   Die Seite einer Figur F ist das doppelte der Seite einer ähnlichen Figur G. Um wie viel Prozent größer ist der Umfang von F als der von G? Um wie viel Prozent kleiner ist der Umfang von G als der von F? Um wie viel Prozent größer ist die Fläche von F als die Fläche von G? Um wie viel Prozent kleiner ist die Fläche von G als die von F?

7. 
   

   Der Radius einer Kugel A ist um 200% größer als der Radius einer Kugel B. Um wie viel Prozent größer ist die Oberfläche von A in Bezug auf B? Um wie viel Prozent größer ist das Volumen von A in Bezug auf B? Um wie viel Prozent kleiner ist der Durchmesser von B in Bezug auf A? Um wie viel Prozent kleiner ist die Oberfläche von B in Bezug auf A?

8. 
   

   Bei den Wahlen in einer Gemeinde hat 70% der Wählerschaft tatsächlich gewählt. Die Partei D (Die Partei) hat 19% der Stimmen bekommen, die Partei U (Partei nur für Uns) 22%, die Partie K (Partei der Keuschheit) 1,5%, die Partei V (Partei für die Vergangenheit) 42%, die Partei Z (Partei für die Zukunft) 15% und der Rest der Stimmen war nicht gültig. Zeigen Sie, dass die am stärksten vertretene Gruppe die nicht-WählerInnen war! Wie viel Prozent mehr waren sie als die Wählerschaft der stärksten Partei? Wie viel Prozent mehr als die ungültigen Stimmen waren die Stimmen der Partei für die Keuschheit? Wie viel Prozent der Stimmen weniger als die Partei V hat die Partei K bekommen? Wie viel Prozent der Stimmen mehr als die Partei K hat die Partei V bekommen? Wie viel Prozent der gesamten Wählerschaft hat die Partei D gewählt? Wie viel Prozent der gültigen Stimmen hat jede Partei durchschnittlich bekommen?

Prozentrechnung vertiefend

1. 
   

   Der Prozentsatz des übrig gebliebenen Mathematik-Wissens nach dem Schulabschluss in Abhängigkeit von der Zeit in Wochen wird durch folgende Gleichung angegeben: $P(t)=7+93\cdot 0{,}702^{t}$ Berechnen Sie, um wie viel Prozent das Wissen nach 23,8 Tagen abgenommen hat! Nach einem anderen Modell ist das Wissen am 8. Tag zwei fünftel des Wissens am 1. Tag nach dem Abschluss. Wie viel Prozent mehr ist das Wissen am 1. Tag als das Wissen am 8. Tag? Die Anzahl der Mathematik-Studierenden in einer Universität wurde in der folgenden Tabelle erfasst: Jahr 1994 1995 1996 1997 Studierende 235 256 301 392 Interpretieren das Ergebnis der Berechnung ${\tfrac {301-235}{235}}$ im gegebenen Sachzusammenhang! Im Jahr 1994 war das Studium 4-jährig, im Jahr 1997 5-jährig. Wie viel war der prozentuelle Anstieg der durchschnittlichen Anzahl der Studenten pro Studiumjahrgang zwischen 1994 und 1997? In einer Zeitung steht, dass in den ersten 2 Wochen das Wissen um 30% abnimmt und zwischen 3. und 5. Woche um 20%. Daher nimmt das Wissen um 50% in diesen 5 Wochen ab. Zeigen Sie, dass das Mathematik-Wissen des Verfassers des Artikels schon stark abgenommen hat. Genauer: Erklären Sie, warum diese Aussage nicht gilt und berechnen Sie, um wie viel Prozent das Wissen tatsächlich abgenommen hat! In einer Mathematik-Prüfung haben 14 Personen 12 Punkte gehabt, 4 Personen 9 Punkte, 3 Personen 16 Punkte und 8 Personen 7 Punkte. Um die Prüfung zu bestehen waren zumindest 11 Punkte notwendig. Wie viel Prozent der Personen haben die Prüfung bestanden? In einer 12 km lange Autobahnstrecke mit 120 km/h Tempolimit wurde dieses um 5% erhöht. Eine Person dachte, dass sie dadurch 5% weniger Zeit brauchen würde (wenn sie immer am Limit fahren wurde). Zeigen Sie, dass diese Annahme nicht stimmt!

2. 
   

   Der prozentuelle Anstieg der Todesfälle in einem Staat, die an das Rauchen zuzuschreiben sind, innerhalb der jeweiligen Jahrzehntewurde in der folgenden Tabelle erfasst: Jahr 1951-60 1961-70 1971-80 1981-90 1991-2000 2001-2010 2011-2020 Anstieg 15,4% 17,7% 12,8% 15,4% 44,0% 23,2% 11,3% Es gab 30459 an das Rauchen zuzuschreibende Todesfälle am Ende der Jahrzehnte zwischen 2001-2010. Das war 48,5% der gesamten Todesfälle. Wie viel waren die an das Rauchen zuzuschreibenden Todesfälle am Anfang der Jahrzehnte zwischen 1981-1990? Wie viele waren die gesamten Todesfälle am Ende der Jahrzehnte zwischen 2001-2010? Zwei siebtel der Todesfälle am Ende der Jahrzehnte zwischen 2001-2010, die an das Rauchen zuzuschreiben sind, sind an Krebs gestorben. Wie viel Prozent der gesamten Todesfälle war das? Erklären Sie warum die absolute Änderung der Todesfälle, die an das Rauchen zuzuschreiben sind, innerhalb der Jahrzehnte zwischen 1951-60 bzw. zwischen 1981-90 nicht gleich ist, obwohl der prozentuelle Anstieg gleich war! In einer Studie wurde ein quadratischer Zusammenhang zwischen der Anzahl der täglichen Zigaretten und der Anzahl der Todesfälle festgestellt. Die Gruppe A in der Studie hat 25 Zigaretten am Tag geraucht, die Gruppe B 27. Jemand behauptet, dass die Todesfälle der Gruppe B 8% mehr als die Todesfälle der Gruppe A sind. Begründen Sie, warum diese Aussage falsch ist! Der Gewinn in € für die Gesellschaft, in Bezug auf die Menschen, die mit dem Rauchen aufhören wird durch die folgende Funktion angegeben: $G(a)=G_{0}\cdot 1{,}0008^{a}$ Was bedeutet in diesem Zusammenhang die Lösung der Gleichung: $2=1{,}0008^{a}?$ Beschreiben Sie, was im gegebenen Sachzusammenhang durch die Rechnung ${\tfrac {G(303)-G(241)}{G(241)}}$ ermittelt wird!

3. 
   

   Die Bevölkerung in einer Provinzstadt in Tausenden Menschen in Abhängigkeit von der Zeit in Jahren wird durch folgende Gleichung angenähert: $B(t)=43+69\cdot 1{,}702^{-t}$ Berechnen Sie, um wie viel Prozent die Bevölkerung nach 57,9 Monaten abgenommen hat! In einer anderen Stadt ist die Bevölkerung am 18. Jahr sieben viertel der Bevölkerung am 1. Jahr. Wie viel Prozent weniger ist die Bevölkerung im 1. Jahr als die Bevölkerung im 18. Jahr? Die Bevölkerung in einer Stadt wurde in der folgenden Tabelle erfasst: Jahr 2000 2001 2002 2003 Tausende Einwohner 203 187 179 178 Interpretieren das Ergebnis der Berechnung ${\tfrac {187-178}{187}}$ im gegebenen Sachzusammenhang! Die Stadt wurde in Bezirke mit der gleichen Bevölkerung geteilt. Im Jahr 2003 wurden die Bezirke der Stadt von 7 auf 6 reduziert. Wie viel war der prozentuelle Anstieg der Einwohner pro Bezirk zwischen 2000 und 2003? In einer Zeitung steht, dass in den ersten 2 Jahren die Bevölkerung einer Stadt um 10% zunimmt und in den folgenden 4 Jahren noch 5% dazu. Daher nimmt die Bevölkerung insgesamt um 15% in diesen 6 Jahren zu. Erklären Sie, warum diese Aussage nicht gilt und berechnen Sie, um wie viel Prozent die Bevölkerung tatsächlich zugenommen hat! In einer Veranstaltung in einer Stadt gab es 34 15-jährige Personen, 103 19-jährige, 207 20-jährige und 14 16-jährige. Die Veranstaltung war allerdings nur ab einem Alter von 18 Jahren erlaubt. Wie viel Prozent der Personen waren illegal? In einer 5 km lange Straße der Stadt wurde das Tempolimit von 50 auf 60 km/h erhöht. Eine Person, die diese Strecke fahren wollte, dachte, dass sie dadurch 20% weniger Zeit brauchen würde (wenn sie immer am Limit fahren wurde). Zeigen Sie, dass diese Annahme nicht stimmt!

4. 
   

   Der prozentuelle Anstieg der durch Atomkraft produzierten Energiemenge in einem Staat innerhalb des jeweiligen Jahres wurde in der folgenden Tabelle erfasst: Jahr 1994 1995 1996 1997 1998 1999 2000 Anstieg 15,4% 18,3% 18,3% 33,9% 144,0% 53,2% 38,4% Die produzierte Menge am Ende des Jahres 2000 war 877,8 MWh. Das war 65,8% der gesamten produzierten Menge. Wie viel war die durch Atomkraft produzierte Energiemenge am Anfang des Jahres 1996? Wie viel MWh war die gesamte Energiemenge am Ende des Jahres 2000? Ein elftel der Atomenergiemenge am Ende des Jahres 2000 wurde für die vollständige Stromversorgung einer Metallindustrie benutzt. Welcher Prozentsatz der gesamten Energiemenge des Jahres 2000 war das? Erklären Sie warum die absolute Änderung der durch Atomkraft produzierten Energiemenge innerhalb des Jahres 1995 bzw. 1996 nicht gleich ist, obwohl der prozentuelle Anstieg gleich war! In einem Physik-Buch liest man: "Hätte ein Atomkern 1 dm Durchmesser, so wäre der Durchmesser des gesamten Atoms 1 km. Das Volumen des Atomkerns macht dann 0,01 % des Gesamtvolumens eines Atoms aus." Begründen Sie, warum diese Aussage falsch ist! Ein (riesiges) Problem der Atomkraft ist der radioaktiver Müll, der für Hunderte bis Tausende Jahre gefährlich bleibt. Der Zerfall des Caesium-Isotops 137Cs wird durch die folgende Funktion angegeben: $M(t)=M_{0}\cdot 0{,}97733^{t}\$(M: Menge der Atome, t Zeit in Jahren) Was bedeutet in diesem Zusammenhang die Lösung der Gleichung: $0{,}5=0{,}97733^{t}?$ Beschreiben Sie, was im gegebenen Sachzusammenhang durch die Rechnung ${\tfrac {M(4)-M(5)}{M(4)}}$ ermittelt wird!