MathemaTriX ⋅ Radiant

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

LINKS

Zumindest eine Aufgabe probieren

	lle	Gaben
	uf-

Theorie in Kürze (mit Geogebra)

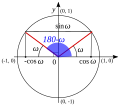
Kreis, dessen Mittelpunkt sich am Anfang des (kartesischen) Koordinatensystems befindet und dessen Radius 1 ist. Der Winkel wird als Drehung im Bezug auf dem rechten Teil der x-Achse gemessen. Da der Radius 1 ist, ist der Umfang 2π. Das wird als Basis für die Winkeleinheit "Radiant" (Symbol: rad) benutzt. 360° Winkel ist so viel wie 2π rad.

• 
  Winkel mit gleichen Kosinus
  $\omega \ {\text{und }}360^{\circ }-\omega$
• 
  Winkel mit gleichen Sinus
  $\omega \ {\text{und }}180^{\circ }-\omega$
• 
  Winkel mit gleichen Sinus und Kosinus
  $\omega \ {\text{und }}360^{\circ }+\omega$

Aufgaben

1. 
   

   Rechnen Sie in Grad ° (Winkelmaß) um! A) $\ 3\pi \ rad$, B)$\ {\frac {5\pi }{9}}\ rad$, C)$\ 0{,}2\ rad$, D)$\ {\frac {5}{9\pi }}\ rad$, E)$\ 360\ rad$ Rechnen Sie in Radiants (Bogenmaß) um A)$\ 300^{\circ }$, B)$\ 0{,}2^{\circ }$, C)$\ 3\pi ^{\circ }$, D)$\ {\frac {170}{9\pi }}^{\circ }$, E)$\ 145^{\circ }$ Sind folgende Winkel mehr oder weniger als ein Halbkreis? Wo befinden sie sich im Einheitskreis? A)$\ 300^{\circ }$, B)$\ 100^{\circ }$, C)$\ 2\ rad$, D)$\ 1\ rad$, E)$\ 390^{\circ }$

2. 
   

   Rechnen Sie in Grad ° (Winkelmaß) um! a) $\ 5\pi \ rad$, B)$\ {\frac {9\pi }{7}}\ rad$, C)$\ 0{,}6\ rad$, D) $\ {\frac {4}{5\pi }}\ rad$, E) $\ 270\ rad$ Rechnen Sie in Radiants (Bogenmaß) um A)$\ 200^{\circ }$, B)$\ 0{,}5^{\circ }$, C)$\ 5\pi ^{\circ }$, D)$\ {\frac {260}{4\pi }}^{\circ }$, E)$\ 342^{\circ }$ Sind folgende Winkel mehr oder weniger als ein Halbkreis? Wo befinden sie sich im Einheitskreis? A)$\ 200^{\circ }$, B)$\ 330^{\circ }$, C)$\ 5\ rad$, D)$\ 0{,}6\ rad$, E)$\ 35^{\circ }$

3. 
   

   Rechnen Sie in Grad ° (Winkelmaß) um! a) $\ 4\pi \ rad$, B)$\ {\frac {7\pi }{5}}\ rad$, C)$\ 0{,}5\ rad$, D)$\ {\frac {5}{8\pi }}\ rad$, E)$\ 315\ rad$ Rechnen Sie in Radiants (Bogenmaß) um A)$\ 250^{\circ }$, B)$\ 0{,}4^{\circ }$, C)$\ 4\pi ^{\circ }$, D)$\ {\frac {310}{7\pi }}^{\circ }$, E)$\ 217^{\circ }$ Sind folgende Winkel mehr oder weniger als ein Halbkreis? Wo befinden sie sich im Einheitskreis? A)$\ 100^{\circ }$, B)$\ 272^{\circ }$, C)$\ 1{,}5\ rad$, D)$\ 8{,}6\ rad$, E)$\ 687^{\circ }$

4. 
   

   Rechnen Sie in Grad ° (Winkelmaß) um! a) $\ 7\pi \ rad$, B)$\ {\frac {7\pi }{6}}\ rad$, C)$\ 1{,}5\ rad$, D)$\ {\frac {7}{9\pi }}\ rad$, E)$\ 420\ rad$ Rechnen Sie in Radiants (Bogenmaß) um A)$\ 15^{\circ }$, B)$\ 0{,}8^{\circ }$, C)$\ 7\pi ^{\circ }$, D)$\ {\frac {430}{7\pi }}^{\circ }$, E)$\ 560^{\circ }$ Sind folgende Winkel mehr oder weniger als ein Halbkreis? Wo befinden sie sich im Einheitskreis? A)$\ 90^{\circ }$, B)$\ 180^{\circ }$, C)$\ 1\ rad$, D)$\ 7{,}6\ rad$, E)$\ 730^{\circ }$