MathemaTriX ⋅ Relative Änderung

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

LINKS

Zumindest eine Aufgabe probieren

	lle	Gaben
	uf-

Theorie in Kürze (mit Geogebra)

• y in Abhängigkeit von x, y in Bezug auf x, je x desto y
• Punkt (x|y), also erst x und dann y.
• Absolute Änderung: $\Delta y$ also nur die y-Änderung $(\Delta y=y_{2}-y_{1})$ für die zwei angegebenen x-Werte. Also die x-Werte sind angegeben, die y-Werte muss man subtrahieren!
• Relative Änderung: ${\tfrac {\Delta y}{y_{1}}}={\tfrac {y_{2}-y_{1}}{y_{1}}}$ keine Einheiten (kann man mit Kommaverschieben als Prozentsatz angeben). Die Differenz der y-Werte durch den ersten y-Wert.
• Mittlere Änderungsrate, auch Differenzenquotient.: ${\tfrac {\Delta y}{\Delta x}}={\tfrac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ Einheit: Einheiten der y-Achse pro eine Einheit der x-Achse. → Steigung der Gerade, die zwei Punkte verbindet.

Der Unterschied zwischen Änderungsrate und relativer Änderung ist daher der Nenner des Bruches.

• Ist er einer der beiden Werte des Zählers, dann geht es (fast immer) um eine relative Änderung.
• Ist er eine Differenz von Werten (der x-Achse), dann geht es um eine mittlere Änderungsrate (Steigung).

Die absolute Änderung hingegen ist (fast immer) kein Bruch sondern einfach eine Differenz von zwei (in der Regel y-) Werten.

Ausdrücke

• Absolute Änderung: Der/Die/Das (Begriff, was auf der y-Achse steht) ist zwischen (was $x_{1}$ und $x_{2}$ ist) mehr/weniger geworden
• Relative Änderung: Der/Die/Das (Begriff, was auf der y-Achse steht) ist zwischen (was $x_{1}$ und $x_{2}$ ist) um so viel Prozent mehr/weniger geworden
• Mittlere Änderungsrate: Der/Die/Das (Begriff, was auf der y-Achse steht) ist zwischen (was $x_{1}$ und $x_{2}$ ist) durchschnittlich um (y-Einheiten pro EINE x-Einheit → Steigung) mehr/weniger geworden

Aufgaben

1. 
   

   Das Diagramm zeigt die Funktion T(t) der Temperatur eines Patienten im Verlauf des Tages. Wie viel war die absolute Temperaturänderung zwischen 2 und 12 Uhr? Wie viel war die relative Temperaturänderung zwischen 6 und 22 Uhr Wie viel war die relative Temperaturänderung zwischen 4 und 14 Uhr? Interpretieren Sie das Ergebnis! Was bedeutet ${\tfrac {T(t_{1})-T(t_{2})}{T(t_{1})}}=0{,}032\$in diesem Zusammenhang? Was bedeutet ${\tfrac {T(t_{1})-T(t_{2})}{T(t_{2})}}=-0{,}024\$in diesem Zusammenhang?

2. 
   

   4 verschiedene Waschmittel wurden auf ihre Effektivität geprüft. Das Diagramm zeigt welcher Anteil (in Prozent) des Schmutzes geblieben ist in Bezug auf die Zeit (in Minuten). Die entsprechenden Funktionen sind L(t) für Linix, B(t) für Blautrex, R(t) für Rotrum und M(t) für Mavrit. Wie viel war die absolute prozentuale Änderung für Rotrum zwischen 5 und 17 Minute? Wie viel war die relative prozentuale Änderung für Mavrit zwischen 3 und 23 Minute Wie viel war die relative prozentuale Änderung für Linix zwischen 8 und 16 Minute? Interpretieren Sie das Ergebnis! Was bedeutet ${\tfrac {B(t_{2})-B(t_{1})}{B(t_{1})}}=-0{,}032\$in diesem Zusammenhang? Was bedeutet ${\tfrac {L(t_{1})-L(t_{2})}{L(t_{2})}}=2{,}024\$in diesem Zusammenhang?

3. 
   

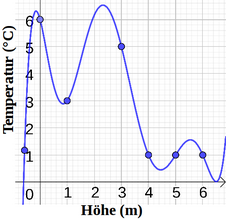
   Das Diagramm stellt die die Funktion T(h) der Temperatur in einem Wassertank in Bezug auf seine Höhe in m dar. Wie viel ist die absolute Temperaturänderung zwischen 2 und 3 m? Wie viel ist die relative Temperaturänderung zwischen 1 und 4 m Wie viel ist die relative Temperaturänderung zwischen 4 und 5 m? Interpretieren Sie das Ergebnis! Was bedeutet ${\tfrac {T(h_{1})-T(h_{2})}{T(h_{1})}}=-3{,}032\$in diesem Zusammenhang? Was bedeutet ${\tfrac {T(h_{1})-T(h_{2})}{T(h_{2})}}=1{,}024\$in diesem Zusammenhang?

4. 
   

   Das Wachstum der Bevölkerung (in Millionen) in 4 verschiedenen (imaginären) Städten in Abhängigkeit von der Zeit in Jahren wurde im Diagramm zusammengefasst. Die entsprechenden Funktionen sind R(t) für Orange, G(t) für Grün, B(t) für Blau und S(t) für Schwarz. Wie viel ist das absolute Bevölkerungswachstum für die blaue Stadt für die ersten 45 Jahren? Wie viel ist das relative Bevölkerungswachstum für die schwarze Stadt für die ersten 60 Jahren? Wie viel ist das relative Bevölkerungswachstum für die schwarze Stadt zwischen 60 und 90 Jahr? Interpretieren Sie das Ergebnis! Was bedeutet ${\tfrac {G(t_{1})-G(t_{2})}{G(t_{1})}}=-0{,}032\$in diesem Zusammenhang? Was bedeutet ${\tfrac {S(t_{2})-S(t_{1})}{S(t_{2})}}=0{,}024\$in diesem Zusammenhang?