MathemaTriX ⋅ Schnittpunkte von Funktionen in einem Diagramm

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

LINKS

Zumindest eine Aufgabe probieren

	lle	Gaben
	uf-

Aufgaben

1. 
   

   Im Bild sehen wir eine Polynomfunktion r(x) (gestrichelt), drei quadratische Funktionen p(x), q(x) und h(x) (zwei Kurven p und h nach oben und eine Kurve q nach unten) und zwei lineare Funktionen g(x) und f(x) (Gerade g nach unten rechts und Gerade f nach oben rechts). Lesen Sie vom Diagramm ab: Die Lösungen (Nullstellen) jeder Funktion. Den y-Achsenabschnitt jeder Funktion. Die Lösungen der Gleischungssysteme, die aus folgenden Funktionen bestehen: i) g und f $\quad$ii) p und r $\quad$iii) p und g iv)f und q $\quad$v) r und f $\quad$vi) g und h

2. 
   

   Im Bild sehen wir eine Polynomfunktion r(x) (gestrichelt), drei quadratische Funktionen p(x), q(x) und h(x) (zwei Kurven p und h nach oben und eine Kurve q nach unten) und zwei lineare Funktionen g(x) und f(x) (Gerade g nach unten rechts und Gerade f nach oben rechts). Lesen Sie vom Diagramm ab: Die Lösungen (Nullstellen) jeder Funktion. Den y-Achsenabschnitt jeder Funktion. Die Lösungen der Gleischungssysteme, die aus folgenden Funktionen bestehen: i) g und f $\quad$ii) p und r $\quad$iii) p und g iv)f und q $\quad$v) r und f $\quad$vi) g und h

3. 
   

   Im Bild sehen wir eine Polynomfunktion r(x) (gestrichelt), drei quadratische Funktionen p(x), q(x) und h(x) (zwei Kurven p und h nach oben und eine Kurve q nach unten) und zwei lineare Funktionen g(x) und f(x) (Gerade g nach unten rechts und Gerade f nach oben rechts). Lesen Sie vom Diagramm ab: Die Lösungen (Nullstellen) jeder Funktion. Den y-Achsenabschnitt jeder Funktion. Die Lösungen der Gleischungssysteme, die aus folgenden Funktionen bestehen: i) g und f $\quad$ii) p und r $\quad$iii) p und g iv)f und q $\quad$v) r und f $\quad$vi) g und h

4. 
   

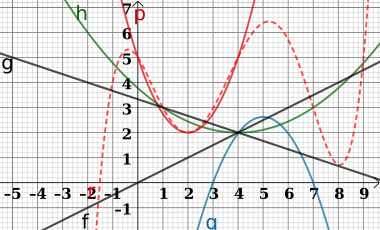
   Im Bild sehen wir eine Polynomfunktion g(x) (gestrichelt), drei quadratische Funktionen c(x), d(x) und e(x) (zwei Kurven c und e nach oben und eine Kurve d nach unten) und zwei lineare Funktionen h(x) und f(x) (Gerade f nach unten rechts und Gerade h nach oben rechts). Lesen Sie vom Diagramm ab: Die Lösungen (Nullstellen) jeder Funktion. Den y-Achsenabschnitt jeder Funktion. Die Lösungen der Gleischungssysteme, die aus folgenden Funktionen bestehen: i) h und f $\quad$ii) g und d $\quad$iii) c und f iv)e und h $\quad$v) g und f $\quad$vi) c und d