Overview: continuity and differentiability – Serlo
In this section we summarise the most important relationships and results between the related terms of continuity and differentiability.
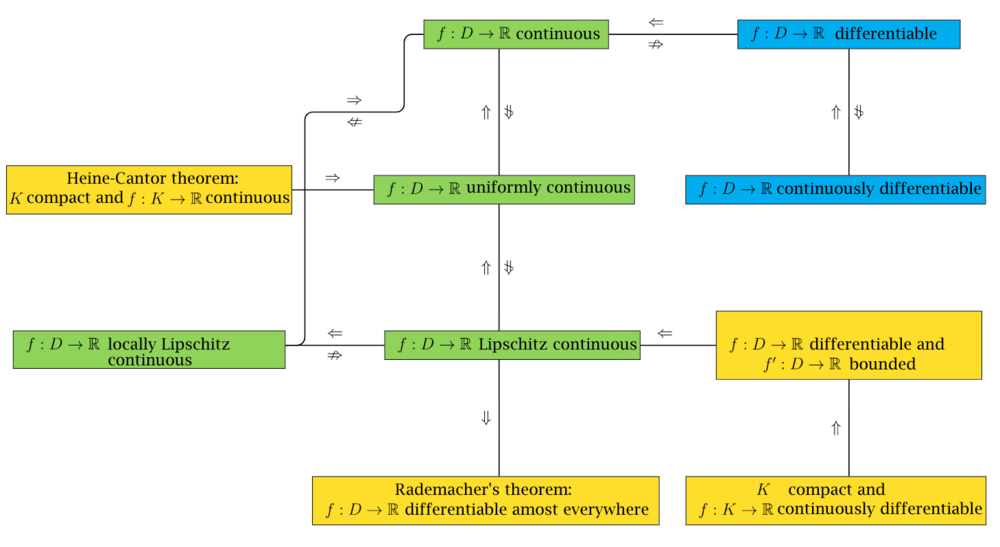
Overview: Relation between continuity and differentiability
[Bearbeiten]We had already proved that every differentiable function is continuous. The converse is generally not correct. Examples are the functions or . In each case, the problem occurs at zero.
A stronger variant of continuity is uniform continuity. In contrast to the "usual" continuity, this is not a local but a global property. Therefore every uniformly continuous function is continuous. The converse is not true, as the example shows. However, every continuous function on a compact interval is uniformly continuous. This result is also known in the literature as Heine–Cantor theorem.
The Lipschitz continuity is, just like the uniform continuity, a global property. There is a weaker, local variant of this, the local Lipschitz continuity. Local Lipschitz continuity and Lipschitz continuity behave exactly like continuity and uniform continuity. I.e. every Lipschitz continuous function is also locally Lipschitz continuous, but not the other way round. An example is again the square root function . It is important that the zero here is not contained in the domain of definition of the root function. On the other hand, the "usual" continuity follows from local Lipschitz continuity, but not the other way round. For example, the function is continuous at zero point, but not locally Lipschitz continuous.
A relationship between differentiability and Lipschitz continuity is provided by in implication of the mean value theorem: Every differentiable function with bounded derivative is Lipschitz continuous. A sufficient condition for this requirement is, according to the extreme value theorem, that the function is defined on a compact interval (or any compact domain) and is continuously differentiable. Finally, it follows the other way round that every Lipschitz continuous function is differentiable almost everywhere (i.e. except for a zero set). This statement is known as Rademacher's theorem.
Questions
[Bearbeiten]Question: Find a function with the respective following properties:
- is uniformly continuous and not compact.
- is continuous and compact, but is not Lipschitz continuous.
- is uniformly continuous, but not Lipschitz continuous.
- is differentiable, but not Lipschitz continuous.
- is continuous differentiable, but not uniformly continuous.
Solutions (there are many more):
- or
- or






![{\displaystyle f:[-1,1]\to \mathbb {R} ,\ f(x)={\sqrt {|x|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68d88ec99e0e892e5a153d309e4318687c09d3b4)




![{\displaystyle f:[0,1]\to \mathbb {R} ,\ f(x)={\sqrt {x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4c56457d1d7f447f2944e70d32afa5752a42e61)

