Formelsammlung Physik: Astronomie
Klassische Mechanik | Wellenlehre | Optik | Akustik | Wärmelehre | Elektrizitätslehre | Elektrodynamik | Atom- und Kernphysik | Quantenphysik | Thermodynamik 2 | Relativitätstheorie | Astronomie | Hydrostatik | Tabellen
Vorwort[Bearbeiten]
Die Astronomie ist eine eigenständige Naturwissenschaft, die aber viele Querverbindungen zu anderen Disziplinen aufweist. Besonders eng ist die Verflechtung mit der Physik und damit zwangsläufig auch der Mathematik. Jedoch bestehen auch Beziehungen zur Chemie, der Biologie und den Geowissenschaften. Aufgrund dieser vielen Schnittmengen mit anderen Wissenschaften enthält diese Sammlung daher zahlreiche Formeln, welche auch in anderen Übersichtswerken aufgelistet sind. Der Unterschied besteht darin, dass solche Formeln hier spezifisch astronomische Anwendungen finden.
Dem Charakter einer Formelsammlung entsprechend, können Beweise für einzelne Beziehungen nur kurz angedeutet bzw. anhand einfach zu behandelnder Spezialfälle plausibel gemacht werden. Hinsichtlich einer exakten Beweisführung muss auf entsprechende Artikel in der Wikipedia und der dort angegebenen Literatur verwiesen werden.
Häufig benutzte Größen und Naturkonstanten[Bearbeiten]
In diesem Kapitel werden in dieser Formelsammlung häufig verwendete Größen und Naturkonstanten vorab zusammengestellt.
Größen der Erde[Bearbeiten]
| Abkürzung | Bezeichnung | Wert in SI-Einheiten |
|---|---|---|
| RE | Mittlerer Radius | 6371 km |
| ME | Masse | 5.974 1024 kg |
| E | Dichte | 5.515 g cm-3 |
| gE | Fallbeschleunigung an Oberfläche | 9.80665 m s-2 |
| aE | Große Halbachse der Bahn um die Sonne | 149.6 10 6 km |
Größen des Erdmondes[Bearbeiten]
| Abkürzung | Bezeichnung | Wert in SI-Einheiten |
|---|---|---|
| RM | Mittlerer Radius | 1738 km |
| MM | Masse | 7.349 1022 kg |
| M | Dichte | 3.341 g cm-3 |
| gM | Fallbeschleunigung an Oberfläche | 1.623 m s-2 |
| aM | Große Halbachse der Bahn um die Erde | 384400 km |
Größen der Sonne[Bearbeiten]
| Abkürzung | Bezeichnung | Wert in SI-Einheiten |
|---|---|---|
| R☉ | Radius | 696342 km |
| M☉ | Masse | 1.9884 1030 kg |
| ☉ | Dichte | 1.408 g cm-3 |
| g☉ | Fallbeschleunigung an Oberfläche | 273.7 m s-2 |
| L☉ | Leuchtkraft | 3.846 1026 W |
Naturkonstanten[Bearbeiten]
| Konstante | Bezeichnung | Wert |
|---|---|---|
| G | Gravitationskonstante | (6.67408 0.00031) 10-11 m3 kg-1 s-2 |
| c | Lichtgeschwindigkeit | 299792458 m s-1 exakt per Definition |
| h | Plancksches Wirkungsquantum | (6.626070040 0.000000081) 10-34 J s |
| k | Boltzmann-Konstante | (1.38064852 0.00000079) 10-23 J K-1 |
| Stefan-Boltzmann-Konstante | (5.670367 0.000013) 10-8 W m-2 K-4 | |
| b | Wiensche Verschiebungskonstante | (2897.7729 0.0017) m K |
| Elektronenmasse | (9.10938356 0.00000011) 10-31 kg | |
| Protonenmasse | (1.672621898 0.000000021) 10-27 kg |
Elektromagnetische Strahlung[Bearbeiten]
Von sehr wenigen Ausnahmen abgesehen (z. B. kosmische Strahlung und Gravitationswellen), beruhen alle von Himmelskörpern empfangenen Signale auf elektromagnetischer Strahlung. In diesem Kapitel sollen daher zahlreiche Gesetzmäßigkeiten zusammengestellt werden, welche zur Interpretation entsprechender Beobachtungen benötigt werden.
Fundamentale Eigenschaften[Bearbeiten]
Wellenlänge und Frequenz
Wie viele klassische Experimente (z. B. der Doppelspalt-Versuch) zeigen, stellt elektromagnetische Strahlung ein Wellenphänomen dar. Wellenlänge und Frequenz einer elektromagnetischen Schwingung sind dabei folgendermaßen über die Lichtgeschwindigkeit miteinander verknüpft:
Doppler-Effekt
Eine der wichtigsten astronomischen Anwendungen der Wellennatur elektromagnetischer Strahlung ist der Doppler-Effekt. Bewegt sich eine Lichtquelle mit einer Geschwindigkeit relativ zum Betrachter weg, kommt das Licht bei diesem im Vergleich zu einer ruhenden Lichtquelle verspätet an, was einer geringen Frequenz bzw. größeren Wellenlänge entspricht. Das strahlende Objekt erscheint somit gerötet. Kommt die Lichtquelle auf den Beobachter zu, verhält es sich umgekehrt, der leuchtende Körper erscheint blauer. Für die Änderung der Frequenz bzw. der Wellenlänge gilt im Falle kleine Geschwindigkeiten :
Kennt man die Wellenlängenverschiebung (z. B. durch Vergleich der beobachteten Wellenlängen von Spektrallinien mit den unverschobenen Werten), so folgt daraus unmittelbar die Geschwindigkeit, mit der sich die Lichtquelle in Blickrichtung relativ zum Beobachter bewegt.
Bei der Beobachtung von Sternen unserer Galaxis liegt üblicherweise in der Größenordnung von 10 bis 100 km/s und damit in der Größenordnung von 10-5 bis 10-4. Im Falle sehr weit entfernter Galaxien kann jedoch eine Größenordnung von 100000 km/s und damit eine solche von 0.1 bis 1 erreichen. Dieses Szenario einer im Vergleich zur Lichtgeschwindigkeit nicht vernachlässigbaren Geschwindigkeit der Lichtquelle wird im Kapitel Relativitätstheorie behandelt.
In der Praxis wird das Verhältnis zwischen der Änderung der Frequenz bzw. Wellenlänge und deren unverschobenem Wert oft mit dem Buchstaben abgekürzt:
Energie eines Lichtquants
Erscheinungen wie der photoelektrische Effekt offenbaren, dass elektromagnetischer Strahlung nicht nur eine Wellen-, sondern zugleich auch eine Teilchennatur innewohnt. Gemäß dieser Vorstellung tritt Licht einer Frequenz nur in bestimmten Energieportionen, sogenannten Lichtquanten oder Photonen auf. Die Energie eines solchen Lichtquants beträgt:
Strahlungsleistung[Bearbeiten]
Die Strahlungsleistung ist eine der wichtigsten Größen in der Astronomie, sowohl in Bezug auf die von einer Lichtquelle abgegebene Leistung, als auch in Bezug auf die von einem Beobachter registrierte. Für die Strahlungsleistung werden etliche nun vorgestellte Größen verwendet, je nachdem ob man sich auf die gesamte Leistung bezieht oder nur auf einen pro Fläche oder Raumwinkel entfallenden Anteil.
Leuchtkraft und Lichtstrom
Die Leuchtkraft bezeichnet die gesamte von einem selbstleuchtenden Himmelskörper abgegebenen Leistung, summiert sowohl über das ganze elektromagnetische Spektrum, als auch über alle Richtungen. Als Einheit wird, wie generell für Leistungen, Watt benutzt.
Die Leistung irdischer Lichtquellen wird meist durch den Lichtstrom ausgedrückt. Im Unterschied zur Leuchtkraft wird nicht die über alle Richtungen summierte Leistung betrachtet, sondern nur der Anteil, der in einen Raumwinkel von 1 Steradiant fällt. Um kenntlich zu machen, dass man sich auf die Leistung einer Lichtquelle bezieht, wird als gesonderte Einheit Lumen (abgekürzt lm) verwendet. Da der alle Richtungen umfassende Raumwinkel beträgt, gilt bei richtungsunabhängiger Ausstrahlung:
Wegen des in Watt üblicherweise sehr hohen Zahlenwertes für die Leuchtkraft eines Himmelskörpers wird diese fast immer als Vielfaches der Sonnenleuchtkraft ausgedrückt. Als logarithmisches Maß für die Leuchtkraft wird häufig zudem die bolometrische Helligkeit verwendet, welche im Kapitel Physik der Sterne näher erläutert wird.
Lichtstärke
Für Lichtquellen, die nicht in alle Richtungen gleichmäßig strahlen, interessiert man sich oft nicht nur für die gesamte Leistung, sondern auch für deren Abhängigkeit von der Strahlrichtung. Zu diesem Zweck dient die Lichtstärke . Diese gibt an, welcher Anteil des Lichtstroms in einen kleinen Raumwinkel fällt:
Die Einheit ist per Definition Lumen pro Steradiant (Watt pro Steradiant), wofür sich als eigenständige Bezeichnung Candela (abgekürzt cd) durchgesetzt hat. In der Astronomie wird die Lichtstärke selten verwendet.
Spezifische Lichtausstrahlung
Anstatt die pro Raumwinkel abgestrahlte kann man auch die durch eine kleine Fläche abgegebene Leistung betrachten. Sie wird als spezifische Lichtausstrahlung bezeichnet, mitunter auch als Ausstrahlungsstromdichte oder Abstrahlungsstärke. Für irdische Lichtquellen lautet die Definition:
Dies entspricht einer Einheit Lumen pro Quadrameter (Watt pro Quadratmeter). Als spezifische Bezeichnung wird Lux (abgekürzt lx) verwendet.
Im Gegensatz zur Lichtstärke ist die spezifische Lichtausstrahlung im Hinblick auf das nachfolgend skizzierte Stefan-Boltzmann-Gesetz für die Astronomie von großer Bedeutung. Jedoch wird für Himmelskörper nicht der Lichtstrom, sondern die gesamte Leuchtkraft im Verhältnis zur Oberfläche betrachtet. Weist z. B. ein Stern einen Radius auf, so gilt:
Leuchtdichte
Die Leuchtdichte (leider ist das gleiche Symbol üblich wie für die Leuchtkraft) gestattet die genaueste Beschreibung einer Lichtquelle, welche Inhomogenitäten der Abstrahlung sowohl hinsichtlich der Richtung als auch der Oberfläche berücksichtigt. Entsprechend wird jetzt der Anteil des Lichtstroms betrachtet, der durch eine kleine Fläche in einen kleinen Raumwinkel ausgesandt wird:
Der Winkel berücksichtigt, dass die Fläche nicht senkrecht zur Blickrichtung ausgerichtet sein muss ( = 0), sondern gegenüber dieser geneigt sein kann. In diesem Fall kommt eine um den Faktor reduzierte Lichtenergie am Beobachter an. Um ein davon unabhängiges Resultat zu erhalten, wird schon bei der Definition der Leuchtdichte dieser Effekt herauskorrigiert.
Die Einheit der Leuchtdichte ist entsprechend der Definition Lumen pro Steradient und Quadratmeter (Watt pro Steradient und Quadratmeter). Eine gesonderte Bezeichnung existiert offiziell nicht. Man kann jedoch anhand der anderen Strahlungsgrößen die Einheiten Candela pro Quadratmeter bzw. Lux pro Steradiant ableiten.
Alle hier vorgestellten Größen kann man im Prinzip anstatt auf das gesamte elektromagnetische Spektrum auch auf einen Ausschnitt desselben beziehen, also auf ein Frequenz- bzw. Wellenlängenintervall. In dieser Form ist gerade die Leuchtdichte eines Schwarzen Körpers als Resultat des Plackschen Strahlungsgesetzes von großer Wichtigkeit.
Beleuchtungsstärke und Intensität
Alle bisher unter dem Thema Strahlungsleistung vorgestellten Größen beziehen sich auf die Lichtquelle. In der Astronomie ist diese jedoch nie direkt zugänglich, sondern nur die am Beobachtungsinstrument ankommende Strahlung. Die wichtigste Größe, um den Lichteinfall zu beschreiben, ist im Falle irdischer Lichtquellen die Beleuchtungsstärke . Sie gibt den Anteil des von der Quelle ausgesandten Lichtstroms an, welcher auf eine kleine Fläche trifft.
Im Falle von Himmelskörpern spricht man anstatt von Beleuchtungsstärke von der Intensität des einfallenden Lichts, welche leider das gleiche Symbol trägt wie die Lichtstärke. Zudem wird nun nicht der vom Lichtstrom, sondern von der Leuchtkraft aufgenommene Anteil betrachtet.
Formell entsprechen diese Definitionen denjenigen der spezifischen Ausstrahlung, doch bezieht sich nun nicht auf eine abstrahlende, sondern eine beleuchtete Fläche. Dementsprechend werden auch die gleichen Einheiten verwendet, nämlich Watt pro Quadratmeter bzw. im Falle einer Beleuchtung durch irdische Lichtquellen Lux. Die von Himmelskörpern ankommende Strahlung ist meist so schwach, dass statt der Intensität als handlicheres (und logarithmisches) Maß die scheinbare Helligkeit verwendet wird (siehe Kapitel Physik der Sterne).
Zusammenfassung
Abschließend seien alle mit der Strahlungsleistung in Zusammenhang stehenden Größen durch nachfolgende Tabelle zusammengefasst.
| Abkürzung | Bezeichnung | SI-Einheit | Dimension |
|---|---|---|---|
| Lichtstrom | Lumen (lm) | W | |
| Leuchtkraft | W | W | |
| Lichtstärke | Candela (cd) | W sr-1 | |
| Spezifische Lichtausstrahlung | Lux (lx) | W m-2 | |
| Leuchtdichte | W m-2 sr-1 | W m-2 sr-1 | |
| Beleuchtungsstärke | Lux (lx) | W m-2 | |
| Intensität | W m-2 | W m-2 |
Strahlungsausbreitung[Bearbeiten]
Photometrisches Entfernungsgesetz
Aus den Definitionen von Lichtstärke und Beleuchtungsstärke lässt sich leicht ableiten, wie diese beiden Größen für eine Lichtquelle in einer Entfernung zusammenhängen. Per Definition ist und . Für den Raumwinkel , welchen ein Empfänger der Fläche von der Quelle aus gesehen einnimmt, gilt wiederum . Einsetzen in die Definition der Beleuchtungsstärke liefert:
Für einen in alle Richtungen gleichmäßig abstrahlenden Himmelskörper besteht zwischen Lichtstärke und Leuchtkraft der Zusammenhang . Daraus resultiert für die Intensität (man achte wieder auf die zusätzliche Verwendung des Symbols auch für die Lichtstärke):
Astronomische Beobachtungen liefern primär die Intensität und die Entfernung, so dass dann das photometrische Entfernungsgesetz die Leuchtkraft der Lichtquelle liefert. Ein Beispiel hierfür ist die Bestimmung der Leuchtkraft der Sonne. Die Solarkonstante, die außerhalb der Erdatmosphäre bei senkrechtem Lichteinfall im Mittel einfallende Intensität, beträgt 1367 W/m2. Die in der Einleitung gegebene mittlere Entfernung der Sonne liefert dann die dort ebenfalls erwähnte Leuchtkraft.
Lambert-Beersches-Gesetz
Das soeben vorgestellte Entfernungsgesetz gilt nur, wenn zwischen Lichtquelle und Empfänger kein absorbierendes bzw. streuendes Medium vorhanden ist. Tatsächlich unterliegen aber alle bodengebundenen astronomischen Beobachtungen der Absorption und Streuung durch die Erdatmosphäre und müssen dementsprechend korrigiert werden. Schon bevor das Sternenlicht die Atmosphäre erreicht, wird es zudem durch interstellare Materie geschwächt (und gerötet). Auf dieses Problem wird später eingegangen, hier sollen nur die Grundtatsachen der Lichtschwächung durch ein Medium dargelegt werden.
Man betrachte eine dünne Schicht der Dicke , auf der Licht mit einer Intensität auftrifft. Der Verlust an Intensität ist der Schichtdicke direkt proportional und natürlich auch zu selbst, d. h. es gilt eine Beziehung der Form . Diese Differentialgleichung lässt sich unmittelbar lösen, woraus das Lambert-Beersche Gesetz folgt ( bezeichnet die vor der schwächenden Schicht ankommende Intensität):
Die von einem Medium durchgelassene Intensität fällt also exponentiell mit zunehmender Schichtdicke ab. wird als Extinktionskoeffizient bezeichnet. Er hängt vom streuenden bzw. absorbierenden Material und vor allem von dessen Teilchendichte (der Anzahl der absorbierenden Partikel pro Volumen) ab.
In der Literatur gibt es unterschiedliche Darstellungen des Lambert-Beersche-Gesetzes. Oft wird die Teilchendichte aus dem Extinktionskoeffizienten herausgezogen, was zu folgender Form führt.
In der Chemie wird anstatt der Teilchendichte zudem meist die Stoffmengenkonzentration verwendet. In diesem Buch soll wie in der Astronomie in der Regel üblich im Extinktionskoeffizienten enthalten sein. Dann wird das Produkt als Optische Tiefe bezeichnet:
Ist dieses sehr viel kleiner als 1, darf die Näherung verwendet werden. In diesem Fall ist der Verlust an Intensität durch die absorbierende Schicht proportional zu deren Dicke als auch dem Extinktionskoeffizienten und damit der Dichte der Absorber. Man spricht dann von einer optisch dünnen Schicht; eine solche ist weitgehend durchsichtig. Umgekehrt entspricht der Fall einer optisch dicken Schicht, welche nahezu undurchsichtig ist.
Sehr oft ist eine absorbierende Schicht inhomogen, wodurch sich längs des Weges ändert. Dann muss anstelle des einfachen Produkts das Integral des Extinktionskoeffizienten über dem Weg genommen werden:
Wellenlängenabhängigkeit der Extinktion
ist nicht nur von der Teilchendichte und der Art des absorbierenden Materials, sondern im Allgemeinen auch von der Wellenlänge des einfallenden Lichts abhängig. Hierfür existieren drei Szenarien. Sind die Partikel viel kleiner als die Wellenlänge (z. B. Luftmoleküle), liegt Rayleigh-Streuung vor. In diesem Fall ist:
Sind Partikel und Wellenlänge etwa gleich groß (z. B. bei Aerosolen), befindet man sich im Bereich der Mie-Streuung. Diese ist mathematisch sehr schwierig zu behandeln, wobei aber ungefähr gilt:
Bei großen Partikeln liegt schließlich eine rein geometrische Abschattung vor, welche von unabhängig ist. In der Praxis wird die Extinktion jedoch von kleinen Partikeln dominiert, so dass stets eine deutliche Wellenlängenabhängigkeit gegeben ist. Die Mie- und erst recht die Rayleigh-Streuung liefert eine deutliche Zunahme der Extinktion zu kürzeren Wellenlängen hin, was die Rötung des Sternenlichts sowohl durch die Erdatmosphäre als auch interstellare Materie erklärt.
Strahlungsgesetze[Bearbeiten]
Sehr oft interessiert man sich nicht nur für die gesamte Leuchtkraft eines Himmelskörpers, sondern auch für deren spektrale Verteilung. Ein recht grobes, aber durchaus schon nützliches Modell hierfür ist die Strahlung eines sogenannten Schwarzen Körpers, deren Spektrum exakt berechnet werden kann. Auf die Herleitung der entsprechenden Gesetzmäßigkeiten muss hier jedoch auf die Wikipedia und die einschlägige Literatur verwiesen werden.
Plancksches Strahlungsgesetz
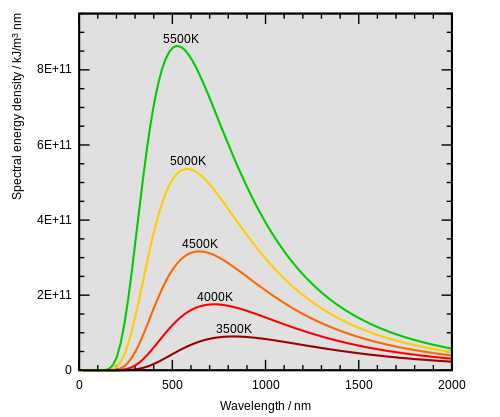
Das Plancksche Strahlungsgesetz gibt die spektrale Verteilung der Leuchtdichte eines Schwarzen Körpers in Abhängigkeit von dessen Temperatur an, wobei nun die Boltzmann-Konstante bezeichnet. Es gibt sowohl eine Frequenz- als auch eine Wellenlängendarstellung, wobei letztere in der astronomischen Praxis bevorzugt wird
Wiensches Strahlungsgesetz und Rayleigh-Jeans-Gesetz
Bei diesen beiden Gesetzmäßigkeiten handelt es sich um Näherungen des Planckschen Strahlungsgesetzes, welche schon vor dessen Herleitung durch Max Planck bekannt waren. Falls , d. h. für genügend kleine Wellenlängen, kann man im Nenner obigen Ausdrucks die 1 gegenüber der Exponentialfunktion vernachlässigen. Dies entspricht dem Wienschen Strahlungsgesetz:
Im umgekehrten Fall , d. h. für ausreichend große Wellenlängen, gilt näherungsweise . Wendet man diese Beziehung auf das Plancksche Strahlungsgesetz an, so ergibt sich das Rayleigh-Jeans-Gesetz:
Wiensches Verschiebungsgesetz
Obige Veranschaulichung des Planckschen Strahlungsgesetzes zeigt, dass die spektrale Verteilung der Leuchtdichte eines Schwarzen Körpers genau ein Maximum aufweist, das mit zunehmender Temperatur sich zu einer immer kürzeren Wellenlänge hin verschiebt. Die Lage dieses Maximum lässt sich durch eine klassische Kurvendiskussion ermitteln, indem man die 1. Ableitung der Plancksche Formel nach bildet und deren Nullstelle bestimmt. Das daraus resultierende Wiensche Verschiebungsgesetz lautet:
Dieser Zusammenhang ermöglicht es, auf einfache Weise die Oberflächentemperatur eines selbstleuchtenden Himmelskörpers abzuschätzen (wobei bei Sternen, die ja keine feste Oberfläche aufweisen, damit die Photosphäre gemeint ist). So erreicht z. B. das Spektrum der Sonne bei etwa 0.45 m sein Maximum, was gemäß dem Wienschen Verschiebungsgesetz einer Temperatur von ungefähr 6400 K entspricht.
Stefan-Boltzmann-Gesetz
Integriert man die von einer kleinen Fläche eines Schwarzen Körpers ausgesandte Strahlung über das gesamte Spektrum und alle Richtungen, so gewinnt man dessen spezifische Ausstrahlung . Die entsprechende Gesetzmäßigkeit, das Stefan-Boltzmann-Gesetz, stellt einen weiteren Zusammenhang zwischen dem Abstrahlverhalten und der Temperatur eines Schwarzen Körpers her. Es gilt:
Betrachtet man einen kugelförmigen Schwarzen Körper mit Radius , so beträgt wegen dessen Leuchtkraft:
Das Stefan-Boltzmann-Gesetz gibt eine zweite Methode an die Hand, um die Oberflächentemperatur eines (kugelförmigen) Himmelskörpers abzuschätzen. Sind dessen Radius und Leuchtkraft bekannt, folgt daraus unmittelbar seine Oberflächentemperatur. Im Fall der Sonne resultiert aus den für und gegebenen Werten eine Oberflächentemperatur von circa 5800 K, was um etwa 600 K von dem Ergebnis des Wienschen Verschiebungsgesetzes abweicht. Die Ursache für diese Differenz liegt darin begründet, dass die Sonne (wie alle Sterne) kein wirklicher Schwarzer Körper ist. Die Spektren von Sternen sind durch Absorptionsvorgänge in deren Photosphären zum Teil sehr diskontinuierlich und zeigen damit von der Planckschen Strahlungsformel erheblich abweichende Leistungsverteilungen.
Die Temperaturbestimmung aus Leuchtkraft und Radius ist nur möglich, solange der Himmelskörper noch als flächiges Objekt beobachtet werden kann. Meist ist ein solcher nur als Punktquelle sichtbar. Sind nun aber Leuchtkraft und Temperatur aus unabhängigen Messungen bekannt, liefern diese umgekehrt den Radius.
Gleichgewichtstemperatur eines Planeten[Bearbeiten]
Die hier zusammengestellten Gesetze über elektromagnetische Strahlung erlauben es, die auf der Oberfläche eines Planeten herrschende durchschnittliche Temperatur abzuschätzen. In einem Abstand von einem Zentralgestirn der Leuchtkraft kommt eine Intensität an. Nur die Tagseite des Planeten nimmt ankommende Strahlung auf, welche zudem meist nicht senkrecht, sondern schräg auf die Oberfläche einfällt. Effektiv trägt so nur der kreisförmige Querschnitt des Planeten mit der Fläche zur Energieaufnahme bei. Weiterhin reflektiert jede Oberfläche und eventuell vorhandene Atmosphäre einen Teil des ankommenden Lichts sofort wieder zurück, welcher Albedo genannt wird. Damit verbleibt eine aufgenommene Leistung .
Gemäß dem Stefan-Boltzmann-Gesetz beträgt die vom Planeten abgestrahlte Leistung . Tatsächlich gibt jedes Material jedoch nur einen Anteil von diesem theoretisch möglichen Höchstwert ab, welcher als Emissionsgrad bezeichnet wird. Im Falle einer Atmosphäre halten Treibhausgase zusätzlich einen Teil der von der Oberfläche abgestrahlten Energie zurück, welchen man formell ebenfalls zurechnen kann. Die abgegebene Leistung lautet also .
Im Mittel müssen die vom Zentralgestirn ankommende und vom Planeten abgestrahlte Leistung gleich sein. Daraus ergibt sich:
Setzt man für die Sonnenleuchtkraft und für den Abstand Erde-Sonne ein, so gewinnt man die auf irdische Verhältnisse zugeschnittene Beziehung:
Für die Erde ist derzeit etwa 0.3 und ungefähr 0.6, was eine Durchschnittstemperatur von circa 289 K bzw. +16° C liefert. Eine Änderung des Emissionsgrads um 0.01 würde bei sonst unveränderten Bedingungen eine solche der Gleichgewichtstemperatur von 1.2 K bewirken. Eine Änderung der Albedo ebenfalls um 0.01 würde eine Temperaturänderung um 1.0 K nach sich ziehen.
Instrumente[Bearbeiten]
Optische Teleskope[Bearbeiten]
Trotz des Vordringens der Astronomie in andere Wellenlängenbereiche spielen optische Beobachtungen weiterhin eine bedeutsame Rolle, wobei man hinsichtlich der Abbildungstechnik auch noch das Ultraviolett und nahe Infrarot mit einschließen kann. Im Folgenden sollen einige wichtige Eigenschaften optischer Teleskope diskutiert werden.
Öffnungsverhältnis
Eine überragende in viele andere Kenngrößen eingehende Eigenschaft eines Teleskops ist dessen Öffnungsverhältnis , das Verhältnis zwischen dem Durchmesser der Eintrittspupille des Objektivs und dessen Brennweite :
Bildgröße
Ein Objektiv erzeugt von einem sehr weit entfernten Gegenstand ein Bild, das direkt in der Fokalebene liegt. Der Abstand des Bilds vom Objektiv beträgt also genau . Erscheint der Gegenstand unter einem Winkeldurchmesser , so weist das Bild folgende lineare Ausdehnung auf:
Bei Himmelsobjekten ist immer sehr klein, so dass die Näherung verwendet werden darf. muss dabei im Bogenmaß eingesetzt werden. Handlicher ist jedoch das Gradmaß, was einen zusätzlichen Umrechnungsfaktor von / 180 bzw. von etwa 0.0175 erfordert. Damit vereinfacht sich obige Formel zu:
Winkelvergrößerung
Das vom Objektiv erzeugte Bild wird anschließend durch ein Okular mit einer kürzeren Brennweite betrachtet. Ein Objekt mit einem vorherigen kleinen Winkeldurchmesse erscheint unter dem wie eine Lupe wirkenden Okular unter einem größeren Winkel . Als Winkelvergrößerung ist folgendes Verhältnis definiert:
Die oben für das Objektiv gegebene Beziehung zwischen linearer Bildgröße und Brennweite gilt analog auch für das Okular. Daraus folgt, dass die Winkelvergrößerung direkt durch das Verhältnis der Brennweiten der beiden Komponenten gegeben ist:
Auflösungsvermögen
Infolge der Beugung des einfallenden Lichts am Objektiv wird auch eine Punktquelle flächenhaft, nämlich als Beugungsscheibchen abgebildet. Zwei unmittelbar benachbarte Punktquellen können noch klar voneinander getrennt werden, wenn das Hauptmaximum des einen Scheibchens auf dem ersten Minimum des benachbarten zu liegen kommt. Nach der Beugungstheorie entspricht dies für Licht einer Wellenlänge folgendem Winkelabstand :
In der Praxis kann man gemäß des Dawes-Kriteriums noch einen etwas geringeren Winkelabstand zulassen, nämlich:
Folgende Abbildung zeigt zwei Beugungsbilder, welche diese Anforderung gerade noch erfüllen.

Für obige Formel ist es wünschenswert, den sehr kleinen Winkel in Bogensekunden anstatt Bogenmaß und die Wellenlänge in Nanometern statt Metern auszudrücken. Dann lautet die Beziehung:
Tatsächlich ist das Auflösungsvermögen bei größeren Instrumenten durch die Luftunruhe und nicht durch die Beugung beschränkt, und zwar auf etwa 1 Bogensekunde. Betrachtet man Licht einer Wellenlänge von 500 Nanometern, bewirkt schon bei einem Objektivdurchmesser von etwa 0.11 Metern die Luftunruhe die gleiche "Verschmierung" einer Punktquelle wie die Beugung.
Die hier skizzierte Gesetzmäßigkeit für die Begrenzung der Auflösung durch Beugung gilt auch außerhalb des optischen Bereichs, z. B. für Radioteleskope.
Aufgenommene Leistung (Punktquelle)
Die von einer Punktquelle aufgenommene Leistung ist der Fläche der Eintrittspupille des Objektivs und somit dem Quadrat dessen Durchmessers direkt proportional:
Aufgenomme Intensität (Flächenquelle)
Wie schon geschildert, ist die lineare Ausdehnung des Abbilds eines flächigen Gegenstands der Brennweite des Objektivs direkt proportional, dementsprechend die Fläche des Abbilds proportional zum Quadrat der Brennweite. Die pro Flächenelement am Empfänger (man denke z. B. an die Pixel einer CCD-Kamera) ankommende Leistung, d. h. die Intensität , ist somit umgekehrt proportional zu . Berücksichtigt man zusätzlich wieder die Rolle des Objektivdurchmessers, so gilt:
Je stärker die Vergrößerung des Teleskops ist, umso dunkler erscheint das Bild, da das einfallende Licht über eine größere Fläche am Empfänger verteilt wird. Dies betrifft auch Punktquellen wie Sterne, welche durch die Beugung bzw. Luftunruhe ebenfalls flächig abgebildet werden. Bei großen Instrumenten () ist der Winkeldurchmesser des Abbilds durch die Luftunruhe bestimmt, wodurch obige Formel zu verwenden ist.
Bei kleinen Teleskopen dominiert die Beugung, welche wie gerade erläutert ein Abbild liefert, dessen Winkeldurchmesser proportional zu und dessen Fläche damit proportional zu ist. Die einfallende Intensität ist so nicht nur zu proportional, sondern auch zu . Die Multiplikation beider Proportionalitäten liefert:
Zwar interessiert man sich bei Sternen nur für die gesamte aufgenommene Leistung, welche weiterhin proportional zu ist. Jedoch wird bei starker Vergrößerung das ankommende Licht infolge des endlichen Winkeldurchmessers des Sternscheibchens wie bei einer echten Flächenquelle über viele Pixel des Empfängers verteilt, was angesichts eines gleichbleibenden Rauschens pro Pixel den Nachweis schwacher Sterne erschwert.
Bei kleinen Teleskopen erzielt man in dieser Hinsicht mit einem größeren Objektivdurchmesser einen enormen Mehrwert, da man nicht nur mehr Licht aufsammelt, sondern dieses zusätzlich auf ein kleineres Beugungsscheibchen konzentriert. Bei großen Instrumenten verbessert wegen der Luftunruhe ein größeres Objektiv die Konzentration des Lichts auf ein kleineres Sternscheibchen nicht mehr. Es bleibt nur noch der zusätzliche Gewinn an einfallendem Licht.
Die hier getätigten Aussagen über die aufgenommene Leistung bzw. Intensität lassen sich ebenfalls auf andere Bereiche des elektromagnetischen Spektrums übertragen.
Radioastronomie[Bearbeiten]
Das Herzstück eines Radioteleskops ist wie bei einem optischen Fernrohr zumeist ein Parabolspiegel. Als Empfänger dient nun aber eine Antenne, welche sich im Brennpunkt des Spiegels befindet. Im Folgenden sollen sowohl einige allgemeine Eigenschaften von Antennen als auch spezifische Eigenheiten von Radioteleskopen genannt werden.
Antennengewinn
Eine Funkantenne strahlt und empfängt nicht gleichmäßig, sondern bevorzugt in bzw. aus bestimmten Richtungen. Dieses gerichtete Abstrahl- und Empfangsverhalten wird im Detail durch das sogenannte Antennendiagramm beschrieben, welches die in/aus einer beliebigen Richtung abgegebene/aufgenommene Leistung pro Raumwinkel mit derjenigen in der Hauptstrahlrichtung (dem Maximum) vergleicht. Das untenstehende Bild zeigt als Beispiel das Antennendiagramm einer Parabolantenne.

Ein übersichtliches Maß, wie stark die Antenne gerichtet ist, stellt der Antennengewinn dar. Hierbei vergleicht man die tatsächliche Leistung pro Raumwinkel in Hauptstrahlrichtung mit derjenigen , welche von einer isotropen Antenne gleicher Gesamtleistung ausgehen würde:
Antennenwirkfläche
Die Antennenwirkfläche gibt die effektiv absorbierende Fläche einer Antenne an. Kommt elektromagnetische Strahlung einer Intensität an und wird dabei eine gesamte Leistung aufgenommen, so gilt aufgrund der Definition der Intensität:
Die Antennenwirkfläche ist mit dem Antennengewinn über folgende Beziehung verknüpft, wobei abermals die Wellenlänge darstellt:
Andererseits hängt von den geometrischen Abmessungen des Radioteleskops (dem Durchmesser des Parabolspiegels) und dem Wirkungsgrad der Empfangsvorrichtung ab:
Die von einem Radioteleskop aufgenommene Leistung ist ebenso dem Quadrat des Durchmessers des Hauptspiegels proportional wie für ein optisches Fernrohr. Der Wirkungsgrad einer Parabolantenne beträgt zumeist etwa 50%.
Auflösungsvermögen
Die beiden obigen Beziehungen für die Antennenwirkfläche liefern einen direkten Zusammenhang zwischen , und . Es zeigt sich, dass der Antennengewinn eines Radioteleskops direkt durch dessen beugungsbegrenztes Auflösungsvermögen gegeben ist:
Wegen der großen Wellenlängen der Radiostrahlung ist das Auflösungsvermögen selbst gewaltiger Radioteleskope bescheiden. Für das Teleskop in Effelsberg erhält man mit einem Durchmesser von 100 m bei einer Wellenlänge von 21 cm (ein wichtiger Bereich für die Messung der Radiostrahlung interstellaren Wasserstoffs) ein Auflösungsvermögen von gerade einmal 0.124 Grad, entsprechend etwa einem Viertel des Winkeldurchmessers von Sonne und Vollmond. Jedoch können mittels der sogenannten Langbasisinterferometrie die von mehreren auch weit voneinander entfernten Radioteleskopen empfangenen Signale rechnerisch kohärent miteinander kombiniert werden. Damit ist das Auflösungsvermögen nicht mehr durch die Durchmesser der Parabolspiegel, sondern die viel größeren Abstände der Teleskope untereinander bestimmt. Mit maximalen Abständen in der Größenordnung von 10000 km lässt sich im Wellenlängenbereich von 21 cm so eine Auflösung von etwa 0.004 Bogensekunden erreichen (die Luftunruhe spielt im Radiobereich keine Rolle).
Spektrographen[Bearbeiten]
Für astronomische Spektroskopie wird im Optischen und den unmittelbar angrenzenden Bereichen des elektromagnetischen Spektrums zumeist ein Beugungsgitter eingesetzt. Die wichtigsten Charakteristika solcher Gitter sollen nun aufgezeigt werden.
Winkeldispersion eines Beugungsgitters
Man betrachte ein Gitter der Ausdehnung , dessen Spalten untereinander einen festen Abstand haben. Der Einfachheit halber soll das Licht senkrecht einfallen (siehe nachfolgende Zeichnung).

Betrachtet man nun aufeinanderfolgende Spalte, so beträgt in Richtung eines Ausfallswinkels der Gangunterschied der entsprechenden Lichtstrahlen . Konstruktive Interferenz liegt vor, wenn ein ganzzahliges Vielfaches der Wellenlänge ist, also . Für kleine Ausfallswinkel darf man (in Bogenmaß) setzen, woraus folgt:
Unter der Winkeldispersion versteht man die Änderung des Ausfallswinkels mit der Wellenlänge, also den Ausdruck . Mit obiger Näherung gilt:
Die Winkeldispersion ist demnach von der Wellenlänge unabhängig, ein Vorteil des Beugungsgitters gegenüber dem Prisma.
Spektrales Auflösungsvermögen
Eine wichtige Eigenschaft eines Spektrographen besteht darin, zwei Spektrallinien mit fast identischen Wellenlängen und noch trennen zu können. Dies ist dann der Fall, wenn unter dem gleichen Ausfallswinkel für die eine Linie das -te Hauptmaximum, für die andere Linie dagegen das entsprechende erste Minimum erscheint. Das Auflösungsvermögen wird durch das dann vorliegende Verhältnis ausgedrückt.
Der kleinste Winkel, der mit einem Gitter der Größe noch aufgelöst werden kann, beträgt analog zu einem Teleskop mit dem gleichen Durchmesser . Andererseits ist wie oben gezeigt für konstruktive Interferenz , woraus durch Gleichsetzen folgt. entspricht der Anzahl der Gitterspalte. Daraus resultiert schließlich:
Das Auflösungsvermögen hängt also allein von der Anzahl der Gitterspalte und der Ordnung ab, unter welcher man das Spektrum betrachtet. Demnach ist es erstrebenswert, ein Beugungsmaximum möglichst hoher Ordnung zu verwenden. Jedoch folgen dann (die Näherung gilt für große nicht mehr) die Maxima immer dichter aufeinander, so dass die Spektren zu überlappen beginnen. Weiterhin nimmt bei einem gewöhnlichen Gitter die Intensität der Maxima mit zunehmender Ordnung stark ab. Zumindest dieses Problem lässt sich durch ein sogenanntes Blazegitter umgehen. Es hat die Eigenschaft, dass bei schrägem Lichteinfall der Ausfallswinkel für eine bestimmte Ordnung demjenigen einer einfachen Reflexion entspricht, wodurch weit mehr Licht in diese Richtung gebeugt wird.
Wie schon geschildert, liegt die relative Dopplerverschiebung für Sterne der Milchstraße zumeist bei etwa 10-5 bis 10-4. Um deren Geschwindigkeiten relativ zu uns mit einer Genauigkeit von 1% messen zu können, ist eine spektrale Auflösung in der Größenordnung von 106 bis 107 erforderlich. Beobachtet man in der 10.Ordnung, werden somit 105 bis 106 Gitterspalte benötigt.
Astrometrie[Bearbeiten]
Die Astrometrie befasst sich mit der Messung und Berechnung der Positionen der Gestirne am Himmel, der sogenannten Sternörter. Sie bezieht sich dabei sowohl auf die (Fix)sterne als auch auf Körper des Sonnensystems wie Sonne, Mond, Planeten und Kometen. Hier soll aber nur die Berechnung von Sternpositionen ausführlicher behandelt werden. Auf die wesentlich kompliziertere Berechnung der Positionen von Mitgliedern des Sonnensystems kann im Rahmen dieser Formelsammlung nicht eingegangen werden.
Sternzeit[Bearbeiten]
Für die Beschreibung der Sternörter wird eine Zeitskala benötigt, welche die scheinbare Bewegung der Gestirne um die Erde aufgrund deren Eigenrotation beschreibt. Diese Zeitskala wird als Sternzeit bezeichnet.
Die Sternzeit wird wie die im Alltag benutzte Sonnenzeit (welche sich auf die scheinbare Bewegung der Sonne um die Erde bezieht) in Tage, Stunden, Minuten und Sekunden eingeteilt. Ein Sterntag (und dementsprechend auch dessen Untereinheiten) ist dabei kürzer als ein Sonnentag. Ursache hierfür ist, dass die scheinbare Bewegung der Sonne um die Erde nicht nur von der Rotation, sondern auch der Bahnbewegung der Erde um die Sonne bestimmt ist. Dadurch bleibt die Sonne auf ihrer scheinbaren Bahn gegenüber den Sternen täglich um einen kleinen Betrag zurück (siehe nachfolgende Abbildung).
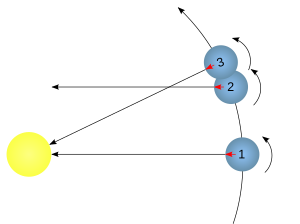
Ein Sterntag ist exakt um den Faktor 1 / 365.2422 (entsprechend der Dauer eines Jahres in Sonnentagen) kürzer als ein Sonnentag. In Einheiten der Sonnenzeit ausgedrückt, dauert ein Sterntag 23 h 56 m 4.091 s. Ungeachtet dessen gilt die Einteilung 1 Sterntag = 24 Sternstunden, 1 Sternstunde = 60 Sternminuten usw.
Die Dauer eines Sterntages lässt sich anschaulich messen, indem man von einem festen Standort aus beobachtet, wann ein bestimmter Stern hinter einer Mauer verschwindet. Wiederholt man diese Beobachtung in der darauffolgenden Nacht, so stellt man fest, dass unterdessen noch keine 24 Sonnenstunden vergangen sind, sondern noch einige Minuten fehlen. In der astronomischen Praxis ist der Sterntag durch die Zeit definiert, die zwischen zwei aufeinanderfolgenden Durchgängen des Frühlingspunkts durch den Nullmeridian verstreicht.
Für die Berechnung von Sternörtern ist die Kenntnis der lokalen Sternzeit unerlässlich. Diese lässt sich durch folgende Schritte ermitteln:
- Julianisches Datum für 0 h mittlere Greenwicher Sonnenzeit
- Mittlere Greenwicher Sternzeit für 0 h mittlere Greenwicher Sonnenzeit
- Mittlere Greenwicher Sternzeit für tatsächliche Beobachtungszeit
- Mittlere lokale Sternzeit für tatsächlichen Standort (geographische Länge) des Beobachters
Julianisches Datum für 0 h mittlere Greenwicher Sonnenzeit
Das Julianische Datum gibt an, wie viele Tage seit dem 1. Januar 4713 v.Chr. 12 h vergangen sind. Es stellt eine fortlaufende Tageszählung dar, welche in der Astronomie oft verwendet wird. Es hat gegenüber im Alltag verwendeten Kalendern den Vorteil, dass Zeitdifferenzen sehr leicht berechnet werden können, ohne sich um Besonderheiten wie ungleich lange Momate und Schaltjahre kümmern zu müssen.
Ist ein Datum mit Tag, Monat und Jahr gegeben, so wird das entsprechende Julianische Datum folgendermaßen berechnet. Für die Monate März bis Dezember wird gleich dem tatsächlichen Monat und gleich dem tatsächlchen Jahr gesetzt. Für Januar und Februar ist jedoch für der Wert Monat + 12 und für der Wert Jahr - 1 zu verwenden. Für wird einfach die Tageszahl genommen. Dann gilt für Daten seit der Einführung des gregorianischen Kalenders am 15. Oktober 1582:
Die Funktion Int bezeichnet das Wegschneiden der Nachkommastellen (es wird unabhängig vom Ergebnis stets auf die nächstkleinere ganze Zahl abgerundet).
Als Beispiel sei der 31. Januar 2018 betrachtet. Gemäß obiger Regel ist dann als Jahreszahl 2017 und als Monatszahl 13 einzusetzen. Es ergibt sich ein Julianisches Datum von 2458149.5.
Mittlere Greenwicher Sternzeit für 0 h mittlere Greenwicher Sonnenzeit
Aus dem Julianischen Datum folgt die mittlere Greenwicher Sternzeit in Sekunden für 0 h mittlere Greenwicher Sonnenzeit gemäß der Vorschrift:
Die aus folgende Zeit muss auf Werte zwischen 0 und 86400 Sekunden normiert werden, wozu die Modulo-Operation dient.
Wieder sei der 31. Januar 2018 diskutiert. Aus obigem Julianischen Datum folgt eine von 31240.5 Sekunden bzw. 8 h 40 m 40.5 s.
Mittlere Greenwicher Sternzeit für tatsächliche Beobachtungszeit
Findet die Beobachtung nicht um 0 h, sondern zu einem beliebigen Zeitpunkt mittlerer Greenwicher Sonnenzeit statt, so muss ausgedrückt in Sternzeit zur hinzuaddiert und das Resultat erneut normiert werden:
Der Faktor 1.00273790935 berücksichtigt den Unterschied zwischen mittlerem Sonnen- und Sterntag.
Man betrachte z. B. eine Beobachtung um 20 h Mitteleuropäischer Zeit, was einer solchen um 19 h Greenwicher Zeit entspricht. 19 Sonnenstunden ergeben 68400 Sonnensekunden, welche wiederum 68587 Sternsekunden entsprechen. Addiert man diesen Betrag zu den oben genannten 31240.5 Sekunden hinzu, ergeben sich normiert 13427.8 Sekunden bzw. 3 h 43 m 47.8 s.
Mittlere lokale Sternzeit für tatsächlichen Standort (geographische Länge) des Beobachters
Schließlich muss berücksichtigt werden, dass der Beobachter sich auf einem beliebigen Längengrad befinden kann. Um aus der Greenwicher die lokale Sternzeit zu gewinnen, muss die Länge in Zeitsekunden ausgedrückt und zur addiert werden:
360 Längengraden entsprechen 24 Zeitstunden. Dementsprechend ist der Umrechnungsfaktor von Winkelsekunden zu Zeitsekunden 24 / 360 bzw. 1 / 15.
Befindet man sich z. B. auf 10 Grad östlicher Länge, so ist man der Greenwicher Zeit 36000 Winkelsekunden bzw. 2400 Zeitsekunden voraus. Zu obigen 13427.8 Sekunden addiert, erhält man eine lokale Sternzeit von 15827.8 Sekunden bzw. 4 h 23 m 47.8 s.
Koordinatensysteme[Bearbeiten]
Horizontsystem[Bearbeiten]
Um die Positionen der Gestirne festzulegen, muss man sich auf exakt definierte Bezugssysteme beziehen. Um ein Teleskop auf einen bestimmten Himmelskörper auszurichten, verwendet man hierbei ein System, welches unmittelbar die Anschauung des Beobachters wiedergibt, das sogenannte Horizontsystem. Der Beobachter befindet sich in dessen Ursprung.

In diesem System gibt man die Position eines Gestirns durch zwei Winkel relativ zum Horizont und der Südrichtung bzw. Nordrichtung an, je nachdem ob man sich auf der nördlichen oder südlichen Hemisphäre befindet. Die Koordinate relativ zum Horizont wird durch die Elevation (Höhenwinkel) repräsentiert, diejenige relativ zur Süd- bzw. Nordrichtung durch den Azimut . Der Azimut wird dabei von der Bezugsrichtung ausgehend im Uhrzeigersinn gemessen. Häufig wird anstatt des Horizonts auch der Zenit als Bezugspunkt genommen. Anstelle der Elevation tritt dann die Zenitdistanz mit .
Äquatorsystem[Bearbeiten]
Ruhendes Äquatorsystem
Das Horizontsystem folgt zwar direkt der Perspektive des Beobachters, doch hat es den Nachteil, dass sich darin die Positionen der Gestirne infolge der Erdrotation fortlaufend ändern. Ein wichtiger Schritt hin zu einem Koordinatensystem, welches der Erdrotation folgt und damit (fast) zeitunabhängige Positionen für die Sterne liefert, ist das ruhende Äquatorsystem. Es unterscheidet sich vom Horizontsystem dadurch, dass als Bezugsebene nicht der Horizont, sondern der Himmelsäquator (die Projektion des Erdäquators an das Firmament) verwendet wird.

An die Stelle des Höhenwinkels über dem Horizont tritt nun derjenige über dem Himmelsäquator, die sogenannte Deklination . Der Azimut wird durch den Stundenwinkel ersetzt, wobei dieser sich jedoch weiterhin auf die Süd- bzw. Nordrichtung bezieht.
Im Gegensatz zur üblichen Konvention wird der Stundenwinkel nicht in Grad, sondern in Stunden angegeben, entsprechend der Tatsache, dass die Änderung des Stundenwinkels der Sonne genau dem Fortschreiten der Tageszeit entspricht. Im Verlauf eines mittleren Sonnentages ändert sich der Stundenwinkel der Sonne um 360 Grad, d. h. pro Stunde um 15 Grad.
Rotierendes Äquatorsystem
Für (Fix)sterne ist die Deklination bereits eine (nahezu) zeitunabhängige Größe. Der Stundenwinkel jedoch unterliegt noch der Erdrotation. Um daraus einen zweiten festen Winkel zu gewinnen, lässt man das Koordinatensystem sich mit der Erde drehen, woraus das rotierende Äquatorsystem hervorgeht.

Die Deklination bleibt hierbei unverändert. An die Stelle des Stundenwinkels tritt nun aber mit der sogenannten Rektaszension wie gewünscht eine zweite von der Erdrotation freie Koordinate. Als Bezugspunkt für die Rektaszension dient der Frühlingspunkt - der Schnittpunkt von Himmelsäquator und Ekliptik, auf welchem sich die Sonne zum Frühlingsanfang befindet. Wie der Stundenwinkel wird auch die Rektaszension in Stunden anstatt Grad angegeben.
Das rotierende Äquatorsystem ist dem für geographische Ortsangaben benutzten Gradnetz völlig analog. Die Deklination entspricht dem Breitengrad, die Rektaszension dem Längengrad.
Transformation Rotierendes Äquatorsystem -> Horizontsystem
Für die Beobachtungspraxis am wichtigsten ist die Umrechnung vom rotierenden Äquatorsystem ins Horizontsystem, um das Teleskop auf ein gewünschtes Objekt ausrichten zu können. Hierfür gelten folgende Beziehungen, wobei die geographische Breite bedeutet:
Der Höhenwinkel kann nur Werte von -90 bis +90 Grad annehmen, so dass die Arcussinus-Funktion eindeutige Werte liefert. Hingegen kann der Azimuth zwischen 0 und 360 Grad liegen, so dass die Arcustangens-Funktion entsprechend den Vorzeichen von Zähler und Nennen ausgewertet muss:
Als Beispiel sei der Stern Beteigeuze betrachtet. Auf das Jahr 2000 bezogen (wie nachfolgend gezeigt wird, ändern sich die Sternörter im Laufe der Zeit vor allem durch die Präzession) hat er eine Deklination von +07 Grad 24 mm 25 ss und eine Rektaszension von 05 h 55 m 10.3 s. Für die oben diskutierte Beobachtung am 31. Januar 2018 um 20 Uhr Mitteleuropäischer Zeit auf 10 Grad östlicher Länge beträgt die Sternzeit wie bereits gezeigt 4 h 23 m 47.8 s. Befindet sich man auf 50 Grad nördlicher Breite, so liefern die Transformationsformeln einen Azimut von 326 Grad 53 mm 45 ss und eine Zenitdistanz von 46 Grad 49 mm 20 ss. Beteigeuze findet sich dann also im Südosten auf mittlerer Höhe über dem Horizont.
Transformation Horizontsystem -> Rotierendes Äquatorsystem
Die umgekehrte Transformation vom Horizont- ins rotierende Äquatorsystem lautet:
Die Arcustangens-Funktion ist genauso zu behandeln wie für die Umrechnung vom Äquator- ins Horizontsystem.
Dauer des längsten Tages
Aus der Transformation des Äquator- ins Horizontsystem lässt sich folgendermaßen die Dauer des längsten Tages ableiten. Man betrachte die Stundenwinkel der Sonne zum Zeitpunkt ihres Aufgangs und Untergangs, wenn also deren Elevation gleich 0 ist. Die Deklination der Sonne am längsten Tag des Jahres ist auf der Nordhalbkugel gleich der Schiefe der Ekliptik (auf der Südhalbkugel entsprechend gleich ). Unter diesen Voraussetzungen liefert die Formel zur Berechnung der Elevation die Beziehung . Da die beiden möglichen Stundenwinkel betragsmäßig gleich sind, folgt daraus für die maximale Tageslänge:
Auf 50 Grad nördlicher Breite erhält man mit einer Schiefe der Ekliptik von 23.45 Grad eine maximale Tageslänge von 16 h 9 m 1 s. Am Polarkreis, entsprechend einer Breite , nimmt der Bruch in obiger Formel den Wert -1 an, d. h. die Sonne geht exakt bei einem Stundenwinkel von -12 h (d. h. genau um Mitternacht) auf und bei einem solchen von +12 h (d. h. erneut exakt um Mitternacht) wieder unter, so dass die maximale Tageslänge über volle 24 Stunden geht. Für Gebiete noch weiter nördlich bleibt der Bruch kleiner als -1, d. h. die Sonne geht dort zur Zeit der Sommersonnenwende überhaupt nicht mehr unter.
Dauer des kürzesten Tages
Für den kürzesten Tag des Jahres ist auf der Nordhalbkugel für die Deklination der Sonne der Wert (und auf der Südhalbkugel analog ) einzusetzen. Aus den Eigenschaften der Sinus- und Cosinusfunktion bezüglich negativer Winkel folgt dann unmittelbar:
Für 50 Grad nördlicher Breite gewinnt man ein Ergebnis von 7 h 50 min 59 s. Am Polarkreis wird der Bruch nun gleich +1. Die Sonne geht dann bei einem Stundenwinkel von genau 0 h auf und wieder unter, d. h. die minimale Tageslänge liegt bei 0. Noch weiter nördlicher ist der Bruch größer als +1, die Sonne geht dort zur Zeit der Wintersonnenwende gar nicht mehr auf.
Bei den hier skizzierten Berechnungen der Tageslänge sind die endliche Ausdehnung der Sonnenscheibe und die nachfolgend behandelte Refraktion nicht berücksichtigt. Durch letztere erscheinen Gestirne am Horizont um 34 Bogenminuten - mehr als der Winkeldurchmesser der Sonne - angehoben. Wenn die Sonne rein geometrisch betrachtet sich schon komplett unter dem Horizont befindet, ist sie tatsächlich noch vollständig sichtbar, was einen entsprechend verlängerten Tag zur Folge hat.
Ekliptikales Koordinatensystem[Bearbeiten]
Um die Positionen von Körpern des Sonnensystems anzugeben, ist es oft praktischer, nicht die vom Himmelsäquator, sondern von der Ekliptik definierte Ebene als Bezugspunkt zu nehmen. Als Ekliptik bezeichnet man den Weg, den die Sonne im Verlauf eines Jahres infolge der Bahnbewegung der Erde vor dem Hintergrund der (Fix)sterne abschreitet.
Anstelle von Deklination und Rektaszension treten nun ekliptikale Breite und Länge . Die Länge bezieht sich wie die Rektaszension auf den Frühlingspunkt.
Für das ekliptikale Koordinatensystem gibt es zwei Varianten. Bei der einen Abart steht die Erde, bei der anderen die Sonne im Ursprung des Koordinatensystems. Ersteres entsteht aus dem rotierenden Äquatorsystem, indem dieses entsprechend der Neigung der Erdachse gegenüber der Erdbahn um 23.45 Grad gekippt wird.
Transformation Äquatorsystem -> Ekliptikales System (Erde im Ursprung)
Für die Umrechnung von Äquator- in ekliptikale Koordinaten werden zunächst Deklination und Rektaszention in geozentrische kartesische Koordinaten transformiert. Hierbei bezeichnet die Neigung der Erdachse gegenüber der Bahnebene.
Aus den kartesischen Koordinaten folgen anschließend ekliptikale Breite und Länge:
Transformation Ekliptikales System -> Äquatorsystem
Due Rückkehr von ekliptikalen zu Äquatorkoordinaten beruht auf folgenden Beziehungen:
Galaktisches Koordinatensystem[Bearbeiten]
Für Objekte der Milchstraße wird als Bezugspunkt für deren Positionen oft das galaktische Zentrum verwendet, wodurch aus dem rotierenden Äquatorsystem das galaktische Koordinatensystem hervorgeht. Im rotierenden Äquatorsystem hat das Milchstraßenzentrum (bezogen auf das Jahr 1950) die Koordinaten 28 Grad 55 mm und 17h 42.4 m. Die Position des galaktischen Nordpols lautet +27 Grad 24 mm und 12h 49.0 m. Die galaktische Ebene ist gegenüber dem Himmelsäquator um 62 Grad 36 mm geneigt.
Aus Deklination unf Rektaszension werden im galaktischen Koordinatensystem galaktische Breite und Länge .
Transformation Äquatorsystem -> Galaktisches System
Die Transformation von Äquator- in galaktische Koordinaten geschieht wie folgt:
Transformation Galaktisches System -> Äquatorsystem
Die Umkehrtransformation lautet:
Korrekturen[Bearbeiten]
Präzession
Die Positionen der Sterne im rotierenden Äquatorsystem sind nicht wirklich fix, sondern ändern sich langsam im Laufe der Zeit. Eine wesentliche Ursache hierfür ist die Präzession der Erdachse, welche nicht fest im Raum orientiert ist, sondern vor allem unter dem Einfluß des Mondes sich wie die Achse eines Kreisels bewegt. Im Verlaufe von etwa 25700 Jahren zeichnet die Erdachse dadurch einen Kegel um den Pol der Ekliptik, dessen Öffnungswinkel mit der Schiefe der Ekliptik identisch ist. Die Kreiselbewegung der Erdachse zieht eine entsprechende Verschiebung des Frühlingspunktes und damit des Koordinatensystems mit sich.
Die jährliche durch den Mond bewirkte Verschiebung des Frühlungspunktes wird als Präzessionskonstante bezeichnet und beläuft sich auf 50"3878 pro Jahr (bezogen auf das Jahr 2000). Die Planeten stören die Erdachse zusätzlich geringfügig und liefern einen weiteren Beitrag zur Präzession von 0"1055 pro Jahr.
Um die jährliche Änderung der Koordinaten eines Sterns zu berechnen, muss man zunächst die allgemeine jährliche Drift des Koordinatensystem in Deklination und in Rektaszension betrachten. Es gilt:
beläuft sich auf 20"0431 = 1.33621 s und auf 46"1244 = 3.07496 s pro Jahr, Aus diesen beiden Größen und den aktuellen Sternkoordinaten folgen deren jährliche Änderungen gemäß:
Aufgrund der durch die Präzession hervorgerufenen Verschiebung der Sternpositionen muss man für solche stets auch den Zeitpunkt angeben, auf welchen sich diese beziehen sollen. Meist wird als Zeitreferenz der Beginn des Jahres 2000 genommen.
Die Präzessionskonstante selbst ist ebenfalls nicht wirklich konstant. Aufgrund geringer Änderungen der Mondbahn nimmt sie gegenwärtig um circa 0"0002 pro Jahr zu. Deshalb muss auch für den Wert von stets der Zeitbezug genannt werden.
Für das hier behandelte Beispiel mit Beteigeuze liefern die Präzessionsformeln für den gewünschten Beobachtungszeitpunkt eine Deklination von +07 Grad 7 mm 59 ss und eine Rektaszension von 5 h 56 m 12.0 s. Für die Deklination fällt hier die Korrektur vergleichsweise gering aus, da die Rektaszension nahe bei 6 h bzw. 90 Grad und damit fast bei 0 liegt. Die Korrektur der Rektaszension ist hier weitgehend durch bestimmt, da die Deklination und damit deren Tangens nur wenig über 0 liegt. Die Umrechnung der korrigierten Koordinaten ins Horizontsystem liefert eine Zenitdistanz von 46 Grad 54 mm 16 ss und einen Azimut von 326 Grad 33 mm 10 ss. Erstere erfährt hier eine Korrektur von etwa 5, letzterer sogar um ungefähr 20 Winkelminuten entsprechend circa 2/3 des scheinbaren Durchmessers des Vollmonds.
Nutation
Zusätzlich zur Kreisel- führt die Erdache eine kleine Nickbewegung aus, welche als Nutation bezeichnet wird. Sie wird überwiegend durch die Präzession der Mondbahn verursacht, deren Knotenlinie eine Umlaufperiode von 18.6 Jahren aufweist. Im Laufe dieser Zeit beschreibt die Erdachse eine Ellipse, deren große und kleine Halbachse 9"21 und 6"86 betragen. Aufgrund dieser kleinen zusätzlichen Bewegung ist der Präzessionskegel nicht glatt, sondern durch kleine wellenförmige Ausschläge leicht deformiert.

Die Nutation zieht zwei Effekte nach sich, eine Änderung der Schiefe der Ekliptik und wiederum eine Verschiebung des Frühlingspunkts in ekliptikaler Länge . Beide folgen unmittelbar aus der ekliptikalen Länge des Mondknotens:
Aus folgt ein zusätzlicher Versatz des Äquatorsystems und in Deklination und Rektaszension.
Neben dem Hauptbeitrag durch die Präzession der Mondbahn existieren noch weitere Komponenten mit kürzeren Perioden und geringeren Amplituden, die unter 1" liegen. Die exakte Behandlung der Nutation ist recht aufwändig, so dass auf den entsprechenden Artikel in der Wikipedia verwiesen sei.
Aberration
Vor allem aufgrund der Bahnbewegung der Erde um die Sonne bewegt sich ein Beobachter mit einer bestimmten Geschwindigkeitskomponente senkrecht zur Einfallsrichtung des Lichts. Deshalb darf er das Teleskop nicht direkt zum Gestirn hin ausrichten, sondern muss es um einen Winkel leicht in Bewegungsrichtung neigen, damit das Licht zunächst die Mitte des Objektivs und anschließend das Okular trifft (so wie ein Spaziergänger seinen Schirm neigen muss, damit der Regen diesen und nicht den Fußgänger trifft).

Da viel kleiner als die Lichtgeschwindigkeit ist, darf klassich gerechnet werden (mit Ergebnis in Bogenmaß) gemäß
Die Aberration ist am stärksten, wenn das Licht senkrecht zur Bahnebene der Erde einfällt. Aus einer Bahngeschwindikeit von 30 km/s folgt daraus ein Aberrationswinkel von etwa 21". Jeder Stern beschreibt am Himmel im Verlaufe eines Jahres eine Ellipse, deren große Halbachse eben jenen Betrag aufweist.
Die Erdrotation liefert ebenfalls einen noch meßbaren, aber sehr geringen Beitrag. Selbst am Äquator wird mit einer Rotationsgeschwindigkeit von ungefähr 0.46 km/s ein von höchstens 0"32 erreicht.
Refraktion
Durch die Brechung des Lichts in der Erdatmosphäre erscheinen die Gestirne angehoben, wie nachfolgendes Bild zeigt. Die aus den Äquatorkoordinaten folgende Höhe über dem Horizont wird dementsprechend um einen Zusatzbeitrag vergrößert. Für reicht es aus, die Atmosphäre als eine Abfolge ebener paralleler Schichten zu betrachten. Dann gilt mit in Bogenmaß:
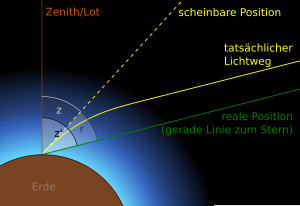
bezeichnet den Brechungsindex der Luft am Beobachtungsstandort. Unter Normalbedingungen ist = 1.000293, was zur folgenden handlicheren Darstellung in Bogensekunden führt:
Für Gestirne, die nahe dem Horizont stehen, muss die Krümmung der Atmosphäre berücksichtigt, diese also als eine Abfolge kugelförmiger Schichten diskutiert werden. Es ergeben sich Korrekturen, die bis zu noch relativ einfach berechnet werden können. Es gilt dann unter Normalbedingungen wiederum in Bogensekunden:
Für das Beteigeuze-Beispiel darf mit einer Zenitdistant von 46 Grad 54 mm 16 ss die einfache Refraktionsformel genommen werden. Es ergibt sich eine Korrektur von 70 Winkelsekunden.
Himmelsmechanik[Bearbeiten]
Die Himmelsmechanik befasst sich mit der Fragestellung, wie sich Himmelskörper unter dem Einfluss der gegenseitigen Massenanziehung bewegen. Im Prinzip lassen sich solche Probleme mit Hilfe der aus der Mechanik bekannten Gesetzmäßigkeiten behandeln. Das Vorgehen wird jedoch oft sehr erleichtert, wenn man auf die konkrete Anwendung zugeschnittene Methoden heranzieht.
Schwerpunkt[Bearbeiten]
Oft ist es sehr nützlich, die Bewegungen der Mitglieder eines Ensembles von Himmelskörpern relativ zu dessen Schwerpunkt zu betrachten. Man betrachte ein System von Körpern mit Massen bis und Positionen (Ortsvektoren) bis . Die Position des Schwerpunkts lautet dann:
Für die Geschwindigkeit des Schwerpunkts gilt analog, wobei bis die Geschwindigkeiten der individuellen Mitglieder des Systems bezeichnen:
Sowohl als auch stellt also ein gewichtetes Mittel dar, wobei jedes Einzelobjekt mit seiner Masse gewichtet wird. Auf den Schwerpunkt bezogene Positionen und Geschwindigkeiten gewinnt man folgendermaßen:
Gravitationsgesetz und einfache Anwendungen[Bearbeiten]
Skalare Formulierung
Die wichtigste Gesetzmäßigkeit der Himmelsmechanik ist das Newtonsche Gravitationsgesetz. Es gibt an, mit welcher Kraft zwei Massen und , welche einen Abstand voneinander aufweisen, sich gegenseitig anziehen:
Vektorielle Formulierung
Das Newtonsche Gravitationsgesetz gibt nicht nur den Betrag der Anziehungskraft an, sondern auch deren Richtung, welche der Verbindungslinie der beiden Massen entspricht. Die Kraft , welche auf ausübt, lautet demgemäß:
Die von auf ausgeübte Kraft ist betragsmäßig der Kraft gleich, doch zeigt diese in die entgegengesetzte Richtung, nämlich .
Greift man aus einem System mit Körpern eine beliebige Masse heraus, muss man über alle von den übrigen Mitgliedern ausgeübten Kräfte vektoriell summieren, um die auf einwirkende Kraft zu erhalten:
Schwerebeschleunigung - nicht rotierender Körper
Das Gravitationsgesetz ermöglicht auf einfache Weise, die auf der Oberfläche eines Himmelskörpers herrschende Schwerebeschleunigung abzuleiten, wobei eine mögliche Rotation zunächst vernachlässigt werden soll. Man betrachte einen kugelförmigen Körper mit Masse und Radius , welcher eine radialsymmetrische Dichteverteilung aufweist (also eine nur vom Abstand vom Mittelpunkt abhängige lokale Dichte). Eine Probemasse auf dessen Oberfläche erfährt eine Kraft . Andererseits ist gemäß des Newtonschen Kraftgesetzes , woraus folgt:
Ist die Schwerebeschleunigung aus unabhängigen Messungen bekannt, liefert sie bei bekanntem Radius die Masse und über die Beziehung auch die mittlere Dichte des Körpers:
Schwerebeschleunigung - rotierender starrer Körper
Rotiert ein Körper, tritt zur Schwerebeschleunigung eine Zentrifugalbeschleunigung hinzu, so dass man in der Summe eine entsprechend verminderte Fallbeschleunigung registriert. Der Effekt hängt von der geographischen Breite ab, er ist am Äquator am stärksten, an den Polen verschwindet er ganz. Da die Breitenabhängigkeit relativ kompliziert ist, sollen hier nur die Verhältnisse am Äquator skizziert werden. Liegt dort eine Rotationsgeschwindigkeit vor, so gilt . Andererseits ist , wobei die Rotationsperiode des Körpers ist. Damit erhält man:
Auf der Erde sollte sich die Korrektur gemäß dieser Formel auf etwa 0.034 m s-2 belaufen, ein zwar kleiner, aber meßbarer Betrag. Um die Masse und somit auch die Dichte des rotierenden Körpers zu bestimmen, muss die Zentrifugalkraft folgendermaén berücksichtigt werden:
Da , ändert sich formell an der Beziehung für nichts. Jedoch liefert eine Messung auf einem rotierenden Körper nicht direkt , sondern nur . Zu dieser gemessenen Fallbeschleunigung muss addiert werden, um ein korrektes Ergebnis zu erhalten.
In der Praxis bewirkt die Zentrifugalkraft zusätzlich eine Verformung des rotierenden Körpers, er wird abgeplattet. Am Äquator ist man weiter vom Schwerezentrum entfernt als an den Polen, wodurch sich eine noch deutlichere Abhängigkeit der Fallbeschleunigung von der Breite einstellt. Tatsächlich nimmt diese auf der Erde vom Äquator zu den Polen hin um 0.054 m s-2 zu, d. h. deutlich stärker als oben berechnet. Auf eine Herleitung der zu erwartenden Abplattung soll hier jedoch verzichtet werden.
Potentielle Energie
Die potentielle Energie in einem Gravitationsfeld bezeichnet die Hubarbeit, welche man an einer Probemasse verrichten muss, um sie vollständig aus dem Anziehungsbereich einer Masse zu entfernen. Der Abstand der beiden Massen betrage zunächst . Um um eine kleine Strecke von wegzubewegen, ist nach dem Prinzip Arbeit = Kraft Weg die Arbeit erforderlich. Die Integration dieses Ausdrucks von bis ins Unendliche liefert:
Das Minuszeichen bringt zum Ausdruck, dass man die genannte Energie aufwenden muss, um die beiden Massen voneinander zu trennen. Betrachtet man die potentielle Energie eines beliebigen Mitglieds eines -Körper-Systems, muss man die Einzelenergien bezüglich aller anderen Massen aufaddieren:
Gravitationspotential
Für viele Probleme der Himmelsmechanik ist auch das Gravitationspotential eine Größe von eminenter Bedeutung. Es gibt die pro Masse auf einen Probekörper entfallende potentielle Energie an, ist also per Definition von dieser unabhängig. Befindet sich die Probemasse in einem Abstand r von der Masse , so herrscht dort ein Potential:
Eine Masse innerhalb eines Ensembles von Körpern unterliegt demgemäß einem Potential:
Das Gravitationspotential wird vor allem für solche Fragestellungen herangezogen, die vorzugsweise auf Grundlage einer kontinuerlichen Dichteverteilung zu bearbeiten sind, anstatt mit einem Modell diskreter Massen. Die sogenannte Poisson-Gleichung gestattet es, aus der Verteilung der Dichte diejenige des Gravitationspotentials und damit auch der Schwerebeschleunigung zu ermitteln.
Kosmische Geschwindigkeiten
Die hier vorgestellten Gesetzmäßigkeiten über die Gravitation und ihr Potential gestatten es, zwei häufig benutze Geschwindigkeitsskalen herzuleiten, welche als kosmische Geschwindigkeiten bezeichnet werden. Die 1. kosmische Geschwindigkeit gibt die Kreisbahngeschwindigkeit im niedrigsten möglichen Orbit um einen Himmelskörper an (dieser soll wieder eine Masse und einen Radius aufweisen). Sie folgt aus der Gleichsetzung der auf einer solchen Bahn herrschenden Zentripetalkraft mit der Anziehungskraft :
Die 2. kosmische Geschwindigkeit gibt an, auf welche Mindestgeschwindigkeit eine Probemasse beschleunigt werden muss, um von der Oberfläche startend die von ausgehende Gravitation überwinden zu können. Man gewinnt diese sogenannte Fluchtgeschwindigkeit, indem man die erforderliche kinetische Energie mit der potentiellen Energie im Gravitationsfeld von gleichsetzt:
Mit den in der Einleitung genannten Werten für die Masse und den Radius der Erde erhält man einen Wert von 7.9 km/s für die 1. und von 11.2 km/s für die 2. kosmische Geschwindigkeit.
Gezeiten[Bearbeiten]
Gezeitenkraft
Für viele Anwendungen der Himmelsmechanik reicht es aus, Himmelskörper als punktförmig zu betrachten. Kommen sich zwei solche aber sehr nahe, ist diese Vorgehensweise nicht mehr zulässig. Die Schwerebeschleunigungen, welche die beiden Körper wechselseitig spüren, unterschieden sich nun auf diesen von Ort zu Ort deutlich. Diese lokalen Differenzen machen sich als Gezeitenkräfte bemerkbar.
Man betrachte einen Körper mit Masse und Radius sowie einen zweiten mit Masse und Radius . Der Abstand der Mittelpunkte sei .
Der Mittelpunkt von erleidet durch eine Schwerebeschleunigung . Der Ort an der Oberfläche von , welcher direkt zugewandt ist, hat von dem zweiten Körper aber nur einen Abstand . Dementsprechend herrscht dort eine höhere Beschleunigung . Subtrahiert man die beiden Beschleunigungen voneinander und benutzt dabei die für zulässige Näherung , so folgt für das Beschleunigungsgefälle innerhalb von
Betrachtet man die Rückseite von , wo ein Abstand vom zweiten Körper von bis zu gegeben ist, erhält man mittels des obigen Vorgehens das gleiche Resultat. Selbstverständlich unterliegt ebenfalls einer Gezeitenkraft, welche analog lautet:
Als Beispiel seien die Gezeitenkräfte betrachtet, welche Mond und Sonne auf die Erde ausüben. Aus den eingangs gegebenen Daten für den Mond folgt eine Gezeitenbeschleunigung von etwa 1.1 10-6 m/s2. Die Sonne liefert einen Beitrag von ungefähr 5.0 10-7 m/s2. Aufgrund ihrer enormen Masse stellt die Sonne trotz ihrer großen Entfernung noch fast 1/3 der auf der Erde herrschenden Gezeitenkraft.
Roche-Grenze
Für das Erde-Mond-System sind die Gezeitenbeschleunigungen im Vergleich zu den absoluten Schwerebeschleunigungen sehr gering. Die -Abhängigkeit der Gezeitenkraft legt jedoch nahe, dass dies bei Abständen, die nur noch wenig größer als die Radien der beteiligten Körper sind, nicht mehr gilt. Tatsächlich gibt es einen Minimalabstand , die sogenannte Roche-Grenze, unterhalb dessen ein Mond nicht mehr stabil ist.
Es seien abermals die beiden obigen Körper betrachtet. Sie sollen zunächst als starr betrachtet werden. Auf der zugewandten Seite von soll ein kleines Steinchen liegen. kann dieses nur festhalten, solange die darauf einwirkende Schwerebeschleunigung mindestens gleich der Gezeitenbeschleunigung ist. Daraus resultiert ein Mindestabstand . Ersetzt man noch die Massen durch die mittleren Dichten und , erhält man die übliche Formulierung:
Nicht nur unter den Einfluss der eigenen Rotation, sondern auch unter demjenigen von Gezeiten verhalten sich Himmelskörper nicht starr, sondern reagieren plastisch mit Verformung (wie man es auch von Ebbe und Flut her kennt). Aus Kugeln werden näherungsweise Ellipsoide, die mit ihren Spitzen aufeinander zeigen. Die großen Halbachsen der Ellipsoide sind natürlich größer als die ursprünglichen Kugelradien, was die lokalen Unterschiede hinsichtlich der Schwerebeschleunigung und damit die Gezeiten noch verstärkt. Je näher sich die beiden Körper kommen, umso mehr weichen sie von der Kugelgestalt ab. Aus diesem Mechanismus folgt ein im Vergleich zum einfachen Modell starrer Körper bedeutend größerer Mindestabstand von:
Der umfangreiche Beweis kann im Rahmen eines Nachschlagewerkes nicht gezeigt werden, es sei daher auf die Wikipedia verwiesen. Gemäß obiger Formel könnte sich der Mond der Erde bis auf circa 18000 km nähern, bevor er von den Gezeiten zerrissen würde.
Maximale Abweichung von der Kugelgestalt[Bearbeiten]
Alle größeren Himmelskörper mit Abmessungen ab etwa 1000 km zeigen kaum Abweichungen von der Kugelgestalt. Um dies zu verstehen, betrachte man einen Körper mit Masse und Radius , auf welchem ein Berg der Höhe errichtet werden soll. Die potentielle Energie des Berges liegt in der Größenordnung , wobei die Masse der Erhebung und die auf dem Himmelskörper herrschende Fallbeschleunigung darstellt. Der Berg bleibt stabil, solange dessen chemische Bindungsenergie der potentiellen Energie im Schwerefeld von zumindest gleich ist.
Besteht der Berg aus Teilchen der Masse , so gilt . Analog gilt mit einer Bindungsenergie pro Teilchen . Drückt man noch die Fallbeschleunigung mit Hilfe der Dichte des Himmelskörpers gemäß aus, so liefert die Gleichgewichtsbedingung folgenden Ausdruck für das die Abweichung von der Kugelgestalt beschreibende Verhältnis :
Die maximal mögliche Abweichung von der Kugelgestalt, welche ein Himmelskörper aufweisen kann, ist umgekehrt proportional zum Quadrat dessen Radius. Absolut betrachtet verhält sich die maximale Höhe eines Berges umgekehrt proportional zum Radius.
Der Ausdruck hat die Dimension einer Fläche , er stellt eine Materialeigenschaft des Körpers dar. Typische Werte sind 0.1 Elektronenvolt, 50 Atommassen und 3 g cm-3, womit sich 500 km ergbt.
Planetenbewegung[Bearbeiten]
Keplersche Gesetze
Diese klassischen Gesetze der Planetenbewegung stellen gleichwohl eine Idealisierung dar. Sie gelten streng genommen nur für ein lediglich aus zwei Körpern bestehendes System. Jedoch ist im Sonnensystem die Anziehungskraft der Sonne so dominant, dass Sonne und ein Planet in guter Näherung als ein Zweikörpersystem betrachtet werden dürfen, das durch die übrigen Planeten und sonstige kleinere Massen nur sehr geringfügig gestört wird. Die Keplerschen Gesetze lauten folgendermaßen:
- Die Bahnen der Planeten sind Ellipsen, in deren einen Brennpunkt die Sonne steht. Exakt betrachtet, steht jedoch nicht die Sonne, sondern der Schwerpunkt von Sonne und Planet in einem Brennpunkt.
- Die Verbindungslinie Sonne - Planet, der sogenannte Fahrstrahl, überstreicht in gleichen Zeiten gleiche Flächen (siehe Abbildung). Physikalisch bedeutet dieses Gesetz die Erhaltung des Bahndrehimpulses.
- Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die Kuben ihrer großen Halbachsen.

Die Keplerschen Gesetze können auf Grundlage des Newtonschen Gravitationsgesetzes hergeleitet werden, wozu jedoch auf die Wikipedia verwiesen wird. Das 3. Keplersche Gesetz kann anhand einer kleinen Masse , die auf einer Kreisbahn mit Radius eine Zentralmasse umläuft, jedoch leicht plausibel gemacht werden. Wie bereits dargelegt, gilt für die Umlaufgeschwindikeit nämlich (analog zum Ausdruck für die 1. kosmische Geschwindigkeit). Andererseits ist , wobei T die Umlaufzeit ist. Das Gleichsetzen der beiden Ausdrücke liefert unmittelbar . Die exakte Herleitung liefert, dass in Wahrheit allerdings die Summe beider beteiligten Massen einzusetzen ist:
Das 3. Keplersche Gesetz stellt eine weitere Methode dar, die Massen von Himmelskörpern zu bestimmen. Sind und bekannt, liefert es ja unmittelbar die Summe der Massen der beiden einander umlaufenden Körper. Als beispielsweise im 18.Jh. auf Grundlage eines Venustransits erstmals der Abstand der Erde zur Sonne exakt bestimmt werden konnte, war damit auch die Sonnenmasse bekannt.
Gesamtenergie auf einer Planetenbahn
Die Gesamtenergie auf einer Planetenbahn kann anhand des soeben skizzierten Kreisbahn-Szenarios ebenfalls plausibel diskutiert werden. Für den kinetischen Anteil gilt . Die potentielle Energie ist wie bereits besprochen . Somit ist:
Dieser Zusammenhang gilt auch für Ellipsenbahnen. Im Fall einer gegen Unendlich tendierenden großen Halbachse geht die Gesamtenergie gegen Null. Die beiden Massen sind dann nicht mehr durch die Schwerkraft aneinander gebunden. Der Begleiter umläuft die Zentralmasse auf einer Parabel ein einziges Mal und verschwindet dann erneut auf Nimmerwiedersehen. Auch das Szenario einer positiven Gesamtenergie ist möglich. In diesem Fall liegt eine Hyperbelbahn vor, auf welcher die kleine Masse der großen bis auf einen Abstand nahekommt und dann abermals wieder verschwindet. Hyperbelbahnen werden oft bei einmalig auftauchenden Kometen beobachtet.
Position und Geschwindigkeit auf einer Planetenbahn
Mit Hilfe der ersten beiden Keplerschen Gesetze, aus welchen wiederum die Kepler-Gleichung folgt, lassen sich Position und Geschwindigkeit eines Planeten auf seiner Bahn in Abhängigkeit von der Zeit bestimmen. Dazu dient die folgende Konstruktion.

Im 1. Schritt zeichnet man um die elliptische Bahn den dazugehörigen Umkreis. Man nimmt zunächst an, dass der Planet auf diesem Kreis anstatt der Ellipse und dementsprechend mit konstanter Winkelgeschwindigkeit umläuft. Nun betrachtet man den Winkel, der durch die Verbindungslinie Kreismittelpunkt - Perihel CZ und die Verbindungslinie Kreismittelpunkt - fiktive Planetenposition auf dem Kreis CY definiert ist. Dieser wird mittlere Anomalie genannt. Wegen der konstanten Winkelgeschwindigkeit des Planeten auf dem Kreis gilt für die Zeitabhängigkeit von einfach (wobei nun die Umlaufdauer mit bezeichnet wird und zu Beginn der Planet sich im Perihel Z befinden soll):
Im 2. Schritt wird die sogenannte exzentrische Anomalie betrachtet. Dazu wird die tatsächliche Position des Planeten auf der Ellipse P in Richtung der kleinen Halbachse b auf den Umkreis projeziert, wodurch man den Punkt X erhält. ist durch die beiden Verbindungslinien CZ und CX festgelegt und kann aus mittels der Keplergleichung bestimmt werden, wobei die Exzentrizität der Bahn angibt.
Algebraisch lässt sich diese Beziehung nicht nach auflösen. Man kann sie jedoch iterativ lösen, z. B. mit dem Ansatz:
Die Kenntnis der exzentrischen Anomalie reicht bereits aus, um den Abstand des Planeten vom Brennpunkt S anzugeben, denn es gilt:
Um die Positionsangabe zu vervollständigen, muss in einem 3. Schritt auch noch der durch die Verbindungslinien SZ und SP definierte Winkel bestimmt werden. Dieser wird wahre Anomalie genannt und kann wie der Abstand aus der exzentrischen Anomalie abgeleitet werden, wofür mehrere Vorschriften bekannt sind:
Die wahre Anomalie liefert ebenfalls den Abstand, und zwar gemäß
Um zusätzlich zur momentanen Position auch die dazugehörige Geschhwindigkeit zu gewinnen, muss man die Erhaltung der Gesamtenergie mit heranziehen. Der gesuchte Zusammenhang zwischen Abstand und Geschwindigkeit ist durch die sogenannte Vis-Viva-Gleichung gegeben.
Obige Gleichung gilt auch für Hyperbelbahnen. In diesem Fall muss für jedoch der Zahlenwert negativ eingesetzt werden. Hinsichtlich der Beweise der Kepler- und Vis-Viva-Gleichung sei ein weiteres Mal auf die Wikipedia verwiesen.
Relativitätstheorie[Bearbeiten]
Eine detaillierte Darstellung der Relativitätstheorie und damit exakte Beweisführung der in diesem Kapitel zusammengestellten Beziehungen kann wegen des dafür erforderlichen Umfangs nicht gegeben werden. Für viele in der Astronomie bedeutsame Effekte kann anhand physikalisch plausibler Argumente aber auch ohne den für eine genaue Beschreibung notwendigen mathematischen Apparat zumindest die Größenordnung abgeschätzt werden.
Speziell[Bearbeiten]
Die spezielle Relativitätstheorie widmet sich der Struktur von Raum und Zeit in Bezugssystemen, die sich mit gleichförmiger Geschwindigkeit gegeneinander bewegen, d. h. sie vernachlässigt auf diese einwirkende Kräfte, insbesondere die Gravitation. Dennoch sind die von ihr gelieferten Resultate von großer Bedeutung.
Lorentzfaktor
Wie die nachfolgend behandelten Beispiele zeigen, ist das quantitative Ausmaß vieler relativistischer Effekte vom Verhältnis bestimmt gemäß folgender, als Lorentzfaktor bezeichnete Größe:
Der Lorentzfaktor ist nachstehend als Funktion von dargestellt.

Beziehung zwischen Gesamtenergie , Ruhemasse und Impuls eines Körpers
Der allgemeine Zusammenhang zwischen diesen Größen lautet:
Der Sonderfall entspricht der berühmten Masse-Energie-Äquivalenz
Weitere Spezialfälle sind sind (klassischer Grenzfall) und (extrem relativistischer Grenzfall):
Relativistische Massenzunahme
Wird ein Körper beschleunigt, so kann die an ihm verrichtete Arbeit nicht beliebig in Bewegungsenergie umgesetzt werden, weil eine Beschleunigung über die Lichtgeschwindigkeit hinaus nicht möglich ist. Nach der Masse-Energie-Äquivalenz muss somit zumindest ein Teil der dem Körper zugeführten Energie sich als zusätzliche Masse bemerkbar machen. Für die bewegte Masse als Funktion der Geschwindigkeit gilt (siehe dazu auch unter relativistische Masse)
Beziehung zwischen Gesamtenergie und Geschwindigkeit eines Körpers
Die klassische Beziehung gilt auch in der Relativitätstheorie, sofern man die bewegte Masse verwendet. Setzt man diese Beziehung mitsamt derjenigen für die relativistischen Massenzunahme in obige Energieformel ein, so ergibt sich:
Zeitdilatation
Die Zeitdilatation ist ebenfalls ein recht bekannter relativistischer Effekt. Er besagt, dass in einem relativ zu einem ruhenden Beobachter bewegten Bezugssystem alle physikalischen Prozesse langsamer abzulaufen scheinen. Ist für den ruhenden Betrachter ein Zeitintervall verstrichen, scheint in dem bewegten System erst eine kürzere Zeit vergangen zu sein gemäß:
Dopplereffekt
Die Zeitdilatation führt in zweierlei Hinsicht zu einer Korrektur für den bereits skizzierten Dopplereffekt. Sie bewirkt eine Modifikation der Frequenzverschiebung für eine relativ zum Beobachter in Blickrichtung sich bewegende Lichtquelle. Sie lautet nun:
Weiterhin gilt, dass sich vom Beobachter weg bewegendes Licht eine Rotverschiebung, auf den Beobachter zukommendes Licht eine Blauverschiebung erleidet.
Die zweite Korrektur ist besonders interessant. Selbst eine senkrecht zur Blickrichtung sich bewegende Lichtquelle erleidet eine Frequenzänderung, was als transversaler Dopplereffekt bezeichnet wird. Für diesen gilt:
Der transversale Dopplereffekt bewirkt immer eine Rotverschiebung. Im Vergleich zum gewöhnlichen Dopplereffekt handelt es sich um einen Beitrag 2.Ordnung. Während der gewöhnliche Dopplereffekt, solange der Lichtgeschwindigkeit nicht sehr nahe kommt, von der Größenordnung ist, liegt der transversale Dopplereffekt hingegen bei einer solchen von .
Allgemein[Bearbeiten]
Die allgemeine Relativitätstheorie betrachtet gegeneinander beschleunigte Bezugssysteme, so dass auf diese einwirkende Kräfte berücksichtigt werden. Sie muss dann herangezogen werden, wenn starke Gravitationsfelder ins Spiel kommen. Wie im Folgenden aufgezeigt wird, ist das wichtigste Maß für die Stärke eines solchen Feldes das Verhältnis zwischen Schwarzschildradius und dem tatsächlichen Radius eines Körpers. Folgerichtig bestimmt es auch die Größenordnung allgemein relativistischer Effekte.
Schwarzschildradius
Der Schwarzschildradius gibt an, auf welchen Radius eine Masse komprimiert werden muss, damit von deren Oberfläche selbst Licht nicht mehr entweichen kann, diese also zu einem Schwarzen Loch wird. Laplace erkannte schon im 18.Jh., dass ein genügend massereicher Körper unsichtbar sein müsse. Setzt man nämlich die Lichtgeschwindigkeit in die klassische Formel für die Fluchtgeschwindigkeit ein, so lautet der entsprechende Radius . Die allgemeine Relativitätstheorie bestätigt, dass die klassische Rechnung bereits die richtige Größenordnung liefert. Für ein nicht rotierendes Schwarzes Loch liefert die exakte Betrachtung jedoch zusätzlich einen Faktor 2:
In der Praxis muss man davon ausgehen, dass viele Schwarze Löcher rotieren, da sie ja aus dem Kollaps von bereits rotierenden Objekten wie massereiche Sterne hervorgehen. Ein rotierendes Schwarzes Loch weist in Abhängigkeit von seinem Drehimpuls einen verminderten Schwarzschildradius auf.
Qualitativ lässt sich das leicht nachvollziehen. Mit der Rotation ist eine der Schwerkraft entgegengesetzte Zentripetalkraft verbunden, so dass man näher an das Gravitationszentrum heranrücken muss, um eine Fluchtgeschwindigkeit gleich zu erreichen.
Der Drehimpuls kann maximal einen Wert annehmen. In diesem Fall verschwindet die Wurzel, und es stellt sich ein minimaler Schwarzschildradius ein, welcher als Gravitationsradius bezeichnet wird. Dieser stimmt sogar mit der einfachen klassischen Rechnung überein:
Für aus Sternen hervorgegangene Schwarze Löcher liegt der Schwarzschildradius in der Größenordnung von einigen 1-10 km. So erhält man z. B. für einen nicht rotierenden Körper mit einer Sonnenmasse einen Wert von 2.953 km. Supermassive Löcher, wie sie in den Zentren von Galaxien vermutet werden, weisen entsprechend ihren Massen Schwarzschildradien in der Größenordnung von Millionen bis Milliarden km auf, d. h. sie können Abmessungen vom Ausmaß des Planetensystems erreichen.
Für Hauptreihensterne wie die Sonne liegt das Verhältnis zwischen und in der Größenordnung 10-6. Für Weiße Zwerge beträgt etwa 10-4. Neutronensterne erreichen ein von einigen 0.1 und Schwarze Löcher per Definition = 1.
Schwarzschilddichte
Aus dem Schwarzschildradius lässt sich unmittelbar eine entsprechende Dichte ableiten, indem man die Masse des Schwarzen Loches mit dem durch definierten Kugelvolumen dividiert. Es ist:
Die Dichte, auf welche Materie komprimiert werden muss, um daraus ein Schwarzes Loch zu bilden, nimmt umgekehrt proportional mit dem Quadrat deren Masse ab. Dies macht zumindest ein Stück weit plausibel,dass eine Entstehung supermassiver Schwarzer Löcher tatsächlich möglich ist. Damit eine Sonnenmasse zu einem Schwarzen Loch wird, muss eine Dichte von 1.843 1019 kg m-3 erreicht werden, was etwa eine Größenordnung über der Dichte eines Neutronensterns liegt. Um eine Milliarde Sonnenmassen in ein Schwarzes Loch zu verwandeln, sind jedoch nur 18.43 kg m-3 erforderlich, also etwa 1/50 der Dichte von Wasser.
Rotverschiebung und Zeitdilatation im Gravitationsfeld
Lichtquanten der Frequenz weisen eine Masse auf. Um dem Gravitationspotential einer Masse mit Radius zu entkommen, müssen sie eine Hubarbeit verrichten. Diese entspricht wiederum einer Verringerung der Frequenz . Setzt man in letztere Beziehung das Potential und die Photonenmasse ein, so gewinnt man für die relative Frequenzänderung den Ausdruck und mit Hilfe des Schwarzschildradius schließlich:
Die Rotverschiebung des Lichts durch ein von einer kugelförmigen Masse ausgehendes Gravitationsfeld ist also direkt durch das Verhältnis zwischen deren Schwarzschild- und tatsächlichem Radius gegeben.
Bei obiger Herleitung handelt es sich um eine Näherung, die nur für schwache Gravitationsfelder gültig ist. Mit der Rotverschiebung ist ja zugleich auch eine Änderung der Photonenmasse gegeben, welche hier vernachlässigt wurde Die genaue Diskussion liefert für die Rotverschiebung das Resultat:
Mit der Regel für folgt daraus wiederum die hergeleitete Approximation. Doch auch gemäß des allgemeingültigen Ergebnisses bleibt das Verhältnis für den Effekt maßgeblich. Schrumpft eine Masse bis auf den Schwarzschildradius zusammen, so wird . Das von dieser ausgesandte Licht kommt dann mit verschwindender Frequenz bzw. unendlich stark gedehnter Wellenlänge an einem weit entfernten Beobachter an.
Die Rotverschiebung im Gravitationsfeld hat unmittebar als weiteren Effekt eine Zeitdilatation zur Folge, welche nicht mit der bei hohen Geschwindigkeiten auftretenden Zeitdilatation der speziellen Relativitätstheorie verwechselt werden darf. Man stelle sich Lichtquanten der Frequenz als Uhr vor. Werden solche am Ort eines weitab der Masse sich aufhaltenden Beobachters emittiert, so registriert dieser tatsächlich Wellenzüge pro Sekunde. Sendet jedoch solche Photonen aus, kommen am Beobachter nur Wellenzüge pro Sekunde an. Von diesem aus gesehen, erscheinen somit alle Vorgänge auf der Oberfläche der Masse verlangsamt abzulaufen. Ist am Ort des Beobachters eine Zeit verflossen, so scheint auf erst eine kürzere Zeit verstrichen zu sein:
Erwartungsgemäß spielt abermals das Verhältnis Schwarzschild- zu wirklichem Radius eine Schlüsselrolle. Mit wird = 0, d. h. von einem fernen Beobachter aus gesehen scheint dann die Zeit auf still zu stehen. Dies hat Schwarzen Löchern im Russischen die Bezeichung "Gefrorener Stern" eingetragen.
Lichtablenkung im Gravitationsfeld
Die Tatsache, dass die Schwerkraft auch auf Licht einwirkt, ruft ein weiteres Phänomen hervor. Passiert ein Lichtstrahl eine Masse in einem Abstand , so erfährt dieser eine Ablenkung um einen Winkel (siehe Zeichnung).

Um abzuschätzen, soll folgendes einfaches Modell angewandt werden. Das Licht soll auf der Strecke in Y-Richtung eine konstante Beschleunigung spüren, sonst sich aber kräftefrei bewegen. Damit lautet die Bewegungsglecichung in X-Richtung und in Y-Richtung . Das Licht umläuft dann die Masse auf einer Parabel . Der Ablenkwinkel ist durch die Steigung derselben an der Stelle gegeben. Es gilt und damit . Mit dem Schwarzschildradius von vereinfacht sich dieser Ausdruck zu . Das Ergebnis stimmt mit der Vorhersage der Allgemeinen Relativitätstheorie der Größenordnung nach überein. Die exakte Rechnung liefert abermals einen zusätzlichen Faktor 2:
Dieses Mal zeigt sich das Verhältnis - das Verhältnis Schwarzschildradius / Mindestabstand zur Zentralmasse - für das Ausmaß des Effekts als entscheidend. Die Lichtablenkung durch große dichte Massen hat z.T. spektakulär verzerrte Abbildungen kosmischer Objekte zur Folge (siehe Gravitationslinseneffekt), da diese dadurch wie eine Linse wirken (siehe untenstehende Skizze)

Periheldrehung der Planeten
Um die Einwirkung der Gravitation auf Licht zu beschreiben, darf die klassische Abhängigkeit vom Abstand zur anziehenden Masse weiterhin als gültig betrachtet werden. Um die relativistische Periheldrehung der Planeten korrekt zu beschreiben, muss jedoch das Newtonsche Gravitationsgesetz um eine Komponente erweitert werden, welche einem Gesetz folgt. Diese setzt sich wiederum aus zwei Anteilen zusammen, der relativistischen Zunahme der Ruhemasse des umlaufenden Trabanten sowie der im Vergleich zur physischen Masse des Zentralgestirns größeren effektiven Masse .
Ein mit einer Geschwindigkeit auf einer Kreisbahn mit Radius sich bewegender Planet weist gemäß der speziellen Relativitätstheorie eine Masse auf. Wegen gilt in guter Näherung . Setzt man und erneut den Schwarzschildradius ein, so gewinnt man den Ausdruck:
Die effektive Masse des Zentralgestirns ist eine Folge des Energiegehalts des Gravitationsfeldes, welches dieses umgibt. So wie ein elektrisches Feld weist auch ein Schwerefeld eine bestimmte Energiedichte auf. Nach dem Masse-Energie-Prinzip entspricht diese wiederum einer Massendichte. Nach dem Birkhoff-Theorem spürt man im Abstand von einer Masse somit nicht nur diese selbst, sondern auch die gesamte zusätzliche Masse, welche sich aufgrund der Energiedichte des Gravitationsfeldes innerhalb einer Kugel mit Radius um herum befindet.
Die lokale Energiedichte eines Schwerefeldes ist unmittelbar mit der lokalen Schwerebeschleunigung verknüpft gemäß:
Setzt man und die Masse-Energie-Äquivalenz ein, so gewinnt man für die entsprechende Massendiche :
Entsprechend der vorliegenden Dichteverteilung spürt man in der Entfernung von so eine effektive Masse
Das Integral über die Kugel um die Masse herum lässt sich am besten mit Hilfe von Kugelkoordinaten auswerten. Die Winkelkomponenten liefern einen Beitrag von , das Volumenelement zudem einen solchen von . Damit bleibt die vereinfachte Beziehung:
Das verbliebene Integral läuft vom Abstand von bis ins Unendliche. Löst man dieses auf und zieht abermals den Schwarzschildradius heran, so lautet das Endresultat:
Wendet man schließlich beide Korekturen auf das Newtonsche Gravitationsgesetz an, so lautet unter Vernachlässigung höherer Potenzen von die auf einen Planeten einwirkende Kraft:
Erneut stellt sich - hier Schwarzschildradius der Zentralmasse / Radius der Kreisbahn um derselben - als Maß aller Dinge heraus. Für eine Kreisbahn liefert die exakte Theorie für die Periheldrehung folgende Winkelgeschwindigkeit, wobei die aus der klassischen Mechanik folgende Umlaufdauer bedeutet:
In der Praxis liefert die Relativitätstheorie nur einen sehr kleinen Anteil der beobachteten Periheldrehung. Diese geht vielmehr größtenteils auf die Bahnstörungen zurück, welche die Planeten gegenseitig auf sich ausüben. Obige Formel liefert für den Perihel selbst des sonnennächsten Planeten Merkur ( = 87.969 Tage, = 57.909 106 km) eine winzige Winkelgeschwindigkeit von nur 6.323 10-14 rad s-1, entsprechend circa 41 Bogensekunden pro Jahrhundert (das Verhältnis liegt nur bei einigen 10-8). Tatsächlich beläuft sich dessen Periheldrehung jedoch auf 5602 Bogensekunden pro Jahrhundert. Um den nicht einmal 1% ausmachenden relativistischen Beitrag zu erkennen, ist also eine extrem sorgfältige Diskussion der klassischen Bahnstörungen erforderlich.
Gravitationswellen
Diese kürzlich weltberühmt gewordene Erscheinung stellt kleine Schwingungen der Raum-Zeit dar, welche sich durch winzige Streckungen und Stauchungen von Längenabmessungen bemerkbar machen. Gravitationswellen werden von beschleunigten Massen mit nicht kugelsymmetrischer Dichteverteilung abgestrahlt, so wie beschleunigte elektrische Ladungen elektromagnetische Strahlung aussenden. Die Abweichung einer Massenverteilung von der Kugelsymmetrie wird durch das Quadrupolmoment ausgedrückt, dieses bestimmt gemäß folgender Beziehung die Strahlungsleistung :
Wiederum soll eine um eine Zentralmasse auf einem Kreis umlaufende Probemasse betrachtet werden. Die Zeitabhängigkeit des Quadrupolmoments ist dann von der Art , wobei die Winkelgeschwindigkeit auf der Kreisbahn angibt. Jede Zeitableitung liefert einen Beitrag . Mit drei derartigen Ableitungen ergibt sich so ein Beitrag und durch das Quadrat von letzlich ein solcher von . Der von der Zeit unabhängige Anteil des Quadrupolmoments ist von der Größenordnung , dessen Quadrat also etwa . Für die Winkelgeschwindigkeit gilt weiterhin . Einsetzen in obige Definition liefert:
Verwendet man zuletzt die Schwarzschildradien beider Massen, so ergibt sich als Endergebnis:
Der Vorfaktor ist mit einer Größenordnung von 1052 W gigantisch, er entspricht der Leuchtkraft von 1026 Sonnen bzw. von 1014 großen Galaxien. Kommen sich zwei sehr kompakte Objekte wie Neutronensterne oder gar schwarze Löcher sehr nahe, können sie für einen Augenblick eine Leistung erbringen, welche die Leuchtkraft aller Sterne des Universums zusammen bei weitem übertirfft.
Physik der Sterne[Bearbeiten]
Zustandsgrößen[Bearbeiten]
Unter den Zustandsgrößen eines Sterns versteht man einen Satz physikalischer Parameter, welche seine wichtigsten Eigenschaften beschreiben. Der bedeutenste dieser Parameter ist die Masse, da diese weitere Größen wie die Temperatur und den Radius (und damit die Leuchtkraft) stark dominiert. Vom Standpunkt des unmittelbaren Beobachtens aus betrachtet, sind die scheinbare Helligkeit und Farbe die naheliegensten Eigenschaften eines Sterns. Um die scheinbare Helligkeit als Anhaltspunkt für die Leuchtkraft verwenden zu können, muss die Entfernung des Himmelskörpers bekannt sein.
Helligkeit[Bearbeiten]
Scheinbare Helligkeit
Die scheinbare Helligkeit ist ein schon von den Astronomen der Antike entwickeltes Maß für die Stärke, mit welcher das von einem Gestirn ankommende Licht mit dem Auge wahrgenommen wird. Die hellsten Sterne bezeichneten sie als solche 1.Größe, die schwächsten gerade noch sichtbaren als solche 6.Größe. Dementsprechend wird auch noch heute die scheinbare Helligkeit in Größenklassen bzw. Magnituden angegeben und dafür das Symbol benutzt, wobei der Buchstabe V für eine visuelle (mit dem Auge erfolgende) Beobachtung steht.
Später stellte sich heraus, dass die Magnitude ein logarithmisches Maß für die Intensität des einfallenden Lichts darstellt und dass ein Helligkeitsunterschied von 5 Größenklassen einem Intensitätsverhältnis von etwa 100 entspricht. Dementsprechend lautet die moderne Definition der Magnitude (es wird bei den folgenden Diskussionen stets der Logarothmus zur Basis 10 verwendet):
Das Minuszeichen berücksichtigt, dass mit zunehmender Helligkeit kleinere Zahlenwerte für die Magnitude auftreten. ist eine Konstante, die durch Beobachtung von Sternen bekannter scheinbarer Helligkeit, sogenannter Standardsterne, für jedes Instrument individuell ermittelt werden muss. In der Praxis ist zudem eine Funktion der Sternfarbe, was hier jedoch nicht weiter diskutiert werden soll.
Schon seit langem wird die scheinbare Helligkeit von Sternen nicht mit Hilfe des Auges, sondern wohldefinierter Filter gemessen, welche jeweils bestimmte Wellenlängenbereiche passieren lassen. Das bekannteste dieser Filtersysteme ist das von Johnson und Morgan 1951 eingeführte UBV-System, welche aus drei Filtern besteht. Der V-Vilter (V = visuell) entspricht weitgehend dem menschlichen Auge, der B-Filter (B = blau) einer klassischen Photoplatte. Der U-Filter (U = ultraviolett) repräsentiert das nahe, von der Erdatmosphäre noch durchgelassene Ultraviolett. Die Schwerpunktewellenlängen der Filter liegen bei 540 nm (V), 442 nm (B) und 364 nm (U).
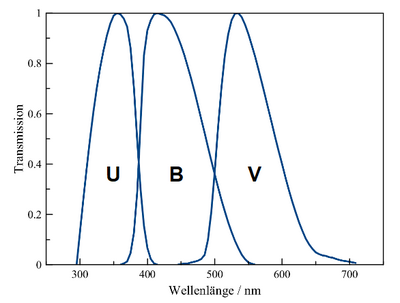
Die Filter liefern jeweils eigene Helligkeitswerte, welcher anstatt mit , und einfach mit , und bezeichnet werden. Mit drei Filtern gibt es auch drei Konstanten ,
und , die wiederum für jede Meßvorrichtung einzeln ermittelt werden müssen und allesamt erneut von der Sternfarbe abhängig sind. Später wurde das UBV-System durch weitere Filter erweitert, welche für Beobachtungen im Roten und Infraroten verwendet werden.
Absolute Hellgkeit
Die scheinbare Helligkeit eines Himmelskörpers hängt von zwei Größen ab: seiner Leuchtkraft innerhalb des vom Fiter erfassten Wellenlängenbereichs und seiner Entfernung. Als ein von der Entfernung unabhängiges, allein die Leuchtkraft widerspiegelndes Helligkeitsmaß wird die absolute Helligkeit benutzt, welche für visuelle Beobachtung mit dem Symbol bezeichnet wird. Diese gibt an, welche scheinbare Helligkeit ein Stern aufweisen würde, wenn er anstatt seiner tatsächlichen Entfernung eine Standartdistanz von 10 Parsec aufweisen würde.
Gemäß dem photometrischen Entfernungsgesetz würde aus der Standardentfernung nicht Licht der Intensität , sondern der Intensität zu uns gelangen. Aus der Definition der Magnitude folgt für die Differenz zwischen scheinbarer und absoluter Helligkeit (welche als Entfernungsmodul bezeichnet wird) und daraus wiederum . Einsetzen der Standartentfernung in Parsec liefert schließlich:
Tatsächlich ist die Beziehung zwischen scheinbarer und absoluter Helligkeit komplizierter. Ein wesentlicher Teil des von einem Stern ausgesandten Lichts wird von interstellarem Staub absorbiert, woraus eine Absenkung der beobachteten scheinbaren Magnitude um einen Betrag resultiert. Damit tatsächlich die Leuchtkraft des Sterns repräsentiert, muss obige Formel entsprechend korrigiert werden.
Die Bestimmung von erfolgt über diejenige der interstellaren Verfärbung, wie nachfolgend erläutert wird.
Wie nachfolgendes Diagramm zeigt, liegt die Sonne hinsichtlich der absoluten Helligkeit im unteren Mittelfeld der Gestirne. Blaue Hauptreihensterne sowie Überriesen generell überbieten sie um mehr als 10 Größenklassen, d. h. um mehr als das 10000-fache. Rote Zwerge liegen um bis zu 8 Größenklassen, d. h. um bis zu einem Faktor 1000 unter unserem Heimatstern.

Bolometrische Helligkeit
Die scheinbare Helligkeit bezieht sich auf die Intensität , welche innerhalb eines durch einen Filter festgelegten Wellenlängenintervalls empfangen wird. Jedoch ist auch ein Hellgkeitsmaß wünschenswert, welches die über das gesamte elektromagnetische Spektrum aufgenommene Intensität repräsentiert. Ein solches ist die scheinbare bolometrische Helligkeit, welche wie die scheinbare Helligkeit in Magnituden ausgedrückt wird:
Die Konstante muss wiederum durch Messungen ermittelt werden und erweist sich als sehr stark von der Sternfarbe abhängig. In der Praxis wird die bolometrische Helligkeit aus der scheinbaren visuellen Helligkeit abgeleitet, indem von dieser eine sogenannte bolometrische Korrektur subtrahiert wird:
Für die Sonne ist auf 0.13 Magnituden festgelegt worden. Für andere Sterntypen kann die bolometrische Korrektur bestimmt werden, indem man deren spektrale Intensitätsverteilung mit derjenigen der Sonne vergleicht. Derartige Messungen sind allerdings extrem aufwendig, da sie je nach Wellenlängenbereich den Einsatz sehr unterschiedlicher Instrumente und wegen der im Ultravioletten und Infraroten sehr beschränkten Durchlässigkeit der Erdatmisphäre den Einsatz von Satelliten erfordern.
Mit bekannter bolometrischer Korrektur kann schließlich die absolute visuelle Helligkeit in eine absolute bolometrische Helligkeit umgerechnet werden:
ist ein unmittelbares Maß für die Leuchtkraft eines Sterns. Kennt man die entsprechenden Größen für die Sonne, so gilt für einen beliebigen Stern:
Für Sterne, deren Energieverteilungen sich sehr stark von derjenigen der Sonne unterschieden, beträgt die bolometrische Korrektur mehrere Größenklassen. Sowohl blaue als auch rote Sterne sind über das gesamte elektromagnetische Spektrum betrachtet wesentlich heller, als der visuelle Sinneseindruck nahelegt. Im Falle blauer Sterne erfasst die visuelle Helligkeit nur noch den langwelligen Schwanz des Spektrums, dessen Schwerpunkt im Ultravioletten liegt. Bei roten Sternen liegt das umgekehrte Extrem vor. Die visuelle Helligkeit deckt nur den kurzwelligen Ausläufer der Energieverteilung ab, der Löwenanteil der ankommenden Intensität fällt in das Infrarote.

Farbe[Bearbeiten]
Farbenindex
Schon mit bloßem Auge kann man bei genügend hellen Sternen nicht nur Unterschiede hinsichtlich der scheinbaren Helligkeit, sondern auch der Farbe erkennen. Das Auge ist wie ein zur Messung von scheinbaren Helligkeiten verwendetes Teleskop mit Filtern ausgestattet, die unterschiedliche Wellenlängenbereiche abdecken (nämlich für rotes, grünes und blaues Licht). Der Farbeindruck entsteht dadurch, dass die in den verschiedenen Bereichen einfallenden Intensitäten miteinander verglichen werden. Rote Lichtquellen liefern im Roten eine höhere Intensität als im Grünen oder gar Blauen, bei blauen Strahlern verhält es sich umgekehrt.
Dies legt folgendes Vorgehen nahe, um die Farbe eines Sterns zu bestimmen. Man betrachtet zunächst das Verhältnis der in verschiedenen Wellenlängenintervallen registrierten Intensitäten und wendet darauf abermals die Definition der Magnitude an. Für das UBV-System können so zwei voneinander unabhängige Farben definiert werden:
Um die Konstanten und - welche erneut von Instrument, aber auch der Sternfarbe selbst abhängig sind - bestimmen zu können, wurde festgelegt, dass für die Wega (ein Hauptreihenstern mit Spektraltyp A0) die Farben und beide den Wert 0 haben. Sterne mit positiven Farbwerten sind also röter, solche mit negativen Farbwerten blauer als dieser Referenzstern.
Üblicherweise wird der das blauere Wellenlängenintervall darstellende Filter zuerst genannt. Anstelle von Farben spricht man in der Regel von Farbenindizes. Durch zusätzliche Filter in anderen Wellenlängenbereichen kann man weitere Farbenindizes definieren.
Eigenfarbe und Verfärbung
Jeweils auf den Verhältnissen zweier Intensitäten beruhend, sind die Farbenindizes eines Sterns von dessen Entfernung unabhängig. Dennoch entsprechen die gemessenen Werte keineswegs dem tatsächlichen Zustand des Himmelskörpers. Das Sternenlicht wird durch den interstellaren Staub nicht nur geschwächt, sondern auch gerötet, da die Absorption in verschiedenen Wellenlängenbereichen unterschiedlich stark ausfällt. Im Ultravioletten ist diese stärker als im Blauen, und dort immer noch stärker als im Visuellen. Die gemessenen Farben bestehen somit aus zwei Komponenten, den tatsächlicne Farben (Eigenfarben) und des Sterns und den erlittenen Rötungen (Verfärbungen) und :
Der Verlauf der Eigenfarben und in Abhängigkeit vom Spektraltyp ist in nachfolgenden Diagrammen für Hauptreihensterne, Riesen und Überriesen zusammengefasst. Während durchgängig einen monotonen Verlauf aufweist, zeigt eine recht komplizierte Abhängigkeit vom Spektraltyp.


Die Verfärbungen und sind miteinander korreliert, worin sich Eigenschaften des interstellaren Staubs wiederspiegeln. Zahlreiche Arbeiten wie z. B. von Turner (1989) zeigen, dass das Verhältnis einem Gesetz der folgenden Form folgt:
Der Hauptbeitrag weist beträchtliche regionale Variationen auf, d. h. der interstellare Staub verhält sich keineswegs überall gleich. So gibt Turner (1989) auf Grundlage von Beobachtungen blauer Sterne in der Milchstraße je nach Ort Werte von 0.62 bis 0.80 an. Der durch repräsentierte Anteil ist dagegen sehr gering, laut der zitierten Arbeit liegt nur bei 0.02.
Die enge Korrelation zwischen und kann man sich im sogenannten Zwei-Farben-Diagramm folgendermaßen zunutze machen, um die Verfärbung eines Sterns zu bestimmen. Man trägt gegen auf und schiebt den Stern gedanklich entlang des durch obige Gesetzmaßigkeit definierten Pfades, dem sogenannten Verfärbungsweg, zurück auf die Kurve, welche durch die Eigenfarben seiner Leuchtkraftklasse definiert ist. Wegen des sehr kleinen Wertes von ist der Verfärbungsweg fast eine Gerade, nur bei sehr starken Verfärbungen ab etwa 1 Magnitude weist er eine signifikante Krümmung auf.
Man hat bei diesem Verfahren jedoch mit mehreren Schwierigkeiten zu kämpfen. Die Eigenfarben eines Stern sind von dessen Leuchtkraftlasse abhängig, so dass diese aus spektroskopischen Beobachtungen abgeleitet werden muss. Im mittleren Bereich des unten gezeigten Zwei-Farben-Diagramms schneidet der Verfärbungsweg die Eigenfarben-Kurve drei Mal, so dass auch der Spektraltyp bekannt sein muss, um die richtige Auswahl zu treffen. Detaillierte Untersuchungen zeigen zudem, dass der Verfärbungsweg für rote Sterne steiler ist als für blaue.

Ist die Verfärbung bekannt, kann daraus schließlich die Absorption ermittelt werden. Seit langem ist bekannt, dass lokal betrachtet das Verhältnis in guter Näherung als konstant betrachtet werden darf:
Wie der Verfärbungsweg unterliegt auch signifikanten regionalen Schwankungen. Turner (1994) findet für blaue Sterne der Galaxis in der Regel Werte zwischen 2.8 und 3.3, doch existieren auch Gebiete mit Werten von 4 und höher. Wird eine solche Anomalie nicht erkannt, wird die interstellare Absorption erheblich unterschätzt.
Für andere Wellenlängenintervalle definierte Farbenindizes unterliegen ebenfalls interstellaren Verfärbungen. Im Roten und Infraroten sind diese jedoch im Vergleich zu den im UBV-Bereich auftretenden Verfärbungen erheblich geringer.
Entfernung[Bearbeiten]
Wie bereits aufgezeigt, muss zur Bestimmung der absoluten Helligkeit eines Sterns dessen Entfernung bekannt sein. Diese lässt sich direkt bestimmen, indem man dessen jährliche Parallaxe misst.
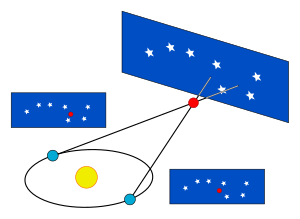
Aufgrund der Bahnbewegung der Erde um die Sonne ändert sich im Laufe des Jahres die Blickrichtung zu einem Stern, wodurch dieser im allgemeinen eine Ellipse gegenüber dem Himmelshintergrund beschreibt, deren große Halbachse einem Winkel entspricht. Wird in Bogensekunden ausgedrückt, so ergibt sich daraus unmittelbar die Entfernung in Parsec:
Die 2013 gestartete Raumsonde Gaia hat inzwischen für circa 1.7 Milliarden Sterne deren Parallaxen mit einer durchschnittlichen Genauigkeit von etwa 0.0001" bestimmt. Dies entspricht einem relativen Fehler von höchstens 10% bis hin zu einer Entfernung von 1000 Parsec. Damit ist es möglich, für viele verschiedene Sterntypen absolute Helligkeiten mit hoher Genauigkeit zu ermitteln, d. h. deren Spektren als Maß für zu eichen.
Dadurch wiederum können auch für solche Sterne zuverlässige Distanzen abgeleitet werden, welche nicht mehr von Gaia erfasst werden. Man leitet für solche die absolute Helligkeit aus deren Spektren ab, woraus sich zusammen mit der scheinbaren Helligkeit und der interstellaren Absorption die Entfernung ergibt:
Radius[Bearbeiten]
Winkeldurchmesser
Bei bekannter Entfernung folgt der Radius eines Sterns unmittelbar aus dessen Winkeldurchmesser . Mit in Bogenmaß und sowohl als auch in km gilt:
In der Praxis ist jedoch der Winkeldurchmesser in Bogensekunden und die Entfernung in Parsec gegeben, womit sich der Radius in Astronomischen Einheiten AE ergibt. Daraus folgt unmittelbar:
Die Winkeldurchmesser der Sterne sind leider extrem klein, selbst für die nähesten (Über)riesen weisen diese nur eine Größenordung von einigen 0.01" auf. Moderne Interferometer erzielen andererseits für ausreichend helle Objekte eine extrem hohe Meßgenauigkeit von bis zu 0.00002", so dass inzwischen für zahlreiche Sterntypen zuverlässige Resultate gewonnen werden konnten.
Bedeckungsveränderliche
Wird ein Doppelsternsystem von der Kante gesehen, bedecken sich dessen beide Mitglieder während eines Umlaufs gegenseitig, was zu meßbaren Helligkeitseinbrüchen führt. Bedeckt der leuchtkräftigere Stern den leuchtschwächeren, tritt nur ein schwach ausgeprägtes Minimum auf. Im umgekehrten Fall ist hingegen ein deutlich ausgeprägter Helligkeitsabfall sichtbar.
Für einen solchen Bedeckungsveränderlichen können die Durchmesser und (und damit die Radien) beider Komponenten bestimmt werden, indem man folgende 4 Zeitpunkte betrachtet.
- der schwächere Stern scheint den helleren gerade zu berühren (Beginn der Verfinsterung)
- der schwächere Stern steht gerade schon komplett vor dem helleren (Beginn des Hauptminimums)
- der schwächere Stern steht gerade noch komplett vor dem helleren, aber auf der anderen Seite dessen Scheibe (Ende des Hauptminimums)
- der schwächere Stern scheint den helleren gerade noch zu berühren (Ende der Verfinsterung)
Während der gesamten Dauer der Verfinsterung legt der schwächere Stern eine Strecke zurüch. Der Dauer des Hauptmaximums entspricht eine Strecke . Kennt man jetzt auch noch die Umlaufdauer des schwächeren Sterns und den Umfang seiner Bahn, so kann man für Kreisbahnen folgende Beziehungen aufstellen, welche durch Addition bzw. Subtraktion nach bzw. aufgelöst werden können.
Die Bahnumfang kann durch spektroskopische Beobachtungen ermittelt werden, indem auf Grundlage des Dopplereffekts die Umlaufgeschwindigkeit des schwächeren Sterns bestimmt wird.
In der Praxis treten mehrere Komplikationen auf. Meist umkreisen sich Doppelsterne auf elliptischen Bahnen. Zudem werden auch Bedeckungsveränderliche oft nicht perfekt von der Kante gesehen, so dass die gegenseitigen Verfinsterungen dann nur partiell sind.
Stefan-Boltzmann-Gesetz
In den meisten Fällen versagen beide hier skizzierten Verfahren. Dann muss der Sternradius indirekt wie bereits erläutert auf Grundlage des Stefan-Boltzmann-Gesetzes aus der Leuchkraft und Oberflächentemperatur abgeleitet werden.
Zusammenfassung
In folgende Tabelle sind typische Werte für Sternradien für Hauptreihensterne, Riesen und Überriesen nach Röser und Tscharnuter (2012) zusammengestellt. Die Radien sind als Vielfaches des Sonnenradius angegeben.
| Spektraltyp | Hauptreihe | Riesen | Überriesen |
|---|---|---|---|
| O5 | 12 | - | 30 |
| B0 | 7.4 | 15 | 30 |
| A0 | 2.4 | 5 | 60 |
| F0 | 1.5 | - | 80 |
| G0 | 1.1 | 6 | 100 |
| K0 | 0.85 | 15 | 200 |
| M0 | 0.60 | 40 | 500 |
| M5 | 0.27 | - | - |
Oberflächentemperatur[Bearbeiten]
Die Oberflächentemperatur eines Sterns kann generell nur indirekt ermittelt werden, wozu mehrere Möglichkeiten existieren. Die meisten dieser Methoden sind eng mit dem Thema Sternatmosphären verknüpft, was im nächsten Abschnitt ausführlich behandelt wird. An dieser Stelle soll daher eine knappe Schilderung genügen.
Spektrale Energieverteilung
Die spektrale Energieverteilung eines selbstleuchtenden Körpers ist stark von dessen Temperatur abhängig, wie das schon erwähnte Plancksche Strahlungsgesetz aufzeigt. Für Sternspektren ist dieses jedoch eine recht grobe Näherung, da Phänomene wie Spektrallinien nicht berücksichtigt werden. Für zuverlässige Resultate ist man auf sehr komplizierte Modelle angewiesen, welche die in Sternatmosphären stattfindenden Emissons- und Absorptionsvorgänge detailliert beschreiben. Zudem muss die beobachtete Energieverteilung hinsichtlich der interstellaren Absorption korrigiert werden.
Breite von Spektrallinien
Die thermische Bewegung von Gasteilchen weist eine temperaturabhängige Geschwindigkeitsverteilung auf und zieht aufgrund des Dopplereffekts eine dementsprechende Verbreiterung der Spektrallinien nach sich. Für dieses Verfahren sind Messungen hoher spektraler Auflösung erforderlich, zudem hängt die Breite von Spektrallinien auch vom Gasdruck ab. Es bietet jedoch den Vorteil, dass es von der interstellaren Absorption unabhängig ist.
Stärke von Spektrallinien
Die Temperatur bestimmt nicht nur die thermische Bewegung von Gasteilchen, sondern auch die Häufigkeit, mit welcher Atome in angeregten Energiezuständen auftreten. Zusammen mit dem Druck entscheidet die Temperatur zudem über die Häufigkeit von Ionisationsstufen und damit letztendlich über die Stärke von Spektrallinien. Abermals ist man auf Beobachtungen hoher Wellenlängenauflösung angewiesen, doch erneut keine Kenntnis der interstellaren Absorption erforderlich.
Eigenfarben
Die soeben skizzierten spektroskopischen Techniken ermöglichen es, Eigenfarben als Maß für die Oberflächentemperatur zu eichen, was in der untenstehenden Abbildung für Hauptreihensterne dargestellt ist. Die Farbe ist vor allem für kühle Sterne mit Oberflächentemperaturen unterhalb von 10000 K, d. h. die Spektraltypen A bis M, ein brauchbares Thermometer. Für heiße Sterne entsprechend den Spektraltypen O und B ist dagegen zu unempfindlich gegenüber selbst großen Temperaturunterschieden, weil die Filter und nur noch den langwelligen Schwanz des Spektrums erfassen. Die Farbe kommt zumindest für B-Sterne - entsprechend Oberflächentemperaturen von 10000 bis 30000 K - noch genügend nahe an das Strahlungsmaximum heran, um auf Temperaturunterschiede hinreichend reagieren zu können. Für O-Sterne ist jedoch auch als Temperaturmaß nicht mehr empfindlich genug. Für kühle Sterne ist generell kaum geeignet, weil der Zusammenhang zwischen Eigenfarbe und Oberflächentemperatur oft nicht eindeutig ist.
Wie bereits ausführlich erläutert, muss für die Temperaturbestimmung auf der Grundlage von Eigenfarben die interstellare Verfärbung bekannt sein. Der Beziehung zwischen Eigenfarbe und Temperatur hängt zudem von der Leuchtkraftklasse der Sterne ab.

Zusammenfassung
Auch für die Oberflächentemperatur seien repräsentative Werte für Hauptreihensterne, Riesen und Überriesen nach Röser und Tscharnuter (2012) genannt. Als Einheit wird K verwendet.
| Spektraltyp | Hauptreihe | Riesen | Überriesen |
|---|---|---|---|
| O5 | 44500 | - | 40300 |
| B0 | 30000 | 29000 | 26000 |
| A0 | 9520 | 10100 | 9730 |
| F0 | 7200 | 7150 | 7700 |
| G0 | 6030 | 5850 | 5550 |
| K0 | 5250 | 4750 | 4420 |
| M0 | 3850 | 3800 | 3650 |
| M5 | 3240 | - | - |
Masse[Bearbeiten]
Visuelle Doppelsterne
Von allen Zustandsgrößen eines Sterns ist seine Masse die wichtigste, denn diese bestimmt weitgehend sowohl seinen inneren Aufbau (und damit Radius, Oberflächentemperatur und Leuchtkraft) als auch seine Entwicklung. Direkt kann jedoch nur für Doppelsterne auf Grundlage des 3.Keplerschen Gesetzes bestimmt werden. Kennt man die Halbachse der relativen Bahn der beiden Komponenten zueinander sowie die Umlaufperiode , so gilt für die Gesamtmasse des Systems:
Die Bahnhalbache kann man leider nur unter günstigen Voraussetzungen bestimmen. Lassen sich beide Sterne voneinander trennen, kann man den Winkeldurchmesser der Bahn ermitteln, also in Bogensekunden messen. Ist nun auch die Entfernung bzw. Parallaxe des Systems in Bogensekunden bekannt, so gibt das Verhältnis direkt die Halbachse in Astronomischen Einheiten an. Setzt man nun noch die Umlaufperiode in Jahren ein, liefert das 3. Keplersche Gesetz die Gesamtmasse in Sonnenmassen:
In der Regel blickt man nicht senkrecht auf ein Doppelsternsystem, sondern unter einem beliebigen Neigungswinkel auf seine Bahn. Diese muss jedoch alle drei Keplerschen Gesetze erfüllen, woraus sich ableiten lässt.
Das 3.Keplersche Gesetz liefert nur die Gesamtmasse beider Mitglieder. Beobachtet man aber zusätzlich deren Bewegungen gegen den Himmelshintergrund, so kann man auch die absoluten Bahnen bzw. Halbachsen und ermitteln. Das Verhältnis beider liefert das Verhältnis der Massen (womit die Gesamtmasse in die beiden Einzelmassen aufgeteilt werden kann):
Spektroskopische Doppelsterne
Oft lassen sich Doppelsterne nicht trennen, sondern verraten sich nur dadurch, dass sich die Spektren zweier verschiedener Sterntypen überlagern. In diesem Fall kann man den Neigungswinkel der Bahn nicht ermitteln, sondern (auf Grundlage des Dopplereffekt) nur die Werte und . Während so das Verhältnis weiterhin beobachtbar ist, kann für die Gesamtmasse nur das Resultat angegeben werden.
Zusammenfassung
Zuletzt seien für Hauptreihensterne, Riesen und Überriesen auch deren typische Massen nach Röser und Tscharnuter (2012) gegeben. Als Einheit dient die Masse der Sonne.
| Spektraltyp | Hauptreihe | Riesen | Überriesen |
|---|---|---|---|
| O5 | 60 | - | 70 |
| B0 | 17.5 | 20 | 25 |
| A0 | 2.9 | 4 | 16 |
| F0 | 1.6 | - | 12 |
| G0 | 1.05 | 1 | 10 |
| K0 | 0.79 | 1.1 | 13 |
| M0 | 0.51 | 1.2 | 13 |
| M5 | 0.21 | - | - |
Sternatmosphären[Bearbeiten]
Wie im vorausgegangenen Abschnitt bereits angedeutet, erfordert die Bestimmung der Zustandsgrößen eines Sterns oftmals eine detaillierte Untersuchung seiner Atmosphäre, sprich dessen Spektrums. Dies gilt vor allem für die bolometrische Leuchtkraft und die Oberflächentempeatur.
Eine der markantesten Erscheinungen eines Sternspektrums sind die sogenannten Fraunhoferlinien. Sie lassen sich durch die nachfolgend besprochenen Größen der Linienbreite und Linienstärke charakterisieren, die wiederum Rückschlüsse auf die Zustandsgrößen des Sterns zulassen.

Breite von Spektrallinien[Bearbeiten]
Natürliche Linienbreite
Jede Spektrallinie hat von Natur aus eine gewisse Breite. Das Abklingen angeregter Zustände in einem Atom kann man durch eine gedämpfte Schwingung beschreiben, welche einen Abklinganteil aufweist, wobei der Kehrwert der mittleren Lebensdauer des angeregten Zustands ist. Indem man auf den zeitlichen Verlauf der Schwingung eine Fouriertransformation anwendet, erhält man den entsprechenden Verlauf des Linienprofils in Abhängigkeit von der Freqenz , das sogenannte Lorentzprofil (mit gleich der Mittenfrequenz der Linie):
Als Maß für die Breite einer Spektrallinie wird sehr oft die Halbwertsbreite verwendet. Für das Lorentzprofil gilt:
In der Astronomie ist es zumeist praktischer, die Halbwertsbreite auf der Wellenlängen- anstatt der Frequenzskala anzugeben. Wegen gilt und damit:
Die natürliche Linienbreite ist unter den in Sternatmosphären gegebenen Bedingungen allerdings bedeutunglos. Tatsächlich beherrschen die nun diskutierten Mechanismen der Linienverbreiterung die Profile der Fraunhoferlinien.
Dopplerverbreiterung
Aufgrund der hohen Temperaturen in Sternatmosphären unterliegen die dort sich befindlichen Atome einer erheblichen thermischen Bewegung. Während des Abklingens eines angeregten Zustands bewegen sich die Atome somit mit unterschiedlichen Geschwindigkeiten auf uns zu bzw. von uns weg, so dass die entsprechenden Spektrallinien aufgrund des bereits geschilderten Dopplereffekts unterschiedliche Blau- bzw. Rotverschiebungen aufweisen. Durch die Überlagerung all dieser individuellen Verschiebungen entsteht in der Gesamtheit ein gegenüber dem natürlichen verbreitertes Linienprofil. Diese Erscheinung wird als Dopplerverbreiterung bezeichnet.
Gemäß der Maxwell-Boltzmann-Verteilung sind die Geschwindigkeitskomponenten in jeder Raumrichtung gaußverteilt. Die Standardabweichung dieser Verteilung lautet, wobei die Temperatur des Gases, die Atommasse und die Boltzmann-Konstante bedeuten:
Die Gaußverteilung der Geschwindigkeiten zieht auch ein gaußförmiges Linienprofil nach sich, wobei sich mittels der Dopplerformel leicht in eine entsprechende Standardabweichung auf der Frequenz- bzw. Wellenlängenskala umrechnen lässt. Die Halbwertbreite einer Gaußkurve entspricht dem -fachen von , woraus schließlich resultiert:
Als Beispiel betrachte man die sogenannte H-Linie des Wasserstoffs bei 656.28 nm. Die tiefste noch durchsichtige Schicht der Sonnenatmosphäre weist eine Temperatur von etwa 6300 K auf, was bei einer Atommasse von ungefähr 1.67 10−27 kg eine Halbwertsbreite von ca. 0.037 nm nach sich zieht.
In der Praxis ist die Sichtweise natürlich umgekehrt. Kennt man die Linienbreite, kann man aus ihr auf die Temperatur schließen. Das Beispiel zeigt, dass man für entsprechende Beobachtungen eine gute spektrale Auflösung benötigt. Im hier geschilderten Fall beträgt das Verhältnis etwa 18000. Um die Halbwertsbreite einer Linie zuverlässig ermitteln zu können, muss das Linienprofil noch erkennbar sein, d. h. für das hier genannte Beispiel ist ein spektrales Auflösungsvermögen von zumindest etwa 100000 erforderlich.
Druckverbreiterung
Das Abklingen eines angeregten Zustands wird oft gestört, weil das Atom währenddessen mit anderen Teilchen zusammenstößt. Die Breite des Lorentzprofils wird dann nicht mehr durch die natürliche Lebensdauer des Zustands, sondern durch die kürzere mittlere Zeit zwischen zwei Stößen bestimmt. Man spricht in diesem Fall von Druckverbreiterung.
ist gegeben durch die mittlere freie Weglänge , welche das Atom zwischen zwei Kollisionen zurücklegen kann, und dessen charakteristische Geschwindigkeit gemäß .
Die mittlere freie Weglänge errechnet sich aus der gesamten Teilchendichte des Gases und der effektiven Querschnittsfläche des Atoms, mit welcher es zu Stößen mit anderen Partikeln beiträgt:
Für die charakteristische Geschwindigkeit kann die aus der Maxwell-Boltzmann-Verteilung folgende wahrscheinlichste Geschwindigkeit genommen werden:
Setzt man all dies in die Halbwertsbreite des Lorentzprofils ein, so gewinnt man als Endergebnis:
Wieder werde die H-Linie als Beispiel herangezogen. Die Teilchendichte in der tiefsten gerade noch durchsichtigen Schicht der Sonne beträgt etwa 1.48 1023 m-3. Der effektive Querschnitt eines Wasserstoffatoms (beruhend auf dem kovalenten Radius von 3.1 10-11 m) liegt bei ca. 3.0 -21 m2. Daraus resultiert eine extrem geringe Halbwertsbreite von nur ungefähr 10-6 nm.
Die Druckverbreiterung schent in Sternatmosphären damit irrelevant zu sein. Jedoch fällt das durch die Dopplerverbreiterung bewirkte Gaußprofil mit zunehmendem Abstand von der Linienmitte viel rascher ab als das durch den Druck hervorgerufene Lorentzprofil. Durch die Überlagerung beider entsteht ein Gesamtprofil, das zwar nahe der Mitte vom Dopplereffekt dominiert wird, weiter außen jedoch vom Druck. Dass dies doch messbare Konsequenzen hat, wird nun detailliert erläutert.
Stärke von Spektrallinien[Bearbeiten]
Definition der Äquivalentbreite
Ein sehr anschauliches und auch sehr häufig benutztes Maß für die Stärke einer Spektrallinie ist die Äquivalentbreite bzw. . Um diese zu bestimmen, trägt man die ankommende Intensität gegen die Wellenlänge bzw. Frequent aus und betrachtet die Fläche , die von dieser Kurve und der durch die ungestörte Intensität außerhalb der Linie definierten Horizontale eingeschlossen wird. Dann ersetzt man diese Fläche durch ein gleich großes Rechteck, dessen Höhe wiederum durch gegeben ist (siehe Abbildung).

Mit dieser Festlegung gilt:
Diese anschauliche Definition hat leider einen Haken. Vor allem bei kühlen Sternen liegen die Spektrallinien oft so dicht beieinander, dass es kaum noch möglich ist, ein ungestörtes Intensitätsniveau anzugeben. In den Spektren heißer Sterne finden sich weite Bereiche mit einem überwiegend glatten Intensitätsverlauf. Dieser entspricht aber auch nicht wirklich , da neben der linienhaften auch eine kontinuierliche Absorption z. B. durch Streuung an freien Elektronen auftritt. Eine zuverlässige Bestimmung der ungestörten Intensität ist nur anhand komplizierter Atmosphärenmodelle möglich, welche alle Absorptions- und Emmissionsvorgänge exakt berücksichtigen.
Lambert-Beersches-Gesetz für Spektrallinien
Gemäß der bisher erläuterten Form des Lambert-Beerschen-Gesetzes kann im Falle einer sehr stark absorbierenden Schicht die ankommende Intensität praktisch bis auf Null abfallen. In Sternatmosphären sind die Verhältnisse jedoch komplizierter. Über dichten, undurchsichtigen Schichten liegen in der Regel dünnere, noch durchsichtige Bereiche, von denen noch Strahlung zu uns gelangen kann. Dadurch bleibt selbst in der Linienmitte noch eine Restintensität erhalten. Dementsprechend muss das Lambert-Beersche-Gesetz folgendermaßen formuliert werden:
Eine Berechnung der zu erwartenden Mindestintensität erfordert abermals ein detailliertes Modell der Sternatmosphäre.
Extinktionskoeffizient für Spektrallinien
Für Spektrallinien ist der Extinktionskoeffizient natürlich sehr stark von der Wellenlänge abhängig, und zwar genau entsprechend dem Linienprofil . Wie gewöhnlich ist der Dichte der absorbierenden Teilchen direkt proportional. Eine weitere wichtige in den Extinktionskoeffizienten eingehende Größe ist die sogenannte Oszillatorstärke . Diese ist ein Maß für die in der Linienmitte absorbierte Energie, wenn die Dichte der Absorber nur 1 Teilchen pro m3 beträgt. Insgesamt gilt folgender Zusammenhang:
Als Beispiele für das Aussehen von Linienprofilen seien jeweils Linien der Form gezeigt, die Restintensität also vernachlässigt. Die optische Tiefe soll im ersten Fall einer normierten Gauß-, im zweiten Fall einer Lorentzverteilung folgen. In den nachfolgenden Abbildungen entspricht der durchgezogenen Linie eine zentrale optische Tiefe von exakt 1, für die weiteren Kurven mit abnehmender Strichelung beträgt sie 2, 5 und 10.
Im Falle einer gaußverteilten optischen Tiefe - entsprechend einer Dopplerverbreiterung - liegt nur nahe der Linienmitte eine deutliche Absorption vor, selbst wenn dort die Materie nahezu völlig undurchsichtig ist. Nur wenige Vielfache der Halbwertsbreite vom Zentrum entfernt liegt die Absorption schon fast bei Null. Ganz anders verhält es sich, wenn die optische Tiefe gemäß dem Szenario einer Druckverbreiterung einer Lorentzverteilung folgt. Selbst im Abstand von einigen 10 Halbwertsbreiten von der Linienmitte liegt noch eine signifikante Absorption vor. Obwohl in Sternatmosphären in der Regel der Dopplereffekt eine deutlich größere Halbwertsbreite bewirkt als der Gasdruck, setzt sich aufgrund des viel langsameren Abfalls des Lorentzprofils in optisch dicken Wellenlängenbereichen dieses gegenüber dem Gaußprofil durch.


Äquivalentbreite als Funktion der Teilchendichte
Mit Hilfe der soeben skizzierten Beziehungen lässt sich die Äquivalentbreite einer Spektrallinie in Abhängigkeit von der Teilchendichte bestimmen. Solange die absorbierende Schicht optisch dünn, also noch weitgehend durchsichtig ist, dominiert das Dopplerprofil die Absorption und damit die Äquivalentbreite. Es ist:
Beginnt die Schicht in der Linienmitte undurchsichtig zu werden, tritt eine Sättigung des Dopplerprofils ein. Aus der Gaußkurve wird mehr und mehr ein kastenförmiges Profil, das bei der Restintensität verharrt. Jetzt dominiert zunehmend die Absorption durch das Lorentzprofil, wobei sich aber der Anstieg der Äquivalentbreite mit der Teilchendichte verlangsamt:
ist wie schon erwähnt die mittlere Zeit zwischen zwei Stößen eines absorbierenden Teilchens.
Die beiden hier skizzierten Gesetzmäßigkeiten lassen sich anhand der oben dargestellten normierten Linienprofile anschaulich darstellen. Sowohl für das Gauß- als auch das Lorentzprofil ist für durchsichtige Materie die Äquivalentbreite der zentralen optischen Tiefe direkt proportional ( nimmt im doppellogarithmischen Diagramm um 1 Größenordnung zu, wenn ebenfalls um 1 Größenordnung ansteigt). Wird die Materie undurchsichtig, wächst für eine dopplerverbreiterte Linie die Äquivalentbreite nur noch sehr langsam mit zunehmender optischer Dicke an. Auch für eine druckverbreiterte Linie verlangsamt sich der Anstieg, doch nicht in so starkem Maße. Ein Anstieg der Äquivalentbreite um 1 Größenordnung erfordert nun eine Zunahme der zentralen optischen Tiefe um 2 Größenordnungen, was genau der genannten Proportionalität entspricht.

Häufigkeit von Energieniveaus[Bearbeiten]
Aus der Äquivalentbreite einer Spektrallinie kann man also auf die Dichte der absorbierenden Teilchen schließen. Diese ist aber nicht gleichbedeutend mit der Dichte des entsprechenden chemischen Elements. Betrachtet man z. B. die H-Linie, so erfasst man als Absorber nur Wasserstoffatome, die sich schon im 1. angeregten Zustand befinden und von dort aus in den 2. angeregten Zustand gelangen. Um alle Atome zu erfassen, muss man zusätzlich die Boltzmann-Formel heranziehen. Diese gibt die relative Häufigkeit eines Energieniveaus in Abhängigkeit von der Temperatur an, wobei die Summe im Nenner über alle Niveaus einschließlich des Grundzustandes läuft:
bezeichnet die Energie, die erforderlich ist, um vom Grundzustand in das Niveau zu gelangen. Das sogenannte statistische Gewicht berücksichtigt, ob das Niveau entartet ist, also in einem elektromagnetischen Feld weiter aufspaltet. Die Summe im Nenner über alle Zustände wird als Zustandssumme bezeichnet. Die Gesamtheit aller relativen Häufigkeiten entspricht hier der Menge aller Atome einer einheitlichen Ionisationsstufe (z. B. alle neutralen Atome).
Bei tiefen Temperaturen, d. h. befinden sich fast alle Atome im Grundzustand. Mit steigender Temperatur finden sich mehr und mehr Atome in zunehmend höheren Zuständen.
Berechnungen auf der Grundlage der Boltzmann-Formel erfordern eine sorgfältige Diskussion. So weist im Wasserstoffatom ein Nievau ein statistisches Gewicht auf. Seine potentielle Energie bezogen auf diejenige des Grundzustands beträgt , dementsprechend seine Anregungsnergie . Damit lautet obige Formel:
Scheinbar steht man nun vor einem unlösbaren Dilemma, denn die Zustandssumme ist nicht endlich. In der Praxis kann jedoch keineswegs beliebig große Werte annehmen, denn hochangeregte Atome sind nicht stabil. Bezeichnet den Radius des Wasserstoffatoms im Grundzustand, so liegt dieser im Zustand bei . Mit zunehmender Anregung bläht sich das Atom also rapide auf, wodurch es jedoch sehr leicht Stöße mit anderen Teilchen erleidet. Gleichzeitig ist es dann sehr leicht ionisierbar, weil nur noch die geringe Energie aufgewandt werden muss, um das nur noch schwach gebundene Elektron vom Atomkern zu lösen. Tatsächlich sind in Sternatmosphären nur der Grund- und der erste angeregte Zustand relevant, d. h. die Zustandssumme umfasst nur die Glieder für gleich 1 und 2. Somit ist auch nur die Häufigkeit von Wasserstoffatomen (bezogen auf alle neutralen H-Atome) im 1. angeregten Zustand interessant (die Häufigkeit des Grundzustands ist einfach 1 - Häufigkeit des 1. angeregten Zustands):
Mit zunehmender Temperatur befindet sich ein immer größerer Anteil der neutralen Wasserstoffatome im 1. angeregten Zustand und steht damit für die Entstehung der in den Spektren von A-Sternen so markanten Balmer-Linien zur Verfügung. Geht man zu den noch heißeren B- und O-Sternen, nimmt die Stärke dieser Linien dennoch wieder ab. Ursache hierfür ist - wie nun aufgezeigt wird - die zunehmende Ionisation, welche mit steigender Temperatur immer weniger neutrale Atome übriglässt.
Häufigkeit von Ionen[Bearbeiten]
Die Boltzmann-Formel erfasst wie gerade skizziert nur die Häufigkeiten unterschiedlich angeregter Atome einer bestimmten Ionisationsstufe, z. B. neutraler Atome. Um ein vollständiges Bild der Häufigkeit eines chemischen Elements in einer Sternatmosphäre zu bekommen, muss man auch noch die relative Häufigkeiten der Ionisationsstufen untereinander ermitteln, in dem man die Boltzmann-Formel auf die Reaktion Ion (Stufe ) <-> Ion (Stufe ) + Elektron anwendet. Dies erfordert neben der Betrachtung der Zustandssummen der beiden Ionisationsstufen auch die Bestimmung der Zustandssumme der freien Elektronen, woraus die Saha-Gleichung hervorgeht. Diese gibt das Verhältnis der Teilchendichten und der beiden Ionisationsstufen und an. Zusätzlich geht auch die Elektronendichte ein:
bedeutet das Plancksche Wirkungsquantum, die Elektronenmasse und die notwendige Energie, um von der Ionisationsstufe zur nächsthöheren zu gelangen, d. h. ein weiteres Elektron vom Atom abzulösen. und stellen die Zustandssummen innerhalb der Ionisationsstufen dar.
Die Saha-Gleichung führt zu analogen Schlussfolgerungen wie die Boltzmann-Formel. Bei tiefen Temperaturen () sind praktisch alle Atome neutral. Mit zunehmender Temperatur werden Ionen immer häufiger, und es treten auch immer höhere Ionisationsstufen auf.
Das Beispiel des Wasserstoffs werde nun auch auf die Saha-Gleichung angewandt. Da ein Wasserstoffatom nur 1 Elektrom aufweist, gibt es nur zwei Ionisationsstufen 0 und 1, neutrale Atome und freie Protonen. Die Teilchendichte der letzteren ist gleich der Teilchendichte der freien Elektronen . Die Zustandsumme der freien Protonen beträgt einfach 1, da solche keine elektronischen Zustände aufweisen. Die Zustandssumme der neutralen Atome ist gleich wie bereits besprochen. Die Ionisationsenergie des Wasserstoffs entspricht seiner potentiellen Energie im Grundzustand . Damit vereinfacht sich die Saha-Gleichung zu:
Führt man jetzt noch die gesamte Teilchendichte ein, kann man eliminieren und man erhält eine quadratische Gleichung für in Abhängigkeit von und der Temperatur . Die Diskussion dieser Gleichung zeigt in der Tat, dass der hohe Anteil angeregter Wasserstoffatome unter den neutralen Atomen in den Atmosphären von B- und erst recht O-Sternen beinahe wirkungslos ist, weil infolge der Ionisation kaum noch neutraler Wasserstoff vorhanden ist.
Innerer Aufbau und Entwicklung[Bearbeiten]
In diesem Abschnitt sollen die im Inneren der Sterne herrschenden Verhältnisse beleuchtet werden. Sowohl für Hauptreihensterne als auch Weiße Zwerge werden anhand eines einfachen Modells die beobachteten Zustandsgrößen qualitativ begründet.
Zeitskalen[Bearbeiten]
Sterne durchlaufen unterschiedliche Entwicklungsphasen von z.T. sehr unterschiedlicher Dauer. Um diese Phasen zu charakterisieren, werden verschiedenen Zeitskalen verwendet, die hier kurz vorgestellt werden sollen
Hydrostatische Zeitskala
Diese Zeitskala gibt an, wie lange Materie einer bestimmten Dichte mit vernachlässigbarem inneren Druck unter ihrer eigenen Schwerkraft kollabiert, ehe sich durch einen während der Kontraktion aufbauenden Drucks ein hydrostatisches Gleichgewicht einstellt. Man betrachte eine kugelförmige Materieansammlung mit einer Masse und einem Radius . An deren Oberfläche herrscht eine Schwerebeschleunigung . Ersetzt man das Differential durch , so gewinnt man die Beziehung . Setzt man an die Stelle von Volumen und Masse noch die Dichte der Kugel, so ergibt sich:
Für die hydrostatische Zeitskala gibt es verschiedene Anwendungen. So lässt sich z. B. mit deren Hilfe abschätzen, wie lange der Kollaps interstellarer Gaswolken dauert, aus denen schließlich Sterne hervorgehen. Am Anfang der Sternentstehung stehen kühle, dichte Wolken, in denen der Wasserstoff in molekularer Form vorliegt. Die Teilchendichte in solchen Gebilden liegt bei etwa 109 Molekülen pro m3 entsprechend einer Massendichte der Größenordnung von 10-18 kg m-3. Daraus folgt eine hydrostatische Zeitskala von wenigen Millionen Jahren.
Ein weiteres Beispiel sind Pulsationen, wie sie vor allem bei Riesen und Überriesen z. B. in Gestalt von Mira-Sternen und Cepheiden beobachtet werden. Erstere weisen Massen vergleichbar der Sonne, aber zugleich extrem große Abmessungen von einigen 100 Sonnenradien auf. Dementsprechend sind ihre mittleren Dichten sehr gering mit einer Größenordnung von 10-4 kg m-3. Dies entspricht einer hydrostatischen Zeitskala von mehreren Monaten, was die langen Pulsationsperioden dieser Sterne verständlich macht.
Thermische Zeitskala
Mit fortschreitender Kontraktion wird das Gas einer interstellaren Wolke dichter und heißer. Dementsprechend steigt dort der Druck, was den Kollaps schließlich zum Stehen bringt. Die durch die Eigengravitation repräsentierte potentielle Energie wird in Wärme umgewandelt, welche vom entstehenden Stern zunehmend durch Strahlung nach außen abgeführt wird. Die thermische Zeitskala gibt an, wie lange ein Himmelskörper mit einer Leuchtkraft von der potentiellen Energie zehren kann. Das Gravitationspotetial - die potentielle Energie pro Masse - einer Kugel beträgt erwa , dementsprechend gilt . Daraus folgt mit :
Für die Sonne liegt die thermische Zeitskala bei circa 30 Millionen Jahren. Angesichts eines schon um 1900 erkannten weit höheren Erdalters blieb dies lange Zeit ein Rätsel, bis der nukleare Ursprung ihrer Energieerzeugung erkannt wurde.
Entwicklungszeit
Die nukleare Energiegewinnung ermöglicht in der Tat eine viel höhere Lebensdauer für einen Stern. Die Entwicklungszeit gibt an, wie lange ein Himmelskörper durch Fusion eines Elements (z. B. Wasserstoff) zu einem Element (z. B. Helium) seine Leuchtkraft aufrecht erhalten kann. Mit einer Energieausbeute pro Masse durch die entsprechende Kernreaktion und einem Anteil des Elements an der Gesamtmasse des Sterns ist dessen Energievorrat . Hierbei muss man jedoch berücksichtigen, dass die nukleare Energie überwiegend in der Kernzone eines Sterns erzeugt wird, so dass effektiv nur etwa 1/10 seiner Masse zur Verfügung steht. Mit gewinnt man die Beziehung:
In der Sonne liegt der Massenanteil des Wasserstoffs bei 70%, d. h. es ist gleich 0.7. Die Umwandlung von Wasserstoff liefert etwa 6 1014 J kg-1. Zusammen mit den schon eingangs genannten Größen der Sonne resultiert daraus eine Entwicklungszeit von etwa 7 Milliarden Jahren.
Nach Ablauf der Entwicklungszeit sind bereits tiefgreifende Veränderungen der Struktur eines Sterns zu erwarten. Das Hauptreihenstadium geht zu Ende, es beginnt die Entwicklung zum Roten (Über)riesen mit Waserstoffbrennen in der Schale und schließlich Heliumbrennen im Kern.
Grundgleichungen des Sternaufbaus[Bearbeiten]
Im Folgenden soll das Modell des inneren Aufbaus eines kugelförmigen, d. h. nicht rotierenden Sterns skizziert werden. Man stelle sich diesen aus dünnen Schichten aufgebaut vor, in welchen je nach Abstand vom Mittelpunkt unterschiedliche Bedingungen herrschen. Betrachtet werden sollen insbesondere Dichte , Druck , Temperatur und Leuchtkraft (nachfolgend kurz , , und geschrieben). Der Stern soll sich überall in lokalem hydrostatischen und thermischen Gleichgewicht befinden.
Massenverteilung
Die Masse einer Schicht ist durch deren Dichte und Volumen gemäß gegeben, wobei wiederum gilt. Damit ist für die pro Schicht nach außen hin erfasste Masse:
Hydrostatische Druckschichtung
Obige Massenverteilung zieht unmittelbar eine entsprechende Druckschichtung nach sich. Jede Schicht weist eine bestimmte Masse pro Fläche auf. Betrachtet man eine Schicht an der Stelle , so übt die unmittelbar darüberliegende eine Gewichtskraft pro Fläche, d. h. einen Druck aus. Nach dem Birkhoff-Theorem trägt für eine radialsymmetrische Massenverteilung nur die innerhalb von sich befindliche Masse zur Gewichtskraft bei. Damit lautet diese . Für die Druckzunahme pro Schicht erhält man so:
Energieerzeugung
Um die Leuchtkraft einer Schicht angeben zu können, muss man die pro Masse generierte Leistung kennen. Dann gilt unmittelbar:
Die Bestimmung von ist eine äußerst schwierige Aufgabe der Kernphysik. Es zeigt sich, dass diese Materialeigenschaft neben der Dichte vor allem sehr empfindlich von der Temperatur und der Art der im Sterninnern ablaufenden nuklearen Reaktionen abhängt. Für den Proton-Proton-Zyklus gilt im Bereich von 10 Millionen K laut Röser und Tscharnuter (2012):
Für den CNO-Zyklus geben für den Bereich um 30 Millionen K obige Autoren an:
Bei diesen Ausdrücken handelt es sich um Näherungsformeln im jeweils dominiereden Temperaturbereich der Reaktion. Im Detail ist die Temperaturabhängigkeit der Energieausbeute wesentlich komplizierter.
Energietransport
Die im Sterninneren erzeugte Energie wird durch verschiedene Transportmechanismen nach außen abgeführt. Sofern das Temperaturgefälle kleiner als der sogenannte adiabatische Temperaturgradient ist, geschieht der Energietransport in der Regel durch Strahlung. Anderenfalls tritt Konvektion auf, welche aufgrund ihrer enormen Komplexität hier nicht näher erläutert werden soll.
Der Energietransport durch Strahlung lässt sich als Diffusionsvorgang beschreiben, in welchem das Strahlungsleitvermögen eine entscheidende Rolle spielt. Es gibt an, welche Leistung pro Weglänge transportiert werden kann, wenn entlang dieses Weges eine Temperaturdifferenz vorliegt. Aufgrund dieser Definition gilt:
Die Bestimmung des Strahlungsleitvermögens als weitere Materialeigenschaft ist ebenfalls sehr anspruchsvoll. hängt von der Dichte, Temperatur und der sogenannten Opazität ab. Letztere gibt an, welcher Anteil der transportierten Energie pro Weglänge wieder absorbiert wird, ist also ein Maß für die Durchsichtigkeit der Materie. Es besteht folgender Zusammenhang (mit gleich der Stefan-Boltzmann-Konstante):
Zustandsgleichungen[Bearbeiten]
Um die den Sternaufbau beschreibenden Gleichungen lösen zu können, benötigt man zusätzlich noch eine Zustandsgleichung, welche Dichte, Druck und Temperatur miteinander verknüpft. Hierfür sind mehrere nachfolgend vorgestellte Fälle zu unterscheiden.
Allgemeine Gasgleichung
In Sternen nicht sehr hoher Dichte stellt sich als wichtigste Gegenkraft der Gasdruck dem von der Gravitation ausgeübten hydrostatischen Druck entgegen. Die Sternmaterie darf als ideales Gas betrachtet werden, so dass als Zustandsgleichung die Allgemeine Gasgleichung verwendet werden kann:
bezeichnet die Boltzmann-Konstante, die mittlere molare Masse des Gases. Mit der thermischen Energie eines Teilchens lässt sich die Allgemeine Gasgleichung auch folgendermaßen darstellen:
Strahlungsdruck
Bei sehr hohen Temperaturen, wie sie im Inneren massereicher Sterne vorliegen, stellt auch der Strahlungsdruck ein signifikantes, im Extremfall sogar das vorherrschende Gegengewicht zur Gravitation dar. Dieser hängt nur von der Temperatur, nicht aber auch der Dichte der Materie ab:
Entartete Materie
In Sternen sehr hoher Dichte liegt Entartete Materie vor, das Gegenstück zur Schwerkraft bildet nun überwiegend der Fermi-Druck. Dieser kommt zustande, wenn durch eine sehr starke Verdichtung ein Teilchen mit einer Masse auf eine sehr kleine Längenskala eingesperrt wird. Nach der Heisenbergschen Unschärferelation hat dieses einen Impuls , welcher als Fermi-Impuls bezeichnet wird. Diesem Impuls entspricht wiederum eine Energie , welche Fermi-Energie genannt wird. Im nicht relativistischen Fall lautet diese:
Bei extrem hoher Dichte kann der Fermi-Impuls so groß werden, dass die Geschwindigkeit der eingezwängten Teilchen der Lichtgeschwindigkeit nahe kommt. Im Extremfall gilt dann:
Wird Sternmaterie stark verdichtet, so sind zunächst nur die Elektronen von Entartung betroffen. Die Fermi-Energie der sehr viel schwereren Nukleonen bleibt, sofern die Verdichtung nur bis zum Stadium des Weißen Zwerges voranschreitet, vernachlässigbar. Im Folgenden wird daher für die Teilchenmasse die Elektronenmasse eingesetzt.
Das der Längenskala entsprechende einem Elektron zur Verfügung stehende Volumen ist durch den Kehrwert der Elektronendichte gegeben. Diese wiederum folgt aus dem Quotienten von Massendichte und mittlerer Masse aller Teilchen (Elektronen und Nukleonen), d. h. es ist , wobei die Masse eines Protons bezeichnet.
Der oben genannte Zusammenhang zwischen Druck und Energie eines Teilchens ist auch für entartete Materie, d. h. die Fermi- anstelle der thermischen Energie gültig. Setzt man in diese Beziehung die Fermi-Energie ein und eliminiert mit Hilfe der Dichte, so gewinnt man die Zustandsgleichung für entartete Elektronen. In dieser hängt der Druck nur noch von der Dichte, nicht aber der Temperatur ab:
Erreicht die Verdichtung das Stadium des Neutronensterns, so entarten auch die Nukleonen. Ganz grob kann man dafür eine Zustandsgleichung aufstellen, indem man in obigen Gleichungen sowohl die Elektronen- als auch Protonenmasse durch die Neutronenmasse ersetzt und für die mittlere molare Masse den Wert 1 verwendet. Tatsächlich aber sind die Verhältnisse aufgrund der Kernkräfte, welche die Neutronen aufeinander ausüben, viel komplizierter.
Hauptreihensterne[Bearbeiten]
Zentrale Dichte
Gibt man adhoc eine einfache Massenverteilung, z. B. eine konstante Dichte vor, so lassen sich die beiden ersten Grundgleichungen des Sternaufbaus zusammen mit der Zustandsgleichung elementar lösen und so die folgenden Beziehungen ableiten. Schwarzschild (1958) zeigte, dass diese für Hauptreihensterne sogar allgemein gelten. Die zentrale Dichte hängt demgemäß folgendermaßen von der Masse und dem Radius des Sterns ab:
Überraschenderweise dominiert hier der Beitrag des Radius. Massearme Hauptreihensterne weisen größere Dichten in ihrer Mitte auf als massereiche.
Zentraler hydrostatischer Druck
Auch in den zentralen Druck gehen Masse und Radius ein. Es besteht der Zusammenhang:
Auch hier hat der Radius gegenüber der Masse das stärkere Gewicht. In massearmen Sternen liegen höhere zentrale Drücke vor als in massereichen.
Zentrale Temperatur
Hier muss man zwischen vom Gasdruck und vom Strahlungsdruck beherrschten Sternen unterscheiden. Im ersten Fall gilt mit der allgemeinen Gasgleichung die Beziehung . Setzt man obige Proportionalitäten ein, so erhält man für die zentrale Temperatur :
Nun setzt sich die Masse gegenüber dem Radius durch. Je massereicher ein Hauptreihenstern, umso heißer ist er im Zentrum. Dominiert der Strahlungsdruck gegenüber dem Gasdruck, so liegt vor, woraus durch abermaliges Einsetzen folgt:
Bei sehr massereichen Sternen liegt demgemäß nur noch ein flacher Anstieg der Mittentemperatur mit zunehmender Masse vor.
Masse-Leuchtkraft-Beziehung
Nimmt man zusätzlich eine konstante Opazität an, so lässt sich auch die Strahlungstransportgleichung elementar lösen. Sie liefert dann für die Leuchtkraft . Setzt man die soeben gezeigten Beziehungen für und ein, so gewinnt man die Masse-Leuchtkraft-Beziehung. Wiederum muss man zwischen einer Dominanz des Gasdrucks und des Strahlungsdrucks differenzieren:
Der flachere Anstieg der Zentraltemperatur mit zunehmender Masse im Falle eines Überwiegens des Strahlungsdrucks hat auch einen flacheren Anstieg der Leuchtkraft zur Folge.
Oberflächentemperatur
Setzt man schließlich in die Leuchtkraft das Stefan-Boltzmann-Gesetz ein, so erhält man abschließend folgende Gesetzmäßigkeiten für die Oberflächentemperatur :
Wie für die Mittentemperatur, dominiert auch für die Oberflächentemperatur der Beitrag der Masse. Massereiche Hauptreihensterne sind auch an der Oberfläche heißer als massearme. Abermals flacht der Trend ab, sobald der Strahlungsdruck gegenüber dem Gasdruck dominiert.
Zusammenfassung
Abschließend seien in nachfolgender Tabelle typische Werte für Hauptreihensterne zusammengestellt.
| Spektraltyp | M/M☉ | R/R☉ | M/M☉ / (R/R☉)3 | (M/M☉)2 / (R/R☉)4 | M/M☉ / R/R☉ | L/L☉ Theorie | L/L☉ Messung | TO/TO☉ Theorie | TO/TO☉ Messung | |
|---|---|---|---|---|---|---|---|---|---|---|
| O5 | 60 | 12 | 0.035 | 0.17 | 5.0 | 220000 | 790000 | 6.2 | 7.7 | |
| B0 | 17.5 | 7.4 | 0.043 | 0.10 | 2.4 | 5400 | 52000 | 3.1 | 5.2 | |
| A0 | 2.9 | 2.4 | 0.21 | 0.25 | 1.2 | 24 | 54 | 1.4 | 1.6 | |
| F0 | 1.6 | 1.5 | 0.47 | 0.51 | 1.1 | 4.1 | 6.5 | 1.2 | 1.2 | |
| G0 | 1.05 | 1.1 | 0.79 | 0.75 | 0.95 | 1.2 | 1.5 | 0.99 | 1.0 | |
| K0 | 0.79 | 0.85 | 1.3 | 1.2 | 0.93 | 0.49 | 0.42 | 0.91 | 0.91 | |
| M0 | 0.51 | 0.6 | 2.4 | 2.0 | 0.85 | 0.13 | 0.077 | 0.78 | 0.66 | |
| M5 | 0.21 | 0.27 | 11 | 8.3 | 0.78 | 0.0093 | 0.011 | 0.60 | 0.56 |
Während die elemenare Theorie die beobachteten Oberflächentemperaturen (genauer Effektivtemperaturen) zumeist gut wiedergibt, werden die Leuchtkräfte heißer Sterne stark unterschätzt. Eine mögliche Erklärung dafür ist, dass in solchen Sternen im Kern der Energietransport durch Konvektion anstatt durch Strahlung erfolgt, wodurch die erzeugte Energie wesentlich schneller in Richtung der Oberfläche befördert wird.
Weiße Zwerge[Bearbeiten]
Masse-Radius-Beziehung
Die für Hauptreihensterne hergeleiteten Beziehungen und gelten auch für Weiße Zwerge. Da für entartete Materie Druck und Dichte ohne zusätzliche Temperaturabhängikeit aber direkt miteinander zusammenhängen, lassen sich durch Eliminierung einer der Größen oder auch Radius und Masse des Sterns direkt miteinander verknüpfen. Im nicht relativistischen Fall ist wie schon dargelegt , unter extrem relativistischen Bedingungen . Daraus folgt:
Die Radien nicht relativistischer Weißer Zwerge werden mit zunehmender Masse kleiner. Im relativistischen Fall sollte der Radius dagegen mit der Masse wieder ansteigen.
Masse-Dichte-Beziehung
Was der relativistische Fall bedeutet, erkennt man, wenn man die zentrale Dichte als Funktion der Sternmasse betrachtet. Es gilt:
Im nicht relativistischen Fall nimmt die Mittendichte mit zu. Umgekehrt bedeutet das, dass stärker verdichtete Elektronen auch mehr Masse tragen können. Für relativistische Weiße Zwerge sollte dagegen die Dichte im Zentrum mit zunehmender Masse abfallen. Werden Elektronen so stark verdichtet, dass diese relativistisch werden, können sie weniger Masse standhalten als vorher. Dies wiederum zieht eine noch stärkere Komprimierung und dementsprechend einen noch schwächeren Widerstand gegen die Gravitation nach sich. Es liegt also eine instabile Konfguration vor. Tatsächlich können Weiße Zwerge oberhalb einer bestimmten Masse, der sogenannten Chandrasekhar-Grenze nicht mehr existieren, sondern kollabieren weiter zu einem Neutronenstern oder gar einem Schwarzen Loch.
Eigenschaften der habitablen Zone[Bearbeiten]
Von allen Feldern der Astronomie stößt die Suche nach erdähnlichen Planeten auf das wohl größte öffentliche Interesse. Daher sollen die Eigenschaften der sogenannten habitablen Zone hier kurz skizziert werden. Sie umfasst jenes Abstandsintervall um ein Zentralgestirn, innerhalb dessen auf einem Planeten flüssiges Wasser existieren könnte. Wegen der extremen Veränderungen, die Sterne im Laufe ihrer Entwicklung erfahren, kommen für eine solche Diskussion nur Hauptreihensterne in Frage
Abstand vom Zentralgestirn
Aufgrund des photometrischen Entfernungsgesetzes, wonach die von einer Strahlungsquelle empfangene Intensität umgekehrt proportional zum Quadrat deren Entfernung abfällt, gilt folgende Beziehung zwischen der Leuchtkraft eines Sterns und dem Abstand der habitablen Zone , woraus durch Anwendung der Masse-Leuchtkraft-Beziehung auch ein Zusammenhang zwischen und der Zentralmasse abgeleitet werden kann:
Im Prinzip weist jeder Hauptreihenstern eine habitable Zone auf. Die Lebensdauer von O-, B- und A-Sternen ist jedoch nach heutigem Verständnis für die Entstehung von Leben zu kurz.
Gezeitenwirkung des Zentralgestirns
Bei leuchtschwachen Sternen ist der Abstand der habitablen Zone zu denselben sehr gering. Dies bedeutet jedoch, dass der Zentralstern auf einen dort sich befindlichen Planeten eine starke Gezeitenkraft ausübt. Es ist nämlich , woraus resultiert:
Ein Planet in der habitablen Zone eines M-Zwergs wird durch die von seinem Zentralgestirn ausgeübte Gezeitenkraft in eine gebundene Rotation gezwungen, er kehrt seinem Stern immer die gleiche Seite zu (vergleichbar der Mond der Erde). Zwischen Tages- und Nachtseite herrschen somit extreme Temperaturunterschiede, insofern nicht eine dichte Atmosphäre effizient Wärme von der einen zur anderen Seite abführt.
Zusammenfassung
Abschließend seien typische Werte für (in Astronomischen Einheiten) und (relativ zur von der Sonne auf die Erde ausgeübten Gezeitenkraft) zusammengestellt.
| Spektraltyp | rH / AE | FH / FH☉ |
|---|---|---|
| O5 | 890 | 8.5 10-8 |
| B0 | 230 | 1.5 10-6 |
| A0 | 7.3 | 0.0073 |
| F0 | 2.5 | 0.097 |
| G0 | 1.2 | 0.57 |
| K0 | 0.65 | 2.9 |
| M0 | 0.28 | 24 |
| M5 | 0.10 | 180 |
Sternhaufen[Bearbeiten]
Sternhaufen sind aus vielen Einzelsternen bestehende Ansammlungen, die sich in zwei völlig unterschiedliche Kategorien gliedern lassen. Offene Sternhaufen enthalten einige 10 bis 1000 Mitglieder, welche sich zwar deutlich vom allgemeinen Himmelshintergrund abheben, aber dennoch nur mäßig zu ihrem Zentrum hin konzentriert sind. Man findet solche Haufen in den Scheiben von Spiralgalaxien wie unserer Milchstraße, aber auch in irregulären Galaxien. Kugelsternhaufen sind mit einigen 100000 bis 1000000 Sternen weit mehr bevölkert als Offene Sternhaufen und weisen eine viel stärkere Konzentration zur Mitte hin auf. Sie befinden sich weiträumig verteilt in den Halos von Galaxien.
Für das Verständnis von Sternhaufen erweist sich der Vergleich mit einem Gas als sehr nützlich, obwohl zwischen diesen beiden Typen von Vielkörpersystemen ein fundamentaler Unterschied besteht. Die zwischen Gasteilchen wirkende Van-der-Waals-Kräfte sind von kurzer Reichweite, so dass ein Gas ein thermodynamisches Gleichgewicht erreichen kann. Einem Sternhaufen ist das nicht möglich, denn die Reichweite der Schwerkraft ist unbegrenzt. Dennoch weisen Sternhaufen einige Eigenschaften auf, die es zulassen, Konzepte aus der Thermodynamik zu übertragen.
Virialsatz[Bearbeiten]
Kinetische und potentielle Energie eines Haufens
Ein gutes Beispiel für die Anwendbarkeit der Thermodynamik auf Sternhaufen ist der Virialsatz. Man betrachte ein abgeschlossenes System aus Körpern mit Ortsvektoren . Jedes Mitglied des Systems unterliege durch alle anderen Mitglieder einer Kraft . Gemäß des Virialsatzes gilt für die über einen genügend langen Zeitraum gemittelte kinetische Energie :
Im Allgemeinen ist die Berechnung der Summe sehr schwierig. Für den Fall, dass die zwischen zwei Körpern herrschende Kraft nur von deren Abstand abhängt, vereinfacht sich die Auswertung jedoch erheblich. Es zeigt sich dann, dass der Virialsatz einen Zusammenhang zwischen mittlerer kinetischer und potentieller Energie herstellt. Für Kräfte mit einer -Abhängigkeit wie die Gravitation lautet dieser:
Masse eines Haufens
Der Viralsatz gestattet es auf folgende Weise, die Masse eines Sternhaufens abzuschätzen. Seine kinetische Energie ist gegeben durch die Summe über die individuellen Energien . Durch Bildung des mittleren Geschwindigkeitsquadrats lässt sich dieser Ausdruck vereinfachen zu . Von der Geschwindigkeit eines Sterns ist mittels des Dopplereffekts nur die Komponente in Richtung zum Beobachter meßbar. In einem sphärisch symmetrischen Haufen, der im Sinne des Virialsatzes (näherungsweise) ein thermodynamisches Gleichgewicht erreicht hat, sind alle Geschwindigkeitsrichtungen jedoch gleich wahrscheinlich, so dass gilt und damit .
Die potentielle Energie eines Haufens ist gegeben durch , wobei den Radius und einen freier Parameter darstellt, der von der radialen Dichteverteilung des Sternsystems abhängig ist. Setzt man kinetische und potentielle Energie in den Virialsatz ein, gewinnt man folgenden Ausdruck:
Sternhaufen haben leider keinen scharfen Rand, sondern gehen diffus in das sie umgebende Sternfeld über, so dass die Bestimmung des Radius problematisch ist. Daher wird in der Praxis oft der sogenannte Halblichtradius verwendet, welcher die Hälfte der Gesamthelligkeit des Haufens einschließt. liegt dann gemäß Röser und Tscharnuter (2012) etwa bei 1.2.
Relaxation[Bearbeiten]
Relaxationszeit
Im Zusammenhang mit dem Virialsatz stellt sich unmittelbar die Frage, welche Zeit seit der Entstehung eines Sternhaufens verstrichen sein muss, damit ein solcher im Sinne dieser Gesetzmäßigkeit ein thermodynamisches Gleichgewicht erreicht hat. Diese Zeit wird Relaxationszeit genannt und ist für Sternhaufen durch die mittlere Zeit zwischen zwei engen Begegnungen eines Mitglieds mit anderen Sternen gegeben, welche die ursprüngliche kinetische Energie um einen Betrag ändern, der im Mittel ebenso groß ist wie selbst.
Um abzuschätzen, ist der Vergleich eines Sternhaufens mit einem Gas erneut sehr fruchtbar. Wie bereits im Abschnitt über die Druckverbreiterung von Spektrallinien gezeigt, gilt in einem Gas der Teilchendichte für die mittlere Zeit zwischen zwei Stößen eines Teilchens , wobei der Wirkungsquerschnitt und die typische Geschwindigkeit eines Teilchens darstellen. Ein entscheidender Punkt ist nun, was unter dem Wirkungsquerschnitt bzw. Wirkungsradius eines Sterns zu verstehen ist. Es zeigt sich, dass hierbei der Abstand, bei dem zwei Sterne gerade noch nicht gravitativ aneinander gebunden sind, ein brauchbares Maß darstellt. Gemäß dem über die 2.kosmische Geschwindigkeit Gesagten ist , bedeutet hierbei die typische Masse eines Sterns. Chandrasekhar hat gezeigt, dass als Wirkungsradius , mithin als Wirkungsquerschnitt zu verwenden ist. Durch Einsetzen erhält man als Zwischenergebnis:
lässt sich mit Hilfe des Virialsatzes durch die Masse und den Radius des Haufens ausdrücken mittels , die Anzahldichte der Sterne durch deren absolute Anzahl und das Volumen des Haufens gemäß und schließlich durch . Daraus folgt:
Dieses Resultat berücksichtigt nur die Wechselwirkung eines Sterns mit jeweils seinem nächsten Nachbarn. Betrachtet man auch den schwächeren Energieaustausch mit weiter entfernten Haufenmitgliedern in seiner Umgebung, so erhält man der Theorie Chandrasekhars zufolge noch einen Korrekturfaktor, für dessen Größe das Verhältnis entscheidend ist:
Indem man erneut die Beziehungen und heranzieht, kann man zeigen, dass gilt. Damit vereinfacht sich Chandrasekhars Ergebnis zu:
Der zusätzliche Energieaustausch eines Sterns auch mit nicht unmittelbaren Nachbarn trägt dazu bei, dass ein Haufen das thermodynamische Gleichgewicht im Sinne des Virialsatzes rascher erreicht.
Die Größen und werden meist in Sonnenmassen und Parsec ausgedrückt, die Relaxationszeit in der Regel in Jahren. Die entsprechende Formulierung obiger Formel lautet:
Für die Plejaden ergibt sich mit 2100 Mitgliedern, einem Radius von 2.5 Parsec und 690 Sonnenmassen eine Relaxationszeit von circa 50 Millionen Jahren. 47 Tucanae weist mit etwa 1 Million Sternen, einem Radius von 18 Parsec und circa 900000 Sonnenmassen ein von ungefähr 7 Milliarden Jahren auf.
Auflösung von Haufen
Durch die Relaxation stellt sich für die Mitglieder eines Sternhaufens eine Geschwindigkeitsverteilung ein, welche einer Maxwell-Verteilung entspricht. Obwohl die Gesamtenergie des Systems negativ ist, erreichen immer wieder einzelne Sterne eine zum Verlassen des Haufens ausreichende Geschwindigkeit. Im Mittel beträgt dieser Verlust 0.78 % der aktuellen Mitgliederzahl pro Relaxationszeit, d. h. es gilt bzw.
Durch das sukzessive einem Verdampfen vergleichbare Entweichen einzelner Mitglieder löst sich ein Sternhaufen im Laufe der Zeit allmählich auf. Nach etwa 130 Relaxationszeiten ist nur noch der ursprünglich vorhandenen Sterne im Haufen verblieben.
Dichteverteilung[Bearbeiten]
Projezierte und radiale Dichteverteilung
Die tatsächliche räumliche Dichteverteilung eines Haufens - welche als radial angenommen werden darf - lässt sich nicht direkt beobachten. Unmittelbar sichtbar ist nur eine projezierte Flächenhelligkeit bzw. eine daraus abgeleitete projezierte Flächendichte (siehe Zeichnung).

Um die radiale Dichteverteilung zu gewinnen, ist eine Deprojektion erforderlich. Die Flächendichte gewinnt man, indem man die räumliche Dichteverteilung entlang der Sichtlinie auf die dazu senkrechte Ebene projeziert gemäß
Die Deprojektion erfolgt, indem man obige Integralgleivhung nach auflöst. Das Ergebnis lautet:
King-Profil
Wie King (1981) zeigte, lässt sich insbesondere für Kugelsternhaufen die Flächendichte durch folgendes nach ihm benannte Profil darstellen:
Die beiden Radien und sind freie Parameter, welche durch Messung der Flächenhelligkeit in Abh. von bestimmt werden müssen. wird als Kernradius (englisch core radius) bezeichnet, gibt also die Größe der Kernzone des Haufens an. wird Gezeitenradius (englisch tidal radius) genannt. Wie ein Mond einem Planeten wegen der schon beschriebenen Roche-Grenze nicht zu nahe bzw eine bestimmte Größe nicht überschreiten kann, ist auch dem Radius eines Sternhaufens durch die von der Muttergalaxie ausgehende Gezeitenkraft eine obere Grenze gesetzt.
Folgende Abbildung zeigt die von King angegebene Beziehung in Abhängigkeit vom Verhältnis der beiden Radien. Je kleiner der Kernradius im Vergleich zum Gezeitenradius ausfällt, umso stärker sind die Sterne zur Mitte des Haufens hin konzentriert.
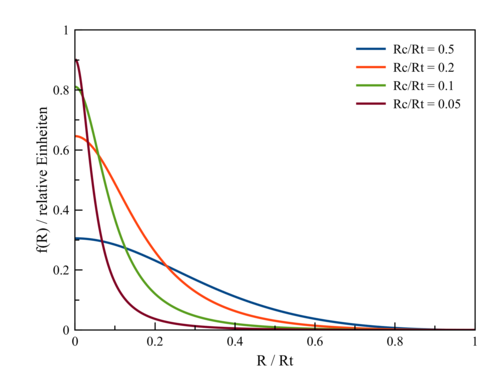
Für das King-Profil lässt sich obiges Deprojektions-Integral explizit lösen, wobei sich allerdings ein sehr komplizierter Ausdruck ergibt:
Galaxien[Bearbeiten]
Entfernungen[Bearbeiten]
Methode der Standardkerzen[Bearbeiten]
Selbst die nächsten Galaxien sind viel zu weit entfernt, als dass selbst die extrem genauen Messungen von Parallaxen durch den Satelliten Gaia noch greifen könnten. Um die Entfernungen solcher Systeme bestimmen zu können, ist man darauf angewiesen, innerhalb derselben Objekte bekannter absoluter Helligkeit zu beobachten. Aus der scheinbaren Helligkeit einer solchen Standardkerze folgt dann unter Berücksichtigung der interstellaren Absorption folgendermaßen die Entfernung :
Als Standardkerzen kommen verschiedene Sterntypen in Frage, die hier kurz vorgestellt werden sollen.
Standardkerzen für nahe Galaxien[Bearbeiten]
Cepheiden
Nahe Galaxien wie z. B. die Andromedagalaxie können am Rand noch in Einzelsterne aufgelöst werden. Als Standardkerzen kommen dabei vor allem die Cepheiden in Frage, eine Klasse pulsierender veränderlicher Sterne, deren absolute Helligkeit eng mit der Pulsationsperiode verknüpft ist. Die folgende von Sandage und Tammann (2006) angegebene Beziehung ist auf etwa 0.1 Größenklassen stabil:
RR-Lyrae-Sterne
RR-Lyrae-Sterne sind eine weitere Klasse pulsierender veränderlicher Himmelskörper. In ihrem Fall korreliert die absolute Helligkeit eng mit der Häufigkeit schwerer Elemente (wobei alle Elemente jenseits von Wasserstoff und Helium als schwer bezeichnet werden). Nach Röser und Tscharnuter (2012) gilt:
Die Häufigkeit schwerer Elemente wird gemäß folgender Konvention angegeben. Zunächst wird diese mit dem für die Sonne gültigen Wert (etwa 2%) verglichen und anschließend der Logarithmus zur Basis 10 genommen. Für einen Stern mit gleichem Anteil schwerer Elemente wie die Sonne ist also gleich 0. Im Allgemeinen weisen RR-Lyrae-Sterne jedoch einen weit geringeren Anteil schwere Elemente wie die Sonne auf. Ist dieser z. B. nur 1/10 im Vergleich zur Sonne, so ist = -1.
Standardkerzen für ferne Galaxien[Bearbeiten]
Selbst leuchkräftige Sterne wie die soeben skizzierten Typen von Veränderlichen können in fernen Galaxien nicht mehr als individuelle Objekte beobachtet werden. Allein Sterne mit sehr starken Helligkeitsausbrüchen, sogenannte eruptive Veränderliche, helfen hier noch weiter. Novae und allem Supernovae kommen in Frage.
Novae
Novae sind Sterne, die starke kurzzeitige Helligkeitsanstiege um bis zu etwa 15 Größenklassen aufweisen. Die absolute Helligkeit zum Zeitpunkt des Maximums gehorcht einem engen Zusammenhang mit der Zeit , die verstreicht, bis anschließend die Helligkeit wieder um 3 Größenklassen abgefallen ist. Röser und Tscharnuter (2012) geben mit einer Genauigkeit von 0.3 Größenklassen an:
Supernovae
Von allen stellaren Körpern liefern Supernovae aufgrund ihrer enormen Leuchtkräfte die größtmöglichen Reichweiten. Vor allem Supernovae des Typs Ia stellen hervorragende Standardkerzen mit einer Stabilität von circa 0.1 Größenklassen da. Es handelt sich um explodierende Weiße Zwerge, d. h. die Ausgangsobjekte weisen allesamt fast exakt die gleiche innere Struktur und chemische Zusammensetzung auf. Die Detonation inklusive Anstieg und Abklingen der Helligkeit läuft somit jedes Mal weitgehend auf die gleiche Weise ab. Tatsächlich weisen alle Supernovae des Typs Ia nahezu die gleiche maximale absolute Blauhelligkeit auf:
Beobachtet man eine Supernova in einer fernen Galaxie, muss man die Rotverschiebung beachten. Bevor man die Blauhelligkeit bestimmt, muss die spektrale Helligkeitsverteilung entsprechend korrigiert werden.
Dynamik der Galaxie als Maß für ihre Leuchtkraft[Bearbeiten]
Eine völlig andere Methode der Entfernungsbestimmung beruht darauf, anhand der Dynamik der Galaxie deren Leuchtkraft zu bestimmen, woraus mit Hilfe der scheinbaren Helligkeit erneut die Entfernung folgt. Die nachfolgend skizzierten Relationen müssen jedoch auf Grundlage von Standardkerzen geeicht werden, d. h. sie stellen nur sekundäre Verfahren dar.
Tully-Fisher-Relation
Die Tully-Fisher-Relation stellt einen empirisch gefundenen Zusammenhang zwischen der absoluter Helligkeit einer Spiralgalaxie und der Äquivalentbreite der 21 cm - Linie des neutralen Wasserstoffs her. Ursprünglich 1977 zum ersten Mal formuliert, gilt gemäß einer neueren Kalibration von Pierce und Tully (1992):
Die Beziehungen weisen eine Genauigkeit von ungefähr 0.1 Größenklassen auf. R, I und H beziehen sich auf Wellenlängenbereiche im Roten, nahen Infraroten (bei 1 m) und mittleren Infraroten (bei 3.6 m).
Ihre Erklärung findet die Tully-Fisher-Relation im Rotationsverhalten der Spiralsysteme. Durch die Rotation bewegen sich manche ihrer Bereiche auf uns zu, anderen dagegen von uns weg. Infolge des Doppler-Effekts werden dadurch alle Spektrallinien und damit auch die 21 cm - Linie verbreitert. Die Äquivalentbreite zeigt die maximale Umlaufgeschwindigkeit an, welche ein Maß für die Masse der Galaxie darstellt. Die Masse aber ist wiederum mit der Leuchtkraft des Systems verknüpft.
Faber-Jackson-Relation
Die Faber-Jackson-Relation betrachtet die Dynamik elliptischer Galaxien und verknüpft deren absolute Helligkeit bzw. Leuchtkraft mit der Streuung der in ihnen auftretenden Sterngeschwindigkeiten. Gemäß Faber und Jackson (1976) ist bzw. auf der Magnitudenskala
Die Konstante muss für jeden Wellenlängenbereich individuell bestimmt werden. Auch diese Gesetzmäßigkeit ist auf etwa 0.1 Größenklassen genau.
Die Faber-Jackson-Relation beruht auf dem Virialsatz, d. h. eine elliptische Galaxie wird als überdimensionaler Sternhaufen mit einer Masse und einem Radius betrachtet. Wie bereits im entsprechenden Kapitel gezeigt, gilt demgemäß . Neben Spiralgalaxien weisen auch elliptische Systeme eine Proportionalität auf, so dass . Nimmt man jetzt noch an, dass alle derartigen Galaxien die gleiche absolute Flächenhelligkeit zeigen, so ist und letztendlich .
Massen[Bearbeiten]
Rotationskurve[Bearbeiten]
Die Massen von Galaxien sind noch erheblich schwieriger zu bestimmen als deren Entfernungen. Im Falle rotierender Galaxien (Spiral- und Baklenspiralsysteme) stellt die Abhängigkeit der Umlaufgeschwindigkeit in der Scheibe vom Abstand zum Zentrum, die sogenannte Rotationskurve, die wichtigste Informationsquelle dar. Betrachtet man eine Probemasse und setzt die von der von der Bahn umschlossenen Masse ausgeübte Gravitation mit der Zentripetalkraft gleich, so folgt unmittelbar:
Anstelle des Abstands zur Mitte der Galaxie ist jedoch nur der Winkelabstand zu derselben direkt beobachtbar. Um aus letzterem die tatsächliche Distanz zum Zentrum zu gewinnen, muss die Entfernung des Systems bekannt sein gemäß (wobei die hier zulässige Näherung benutzt wird). In handlichen Einheiten gilt dann:
Beobachtet man eine (Balken)spiralgalaxie an deren sichtbaren Randbereich, sollte proportional zu abfallen. Tatsächlich ist aber schon lange bekannt, dass die Umlaufgeschwindigkeit in vielen derartigen Systemen nach außen hin bis zur Beobachtungsgrenze auf unverändert hohem Niveau verharrt. Dies bedeutet, dass selbst an der Sichtbarkeitsgrenze nur einen kleinen Teil der tatsächlichen Masse der Galaxie ausmacht. Um diese zu ermitteln, muss man ein kompliziertes Modell für die Massenverteilung aufstellen, welches die beobachtete Rotationskurve möglichst gut widerspiegelt. Ein solches wird im nächsten Abschnitt vorgestellt.

Virialsatz[Bearbeiten]
Wie die weiter oben beschriebene Faber-Jackson-Relation beweist, können elliptische Galaxien näherungsweise wie Sternhaufen behandelt werden. Dann kann wie bereits behandelt die Masse aus der Sreuung der Sterngeschwindigkeiten abgeleitet werden. Letztere folgt wiederum aus der Dopplerverbreiterung der Spektrallinien.
Modell einer Spiralgalaxie[Bearbeiten]
Abschließend soll hier der typische Aufbau einer Spiralgalaxie skizziert werden. Eine solche besteht aus einer im Vergleich zu ihrem Durchmesser sehr dünnen Scheibe, einer als Linse bezeichneten Verdickung nahe des Zentrums und einem sehr ausgedehnten Halo.
Massenverteilung[Bearbeiten]
Scheibe
Die Dichteverteilung entspricht in guter Näherung derjenigen einer isothermen Scheibe, welche durch ihre eigene Schwerkraft stabilisiert wird. Die Dichte nimmt sowohl mit zunehmender Entfernung von der Rotationsachse als auch Abstand von der Äquatorebene exponentiell ab:
Hierbei bezeichnen die Masse der Scheibe, ihren Skalenradius und ihre Skalenhöhe. Für die Milchstraße beträgt neueren Forschungen zufolge, z. B. von McMillan (2011), etwa 57 Milliarden Sonnenmassen. liegt bei circa 3000 Parsec. Für gibt der Autor einen Wert von 300 Parsec an. Die interstellare Materie und unmittelbar aus ihr hervorgegangene junge Sterne sind jedoch wesentlich stärker zur Äquatorebene hin konzentriert. Bahcall und Sonaira gaben schon 1980 für diese eine Skalenhöhe von nur 100 bis 125 Parsec an. Lediglich langlebige Sterne wie die Sonne entfernen sich weiter von der Äquatorebene.
Die starke Konzentration des interstellaren Mediums ist vor allem bei extragalaktischen Systemen, welche sich von der Kante zeigen, sehr schön zu sehen. Der interstellare Staub zeigt sich als schmales dunkles Band, welches die Scheibe genau in zwei leuchtende Hälften teilt.

Linse
Die Linse wirkt ihrem äußeren Erscheinungsbild nach wie ein überdimensionaler Kugelsternhaufen. Näherungsweise kann ihre Dichteverteilung als radial, d. h. als Funktion des Abstandes zum Koordinatenursprung betrachtet werden. Gemäß McMillan fällt die Dichte nahe des Ursprungs einem Potenzgesetz folgend ab, weiter außen stellt sich vergleichbar der Scheibe ein exponentieller Abfall ein. Der Autor schlägt folgende Beziehung vor:
ist der Skalenradius für den inneren Bereich der Linse, wo das Potenzgesetz dominiert. bezeichnet den Skalenradius für die Außenzone, welche durch den exponentiellen Dichteabfall charakterisiert ist. Für die beiden Radien nennt McMillan für die Galaxis Werte von 75 und 2100 Parsec. Der Exponent beläuft sich ihm zufolge auf 1.8. ist eine Proportionalitätskonstante, welche von der Masse der Linse abhängt. Für die Milchstraße liegt diese bei 9 Milliarden Sonnenmassen.
Streng genommen nimmt auch die Linse an der Rotation ihrer Muttergalaxie teil und ist dadurch etwas abgeplattet. Darauf wird hier aber nicht weiter eingegangen.
Halo
Wie bereits erwähnt, werden selbst am gerade noch sichtbaren Rand rotierender Galaxien sehr hohe Umlaufgeschwindigkeiten beobachtet, welche durch die von der sichtbaren Materie ausgeübten Schwerkraft nicht erklärt werden können. Um eine Übereinstimmung mit dem Newtonschen Gravitationsgesetz herzustellen, ist man gezwungen, einen Halo enormer Ausdehnung und Masse anzunehmen, dessen Materie jedoch unsichtbar und bis heute nicht identifiziert ist. Die Dichteverteilung in diesem dunklen Halo wird in der Regel als kugelsymmetrisch betrachtet. Gemäß McMillan fällt die Dichte selbst zu sehr großen Entfernungen hin nur langsam, d. h. einem Potenzgesetz entsprechend ab:
Für den Skalenradius gibt McMillan einen Wert von 20200 Parsec an. ist wiederum eine Proportionalitätskonstante, in welche jetzt die Masse des Halo eingeht.
McMillans Potenzgesetz erfordert die Einführung eines maximal zulässigen Abstandes , da es ansonsten eine unendliche Masse für den Halo liefern würde. Gibt man eine endliche Halomasse vor, kann man aus dieser zusammen mit die Konstante folgendermaßen bestimmen:
Laut McMillan schließt der galaktische Halo bis zu einem Abstand von 50000 Parsec vom Milchstraßenzentrum 540 Milliarden Sonnenmassen ein. Seine Gesamtmasse soll sogar 1400 Milliarden Sonnenmassen betragen, was mit der hier genannten Dichteverteilung einem Radius von 180000 Parsec entspräche.
Zusammenfassung der Komponenten
Die nachfolgenden Diagramme fassen die in der Äquatorebene der Galaxis vorliegenden Verhältnisse zusammen. Nur ganz nahe des Zentrums, bis zu einem Abstand von etwa 1000 Parsec, beherrscht die Linse die Materiedichte. Danach dominiert bis zu einer Entfernung von etwa 20000 Parsec die Scheibe. Nur ganz außen, wo die Sterndichte bereits sehr gering ist, überwiegt selbst in der Äquatorebene der Beitrag des Halo.

Für die Kreisbahngeschwindigkeit ergibt sich ein ganz anderes Bild. Nur die Linse zeigt einen ähnlichen Dominanzbereich wie in Bezug auf die Materiedichte, sie bestimmt die Umlaufgeschwindigkeit bis zu einer Distanz von etwa 1500 Parsec vom Zentrum. Der Herrschaftsbereich der Scheibe ist nun aber deutlich beschnitten, nur bis zu einem Abstand von circa 6000 Parsec dominiert sie die Kreisbahngeschwindigkeit. Die Dynamik selbst der stellaren Komponente der Milchstraße wird also überwiegend vom Halo geprägt.

Geschwindigkeiten der Sterne[Bearbeiten]
Scheibe
Ganz grob betrachtet, laufen die in der Scheibe einer Spiralgalaxie sich befindlichen Sterne in Kreisbahnen um das Zentrum des Sternsystems. Die Umlaufgeschwindigkeit ist dabei durch den Abstand vom Zentrum und die von der Bahn eingeschlossenen Masse gegeben:
Tatsächlich üben die Sterne aber Gravitationskräfte aufeinander aus und stören sich so auf ihren Bahnen gegenseitig. Für die Bewegung senkrecht zur Äquatorebene stellt sich gemäß dem Modell einer isothermen Scheibe eine gaußförmige Geschwindigkeitsverteilung ein, deren Mittelwert gleich 0 ist und deren Streuung von der Dicke der Scheibe und der lokalen Dichte am Äquator abhängt:
Legt man das hier skizzierte Dichtemodell zugrunde, findet man in der Sonnenumgebung senkrecht zur galaktischen Ebene eine Geschwindigkeitsstreuung von 16 km/s.
Um die Bedingungen parallel zur Äquatorebene zu verstehen, muss man folgenden Effekt betrachten. Nachbarn, die im Vergleich zu einem bestimmten herausgegriffenen Stern näher am Zentrum stehen, überholen diesen fortlaufend. Umgekehrt lässt der Referenzstern weiter außen laufende Nachbarn ständig hinter sich. Gemäß Oort (1965) bilden sich dadurch Bahnen heraus, die an das ptolemäische Modell der Planetenbewegung erinnern. Die Sterne schwingen auf Epizykeln um ihre idealen Kreisbahnen herum, wobei erstere aber in der Regel nicht kreisförmig, sondern elliptisch sind. Dadurch entstehen auch tangential zu den Kreisbahnen und in radialer Richtung gaußförmige Geschwindigkeitsverteilungen, welche durch Streuungen und charakterisiert sind. Das Verhältnis der beiden Streuungen ist nach Oort durch das Verhältnis der Winkelgeschwindigkeiten und bestimmt, mit welchen die Sterne auf ihren Kreisen und Epizykeln sich bewegen:
Das Verhältnis der beiden Winkelgeschwindigkeiten wiederum hängt von selbst und ab:
Mit dem gegebenen Dichtemodell sind über weite Bereiche der galaktischen Scheibe die beiden Winkelgeschwindigkeiten nahezu gleich, d. h. einem Umlauf auf der Kreisbahn um das Zentrum entspricht fast genau einem Umlauf auf dem Epizykel. Damit liegt das Verhältnis tangentiale / radiale Geschwindigkeitsstreuung nahe bei 1/2.
Das Verhältnis der Geschwindigkeitsstreuungen senkrecht / parallel zur Äquatorebene entzieht sich einer einfachen Erklärung. Bottema (2003) gibt an:
ist eine Korrekturfunktion, die gemäß des Autors je nach Entfernung zur Rotationsachse etwa zwischen 0.6 und 0.9 liegt. In der Umgebung der Sonne ist somit in radialer Richtung eine Geschwindigkeitsstreuung von ungefähr 35 km/s zu erwarten.
Linse
Für die Geschwindigkeiten der in der Linse sich aufhaltenden Sterne gibt es kein anschauliches Modell. Man ist auf Messungen der Radialgeschwindigkeit vieler Einzelsterne angewiesen, die für die Milchstraße folgendes Bild zeigen. Gemäß Howard und anderen (2008) sowie Kunder und anderen (2012) bewegen sich die Linsensterne weniger regellos als in einem Sternhaufen. Sie nehmen noch an der galaktischen Rotation teil, wobei die mittlere Umlaufgeschwindigkeit aber deutlich unter der Streuung derselben liegt, d. h. der Sternhaufencharakter überwiegt.
Kosmologie[Bearbeiten]
Mitbewegte Koordinaten[Bearbeiten]
Seit der Entdeckung der Galaxienflucht in den 1920er Jahren ist bekannt, dass das Universum sich ausdehnt. Dies bedeutet, dass in einem festen Koordinatensystem alle Körper ihre Positionen nicht nur aufgrund der wechselseitig ausgeübten Gravitation ändern, sondern auch wegen der Expansion des Kosmos. Um diese beiden Arten von Bewegung getrennt voneinander beschreiben zu können, sind Koordinaten wünschenswert, welche der Ausdehnung des Weltalls folgen. In einem solchen System bleibt, wie untenstehende Abbildung zeigt, die Position eines Körpers von der Expansionsbewegung unberührt, sie unterliegt allein der von anderen Körpern ausgehenden Schwerebeschleunigung .

Um die Position eines Körpers in festen Koordinaten in eine Position in mitbewegten Koordinaten umzurechnen, wird ein Skalenfaktor folgendermaßen eingeführt:
Der Faktor beschreibt das Ausdehnungsverhalten des Universums. Er gibt an, wie groß es zu einem Zeitpunkt im Vergleich zu einem bestimmten Bezugspunkt = 0 ist.
Friedmannsche Gleichungen[Bearbeiten]
Klassisches Modell einer expandierenden homogenen Kugel[Bearbeiten]
Beschleunigung des Skalenfaktors
Ein einfaches Modell, die Expansion des Weltalls zu beschreiben, ist das einer homogenen Kugel, welche vom Mittelpunkt ausgehend einen Schubs gleichmäßig in alle Richtungen erhalten hat. Man betrachte ein Teilchen an der Oberfläche der Kugel, das in festen Koordinaten einen Abstand und in mitbewegten Koordiaten einen solchen von vom Zentrum aufweisen soll. Da für eine gleichmäßig sich ausdehnende Kugel gemäß der Konstruktion des Koordinatensystems zeitunabhängig ist, folgt aus unmittelbar und .
Das Probeteilchen an der Kugeloberfläche spürt in festen Koordinaten eine Schwerebeschleunigung wobei die Masse der Kugel darstellt. Rechnet man diese Beziehung in mitbewegte Koordinaten um und ersetzt man die Masse durch die Dichte der Kugel gemäß , so gewinnt man die Beschleunigungsgleichung des Skalenfaktors.
Geschwindigkeit des Skalenfaktors
Verwendet man anstelle der Dichte die Masse der Kugel, lautet obige Gleichung . Multipliziert man beide Seiten mit , kann man unmittelbar über die Zeit integrieren mit dem Ergebnis . bezeichnet eine aus den Anfangsbedingungen zu bestimmende Konstante. Setzt man jetzt abermals die Dichte anstelle der Masse ein, lautet die Geschwindigkeitsgleichung des Skalenfaktors:
Allgemeinrelativistisches Modell nach Friedmann[Bearbeiten]
Beschleunigung des Skalenfaktors
Die Anwendung der allgemeinen Relativitätstheorie auf das Modell der expandierenden Kugel liefert im Vergleich zur klassischen Lösung mehrere Zusatzterme. Die vollständige Beschleunigungsgleichung für den Skalenfaktor lautet nach Friedmann:
bezeichnet den Druck innerhalb der Kugel, welcher sich aus dem Gas- und Strahlungsdruck zusammensetzt. Ersterer kann vernachlässigt werden, doch letzterer muss zumindest für die frühen Entwicklungsstadien des Universums berücksichtigt werden.
Eine besonders interessante Korrektur wird durch die sogenannte kosmologische Konstante repräsentiert. Sie ist gegenüber dem Dichte- und Druckbeitrag von entgegengesetztem Vorzeichen, d. h. beschreibt eine im Gegensatz zur Gravitation abstoßende Kraft.
Geschwindigkeit des Skalenfaktors
Auch die Geschwindigkeitsgleichung des Skalenfaktors erfährt einige Änderungen. Gemäß Friedmann gilt:
Wieder tritt die kosmologische Konstante in Erscheinung. Als weitere Korrektur taucht die Krümmung auf, welche die Werte -1, 0 und 1 annehmen kann. Der Fall -1 entspricht einer negativen Krümmung des Raums (analog einer Sattelfläche), der Fall +1 einer positiven Krümmung (vergleichbar einer Kugeloberfläche). Der Fall 0 stellt einen flachen Raum (analog einer Ebene) dar.
Normierte Darstellung des Friedmannschen Modells[Bearbeiten]
Der Skalenfaktor, seine Geschwindigkeit und Beschleunigung lassen sich als Vielfache beobachtbarer Größen darstellen. Dies gestattet es, eine übersichtlichere Darstellung der Friedmannschen Gleichungen zu gewinnen.
Hubble-Konstante
In den 1920 Jahren wurde nicht nur entdeckt, dass sich (von regionalen Abweichungen abgesehen) sämtliche Galaxien von uns entfernen, sondern auch dass deren sogenannte Fluchtgeschwindigkeiten proportional zu ihren Entfernungen sind:
Die Proportionalitätskonstante wird Hubble-Konstante genannt. Tatsächlich ist sie jedoch zeitabhängig, weshalb oft die Bezeichnung Hubble-Parameter bevorzugt wird. Der heutige Wert beträgt etwa 70 km/s pro 1 Million Parsec, siehe z. B. Ling und andere (2010).
Überträgt man obige Beziehung auf das Modell der expandierenden homogenen Kugel und rechnet diese in mitbewegte Koordinaten um, so zeigt sich, dass die Geschwindigkeit des Skalenfaktors zu dessen Absolutwert proportional ist:
Kritische Dichte
Aus der soeben skizzierten Definition der Hubble-Konstanten folgt, dass die linke Seite der Friedmannschen Geschwindigkeitsgleichung gleich ist. Dies bedeutet aber wiederum, dass folgender Ausdruck die Dimension einer Dichte hat:
wird als kritische Dichte bezeichnet. Eine weitere wichtige Größe ist das Verhältnis zwischen tatsächlicher unf kritischer Dichte:
Für das heutige Verhältnis der beiden Dichten wird die Bezeichnung benutzt.
Dunkle Energie
Formell lässt sich auch der kosmologischen Koordinate eine Dichte zuordnen. Diese lautet:
Die der kosmologischen Konstante entsprechende Komponente des Weltalls wird als dunkle Energie bezeichnet.
Die Dichte wird in der Kosmologie ebenfalls mit der kritsichen Dichte verglichen:
Für die Gegenwart lautet die Bezeichnung .
Dichte und Krümmung des Kosmos
Betrachtet man die Friedmannsche Geschwindigkeitsgleichung für den heutigen Zustand und setzt sämtliche soeben eingeführte Größen ein, so nimmt diese folgende Gestalt an:
und bezeichnen die heutige Werte für die Hubble-Konstante und den Skalenfaktor. Man betrachte die Gleichung zunächst ohne kosmologische Konstante, also für = 0. Unter dieser Bedingung verschwindet die linke Seite und damit die Krümmung, wenn genau gleich 1, d. h. die Dichte des Universums gleich der kritischen Dichte ist. Damit wird diese Bezeichnung verständlich: Der Kosmos muss genau die Dichte aufweisen, damit dieser eine flache Geometrie aufweist. Ist > 0, so genügt dazu bereits ein . Gemäß Riess und anderen (1998) sowie Perlmutter und anderen (1998) ist das Universum tatsächlich flach mit einem von etwa 0.3 und dementsprechend einem von circa 0.7. Sichtbare und dunkle Materie stellen demgemäß nur 30%, die dunkle Energie 70% der Dichte des heutigen Weltalls.
Normierte Gestalt der Friedmannschen Geschwindigkeitsgleichung
Unter Zuhilfenahme der Hubble-Konstanten und der normierten Dichten lautet die Friedmannsche Geschwindigkeitsgleichung für beliebige Zeiten:
Für einen flachen Kosmos verschwindet dabei der mittlere Term auf der rechten Seite, so dass die normierte Gleichung dann folgendermaßen aussieht:
Lösungen der Friedmannschen Gleichungen für ein flaches Universum[Bearbeiten]
Zeitliche Entwicklung des Skalenfaktors
Für ein flaches Weltall nehmen die Lösungen der Friedmannschen Gleichungen eine recht überschaubare Gestalt an. Der heutige Skalenfaktor wird auf 1 gesetzt, zudem die Hilfsgröße verwendet. Dann gilt ohne bzw. mit kosmologische Konstante, was durch nachfolgendes Diagramm veranschaulicht wird.

Weltalter
Setzt man in obigen Gleichungen auf 1 und löst nach auf, so erhält man die Zeit , welche seit der Entstehung des Kosmos - definiert durch = 0 - vergangen ist:
Ohne kosmologische Konstante liefert die heutige Hubble-Konstante ein Weltalter von etwa 9.3 Milliarden Jahren. Dies widerspricht jedoch den gängigen Modellen der Sternenwicklung, welche für Kugelsternhaufen ein Alter von bis zu circa 13 Millarden Jahren anzeigen. Mit dem gegenwärtig angenommenen Wert für die kosmologische Konstante ergibt sich ein wesentlich besser mit diesen Befunden übereinstimmendes Weltalter von ungefähr 13.4 Milliarden Jahren.
Zeitliche Entwicklung der Hubble-Konstanten
Für die Hubble-Konstante lauten die wiederum graphisch veranschaulichgten Lösungen:

Ohne kosmologische Konstante konvergiert die Hubble-Konstante gegen 0, d. h. die Expansion eines dementsprechenden flachen Kosmos verlangsamt sich immer mehr, ohne jedoch gänzlich zum Stehen zu kommen. Mit kosmologischer Konstante nähert sich die Hubble-Konstante dagegen immer mehr einem endlichen Wert > 0 an. Einem tatsächlich konstanten entspricht für alle Zeiten eine lineare Zunahme der Fluchtgeschwindigkeit mit der Entfernung. Da das Universum sich aber gleichzeitig immer mehr ausdehnt, bedeutet dies eine fortlaufende Beschleunigung der Expansion.
Literaturverzeichnis[Bearbeiten]
Allgemeine weiterführende Literatur[Bearbeiten]
- Schneider Peter: Einführung in die extragalaktische Astronomie und Kosmologie, Springer-Verlag, Berlin, Heidelberg, New York, 2006
- Schwarzschild Martin: Structure and Evolution of the Stars, Princeton University Press, Princeton, 1958
- Sexl Roman, Sexl Hannelore: Weiße Zwerge - Schwarze Löcher. Einführung in die relativistische Astrophysik, Friedrich Vieweg & Sohn Verlagsgesellschaft GmbH, Braunschweig, 1979
- Unsöld Albrecht, Baschek Bodo: Der neue Kosmos. Einführung in die Astronomie und Astrophysik, Springer-Verlag, Berlin, Heidelberg, New York, 2002
- Röser H.J., Tscharnuter W. (Herausgeben): Abriss der Astronomie, Wiley-VCH, Berlin, 2012
- Weigert Alfred, Wendker Heinrich J., Wisotzki Lutz: Astronomie und Astrophysik. Ein Grundkurs, Wiley-VCH, Berlin, 2012
Spezielle Einzelnachweise[Bearbeiten]
- Bahcall J.N., Soneira R.M., The universe at faint magnitudes. I. Models for the Galaxy and the predicted star counts, in: The Astrophysical Journal Supplement Series Band 44, S.73 ff, 1980
- Bottema R., Simulations of normal spiral galaxies, in: Monthly Notices of the Royal Astronomical Society Band 344, S.358 ff, 2003
- Faber S.M., Jackson R.E., Velocity Dispersions and Mass to Light Ratios for Elliptical Galaxies, in: The Astrophysical Journal Band 264, S.668 ff, 1976
- Howard C.D., Rich R.M., Reitzel D.B., Koch A., De Propris R. und Zhao H.S., The bulge radial velocity assay. I. Sample selection and a rotation curve, in: The Astrophysical Journal Band 688, S.1060 ff, 2008
- King I.R., The Dynamic of Globular Clusters, in Quarterly Journal of the Royal Astronomical Society, Band 22, S. 227 ff, 1981
- Kunder A., Koch A., Rich R.M., De Propries R., Howard C.D., Stubbs S.A. und 10 weitere Autoren, The bulge radial velocity assay. II. Complete sample and data release, in: The Astronomical Journal Band 143, S.57 ff, 2012
- Ling F.-S., Nezri E., Athanassoula E., Teyssier R., Dark matter direct detection signals inferred from a cosmological N-body simulation with baryons, in: Journal of Cosmology and Astroparticle Physics Band 2, 2010
- Pierce M.J., Tully R.B., Luminosity-Line Width Relations and the Extragalactic Distance Scale. I Absolute Calibration, in: The Astrophysical Journal Band 387, S.47 ff, 1992
- Perlmutter S, Aldering G, Boyle. B.J., Castro P.G., Couch W.J., Deustua S. und 27 weitere Autoren, Measurements of Omega and Lambda from 42 High-Redshift Supernovae, in: Abstracts of the 19th Texas Symposium on Relativistic Astrophysics and Cosmology, held in Paris, France, Dec. 14-18, 1998. Herausgeber: J. Paul, T. Montmerle und E. Aubourg (CEA Saclay)
- Riess A.G., Filippenko A.V., Challis P., Clocchiatti A., Diercks A., Garnavich P.M. und 14 weitere Autoren, Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant, in: The Astronomical Journal Band 116, S.1009 ff, 1998
- McMillan P.J., Mass models of the Milky Way, in: Monthly Notices of the Royal Astronomical Society Band 414, S.2446 ff, 2011
- Röser H.J., Tscharnuter W. (Herausgeben): Abriss der Astronomie, Wiley-VCH, Berlin, 2012, S.324
- Röser H.J., Tscharnuter W. (Herausgeben): Abriss der Astronomie, Wiley-VCH, Berlin, 2012, S.429
- Röser H.J., Tscharnuter W. (Herausgeben): Abriss der Astronomie, Wiley-VCH, Berlin, 2012, S.626
- Röser H.J., Tscharnuter W. (Herausgeben): Abriss der Astronomie, Wiley-VCH, Berlin, 2012, S.826/827
- Sandage, A., Tammann, G. A.: Absolute Magnitude Calibrations of Population I and II Cepheids and Other Pulsating Variables in the Instability Strip of the Hertzsprung-Russell Diagram, in: Annual Review of Astronomy & Astrophysics, Band 44, S.93 ff, 2006
- Turner D.G.: Comments on the Cluster Main Sequence Fitting Method. III Empirical UBV Reddening Lines for Early Type Stars, in The Astronomical Journal Band 98, S.2300 ff, 1989
- Turner D.G.: The Interstellar Extinction Law, in Revista Mexicana de Astronomia y Astrofisica, Band 29, S.163ff, 1994
- Oort J.H., Stellar Dynamics, in Stars and stellar systems Band V, Kap.21, S.455 ff, 1965





















































































![{\displaystyle T[K]=278.7\left({\frac {1-A}{\epsilon }}\right)^{1/4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f800fb6f5ae287dec8759430b0eb085f027a0350)









![{\displaystyle l[m]=0.0175f_{\text{Ob}}[m]\omega [^{\circ }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18107c3c79fc6eb4b3dca436f54b7e7e794f9013)








![{\displaystyle \alpha [^{\prime \prime }]={\frac {\lambda [nm]}{4848D[m]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/374d4b4731fb011f839610d301c3bcdbc28d4a94)














































![{\displaystyle JD=Int[365.25\cdot (YYYY+4716)]+Int[30.6001\cdot (MM+1)]+DD+B-1524.5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97fefec8d6b476e32d5490e5c99d0b2280ce76c5)


![{\displaystyle GMST(0)[s]=(24110.54841+8640184.812866\cdot T+0.093104\cdot T^{2}-0.0000062\cdot T^{3}){\bmod {8}}6400}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25bf3e0be9b9c1cbe13a797082a88d56e8bbee64)

![{\displaystyle GMST(t)[s]=(GMST(0)+1.00273790935\cdot t){\bmod {8}}6400}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b42f663e51a2b926ec41f8b53054b6c4ceeb88e)

![{\displaystyle ST(t,\lambda )[s]=\left(GMST(t)+{\frac {\lambda [\prime \prime ]}{15}}\right){\bmod {8}}6400}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0399021536492fee6fd34e87dc8d50ca16428a70)



































































































































































































































































![{\displaystyle m_{V}-M_{V}=5\lg r[pc]-5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fbf45a2c65e751f1a23a6fe4b4a569dfd1fd725)

![{\displaystyle m_{V}-M_{V}=5\lg r[pc]-5+A_{V}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a8b663fa12192946b201a50d12afd1294f17e87)


























![{\displaystyle r[pc]={\frac {1}{p[^{\prime \prime }]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27ce7af8ccfe3765a3751cfdc8a6111cea71d2b3)

![{\displaystyle \lg r[pc]={\frac {m_{V}-M_{V}-A_{V}}{5}}+1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfb6a4792630de0b090ac5fb71471e7bf7e8f427)

![{\displaystyle R[km]=149.6\cdot 10^{6}{\frac {\phi [^{\prime \prime }]r[pc]}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66f0795204cc0c2fddf16b9daabf92fd591addc1)












![{\displaystyle (M_{1}+M_{2})[M_{S}]={\frac {a[^{\prime \prime }]^{3}}{p[^{\prime \prime }]^{3}T[a]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bc90318cd6d70197f8f24602814ff62b1974cb2)

























































































































































































![{\displaystyle t_{R}[a]=1.24\cdot 10^{6}{\frac {N}{\ln N}}{\sqrt {\frac {R[pc]^{3}}{M[M_{S}]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3368276cfa33273c78f07c3a08ff111244cdc01)














![{\displaystyle \lg r[pc]={\frac {m-M_{V}-A_{V}}{5}}+1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07eb5f14cc3334f9fcc886077a42af49e85ad885)
![{\displaystyle M_{v}=-0.914-3.087\lg P[d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3789d72435dff8b21244c175c5bb78c69f31f112)
![{\displaystyle [Fe/H]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbef27f4f089d5e2c9b5a9cc3a5202ae4e5046fb)
![{\displaystyle M_{v}=0.82+0.20[Fe/H]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a40698a2756259f719c16ce72b64b461b7a7bfa9)






















![{\displaystyle M(r)[M_{\text{Sonne}}]=0.00113R[pc]\phi [^{\prime \prime }](v[km/s])^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1219d488a8ced93518ff60d06eb753d24be6607)





























































