Formelsammlung Physik: Elektrizitätslehre

Formelsammlung Physik

Klassische Mechanik |  Wellenlehre |  Optik |  Akustik |  Wärmelehre |  Elektrizitätslehre |  Elektrodynamik |  Atom- und Kernphysik |  Quantenphysik |  Thermodynamik 2 |  Relativitätstheorie |  Astronomie |  Hydrostatik |  Tabellen

Siehe auch: Formelsammlung_Elektrotechnik.

Elektrostatik

${\sqrt[{n}]{x}}$

Dieses ist eine Formelsammlung zum Thema Elektrostatik. Es werden mathematische Symbole verwendet, die im Wikipedia-Artikel Mathematische Symbole erläutert werden.

Ladung / Verschiebungsfluss

Einheit

Q bzw. q = $\Psi$. Einheit: [Q] = C = As (Coulomb = Ampere Sekunde)

Elektrische Elementarladung

$e=\,1{,}60217662\cdot 10^{-19}\mathrm {As}$

Die Ladung ist vielfaches der elektrische Elementarladung $e$

$Q=eN\quad {\text{mit}}\quad N\in \mathbb {Z}$

Ladungsdichte

Linienladungsdichte

$\lambda ({\vec {r}})={\frac {\mathrm {d} Q}{\mathrm {d} l}}\quad \Leftrightarrow \quad Q=\int _{l}\lambda ({\vec {r}})\,\mathrm {d} l.$

Oberflächenladungsdichte

$\sigma ({\vec {r}})={\frac {\mathrm {d} Q}{\mathrm {d} A}}\quad \Leftrightarrow \quad Q=\int _{A}\sigma ({\vec {r}})\,\mathrm {d} A$

Raumladungsdichte

$\rho ({\vec {r}})={\frac {\mathrm {d} Q}{\mathrm {d} V}}\quad \Leftrightarrow \quad Q=\int _{V}\rho ({\vec {r}})\,\mathrm {d} V$,

Ladungserhaltung

$Q_{\mathrm {tot} }=\sum _{i}Q_{i}=\int \limits _{V}{q_{i}\,\cdot \,\mathrm {d} V}$

$Q_{\mathrm {tot} }\,$: Gesamtladung im abgeschlossenen System

$Q_{i}/q_{i}$: Einzelladungen

$V,\mathrm {d} V$: Volumen , w:infinitesimales Volumenelement

Anziehungskraft zweier Punktladungen

skalar:

$F={\frac {1}{4\pi \varepsilon }}\,\cdot \,{\frac {Q_{1}Q_{2}}{r^{2}}}\qquad {\text{mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\rm {r}}$

vektoriell:

${\vec {F}}\,=\,{\frac {1}{4\pi \varepsilon }}\,\cdot \,{\frac {Q_{1}Q_{2}}{r^{2}}}\,\cdot \,{\frac {\vec {r}}{r}}\qquad {\text{mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\rm {r}}$

$\varepsilon \,$: w:Permittivität (Dielektrizitätszahl)

$\varepsilon _{0}\,$: w:elektrische Feldkonstante $=\,8{,}85418782\dots \cdot 10^{-12}\,{\frac {\rm {As}}{\rm {Vm}}}$

$\varepsilon _{\mathrm {r} }\,$: relative Permittivität (relative Dielektrizitätszahl)

$\pi \,$: (Pi) w:Kreiszahl $=\,3{,}14159265\dots$

$Q_{1},Q_{2}$: Ladungen

${\vec {r}}\,$: Abstandsw:vektor der Ladungen

$r=|{\vec {r}}|\,$: Abstand der Ladungen

Verschiebungsfluss

skalar:

$\Psi =Q=\sum {\varepsilon \,\cdot E_{N}\,\cdot \,\Delta A}\qquad {\textrm {mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{r}$

wenn homogen:

$\Psi =Q=$ $A$ $D\,\cdot \,\mathrm {d} A$

vektoriell:

$\Psi =Q=$ $A$ $\varepsilon \,\cdot {\vec {E}}\,\cdot \,{\vec {\mathrm {d} A}}\quad \mathrm {mit} \quad \varepsilon =\varepsilon _{0}\varepsilon _{\mathrm {r} }$

$\Psi =Q=$ $A$ ${\vec {D}}\,\cdot \,{\vec {\mathrm {d} A}}$

geschlossene Fläche:

$\Psi \,=\,\sum _{A}{Q_{e}}$

$Q_{e}$: eingeschlossene Ladung

$\varepsilon \,$: Permittitvität (Dielektrizitätszahl)

$\varepsilon _{0}\,$: elektrische Feldkonstante $=\,8{,}85418782\dots \cdot 10^{-12}\,{\frac {\mathrm {As} }{\mathrm {Vm} }}$

$\varepsilon _{\mathrm {r} }\,$: relative Permittivität (relative Dielektrizitätszahl)

$E_{\mathrm {N} }=|{\vec {E}}|\cdot \,\cos(\varphi )\,$: Normalkomponente

nach oben

elektrische Feldstärke

die elektrische Feldstärke (E-Feld) und deren Einheit

Die elektrische Feldstärke ist eine vektorielle Größe; sie hat somit einen Betrag und eine Richtung.

${\vec {E}}\qquad {\text{Einheit:}}\,{\frac {\mathrm {V} }{\mathrm {m} }}\quad {\text{bzw.}}\quad {\frac {\mathrm {N} }{\mathrm {C} }}$

Die Einheiten veranschaulichen die einfachste Berechnungen des E-Feldes:

${\vec {E}}={\frac {\vec {F}}{q}}={\frac {\mathrm {d} U}{\vec {\mathrm {d} l}}}$

Feldstärke im Potenzialfeld:

${\vec {E}}=-\operatorname {grad} (\varphi )$

E-Feld einer Punktladung

skalar:

$E={\frac {1}{4\pi \varepsilon }}\,\cdot \,{\frac {Q}{r^{2}}}\quad {\text{mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\mathrm {r} }$

vektoriell:

${\vec {E}}={\frac {1}{4\pi \varepsilon }}\,\cdot \,{\frac {Q}{r^{2}}}\,\cdot \,{\frac {\vec {r}}{r}}\quad {\text{mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\mathrm {r} }$

$\varepsilon _{0}$: Elektrische Feldkonstante $=8{,}85418782\dots \cdot 10^{-12}\,{\frac {\mathrm {As} }{\mathrm {Vm} }}$

$\varepsilon _{\mathrm {r} }$: Dielektrizitätszahl

E-Feld eines geladenen Leiters

äußeres Feld:

skalar:

$E={\frac {Q}{2\pi \varepsilon lr}}={\frac {\rho }{2\pi \varepsilon r}}\quad {\text{mit}}\quad \rho ={\frac {Q}{l}}$

vektoriell:

${\vec {E}}(P)={\frac {Q}{2\pi \varepsilon l({\vec {p}}\times {\vec {e_{l}}})^{2}}}\cdot ({\vec {e_{l}}}\times ({\vec {p}}\times {\vec {e_{l}}}))={\frac {\rho }{2\pi \varepsilon ({\vec {p}}\times {\vec {e_{l}}})^{2}}}\cdot ({\vec {e_{l}}}\times ({\vec {p}}\times {\vec {e_{l}}}))\quad {\text{mit}}\quad {\vec {e_{l}}}={\frac {\vec {l}}{|{\vec {l}}|}},\quad {\vec {p}}={\vec {OP}}$

inneres Feld:

Für eine Statische Ladungsverteilung muss die Summe aller Kräfte auf jede Ladung 0 sein. Da Ladungen im inneren eines Leiters frei beweglich sind gilt, darf es kein Feld geben. Diesem würde jede Ladung folgen, bis auftretende Ladungsverteilungen das Ursprungsfeld kompensieren. Das heißt, dass es keine Potentialdifferenz gibt:

$\Delta U=0$.

$U({\vec {r}})={\text{const.}}$ erfüllt diese Bedingung. Wonach das Feld 0 sein muss:

${\vec {E}}({\vec {r}})=-\nabla U({\vec {r}})=0$

Nach dem Eindeutigkeitssatz, ist dies die richtige Lösung.

nach oben

Spannung / Potential

die Spannung / das Potential und deren Einheit

$U\qquad {\text{Einheit ist Volt: }}\mathrm {V} ={\frac {\mathrm {J} }{\mathrm {C} }}$

$\varphi \qquad {\text{Einheit: }}\mathrm {V}$

Spannung zwischen zwei Punkten im E-Feld

$U_{AB}={\frac {W_{AB}}{q}}$

$U_{AB}=\int \limits _{A}^{B}{{\vec {E}}\cdot {\vec {\mathrm {d} s}}}$

im homogenen Feld:

$U_{AB}={\vec {E}}\cdot {\vec {s}}$

Potential im E-Feld

$\varphi _{A}=U_{AZ}=-\int \limits _{Z}^{A}{{\vec {E}}\cdot {\vec {\mathrm {d} s}}}$

$Z$: Bezugspunkt; $\varphi _{Z}=0$

Kirchoff: Maschenregeln

Wenn kein bewegendes Magnetischesfeld vorhanden ist.

$\oint {\vec {E}}\cdot {\rm {d}}{\vec {s}}=0$

Elektromotorische Kraft

$\oint {\vec {E}}\cdot \mathrm {d} {\vec {s}}=-\int {\frac {\partial {\vec {B}}}{\partial t}}\mathrm {d} {\vec {A}}={\mathcal {E}}$

nach oben

Kondensatoren

Kapazität

die Kapazität und deren Einheit

die Kapazität ist ein Maß für die Speicherfähigkeit eines Kondensators. Ihr Symbolbuchstabe ist:

$C\$

Ihre Einheit ist das Farad:

$[C]=1\,\mathrm {F} ={\frac {\mathrm {C} }{\mathrm {V} }}$

Die Einheit veranschaulicht die einfachste Berechnung der Kapazität:

$C={\frac {Q}{U}}$

Kapazität einer beliebigen Ladungsverteilung

$C={\frac {Q}{U}}={\frac {\oint _{A}\varepsilon {\vec {E(A)}}\cdot d{\vec {A}}}{\int _{A}^{B}{\vec {E(s)}}\cdot d{\vec {s}}}}$

Kapazität eines Plattenkondensators

$C=\varepsilon {\frac {A}{d}}\quad {\text{mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\mathrm {r} }$

$\varepsilon$: Permittivität (Dielektrizitätszahl)

$\varepsilon _{0}$: elektrische Feldkonstante $=8{,}85418782\ldots \cdot 10^{-12}\,\mathrm {\frac {\mathrm {A} s}{\mathrm {V} m}}$

$\varepsilon _{\mathrm {r} }$: relative Permittivität (relative Dielektrizitätszahl)

Kapazität eines Zylinderkondensators

könnte z.B. ein Koax-Kabel sein

$C={\frac {2\pi \varepsilon l}{\ln {\frac {r_{\mathrm {a} }}{r_{\mathrm {i} }}}}}\quad {\text{mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\mathrm {r} }$

$r_{\mathrm {a} }$: Außenradius

$r_{\mathrm {i} }$: Innenradius

$l$: Zylinderlänge

Kapazität einer freistehenden Kugel

$C=4\pi \varepsilon r\quad {\text{mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\mathrm {r} }$

$r$: Kugelradius

Kapazität eines Kugelkondensators

$C={\frac {4\pi \varepsilon }{\left({{\frac {1}{r_{\rm {i}}}}-{\frac {1}{r_{\rm {a}}}}}\right)}}\quad {\rm {mit}}\quad \varepsilon =\varepsilon _{0}\varepsilon _{\rm {r}}$

$r_{\mathrm {a} }$: äußerer Kugelradius

$r_{\mathrm {i} }$: innerer Kugelradius

Elektrotechnik

Grundlagen

Ladung

Formelzeichen	Einheit
Q Ladung	C Coulomb
$[Q]=[I]\cdot [t]$	$C=A\cdot s$

$Q=\int _{t}I(t)\mathrm {d} t\$

Kapazität

Allgemein
Ladung Q im Kondensator	$Q=C\cdot U$
Energie W im Kondensator	$W={\frac {1}{2}}\ C\cdot U^{2}$
Strom in den Kondensator	$I=C\cdot {\frac {dU}{dt}}\$
Laden / Entladen in Reihenschaltung
Anfangsladestrom	$I={\frac {U}{R}}$
Zeitkonstante $\tau$	$\tau =R\cdot C$
Kondensatorspannung beim Ladevorgang	$u_{c}=U\cdot (1-e^{-{\frac {t}{\tau }}})$
Ladestrom	$i_{c}={\frac {U}{R}}\cdot e^{-{\frac {t}{\tau }}}$
Kondensatorspannung beim Entladevorgang	$u_{c}=U\cdot e^{-{\frac {t}{\tau }}}$
Entladestrom	$i_{c}=-{\frac {U}{R}}\cdot e^{-{\frac {t}{\tau }}}$

Reihenschaltung von Kondensatoren	Parallelschaltung von Kondensatoren
$U_{g}=U_{1}+U_{2}+\dots +U_{n}\$	$Q_{g}=Q_{1}+Q_{2}+\dots +Q_{n}\$
${\frac {1}{C_{g}}}={\frac {1}{C_{1}}}+{\frac {1}{C_{2}}}+\dots +{\frac {1}{C_{n}}}$	$C_{g}=C_{1}+C_{2}+\dots +C_{n}\$
${\frac {U_{1}}{U_{2}}}={\frac {C_{2}}{C_{1}}}$	${\frac {Q_{1}}{Q_{2}}}={\frac {C_{1}}{C_{2}}}$
Für n gleiche C $C_{g}={\frac {C}{n}}$	Für n gleiche C $C_{g}=n\cdot C$

Stromstärke

Formelzeichen

$I\$

Einheit

Ampere

Das Ampere ist eine SI-Basiseinheit und hat daher keine Definitionsgleichung

$\mathrm {A} \$

Beweglichkeit

Elektronen werden durch Kraftwirkung Beschleunigt

$\mathrm {\vec {F}} =-e{\vec {E}}$

Elektronen werden beschleunigt bis es z. B. ein Gitteratom stößt:

${\vec {v_{D}}}=\int _{0}^{\tau _{m}}{\frac {(-e){\vec {E}}}{m_{e}}}=-\left({\frac {e\tau _{m}}{m}}\right){\vec {E}}=-\mu _{n}{\vec {E}}$

wobei

$\tau _{m}$: Mittlere zwischen zwei Stößen

$v_{D}$: Driftgeschwindigkeit: Ist die mittlere Geschwindigkeit, die von Feldstärke verursachen wird.

$m_{e}$: Elektronenmasse

$\mu _{n}$: Beweglichkeit der Elektronen

Stromdichte

Einheit

Ampere*Meter^-2

${\vec {J}}=\rho \;{\vec {v}}_{D}=n\;e\;{\vec {v_{D}}}$

wobei

$\rho$: Volumenladungsichte

$n$: Anzahl der Elektronen

$e$: Elementarladung

$I=\iint \limits _{A}{\vec {J}}\cdot \mathrm {d} {\vec {A}}$

Wenn Homogen

$I=J\cdot A$

Kirchhoff: Knotenregel

Es gilt nur wenn Strom konstant ist, und wenn es keine Ladung in die Hüllfläche gibt.

$0=$ $A$ ${\vec {J}}\cdot \mathrm {d} {\vec {A}}$

Widerstand

Formelzeichen

$R={\frac {U}{I}}$

Einheit

Ohm

$1\Omega ={\frac {\mathrm {V} }{\mathrm {A} }}={\frac {\mathrm {kg} \cdot \mathrm {m} ^{2}}{\mathrm {s} ^{3}\cdot \mathrm {A} ^{2}}}$

Dass der Widerstand konstant ist, gilt übrigens nur bei konstanter Temperatur und metallischen Leitern! Für den Fall, dass der Widerstand sich mit der Temperatur ändert, gilt folgende Gesetzmäßigkeit:

$R_{\theta }=R_{20}\cdot \left(1+\alpha \cdot \Delta \theta \right)$

Der Widerstand bei einer Temperatur ist der Widerstand bei einer bekannten Temperatur multipliziert mit einem Faktor, der von einer Materialkonstante α abhängt und der Temperaturdifferenz $\Delta \theta$.

Spannung, Stromstärke, Widerstand, Leitwert

Formelzeichen	Einheit
U Spannung	V Volt
I Stromstärke	A Ampère
R Widerstand	Ω Ohm
G Leitwert	S Siemens

$U=I\cdot R$	$I={\frac {U}{R}}$	$R={\frac {U}{I}}$
$I=U\cdot G$	$U={\frac {I}{G}}$	$G={\frac {I}{U}}$
$1=R\cdot G$	$R={\frac {1}{G}}$	$G={\frac {1}{R}}$

Leistung

Formelzeichen	Einheit
P Leistung	W Watt

$P=U\cdot I$	$U={\frac {P}{I}}$	$I={\frac {P}{U}}$
$P={\frac {U^{2}}{R}}$	$P={I^{2}}\cdot {R}$ (Ohmsche Verluste)
$U={\sqrt {P\cdot R}}$	$I={\sqrt {\frac {P}{R}}}$
$R={\frac {U^{2}}{P}}$	$R={\frac {P}{I^{2}}}$

Elektrische Arbeit

Formelzeichen	Einheit
W Arbeit	Ws Wattsekunde = J w:Joule
t w:Zeit	s Sekunden

$W=P\cdot t$	$P={\frac {W}{t}}$	$t={\frac {W}{P}}$
$W=U\cdot I\cdot t$

Reihenschaltung von Widerständen

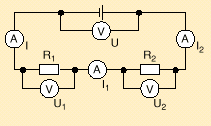
2. Kirchhoff'sches Gesetz, auch Maschenregel genannt.

Die Summe aller Teilspannungen ist genauso groß wie die Gesamtspannung

Formelzeiche	Beschreibung	Formelzeichen	Beschreibung	Formelzeichen	Beschreibung
Rges	Gesamtwiderstand	R1	Teilwiderstand	R2	Teilwiderstand
Uges	Gesamtspannung	UR1	Spannung an R1	UR2	Spannung an R2
Pges	Gesamtleistung	PR1	Leistung an R1	PR2	Leistung an R2

$I_{\mathrm {ges} }=I_{R_{1}}=I_{R_{2}}=\dots =I_{R_{n}}$

$R_{\mathrm {ges} }=R_{1}+R_{2}+\dots +R_{n}$

$U_{\mathrm {ges} }=U_{R_{1}}+U_{R_{2}}+\dots +U_{R_{n}}$

$P_{\mathrm {ges} }=P_{R_{1}}+P_{R_{2}}+\dots +P_{R_{n}}$

$P_{R_{1}}=U_{R_{1}}\cdot I$

$U_{R_{1}}=U_{\mathrm {ges} }\cdot {\frac {R_{1}}{R_{\mathrm {ges} }}}$

Parallelschaltung von Widerständen

1. Kirchhoff'sches Gesetz, auch Knotenregel genannt.

Die Summe aller Teilströme ist genauso groß wie der Gesamtstrom

Formelzeichen	Beschreibung	Formelzeichen	Beschreibung	Formelzeichen	Beschreibung
Rges	Gesamtwiderstand	R1	Teilwiderstand	R2	Teilwiderstand
Gges	Gesamtleitwert	G1	Leitwert von Teilwiderstand R1	G2	Leitwert von Teilwiderstand R2
Iges	Gesamtstromstärke	IR1	Stromstärke an R1	IR2 Stromstärke an R2
Pges	Gesamtleistung	PR1	Leistung an R1	PR2	Leistung an R2

$U_{\mathrm {ges} }=U_{R_{1}}=U_{R_{2}}=\dots =U_{R_{n}}$

$R_{\mathrm {ges} }={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\dots +{\frac {1}{R_{n}}}}}$

$G_{\mathrm {ges} }=G_{1}+G_{2}+\dots +G_{n}$

$R_{\mathrm {ges} }={\frac {1}{G_{1}+G_{2}+\dots +G_{n}}}$

$I_{\mathrm {ges} }=I_{R_{1}}+I_{R_{2}}+\dots +I_{R_{n}}$

$P_{\mathrm {ges} }=P_{R_{1}}+P_{R_{2}}+\dots +P_{R_{n}}$

$P_{R_{1}}=U\cdot I_{R_{1}}$

Spezifischer Widerstand

Formelzeichen	Einheit
ρ Spezifischer Widerstand	(Ω·mm²)/m

$[\rho ]={\frac {\Omega \cdot \mathrm {mm} ^{2}}{\mathrm {m} }}$

Tabelle für den spezifischen Widerstand

Leiterwiderstand

Formelzeichen	Einheit
l Länge	m w:Meter
A w:Fläche	m² w:Quadratmeter

$R={\frac {\rho \cdot l}{A}}$

Leitfähigkeit

Formelzeichen	Einheit
γ Leitfähigkeit	m / (Ω·mm²)

$[\gamma ]={\frac {\mathrm {m} }{\Omega \cdot \mathrm {mm} ^{2}}}$

Leiterwiderstand

$R={\frac {l}{\gamma \cdot A}}$

Einfacher Gleichstromkreis

elektrische Spannung U	$U={\frac {W}{Q}}$	$t$ = Zeit $Q$ = elektrische Ladung $W$ = mechanische Arbeit $\vartheta$ = Temperatur $\rho =$ spezifischer elektrischer Widerstand
elektrische Strom- stärke I	$I={\frac {dQ}{dt}}$ Unter der Bedingung eines stationären Stromes (I = konstant) gilt: $I={\frac {Q}{t}}$
elektrischer Wider- stand R	$R={\frac {U}{I}}$
elektrischer Leitwert G	$G={\frac {1}{R}}$
elektrische Leistung P	$P=U\cdot I$
elektrische Arbeit W	$W=P\cdot t$
ohmsches Gesetz	Unter der Bedingung $\vartheta =\mathrm {konstant}$ gilt: $U\sim I,{\frac {U}{I}}=\mathrm {konstant}$
Widerstandsgesetz	$R={\frac {\rho \cdot l}{A}}$
elektrische Leitfähigkeit	$\gamma ={\frac {1}{\rho }}$

Unverzweigter und verzweigter Gleichstromkreis

Reihenschaltung von Widerständen	Parallelschaltung von Widerständen
$I=I_{1}=I_{2}=\dots =I_{n}\$	$I=I_{1}+I_{2}+\dots +I_{n}\$
$U=U_{1}+U_{2}+\dots +U_{n}\$	$U=U_{1}=U_{2}=\dots =U_{n}\$
$R=R_{1}+R_{2}+\dots +R_{n}\$	${\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\dots +{\frac {1}{R_{n}}}\$
Spannungsteilerregel: ${\frac {U_{1}}{U_{2}}}={\frac {R_{1}}{R_{2}}}\qquad {\frac {U_{1}}{U}}={\frac {R_{1}}{R}}$	Stromteilerregel: ${\frac {I_{2}}{I_{1}}}={\frac {R_{1}}{R_{2}}}\qquad {\frac {I_{1}}{I}}={\frac {R}{R_{1}}}$
Reihenschaltung von Spannungsquellen	Parallelschaltung von Spannungsquellen
$U=U_{1}+U_{2}+\dots +U_{n}$	Unter der Bedingung gleicher Spannungsquellen gilt: $U=U_{1}=U_{2}=...=U_{n}$

Magnetisches Feld

Lorentzkraft

Magnetische Flussdichte

Formelzeichen	Einheit
${\vec {B}}$ Magnetische Flussdichte	T Tesla
$[{\vec {B}}]={\frac {[U]\cdot [t]}{[s]^{2}}}$	$T={\frac {V\cdot s}{m^{2}}}$

$\mathbf {\vec {B}} =\mu _{0}(\mathbf {{\vec {H}}+{\vec {M}}} )=\mu \mathbf {\vec {H}}$

Allgemein

Magnetische Wirkung eine ladung in andere Ladung:

${\vec {F}}_{mag,Q_{2}}=(Q_{2}{\vec {v}}_{2})\times \mu {\frac {(Q_{1}{\vec {v_{1}}})\times {\vec {r}}}{r^{3}}}=(Q_{2}{\vec {v}}_{2})\times {\vec {\mathbf {B} }}$

wobei

$\mu =\mu _{0}\mu _{r}$

$\mu$: Permeabilität

$\mu _{0}\,$: magnetische Feldkonstante $\approx 4\pi \cdot 10^{-7}{\frac {\mathrm {N} }{\mathrm {A} ^{2}}}$

$\mu _{\rm {r}}\,$: relative Permeabilität

$\pi \,$: (Pi) Kreiszahl $=\,3{,}14159265\dots$

$Q_{1}\,,\,Q_{2}$: Ladungen

${\vec {v}}_{1}\,,\,{\vec {v}}_{2}$: Ladungen geschwindigkeit

${\vec {r}}\,$: Abstandsvektor der Ladungen

$r\,=\,|{\vec {r}}|\,$: Abstand der Ladungen

und

${\overrightarrow {\mathbf {B} }}=\mu _{0}{\overrightarrow {\mathbf {H} }}$

$\mu _{0}\varepsilon _{0}={\frac {1}{c^{2}}}$

Magnetische Feldstärke

Formelzeichen	Einheit
${\vec {H}}$ Magnetische Feldstärke	A/m
$[H]$	${\frac {A}{m}}$

$\mathbf {\vec {B}} =\mu _{0}(\mathbf {{\vec {H}}+{\vec {M}}} )=\mu \mathbf {\vec {H}}$

Lorenzkraft

${\boldsymbol {F}}_{L}=q\left({\boldsymbol {v}}\times {\boldsymbol {B}}\right)=I\,\mathbf {\ell } \times \mathbf {B}$

Flussdichte eines Leiters

Für einer unendliche lange Leiter gilt:

${\vec {B}}={\frac {\mu \;I}{2\pi \rho }}{\vec {e_{\rho }}}$

Oerstedsche Gesetz

$\oint {\vec {H}}\cdot d{\vec {s}}=\Theta$

Magnetischer Fluss

Formelzeichen	Einheit
$\Phi$ Magnetischer Fluss	Weber
$[\Phi ]=[U]\cdot [t]$	$Wb=V\cdot s$

$\Phi =\oint \limits _{\partial V}{\vec {B}}\cdot \mathrm {d} {\vec {A}}=\int \limits _{V}\nabla \cdot {\vec {B}}\;\mathrm {d} V$

Induktivität

Formelzeichen	Einheit
$L$ Induktivität	Henry
$[L]={\frac {[\Phi ]}{[I]}}$	$H={\frac {Wb}{A}}$

Induktivität ist verketterter magnetische Fluss durch Ström

Elektromagnetisches Feld

Braunsche Röhre

Ablenkung im Kondensator	$y_{1}={\frac {1}{4}}\cdot {\frac {U_{y}}{U_{A}}}\cdot {\frac {l^{2}}{d}}$	$U_{y}$ = Ablenkspannung $U_{A}$ = Beschleunigungsspannung $l$ = Kondensatorlänge $d$ = Plattenabstand $s$ = Abstand von Kondensator zum Schirm
Ablenkung außerhalb des Kondensator	$y_{2}={\frac {1}{2}}\cdot {\frac {U_{y}}{U_{A}}}\cdot {\frac {l\cdot s}{d}}$
Gesamte Ablenkung	$y={\frac {1}{2}}\cdot {\frac {U_{y}}{U_{A}}}\cdot {\frac {l}{d}}\left({\frac {l}{2}}+s\right)$

Wechselstromkreis

Stromstärke i im Wech- selstromkreis	Momentanwert: $i={\hat {i}}\cdot \sin \left(\omega \cdot t+\varphi _{0}\right)$ Effektivwert: $I={\frac {1}{\sqrt {2}}}\ {\hat {i}}\approx 0{,}707\ {\hat {i}}$	$\omega =2\pi \cdot f$ $i\$ = Momentanwert $t\$ = Zeit ${\hat {i}}$ = Scheitelwert $I\$ = Effektivwert $\varphi _{0}$ = Phasenwinkel $u\$ = Momentanwert ${\hat {u}}$ = Scheitelwert $U\$ = Effektivwert $\cos \varphi$ = Leistungsfaktor $\varphi$ = Phasenverschiebungswinkel
Spannung u im Wech- selstromkreis	Momentanwert: $u={\hat {u}}\cdot \sin \left(\omega \cdot t+\varphi _{0}\right)$ Effektivwert: $U={\frac {1}{\sqrt {2}}}\ {\hat {u}}\approx 0{,}707\ {\hat {u}}$
Scheinleistung S	$S=U\cdot I$
Wirkleistung P	$P=U\cdot I\cdot \cos \varphi$
Blindleistung Q	$Q=U\cdot I\cdot \sin \varphi$

Widerstände im Wechselstromkreis

kapazitiver Widerstand

$X_{C}={\frac {1}{2\cdot \pi \cdot f\cdot C}}$

$f\$ = Frequenz $C\$ = Kapazität

induktiver Widerstand

$X_{L}={2\cdot \pi \cdot f\cdot L}$

$f\$ = Frequenz $L\$ = Induktivität

Transformator

${\frac {U_{1}}{U_{2}}}={\frac {N_{1}}{N_{2}}}$

${\frac {I_{1}}{I_{2}}}={\frac {N_{2}}{N_{1}}}$

${\frac {I_{1}}{I_{2}}}={\frac {U_{2}}{U_{1}}}$

---

$U_{1}$ = Spannung in der Primärspule
$U_{2}$ = Spannung in der Sekundärspule
$N_{1}$ = Windungen der Primärspule
$N_{2}$ = Windungen der Sekundärspule
$I_{1}$ = Stromstärke in der Primärspule
$I_{2}$ = Stromstärke in der Sekundärspule

Weblinks

• http://www.elektrotechnik-fachwissen.de/
• http://www.elektronik-kompendium.de/
• http://www.formelsammlung24.de/
• Formelsammlung für TI Grafiktaschenrechner - speziell für Elektroberufe

Formelsammlung Physik

Klassische Mechanik |  Wellenlehre |  Optik |  Akustik |  Wärmelehre |  Elektrizitätslehre |  Elektrodynamik |  Atom- und Kernphysik |  Quantenphysik |  Thermodynamik 2 |  Relativitätstheorie |  Astronomie |  Hydrostatik |  Tabellen