Zu berechnen ist ein Beulfeld in einem 33m langen Zweifeldträger. Um die Tragfähigkeit zu erhöhen, wird eine Längssteife bei der Stütze in 0,4m Höhe eingebaut. Da diese Längssteife im Feld woanders gebraucht wird, wird eine Quersteife 7,1m von der Stütze entfernt eingebaut. Dort endet die Längssteife.
Maße des Trägers
Alle Eingangsdaten für das zweite Rechenbeispiel
oberer Flansch
bf2 =0,37m
tf2 =11mm
Quersteifen
a'= 7,1m
unterer Flansch
bf1 =0,53m
tf1 =17mm
Träger links
l1 = 33m
Steg
hw =2,9m
tw =9mm
Träger rechts
l2 = 33m
Steife
bsl =0,1m
tsl =8mm
Belastung
qEd = 55,4kN/m
untere Steife
hw1 =0,4m
Streckgrenze Eurocode
fyk = 235N/mm²
Streckgrenze DIN
fyk = 240N/mm²
Teilsicherheitsbeiwert
γM0 = 1
Teilsicherheitsbeiwert DIN
γM = 1,1
Teilsicherheitsbeiwert
γM0 = 1
Bezugsspannung
σE = 1,83N/mm²
ε= 1
η= 1,2
Schnittgrößen
Schubverzerrung
b0 = 0,37/2= 0,185
b0 = 0,53/2= 0,265 Le = 0,25∙(L1 + L2 )
Le = 16,5m
K
=
a
0
⋅
b
0
L
e
=
1
⋅
0,265
16
,
5
{\displaystyle K={\frac {a_{0}\cdot b_{0}}{L_{e}}}={\frac {1\cdot 0{,}265}{16{,}5}}}
K= 0,016 <0,02
ß=1 Schubverzerrung tritt nicht auf
Grenz c/t
c
t
<
14
c
t
=
0
,
53
−
0,009
2
⋅
0,017
{\displaystyle {\frac {c}{t}}<14{\frac {c}{t}}={\frac {0{,}53-0{,}009}{2\cdot 0{,}017}}}
15
,
32
≮
14
{\displaystyle 15{,}32\not <14}
Beulnachweis erforderlich
kσ = 0,43
λ
¯
p
=
b
t
⋅
28
,
43
⋅
ϵ
⋅
k
σ
{\displaystyle {\overline {\lambda }}_{p}={\frac {b}{t\cdot 28{,}43\cdot \epsilon \cdot {\sqrt {k_{\sigma }}}}}}
λ
¯
p
=
0
,
53
⋅
0
,
5
0,017
⋅
28
,
43
⋅
1
⋅
0
,
43
{\displaystyle {\overline {\lambda }}_{p}={\frac {0{,}53\cdot 0{,}5}{0{,}017\cdot 28{,}43\cdot 1\cdot {\sqrt {0{,}43}}}}}
λ
¯
p
=
0,836
{\displaystyle {\overline {\lambda }}_{p}=0{,}836}
ρ
=
λ
¯
p
−
0,188
λ
¯
p
2
{\displaystyle \rho ={\frac {{\overline {\lambda }}_{p}-0{,}188}{{\overline {\lambda }}_{p}^{2}}}}
ρ
=
0,836
−
0,188
0,836
2
{\displaystyle \rho ={\frac {0{,}836-0{,}188}{0{,}836^{2}}}}
ρ= 0,927 bf := bf ∙ρ= 0,53∙0,927
bf := 0,4915 Mit der kürzeren Länge des Druckflansches wird gerechnet.
As = bf2 ∙tf2 + hw ∙tw + bf1 ∙tf1
As = 0,37∙0,011 + 0,009∙2,9 + 0,4915∙0,017
As = 0,03852m² Der Schwerpunkt hs wird vom unteren Stegende aus nach oben gemessen.
h
s
=
b
f
2
⋅
t
f
2
⋅
(
h
w
+
0
,
5
⋅
t
f
2
)
+
0
,
5
⋅
h
w
2
⋅
t
w
−
0
,
5
⋅
b
f
1
⋅
t
f
1
2
A
{\displaystyle h_{s}={\frac {b_{f2}\cdot t_{f2}\cdot (h_{w}+0{,}5\cdot t_{f2})+0{,}5\cdot h_{w^{2}}\cdot t_{w}-0{,}5\cdot b_{f1}\cdot t_{f1^{2}}}{A}}}
h
s
=
0
,
37
⋅
0,011
⋅
(
2
,
9
+
0
,
5
⋅
0,011
)
+
0
,
5
⋅
2
,
9
2
⋅
0,009
−
0,491
5
⋅
0,017
2
/
2
0,038
52
{\displaystyle h_{s}={\frac {0{,}37\cdot 0{,}011\cdot (2{,}9+0{,}5\cdot 0{,}011)+0{,}5\cdot 2{,}9^{2}\cdot 0{,}009-0{,}4915\cdot 0{,}017^{2}/2}{0{,}03852}}}
h
s
=
0,011
83
+
0,037
8
−
7
,
65
⋅
10
−
5
0,038
52
{\displaystyle h_{s}={\frac {0{,}01183+0{,}0378-7{,}65\cdot 10^{-5}}{0{,}03852}}}
hs = 1,2874m Das Flächenträgheitsmoment I besteht aus 3 Steineranteilen und 3 Eigenanteilen.
I
=
∑
(
3
E
i
g
e
n
b
f
1
⋅
t
f
1
⋅
(
h
s
+
0
,
5
⋅
t
f
1
)
2
b
f
2
⋅
t
f
2
⋅
(
h
w
−
h
s
+
0
,
5
⋅
t
f
2
)
2
h
w
⋅
t
w
⋅
(
0
,
5
⋅
t
w
−
h
s
)
2
)
{\displaystyle I=\sum {\begin{pmatrix}3Eigen\\b_{f1}\cdot t_{f1}\cdot (h_{s}+0{,}5\cdot t_{f1})^{2}\\b_{f2}\cdot t_{f2}\cdot (h_{w}-h_{s}+0{,}5\cdot t_{f2})^{2}\\h_{w}\cdot t_{w}\cdot (0{,}5\cdot t_{w}-h_{s})^{2}\end{pmatrix}}}
I
=
∑
(
0,018
23
0,491
5
⋅
0,017
⋅
(
1,287
4
+
0
,
5
⋅
0,017
)
2
0
,
37
⋅
0,011
⋅
(
2
,
9
−
1,287
4
+
0,017
⋅
0
,
5
)
2
2
,
9
⋅
0,009
⋅
(
0
,
5
⋅
2
,
9
−
1,287
)
2
)
{\displaystyle I=\sum {\begin{pmatrix}0{,}01823\\0{,}4915\cdot 0{,}017\cdot (1{,}2874+0{,}5\cdot 0{,}017)^{2}\\0{,}37\cdot 0{,}011\cdot (2{,}9-1{,}2874+0{,}017\cdot 0{,}5)^{2}\\2{,}9\cdot 0{,}009\cdot (0{,}5\cdot 2{,}9-1{,}287)^{2}\end{pmatrix}}}
I= 10-3 ∙(18,23 + 14,03 + 10,65 + 0,69)
I= 0,04367m4 Spannung σ2 im oberen Stegende
σ
2
=
−
M
⋅
z
I
+
N
A
=
−
7541
⋅
(
2
,
9
−
1,287
4
)
0,043
67
+
0
0,038
53
{\displaystyle \sigma _{2}={\frac {-M\cdot z}{I}}+{\frac {N}{A}}={\frac {-7541\cdot (2{,}9-1{,}2874)}{0{,}04367}}+{\frac {0}{0{,}03853}}}
σ2 = 278 - 0
σ2 = 278,5N/mm² Spannung σ1 im unteren Stegende
σ
1
=
−
7541
⋅
1,287
4
0,043
67
{\displaystyle \sigma _{1}={\frac {-7541\cdot 1{,}2874}{0{,}04367}}}
σ1 = - 222,3N/mm² Spannungsnulllinie S
S
=
h
w
⋅
(
1
−
σ
2
σ
2
−
σ
1
)
=
2
,
9
⋅
(
1
−
278
,
5
278
,
5
+
222
,
3
)
{\displaystyle S=h_{w}\cdot \left(1-{\frac {\sigma _{2}}{\sigma _{2}-\sigma _{1}}}\right)=2{,}9\cdot \left(1-{\frac {278{,}5}{278{,}5+222{,}3}}\right)}
S= 1,2874m Die Spannungsnulllinie geht durch den Schwerpunkt, weil keine Normalkraft wirkt.
Spannung σsl in der Steife
σ
s
l
=
−
M
⋅
z
I
+
N
A
{\displaystyle \sigma _{sl}={\frac {-M\cdot z}{I}}+{\frac {N}{A}}}
σ
s
l
=
−
M
⋅
(
S
−
h
w
1
)
I
+
N
A
{\displaystyle \sigma _{sl}={\frac {-M\cdot (S-h_{w1})}{I}}+{\frac {N}{A}}}
σ
s
l
=
−
7541
⋅
(
1,287
4
−
0
,
4
)
0,043
67
{\displaystyle \sigma _{sl}={\frac {-7541\cdot (1{,}2874-0{,}4)}{0{,}04367}}}
σsl = - 153,2N/mm²
Jetzt wird für beide Einzelfelder der Beulnachweis parallel geführt. Die angrenzenden Stegteile werden mit dem Abminderungsfaktor multipliziert.
b= hw1 - tsl /2= 0,4 - 0,004
b= MIN(S;hw ) - hw1 - tsl /2= 1,2874 - 0,4 - 0,004
b= 0,396m
b= 0,8834m
Randspannungsverhältnis ψ
Ψ
=
σ
s
l
σ
1
=
−
153
−
222
{\displaystyle \Psi ={\frac {\sigma _{sl}}{\sigma _{1}}}=-{\frac {153}{-222}}}
Ψ
=
σ
2
σ
s
l
=
278
−
153
{\displaystyle \Psi ={\frac {\sigma _{2}}{\sigma _{sl}}}={\frac {278}{-153}}}
ψ= 0,689
ψ= - 1,817
Beulwert kσ (Eurocode 1993-1-5 Tabelle 4.1)
k
σ
=
8
,
2
1
,
05
+
Ψ
=
8
,
2
1
,
05
+
0,689
{\displaystyle k_{\sigma }={\frac {8{,}2}{1{,}05+\Psi }}={\frac {8{,}2}{1{,}05+0{,}689}}}
kσ =5,98∙(1 - ψ)²σ =5,98∙(1 + 1,817)²
kσ = 4,715
kσ = 47,46
Beulschlankheitsgrad
λ
¯
p
{\displaystyle {\overline {\lambda }}_{p}}
λ
¯
p
=
b
t
w
⋅
28
,
43
⋅
ϵ
⋅
k
σ
{\displaystyle {\overline {\lambda }}_{p}={\frac {b}{t_{w}\cdot 28{,}43\cdot \epsilon \cdot {\sqrt {k_{\sigma }}}}}}
λ
¯
p
=
b
t
w
⋅
28
,
43
⋅
ϵ
⋅
k
σ
{\displaystyle {\overline {\lambda }}_{p}={\frac {b}{t_{w}\cdot 28{,}43\cdot \epsilon \cdot {\sqrt {k_{\sigma }}}}}}
λ
¯
p
=
0,396
0,009
⋅
28
,
43
⋅
1
⋅
4,715
{\displaystyle {\overline {\lambda }}_{p}={\frac {0{,}396}{0{,}009\cdot 28{,}43\cdot 1\cdot {\sqrt {4{,}715}}}}}
λ
¯
p
=
0,883
4
0,009
⋅
28
,
43
⋅
1
⋅
47
,
46
{\displaystyle {\overline {\lambda }}_{p}={\frac {0{,}8834}{0{,}009\cdot 28{,}43\cdot 1\cdot {\sqrt {47{,}46}}}}}
λ
¯
p
=
0,712
{\displaystyle {\overline {\lambda }}_{p}=0{,}712}
λ
¯
p
=
0,501
{\displaystyle {\overline {\lambda }}_{p}=0{,}501}
Abminderungsfaktor ρ(Eurocode 1993-1-5 Gleichung 4.2)
λ
¯
p
=
b
t
w
⋅
28
,
43
⋅
ϵ
⋅
k
σ
{\displaystyle {\overline {\lambda }}_{p}={\frac {b}{t_{w}\cdot 28{,}43\cdot \epsilon \cdot {\sqrt {k_{\sigma }}}}}}
λ
¯
p
=
b
t
w
⋅
28
,
43
⋅
ϵ
⋅
k
σ
{\displaystyle {\overline {\lambda }}_{p}={\frac {b}{t_{w}\cdot 28{,}43\cdot \epsilon \cdot {\sqrt {k_{\sigma }}}}}}
ρ
=
0,712
−
0,055
⋅
(
3
+
0,689
)
0,712
2
{\displaystyle \rho ={\frac {0{,}712-0{,}055\cdot (3+0{,}689)}{0{,}712^{2}}}}
ρ
=
0,501
−
0,055
⋅
(
3
−
18
,
17
)
0,501
2
{\displaystyle \rho ={\frac {0{,}501-0{,}055\cdot (3-18{,}17)}{0{,}501^{2}}}}
ρ = 1
ρ = 1
Bruttobreiten Von dem druckbeanspruchten Stegteil wird berechnet,
b
u
=
2
⋅
b
5
−
Ψ
=
2
⋅
0,396
5
−
0,689
{\displaystyle b_{u}={\frac {2\cdot b}{5-\Psi }}={\frac {2\cdot 0{,}396}{5-0{,}689}}}
b
u
=
2
⋅
b
5
−
Ψ
=
2
⋅
0,883
4
5
−
0
{\displaystyle b_{u}={\frac {2\cdot b}{5-\Psi }}={\frac {2\cdot 0{,}8834}{5-0}}}
bu = 0,1837
bu = 0,3533
bo = b - bu
bo = b - bu
bo = 0,396 - 0,1837
bo = 0,8834 - 0,3533
bo = 0,2122
bo = 0,53007
wirksame Breiten
bu1,eff = bu ∙ρ = 0,1837∙1
bu2,eff = bu ∙ρ = 0,3533∙1
bu1,eff = 0,1837
bu2,eff = 0,3533
bo1,eff = bo ∙ρ = 0,2122∙1
bo2,eff = bo ∙ρ = 0,53007∙1
bo1,eff = 0,2122
bo2,eff = 0,53007
Σbeff = 0,2122 + 0,1837
Σbeff = 0,53 + 0,3533
Σbeff = 0,396
Σbeff = 0,8834
Verlust= b - Σbeff
Verlust= b - Σbeff
Verlust= 0,396 - 0,396
Verlust= 0,8834 - 0,8834
Verlust= 0m
Verlust= 0m
Es geht nichts durch Einzelfeldbeulen verloren. Trotzdem wird so weiter gerechnet, als wäre ρ ein anderer Wert als 1.
Bruttobreiten Querschnittswerte der Steife
Asl = tw ∙(b1o + b2u + tsl ) + bsl ∙tsl
Asl = 0,009∙(0,2122 + 0,3534 + 0,008) + 0,1∙0,008
Asl = 0,005963
x
s
l
=
t
s
l
⋅
b
s
l
⋅
(
b
s
l
/
2
+
t
w
/
2
)
A
s
l
{\displaystyle x_{sl}={\frac {t_{sl}\cdot b_{sl}\cdot (b_{sl}/2+t_{w}/2)}{A_{sl}}}}
x
s
l
=
0,008
⋅
0
,
1
⋅
(
0
,
05
+
0,004
5
)
0,005
963
{\displaystyle x_{sl}={\frac {0{,}008\cdot 0{,}1\cdot (0{,}05+0{,}0045)}{0{,}005963}}}
xsl = 0,007312 Isl = 2 Eigen + 2 Steiner
I
s
l
=
∑
(
t
w
3
⋅
(
b
e
f
f
1
o
+
b
e
f
f
2
u
+
t
s
l
)
/
12
b
s
l
3
⋅
t
s
l
/
12
t
w
⋅
(
b
e
f
f
1
o
+
b
e
f
f
2
u
+
t
s
l
)
⋅
x
s
l
2
b
s
l
⋅
t
s
l
⋅
(
b
s
l
/
2
+
t
w
/
2
−
x
s
l
)
2
)
{\displaystyle I_{sl}=\sum {\begin{pmatrix}t_{w}^{3}\cdot (b_{eff1o}+b_{eff2u}+t_{sl})/12\\b_{sl}^{3}\cdot t_{sl}/12\\t_{w}\cdot (b_{eff1o}+b_{eff2u}+t_{sl})\cdot x_{sl}^{2}\\b_{sl}\cdot t_{sl}\cdot (b_{sl}/2+t_{w}/2-x_{sl})^{2}\end{pmatrix}}}
I
s
l
=
∑
(
0,009
3
⋅
(
0,573
6
)
/
12
0
,
1
3
⋅
0,008
/
12
0,009
⋅
(
0,573
6
)
⋅
0,007
312
2
0
,
1
⋅
0,008
⋅
(
0
,
05
+
0,004
5
−
0,007
312
)
2
)
{\displaystyle I_{sl}=\sum {\begin{pmatrix}0{,}009^{3}\cdot (0{,}5736)/12\\0{,}1^{3}\cdot 0{,}008/12\\0{,}009\cdot (0{,}5736)\cdot 0{,}007312^{2}\\0{,}1\cdot 0{,}008\cdot (0{,}05+0{,}0045-0{,}007312)^{2}\end{pmatrix}}}
Isl = (0,035 + 0,666 + 0,276 + 1,781)∙10-6
Isl = 2,759∙10-6 m4 Beulen des Gesamtfeldes plattenartiges Verhalten
b1 = hw1 = 0,4
b= B1 = hw = 2,9
b2 = B1 - hw = 2,5
a
c
=
4
,
33
⋅
I
s
l
,
1
⋅
b
1
2
⋅
b
2
2
t
3
⋅
b
4
{\displaystyle a_{c}=4{,}33\cdot {\sqrt[{4}]{\frac {I_{sl{,}1}\cdot b_{1}^{2}\cdot b_{2}^{2}}{t^{3}\cdot b}}}}
a
c
=
4
,
33
⋅
2,759
⋅
0
,
4
2
⋅
2
,
5
2
10
6
⋅
2
,
9
⋅
0,009
3
4
{\displaystyle a_{c}=4{,}33\cdot {\sqrt[{4}]{\frac {2{,}759\cdot 0{,}4^{2}\cdot 2{,}5^{2}}{10^{6}\cdot 2{,}9\cdot 0{,}009^{3}}}}}
ac = 4,628m ac < a=7,1m
σ
c
r
,
s
l
=
π
2
⋅
E
⋅
I
s
l
,
1
A
s
l
,
1
⋅
a
2
+
E
⋅
t
3
⋅
b
⋅
a
2
4
⋅
π
2
⋅
(
1
−
ν
2
)
⋅
A
s
l
,
1
⋅
b
1
2
⋅
b
2
2
{\displaystyle \sigma _{cr{,}sl}={\frac {\pi ^{2}\cdot E\cdot I_{sl{,}1}}{A_{sl{,}1}\cdot a^{2}}}+{\frac {E\cdot t^{3}\cdot b\cdot a^{2}}{4\cdot \pi ^{2}\cdot (1-\nu ^{2})\cdot A_{sl{,}1}\cdot b_{1}^{2}\cdot b_{2}^{2}}}}
c
σ
c
r
,
s
l
=
1
,
05
⋅
E
A
s
l
,
1
⋅
I
s
l
,
1
⋅
t
3
⋅
b
b
1
⋅
b
2
{\displaystyle \sigma _{cr{,}sl}={\frac {1{,}05\cdot E}{A_{sl{,}1}}}\cdot {\frac {\sqrt {I_{sl{,}1}\cdot t^{3}\cdot b}}{b_{1}\cdot b_{2}}}}
c
σ
c
r
,
s
l
=
10
,
5
⋅
210
⋅
10
9
0,005
963
⋅
2,759
⋅
10
−
6
⋅
0,009
3
⋅
2
,
9
0
,
4
⋅
2
,
5
{\displaystyle \sigma _{cr{,}sl}={\frac {10{,}5\cdot 210\cdot 10^{9}}{0{,}005963}}\cdot {\frac {\sqrt {2{,}759\cdot 10^{-6}\cdot 0{,}009^{3}\cdot 2{,}9}}{0{,}4\cdot 2{,}5}}}
σcr,sl = 3,6978∙1013 ∙2,4∙10-6 = 8,93∙107 N/m²
σcr,sl = 89,3∙N/mm² Die Beulspannung darf erhöht werden. Dabei wird die ideale Beulspannung auf den Ort der Steife bezogen.
σ
c
r
,
p
=
σ
c
r
,
s
l
⋅
S
S
−
h
w
1
=
8
,
93
⋅
1,287
4
⋅
10
7
12,874
−
0
,
4
{\displaystyle \sigma _{cr{,}p}={\frac {\sigma _{cr{,}sl}\cdot S}{S-h_{w1}}}={\frac {8{,}93\cdot 1{,}2874\cdot 10^{7}}{12{,}874-0{,}4}}}
σcr,p = 129,56N/mm² Ac = ΣAsl,eff + Σρ∙bc,loc ∙b
Ac = 0,005963
Ac,eff,loc = Asl + (beffo1 + tsl + beffu2 )∙tw
Ac,eff,loc = 0,0008 + (0,2122 + 0,008 + 0,353)∙0,009
Ac,eff,loc = 0,005963
β
A
,
c
=
A
c
,
e
f
f
,
l
o
c
A
c
=
1
{\displaystyle \beta _{A{,}c}={\frac {A_{c{,}eff{,}loc}}{A_{c}}}=1}
λ
¯
p
=
β
A
c
⋅
f
y
k
/
σ
c
,
r
c
{\displaystyle {\overline {\lambda }}_{p}={\sqrt {\beta _{Ac}\cdot f_{yk}/\sigma _{c{,}rc}}}}
λ
¯
p
=
235
/
129
,
56
{\displaystyle {\overline {\lambda }}_{p}={\sqrt {235/129{,}56}}}
λ
¯
p
=
1,347
{\displaystyle {\overline {\lambda }}_{p}=1{,}347}
Ψ
=
278
,
5
−
222
,
3
=
−
1,252
{\displaystyle \Psi ={\frac {278{,}5}{-222{,}3}}=-1{,}252}
ρ
=
λ
¯
p
−
0,055
⋅
(
3
+
Ψ
)
λ
¯
p
2
{\displaystyle \rho ={\frac {{\overline {\lambda }}_{p}-0{,}055\cdot (3+\Psi )}{{\overline {\lambda }}_{p}^{2}}}}
ρ
=
1,347
−
0,055
⋅
(
3
−
1,252
)
1,347
2
{\displaystyle \rho ={\frac {1{,}347-0{,}055\cdot (3-1{,}252)}{1{,}347^{2}}}}
ρ= 0,68952 Knickstabverhalten
Ac,eff = ρ∙Ac,eff,loc + bedge,eff ∙t
Ac,eff = 0,6895∙0,005963 + 0,009∙(0,1837 + 0,53007)
Ac,eff = 0,01053 Asl = tw ∙(b1o + b2u + tsl ) + bsl ∙tsl = 0,005936
Asl,1,eff = tw ∙(b1o,eff + b2u,eff + tsl ) + bsl ∙tsl = 0,005936
β
A
,
c
=
A
s
l
,
1
,
e
f
f
A
s
l
=
1
{\displaystyle \beta _{A{,}c}={\frac {A_{sl{,}1{,}eff}}{A_{sl}}}=1}
Isl = 2,759∙10-6 m4
σ
c
r
,
s
l
=
π
2
⋅
E
⋅
I
s
l
A
s
l
⋅
a
2
{\displaystyle \sigma _{cr{,}sl}={\frac {\pi ^{2}\cdot E\cdot I_{sl}}{A_{sl}\cdot a^{2}}}}
σ
c
r
,
s
l
=
π
2
⋅
210
⋅
10
9
⋅
2,759
⋅
10
−
6
0,005
963
⋅
7
,
1
2
{\displaystyle \sigma _{cr{,}sl}={\frac {\pi ^{2}\cdot 210\cdot 10^{9}\cdot 2{,}759\cdot 10^{-6}}{0{,}005963\cdot 7{,}1^{2}}}}
σcr,sl = 19,02N/mm²
σ
c
r
,
c
=
19
,
02
⋅
S
S
−
h
w
1
=
19
,
02
⋅
1,287
4
1,287
4
−
0
,
4
{\displaystyle \sigma _{cr{,}c}={\frac {19{,}02\cdot S}{S-h_{w1}}}={\frac {19{,}02\cdot 1{,}2874}{1{,}2874-0{,}4}}}
σcr,c = 27,6N/mm²
λ
¯
p
=
β
A
c
⋅
f
y
k
/
σ
c
,
r
c
{\displaystyle {\overline {\lambda }}_{p}={\sqrt {\beta _{Ac}\cdot f_{yk}/\sigma _{c{,}rc}}}}
λ
¯
p
=
235
/
27
,
6
{\displaystyle {\overline {\lambda }}_{p}={\sqrt {235/27{,}6}}}
λ
¯
p
=
2,918
{\displaystyle {\overline {\lambda }}_{p}=2{,}918}
Definition der Abstände e1 und e2 e2 = xsl = 0,00731
e1 =(tw + bsl )/2 – xsl
e1 =(0,009 + 0,1)/2 – 0,00731
e1 =0,04719
e= MAX(e1 ;e2 )
e= 0,04719
α= 0,49 für offene Querschnitte
i
=
I
s
l
,
1
A
s
l
,
1
=
2,759
10
6
⋅
0,005
963
{\displaystyle i={\sqrt {\frac {I_{sl{,}1}}{A_{sl{,}1}}}}={\sqrt {\frac {2{,}759}{10^{6}\cdot 0{,}005963}}}}
i= 0,02151m αe = α + 0,09e/i(Eurocode 1993-1-5 Gleichung 4.12)
αe = 0,49 + 0,09∙0,04919/0,02151
αe = 0,687
k
=
0
,
5
⋅
(
1
+
α
e
⋅
(
λ
¯
p
−
0
,
2
)
+
λ
¯
p
2
)
{\displaystyle k=0{,}5\cdot \left(1+\alpha _{e}\cdot \left({\overline {\lambda }}_{p}-0{,}2\right)+{\overline {\lambda }}_{p^{2}}\right)}
k= 0,5∙(1 + 0,687∙(2,918 - 0,2) + 2,918²)
k= 5,69
χ
c
=
M
I
N
(
1
;
1
k
+
k
2
−
λ
¯
p
2
)
{\displaystyle \chi _{c}=MIN\left(1;{\frac {1}{k+{\sqrt {k^{2}-{\overline {\lambda }}_{p^{2}}}}}}\right)}
χ
c
=
M
I
N
(
1
;
1
5
,
69
+
5
,
69
2
−
2,918
2
)
{\displaystyle \chi _{c}=MIN\left(1;{\frac {1}{5{,}69+{\sqrt {5{,}69^{2}-2{,}918^{2}}}}}\right)}
χc = 0,09453 Interaktion
ξ
=
(
σ
c
r
,
p
σ
c
r
,
c
−
1
)
{\displaystyle \xi =\left({\frac {\sigma _{cr{,}p}}{\sigma _{cr{,}c}}}-1\right)}
ξ
=
(
129
,
56
27
,
16
−
1
)
{\displaystyle \xi =\left({\frac {129{,}56}{27{,}16}}-1\right)}
ξ= 1 ρc = (ρ - χc )∙ ξ∙(2 - ξ) + χc (Eurocode 1993-1-5 Gleichung 4.1)3
ρc = (0,68952 - 0,09453)∙1∙(2 - 1) + 0,09453
ρc = 0,68952 Notwendige Maße für die Quertschnittswerte Ac,eff = 0,01053 tw,red = tw ∙ρc = 0,009∙0,68952
tw,red = 0,006206
tsl,red = tsl ∙ρc = 0,008∙0,68952
tsl,red = 0,005516
A
=
∑
(
b
f
2
⋅
t
f
2
(
Z
u
g
s
t
e
g
+
b
e
f
f
2
o
)
⋅
h
w
(
b
e
f
f
2
u
+
t
s
l
+
b
e
f
f
1
o
)
⋅
h
w
b
e
f
f
1
u
⋅
h
w
b
f
1
⋅
t
f
1
)
{\displaystyle A=\sum {\begin{pmatrix}b_{f2}\cdot t_{f2}\\(Zugsteg+b_{eff2o})\cdot h_{w}\\(b_{eff2u}+t_{sl}+b_{eff1o})\cdot h_{w}\\b_{eff1u}\cdot h_{w}\\b_{f1}\cdot t_{f1}\end{pmatrix}}}
A
=
∑
(
0
,
37
⋅
0,011
(
1,612
+
0
,
53
)
⋅
0,009
(
0,353
3
+
0,008
+
0,212
2
)
⋅
0,009
0,183
7
⋅
0,009
0,491
5
⋅
0,017
)
{\displaystyle A=\sum {\begin{pmatrix}0{,}37\cdot 0{,}011\\(1{,}612+0{,}53)\cdot 0{,}009\\(0{,}3533+0{,}008+0{,}2122)\cdot 0{,}009\\0{,}1837\cdot 0{,}009\\0{,}4915\cdot 0{,}017\end{pmatrix}}}
Grafik 12 notwendige Maße für die Querschnittswerte
Schwerpunkt
bs = beff2u + tsl + beff1o = 0,3533 + 0,008 + 0,2122
bs = 0,573
bz = Zugsteg + beff2o = 1,612 + 0,53007
bz = 2,142
A
⋅
h
s
=
∑
(
−
b
f
1
⋅
t
f
1
2
/
2
b
e
f
f
u
1
2
)
⋅
t
w
/
2
b
f
2
⋅
t
f
2
⋅
(
h
w
+
t
f
2
/
2
)
b
s
⋅
t
w
,
r
e
d
⋅
(
b
s
/
2
+
b
e
f
f
1
u
)
b
z
⋅
t
w
⋅
(
h
w
−
b
z
/
2
)
)
{\displaystyle A\cdot h_{s}=\sum {\begin{pmatrix}-b_{f1}\cdot t_{f1^{2}}/2\\b_{effu1}^{2})\cdot t_{w}/2\\b_{f2}\cdot t_{f2}\cdot (h_{w}+t_{f2}/2)\\b_{s}\cdot t_{w{,}red}\cdot (b_{s}/2+b_{eff1u})\\b_{z}\cdot t_{w}\cdot (h_{w}-b_{z}/2)\end{pmatrix}}}
A
⋅
h
s
=
∑
(
−
0,491
5
⋅
0,017
2
/
2
0
,
37
⋅
0,011
⋅
(
2
,
9
+
0,011
/
2
)
0,183
2
2
⋅
0,009
/
2
0,573
⋅
0,006
206
⋅
(
0,573
/
2
+
0,183
2
)
2,142
⋅
0,009
⋅
(
2
,
9
−
2,142
/
2
)
)
{\displaystyle A\cdot h_{s}=\sum {\begin{pmatrix}-0{,}4915\cdot 0{,}017^{2}/2\\0{,}37\cdot 0{,}011\cdot (2{,}9+0{,}011/2)\\0{,}1832^{2}\cdot 0{,}009/2\\0{,}573\cdot 0{,}006206\cdot (0{,}573/2+0{,}1832)\\2{,}142\cdot 0{,}009\cdot (2{,}9-2{,}142/2)\end{pmatrix}}}
hs = 1,3229 Ieff = 5 Steineranteile + 5 Eigenanteile
I
e
f
f
=
∑
(
0,491
5
⋅
0,017
3
/
12
0,183
7
3
⋅
0,009
/
12
0,573
3
⋅
0,006
206
/
12
2,142
3
⋅
0,009
/
12
0
,
37
⋅
0,011
3
/
12
)
+
∑
(
0,573
⋅
0,006
2
⋅
0,851
8
2
0,183
7
⋅
0,009
⋅
1
,
23
2
0,008
3555
⋅
1
,
33
2
2,142
⋅
0,009
⋅
0,506
2
0,004
07
⋅
1,582
5
2
)
{\displaystyle I_{eff}=\sum {\begin{pmatrix}0{,}4915\cdot 0{,}017^{3}/12\\0{,}1837^{3}\cdot 0{,}009/12\\0{,}573^{3}\cdot 0{,}006206/12\\2{,}142^{3}\cdot 0{,}009/12\\0{,}37\cdot 0{,}011^{3}/12\end{pmatrix}}+\sum {\begin{pmatrix}0{,}573\cdot 0{,}0062\cdot 0{,}8518^{2}\\0{,}1837\cdot 0{,}009\cdot 1{,}23^{2}\\0{,}0083555\cdot 1{,}33^{2}\\2{,}142\cdot 0{,}009\cdot 0{,}506^{2}\\0{,}00407\cdot 1{,}5825^{2}\end{pmatrix}}}
Ieff = 0,00745 + 0,035
Ieff = 0,04251m4
wirksame Widerstandmomente
W
e
f
f
u
=
I
e
f
f
z
=
I
e
f
f
h
s
e
f
f
+
b
f
1
/
2
{\displaystyle W_{effu}={\frac {I_{eff}}{z}}={\frac {I_{eff}}{h_{seff}+b_{f1}/2}}}
W
e
f
f
o
=
I
e
f
f
z
=
I
e
f
f
h
w
−
h
s
e
f
f
+
b
f
2
/
2
{\displaystyle W_{effo}={\frac {I_{eff}}{z}}={\frac {I_{eff}}{h_{w}-h_{seff}+b_{f2}/2}}}
W
e
f
f
u
=
0,042
5
1,322
9
+
0,017
/
2
{\displaystyle W_{effu}={\frac {0{,}0425}{1{,}3229+0{,}017/2}}}
W
e
f
f
o
=
0,042
5
2
,
9
−
1,322
9
+
0,011
/
2
{\displaystyle W_{effo}={\frac {0{,}0425}{2{,}9-1{,}3229+0{,}011/2}}}
Weffu = 0,03193m³
Weffo = 0,02686m³
MRd,u = Weffu •fyd
MRd,o = Weffo •fyd
MRd,u = 0,03193∙235000
MRd,o = 0,02686∙235000
MRd,u = 7503,1kNm
MRd,o = 6312,3kNm
MEd = 7541,325kNm Nachweis, ob die Stegdicken weiter verringert werden müssen.
σ
c
o
m
,
E
d
=
M
⋅
z
I
=
M
⋅
(
h
s
,
e
f
f
−
b
f
1
)
I
{\displaystyle \sigma _{com{,}Ed}={\frac {M\cdot z}{I}}={\frac {M\cdot (h_{s{,}eff}-b_{f1})}{I}}}
σ
c
o
m
,
E
d
=
7,541
325
⋅
(
1,322
9
−
0
,
4
)
0,042
51
{\displaystyle \sigma _{com{,}Ed}={\frac {7{,}541325\cdot (1{,}3229-0{,}4)}{0{,}04251}}}
σcom,Ed = 163,7N/mm²
σ
c
o
m
,
E
d
ρ
c
⋅
f
y
/
γ
M
=
163
,
7
0,689
52
⋅
235
{\displaystyle {\frac {\sigma _{com{,}Ed}}{\rho _{c}\cdot f_{y}/\gamma _{M}}}={\frac {163{,}7}{0{,}68952\cdot 235}}}
1 < 1
keine weitere Abminderung erforderlich
Nachweise
M
E
d
M
R
d
,
u
=
M
E
d
W
e
f
f
u
⋅
f
y
d
=
7541,325
7503
,
1
{\displaystyle {\frac {M_{Ed}}{M_{Rd{,}u}}}={\frac {M_{Ed}}{W_{effu}\cdot f_{yd}}}={\frac {7541{,}325}{7503{,}1}}}
1,005
≮
1
{\displaystyle 1{,}005\not <1}
M
E
d
M
R
d
,
o
=
7541,325
6312
,
3
{\displaystyle {\frac {M_{Ed}}{M_{Rd{,}o}}}={\frac {7541{,}325}{6312{,}3}}}
1,194
7
≮
1
{\displaystyle 1{,}1947\not <1}
Nachweis nicht erfüllt
genauerer Nachweis mit Abstand
x
=
M
I
N
(
h
w
−
h
1
2
;
0
,
4
⋅
a
)
{\displaystyle x=MIN\left({\frac {h_{w}-h_{1}}{2}};0{,}4\cdot a\right)}
x
=
M
I
N
(
2
,
9
−
0
,
4
2
;
0
,
4
⋅
7
,
1
)
{\displaystyle x=MIN\left({\frac {2{,}9-0{,}4}{2}};0{,}4\cdot 7{,}1\right)}
x= 1,25m abgemindertes Moment
MEd = MEd,N - x∙V + x²∙q/2
MEd = 7541,325 - 1,25∙1142,625 + 1,25²∙55,4/2
MEd = 6156,325 Nachweis
M
E
d
M
R
d
,
u
=
6156,325
7503
,
1
{\displaystyle {\frac {M_{Ed}}{M_{Rd{,}u}}}={\frac {6156{,}325}{7503{,}1}}}
0,8205 < 1 Nachweis erfüllt
Da der Nachweis mit Abstand geführt wurde, muss über der Stütze ein zusätzlicher Klasse 3 Querschnittsnachweis geführt werden.
hs =1,2874m
I= 0,04367m4
η
1
u
=
M
⋅
z
I
⋅
f
y
d
=
M
⋅
(
h
s
+
t
f
1
/
2
)
I
⋅
f
y
d
{\displaystyle \eta _{1u}={\frac {M\cdot z}{I\cdot f_{yd}}}={\frac {M\cdot (h_{s}+t_{f1}/2)}{I\cdot f_{yd}}}}
η
1
u
=
7,541
325
⋅
(
1,287
4
+
0,017
/
2
)
0,043
67
⋅
235000
{\displaystyle \eta _{1u}={\frac {7{,}541325\cdot (1{,}2874+0{,}017/2)}{0{,}04367\cdot 235000}}}
η1u = 0,952 <1 OK
η
1
o
=
M
⋅
z
I
⋅
f
y
d
=
M
⋅
(
h
w
−
h
s
+
t
f
2
/
2
)
I
⋅
f
y
d
{\displaystyle \eta _{1o}={\frac {M\cdot z}{I\cdot f_{yd}}}={\frac {M\cdot (hw-h_{s}+t_{f2}/2)}{I\cdot f_{yd}}}}
η
1
o
=
7,541
325
⋅
(
2
,
9
−
1,287
4
+
0,011
/
2
)
0,043
67
⋅
235000
{\displaystyle \eta _{1o}={\frac {7{,}541325\cdot (2{,}9-1{,}2874+0{,}011/2)}{0{,}04367\cdot 235000}}}
η
1
o
=
1,189
≮
1
{\displaystyle \eta _{1o}=1{,}189\not <1}
Nachweis nicht erfüllt
Der Eurocode erlaubt plastifizieren im Zugbereich für Klasse 3 Querschnitte.
a
=
(
A
1
−
A
2
+
N
f
y
d
)
t
w
=
(
0,083
555
−
0,004
07
)
0,009
{\displaystyle a={\frac {\left(A_{1}-A_{2}+{\frac {N}{f_{yd}}}\right)}{t_{w}}}={\frac {(0{,}083555-0{,}00407)}{0{,}009}}}
a= 0,476m (plastifizierte Steglänge)
b
=
h
w
2
−
a
2
=
2
,
9
2
−
0,476
2
{\displaystyle b={\frac {h_{w}}{2}}-{\frac {a}{2}}={\frac {2{,}9}{2}}-{\frac {0{,}476}{2}}}
b= 1,212
M
P
E
,
R
d
=
∑
(
2
⋅
b
2
⋅
t
w
⋅
f
y
w
3
A
1
⋅
f
y
d
1
⋅
(
b
+
t
f
1
2
)
t
w
⋅
a
⋅
f
y
w
⋅
(
b
+
a
2
)
A
2
⋅
f
y
d
2
⋅
(
a
+
b
+
t
f
2
2
)
−
N
⋅
(
a
+
b
+
S
−
h
w
)
)
{\displaystyle M_{PE{,}Rd}=\sum {\begin{pmatrix}{\frac {2\cdot b^{2}\cdot t_{w}\cdot f_{yw}}{3}}\\A_{1}\cdot f_{yd1}\cdot \left(b+{\frac {t_{f1}}{2}}\right)\\t_{w}\cdot a\cdot f_{yw}\cdot \left(b+{\frac {a}{2}}\right)\\A_{2}\cdot f_{yd2}\cdot \left(a+b+{\frac {t_{f2}}{2}}\right)\\-N\cdot \left(a+b+S-h_{w}\right)\end{pmatrix}}}
M
P
E
,
R
d
=
∑
(
2
⋅
1,212
2
⋅
0,009
3
0,008
3555
⋅
(
1,212
+
0,017
2
)
0,009
⋅
0,476
⋅
(
1,212
+
0,476
2
)
0,004
07
⋅
(
0,476
+
1,212
+
0,011
2
)
0
)
⋅
f
y
d
{\displaystyle M_{PE{,}Rd}=\sum {\begin{pmatrix}{\frac {2\cdot 1{,}212^{2}\cdot 0{,}009}{3}}\\0{,}0083555\cdot \left(1{,}212+{\frac {0{,}017}{2}}\right)\\0{,}009\cdot 0{,}476\cdot \left(1{,}212+{\frac {0{,}476}{2}}\right)\\0{,}00407\cdot \left(0{,}476+1{,}212+{\frac {0{,}011}{2}}\right)\\0\end{pmatrix}}\cdot f_{yd}}
M
P
E
,
R
d
=
∑
(
0,008
81
0,010
19
0,006
21
0,006
89
0
)
⋅
f
y
d
{\displaystyle M_{PE{,}Rd}=\sum {\begin{pmatrix}0{,}00881\\0{,}01019\\0{,}00621\\0{,}00689\\0\end{pmatrix}}\cdot f_{yd}}
MPE,Rd = 7547,3kN verbesserter Nachweis
M
E
D
M
P
E
,
R
d
=
7541,325
7547
,
3
{\displaystyle {\frac {M_{ED}}{M_{PE{,}Rd}}}={\frac {7541{,}325}{7547{,}3}}}
0,9992 < 1
Nachweis erfüllt
Beim Schubbeulen wirken andere Breiten mit.
wirksame Breiten für Schubbeulen beff = 15∙ε∙tw = 15∙1∙0,009
beff = 0,135m Asl = (beff ∙2 + tsl )∙tw + bsl ∙tsl
Asl = (0,27 + 0,008)∙0,009 + 0,008∙0,1
Asl = 0,003302
x
s
l
=
b
s
l
⋅
t
s
l
⋅
(
b
s
l
2
+
t
w
2
)
A
s
l
=
0,000
8
⋅
(
0,054
5
)
0,003
302
{\displaystyle x_{sl}={\frac {b_{sl}\cdot t_{sl}\cdot \left({\frac {b_{sl}}{2}}+{\frac {t_{w}}{2}}\right)}{A_{sl}}}={\frac {0{,}0008\cdot (0{,}0545)}{0{,}003302}}}
xsl = 0,013204m
I
s
l
=
∑
(
b
e
f
f
⋅
t
w
3
/
12
b
s
l
3
/
12
x
s
l
2
⋅
b
e
f
f
⋅
t
w
b
s
l
⋅
t
s
l
⋅
(
b
s
l
/
2
+
t
w
/
2
−
x
s
l
)
2
)
{\displaystyle I_{sl}=\sum {\begin{pmatrix}b_{eff}\cdot t_{w^{3}}/12\\b_{sl^{3}}/12\\x_{sl^{2}}\cdot b_{eff}\cdot t_{w}\\b_{sl}\cdot t_{sl}\cdot (b_{sl}/2+t_{w}/2-x_{sl})^{2}\end{pmatrix}}}
I
s
l
=
∑
(
0,278
⋅
0,009
3
/
12
0
,
1
3
⋅
0,008
/
12
0,013
204
2
⋅
0,278
⋅
0,009
0
,
1
⋅
0,008
⋅
(
0,054
5
−
0,013
204
)
2
)
=
∑
(
0
0,666
0,436
1
,
36
)
⋅
10
−
6
m
4
{\displaystyle I_{sl}=\sum {\begin{pmatrix}0{,}278\cdot 0{,}009^{3}/12\\0{,}1^{3}\cdot 0{,}008/12\\0{,}013204^{2}\cdot 0{,}278\cdot 0{,}009\\0{,}1\cdot 0{,}008\cdot (0{,}0545-0{,}013204)^{2}\end{pmatrix}}=\sum {\begin{pmatrix}0\\0{,}666\\0{,}436\\1{,}36\end{pmatrix}}\cdot 10^{-6}m^{4}}
Isl = 2,484∙ 10-6 m4 Berechnung des Schubbeulwertes
Gesamtfeld
kτsl = MAX( Formel 1; Formel 2) (Eurocode 1993-1-5 Gleichung A.5)
F
o
r
m
e
l
1
=
9
⋅
(
h
w
a
)
2
⋅
(
I
s
l
t
3
⋅
h
w
)
0
,
75
{\displaystyle Formel1=9\cdot \left({\frac {h_{w}}{a}}\right)^{2}\cdot \left({\frac {I_{sl}}{t^{3}\cdot h_{w}}}\right)^{0{,}75}}
F
o
r
m
e
l
1
=
9
⋅
(
2
,
9
7
,
1
)
2
⋅
(
2,484
10
6
⋅
0,009
3
⋅
2
,
9
)
0
,
75
{\displaystyle Formel1=9\cdot \left({\frac {2{,}9}{7{,}1}}\right)^{2}\cdot \left({\frac {2{,}484}{10^{6}\cdot 0{,}009^{3}\cdot 2{,}9}}\right)^{0{,}75}}
Formel 1= 1,694
F
o
r
m
e
l
2
=
2
,
1
t
⋅
I
s
l
h
w
3
{\displaystyle Formel2={\frac {2{,}1}{t}}\cdot {\sqrt[{3}]{\frac {I_{sl}}{h_{w}}}}}
F
o
r
m
e
l
2
=
2
,
1
0,009
⋅
2,484
10
6
⋅
2
,
9
3
{\displaystyle Formel2={\frac {2{,}1}{0{,}009}}\cdot {\sqrt[{3}]{\frac {2{,}484}{10^{6}\cdot 2{,}9}}}}
Formel 2= 2,215
kτsl = MAX( 1,694; 2,215)
kτsl = 2,215
k
τ
=
5
,
34
+
4
⋅
(
h
w
a
)
2
+
k
τ
s
l
{\displaystyle k_{\tau }=5{,}34+4\cdot \left({\frac {h_{w}}{a}}\right)^{2}+k_{\tau sl}}
k
τ
=
5
,
34
+
4
⋅
(
7
,
1
2
,
9
)
2
+
2,215
{\displaystyle k_{\tau }=5{,}34+4\cdot \left({\frac {7{,}1}{2{,}9}}\right)^{2}+2{,}215}
kt = 8,2233 Da das Beulfeld
(
a
=
a
h
w
=
7
,
1
2
,
9
=
2
,
45
<
3
)
{\displaystyle \left(a={\frac {a}{h_{w}}}={\frac {7{,}1}{2{,}9}}=2{,}45<3\right)}
und (1 oder 2 Längssteifen) hat, darf Gleichung A.6 verwendet werden.
k
τ
=
4
,
1
+
6
,
3
α
2
+
0
,
18
⋅
I
s
l
t
3
⋅
h
w
⋅
α
2
+
2
,
2
⋅
I
s
l
t
3
⋅
h
w
3
{\displaystyle k_{\tau }=4{,}1+{\frac {6{,}3}{\alpha ^{2}}}+{\frac {0{,}18\cdot I_{sl}}{t^{3}\cdot h_{w}\cdot \alpha ^{2}}}+2{,}2\cdot {\sqrt[{3}]{\frac {I_{sl}}{t^{3}\cdot h_{w}}}}}
k
τ
=
4
,
1
+
6
,
3
2
,
45
2
+
0
,
18
⋅
2,484
⋅
10
−
6
0,009
3
⋅
2
,
9
⋅
2
,
45
2
+
2
,
2
⋅
2,484
⋅
10
−
6
0,009
3
⋅
2
,
9
3
{\displaystyle k_{\tau }=4{,}1+{\frac {6{,}3}{2{,}45^{2}}}+{\frac {0{,}18\cdot 2{,}484\cdot 10^{-6}}{0{,}009^{3}\cdot 2{,}9\cdot 2{,}45^{2}}}+2{,}2\cdot {\sqrt[{3}]{\frac {2{,}484\cdot 10^{-6}}{0{,}009^{3}\cdot 2{,}9}}}}
kτ = 4,1 + 1,051 + 0,0353 + 2,3215
kτ = 7,5078 Da diese Gleichung keinen höheren Beulwert bringt, bleibt es bei
kt = 8,2233 Schubbeilschlankheit
λ
¯
w
{\displaystyle {\overline {\lambda }}_{w}}
λ
¯
w
=
h
w
37,421
⋅
t
⋅
ϵ
⋅
k
τ
{\displaystyle {\overline {\lambda }}_{w}={\frac {h_{w}}{37{,}421\cdot t\cdot \epsilon \cdot {\sqrt {k_{\tau }}}}}}
λ
¯
w
=
2
,
9
37,421
⋅
0,009
⋅
1
⋅
8,223
3
{\displaystyle {\overline {\lambda }}_{w}={\frac {2{,}9}{37{,}421\cdot 0{,}009\cdot 1\cdot {\sqrt {8{,}2233}}}}}
λ
¯
w
=
3,003
{\displaystyle {\overline {\lambda }}_{w}=3{,}003}
Einzelfeld
Feldhöhe = hw - h1 = 2,9 - 0,4=2,5m
k
τ
=
5
,
34
+
4
⋅
(
h
w
a
)
2
{\displaystyle k_{\tau }=5{,}34+4\cdot \left({\frac {h_{w}}{a}}\right)^{2}}
k
τ
=
5
,
34
+
4
⋅
(
2
,
5
7
,
1
)
2
{\displaystyle k_{\tau }=5{,}34+4\cdot \left({\frac {2{,}5}{7{,}1}}\right)^{2}}
kτ = 5,836 Schubbeulschlankheit
λ
¯
w
{\displaystyle {\overline {\lambda }}_{w}}
λ
¯
w
=
h
w
37,421
⋅
t
⋅
ϵ
⋅
k
τ
{\displaystyle {\overline {\lambda }}_{w}={\frac {h_{w}}{37{,}421\cdot t\cdot \epsilon \cdot {\sqrt {k_{\tau }}}}}}
λ
¯
w
=
2
,
5
37,421
⋅
0,009
⋅
1
⋅
5,836
{\displaystyle {\overline {\lambda }}_{w}={\frac {2{,}5}{37{,}421\cdot 0{,}009\cdot 1\cdot {\sqrt {5{,}836}}}}}
λ
¯
w
=
3,073
{\displaystyle {\overline {\lambda }}_{w}=3{,}073}
Einzelfeldbeulen ist maßgebend.
λ
¯
w
=
M
I
N
(
3,003
;
3,073
)
=
3,073
{\displaystyle {\overline {\lambda }}_{w}=MIN(3{,}003;3{,}073)=3{,}073}
für
λ
¯
w
{\displaystyle {\overline {\lambda }}_{w}}
χ
w
=
1
,
37
0
,
7
+
λ
¯
w
=
1
,
37
0
,
7
+
3,073
{\displaystyle \chi _{w}={\frac {1{,}37}{0{,}7+{\overline {\lambda }}_{w}}}={\frac {1{,}37}{0{,}7+3{,}073}}}
χw= 0,363
V
b
,
w
,
R
d
=
χ
w
⋅
f
y
w
⋅
h
w
⋅
t
γ
M
0
⋅
3
{\displaystyle V_{b{,}w{,}Rd}={\frac {\chi _{w}\cdot f_{yw}\cdot h_{w}\cdot t}{\gamma _{M0}\cdot {\sqrt {3}}}}}
V
b
,
w
,
R
d
=
0,363
⋅
235
⋅
2
,
9
⋅
9
1
⋅
3
{\displaystyle V_{b{,}w{,}Rd}={\frac {0{,}363\cdot 235\cdot 2{,}9\cdot 9}{1\cdot {\sqrt {3}}}}}
Vb,w,Rd = 1285,9kN Beitrag der Flansche
Mf,Rd = MIN(A1 ;A2 )∙ (hw + tf1 /2 + tf2 /2)∙fyd
Mf,Rd = 0,00407∙(2,9 + 0,015)∙235
Mf,Rd = 2,787MN Mf,Rd < MEd =7541
Vbf,Rd =0 Flansch trägtnicht mit Gesamtquerkrafttragfähigkeit Vb,Rd
Vb,Rd = 0 + 1285,9= 1285,9kN Schubbeulnachweis
η
3
=
V
E
d
V
b
,
R
d
=
1142,625
1285
,
9
{\displaystyle \eta _{3}={\frac {V_{Ed}}{V_{b{,}Rd}}}={\frac {1142{,}625}{1285{,}9}}}
η3 = 0,88856<1 Nachweis erfüllt
Der Träger kann noch eine lokale Einzellast aufnehmen. Wie groß sie sein kann, wird hier gezeigt. Die Einzellast verursacht keine Schnittgrößen.
F= 330kN
ss = 0,1m Formelzeichen für Maße Beulwert kf
k
f
=
6
+
2
⋅
h
w
2
a
2
+
(
5
,
44
⋅
b
1
a
−
0
,
21
)
⋅
γ
s
{\displaystyle k_{f}=6+{\frac {2\cdot h_{w}^{2}}{a^{2}}}+\left({\frac {5{,}44\cdot b_{1}}{a}}-0{,}21\right)\cdot {\sqrt {\gamma _{s}}}}
Der dritte Term gilt für Längssteifen und ist nur gültig, wenn gilt:
0,05 < b1 /a und b1 /hw < 0,3 b1 = hw - h1
b1 = 2,9 - 0,4
b1 = 2,5
b
1
a
=
2
,
5
7
,
1
=
0
,
38
>
0
,
05
O
K
{\displaystyle {\frac {b_{1}}{a}}={\frac {2{,}5}{7{,}1}}=0{,}38>0{,}05OK}
b
1
h
w
=
2
,
5
2
,
9
=
0
,
86
≮
0
,
3
{\displaystyle {\frac {b_{1}}{h_{w}}}={\frac {2{,}5}{2{,}9}}=0{,}86\not <0{,}3}
Längssteife trägt nicht mit
Beulwert
k
f
=
6
+
2
⋅
2
,
9
2
7
,
1
2
{\displaystyle k_{f}=6+{\frac {2\cdot 2{,}9^{2}}{7{,}1^{2}}}}
kf = 6,3336 Fcr = 0,9∙kf ∙E∙tw ³/hw (Eurocode 1993-1-5 Gleichung 6.5)
Fcr = 0,9∙ 6,3336∙ 210∙109 ∙0,009³/2,9
Fcr = 300916N
m
1
=
f
y
f
⋅
b
f
f
y
w
⋅
t
w
=
235
⋅
0
,
37
235
⋅
0,009
{\displaystyle m_{1}={\frac {f_{yf}\cdot b_{f}}{f_{yw}\cdot t_{w}}}={\frac {235\cdot 0{,}37}{235\cdot 0{,}009}}}
m1 = 41,111 m2 = Wenn(
λ
¯
F
{\displaystyle {\overline {\lambda }}_{F}}
m2 = 0,02∙hw ²/tf ² = 0,02∙2,9²/0,011²
m2 = 1390,1 ly = MIN(a; ss + 2∙tf2 ∙(1 + (m1 + m2 )0,5 )) (Eurocode 1993-1-5 Gleichung 6.10)
ly = 0,1 + 2∙0,011∙(1 + (41,1 + 1390)0,5 ) (Eurocode 1993-1-5 Gleichung 6.10)
ly = 0,954
λ
¯
F
=
l
y
⋅
t
w
⋅
f
y
w
F
c
r
{\displaystyle {\overline {\lambda }}_{F}={\sqrt {\frac {l_{y}\cdot t_{w}\cdot f_{yw}}{F_{cr}}}}}
λ
¯
F
=
0,954
⋅
0,009
⋅
235
⋅
10
6
300916
{\displaystyle {\overline {\lambda }}_{F}={\sqrt {\frac {0{,}954\cdot 0{,}009\cdot 235\cdot 10^{6}}{300916}}}}
λ
¯
F
=
2
,
56
{\displaystyle {\overline {\lambda }}_{F}=2{,}56}
Die Voraussetzung
λ
¯
F
≮
0
,
5
{\displaystyle {\overline {\lambda }}_{F}\not <0{,}5}
χ
F
=
0
,
5
λ
¯
F
=
0
,
5
2
,
56
{\displaystyle \chi _{F}={\frac {0{,}5}{{\overline {\lambda }}_{F}}}={\frac {0{,}5}{2{,}56}}}
χF = 0,193 Leff = χf ∙ Ly =0,193∙0,954 (Eurocode 1993-1-5 Gleichung 6.2)
Leff = 0,1842 FRd = fyd ∙ Leff ∙ tw (Eurocode 1993-1-5 Gleichung 6.1)
FRd = 235000∙0,1842∙0,009
FRd = 389,6kN Nachweis
η
2
=
F
E
d
f
y
w
d
⋅
L
e
f
f
⋅
t
w
=
330
389
,
6
{\displaystyle \eta _{2}={\frac {F_{Ed}}{f_{ywd}\cdot L_{eff}\cdot t_{w}}}={\frac {330}{389{,}6}}}
η2 = 0,84689 Nachweis erfüllt
Zuerst muss das plastische Moment ausgerechnet werden. Die Steife trägt hier mit.
Maße zur Berechnung des plastischen Momentes A= 0,00407 + 0,026 + 0,0008 + 0,00901
A= 0,03998m²
A/2= 0,01999m² Die Flächenhalbierende liegt im Steg über der Steife.
Die Skizze hat keinen relativen Maßstab.
W
=
∑
(
1,768
88
2
/
2
⋅
0,009
1,131
11
2
/
2
⋅
0,009
0,004
07
⋅
1,774
0,000
8
⋅
0,731
11
0,009
01
⋅
1,139
6
)
=
∑
(
0,014
066
0,005
75
0,007
22
0,000
585
0,010
267
)
{\displaystyle W=\sum {\begin{pmatrix}1{,}76888^{2}/2\cdot 0{,}009\\1{,}13111^{2}/2\cdot 0{,}009\\0{,}00407\cdot 1{,}774\\0{,}0008\cdot 0{,}73111\\0{,}00901\cdot 1{,}1396\end{pmatrix}}=\sum {\begin{pmatrix}0{,}014066\\0{,}00575\\0{,}00722\\0{,}000585\\0{,}010267\end{pmatrix}}}
W= 0,03791m³ MPl,Rd = W∙fyd
MPl,Rd = 0,03791∙235000
MPl,Rd = 8909,4kNm Mf,Rd = 2787,1kNm Der Interaktionsnachweis darf im Abstand x geführt werden
x
=
h
w
−
h
1
2
=
2
,
9
−
0
,
5
2
{\displaystyle x={\frac {h_{w}-h_{1}}{2}}={\frac {2{,}9-0{,}5}{2}}}
x= 1,25 MEd = 6156,325
VEd := VEd - x∙q
VEd = 1142,625 - 1,25∙55,4
VEd = 1073,375kN
η
¯
1
=
M
A
X
(
M
E
d
M
p
l
,
R
d
;
M
f
,
R
d
M
P
l
,
R
d
)
{\displaystyle {\overline {\eta }}_{1}=MAX\left({\frac {M_{Ed}}{M_{pl{,}Rd}}};{\frac {M_{f{,}Rd}}{M_{Pl{,}Rd}}}\right)}
η
¯
1
=
6156,325
8909
,
4
{\displaystyle {\overline {\eta }}_{1}={\frac {6156{,}325}{8909{,}4}}}
η
¯
1
=
0,690
99
{\displaystyle {\overline {\eta }}_{1}=0{,}69099}
η
¯
3
=
V
V
R
d
=
1073,375
1285
,
9
{\displaystyle {\overline {\eta }}_{3}={\frac {V}{V_{Rd}}}={\frac {1073{,}375}{1285{,}9}}}
η
¯
3
=
0,834
7
{\displaystyle {\overline {\eta }}_{3}=0{,}8347}
Nachweis
η
¯
1
+
(
1
−
M
f
,
R
d
M
p
l
,
R
d
)
⋅
(
2
⋅
η
¯
3
−
2
)
2
<
1
{\displaystyle {\overline {\eta }}_{1}+\left(1-{\frac {M_{f{,}Rd}}{M_{pl{,}Rd}}}\right)\cdot (2\cdot {\overline {\eta }}_{3}-2)^{2}<1}
0,690
99
+
(
1
−
2787
,
1
8909
,
4
)
⋅
(
2
⋅
0,834
7
−
1
)
2
{\displaystyle 0{,}69099+\left(1-{\frac {2787{,}1}{8909{,}4}}\right)\cdot (2\cdot 0{,}8347-1)^{2}}
0,69099 + 0,30793= 0,99892 < 1 Nachweis erfüllt
Interaktion zwischen η1 und η2
η
2
+
0
,
8
⋅
η
1
1
,
4
<
1
{\displaystyle {\frac {\eta _{2}+0{,}8\cdot \eta _{1}}{1{,}4}}<1}
0,846
89
+
0
,
8
⋅
0,690
99
1
,
4
{\displaystyle {\frac {0{,}84689+0{,}8\cdot 0{,}69099}{1{,}4}}}
1 < 1 Nachweis erfüllt.
Allgemein:Inhaltsverzeichnis ; Glossar ; Zahlen
Rechenbeispiel: Allgemeiner Lösungsweg ; erstes ; zweites ; drittes ; viertes
Norm: EuroB ;DINS ;EuroS ;DINB ;Zusammenfassung ;Variation der Geometrie 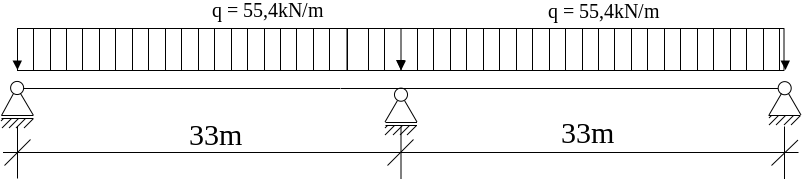
















































![{\displaystyle a_{c}=4{,}33\cdot {\sqrt[{4}]{\frac {I_{sl{,}1}\cdot b_{1}^{2}\cdot b_{2}^{2}}{t^{3}\cdot b}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8041d1989607b0751a0ad3cc51bd7e4a5fcecb21)
![{\displaystyle a_{c}=4{,}33\cdot {\sqrt[{4}]{\frac {2{,}759\cdot 0{,}4^{2}\cdot 2{,}5^{2}}{10^{6}\cdot 2{,}9\cdot 0{,}009^{3}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/732da6210d9c0ec8cafe8a37e977e65f9db23b4c)


























































![{\displaystyle Formel2={\frac {2{,}1}{t}}\cdot {\sqrt[{3}]{\frac {I_{sl}}{h_{w}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ef347646fbcfbc61d9c2d422f97323da4e0cd78)
![{\displaystyle Formel2={\frac {2{,}1}{0{,}009}}\cdot {\sqrt[{3}]{\frac {2{,}484}{10^{6}\cdot 2{,}9}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55c06042bbdfaeb8001bf031ab36c71ac0d0b085)



![{\displaystyle k_{\tau }=4{,}1+{\frac {6{,}3}{\alpha ^{2}}}+{\frac {0{,}18\cdot I_{sl}}{t^{3}\cdot h_{w}\cdot \alpha ^{2}}}+2{,}2\cdot {\sqrt[{3}]{\frac {I_{sl}}{t^{3}\cdot h_{w}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee7e361a3d8fed45de79460c71e2976e48899631)
![{\displaystyle k_{\tau }=4{,}1+{\frac {6{,}3}{2{,}45^{2}}}+{\frac {0{,}18\cdot 2{,}484\cdot 10^{-6}}{0{,}009^{3}\cdot 2{,}9\cdot 2{,}45^{2}}}+2{,}2\cdot {\sqrt[{3}]{\frac {2{,}484\cdot 10^{-6}}{0{,}009^{3}\cdot 2{,}9}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb99fb6fe43d2a213cd68276389d17a9a72e94e6)



































