Plattenbeulen/ drittes Rechenbeispiel/ EuroB

Geometrie

Es wird ein Zweifeldträger mit 2 Längssteifen und ohne Quersteifen an der Stütze untersucht. Er wird durch eine Gleichlast und einer Einzellast im ersten Feld belastet. Die Stahlgüte ist S355.

Träger- querschnitt

allgemeine Formelzeichen

Eingangsdaten für das dritte Rechenbeispiel

Quersteifen	a' keine
Träger links	l1= 5m
Träger rechts	l2= 6,4m
Belastung links	qEd= 18kN/m
Belastung rechts	qEd= 18kN/m
Einzellast	F= 9,3kN

Querschnittsdaten in mm

oberer Flansch	bf2 =71	tf2 =3
unterer Flansch	bf1 =91	tf1 =7
Steg	hw =600	tw =3
Steife	bsl =30	tsl =4
Steifenflansch	hsl =24	tsl2 =3
obere Steife	hw2 =300
untere Steife	hw1 =150

Da bei diesem kleinen Träger sehr viele Nullen in den Formeln stehen, wird für die Länge öfter der Präfix Milli verwendet. Dabei entstehen natürliche Zahlen ohne Komma.

Schnittgrößen

$M={\frac {-q_{1}\cdot L_{1}^{3}-q_{2}\cdot L_{2^{3}}}{8\cdot L_{1}+8\cdot L_{2}}}-{\frac {F\cdot L_{1}^{2}\cdot 3}{(L_{1}+L_{2})\cdot 16}}={\frac {-18\cdot 5^{3}-18\cdot 6{,}4^{3}}{8\cdot 5+8\cdot 6{,}4}}-{\frac {9{,}3\cdot 5^{2}\cdot 3}{(5+6{,}4)\cdot 16}}$

$M={\frac {6969}{91{,}2}}+{\frac {697{,}5}{182{,}4}}=M_{q}+M_{F}=-76{,}41-3{,}82$

M= - 80,23kNm

$V_{links}=-{\frac {q_{1}\cdot L_{1}}{2}}+{\frac {M_{q}}{L_{1}}}+{\frac {M_{F}}{L_{1}}}-{\frac {F}{2}}$

$V_{links}=-{\frac {18\cdot 5}{2}}+{\frac {-76{,}41}{5}}+{\frac {-3{,}82}{5}}-{\frac {9{,}3}{2}}$

V_links= - 45 - 15,28 - 0,76 - 4,65

V_links= - 65,7

$V_{rechts}={\frac {q_{2}\cdot L_{2}}{2}}-{\frac {M_{q}}{L_{2}}}-{\frac {M_{F}}{L_{2}}}$

$V_{rechts}={\frac {18\cdot 6{,}4}{2}}-{\frac {-76{,}41}{6{,}4}}-{\frac {-3{,}82}{6{,}4}}$

V_rechts= 57,6 + 11,93 + 0,59

V_rechts= 70,14

N= - 251,5kN

Schubverzerrung

b₀= 0,091/2= 0,0455

L_e= 0,25∙(L₁ + L₂)

L_e= 2,85m

$K={\frac {a_{0}\cdot b_{0}}{L_{e}}}={\frac {1\cdot 0{,}0455}{2{,}85}}$ (Eurocode 1993-1-5 Tabelle 3.1)

K= 0,01592 <0,02

ß=1

keine Schubverzerrung

Grenz c/t

${\frac {c}{t}}<14\cdot \epsilon ={\frac {91-3}{2\cdot 7}}$ (Eurocode 1993-1-1 Tabelle 5.2)

$\epsilon ={\sqrt {\frac {f_{yd}}{235}}}={\sqrt {\frac {355}{235}}}=0{,}8165$

6,28 < 11,39 Flansch trägt vollständig mit

Bruttoquerschnittswerte

Da diese Berechnung schon zweimal durchgeführt wurde, werden jetzt nur die Ergebnisse gezeigt:

Fläche A= 0,00265m²

Schwerpunkt h_s= 0,251m

Spannungsnulllinie S= 0,4m

Flächenmoment zweiten Grades I= 0,0001258m⁴

Spannung oben σ₂= 127,6 N/mm²

Spannung neben der oberen Steife σ_sl2= - 63,8 N/mm²

Spannung neben der unteren Steife σ_sl1= - 159,5 N/mm²

Spannung unten σ₁= - 255,2 N/mm²

Berechnung von ρ_c

Zuerst werden die wirksamen Breiten der Einzelfelder berechnet. So geht man da für jedes Feld vor:

Randspannungsverhältnis ψ ausrechnen.

Beulwert k_σ aus Tabelle Eurocode 4.1 berechnen.

Beulschlankheitsgrad ${\overline {\lambda }}_{p}$ nach Gleichung 4.3 ermitteln.

Abminderungsfaktor ρ Gleichung 4.2 errechnen.

Bruttobreiten b_u und b_o bestimmen.

wirksame Breiten mit b_u1,eff= b_u∙ρ berechnen

Da dies bereits in den vorherigen Rechenbeispielen vorgeführt wurde, wird dreimal derselbe Rechengang in einer Tabelle zusammengefasst.

Zusammenfassung des Rechengangs für alle 3 Beulfelder

	Feld 1	Feld 2	Feld 3
b	0,148	0,146	0,098
ψ	0,625	0,4	-2
kσ	4,8954	5,6549	53,794
${\overline {\lambda }}_{p}$	0,9638	0,8846	0,5861
ρ	0,8229	0,8915

Kontrolle:

(b₁ + t_sl/2) + (b₂ + t_sl) + (b₃ + t_ls/2)= S

0,15 + 0,15 + 0,1= 0,4 OK

wirksame Breiten

	Feld 1	Feld 2	Feld 3
bu	0,06767	0,06348	0,03921
bo	0,08034	0,08252	0,05881
bu eff	0,05567	0,05659	0,03921
bo,eff	0,06611	0,07356	0,05881
Σ beff	0,12179	0,13015	0,09802
verlust	0,02621	0,01585	0

Querschnittswerte der Steifen

wirksame Breiten an der oberen Steife

wirksame Breiten an der oberen Steife

Fläche der Längssteife ohne mitwirkende Breiten

A_s= b_sl∙t_sl + h_sl∙ t_sl2 - t_sl∙ t_sl2

A_s= 30∙4 + 24∙3 - 4∙3

A_s= 180mm²

b_u,eff3 + b_o,eff2 + t_sl= 73,56 + 39,21 + 4= 116,8

b_u + b_o + t_sl= 82,52 + 39,21 + 4= 125,73

A_sl= t_w∙(b_2o + b_3u + t_sl) + A_s

A_sl= 3∙(82,52 + 39,21 + 4) + 180

A_sl= 557,1mm²

Der Schwerpunkt x_sl wird auf die Stegmitte bezogen.

$x_{sl}={\frac {t_{sl}\cdot b_{sl}\cdot (b_{sl}/2+t_{w}/2)+(h_{sl}-t_{sl})\cdot t_{sl2}\cdot (t_{w}/2+b_{sl}-t_{sl}/2)}{A_{sl}}}$

$x_{sl}={\frac {4\cdot 30\cdot (15+1{,}5)+(24-4)\cdot 3\cdot (1{,}5+30-1{,}5)}{557{,}1}}$

x_sl= 6,784mm

I_sl= 3 Eigen + 3 Steiner

$I_{sl}=\sum {\begin{pmatrix}t_{w}^{3}\cdot (b_{2o}+b_{3u}+t_{sl})/12\\b_{sl}^{3}\cdot t_{sl}/12\\(h_{sl}-t_{sl})\cdot t_{sl2}^{3}/12\\t_{w}\cdot (b_{2o}+b_{3u}+t_{sl})\cdot x_{sl}^{2}\\b_{sl}\cdot t_{sl}\cdot (b_{sl}/2+t_{w}/2-x_{sl})^{2}\\(h_{sl}-t_{sl})\cdot t_{sl2}\cdot (t_{w}/2+b_{sl}-t_{sl}/2-x_{sl})^{2}\end{pmatrix}}$

$I_{sl}=\sum {\begin{pmatrix}3^{3}\cdot (125{,}7)/12\\30^{3}\cdot 4/12\\(24-4)\cdot 3^{3}/12\\3\cdot (125{,}7)\cdot 6{,}784^{2}\\30\cdot 4\cdot (15+1{,}5-6{,}784)^{2}\\(24-4)\cdot 3\cdot (1{,}5+30-1{,}5-6{,}784)^{2}\end{pmatrix}}=\sum {\begin{pmatrix}283\\9000\\45\\17360\\11328\\32338\end{pmatrix}}$

I_sl= 70354mm⁴

Druckkraft F_s in der Steife

F_s= σ_sl2∙ A_sl2 = 63,8∙ 557,1

F_s= 35,56kN

wirksame Breiten an der unteren Steife

A_s= 180mm²

b_{u,eff2 +} b_o,eff1 + t_sl= 56,59 + 66,12 + 4= 126,71

b_u + b_o + t_sl= 80,34 + 63,48 + 4= 147,82

Fläche mit wirksamen Breiten

A_sl= t_w∙(b_1o + b_2u + t_sl) + A_s

A_sl= 3∙147,82 + 180

A_sl= 623,5mm²

Schwerpunkt x_sl

$x_{sl}={\frac {t_{sl}\cdot b_{sl}\cdot (b_{sl}/2+t_{w}/2)+(h_{sl}-t_{sl})\cdot t_{sl2}\cdot (t_{w}/2+b_{sl}-t_{sl}/2)}{A_{sl}}}$

$x_{sl}={\frac {4\cdot 30\cdot (15+1{,}5)+(24-4)\cdot 3\cdot (1{,}5+30-1{,}5)}{623{,}5}}$

x_sl= 6,289mm

I_sl= 3 Eigen + 3 Steiner

$I_{sl}=\sum {\begin{pmatrix}t_{w}^{3}\cdot (b_{1o}+b_{2u}+t_{sl})/12\\b_{sl^{3}}\cdot t_{sl}/12\\(h_{sl}-t_{sl})\cdot t_{sl2}^{3}/12\\t_{w}\cdot (b_{1o}+b_{2u}+t_{sl})\cdot x_{sl}^{2}\\b_{sl}\cdot t_{sl}\cdot (b_{sl}/2+t_{w}/2-x_{sl})^{2}\\(h_{sl}-t_{sl})\cdot t_{sl2}\cdot (t_{w}/2+b_{sl}-t_{sl}/2-x_{sl})^{2}\end{pmatrix}}$

$I_{sl}=\sum {\begin{pmatrix}3^{3}\cdot (147{,}8)/12\\30^{3}\cdot 4/12\\(24-4)\cdot 3^{3}/12\\3\cdot (147{,}8)\cdot 6{,}29^{2}\\30\cdot 4\cdot (15+1{,}5-6{,}29)^{2}\\(24-4)\cdot 3\cdot (1{,}5+30-1{,}5-6{,}29)^{2}\end{pmatrix}}=\sum {\begin{pmatrix}333\\9000\\45\\17539\\12511\\33732\end{pmatrix}}$

I_sl= 73130mm⁴

Druckkraft F_s in der Steife

F_s= σ_sl1∙ A_sl1 = 159,5∙ 623,5

F_s= 99,46kN

Querschnittswerte der zusammengeführten Steife. Nach dem Eurocode sind 3 Fälle zu untersuchen. Die ersten beiden sind das einzelne Beulen und Knicken der Längssteifen und der dritte Fall ist das Beulen und Knicken beider Längssteifen gleichzeitig. Dabei wird eine Ersatzlängssteife geschaffen. Diese hat die Querschnittswerte der einzelnen Steifen zusammen und die Lage errechnet sich aus der Resultierenden der Kräfte der Steifen.

A_L= A_sl1 + A_sl2 = 557,1 + 623,5

A_L= 1180,6mm²

I_L= I_sl1 + I_sl2 = 70354 + 73160

I_L= 143514mm⁴

$h_{wL}=h_{w1}+{\frac {(h_{w2}-h_{w1})\cdot F_{s1}}{F_{s2}+F_{s1}}}$

$h_{wL}=0{,}15+{\frac {(0{,}3-0{,}15)\cdot 35{,}5}{99{,}46+35{,}56}}$

h_wL= 0,1895

	untere	obere	zusammen
Asl	623,46	557,19	1180,7
xsl	6,0629	6,784
Isl	73130	70354	143484
hw	0,15	0,3	0,1895

Berechnung der idealen Beulspannung

drei Möglichkeiten des Ausbeulens

Bei der Berechnung der idealen Beulspannung gibt es die 3 Fälle zu untersuchen. In den ersten beiden Fällen wird das Beulen der einzelnen Steife untersucht, wobei die andere als starr angenommen wird. Der dritte Fall wird mit der zusammengeführten Steife gerechnet. Dabei besteht das Teilfeld immer aus der Steife und den benachbarten Einzelfeldern.

Jetzt wird dreimal der gleiche Rechenweg durchlaufen.
Beulen der unteren Steife

b₁= h_w1= 0,15m

b₂= h_w2 - h_w1= 0,15m

b= B₁= b₁ + b₂= 0,3m

$a_{c}=4{,}33\cdot {\sqrt[{4}]{\frac {I_{sl{,}1}\cdot b_{1}^{2}\cdot b_{2}^{2}}{t^{3}\cdot b}}}$

$a_{c}=4{,}33\cdot {\sqrt[{4}]{\frac {7{,}313\cdot 10^{-8}\cdot 0{,}15^{2}\cdot 0{,}15^{2}}{0{,}3\cdot 0{,}003^{3}}}}$

a_c= 1,126m

a_c < a=5m

a= Quersteifenabstand

Ideale Beulspannung nach Eurocode 1993-1-5 Gleichung A.4

$\sigma _{cr{,}sl}={\frac {\pi ^{2}\cdot E_{Isl1}}{A_{sl{,}1}\cdot a^{2}}}+{\frac {E\cdot t^{3}\cdot b\cdot a^{2}}{4\cdot \pi \cdot (1+\nu )^{2}\cdot \sigma _{l{,}1}\cdot b_{1}^{2}\cdot b_{2}^{2}}}$ für a_c > a

$\sigma _{cr{,}sl}={\frac {1{,}05\cdot E}{A_{sl{,}1}}}\cdot {\frac {\sqrt {I_{sl{,}1}\cdot t^{3}\cdot b}}{b_{1}\cdot b_{2}}}$für a_c < a

$\sigma _{cr{,}sl}={\frac {1{,}05\cdot 210\cdot 10^{9}}{623{,}46\cdot 10^{-6}}}\cdot {\frac {\sqrt {7{,}313\cdot 10^{-8}\cdot 0{,}003^{3}\cdot 0{,}3}}{0{,}15\cdot 0{,}15}}$

σ_cr,sl= 3,536∙10¹⁴∙1,08∙10^-6= 382∙10⁶N/m²

σ_cr,sl= 382,6N/mm²

Die Beulspannung darf erhöht werden. Dabei wird die ideale Beulspannung auf den Ort der Steife bezogen.

$\sigma _{cr{,}p{,}1}={\frac {\sigma _{cr{,}sl}\cdot S}{S-h_{w1}}}$

$\sigma _{cr{,}p{,}1}={\frac {382{,}6\cdot 0{,}4}{0{,}4-0{,}15}}$

σ_cr,p,1= 612,1N/mm²

Beulen der oberen Steife

b₁= h_w2 - h_w1= 0,15m

b₂= h_w - h_w2= 0,3m

b= B₁= b₁ + b₂= 0,45m

$a_{c}=4{,}33\cdot {\sqrt[{4}]{\frac {I_{sl{,}1}\cdot b_{1}^{2}\cdot b_{2}^{2}}{t^{3}\cdot b}}}$

$a_{c}=4{,}33\cdot {\sqrt[{4}]{\frac {7{,}035\cdot 10^{-8}\cdot 0{,}15^{2}\cdot 0{,}3^{2}}{0{,}45\cdot 0{,}003^{3}}}}$

a_c= 1,4248m

a_c < a=5m

Ideale Beulspannung nach Eurocode 1993-1-5 Gleichung A.4

$\sigma _{cr{,}sl}={\frac {1{,}05\cdot E}{A_{sl{,}1}}}\cdot {\frac {\sqrt {I_{sl{,}1}\cdot t^{3}\cdot b}}{b_{1}\cdot b_{2}}}$ für a_c < a

$\sigma _{cr{,}sl}={\frac {1{,}05\cdot 210\cdot 10^{9}}{557{,}19\cdot 10^{-6}}}\cdot {\frac {\sqrt {7{,}035\cdot 10^{-8}\cdot 0{,}003^{3}\cdot 0{,}45}}{0{,}3\cdot 0{,}15}}$

σ_cr,sl= 3,957∙10¹⁴∙0,65∙10^-6= 257∙10⁶N/m²

σ_cr,sl= 257,1N/mm²

$\sigma _{cr{,}p{,}2}={\frac {\sigma _{cr{,}sl}\cdot S}{S-h_{w2}}}$

$\sigma _{cr{,}p{,}2}={\frac {257{,}1\cdot 0{,}4}{0{,}4-0{,}3}}$

σ_cr,p,2= 1028,3N/mm²

Beulen der gemeinsamen Steife

b₁= h_wL= 0,1895m

b₂= h_w - h_wL= 0,4105m

b= B₁= h_w= 0,6m

$a_{c}=4{,}33\cdot {\sqrt[{4}]{\frac {I_{sl{,}1}\cdot b_{1}^{2}\cdot b_{2}^{2}}{t^{3}\cdot b}}}$

$a_{c}=4{,}33\cdot {\sqrt[{4}]{\frac {14{,}348\cdot 10^{-8}\cdot 0{,}1895^{2}\cdot 0{,}4105^{2}}{0{,}6\cdot 0{,}003^{3}}}}$

a_c= 2,083m

a_c < a = 5m

Ideale Beulspannung nach Eurocode 1993-1-5 Gleichung A.4

$\sigma _{cr{,}sl}={\frac {1{,}05\cdot E}{A_{sl{,}1}}}\cdot {\frac {\sqrt {I_{sl{,}1}\cdot t^{3}\cdot b}}{b_{1}\cdot b_{2}}}$ für a_c < a

$\sigma _{cr{,}sl{,}lumped}={\frac {1{,}05\cdot 210\cdot 10^{9}}{1180{,}7\cdot 10^{-6}}}\cdot {\frac {\sqrt {14{,}348\cdot 10^{-8}\cdot 0{,}003^{3}\cdot 0{,}6}}{0{,}1895\cdot 0{,}4105}}$

σ_cr,sl,lumped= 1,867∙10¹⁴∙0,619∙10^-6= 115,7∙10⁶N/m²

σ_cr,sl,lumped= 115,7N/mm²

$\sigma _{cr{,}p{,}lumped}={\frac {\sigma _{cr{,}sl{,}lumped}\cdot S}{S-h_{w2}}}$

$\sigma _{cr{,}p{,}lumped}={\frac {115{,}7\cdot 0{,}4}{0{,}4-0{,}1895}}$

σ_cr,p,lumped = 219,9N/mm²

Von den 3 idealen Beulspannungen ist die geringste maßgebend.

σ_cr,p= MIN(σ_cr,p,1 ;σ_cr,p,2 ;σ_cr,p,lumped)

σ_cr,p= MIN(612,1;1028,3;219,9)

σ_cr,p= 219,9N/mm²

Mit dieser Spannung kann der Beulnachweis für das Teilfeld geführt werden.

A_c= A_sl1 + A_sl2 = 623,46 + 557,19

A_c= 1180,7mm²

b_{u3,eff +} b_o2,eff + t_sl= 56,6 + 66,1 + 4= 126,7

b_u2,eff + b_o1,eff + t_sl= 73,6 + 39,2 + 4= 116,8

A_c,eff,loc= t_w∙(b_{u3,eff +} b_o2,eff + t_sl) + :A_s + t_w∙( b_u2,eff + b_o1,eff + t_sl) + A_s

A_c,eff,loc= 3∙126,7 + 180 + 3∙116,8 + 180

A_c,eff,loc= 1090,4mm²

$\beta _{A{,}c}={\frac {A_{c{,}eff{,}loc}}{A_{c}}}={\frac {1090{,}4}{1180{,}7}}$

ß_A,c= 0,923

${\overline {\lambda }}_{p}={\sqrt {\frac {\beta _{Ac}\cdot f_{yk}}{\sigma _{c{,}rc}}}}={\sqrt {\frac {0{,}923\cdot 355}{220}}}$

${\overline {\lambda }}_{p}=1{,}2209$

$\Psi ={\frac {255{,}2}{-127{,}6}}=-0{,}5$

$\rho ={\frac {{\overline {\lambda }}_{p}-0{,}055\cdot (3+\Psi )}{{\overline {\lambda }}_{p^{2}}}}$ (Eurocode 1993-1-5 Gleichung 4.2)

$\rho ={\frac {1{,}2209-0{,}055\cdot (3-0{,}5)}{1{,}2209^{2}}}$

ρ = 0,72679

Knickstabverhalten
Beim knickstabähnlichen Verhalten wird nur das Ausknicken der unteren Steife untersucht.

A_sl1,eff= untere Steife mit wirksamen Breiten

A_sl1,eff= t_w∙(b_1o,eff + b_2u,eff + t_sl) + A_s

A_sl1,eff= 3∙(56,6 + 66,1 + 4) + 180

A_sl1,eff= 560,1mm²

A_sl1= untere Steife mit Bruttobreiten

A_sl1= t_w∙(b_1o + b_2u + t_sl) + A_s

A_sl1= 3∙(80,3 + 63,5 + 4) + 180

A_sl1= 623,4mm²

$\beta _{A{,}c}={\frac {A_{sl{,}1{,}eff}}{A_{sl}}}={\frac {560}{623{,}4}}$

ß_A,c= 0,898

I_sl1= 7,313∙10^-8m⁴

$\sigma _{cr{,}sl}={\frac {\pi ^{2}\cdot E\cdot I_{sl}}{A_{sl}\cdot a^{2}}}$ (Eurocode 1993-1-5 Gleichung 4.9)

$\sigma _{cr{,}sl}={\frac {\pi ^{2}\cdot 210\cdot 10^{9}\cdot 7{,}313\cdot 10^{-8}}{0{,}000623\cdot 5^{2}}}$

σ_cr,sl= 9,72N/mm²

$\sigma _{cr{,}c}={\frac {19\cdot S}{S-h_{w1}}}={\frac {9{,}72\cdot 0{,}4}{0{,}4-0{,}15}}$

σ_cr,c= 15,56N/mm²

${\overline {\lambda }}_{p}={\sqrt {\frac {\beta _{Ac}\cdot f_{yk}}{\sigma _{c{,}rc}}}}={\sqrt {\frac {0{,}898\cdot 355}{15{,}6}}}$

${\overline {\lambda }}_{p}=4{,}52$

Im Kommentar [7] zum Eurocode 1993-1-5 wird für e₁ eine gigantische Formel (mit Tippfehlern) verwendet. Bildet man das Momentengleichgewicht um den Steg, so lässt sich eine einfache Formel erzeugen.

Definition der Abstände e₁ und e₂

e₂= x_sl= 6,06mm

e₂∙A_sl= (e₁ + e₂)∙A_s

$e_{1}={\frac {e_{2}\cdot A_{sl}}{A_{s}}}-e_{2}={\frac {6{,}06\cdot 623}{180}}-6{,}06$

e₁= 14,94mm

e= MAX(e₁;e₂)

e= 14,94mm

α= 0,49 für offene Querschnitte

$i={\sqrt {\frac {I_{sl{,}1}}{A_{sl{,}1}}}}={\sqrt {\frac {73130}{623{,}4}}}$

i= 10,83mm

α_e= α + 0,09e/i (Eurocode 1993-1-5 Gleichung 4.1)2

α_e= 0,49 + 0,09∙14,9/10,8

α_e= 0,614

$k=0{,}5\cdot \left(1+\alpha _{e}\cdot \left({\overline {\lambda }}_{p}-0{,}2\right)+{\overline {\lambda }}_{p^{2}}\right)$

k= 0,5∙(1 + 0,614∙(4,52 - 0,2) + 4,52²)

k= 12,08

$\chi _{c}=MIN\left(1;{\frac {1}{k+{\sqrt {k^{2}-{\overline {\lambda }}_{p^{2}}}}}}\right)$

$\chi _{c}=MIN\left(1;{\frac {1}{12{,}08+{\sqrt {12{,}08^{2}-4{,}52^{2}}}}}\right)$

χ_c= 0,042963

Interaktion

$\xi =\left({\frac {\sigma _{cr{,}p}}{\sigma _{cr{,}c}}}-1\right)$ und ξ wird zwischen 0 < ξ < 1 begrenzt

$\xi =\left({\frac {220}{15{,}6}}-1\right)$

ξ= 1

ρ_c = (ρ - χ_c)∙ ξ∙(2 - ξ) + χ_c (Eurocode 1993-1-5 Gleichung 4.1)3

ρ_c = (0,72679 - 0,042963)∙1∙(2 - 1) + 0,042963

ρ_c = 0,72679

Wirksame Querschnittswerte

Die wirksamen Querschnittswerte werden in einer Exceltabelle berechnet. So wird in Excel gerechnet: Zuerst wird der Steg in viele Bereiche unterteilt: Ein Beulfeld unterteilt sich in 2 wirksame Breiten. In der Mitte des Beulfeldes ist ein Loch. Zwischen den Beulfeldern befindet sich die Steife. Das Beulfeld, das Zug enthält wird in einen Zug- und Druckbereich unterteilt (der Zugbereich ist 0 bei reinem Druck). Ist eine Steife nicht vorhanden, so werden die Steglängen des Beulfeldes auf 0 gesetzt. Dann wird der Schwerpunktabstand der Flächen zum unteren Stegende berechnet. Der Querschnitt besteht aus sehr vielen Rechtecken mit unterschiedlicher Dicke. Die Stegteile, die am Zugbereich oder Flansch anschließen haben die volle Stegdicke. Die Stegteile, die an einer Steife angrenzen haben eine mit ρc multiplizierte Stegdicke. Die Löcher haben eine Stegdicke von 0. Zu jedem Stegstück werden Fläche, Steineranteil, Eigenträgheitsanteil und A∙ Abstand berechnet, die in weiteren Formeln zu Querschnittswerte verarbeitet werden.

Damit lauten die Querschnittswerte

A_eff= 0,002324m²

h_s,eff= 0,2616m

I_eff= 0,0001213m⁴

Widerstandsmoment unten	Widerstandsmoment oben
$W_{eff{,}u}={\frac {I}{Z}}={\frac {I_{eff}}{h_{s{,}eff}+t_{f1}/2}}$	$W_{eff{,}o}={\frac {I}{Z}}={\frac {I_{eff}}{h_{w}-h_{s{,}eff}+t_{f2}/2}}$
$W_{eff{,}u}={\frac {0{,}0001213}{0{,}2616+0{,}007/2}}$	$W_{eff{,}o}={\frac {0{,}0001213}{0{,}6-0{,}2616+0{,}003/2}}$
Weff,u= 4,576∙10-4m³	Weff,o= 3,569∙10-4m³
MRd= Weff,u∙fyd	MRd,o= Weff,o∙fyd
MRd= 4,576∙10-4∙355000	MRd,o= 3,569∙10-4∙355000
MRd= 162,4kNm	MRd,o= 126,7kNm

Der verschobene Schwerpunkt erhöht das Moment.

M_Ed,N= - M_Ed + N_Ed∙(H_s - H_s,eff)

M_Ed,N= 80,23 + ( - 251,5)∙(0,2513 - 0,2616)

M_Ed,N= 82,83kNm

Nachweis

$\eta _{1}={\frac {M_{Ed{,}N}}{f_{yd}\cdot W_{eff{,}u}}}-{\frac {N}{f_{yd}\cdot A_{eff}}}$

$\eta _{1}={\frac {0{,}08283}{0{,}0004576\cdot 355}}+{\frac {0{,}2515}{355\cdot 0{,}002324}}$

η₁= 0,5099 + 0,3048

η₁= 0,8147

Nachweis erfüllt

Nachweis oben

$\eta _{1}={\frac {M_{Ed{,}N}}{f_{yd}\cdot W_{eff{,}o}}}-{\frac {N}{f_{yd}\cdot A_{eff}}}$

$\eta _{1}={\frac {0{,}08283}{0{,}0003569\cdot 355}}+{\frac {0{,}2515}{355\cdot 0{,}002324}}$

η₁= 0,65376 + 0,30484

η₁= 0,9586

Nachweis erfüllt

Nachweis, ob die Stegdicken weiter verringert werden müssen.

$\sigma _{com{,}Ed}={\frac {M\cdot z}{I}}+{\frac {N}{A}}={\frac {M\cdot (h_{s{,}eff}-h_{w1})}{I}}+{\frac {N}{A_{eff}}}$

$\sigma _{com{,}Ed}={\frac {0{,}08283\cdot (0{,}2616-0{,}15)}{0{,}0001213}}+{\frac {0{,}2515}{0{,}002324}}$

σ_com,Ed= 184,4N/mm²

${\frac {\sigma _{com{,}Ed}}{\rho _{c}\cdot f_{y}/\gamma _{M}}}={\frac {184{,}4}{0{,}727\cdot 355}}$ <1 (Eurocode 1993-1-5 Gleichung A.3)

0,7147 < 1 Keine weitere Abminderung erforderlich

Die Nachweise sind zwar erfüllt, doch der Nachweis kann auch genauer geführt werden. Dazu errechnet man sich den Abstand, in dem der Nachweis geführt wird und führt bei der Quersteife den Querschnittsnachweis. Kann die Zugkraft nicht aufgenommen werden, so kann der Nachweis semiplastisch geführt werden.

Das Ergebnis würde so aussehen:

η₁= 0,7512 statt 0,8147

und beim Querschnittsnachweis

η_1u= 0,7252 (Nachweisunten)

η_1o= 0,3621 (Nachweisoben)

Der semiplastische Nachweis kann nicht geführt werden, weil der Druckflansch zuerst plastifiziert.

Schubbeulen

Beim Schubbeulen wirken andere Breiten mit.

b_eff= 15∙ε∙t_w = 15∙0,8136∙3

b_eff= 36,61mm

A_sl= (b_eff∙2 + t_sl)∙t_w + A_s

A_sl= (36,61∙2 + 4)∙3 + 180

A_sl= 411,7mm²

$x_{sl}={\frac {b_{sl}\cdot t_{sl}\cdot (b_{sl}/2+t_{w}/2)+(h_{sl}-t_{sl})\cdot t_{sl2}\cdot (t_{w}/2+b_{sl}-t_{sl2}/2)}{A_{sl}}}$

$x_{sl}={\frac {30\cdot 4\cdot (30/2+3/2)+(24-4)\cdot 3\cdot (3/2+30-3/2)}{411{,}7}}$

x_sl= 9,182mm

I_sl= 3 Eigen + 3 Steiner

$I_{sl}=\sum {\begin{pmatrix}b_{sl}^{3}\cdot t_{sl}/12\\(h_{sl}-t_{sl})\cdot t_{sl2^{3}}/12\\t_{w^{3}}\cdot (2\cdot b_{eff}+t_{sl})/12\\t_{w}\cdot (2\cdot b_{eff}+t_{sl})\cdot x_{sl}^{2}\\b_{sl}\cdot t_{sl}\cdot (b_{sl}/2+t_{w}/2-x_{sl})^{2}\\(h_{sl}-t_{sl})\cdot t_{sl2}\cdot (t_{w}/2+b_{sl}-t_{sl}/2-x_{sl})^{2}\end{pmatrix}}$

$I_{sl}=\sum {\begin{pmatrix}30^{3}\cdot 4/12\\(24-4)\cdot 3^{3}/12\\3^{3}\cdot (77{,}4)/12\\3\cdot (77{,}4)\cdot 9{,}17^{2}\\30\cdot 4\cdot (15+1{,}5-9{,}17)^{2}\\(24-4)\cdot 3\cdot (1{,}5+30-1{,}5-9{,}17)^{2}\end{pmatrix}}=\sum {\begin{pmatrix}9000\\45\\174\\19525\\6447\\26033\end{pmatrix}}$

I_sl= 61181mm⁴

Berechnung des Schubbeulwertes
Es werden vom Einzelfeld und vom Gesamtfeld die Schlankheiten errechnet. Die kleinere ist maßgebend.

Gesamtfeld

k_τsl= MAX( Formel 1; Formel 2)

$Formel1=9\cdot \left({\frac {h_{w}}{a}}\right)^{2}\cdot \left({\frac {I_{sl}}{t^{3}\cdot h_{w}}}\right)^{0{,}75}$ I_sl:= 2∙I_sl, weil es 2 Steifen gibt

$Formel1=9\cdot \left({\frac {0{,}6}{5}}\right)^{2}\cdot \left({\frac {2\cdot 6{,}118\cdot 10^{-8}}{0{,}003^{3}\cdot 0{,}6}}\right)^{0{,}75}$

Formel 1= 0,5905

$Formel2={\frac {2{,}1}{t}}\cdot {\sqrt[{3}]{\frac {I_{sl}}{h_{w}}}}$

$Formel2={\frac {2{,}1}{0{,}003}}\cdot {\sqrt[{3}]{\frac {2\cdot 6{,}118\cdot 10^{-8}}{0{,}6}}}$

Formel 2= 4,12

k_τsl= MAX(0,5905; 4,1203)

k_τsl= 4,1203

$k_{\tau }=5{,}34+4\cdot \left({\frac {h_{w}}{a}}\right)^{2}+k_{\tau sl}$ (Eurocode 1993-1-5 Gleichung A.5)

$k_{\tau }=5{,}34+4\cdot \left({\frac {0{,}6}{5}}\right)^{2}+4,1203$

k_t= 9,518

Schubbeulschlankheit ${\overline {\lambda }}_{w}$

${\overline {\lambda }}_{w}={\frac {h_{w}}{37{,}421\cdot t\cdot \epsilon \cdot {\sqrt {k_{\tau }}}}}$ (Eurocode 1993-1-5 Gleichung 5.6)

${\overline {\lambda }}_{w}={\frac {0{,}6}{37{,}421\cdot 0{,}003\cdot 0{,}813\cdot {\sqrt {9{,}518}}}}$

${\overline {\lambda }}_{w}=2{,}129$

Einzelfeld
Feldhöhe = größtes Schubbeulfeld= 0,3m

$k_{\tau }=5{,}34+4\cdot \left({\frac {h_{w}}{a}}\right)^{2}$

$k_{\tau }=5{,}34+4\cdot \left({\frac {0{,}3}{5}}\right)^{2}$

k_τ= 5,3544

Schubbeulschlankheit ${\overline {\lambda }}_{w}$

${\overline {\lambda }}_{w}={\frac {h_{w}}{37{,}421\cdot t\cdot \epsilon \cdot {\sqrt {k_{\tau }}}}}$ (Eurocode 1993-1-5 Gleichung 5.6)

${\overline {\lambda }}_{w}={\frac {0{,}3}{37{,}421\cdot 0{,}003\cdot 0{,}813\cdot {\sqrt {5{,}35}}}}$

${\overline {\lambda }}_{w}=1{,}419$

Einzelfeldbeulen ist nicht maßgebend.

${\overline {\lambda }}_{w}$= MIN(1,419;2,129)= 2,129

für ${\overline {\lambda }}_{w}$> 0,82/η gilt:

$\chi _{w}={\frac {1{,}37}{0{,}7+{\overline {\lambda }}_{w}}}={\frac {1{,}37}{0{,}7+2{,}129}}$(Eurocode 1993-1-5 Tabelle 5.1)

χ_w= 0,4842

$V_{b{,}w{,}Rd}={\frac {\chi _{w}\cdot f_{yw}\cdot h_{w}\cdot t}{\gamma _{M0}\cdot {\sqrt {3}}}}$ (Eurocode 1993-1-5 Gleichung 5.2)

$V_{b{,}w{,}Rd}={\frac {0{,}484\cdot 355\cdot 0{,}6\cdot 3}{1\cdot {\sqrt {3}}}}$

V_b,w,Rd= 178,6kN

Der Beitrag der Flansche wird vernachlässigt, weil die Flansche stark ausgelastet sind.

V_b,Rd= V_b,w,Rd = 178,6kN

Schubbeulnachweis

$\eta _{3}={\frac {V_{Ed}}{V_{b{,}Rd}}}={\frac {70{,}13}{178{,}6}}$(Eurocode 1993-1-5 Gleichung 5.1)0

η₃= 0,3926 < 1

Nachweis erfüllt

Lokales Beulen aus einer Einzellast

Der Träger muss die Einzellast von 9,3 aufnehmen können. Da dies ein langer Formelapparat ist, bei dem nichts neu ist und der schon einmal im zweiten Rechenbeispiel Kapitel VI durchgearbeitet wurde, wird die Berechnung übersprungen. Die Längssteife trägt nicht mit.

L_eff= 0,0524

F_Rd= f_yd∙ L_eff∙ t_w (Eurocode 1993-1-5 Gleichung 6.1)

F_Rd= 355000∙0,0524∙0,003

F_Rd= 55,81kN

Nachweis

$\eta _{2}={\frac {F_{Ed}}{F_{Rd}}}={\frac {9{,}3}{55{,}81}}$ (Eurocode 1993-1-5 Gleichung 6.14)

η₂= 0,16662

Nachweis erfüllt

Interaktion

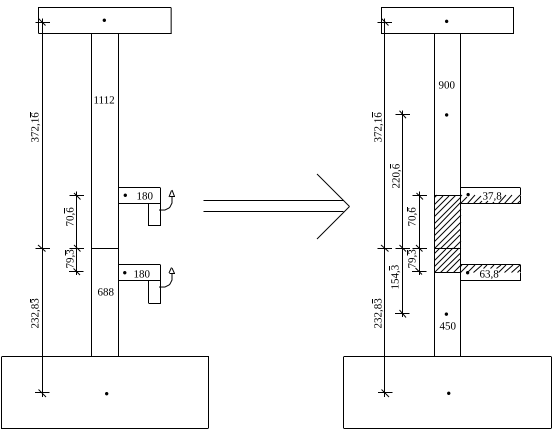
Zuerst muss das plastische Moment ausgerechnet werden. Die Steife trägt mit. Die Skizze hat keinen relativen Maßstab und ist auf das wichtigste reduziert. Flächenhalbierende

A= 213 + 1112 + 688 + 637 + 180 + 180

A= 3010mm²

A/2= 1505mm²

Die Flächenhalbierende liegt im Steg über der unteren Steife.

Die wirkende Normalkraft zehrt den Steg von der Flächenhalbierenden beginnend auf.

$A_{N}={\frac {N}{f_{yd}}}={\frac {251{,}5}{35{,}5}}=7{,}085cm^{2}$

A_N= 708,5mm²

A_N/2= 352,2mm²

Diese Fläche zehrt den gesamten Steg zwischen den Steifen auf. Dann werden die Steifen geschwächt. Die Flächen der Steifen werden zur Vereinfachung in einem Punkt konzentriert. Restflächen der Steifen

A_s,o= A_s + 70,666 ∙3 - 352,2

A_s,o= 180 + 212 -352,2

A_s,o= 37,8mm²

A_s,u= A_s + 79,333 ∙3 - 352,2

A_s,u= 180 + 238 - 352,2

A_s,u= 63,8mm²

$W=\sum {\begin{pmatrix}213\cdot 372{,}1{\overline {6}}\\637\cdot 232{,}8{\overline {3}}\\900\cdot 220{,}{\overline {6}}\\450\cdot 154{,}3\\37{,}8\cdot 70{,}{\overline {6}}\\63{,}8\cdot 79{,}{\overline {3}}\end{pmatrix}}=\sum {\begin{pmatrix}7927\\148315\\19860\\69450\\2670\\5059\end{pmatrix}}$

W= 503473mm³

M_Pl,Rd= W∙f_yd = 0,503473∙355

M_Pl,Rd= 178,7

Tragfähigkeit M_f,Rd der Flansche allein

M_f,Rd= MIN(A₁;A₂)∙ (h_w + t_f1/2 + t_f2/2)∙f_ydEurocode 7.1.3

M_f,Rd= 213∙(600 + 1,5 + 3,5)∙355

M_f,Rd= 45,747kN

Da noch eine Normalkraft wirkt, muss M_f,Rd reduziert werden.

$Faktor=1-{\frac {|N_{Ed}|}{(A_{f1}+A_{f2})\cdot f_{yd}}}$ (Eurocode 1993-1-5 Gleichung 5.9)

$Faktor=1-{\frac {251{,}5}{(213+637)\cdot 0{,}355}}$

Faktor= 0,1665

M_f,Rd:= M_f,Rd∙ Faktor

M_f,Rd= 45,747∙ 0,1665kN

M_f,Rd= 7,618kN

Der Interaktionsnachweis darf im Abstand x geführt werden. Die Höhe ist das größte Beulfeld.

$x={\frac {h_{w}-h_{2}}{2}}={\frac {0{,}6-0{,}3}{2}}$

x= 0,15

M_Ed= M_Ed,N - x∙V + x²∙q/2

M_Ed= 82,83 - 0,15∙70,13 + 0,15²∙18/2

M_Ed= 72,51

V_Ed:= V_Ed - x∙q

V_Ed= 70,13 - 0,15∙18

V_Ed= 67,43kN

${\overline {\eta }}_{1}=MAX\left({\frac {M_{Ed}}{M_{pl{,}Rd}}};{\frac {M_{f{,}Rd}}{M_{Pl{,}Rd}}}\right)$

${\overline {\eta }}_{1}={\frac {72{,}51}{178{,}7}}$

${\overline {\eta }}_{1}=0,4057$

${\overline {\eta }}_{3}={\frac {V}{V_{Rd}}}={\frac {67{,}43}{178{,}6}}$

${\overline {\eta }}_{3}$= MIN(0,5;0,3788)

${\overline {\eta }}_{3}=0,5$

Nachweis

${\overline {\eta }}_{1}+\left(1-{\frac {M_{f{,}Rd}}{M_{pl{,}Rd}}}\right)\cdot (2\cdot {\overline {\eta }}_{3}-2)^{2}<1$ (Eurocode 1993-1-5 Gleichung 7.1)

$0{,}4057+\left(1-{\frac {7{,}61}{178{,}7}}\right)\cdot (2\cdot 0{,}5-1)^{2}$

0,4057 < 1

Nachweis erfüllt

Interaktion zwischen η₁ und η₂

${\frac {\eta _{2}+0{,}8\cdot \eta _{1}}{1{,}4}}<1$

${\frac {0{,}16663+0{,}8\cdot 0{,}4057}{1{,}4}}$

0,35084 < 1

Nachweis erfüllt.

Sonstige Nachweise

Für den Träger sind bestimmte Mindestanforderungen zu erfüllen. Die Mindestanforderungen sind in allen Rechenbeispielen eingehalten.

Mindestanforderungen an die Längssteife
Eine Längssteife muss mindestens so steif sein, dass sie nicht biegedrillknickt. Dies ist der Fall, wenn

${\frac {I_{T}}{I_{p}}}>5{,}3\cdot {\frac {f_{y}}{E}}$(Eurocode 1993-1-5 Gleichung 9.3)

Dieser Nachweis wird auf das einheitliche Format umgeformt:

${\frac {5{,}3\cdot f_{y}\cdot I_{p}}{I_{T}\cdot E}}<1$

Torsionsträgheitsmoment I_t

$I_{t}={\frac {b_{sl}\cdot t_{sl}^{3}}{3}}+{\frac {(h_{sl}-t_{sl})\cdot t_{sl2}^{3}}{3}}$

$I_{t}={\frac {30\cdot 4^{3}}{3}}+{\frac {20\cdot 3^{3}}{3}}$

I_t= 820mm⁴

Polares Trägheitsmoment I_p um den Anschlusspunkt der Steife an den Steg.

$I_{y}={\frac {t_{sl}\cdot b_{sl}^{3}}{3}}+{\frac {(h_{sl}-t_{sl})\cdot t_{sl2}^{3}}{12}}+t_{sl2}\cdot (h_{sl}-t_{sl})\cdot \left(b_{sl}-{\frac {t_{sl2}}{2}}\right)^{2}$

$I_{y}={\frac {4\cdot 30^{3}}{3}}+{\frac {20\cdot 3^{3}}{12}}+3\cdot (20)\cdot \left(30-{\frac {3}{2}}\right)^{2}$

I_y= 36000 + 45 + 48735

I_y= 84780mm⁴

$I_{z}={\frac {b_{sl}\cdot t_{sl}^{3}}{12}}+{\frac {(h_{sl}-t_{sl})^{3}\cdot t_{sl2}}{12}}+t_{sl2}\cdot (h_{sl}-t_{sl})\cdot \left({\frac {h_{sl}}{2}}\right)^{2}$

$I_{z}={\frac {4^{3}\cdot 30}{12}}+{\frac {20^{3}\cdot 3}{12}}+3\cdot (20)\cdot \left({\frac {24}{2}}\right)^{2}$

I_z= 160 + 2000 + 8640

I_z= 10800mm⁴

I_p= I_y + I_z

I_p= 84780 + 10800

I_p= 95580mm⁴

Die Formel für I_w ist höchstwahrscheinlich falsch. Sie ist aus dem Kommentar [7] zum Eurocode entnommen, im dem zwischen t_sl und t_sl2 nicht unterschieden wird.

$I_{w}=\left(b_{sl}-{\frac {t_{sl}+t_{sl2}}{4}}\right)^{2}\cdot h_{sl}^{2}\cdot {\frac {t_{sl}+t_{sl2}}{6}}$

$I_{w}=\left(30-{\frac {7}{4}}\right)^{2}\cdot 24^{3}\cdot {\frac {7}{6}}=798\cdot 16128$

I_w= 12870144mm⁶= 1,287∙10^-11m⁴

Nachweis

${\frac {5{,}3\cdot f_{y}\cdot I_{p}}{I_{T}\cdot E}}<1$ (Eurocode 1993-1-5 Gleichung 9.3)

${\frac {5{,}3\cdot 355\cdot 10^{6}\cdot 95580}{210\cdot 10^{9}\cdot 820}}=1{,}0443\not <1$

Nachweis nicht erfüllt

Es kann auch ein genauerer Nachweis geführt werden. Der Eurocode fordert σ_cr > θ∙ f_yd mit θ=6, gibt aber keine Formel für die Berechnung von σ_cr an. Der Kommentar [7] zum Eurocode 1993-1-5 enthält im letzten „worked Example“ den benötigten Formelapparat. Der Nachweis wird vereinheitlicht zu

${\frac {6\cdot f_{yd}}{\sigma _{cr}}}<1$ (Eurocode 1993-1-5 Gleichung 9.4)

Drehfedersteifigkeit c_θ

$c_{\theta }={\frac {E\cdot t_{w}^{3}}{3\cdot b}}={\frac {210\cdot 10^{9}\cdot 0{,}003^{3}}{3\cdot 0{,}15}}$

mit b= Abstand zwischen den Steifen

c_θ = 12600N

Dann errechnet man eine Länge L_cr, die kleiner sein muss, als der Quersteifenabstand, damit die Formel angewendet werden darf.

$L_{cr}=\pi \cdot {\sqrt[{4}]{\frac {EI_{w}}{c_{\theta }}}}$

$L_{cr}=\pi \cdot {\sqrt[{4}]{\frac {210\cdot 10^{9}\cdot 1{,}287\cdot 10^{-11}}{12600}}}$

L_cr= 0,38m < a=5m

Formel ist gültig

$\sigma _{cr}={\frac {2\cdot {\sqrt {c_{\theta }\cdot E\cdot I_{w}}}+GI_{t}}{I_{p}}}$

$\sigma _{cr}={\frac {2\cdot {\sqrt {12600\cdot 210\cdot 10^{9}\cdot 1{,}287\cdot 10^{-11}}}+80{,}77\cdot 10^{9}\cdot 820\cdot 10^{-12}}{9{,}558\cdot 10^{-8}}}={\frac {369+66}{9{,}558\cdot 10^{-8}}}$

σ_cr= 4554N/mm²

${\frac {6\cdot f_{yd}}{\sigma _{cr}}}<1$

${\frac {6\cdot 355}{4554}}=0,4677<1$

Nachweis erfüllt

Starres Auflager Einheiten der Kampfkrafttheorie

Mindestanforderungen an die Quersteifen
Es sind keine Quersteifen vorhanden. Für Quersteifen muss ein Nachweis gegen Biegedrillknicken geführt werden und die Anforderungen nach Eurocode 9.2.1 müssen eingehalten werden. Im Mittelauflager soll eine beidseitige steife Quersteife eingebaut werden.

An den Trägerenden müssen 2 Quersteifen als starre Auflagersteife eingebaut werden. Die Fläche einer solchen Quersteife muss mindestens sein:

$A={\frac {4\cdot h_{w}\cdot t^{2}}{e}}$ (Eurocode 1993-1-5 9.3.1.3)

Dabei ist e der Steifenabstand. Er muss größer als ein Zehntel der Steghöhe sein.

Sind die Quersteifen 10cm entfernt, 6mm dick und 36mm hoch, so ist der Nachweis erfüllt

$6\cdot 36={\frac {4\cdot 600\cdot 3^{2}}{100}}$

216= 216 OK

flanschinduziertes Stegbeulen
Dass der Flansch in den Steg einbeult, wird verhindert, wenn folgendes Kriterium eingehalten ist:

${\frac {h_{w}}{t_{w}}}<{\frac {k\cdot E}{f_{yd}}}\cdot {\sqrt {\frac {A_{w}}{A_{fc}}}}$(Eurocode 1993-1-5 Gleichung 8.1)

mit

A_w= Stegfläche

A_cf= effektive Querschnittsfläche des Druckflansches

k= 0,55 für elastische Bemessung

${\frac {h_{w}}{t_{w}}}={\frac {600}{3}}=200$

${\frac {k\cdot E}{f_{yd}}}\cdot {\sqrt {\frac {A_{w}}{A_{fc}}}}={\frac {0{,}55\cdot 210000}{355}}\cdot {\sqrt {\frac {3\cdot 600}{7\cdot 91}}}=546{,}9$

200 < 546,9

Flanschinduziertes Stegbeulen ist ausgeschlossen.

---

Allgemein:Inhaltsverzeichnis ; Glossar ; Zahlen

Rechenbeispiel: Allgemeiner Lösungsweg ; erstes ; zweites ; drittes ; viertes

Norm: EuroB ;DINS ;EuroS ;DINB ;Zusammenfassung ;Variation der Geometrie