Gehirn und Sprache: Gehirn und Musik
Wir haben es geschafft, die komprimierende Tätigkeit der Sprache mit mathematischen und neurophysiologischen Überlegungen in einen skizzierten Zusammenhang zu stellen. Die menschlichen Sprachfähigkeiten sind jedoch nicht vollständig erfasst, solange der musikalische Bereich darin fehlt.
Musik ist auch eine Sprache, aber sie teilt nicht klar umgrenzte Vorstellungen mit wie die Wörter, sondern eher klar umrissene Gefühle. Trauer kann nicht überwältigender dargestellt werden, als im zweiten Satz von Beethovens Eroica oder in Bruckners 7. Sinfonie. Religiöse Gefühle sind bei J.S. Bachs Orgelmusik so wenig zu überhören wie in einem Gospelsong, und in Mozarts Opern werden durchgängig die wandelbaren Gefühle der Darsteller in Töne umgesetzt, so dass deren Innenleben in allen Nuancen verständlich hörbar wird.
Fragen wir also weiter: Mit welchen mathematischen und neurophysiologischen Mitteln können die Menschen den Bereich der Töne zur Darstellung und Modulation ihrer Gefühlswelt nutzbar machen.?
Die Grundlagen
[Bearbeiten]Die Grundlagen der musikalischen Sprache sind Rhythmus und Harmonie, die beide bekanntlich in einer mathematischen Darstellung erfasst werden können: Die Mathematik der Harmonie ergibt sich aus den ganzzahligen Schwingungsverhältnissen der Intervalle, im Rhythmus können wir die messbare und abzählbare zeitliche Gestaltung von Metrum, Betonungen usw. zur mathematischen Betrachtung heranziehen.
Es macht Staunen, dass die Sprache der Gefühle so fest mit mathematisch beschreibbaren Prinzipien verbunden ist, und das Staunen wird noch verstärkt durch die Tatsache, dass die musikalische Sprache keine nationalen Grenzen wie andere Sprachen hat; Musik wird international von allen Menschen verstanden (wie auch die Mathematik!).
Um diesem Staunen nachzugehen, schlage ich einen gedanklichen Weg ein, der die Musik vorwiegend als eine Sprache des Körpers auffasst. Gefühle spüren wir ja über den Körper, wenn wir verliebt sind (Herzklopfen), Wut haben (Bauchschmerzen), meditieren (Wohlgefühl), Hunger und Durst leiden usw. Dementsprechend kann Musik nicht nur die Gefühle, sondern den ganzen Körper beeinflussen, mit Macht in die Beine gehen, eine Gänsehaut verursachen, einschläfern, Tränen erzeugen usw., und die dazugehörigen Gefühle stellen sich ein.
Für ein mathematisches Verständnis liegt ein Vorteil der körperlichen Betrachtung darin, dass von unserem Körper bestimmte Eigenschaften, die der Musik zu Grunde liegen, in Zahlenverhältnissen erfasst werden können. Gefühle lassen sich nicht direkt messen, sie werden nur über dem Umweg der körperlichen Symptome in Zahlen erfassbar.
Rhythmus
[Bearbeiten]Eine messbare Grundlage jeder Musik, ihr Rhythmus, geht aus der rhythmischen Natur der Lebensvorgänge hervor.
Musik ist eine rhythmische Tätigkeit im bewußten Dasein der Menschen. In den vorangegangenen Abschnitten wurde beschrieben, wie nicht nur die Bewegungen, sondern auch die dahinter wirksamen Gehirnaktivitäten der bewußten Wahrnehmung und Handlungskontrolle auf einer rhythmischen Grundlage basieren.
Man kann demnach erwarten, dass ein „Pulsschlag des Geistes“ sich in der rhythmischen Dimension der Musik besonders deutlich zu erkennen gibt.
Betrachten wir den Tempobereich, in dem sich gewöhnlich der musikalische Rhythmus bewegt: Grob liegt das Spektrum musikalischer Tempi zwischen 60 und 140 bpm (Taktschläge pro Minute). Diese Taktschläge beziehen sich im Normalfall auf Viertelnoten, die noch in Achtel und Sechzehntel unterteilt werden können. Dieser Bezug auf Viertelnoten wird auch die Zählzeit genannt, weil es ein gut mitzählbares Tempo ist, während die schnelleren Notenwerte zum Zählen nicht mehr geeignet sind.
Tempo 140 ist das schnellste Tempo, das noch kontrolliert (von Virtuosen) in Sechzehntelnoten gespielt werden kann. In einer Sekunde werden dann 140x4/60=9,3 Töne gespielt.
Unkontrolliert können noch mehr Töne gespielt werden, wenn z. B. ein Pianist mit der Faust in einer Sekunde über die ganze Tastatur gleitet.
Interessant ist in diesem Zusammenhang die moderne elektronische Musik. Obwohl die körperlichen Beschränkungen bei dieser Musik wegfallen, weil die Musikcomputer mühelos noch schnellere Tempi erzeugen können, zeigt die Praxis der Diskotheken auch bei dieser Musik eine Grenze bei ca. 140 bpm. Es scheint so, dass bei diesem exstatischen Tempo von den Tänzern keine Steigerung mehr erwünscht ist, eine ästhetische Grenze.
Wichtiger als das schnellste Tempo sind die beliebigen Variationen des Tempos, in denen die Musiker stufenlos jeden von einem Metronom, Dirigenten oder Mitspieler vorgegebenen Wert aufnehmen können. Wie schnell der innere Arbeitstakt einen Rhythmus aufnehmen kann, weiß jeder Musiker. In der Regel genügen drei bis vier vorgegebene Taktschläge, damit alle Mitspieler exakt synchron das betreffende Tempo beginnen und zeitgleich durchhalten können.
Aber nicht nur die Ausführenden, auch die Zuhörer geraten augenblicklich unter den Einfluß, welchen ein spezieller Rhythmus auf unser Gehirn ausübt, und diese Resonanz des internen Taktgebers moduliert die Gefühle der Anwesenden in einer ganz spezifischen Weise. Dazu wippen viele mit den Füßen oder nehmen den Rhythmus in anderen Bewegungen ihres Körpers auf. Es gibt keine traurige Musik in flottem Tempo und keine jauchzende Freude in sehr langsamer Musik, aber das Gegenteil hört man oft, weil die musikalische Manipulation der Rhythmen eine genau bestimmbare, physiologische Wirkung auf die Gefühle hat.
Mit steigender Beatfrequenz wird die innere Anspannung bis zur Grenze von 140 bpm immer größer, sehr langsame Rhythmen wirken entspannend, können einschläfern. So verstehen wir, dass der Schlußsatz in allen Sinfonien immer der Schnellste ist, und ähnliche Gesetze auch in der Diskothek gelten. Die Aufgabe des DJ, des Mannes, der in der Disco die Platten auflegt und für die Stimmung sorgt, besteht darin, im Laufe des Abends durch gezielte Auswahl der Titel eine kontinuierliche Steigerung des Tempos von ca. 80-140 bpm auf der Tanzfläche zu steuern. Man könnte sagen, er führt sein Publikum an der rhythmischen Leine.
Wie exakt sich die Menschen aller Erdteile in ihrem musikalisch-rhythmischen Verhalten ähnlich sind, ist in allen Musikkulturen, besonders natürlich bei den Trommlern, feststellbar.
So genaue interkulturelle Übereinstimmung läßt sich als biologisch bedingte Ähnlichkeit verstehen, der „Pulsschlag des Geistes“ ist in allen menschlichen Gehirnen ähnlich wirksam.
Es wurde im vorigen Kapitel bereits erörtert, wie dieser cerebrale Pulsschlag die sensomotorischen Handlungen durch den ständigen Wechsel von Handlung und Kontrolle optimieren kann, weshalb der Handlungsrhythmus auf die halbe Taktfrequenz begrenzt ist. Bei Musikern können wir davon ausgehen, dass ihre Handlungskontrolle durch tägliche Übungen optimal trainiert ist. Wenn wir von der 140 bpm-Grenze ausgehen, kommen wir bei 9,3 Tönen pro Sekunde auf eine Taktfrequenz von 18,6 Hz. Es kommt nicht genau auf die Zahl hinter dem Komma an, aber genau diesen Frequenzbereich kennen wir bereits als eine wichtige Grenze in der Musik; sie trennt den Bereich des Rhythmus vom Bereich der Töne.
Schallwellen, deren Frequenz langsamer ist(<18), hören wir als einzelne (diskrete) Ereignisse, während wir oberhalb 18Hz nur noch kontinuierliche Töne hören. Weil diese Verschmelzungsgrenze bei ca. 18Hz auch im optischen Kanal (Kino) feststellbar ist, können wir in den Hirnwellen gleicher Frequenz den umfassenden Taktgeber vermuten, der im Gehirn die Grenze der zeitlichen Auflösung festlegt. Dann läßt sich das Verschmelzungsphänomen so deuten, dass der Eindruck von ununterbrochener Dauer entsteht, wenn jede Periode des Arbeitstaktes über einen längeren Zeitraum hinweg die gleiche oder wenig veränderte Information erhält.
Harmonie
[Bearbeiten]Man könnte nach dem Sinn dieser Grenze fragen, wofür dient diese Umwandlung diskreter Wellen in kontinuierliche Töne? Eine sinnvolle Antwort ist die: Wenn wir diskrete Ereignisse >18Hz nicht mehr wahrnehmen können, weil unser cerebraler Taktgeber dafür zu langsam ist, dann ist uns mit der Unterscheidung von Tonhöhen immer noch sehr gut zur Orientierung gedient. Das Gehör ist zur Orientierung wichtiger als die Augen, weil es auch in der Dunkelheit oder im Wald aus allen Himmelsrichtungen noch Signale aufnehmen kann, wo die Augen versagen. Unsere Umwelt ist oft erfüllt mit unterschiedlichsten Frequenzgemischen, die viel zu schnell und zu kompliziert schwingen, um von uns als diskrete Wellenform erkannt zu werden. Unser Gehör kann aber aus dem Kontinuum der Töne nicht nur die Grundschwingungen, sondern gleichzeitig auch die Obertöne sehr fein differenziert erkennen, wenn es zum Beispiel eine Flöte von einer Klarinette unterscheidet. Mit ihrer Tonhöhe können wir die Unterschiede der Frequenzen sehr genau wahrnehmen und damit die feinsten Verstimmungen zwischen zwei Saiten oder Instrumenten korrigieren. Darüber hinaus können wir, wie Pythagoras von Samos vor Jahrtausenden bewies, mit dem Gehör sehr genau harmonische bzw. ganzzahlige Verhältnisse zwischen verschiedenen Tönen identifizieren und damit die Intervalle bestimmen. Der Philosoph fand heraus, dass die musikalischen Intervalle (Sekunde, Terz, Quarte, Quinte, Sexte, Septime und Oktave ) auf ganzzahligen, „harmonischen“ Verhältnissen der Saitenlängen beruhen, das Gehör also mathematische Verhältnisse der Tonhöhen sehr genau analysieren und bestimmen kann. Die Grundlagen der abendländischen Harmonielehre wurden aus dieser Erkenntnis entwickelt.
Diese gut bekannte Tatsache dient als Grundlage für alle Musik, die nicht nur Rhythmus, sondern auch Harmonie und Melodie in ihren Ablauf einschließt. Die musikalischen Intervalle sind die Basis von Harmonie und Melodie, und mit der Oktave und der Quinte ist dieses Fundament ebenso international wie die rhythmischen Grundlagen. Oktave und Quinte sind in allen Musikkulturen als herausragende Intervalle vertreten, deren exakte Bestimmung nur der analysierenden Qualität des menschlichen Gehörs zu verdanken ist.
Diese Fähigkeit, harmonische Frequenzverhältnisse mit großer Genauigkeit wahrzunehmen, ist Voraussetzung für Musik, aber sie bedarf immer noch einer Erklärung.
Die Frage lautet: Wie ist es uns möglich, in zwei Tönen mit sehr verschiedener Höhe eine Art von Verwandtschaft zu hören, der wir den Begriff „Harmonie“ zuordnen, wohinter sich ein ganzzahliges Verhältnis der Schwingungen verbirgt?
Wenn wir zwei Töne im Abstand einer Oktave hören, dann ist das Gefühl der Verwandtschaft beider Töne derartig stark, dass wir beiden Tönen sogar den gleichen Namen geben, zum Beispiel den tiefen Ton C nennen und den höheren c, dann folgend c´, usw. Die Oktavverwandtschaft ist bekanntlich Grundlage der Tonleiter, aber woraus erhält das Gehör diese Information von Verwandtschaft?
Bei der Beantwortung dieser Frage hilft uns auch nicht die Erkenntnis von Pythagoras, dass die Saitenlängen der Oktaven immer im Verhältnis 2:1 stehen, denn die Musiker oder Zuhörer wissen oft nichts von den Saitenlängen, wenn sie Oktaven wahrnehmen. Wenn ein Mann und ein Kind die gleiche Melodie singen, dann singen sie immer im Oktavabstand, auch ohne Bestimmung von Saitenlängen oder Frequenzverhältnissen, die diesen Saitenlängen entsprechen.
Es ist zunächst ein Rätsel, worauf das Gefühl von Verwandtschaft oder Ähnlichkeit basiert, das sich beim Hören einer Oktave einstellt. Die Frage erscheint noch schwieriger, wenn man bedenkt, dass die eng benachbarten Intervalle der Oktave, die große Septime und die kleine None, als starke Dissonanzen gelten und keinerlei Verwandtschaftsgefühl zum Grundton aufkommen lassen, sondern eine Spannung, die sich erst in der Oktave völlig auflöst.
Ähnliches gilt auch für die Quinte, die ein geschultes Gehör sehr genau aus allen Tonverhältnissen herausfinden kann und die immer ein Schwingungsverhältnis von 3:2 als Grundlage hat. Die Saiten der Streichinstrumente werden in Quinten gestimmt. So ist auch die Quinte weltweit in allen musikalischen Formen als vorherrschendes Intervall zu finden. Auch bei der Quinte finden wir eng benachbarte Töne (Tritonus = verminderte Quinte), die sehr unverwandt zum Grundton klingen und eine Spannung erzeugen, die sich in der Quinte auflöst.
Dialektik: Spannung und Entspannung
[Bearbeiten]Eine musikalische Grundregel lautet: Immer nur Entspannung ist langweilig, ständige Spannung ist unerträglich. Deshalb ist die meiste Musik auf einen häufigen Wechsel von Entspannung und Spannung ausgerichtet, wozu die konsonanten und dissonanten Intervalle gute Dienste leisten. Viele Musikstücke bestehen harmonisch hauptsächlich auf dem ewigen Wechsel von Tonika und Dominante, womit die Musik im Wechsel von Entspannung und Spannung voranschreitet. Der Dreiklang „Dominante“ baut auf der Quinte auf und enthält die große Septime und die None zur Tonika, also zwei Intervalle mit sehr dissonanter Spannung zum Grundton. Seinen Namen erhielt der Dreiklang auf der 5.Stufe sicher durch das dominante Streben zur Grundtonart, das wir in dieser harmonischen Stufe erleben.
Die Gefühle zwischen Entspannung und Spannung sind demnach sowohl mit rhythmischen als auch mit harmonischen Mitteln zu erzeugen und über die Wahl des Tempos und der Intervalle musikalisch zu beeinflussen.
Hörgewohnheiten
[Bearbeiten]Die Entwicklung der abendländischen Musiktheorie hat den harmonischen Bereich im Lauf der Jahrhunderte noch weiter differenziert, zum Beispiel in den Kategorien von Dur und Moll, in der Kadenzlehre und dem Kontrapunkt. Es ist hier nicht möglich, diese Entwicklung nachzuzeichnen, aber rückblickend kann gesagt werden, dass die harmonische Entwicklung der Musik auch eine Entwicklung der Hörgewohnheiten bewirkt hat.
Zum Beispiel war eine kleine Septime vor 300 Jahren noch eine heftige Dissonanz, die nur in der Dominante verwendet werden durfte und unbedingt in die Terz der Tonika aufgelöst werden mußte. Die vom Jazz beeinflußten Hörgewohnheiten empfinden diese Notwendigkeit und den dissonanten Charakter der Septime heute nicht mehr.
Unberührt vom Wandel der Hörgewohnheiten sind die Oktave und die Quinte immer noch die grundlegenden konsonanten Intervalle geblieben.. Eine Erklärung für dieses Phänomen haben wir bisher noch nicht.
Unbeantwortet ist die Frage, worauf das starke Gefühl einer Tonverwandtschaft beruht, wenn zu einem beliebigen Ton noch dessen Oktave oder Quinte gespielt wird. Warum erkennen wir präzise mit dem Gehör ein mathematisches Verhältnis in den Tönen und nehmen das 2:1-Verhältnis als Basis und Länge der Tonleiter?
Naturtöne
[Bearbeiten]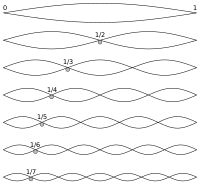
Vielleicht finden wir diese Erklärung eher in physikalischen und psychologischen Erkenntnissen. Der Physik (Akustik) verdanken wir die Erkenntnis, dass die natürlichen Töne nie aus reinen Tönen (Sinusschwingungen) bestehen, sondern immer die sogenannten Obertöne enthalten, die jedem Klang seine spezielle Klangfarbe geben. Die genau festgelegte Reihenfolge von harmonischen Intervallen, die mit jedem Ton zusammen schwingen, ist als Naturtonreihe bekannt. Jeder Klangerzeuger, zum Beispiel jedes Musikinstrument, bekommt durch seine Obertöne einen individuellen Klangcharakter, der nur mit Meßinstrumenten oder feinen Ohren erkannt werden kann. In der Obertonreihe sind alle Intervalle der Tonleiter enthalten, aber sie werden in sehr unterschiedlicher Ausprägung von den Instrumenten erzeugt. Die stärksten Obertöne sind bei den meisten Instrumenten die Oktaven und die Quinten.
Es ist sogar praktisch unmöglich, einen völlig reinen Sinuston zu erzeugen. Jeder Lautsprecher hat eine Resonanzfrequenz und einen Klirrfaktor, erzeugt also zu jeder Schwingung noch Obertöne. Mit Orgelpfeifen kommt man dem reinen Sinuston nahe, aber man vermeidet im Orgelbau diese Reinheit der Töne absichtlich und gibt den Registern der Orgel lieber Eigenschaften, die den Klang von Blasinstrumenten imitieren, z. B. Schalmei oder Trompete. Der Grund dafür liegt darin, dass die obertonarmen Töne, die reinen Sinusschwingungen, für uns leer und langweilig klingen.
Um diese uninteressante Wirkung der reinen Sinustöne zu verstehen, können wir einen Vergleich mit dem Wasser heranziehen: Es gibt in der Natur kein reines (destilliertes) Wasser. Aus jeder Quelle und Wasserleitung kommt das Wasser mit einer kleinen Menge von Salzen und Mineralien, die den Geschmack des Wassers beeinflussen. Deshalb schmeckt das Wasser aus verschiedenen Quellen unterschiedlich. Destilliertes Wasser können wir zwar herstellen, aber zum Trinken ist es völlig ungeeignet, weil ihm mit den Salzen jeder Geschmack fehlt, es schmeckt äußerst fade.
Genau so ist es mit den reinen Sinustönen, denen etwas fehlt, an dessen gesetzmäßige Coexistenz wir von Geburt an gewohnt sind. Gewohnt sind unsere Ohren besonders an die kräftigen Obertöne, die Oktave und die Quinte, und allein aus dieser Hörgewohnheit kann sich die starke subjektive Verwandtschaftsbeziehung ableiten lassen. Oktave und Quinte gehören als die kräftigsten Obertöne nun einmal zu jedem Ton, und so ergibt sich genau dann ein stimmiges Gefühl, wenn diese Töne auch noch durch andere Instrumente verstärkt werden, das paßt gut zusammen.
Umgekehrt sind die dissonanten Intervalle Tritonus, große Septime und kleine None in der Obertonreihe nicht ausgeprägt. Erklingen sie trotzdem, dann vermitteln unsere erschreckten Ohren das dissonante Gefühl, dass etwas nicht dazu gehört, nicht stimmt.
Es ist wie beim Wasser: Salz im Wasser sind wir gewöhnt, es ist auch in unserem Blut, Speichel, Urin und Schweiß vorhanden und wird von uns gern zum Würzen von Speisen genommen. Schmeckt das Wasser aber bitter, dann erregt es Abscheu und wird höchstens als Medizin getrunken. Gifte sind oft bitter, so dass die Abscheu vor Bitterem eine lebensrettende Reaktion sein kann.
Wie empfindlich unser Gehör auf unpassende Geräusche reagiert, kennt jeder Autofahrer. Das Motorgeräusch ist nicht zu überhören, aber es hat eine beruhigende Wirkung, solange keine ungewohnten Töne darin auftauchen. Fremde Geräusche wirken sofort als Alarmsignal.
So ähnlich können wir uns auch die konsonante und dissonante Wirkung der Intervalle psychologisch erklären.
Gemeinsamkeiten von Musik und Sprache
[Bearbeiten]Wir haben damit für die rhythmischen und harmonischen Elemente der Musik eine Verbindung zu körperlichen und psychologischen Vorgängen sowie mathematischen Verhältnissen grob beschrieben. Man kann in diesem Zusammenhang noch der Frage nachgehen, wie weit die Sprache der Wörter mit der Sprache der Töne auf Gemeinsamkeiten zurückgreift.
Rhythmus ist nur in der Poesie so prägnant wie in der Musik, aber auch beim normalen Sprechen kann das Sprechtempo den Gefühlszustand des Sprechers ausgedrücken, mit aufgeregtem, hastigen Gerede, Gestammel, betont langsamem Reden usw. Beim Singen treten die gemeinsamen rhythmischen Wurzeln von Musik und Sprache im Pulsschlag des Geistes klar hervor.
Unser feines Gehör für Obertöne bestimmt die harmonischen Gesetze, aber es hat auch bei der Sprache eine wichtige Aufgabe: Wir können durch die Obertöne die Stimmen von Männern, Frauen, Kindern, Freunden und Fremden sehr genau identifizieren, sogar am Telefon. Noch wichtiger sind die Obertöne für das Sinnverständnis von gesprochener Sprache, denn die Vokale und Konsonanten können von uns nur im hohen Frequenzbereich gut unterschieden werden. Der Grundton kann sogar fehlen, wie es technisch bei jedem Telefon der Fall ist. Die Sprache moduliert besonders die Frequenzen über 1000Hz, und die werden vom Telefon gut übertragen. Menschen, die durch einen Hörsturz der Tonbereich über 1000Hz nicht hören können, nehmen von der Sprache nur die Grundtöne als dumpfes Geräusch ohne erkennbaren Sinn auf. Auch die Altersschwerhörigkeit betrifft die hohen Frequenzen und beeinträchtigt deshalb das Sprachverständnis.
Die Leistungen, die unser Gehör im sprachlichen und musikalischen Handeln störungsfrei in jedem Augenblick beherrschen muß, sind nicht ohne Gedächtnis zu bewältigen. Hörgewohnheiten, wie sie in der Wirkung der Intervalle bemerkbar werden, sind tiefe Gedächtnisspuren aus dem ganzen Leben. Dass sprachliche Kommunikation auch an Lernprozesse in unserem bewußten Gedächtnisspeicher gebunden ist, mag trivial erscheinen, aber die besondere Art dieser Speicherung ist immer noch ungeklärt, und deshalb kann eine weitere Gemeinsamkeit von Sprache und Musik hier noch bedacht werden.
Artikulation
[Bearbeiten]Artikulation (Gliederung) ist seit Wilhelm v.Humboldts sprachtheoretischen Erkenntnissen die eigentliche Aufgabe des tätigen (sprechenden oder denkenden) Geistes.
Zitat: „...die Artikulation ist das eigentliche Wesen der Sprache, der Hebel, durch welchen sie und der Gedanke zu Stande kommt, der Schlußstein ihrer beiderseitigen, innigen Verbindung. Dasjenige aber, wessen das Denken, um den Begriff zu bilden, in der Sprache streng genommen bedarf, ist nicht eigentlich das dem Ohr wirklich Vernehmbare, oder um es anders auszudrücken, wenn man den artikulierten Laut in die Articulation und das Geräusch zerlegt, nicht dieses, sondern jene. Die Articulation beruht auf der Gewalt des Geistes über die Sprechwerkzeuge, sie zur Behandlung des Tons zu nötigen, welche der Form seines (des Geistes) Wirken entspricht...“ (III:192)
Buchstaben oder Silben werden artikuliert zu Wörtern, diese zu Sätzen, jene zu Abschnitten und Kapiteln, ganzen Bänden und Bibliotheken. Das Durchgängige ist dabei die Gliederung, die genau festlegende Reihenfolge der einzelnen Elemente, die nach Humboldt das Wesen der Sprache ausmacht.
Auch in der Musik stoßen wir auf genau vorgeschriebene Gliederungen, wenn wir die melodischen Abläufe ins Auge fassen. So wie in der Sprache die kleinsten Bauteile in beliebigen Verknüpfungen gegliedert werden können, ist es auch in der Musik mit den Tönen möglich. In der Sprache entstehen so ganze Sätze, und auch in der Musik benennt man größere melodische Zusammenhänge als Sätze.
Gliederung von Reihenfolgen ist in der Sprache wie in der Musik eine stetige Arbeit des rhythmisch tätigen Geistes. Wir können sprachlich und musikalisch beliebige Reihenfolgen erzeugen und uns diese Reihenfolgen genau merken.
Professionelle Schachspieler können sich tausende an Schachpartien Zug für Zug erinnern, Dirigenten haben ihr ganzes Repertoire verinnerlicht, Schauspieler ihre Rollen, Pianisten und viele Arten von Künstlern haben ein abendfüllendes Program genau vorgeschriebener Reihenfolgen in ihrem Gedächtnis.
Für eine theoretische Vorstellung von unserem Gedächtnis folgt daraus, dass es nicht nur als Speicher von Fakten, also von feststehenden Begriffen und Objekten, zu betrachten ist, sondern vorwiegend als Speicher für Reihenfolgen beliebiger Art.
Beispiel: Von einem Tag oder von einer Reise sind uns nicht nur die einzelnen Ansichten, Personen oder Ereignisse in Erinnerung, sondern besonders auch deren genaue zeitliche Reihenfolge.
Mit dieser alltäglich benutzten Fähigkeit zur Bildung und Speicherung von gegliederten Reihenfolgen kann der Mensch in der Sprache wie in der Musik zeitlich gestaltend tätig sein, das heißt, er kann beliebige Gliederungen erfinden und diese ganzheitlich zu einer Gestalt verbinden.
Invarianz
[Bearbeiten]Was genau unter dem Begriff Gestalt zu verstehen ist, läßt sich an einer Melodie erklären. Man kann eine Melodie in beliebig hoher oder tiefer Stimmlage singen und ihr Tempo willkürlich langsam oder schnell wählen, aber in jeder Variation wird diese Melodie als ganzheitliches Gebilde erkennbar bleiben. Die einzelnen Variationen der Melodie sind durch ihre Ähnlichkeit verbunden, das grundlegende Muster aller Varianten wird ihre Gestalt genannt.
Auch Mathematiker haben schon seit ewigen Zeiten großes Interesse an Gestalten (z. B. Dreieck, Kreis usw.). Sie benutzen für den Begriff Gestalt lieber den Begriff Invariante, meinen damit aber das Gleiche: invariant ist eine Struktur, die bei Tranformationen erhalten bleibt, zum Beispiel ein Kreis, der groß oder klein sein kann, mit roter oder blauer Farbe gezeichnet, er bleibt als Gestalt oder Invariante immer Kreis.
Invarianten bzw. Gestalten sind den Ideen Platons vergleichbar, aber ihre Herkunft ist nach heutiger Sicht nicht der Himmel, sondern die Gehirne von Säugetieren, besonders Menschen.
Genau wie Melodien oder geometrische Figuren lassen sich auch die Zahlen, Buchstaben, Wörter und sonstige Symbole unter dem Begriff Gestalt oder Invariante als Ergebnisse der artikuliernden Tätigkeit des Geistes begreifen.
In mathematisch knapper Sprache dürfen wir also sagen, dass der Sprache und der Musik die Bildung von artikulierten Invarianten gemeinsam ist.
Schrift
[Bearbeiten]Gemeinsam ist beiden menschlichen Ausdrucksmitteln auch eine Schriftform, die als eine Herstellungsvorschrift verstanden werden kann. So wie die Noten als Vorschrift zur Erzeugung musikalischer Gestalten dienen, sind die Buchstabenfolgen für uns Bauanleitungen für Wörter und Sätze.
Es wurde schon darauf hingewiesen, dass Herstellungsvorschriften mit genau festgelegten Reihenfolgen in der Mathematik unter dem Begriff Algorithmus zusammengefaßt werden. Ein Algorithmus, der die Vorschrift enthält, Zeichensequenzen zu produzieren, kann als komprimierte Darstellung dieser Sequenzen aufgefasst werden.
Zusammenfassung
[Bearbeiten]Will man die Gemeinsamkeiten von Sprache und Musik mit wenigen Worten, mathematisch, zusammenfassen, kann man demnach sagen:
Beide Formen der menschlichen Kommunikation artikulieren im rhythmischen Spektrum der Gehirnwellen und im Bereich der Töne invariante Reihenfolgen zur Gestaltung von Vorstellungen und Gefühlen. Beide können auch in einer Schriftform komprimiert werden.
