Gehirn und Sprache: Mandelbrot-Mengen
Mandelbrot-Menge oder Z n+1 = Z n2 + c
Einen Kontinent kann man allein durch Bilder schon kennen lernen, aber reichhaltiger sind die Eindrücke einer Reise.
Ähnlich ist es mit der MM (Abkürzung für Mandelbrot-Menge), die in vielen Ausschnitten in Wiki Commons unter Mathematik/ Fraktale/ Mandelbrot-set zu sehen ist.
Ein tieferes Verständnis ergibt sich mit jedem Computer, wenn darin ein kleines Programm (z. B. Winfrakt) aus dem Internet installiert wird, das die Figur selbst auf dem Bildschirm erzeugt. Wie mit einem Mikroskop kann man dabei Ausschnitte der Grenze vergrößern und wie auf einer Reise den unendlichen Formenreichtum erleben. Indem die Auswahl der Farben variiert wird, lassen sich unendlich viele schöne Bilder mit künstlerischem Reiz herstellen.
Zum philosophischen Staunen muss schon der extreme Kontrast zwischen den unendlichen Strukturen der MM und der simplen Formel ihrer Herstellung anregen.
Mit ihren Symmetrieeigenschaften, den Spiralen, Verästelungen und dem organischen Zusammenhang erinnert die MM auch an biologische Systeme, die ebenfalls aus kleinen Vorschriften äußerst komplexe Strukturen erzeugen.
Die Möglichkeit, die Ergebnisse dieses kurzen Algorithmus mit dem Computer sichtbar zu machen, ist auch hilfreich dabei, ihn als anschauliches Modell für Sinn und Sprache zu benutzen.
Betrachten wir die folgenden Bilder, auf denen die Ergebnisse der ersten Arbeitsschritte der Formel erkennbar sind.

Die erste Quadrierung erzeugt eine kreisförmige Grenze zwischen Blau und Schwarz, eine informationsarme Linie.
Wir können diese Grenze als Modell für den geistigen Zustand betrachten, den ein neugeborenes Kind am Beginn seiner geistigen Entwicklung hat, die berühmte „Tabula rasa“, noch völlig ohne Information.

Der zweite Iterationsschritt erscheint als symmetrische grüne Einbeulung, die zu einer Birnenform der Grenze führt..
Wenn wir darin ein Modell für die ersten Eindrücke sehen, die ein Baby erhält, kann auch wieder an die biblische Schöpfungsgeschichte erinnert werden.
Demnach entstand die Vielfältigkeit der Welt am Anfang aus groben, symmetrischen Einteilungen in Licht und Dunkel, Wasser und Land, Himmel und Erde usw.
Ähnlich muss das Neugeborene seine ersten Eindrücke in grobe Kategorien wie z. B. hell und dunkel, laut und still, warm und kalt usw. abgrenzen, wenn es sein eigenes Wissen von der Welt aufzubauen beginnt.

Der dritte Schritt macht mit neuen Dellen das Prinzip aller weiteren Schritte deutlich: Jede vorangegangene Einbuchtung wird durch zwei neue, kleinere Eindrücke verformt, wobei eine strenge Spiegelsymmetrie erhalten bleibt, aber eine Differenzierung der nun sich herausbildenden Längsachse bemerkbar ist.
Die Spitze im linken Teil der Längsachse steht als einziger Punkt noch mit dem ursprünglichen Kreis in Verbindung und wird es auch nach allen folgenden Arbeitsschritten des Algorithmus immer bleiben.
Die folgenden Schritte lassen das Prinzip immer klarer sichtbar werden: So wie man bei einem Menschenkind von seinen ersten Eindrücken spricht, die durch ständige Verfeinerung ein ständig sich differenzierendes Weltbild entstehen lassen, so entwickelt die Grenze der MM aus immer feiner werdenden Einbuchtungen einen kosmischen Formenreichtum in organischem Zusammenhang.
- 4.-30.Iteration
-
-
5.Schritt der MM
-
left
-
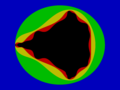
30. Schritt der MM
Die Bilder zeigen die ersten Wiederholungen eines endlos wiederholbaren Vorgangs. In den symmetrischen Umrissen der Grenzlinie wird schon eine „quasi natürliche“ Gestalt wie ein Käfer oder Blatt sichtbar. Es lässt sich auch erkennen, dass die Grenzlinie durch die neuen Eindrücke nie unterbrochen wird, also immer in ganzheitlichem Zusammenhang bleiben muss.
Bei dreißig Iterationen sind die neu hinzugefügten Einbuchtungen schon so klein, dass die Grenzveränderungen in der Grundfigur kaum noch erkennbar sind. Der Computer ermöglicht es aber, sehr kleine Ausschnitte wie mit einem Mikroskop zu betrachten.

Der Ausschnitt zeigt schon sehr deutlich die Selbstähnlichkeit der Grenze, die unendlich viele kleine Kopien der Grundfigur enthält. Auch die immer feiner werdende Verästelung der Grenze ist sichtbar, lässt aber nicht erahnen, welche unendlich feinen Strukturen noch darin verborgen sind.
Ich denke, dass mit diesen Bildern gezeigt werden kann, wie das mathematische Modell den Beginn des kindlichen Weltwissens und seine endlose Verfeinerung anschaulich machen kann.
Für ein Verständnis der sprachlichen Minimierung, zu dem die anfängliche Frage hinführen sollte, kann der C-Wert der Formel herangezogen werden. Das ist die (komplexe) Zahlenfolge, die jedem Teil der Grenze in der komplexen Ebene zugeordnet ist und diesen Teil konstruiert, wenn er in die Formel eingesetzt wird. Vergleichbar den Samen und den sprachlichen Zeichenfolgen ist auch der C-Wert eine kurze Zeichenfolge, die sehr komplexe Strukturen mit „pars pro toto“– Funktion erzeugen kann.
Um den Vorteil dieser Fähigkeit leicht zu begreifen, genügt wieder einmal der Vergleich mit der Digitaltechnik:
Jedes der obigen Bilder wird vom Computer aus 768x1024 Pixeln hergestellt und benötigt zur Speicherung 2,2 MB Speicherplatz. Um die Speichermenge zu verringern, lassen sich technische Algorithmen einsetzen, die „überflüssige Information“ heraussuchen und eine „abgespeckte Version“ erzeugen, die aber immer noch über 100 KB Speicher benötigen wird, um das Bild ohne bemerkbare Verluste zu rekonstruieren.
Wenn das Bild aber anstatt dessen als Ergebnis eines ständig wiederholten Algorithmus mit einem kurzen Controll-Wert C herstellbar ist, dann genügt es, diesen C-Wert zu speichern, um das Bild völlig verlustfrei wieder daraus zu rekonstruieren.
Es liegt auf der Hand, dass die Speicherung einer kurzen Zahlenfolge den Speicherbedarf extrem vermindert. Auch die Übertragungszeit hängt von der Größe einer Datei ab und wird durch die knappe Zeichenfolge so kurz, dass eine Kommunikation in „Echtzeit“ überhaupt erst möglich ist.
Zusammenfassend lässt sich sagen, dass die Visualisierung der MM am Computer wesentliche Aspekte von Sinn und Sprache anschaulich und begreifbar macht.
Wir haben damit ein Grundprinzip der sprachlichen Tätigkeit in einem sehr abstrakten, aber mit Hilfe des Computers sichtbar gemachten Algorithmus vor Augen. Das Prinzip besteht in der Sprache wie in der MM in einer Minimierung der unendlich komplexen Strukturen in kurze Folgen von Werten, die einen ständig wiederholenden Algorithmus steuern, der die Strukturen in einer organisch verbundenen Grenze rekonstruiert und das weitere Wachstum dieser Grenze modifiziert.
Das Modell bietet eine Erklärung für die nahezu unbegrenzte Speicherkapazität und die extrem schnelle Kommunikation der Menschen mit Hilfe der Sprache.
Ich will nicht verschweigen, dass diese Verbindung der geistigen Tätigkeit mit der Mandelbrot-Menge nicht über das rational-diskursive Denken hergestellt wurde, sondern mehr intuitiv mit einer unmittelbaren Einsicht begann, die mich durch ihre Einfachheit und Schönheit überzeugte...
Ich bin deshalb dankbar, hier die Möglichkeit zur komfortablen Darstellung mit Links und Bildern zu erhalten.
Hinweis:
Wer kein Programm zur Erzeugung der Mandelbrotmenge nutzen möchte, kann Videos im Internet dazu finden. Zum Beispiel dieses Video auf YouTube.