MathemaTriX ⋅ Exponentialfunktion

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

LINKS

 ACHTUNG! 
Zumindest Aufgabe 1 von jedem Aufgabentyp probieren,
sie sind unterschiedlich!

	lle	Gaben
	uf-

Theorie in Kürze (mit Geogebra)

$N(t)=N_{0}\cdot a^{t}$

N(t) ist die y-Achse (das y), t die x-Achse (das x). $N_{0}\$ist der "Anfangswert", also der Wert der Funktion (y-Wert) da, wo x Null ist (y-Achsenabschnitt). Die Basis der Potenzzahl (das ist ein "Änderungsfaktor") kann man auch als "Prozentsatz" interpretieren, z.B. $N(t)=N_{0}\cdot 0{,}964^{t}$ bedeutet, dass bei jeder Änderung der x-Achse (z.B. t Zeit in Jahren) um 1 (z.B. jährlich) bleiben (0,964=) 96,4% des vorherigen Wertes, also 3,6% (100%−96,4%) weniger.

Extra Merkmal der Exponentialfunktion: Halbwertszeit: Nach der gleichen Änderung des x-Wertes wird der Wert der Funktion (y-Wert) immer halbiert. Im Bild: Am Anfang (also an der Stelle 0) ist der Wert der Funktion $N(0)=N_{0}\cdot a^{t}=8000\cdot a^{0}=8000\cdot 1=8000$, nach 3,5 auf der x-Achse (also an der Stelle 3,5) ist N(t) =N(3,5)=4000 (also die Hälfte), nach noch 3,5 auf der x-Achse (also an der Stelle 7) ist N(t) 2000 (also die Hälfte der Hälfte) usw.
Die Halbwertszeit kann man berechnen, indem man am Wert Funktion die Hälfte des Anfangswerts einsetzt, z.B. $2350=4700\cdot 0{,}9^{t}$ (2350 ist die Hälfte von 4700) oder $0{,}5=0{,}6^{t}$ (hier "fehlt" der Anfangswert, er ist also 1, und die Hälfte von 1 ist ja 0,5). Entsprechend für eine "Verdoppelungszeit" oder ähnliches: $2=0{,}7^{t}$, $7{,}6=3{,}8\cdot 0{,}9^{t}$ usw.

Noch dazu: die Exponentialfunktion hat keine "Nullstellen": sie kommt immer näher zur x-Achse aber trifft diese nie!

Vergleich linearer und exponentieller Funktion:

	Lineare Funktion	Exponentialfunktion
Formel	$f(x)=s\cdot x+A_{y}$	$N(t)=N_{0}\cdot a^{t}$
Im Text erkennen durch	Steigung der Gerade (in der Formel: s) Änderungsrate y-Einheiten PRO eine x-Einheit	Basis der Hochzahl (in der Formel: a) Relative Änderung ("Prozent"-Änderung) des y-Wertes bei Änderung des x-Wertes um 1
Änderungsrate	Absolut (genauer Wert)	Relativ (Anteil, Prozent, -fach)
steigend ("nach oben") Wachstum	s>0 (positiv)	a>1
fallend ("nach unten") Abnahme	s<0 (negativ)	0<a<1
y-Achsenabschnitt (i.d.R. "Anfangswert")	$A_{y}$	$N_{0}$
Diagramme

Etwas leichter

1. 
   

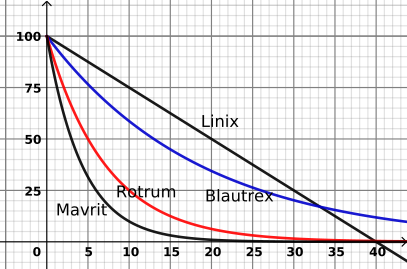
   4 verschiedene Waschmittel wurden auf ihre Effektivität geprüft. Das Diagramm zeigt welcher Anteil (in Prozent) des Schmutzes geblieben ist in Bezug auf die Zeit (in Minuten) Welches Waschmittel ist das wirksamste? Die Funktion für Rotrum lautet: $f(x)=k\cdot e^{-m\cdot x}.\$Lesen Sie aus dem Diagramm den Parameter $k$ ab! Die Halbwertszeit des Schmutzes für Blautrex ist 13 Minuten. Stellen Sie die entsprechende Exponentialfunktion auf! Bei Blautrex wurde die Dosis des Waschmittels erhöht, sobald 12% des Schmutzes übrig geblieben sind. Zum welchen Zeitpunkt war das? Benutzen Sie für die Lösung die Antwort der vorherigen Frage! Die Halbwertszeit für ein anderes Waschmittel ist 7 Minuten. Zeichnen Sie die entsprechende Exponentialfunktion (in dieses Diagramm)! Die Gleichung für Panax lautet: $100\ e^{-{\ln(2)x} \over 2}$. Um wie viel Prozent reduziert sich die Menge des Schmutzes nach 616 Sekunden? Für ein weiteres Waschmittel gilt folgende Gleichung: $M(t)=1,271\cdot 0,7417^{t}$ t die Zeit in Minuten M(t) die Menge des Schmutzes in g Kreuzen Sie die zutreffende(n) Aussage(n) an! Die Menge nimmt linear ab Die Menge nimmt um 25,83% pro Minute ab Die Menge nimmt um 27,1% pro Minute zu Die Menge nimmt im Laufe der Zeit immer schneller ab Die Menge nimmt um 74,17% pro Minute ab Die Menge am Anfang ist 1,271 g Linix weist im dargestellten Intervall eine lineare Abhängigkeit auf. Wie viel ist die Steigung der entsprechenden Funktion? Bitte auch die entsprechenden Einheiten angeben! Die allgemeine Gleichung für die hier dargestellte Vorgänge lautet: $M(t)=M_{0}\cdot a^{t}$. Geben Sie die Intervalle für a, t und M an! Die entsprechende Gleichung eines anderen Waschmittels lautet: $M(t)=2450\cdot 0{,}617^{t}$. Um wie viel Prozent reduziert sich der Schmutz nach 1 Minute? Wie viel ist die Halbwertszeit für Mavrit?

2. 
   

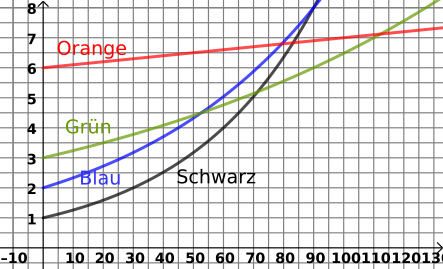
   Das Wachstum der Bevölkerung (in Millionen) in 4 verschiedenen (imaginären) Städten in Abhängigkeit von der Zeit in Jahren wurde im Diagramm zusammengefasst. In welcher Stadt wächst die Bevölkerung am schnellsten? Die allgemeine Funktion für das Wachstum lautet: $w(z)=m\cdot r^{z}.\$Lesen Sie aus dem Diagramm den Parameter $m$ für die Grüne Stadt ab! Die Verdoppelungszeit für die orangen-Stadt ist 50 Jahren. Stellen Sie die entsprechende Exponentialfunktion auf! In der orangen-Stadt hat das Wachstum aufgehört, nachdem die Bevölkerung sich verfünffacht hat. Zum welchen Zeitpunkt war das? Benutzen Sie für die Lösung die Antwort der vorherigen Frage! Die Verdoppelungszeit für eine andere Stadt, die am Anfang 1000000 Bewohner hat, ist drei Jahrzehnten. Zeichnen Sie die entsprechende Exponentialfunktion (in dieses Diagramm)! Die Gleichung für die blaue Stadt lautet: $B(x)=3\ e^{\frac {\ln(2)x}{100}}$. Um wie viel Prozent erhöht sich die Bevölkerung nach 61,5 Monate? Für eine andere Stadt gilt folgende Gleichung: $w(z)=1,0241\cdot 1,0138^{z}$ z die Zeit in Jahren w(z) die Bevölkerung in Millionen Kreuzen Sie die zutreffende(n) Aussage(n) an! Die Bevölkerung nimmt um 2,41% pro Jahr zu Die Bevölkerung nimmt um 1,38% pro Jahr ab Die Bevölkerung nimmt linear ab Die Bevölkerung nimmt um 1,38% pro Jahr zu Die Bevölkerung am Anfang ist 1,0241 Millionnen Die Bevölkerung nimmt im Laufe der Zeit immer schneller zu Die Schwarze Stadt weist im dargestellten Intervall eine lineare Abhängigkeit auf. Wie viel ist die Steigung der entsprechenden Funktion? Bitte auch die entsprechenden Einheiten angeben! Die allgemeine Gleichung für die hier dargestellte Vorgänge lautet: $w(z)=w_{0}\cdot r^{z}$. Geben Sie die Intervalle für w, r und z an! Die entsprechende Gleichung einer anderen Stadt lautet: $w(z)=4{,}1\cdot 1{,}003^{z}.\$ Um wie viel Prozent erhöht sich die Bevölkerung pro Jahr? Wie viel ist die Verdoppelungszeit für die grüne Stadt? Nach wie vielen Jahren haben die grüne und die Schwarze Stadt die gleiche Bevölkerung? Wie viel ist diese?

3. 
   

   4 verschiedene Antibiotika wurden in Petrischalen getestet. Im folgendem Diagramm ist der Prozentsatz der gebliebenen Bakterien in Abhängigkeit von der Zeit in Stunden dargestellt, sie nehmen Exponentiell ab (mit der Ausnahme von Baktrex). Welches Antibiotikum ist das wirksamste? Die Funktion für Vaktrin lautet: $f(x)=b\cdot e^{-m\cdot x}.\$Lesen Sie aus dem Diagramm den Parameter $b$ ab! Die Halbwertszeit der Anzahl der Bakterien für Vaktrin ist 9 Stunden. Stellen Sie die entsprechende Exponentialfunktion auf! In der Vaktrin-Petrischale wurde die Dosis des Antibiotikums erhöht, sobald 14% der Bakterien übrig geblieben sind. Zum welchen Zeitpunkt war das? Benutzen Sie für die Lösung die Antwort der vorherigen Frage! Ein im Land entwickeltes Antibiotikum hat 6 Stunden Halbwertszeit. Zeichnen Sie die entsprechende Exponentialfunktion (in dieses Diagramm)! Zeichnen Sie die entsprechende Exponentialfunktion (in dieses Diagramm)! Die Gleichung für Antibiox lautet: $100\ e^{-{\ln(2)x} \over 2}$. Um wie viel Prozent reduziert sich die Anzahl der Bakterien nach 504 Minuten? Für ein weiteres Antibiotikum gilt folgende Gleichung: $A(t)=1,471\cdot 0,8372^{t}$ t die Zeit in Stunden A(t) die Anzahl der Bakterien in Millionen. Kreuzen Sie die zutreffende Aussage an! Die Anzahl nimmt linear ab Die Anzahl nimmt um 83,72% pro Stunde ab Die Anzahl nimmt um 47,1% pro Stunde zu Die Anzahl nimmt im Laufe der Zeit immer schneller ab Die Anzahl nimmt um 16,28% pro Stunde ab Baktrex weist im dargestellten Intervall eine lineare Abhängigkeit auf. Wie viel ist die Steigung der entsprechenden Funktion? Bitte auch die entsprechenden Einheiten angeben! Die allgemeine Gleichung für die hier dargestellte Vorgänge lautet: $A(n)=a\cdot c^{n}$. Geben Sie die Intervalle für n, A und c an! Die entsprechende Gleichung eines anderen Antibiotikums lautet: $A(n)=476\cdot 0{,}8403^{t}$. Um wie viel Prozent reduziert sich die Anzahl der Bakterien nach 1 Stunde? Wie viel ist de Halbwertszeit für Antibiox?

4. 
   

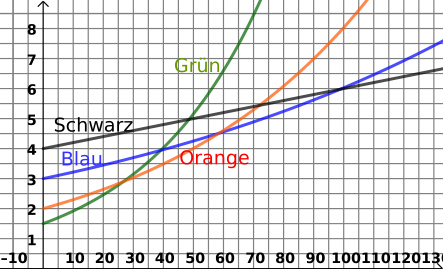
   Das Wachstum der Bevölkerung (in Millionen) in 4 verschiedenen (imaginären) Städten in Abhängigkeit von der Zeit in Jahren wurde im Diagramm zusammengefasst. In welcher Stadt wächst die Bevölkerung am schnellsten? Die allgemeine Funktion für das Wachstum lautet: $N(b)=v\cdot r^{b}.\$Lesen Sie aus dem Diagramm den Parameter $v$ für die Grüne Stadt ab! Die Verdoppelungszeit für die grüne Stadt ist 100 Jahren. Stellen Sie die entsprechende Exponentialfunktion auf! In der grünen Stadt hat das Wachstum aufgehört, nachdem die Bevölkerung sich verdreifacht hat. Zum welchen Zeitpunkt war das? Benutzen Sie für die Lösung die Antwort der vorherigen Frage! Die Verdoppelungszeit für eine andere Stadt, die am Anfang 500000 Bewohner hat, ist 0,1 Jahrhundert. Zeichnen Sie die entsprechende Exponentialfunktion (in dieses Diagramm)! Die Gleichung für die blaue Stadt lautet: $B(x)=3\ e^{\frac {\ln(2)x}{45}}$. Um wie viel Prozent erhöht sich die Bevölkerung nach 61,5 Monate? Für eine andere Stadt gilt folgende Gleichung: $w(z)=1,9241\cdot 0,9138^{z}$ z die Zeit in Jahren w(z) die Bevölkerung in Millionen Kreuzen Sie die zutreffende(n) Aussage(n) an! Die Bevölkerung nimmt um 8,62% pro Jahr zu Die Bevölkerung nimmt um 8,62% pro Jahr ab Die Bevölkerung nimmt linear zu Die Bevölkerung nimmt um 92,41% pro Jahr zu Die Bevölkerung am Anfang ist 1,9241 Millionnen Die Bevölkerung nimmt im Laufe der Zeit immer langsamer ab Die Orangen-Stadt weist im dargestellten Intervall eine lineare Abhängigkeit auf. Wie viel ist die Steigung der entsprechenden Funktion? Bitte auch die entsprechenden Einheiten angeben! Die allgemeine Gleichung für die hier dargestellte Vorgänge lautet: $N(b)=v\cdot r^{b}.\$Geben Sie die Intervalle für N, b und r an! Die entsprechende Gleichung einer anderen Stadt lautet: $N(b)=2{,}7\cdot 1{,}0023^{b}.\$ Um wie viel Prozent erhöht sich die Bevölkerung pro Jahr? Wie viel ist die Verdoppelungszeit für die grüne Stadt? Nach wie vielen Jahren haben die grüne und die Schwarze Stadt die gleiche Bevölkerung? Wie viel ist diese?

Etwas schwieriger

Hier klicken!

Exponentialfunktion Diagramm

Hier klicken!

Exponentialfunktion und Logarithmus

Hier klicken!