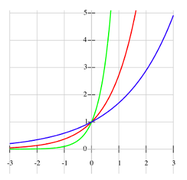
MathemaTriX ⋅ Funktionen allgemein
Erscheinungsbild
| ||||||||||||||||||
ACHTUNG!
Zumindest Aufgabe 1 von jedem Aufgabentyp probieren,
sie sind unterschiedlich!
Zumindest Aufgabe 1 von jedem Aufgabentyp probieren,
sie sind unterschiedlich!
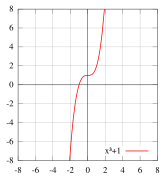
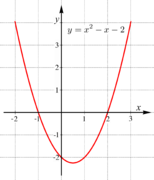
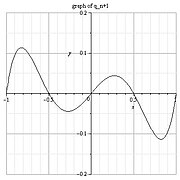
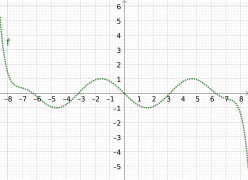
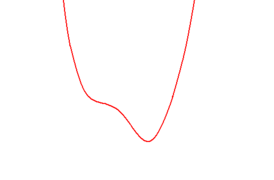
Polynomfunktionen Diagramm
[Bearbeiten]
-
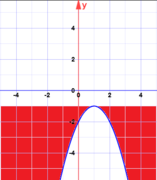
In den folgenden Diagrammen bestimmen Sie den
Grad der dargestellten Polynomfunktion, die Anzahl
ihrer Lösungen, ihr Monotonieverhalten in den
verschiedenen Intervallen, das Vorzeichen der
Koeffizienten der Potenz mit dem höchsten Grad und
wenn möglich den Wert des y-Achsenabschnitts!
-
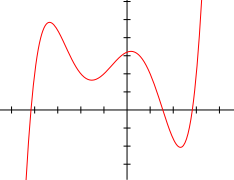
In den folgenden Diagrammen bestimmen Sie den
Grad der dargestellten Polynomfunktion, die Anzahl
ihrer Lösungen, ihr Monotonieverhalten in den
verschiedenen Intervallen, das Vorzeichen der
Koeffizienten der Potenz mit dem höchsten Grad und
wenn möglich den Wert des y-Achsenabschnitts!
-
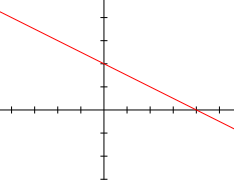
In den folgenden Diagrammen bestimmen Sie den
Grad der dargestellten Polynomfunktion, die Anzahl
ihrer Lösungen, ihr Monotonieverhalten in den
verschiedenen Intervallen, das Vorzeichen der
Koeffizienten der Potenz mit dem höchsten Grad und
wenn möglich den Wert des y-Achsenabschnitts!
-
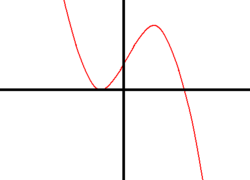
In den folgenden Diagrammen bestimmen Sie den
Grad der dargestellten Polynomfunktion, die Anzahl
ihrer Lösungen, ihr Monotonieverhalten in den
verschiedenen Intervallen, das Vorzeichen der
Koeffizienten der Potenz mit dem höchsten Grad und
wenn möglich den Wert des y-Achsenabschnitts!
Schnittpunkte von Funktionen in einem Diagramm
[Bearbeiten]
- Die Lösungen (Nullstellen) jeder Funktion.
- Den y-Achsenabschnitt jeder Funktion.
- Die Lösungen der Gleischungssysteme,
die aus folgenden Funktionen bestehen: - i) g und f ii) p und r iii) p und g
- iv)f und q v) r und f vi) g und h

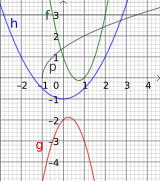
Im Bild sehen wir eine Polynomfunktion r(x) (gestrichelt),
drei quadratische Funktionen p(x), q(x) und h(x)
(zwei Kurven p und h nach oben und eine Kurve q nach
unten) und zwei lineare Funktionen g(x) und f(x)
(Gerade g nach unten rechts und Gerade f nach
oben rechts). Lesen Sie vom Diagramm ab:
- Die Lösungen (Nullstellen) jeder Funktion.
- Den y-Achsenabschnitt jeder Funktion.
- Die Lösungen der Gleischungssysteme,
die aus folgenden Funktionen bestehen: - i) g und f ii) p und r iii) p und g
- iv)f und q v) r und f vi) g und h
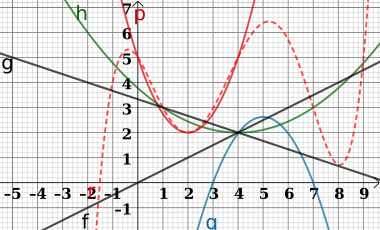
Im Bild sehen wir eine Polynomfunktion r(x) (gestrichelt),
drei quadratische Funktionen p(x), q(x) und h(x)
(zwei Kurven p und h nach oben und eine Kurve q nach
unten) und zwei lineare Funktionen g(x) und f(x)
(Gerade g nach unten rechts und Gerade f nach
oben rechts). Lesen Sie vom Diagramm ab:
- Die Lösungen (Nullstellen) jeder Funktion.
- Den y-Achsenabschnitt jeder Funktion.
- Die Lösungen der Gleischungssysteme,
die aus folgenden Funktionen bestehen: - i) h und f ii) g und d iii) c und f
- iv)e und h v) g und f vi) c und d

Im Bild sehen wir eine Polynomfunktion g(x) (gestrichelt),
drei quadratische Funktionen c(x), d(x) und e(x)
(zwei Kurven c und e nach oben und eine Kurve d nach
unten) und zwei lineare Funktionen h(x) und f(x)
(Gerade f nach unten rechts und Gerade h nach
oben rechts). Lesen Sie vom Diagramm ab:
Schnittpunkte von Funktionen in einem Text
[Bearbeiten]
-
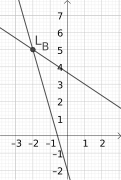
Gegeben sind die Funktionen
- Berechnen Sie die Lösungen (Nullstellen) jeder Funktion!
- Lesen Sie den y-Achsenabschnitt jeder Funktion ab!
- Finden Sie, ob der Punkt P:(2|−5)
- zu mancher der Funktionen gehört!
- Lesen Sie die Steigung der beiden Geraden ab!
- Berechnen Sie die Lösungen der folgenden Gleichungssysteme
- i) g und f, ii) p und q, iii) p und g
-
Gegeben sind die Funktionen
- Berechnen Sie die Lösungen (Nullstellen) jeder Funktion!
- Lesen Sie den y-Achsenabschnitt jeder Funktion ab!
- Finden Sie, ob der Punkt P:(2|−5)
- zu mancher der Funktionen gehört!
- Lesen Sie die Steigung der beiden Geraden ab!
- Berechnen Sie die Lösungen der folgenden Gleichungssysteme
- i) g und f, ii) p und q, iii) f und q
-
Gegeben sind die Funktionen
- Berechnen Sie die Lösungen (Nullstellen) jeder Funktion!
- Lesen Sie den y-Achsenabschnitt jeder Funktion ab!
- Finden Sie, ob der Punkt P:(0{,}625|−0{,}6875)
- zu mancher der Funktionen gehört!
- Lesen Sie die Steigung der beiden Geraden ab!
- Berechnen Sie die Lösungen der folgenden Gleichungssysteme
- i) g und f, ii) p und q, iii) p und g
-
Gegeben sind die Funktionen
- Berechnen Sie die Lösungen (Nullstellen) jeder Funktion!
- Lesen Sie den y-Achsenabschnitt jeder Funktion ab!
- Finden Sie, ob der Punkt P:(1|)
- zu mancher der Funktionen gehört!
- Lesen Sie die Steigung der beiden Geraden ab!
- Berechnen Sie die Lösungen der folgenden Gleichungssysteme
- i) g und f, ii) h und q, iii) p und g
Umkehrfunktionen mit Umformen finden
[Bearbeiten]
-
Finden Sie die Umkehrfunktion:
-
Finden Sie die Umkehrfunktion:
-
Finden Sie die Umkehrfunktion:
-
Finden Sie die Umkehrfunktion:
Funktionserkennung in Diagramm
[Bearbeiten]
A) lineare Funktion, B) Polynomfunktion 2. Grades C) Wurzelfunktion, D) Polynomfunktion 3. Grades E) Polynomfunktion 4. Grades, F) Sinusfunktion G) Kosinusfunktion, H) quadratische Funktion, K) (natürlichen) Logarithmusfunktion, L) M) Exponentialfunktion, N) Umkehrfunktionenpaar |
|
Funktionserkennung in Text
[Bearbeiten]
|
| |||||||
Funktionsdiagramme Eigenschaften erkennen
[Bearbeiten]
-
Wählen Sie das jeweils richtige Diagramm und
- Wie viel ist der y-Achsenabschnitt bei jedem Diagramm?
- Wie viel ist die Steigung der linearen Funktionen?
- ist die quadratische Funktion.
- Bei welcher Funktion ist a negativ bzw. positiv?
- ist die exponentielle Funktion.
- ist die indirekte Proportionalität.
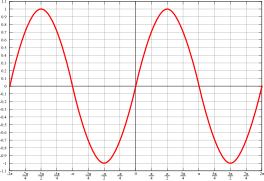
Bei welcher Funktion ist a negativ bzw. positiv? - In welchen Intervallen sind die quadratischen und die linearen
Funktionen, die Sinusfunktionen bzw die indirekte
Proportionalität steigend bzw. fallend? - Gibt es in irgendeinem Diagramm eine Funktion und
ihre Umkehrfunktion? - Gibt es in irgendeinem Diagramm eine Funktion und
ihre auf der y-Achse gespeigelte Funktion? Was gilt
in diesem Fall für f(x) und ihre Spiegelfunktion fs(x)?
beantworten Sie die entsprechende Frage!
-
Wählen Sie das jeweils richtige Diagramm und
- Wie viel ist der y-Achsenabschnitt bei jedem Diagramm?
- Wie viel ist die Steigung der linearen Funktionen?
- ist die quadratische Funktion.
- Bei welcher Funktion ist a negativ bzw. positiv?
- Wo ist der Betrag von a größer?
- ist die exponentielle Funktion.
- Bei welcher Funktion ist a negativ bzw. positiv?
- Wo ist der Betrag von a größer?
- Bei welcher Funktion ist a negativ bzw. positiv?
- Wo ist der Betrag von a größer?
- ist die indirekte Proportionalität.
Bei welcher Funktion ist a negativ bzw. positiv? - In welchen Intervallen sind die quadratischen und die linearen
Funktionen, die Sinusfunktionen bzw die indirekte
Proportionalität steigend bzw. fallend? - Gibt es in irgendeinem Diagramm eine Funktion und
ihre Umkehrfunktion? - Gibt es in irgendeinem Diagramm eine Funktion und
ihre auf der y-Achse gespeigelte Funktion? Was gilt
in diesem Fall für f(x) und ihre Spiegelfunktion fs(x)? - Wie viel ist die Amplitude und die Periode in den Sinusfunktionen?
Gibt es bei manchen eine Winkelverschiebung?
beantworten Sie die entsprechende Frage!
































































![{\displaystyle d(V)={\sqrt[{3}]{\frac {V+7}{\pi }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/657b9d1aec0c3dcd9daa6f3f545f354cb503da44)
![{\displaystyle \ p(t)={\sqrt[{4}]{t^{3}-5\ }}\ +k}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cac5741eb9f03317adb2b1085405085aa2105303)
![{\displaystyle t(p)={\sqrt[{3}]{(p-k)^{4}+5}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0634335dceb7664b06bfafed1b7dae718e9f196d)
![{\displaystyle \ n(y)=\tan({{\sqrt[{5}]{y}}-5\ })\ +\pi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e0445a173ee4d4ca8d9506489abf71315597970)