MathemaTriX ⋅ Theorie. Geometrische Konstruktionen

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Inhalt Ein-Aus- klappen

AUFGABEN

KAPITEL Grundrechenarten Bruchrechnungen $-{\tfrac {\cdot \ +}{\ :\ }}$ Schlussrechnung Prozentrechnung Exponentialfunktion Logarithmus Arbeiten mit Termen $\mathbb {X} ^{2}$ Zahlendarstellungen Mengentheorie Aussagenlogik ${\begin{matrix}\mathbb {R} :=\\\mathbb {Q} \cup \mathbb {I} \end{matrix}}$ Einheiten $cm^{2}$ Statistik und Wahrscheinlichkeit Geometrische Konstruktionen Geometrie der Ebene Geometrie des Raums Diagramme Funktionen $f(x)$ Lineare Gleichungssysteme ${\begin{smallmatrix}{a_{1}\ b_{2}}\\{a_{2}\ b_{2}}\end{smallmatrix}}$ Trigonometrische Funktionen Vektoren Differentialrechnung $^{dy}/_{dx}$ Integralrechnung $\textstyle \int _{a}^{b}dx$ Folgen $a_{n}$ Beweise $a\rightarrow b$

Dreieckskonstruktionen

Dreieckskonstruktionen Einführung

Ein Dreieck ist eine geschlossene ebene Figur mit drei Strecken als Seiten. Die Dreieckkonstruktion ist von selber aus eine Herausforderung und ein Weg, einige Fertigkeiten zu üben. Sie gilt als Vorbereitung und Einführung allgemein für die Geometrie. Ziel ist ein Dreieck mit drei vorgegebenen Größen nur mit Hilfe eines Zirkels und eines Lineals zu konstruieren. Solche Konstruktionen waren sehr beliebt schon in der Antike. Wichtig ist zu wissen, dass die Summe aller Winkel genau 180° und jeder Winkel kleiner als 180° ist und dass keine Seite größer als die Summe der anderen zwei sein darf.

Es gibt vier verschiedenen Aufgabensorten, je nachdem, was gegeben ist. Wenn drei Seiten gegeben sind, dann spricht man von der SSS (Seite-Seite-Seite) Konstruktion. Wenn zwei Seiten und der dazwischen liegender Winkel gegeben sind, spricht man von der SWS (Seite-Winkel-Seite) Konstruktion. Wenn zwei Seiten und ein Winkel, der nicht zwischen den Seiten liegt, gegeben sind, dann spricht man von der SSW Konstruktion (Seite-Seite-Winkel). Wenn zwei Winkel und eine Seite gegeben sind, dann spricht man von der WSW Konstruktion (Winkel-Seite-Winkel).

Konventionen

Die Seiten jedes Dreiecks werden klein geschrieben (mit a, b und c). Die gegenüber liegenden Eckpunkte werden entsprechend groß geschrieben mit (A, B und C). Für die entsprechenden Winkel werden die griechischen klein Buchstaben α, β und γ benutzt (Alpha, Beta und Gamma). Also, wenn A der Eckpunkt ist, ist der Winkel an diesem Punkt α und die gegenüberliegende Seite a. Man zeichnet die Seiten nacheinander im Gegenuhrzeigersinn. Unten zeichnet man i.d.R. die Seite a.

SSS Konstruktion

Wenn drei Seiten gegeben sind, geht man wie in den folgenden Bildern vor. Die Schritte sieht man am Rand jedes Bildes.

Die ganzen Schritten kann man in der folgenden Animation sehen:

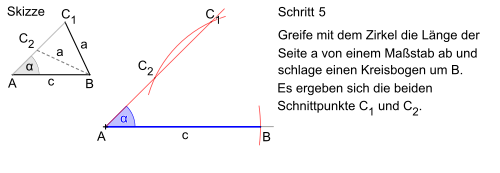
SWS Konstruktion

Wenn zwei Seiten und der Winkel dazwischen gegeben sind, geht man wie in den folgenden Bildern vor. Die Schritte sieht man am Rand jedes Bildes.

Die ganzen Schritten kann man in der folgenden Animation sehen:

SSW Konstruktion

Wenn zwei Seiten und ein Winkel, der nicht zwischen diesen Seiten steht, gegeben sind, geht man wie in den folgenden Bildern vor. Die Schritte sieht man am Rand jedes Bildes.

Die ganzen Schritten kann man in der folgenden Animation sehen:

WSW Konstruktion

Wenn zwei Winkel und eine Seite gegeben sind, gibt es zwei Möglichkeiten. Wenn die zwei Winkel am Rand der gegebenen Seite stehen, dann geht man wie in den folgenden Bildern vor. Wenn einer der gegebenen Winkel, der Winkel gegenüber der gegebenen Seite ist, dann berechnet man erst den dritten Winkel (180°− die anderen beiden Winkel) und geht dann vor, wie in den folgenden Bildern. Die Schritte sieht man am Rand jedes Bildes.

Die ganzen Schritten kann man in der folgenden Animation sehen:

Herzlichem Dank an Petrus3743, der die Seite vorbereitet hat und die Erlaubnis gegeben hat, sie hier zu benutzen. Für weitere Konstruktionen kann man seinem Link folgen

Die Klassischen Probleme der antiken Mathematik

Als Die drei antiken Probleme oder Klassische Probleme der antiken Mathematik werden bezeichnet:

• die Quadratur des Kreises
• die Dreiteilung des Winkels
• die Verdoppelung des Würfels

Sie sind erwiesenermaßen als sogenannte Konstruktion mit Zirkel und Lineal nicht (exakt) lösbar. Lässt man jedoch ein weiteres Hilfsmittel zu, sind exakte Lösungen machbar. Im Folgenden werden Konstruktionen mit Hilfsmitteln, wie z. B. ein Lineal mit Markierung des relevanten Wertes, die Verwendung von Kurven sowie Näherungskonstruktionen (Approximationen) beschrieben.

Die Quadratur des Kreises

Die Quadratur des Kreises ist eines der bekanntesten Probleme aus der Geometrie der Antike. Viele Mathematiker und Laien versuchten vergeblich eine exakte Lösung allein mit Zirkel und Lineal (die euklidischen Werkzeuge) zu finden. Ferdinand von Lindemann bewies 1882 die Unmöglichkeit einer solchen Konstruktion. Sie ist äquivalent mit der Rektifikation des Kreises, bei der man versucht konstruktiv den Kreisumfang als gerade Strecke darzustellen.

In vielen Ländern ist Quadratur des Kreises der Begriff für eine unlösbare Aufgabe.

Die Aufgabe

Die Aufgabe besteht darin, in endlich vielen Konstruktionsschritten ein Quadrat zu konstruieren, dessen Flächeninhalt gleich dem Flächeninhalt eines vorgegebenen Kreises ist. Die Länge der Seite des gesuchten Quadrates ist gleich $r\cdot {\sqrt {\pi }}$; darin ist $r$ der Radius des vorgegebenen Kreises.

Konstruktion mithilfe der Quadratrix des Hippias

Für die Rektifikation des Kreises fand der griechische Sophist Hippias von Elis (um 350 v. Chr.) die nach ihm benannte Kurve Quadratrix des Hippias als zusätzliches Konstruktionsmittel. Darstellbar ist diese Kurve z. B. mit einer Software für Dynamische Geometrie (wie die nebenstehende Zeichnung), als Ausdruck der Kurve auf Papier oder als eine maschinell angefertigte Schablone.

Im kartesischen Koordinatensystem wird die Quadratrix ($a=1$) beschrieben durch die Gleichung:

$x=y\cdot \cot \left({\frac {\pi }{2a}}\cdot y\right)$

Konstruktionsschritte

1. Keis mit Radius ${\overline {AB}}=a=1$
2. Halbgerade ab $A$
3. Senkrechte ${\overline {DE}}$ zu ${\overline {AB}}$ durch $A$
4. Quadrat $ABCD$ sowie Quadratrix (rote Linie) durch $D$ und $E$ nach obiger Formel; dabei ergibt sich der Punkt $F={\tfrac {2}{\pi }}$
5. Strecke ${\overline {BC}}$ ab $C$ verlängern
6. Senkrechte zu ${\overline {AB}}$ mit Fußpunkt $F$ bis sie den Kreis in $G$ schneidet
7. Linie von $A$ durch $G$, bis sie die Verlängerung der Strecke ${\overline {BC}}$ in $H$ schneidet
8. Kreisbogen mit Radius ${\overline {AH}}$ bis auf die Halbgerade, dabei ergibt sich der Schnittpunkt ${\tfrac {\pi }{2}}$
9. Strecke ${\tfrac {\pi }{2}}$ verdoppeln, dabei ergibt sich der halbe Kreisumfang $\pi$
10. Halbkreis über ${\overline {A\pi }}$
11. Abschließende Linie ab $A$ bis auf die Verlängerung der Strecke ${\overline {BC}}$

• Somit ergibt sich mit ${\overline {AI}}={\sqrt {\pi }}$ die gesuchte Seite des Quadrates, dessen Flächeninhalt exakt gleich dem des Kreises ist.

Näherungskonstruktion

Mit mehr oder weniger Konstruktionsaufwand kann jede gewünschte Genauigkeit (geringer Fehler bezogen auf den Sollwert ${\sqrt {\pi }}$) erreicht werden. Die nun folgende weniger bekannte Näherung hat eine Genauigkeit die geringfügig besser ist als die, die mit dem Zu Chongzhi-Bruch ${\tfrac {355}{113}}$ (5. Jahrhundert) zu erreichen ist.

Konstruktionsschritte

1. Kreis mit beliebigem Radius $r$ um Mittelpunkt $M$
2. Quadrat $MBCA$ mit $r$ als Seitenlänge sowie Strecke ${\overline {CB}}$ über $B$ hinaus verlängern
3. Diagonale ${\overline {MC}},$ ergibt Schnittpunkt $D$
4. Parallele zu ${\overline {BC}}$ durch $D$ bis ${\overline {AC}},$ ergibt Schnittpunkt $E$
5. Halbkreis um $D$ ab $E$ im Uhrzeigersinn, ergibt Schnittpunkt $F$
6. Strecke ${\overline {DE}}$ halbieren in $G$
7. $G$ mit $C$ verbinden, ergibt Schnittpunkt $H$
8. Punkt $J$ so bestimmen, dass $|FJ|={\overline {MC}}={\sqrt {2}}\cdot r$
9. Punkt $J$ mit $H$ verbinden, ergibt Schnittpunkt $K$
10. Parallele zu ${\overline {BC}}$ ab $K$ bis Strecke ${\overline {MB}}$, ergibt Schnittpunkt $L$

• Wird die Strecke ${\overline {KL}}$ verdoppelt, ergibt dies die Seitenlänge $a$ eines Quadrates mit einem Flächeninhalt, der nahezu gleich dem des Kreises ist.

Fehlerbetrachtung bei einem Kreis mit Radius r = 1 [LE]:

Konstruierte Seite des Quadrates a = 1,772453865554221... [LE]

Soll-Seite des Quadrates a_s = ${\sqrt {\pi }}\cdot 1[LE]$ = 1,772453850905516... [LE]

Absoluter Fehler = a - a_s = 0,000000014648705... = 1,4648...E-8 [LE]

Fläche des konstruierten Quadrates A = a² = ‭3,141592705518100‬... [FE]‬‬

Soll-Fläche des Quadrates A_s = ${\pi }\cdot 1[FE]$ = 3,141592653589793... [FE]

Absoluter Fehler = A - A_s = 0,000000051928307... = 5,1928...E-8 [FE]

Fazit:

Sieben Nachkommastellen sind gleich denen von ${\sqrt {\pi }}$ bzw. sechs Nachkommastellen sind gleich denen von $\pi$.

• Bei einem Kreis mit dem Radius r = 100 km wäre der Fehler der Seite a ≈ 1,5 mm
• Bei einem Kreis mit dem Radius r = 10 m wäre der Fehler der Fläche A ≈ 5,2 mm²

Weblinks

 Quadratur des Kreises

 Beweis der Unmöglichkeit

 Konstruktion mit Zirkel und Lineal

 Hippias von Elis

 Quadratrix des Hippias

 Software für Dynamische Geometrie

 Nachkommastelle

 Zu Chongzhi-Bruch

 Konstruktion von Jacob de Gelder

Die Dreiteilung des Winkels

Die Dreiteilung des Winkels ist ein klassisches Problem, für das bereits die alten Griechen (5. Jahrhundert v. Chr.) versuchten eine Lösung zu finden.

Spezielle Winkel (siehe nebenstehendes Bild) können jedoch mit den euklidischen Werkzeugen gedrittelt werden, z. B. Winkel die ein ganzzahliges Vielfaches von 9° sind.

Die Aufgabe

Die Aufgabe besteht darin, in endlich vielen Konstruktionsschritten einen beliebigen Winkel allein mit Zirkel und unskaliertem Lineal in drei gleich große Winkel zu teilen. Erst 1837 gelang Pierre-Laurent Wantzel der Beweis, dass dies unmöglich ist.

Konstruktion mithilfe eines rechtwinkligen dreieckigen Lineals

Ludwig Bieberbach fand 1932 eine bemerkenswerte einfache Lösung. Hierfür benutze er einen – wie er ihn nannte – Rechtwinkelhaken als zusätzliches Konstruktionsmittel.

Konstruktionsschritte

(Die Animation hat am Ende 60 s Pause.)

1. Kreis mit beliebigem Radius $r$ um Mittelpunkt $A$
2. Erster Winkelschenkel ${\overline {PB}}$
3. Kreis um $P$ mit Radius ${\overline {PA}}$
4. Ersten Winkelschenkel ${\overline {PB}}$ ab $P$ verlängern, ergibt den Schnittpunkt $O$
5. Kreisbogen um $P$ mit Radius ${\overline {PB}}$
6. Zweiter Winkelschenkel ${\overline {PC}}$, ergibt im Scheitel $P$ den zu drittelnden Winkels $\delta$
7. Dreieckiges Lineal (z.B. ein Geodreieck) folgendermaßen auf die Zeichnung legen:

Der Scheitel des Winkels $90^{\circ }$ bestimmt auf dem Winkelschenkel ${\overline {PC}}$ den Punkt $S$, eine Kathete des Dreiecks verläuft durch den Punkt $O$ und die andere tangiert den Kreis um $A$.

8. Punkt $O$ mit $S$ verbinden sowie Tangente ab $S$ an den Kreis um $A$

Somit zeigt sich der oben genannte Rechtwinkelhaken (rot). Der von den Strecken ${\overline {OS}}$ und ${\overline {PS}}$ eingeschlossene Winkel ist exakt ${\tfrac {\delta }{3}}$

9. Parallele ab $P$ zu ${\overline {OS}}$, dabei ergeben sich der Wechselwinkel oder Z-Winkel ${\tfrac {\delta }{3}}$ und der Punkt $D$ auf dem Kreisbogen um $P$
10. Parallele ab $A$ zu ${\overline {PD}}$, dabei ergibt sich der Berührungspunkt $E$ der Tangente an den Kreis um $A$
11. Abschließende Linie ab $P$ durch $E$, bis sie den Kreisbogen um $P$ in $F$ schneidet

• Somit ist der Winkel $\delta$ exakt gedrittelt, denn es gilt

${\overline {PS}}=2\cdot \cos \left({\frac {\delta }{3}}\right)$

Näherungskonstruktion

Im Jahr 2011 sandte Chris Alberts eine außerordentlich gute Näherung einer Winkeldreiteilung an Rouben Rostamian (University of Maryland, Baltimore County). Die hier beschriebene Näherungskonstruktion ist eine starke Vereinfachung des Originals mit der folgendes erreicht wird:

• Ein großer Teil der Konstruktion liegt meist in der unteren Hälfte des Kreises $k_{1}$.
• Eine praktikable Dreiteilung des Winkels ab nahe $0^{\circ }$ bis $180^{\circ }$.

Konstruktionsschritte

1. Kreis $k_{1}$ mit beliebigem Durchmesser ${\overline {AB}}$ um Mittelpunkt $O.$
2. Winkelschenkel ${\overline {OA}}$ und Winkelschenkel ${\overline {OC}}$ schließen den Winkel $\alpha$ im Scheitel $O$ ein, ${\overline {OB}}$ und ${\overline {OC}}$ den Ergänzungswinkel $\gamma .$
3. Kreis $k_{2}$ um $O$ mit Radius ${\tfrac {1}{3}}{\overline {OA}}$; die Verlängerung des Winkelschenkels ${\overline {CO}}$ schneidet Kreis $k_{2}$ in $D.$
4. Durchmesser ${\overline {EF}}$ mit $\angle {EOA=45^{\circ }}$ und Verbindung des Punktes $D$ mit $E.$
5. Punkt $G$ auf Kreis $k_{2}$ so, dass $|EG|={\overline {EO}}.$
6. Strecke ${\overline {OF}}$ in $H$ halbieren, die anschließende Mittelsenkrechte von $|GH|$ schneidet ${\overline {OE}}$ in $I,$ ergibt $|IG|={\overline {IH}}.$
7. Parallele zu ${\overline {ED}}$ ab $I$ erreicht Kreis $k_{2}$ in $J.$
8. Parallele zu ${\overline {IJ}}$ ab $D,$ Punkt $K$ darauf so, dass ${\overline {JK}}={\overline {JE}}.$
9. Linie ab $J$ durch $K$ erreicht Kreis $k_{1}$ in $L,$ anschließend Linie ab $L$ bis $O.$
10. Parallele zu ${\overline {LO}}$ ab $D$ erreicht Kreis $k_{2}$ in $M.$
11. Strecke ${\overline {KE}}$ über $E$ hinaus verlängern, Punkt $N$ darauf so, dass ${\overline {MN}}={\overline {MD}}.$
12. Linie ab $M$ durch $N$ erreicht Kreis $k_{1}$ in $P.$
13. Bestimme Punkt $Q$ so, dass Winkel $POQ=30^{\circ },$ Verbindung $Q$ mit $O$ ergibt den Winkel $AOQ=\beta .$
14. Mittelsenkrechte von $|CQ|$ schneidet $k_{1}$ in $R,$ verbinde $R$ mit $O.$
15. Bestimme Punkt $S$ so, dass Winkel $QOS=120^{\circ }.$
16. Abschließende Verbindung $S$ mit $O$ ergibt Winkel $SOB=\delta .$

• Der Winkel $AOQ=\beta$ ist nahezu gleich einem Drittel des Winkels $AOC=\alpha .$
• Der Winkel $SOB=\delta$ ist nahezu gleich einem Drittel des Winkels $COB=\gamma .$

Fehlerbetrachtung

Eine Fehleranalyse, ähnlich Chris Alberts' Konstruktion, ist nicht vorhanden.

Die dargestellte Konstruktion wurde mit der Dynamische-Geometrie-Software (DGS) GeoGebra angefertigt; darin werden in diesem Fall die Winkelgrade meist mit signifikanten dreizehn Nachkommastellen angezeigt. Die sehr kleinen Fehler des Winkels $\beta$ bzw. $\delta$, sprich, die Differenzwerte aus ${\frac {\alpha }{3}}-\beta$ bzw. ${\frac {\gamma }{3}}-\delta ,$ werden von GeoGebra stets mit $0^{\circ }$ angezeigt.

Betrachtet man die Grafik in GeoGebra, in sehr kleinen Schritten, die zu- oder abnehmenden Winkelweiten des Winkels $\beta$ bzw. $\delta$ mithilfe des Schiebereglers oder der Animation, ist vereinzelt eine max. Abweichung $1\cdot 10^{-13}\mathrm {^{\circ }}$ vom SOLL-Wert ${\frac {\alpha }{3}}$ bzw. ${\frac {\gamma }{3}}$ ablesbar.

Fazit

Der in GeoGebra ablesbare Differenzwert von max. $1\cdot 10^{-13}\mathrm {^{\circ }}$ entspricht einem absoluten Fehler $F$ der – nicht eingezeichneten – Sehne $|AQ|$ bzw. $|BS|,$ der sich wie folgt ergibt:

$F=2\cdot \sin \left({\frac {1\cdot 10^{-13}\mathrm {^{\circ }} }{2}}\right)=0{,}000\;000\;000\;000\;001\;745\ldots =1{,}745\ldots \cdot 10^{-15}\;[\mathrm {LE} ]$

Hätten die Winkelschenkel die Länge gleich 1 Milliarde km (das Licht bräuchte für diese Strecke ≈ 56 Minuten, das ist etwas weniger als 7-mal die Entfernung Erde – Sonne), wäre der absolute Fehler der beiden – nicht eingezeichneten – Sehnen $|AQ|$ bzw. $|BS|$ ≈ 1,7 mm.

Weblinks

 Dreiteilung des Winkels

 Beweis der Unmöglichkeit

 Winkel

 Tangente

 Wechselwinkel oder Z-Winkel

 Commons: Dreiteilung des Winkels von Chris Alberts – Album mit Bildern, Videos und Audiodateien

 GeoGebra

 Lichtgeschwindigkeit

• Dreiteilung des Winkels, interaktiv

Die Würfelverdoppelung

Das Problem der Würfelverdoppelung auch Delisches Problem genannt, ist seit dem 5. Jahrhundert v. Chr. bekannt. Nach div. Autoren aus der Antike geht die Aufgabe aus einer Episode zurück. Nachdem auf der griechischen Insel Delos eine schwere Seuche ausbrach, befragten die Einwohner ein Orakel, was für eine Besserung zu tun sei. Das Orakel verlangte hierfür den würfelförmigen Altar im Apollontempel der Insel in seinem Volumen zu verdoppeln. Im späten 5. Jahrhundert v. Chr. war Hippokrates von Chios der Erste, der den mathematischen Ansatz zur theoretischen Lösung fand. Das Problem gleicht dem der Bestimmung von zwei mittleren Proportionalen zweier Größen. Sprich, ist für eine Strecke der Länge $a$ nach zwei Strecken der Längen $x$ und $b$ gesucht, gilt folgender Zusammenhang:

${\frac {a}{x}}={\frac {x}{y}}={\frac {y}{2a}}$.

Daraus folgt $x={\sqrt[{3}]{2}}\cdot a$.

Da die Kubikwurzel aus $2={\sqrt[{3}]{2}}$ als Länge einer Strecke nicht in endlich vielen Konstruktionsschritten darstellbar ist, gibt es keine konstruktive Lösung allein mit Zirkel und unmarkierten Lineal. Den Beweis hierzu fand Pierre Wantzel im Jahr 1837.

Die Aufgabe

Die Aufgabe besteht darin, zu einem gegebenen Würfel einen zweiten Würfel in endlich vielen Konstruktionsschritten zu konstruieren, der (exakt) das doppelte Volumen vom Ausgangswürfel hat.

Konstruktion mithilfe eines markierten Lineals

Nimmt man jedoch als zusätzliches Hilfsmittel ein Lineal mit der Markierung der Kantenlänge des Ausgangswürfels, ist eine exakte Lösung, wie z. B. die folgende von Isaac Newton, möglich.

Die nebenstehende Darstellung und folgende sinnmäßig übersetzte Beschreibung, sind nach Isaac Newton.

Ich ziehe eine beliebige Linie, K A = a, halbiere sie in C und ziehe um den Mittelpunkt K mit Abstand K C einen Kreisbogen, ich bestimme C X = b und ziehe eine gerade Linie durch A X und eine durch C X, ich markiere E Y = C A, sodass eine gerade Linie durch E Y sowie durch den Punkt K gehen kann. [...]

Das Bild zeigt eine sogenannte Neusis-Konstruktion, darin sind ${\overline {XY}}$ und ${\overline {KE}}$ die mittleren Proportionalen von $a$ und $b$, wobei $b$ die Kante des Ausgangswürfels und $b\cdot {\sqrt[{3}]{2}}$ die Kante des verdoppelten Würfels ist.

Näherungskonstruktion

Die folgende Näherungskonstruktion hat eine außergewöhnliche Genauigkeit. Darin ist $a_{1}$ die Kantenlänge des Ausgangswürfels und $a_{2}$ die des verdoppelten Würfels.

Konstruktionsschritte

(Die Animation hat am Ende 10 s Pause)

• Der Radius des Kreises um Mittelpunkt $O$ ist gleich der Kantenlänge des Ausgangswürfels $a_{1}$.

Im folgenden Beispiel wurde einfachheitshalber $a_{1}=1$ gewählt.

1. Kreis mit Radius $a_{1}=1$ um Mittelpunkt $O$
2. Durchmesser ${\overline {AB}}$
3. Senkrechte ${\overline {CD}}$ zu ${\overline {AB}}$ durch $O$
4. Kreisbogen mit Radius $a_{1}$ um $A$, ergibt die Schnittpunkte $E$ und $E'$
5. Kreisbogen mit Radius $a_{1}$ um $B$, ergibt die Schnittpunkte $F$ und $F'$
6. Punkt $G$ mithilfe der nicht eingezeichneten Mittelsenkrechten des Abstandes $|E'D|$
7. Parallele zu ${\overline {AB}}$ ab $G$ ergibt Schnittpunkt $H$
8. Punkt $I$ mithilfe der nicht eingezeichneten Mittelsenkrechten des Abstandes $|HF'|$
9. Abstand $|IF'|$ übertragen ab $E$ ergibt $J$
10. Parallele zu ${\overline {AB}}$ ab $J$ ergibt Schnittpunkt $K$
11. Punkt $L$ mithilfe der nicht eingezeichneten Mittelsenkrechten des Abstandes $|KF|$
12. Abschließende Linie von $A$ bis $L$ ergibt Schnittpunkt $M$

• Die Länge der Strecke ${\overline {AM}}$ ist nahezu gleich dem Sollwert ${\sqrt[{3}]{2}}$.

Fehlerbetrachtung bei einem Kreis mit Radius ${\overline {OA}}=a_{1}=1$ [LE]:

In GeoGebra werden max. 15 Nachkommastellen angezeigt.

${\begin{alignedat}{2}{\text{in GeoGebra konstruierte Länge der Strecke }}\qquad {\overline {AM}}&=&&1{,}259921049894873\;[\mathrm {LE} ]\\-{\text{Sollwert }}\qquad -{\sqrt[{3}]{2}}&=-&&1{,}259921049894873\dots \;[\mathrm {LE} ]\\\hline {\text{absoluter Fehler in GeoGebra nicht evaluierbar }}\qquad F&=&&0{,}000000000000000\dots \;[\mathrm {LE} ]\end{alignedat}}$

Fazit

• Bei einem Würfel 1 mit der Kantenlänge a₁ = 1 Mrd. km (das Licht bräuchte für diese Strecke ca. 56 min) wäre bezüglich der konstruierten Kantenlänge a₂ des verdoppelten Würfels 2 kein Fehler evaluierbar.

Somit liegt die Vermutung nahe, dass der absolute Fehler < 1 mm ist.

• Bei einem Würfel 1 mit der Kantenlänge a₁ = 10 km wäre der Fehler des Volumens vom verdoppelten Würfels 2 vermutlich < 0,7 dm³ oder < 1  Liter.

Weblinks

 Würfelverdoppelung, Delisches Problem

 Hippokrates von Chios

 Neusis-Konstruktion nach Isaac Newton

 Neusis-Konstruktion

 Mittelsenkrechte

Konstruktionen von regelmäßigen Vielecken

Das Regelmäßige Fünfeck und der goldene Schnitt