MathemaTriX ⋅ Theorie. Geometrie der Ebene

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT

${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$	DEINE FESTE BEGLEITERIN
	FÜR DIE SCHULMATHEMATIK

EINFACH UND
VERSTÄNDLICH

GRATIS!^*

STARTEN!

MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS!

Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Inhalt
Ein-Aus-
klappen

AUFGABEN

KAPITEL

Grundrechenarten Bruchrechnungen	$-{\tfrac {\cdot \ +}{\ :\ }}$
Schlussrechnung Prozentrechnung
Exponentialfunktion Logarithmus
Arbeiten mit Termen	$\mathbb {X} ^{2}$
Zahlendarstellungen Mengentheorie Aussagenlogik	${\begin{matrix}\mathbb {R} :=\\\mathbb {Q} \cup \mathbb {I} \end{matrix}}$
Einheiten	$cm^{2}$
Statistik und Wahrscheinlichkeit
Geometrische Konstruktionen
Geometrie der Ebene
Geometrie des Raums
Diagramme
Funktionen	$f(x)$
Lineare Gleichungssysteme	${\begin{smallmatrix}{a_{1}\ b_{2}}\\{a_{2}\ b_{2}}\end{smallmatrix}}$
Trigonometrische Funktionen
Vektoren
Differentialrechnung	$^{dy}/_{dx}$
Integralrechnung	$\textstyle \int _{a}^{b}dx$
Folgen	$a_{n}$
Beweise	$a\rightarrow b$

Definitionen der ebenen Geometrie

Grundbegriffe der Geometrie

Strecke

Strecke ist der kürzeste Weg zwischen zwei Punkten. Z.B von den beiden gezeichneten Möglichkeiten zwischen A und B im Bild "Strecken Definition", welche ist die kürzeste?

Gerade und Strahl

Wenn ich eine Strecke auf einer Seite unendlich lang verlängere, dann habe ich einen Strahl. Wenn ich das an beiden Seiten tue, dann hab ich eine Gerade.

Winkel

Winkel Darstellung

Zwischen zwei Strahlen, die vom gleichen Punkt ausgehen, entsteht ein Winkel. Mit einem Winkel misst man eine Drehung.

Rechter Winkel

vier rechte Winkel

Wenn sich zwei Geraden einander so schneiden, dass vier gleichen Winkel entstehen, dann ist jeder von diesen Winkeln ein rechter Winkel.

Parallelen

Wenn zwei Geraden so nebeneinander liegen, dass sie nie einander schneiden und immer den Gleichen Abstand haben, dann sind sie parallel zueinander.

Punkt

Um alle Begriffe bisher zu definieren, haben wir den Punkt gebraucht. Was ist aber wieder ein Punkt? Diese ist die schwerste Definition. Wenn man beispielsweise den Abstand zwischen Wien und Linz berechnen will, muss man einen Ort in jeder Stadt wählen, sonst kann der Abstand bis 15km mehr oder weniger sein! Dieser Ort könnte z.B. eine Säule in der Mitte von jeder Stadt sein. Für so einen großen Abstand reicht eine Säule schon. Sie ist sozusagen ein Punkt.

Wenn man aber die Säule selber messen will, geht es nicht mehr. Man nimmt dann zwei winzigen Flächen am Rand der Säule. Je kleiner das Objekt ist, das wir messen wollen, desto kleiner muss der „Punkt“ sein.

Im idealen Fall ist der Punkt gar nichts, hat selber keine Länge, keine Breite und keine Höhe! So kann man sich einen Punkt vorstellen und so wird er auch definiert.

Eckpunkt

In einer ebenen Figur sind die Eckpunkte, die Punkte bei denen sich zwei Seiten einander schneiden.

Seite und Diagonale

Die Seiten einer ebenen Figur sind die Abgrenzungen der Figur vom Rest der Ebene. Im folgenden Bild eines Quadrats werden alle seine Seiten mit a bezeichnet, im Bild des Rechtecks werden zwei Seiten mit a und zwei mit b bezeichnet. Eine Seite verbindet zwei Punkte die nacheinander liegen. Die Diagonale verbindet hingegen zwei gegenüberliegenden Eckpunkte, die sich nicht am Rand der gleichen Seite befinden. Ein Quadrat und ein Rechteck haben jeweils zwei Diagonalen, die gleich lang sind, in einem Parallelogramm hingegen sind sie nicht gleich lang.

Figuren

Quadrat

Ein Quadrat ist eine viereckige geschlossene Figur, deren Seiten als auch deren Winkel gleich zu einander sind. Formeln: u=4a, A=a² (u ist der Umfang, a die Seite, A die Fläche). Mit d ist hier die sogenannte Diagonale gezeigt (verbindet zwei gegenüberliegende Eckpunkte).

Rechteck

Ein Rechteck ist eine viereckige geschlossene Figur, deren Winkel gleich zueinander sind und deren gegenüberliegenden Seiten auch gleich sind. Formeln: u=2a+2b oder u=2(a+b), A=a·b. Mit d ist wieder die Diagonale bezeichnet, mit a und b die Seiten (in der Figur ist a für die Länge, also die längere Seite und b für die Breite, also die kürzere Seite).

Parallelogramm

Ein Parallelogramm ist eine viereckige geschlossene Figur, deren gegenüberliegenden Seiten gleich sind. Daher sind sie auch parallel. Formeln: u=2a+2b oder u=2(a+b), A=a·h_a oder A=b·h_b. In der Figur ist h_a die Höhe zur Seite a und h_b die Höhe zur Seite b. Mit d wird eine der beiden Diagonalen bezeichnet (hier die kürzeste).

Raute (Rhombus)

Eine Raute ist eine viereckige geschlossene Figur, deren Seiten gleich sind. Daher sind auch alle Winkeln gleich. Formeln: u=4a, A= $\textstyle {\frac {e\cdot f}{2}}$ . Mit e und f sind die beiden Diagonale bezeichnet, mit a die Seite.

Trapez

Ein Trapez ist eine viereckige geschlossene Figur mit zwei gegenüberliegenden parallele Seiten. Formeln: u=a+b+c+d, $\textstyle A={\frac {a+c}{2}}\cdot h$ . Mit a, b, c und d werden die vier (nicht unbedingt gleichen) Seiten bezeichnet, mit h die Höhe auf die Basis (Basis ist nicht nur beim Trapez, sondern bei jeder Figur die untere Seite, beim Trapez im Bild hier die Seite a, also die Seite die im Bild unten steht). In der Figur sieht man auch die Diagonalen (ohne Symbol).

Deltoid

Ein Deltoid ist eine viereckige geschlossene Figur mit zwei Paaren nacheinander liegenden gleichen Seiten.

Vieleck (regelmäßiges)

Ein Vieleck ist eine Figur mit mehreren Winkeln. Wenn die Figur geschlossen ist und alle Seiten (und Winkel) gleich zueinander, dann ist das Vieleck regelmäßig. Im Bild sieht man ein regelmäßiges Siebeneck, die Seite ist hier mit s bezeichnet.

Fragen zu Figuren

Ist jedes Rechteck ein Parallelogramm? Umgekehrt?

Ist jede Raute ein Quadrat? Umgekehrt?

Ist jedes Trapez ein Parallelogramm? Umgekehrt?

Ist jedes Quadrat auch ein Rechteck? Umgekehrt?

Dreieck, Besondere Dreiecke

spitz
gleichseitiges
gleichschenkliges
rechtwinkeliges
stumpfwinkeliges

Ein Dreieck ist eine geschlossene Figur mit drei Winkel. Ist einer Winkel mehr als 90°, dann heißt das Dreieck stumpfwinkeliges, wenn alle Winkel kleiner als 90° sind, dann spitzwinkeliges.

Bei allen Dreiecken gilt für den Umfang: u=a+b+c, wobei a, b und c die Symbole für die Seiten sind. Die allgemeinen Formeln für die Fläche sind $\textstyle A={\frac {a\cdot h_{a}}{2}}={\frac {b\cdot h_{b}}{2}}={\frac {c\cdot h_{c}}{2}}$ , wobei h_a, h_b und h_c die Höhen zu den entsprechenden Seiten sind (im Bild nicht zu sehen).

Ist einer der Winkeln 90°, dann wird das Dreieck rechtwinkelig genannt. Die Formel für die Fläche ist in diesem Fall $\textstyle A={\frac {a\cdot b}{2}}$ , wobei hier a und b die kleineren Seiten sind (Katheten genannt). Die größte Seite (dem rechten Winkel gegenüber) nennt man Hypotenuse.

Sind zwei der drei Winkel (und auch zwei Seiten) gleich, dann nennt man das Dreieck gleichschenklig. Sind alle Winkel (und Seiten) gleich, dann ist es ein gleichseitiges Dreieck (mit Seite a). Für die Fläche des gleichseitigen Dreiecks gilt: $\textstyle A={\frac {\sqrt {3}}{4}}\cdot a^{2}$ .

Kreis, Kreissektor, Kreisring

Kreis
Kreisteile
Kreisring

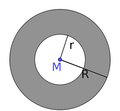
Ein Kreis ist die Menge aller Punkten, die von einem Punkt M (Mittelpunkt genannt) den gleichen Abstand r (Radius genannt) haben. Formeln: u=2πr, A=πr². r ist der Radius. Hier wird mit d der Durchmesser bezeichnet. π ist eine Zahl (wie 2 oder 5,632), mit dem Unterschied, dass man diese Zahl (π) nicht genau angeben kann. π ist ungefähr 3,14159... Sie ist das Verhältnis (also der Bruch) des Umfangs zum Durchmesser $\textstyle ({\boldsymbol {\pi }}={\frac {\boldsymbol {u}}{\boldsymbol {d}}})$ .

Schneidet man einen Kreis wie einen Torten-schnitt (also zwei Schnitte von Mittelpunkt aus bis am Rand), dann hat man einen Kreissektor. Schneidet man ein Stück mit einer Strecke von einem zu einem anderen Punkt des Kreises, hat man ein Kreissegment. Im Bild steht für den Bogen das englische Wort "arc". Schneidet man von der Mitte eines Kreises einen kleineren Kreis mit den selben Mittelpunkt ab, dann bekommt man ein Kreisring.

Ellipse

Schneidet man einen Zylinder schief, dann entsteht eine Ellipse. Die sieht wie ein zerquetschter Kreis aus. Die genauere Definition ist kompliziert:

Man nimmt zwei Punkte, die Brennpunkte (im Bild B₁ und B₂). Jeder Punkt der Ellipse (im Bild z.B. X) hat zu jedem Brennpunkt einen gewissen Abstand (im Bild z.B. ist der Abstand zum Brennpunkt B₁ mit s bezeichnet und zum B₂ mit p). In einer Ellipse ist die Summe der beiden Abständen (also s+p) immer gleich (im Bild gleich 2a, wobei a die sogenannte große Halbachse ist). Mit b wird hier die sogenannte kleine Halbachse bezeichnet.

Intuitiver Beweis der Formeln des Flächeninhalts mancher ebenen Figuren

Definition des Quadratzentimeters

Ein Zentimeter Quadrat (1 cm², ein Zentimeter hoch zwei) ist ganz einfach ein Quadrat, dessen Seite ein Zentimeter ist (erstes Bild).

Fläche des Rechtecks

Im zweiten Bild sieht man ein Rechteck, dass aus mehreren Quadrat Zentimeter besteht. Hier haben wir zwei Zeilen, jede mit 3 Quadraten. Insgesamt 2x3=6 (cm²). Man kann offenbar sagen, dass der Flächeninhalt A eines Rechtecks die Länge a der einer Seite mal die Länge b der anderen ist.

A = a · b

Sonderfall: Das Quadrat. Da gilt A = a · a = a², da die Seiten gleich sind.

Fläche des Parallelogramms

Im Fall eines Parallelogramms kann man sich vorstellen, dass ein Stück der Figur so wie im Bild geschnitten und auf der anderen Seite wieder hinzugefügt werden kann. Dadurch entsteht wieder ein Rechteck, dessen Seiten jetzt die Basis a und die Höhe h_a des Parallelogramms sind. Die Fläche des dadurch entstandenen Rechtecks ist daher der Flächeninhalt des Parallelogramms:

A= a · h_a

Fläche des Dreiecks

Im Fall eines Dreiecks kann man sich wie im Bild vorstellen, dass ein zweites Dreieck, gleich groß wie das erste, umgedreht und auf das erste zugefügt wird. So entsteht wieder ein Parallelogramm, dessen Flächeninhalt A = b · h_b ist. Weil aber dieses Parallelogramm aus 2 gleiche Dreiecke besteht, muss man für den Flächeninhalt des Dreiecks das ganze mit 2 dividieren:

$A={\frac {b\cdot h_{b}}{2}}$

Entsprechend für die anderen Seiten kann man schreiben:

$A={\frac {a\cdot h_{a}}{2}}$

$A={\frac {c\cdot h_{c}}{2}}$

Sonderfälle: Rechtwinkeliges, gleichschenkeliges und gleichseitiges Dreieck. In den zwei letzten Fällen kann man den Satz des Pythagoras benutzen, um eine Formel zu erzeugen (machen wir aber hier nicht).

Fläche des Trapezes

Genauso geht man bei einem Trapez vor. Es entsteht ein Parallelogramm, dessen Basis aber jetzt a+b ist und den Flächeninhalt daher (a+b) · h. Weil, wie vorher beim Dreieck, das Trapez zwei mal vorkommt, muss man wieder für den Flächeninhalt des Trapezes das ganze durch 2 dividieren:

$A={\frac {a+c}{2}}\cdot h$

Anwendung der Formeln

Variablen in der Geometrie

Bei allen Formeln gibt es sogenannten „Variablen“. Es geht in der Regel um ein Buchstabe, der für irgendwas steht. Hier schreiben wir, wofür diese Symbole in der Geometrie stehen.

Ein großes A, steht in der Regel für die Fläche (genauer für den Flächeninhalt)

Ein u steht i.d.R. für den Umfang (also wie lang das Rum-herum der Figur ist)

a, b, c usw. stehen i.d.R. für die Seiten (auch Länge oder Breite) von Figuren

h (oder H) steht i.d.R. für die Höhe einer Figur. Oft gibt es dann ein Index, z.B. h_b, was dann bedeutet, dass diese die Höhe für die Seite b ist.

r (oder R) steht i.d.R. für den Radius eines Kreises.

d steht bei einem Kreis für den Durchmesser des Kreises, bei einem Parallelogramm (oder Rechteck, Quadrat, Trapez, Vieleck) aber für die Diagonale!

Griechische kleine Buchstaben (α, β, γ, δ, ε, θ, φ) stehen i.d.R. für Winkel.

Allerdings ist mit dem griechischen Buchstabe π die Kreiszahl bezeichnet (π≈3,1415...).

Formel Einsetzen in der ebenen Geometrie

$\$	$\$

$\$

Bei einer Aufgabe sind immer gewisse Informationen gegeben, z.B.:

Ein Zimmer ist 4m lang und 2,8m breit. Finden Sie seinen Umfang und seine Fläche heraus!

In solchen Problemen soll man die gegebenen Zahlen in die Formel sinnvoll einsetzen. Das bedeutet, dass man die Buchstaben in der Formel durch Zahlen ersetzt. In diesem Beispiel sucht man in einer Formelsammlung das Rechteck (da ein Zimmer die Form eines Rechtecks hat).

In der Figur, die man in der Formelsammlung finden kann, kann man sehen, dass mit a die Länge und mit b die Breite bezeichnet wird. In der Formelsammlung kann man auch die Formel für den Umfang finden:

u=2a+2b

Die Länge a ist gegeben: 4m. Die Breite b auch: 2,8m. Wenn nichts zwischen einer Zahl und einer Variable steht (hier z.B. 2a), dann ist mal gemeint (2 mal a). Man schreibt also an der Stelle von a und b die Zahlen 4 und 2,8:

$u=2a+2b=2{\cancel {a}}^{=4}+2{\cancel {b}}^{=2{,}8}=2\cdot 4+2\cdot 2,8=13,6\ (m$ , da wie m mit m addiert haben)

In der Spalte für die Fläche steht beim Rechteck:

A=a·b also

$A=a\cdot b={\cancel {a}}^{=4}\cdot {\cancel {b}}^{=2{,}8}=4\cdot 2,8=11,2\ (m^{2}$ , da wie m mit m multipliziert haben)

Man soll auch auf die Einheiten aufpassen:

Der Umfang ist eine Strecke, also er wird in Streckeneinheiten gemessen (hier m), die Fläche hingegen in Flächeneinheiten (hier in m²).

Andererseites kann es sein, dass eine Größe in verschiedenen Einheiten gegeben wird, z.B.:

Die Länge eines Rechtecks ist 5dm und seine Breite 32cm. Finden Sie seinen Umfang und seine Fläche heraus!

Das Einsetzen von Werten in einer Formel setzt voraus, dass die Einheiten übereinstimmen. Man muss z.B. überall in der Formel Werte in Stunden haben und nicht irgendwo Stunden, an einer anderen Stelle Minuten usw. Hier muss man den Wert einer der beiden Seiten umwandeln, z.B.:

32cm=32:10 dm = 3,2 dm

Jetzt sind beide Seiten (Länge und Breite) in dm und es kann weiter berechnet werden:

u=2a+2b und A=a·b

Die Länge a ist gegeben: a=5dm. Die Breite b haben wir jetzt auch in dm umgerechet: b=3,2dm:

$u=2a+2b=2{\cancel {a}}^{=5}+2{\cancel {b}}^{=3{,}2}=2\cdot 5+2\cdot 3{,}2=16{,}4\ (dm$ , da wie hier dm mit dm addiert haben) und

$A=a\cdot b={\cancel {a}}^{=5}\cdot {\cancel {b}}^{=3{,}2}=5\cdot 3{,}2=16\ (dm^{2}$ ,da wie hier dm mit dm multipliziert haben)

Hätten wir die Einheiten (die 32cm) nicht umgewandelt, hätten wir Probleme mit dem Einheit am Ende oder sogar ein völlig falsche Antwort:

Bei der Multiplikation hätten wir:

\textstyle A=a\cdot b={\cancel {a}}^{=5}\cdot {\cancel {b}}^{=32}=5\cdot 32=160\qquad

FALSCH! Wenn man hier dm² oder cm² als Einheit schreibt, ist das Ergebnis völlig falsch, die Einheit, die wir schreiben hätten sollen, wäre dm⋅cm, das wäre zwar richtig, aber diese Einheit wird für die Fläche nie benutzt.

Bei der Addition hätten wir:

u=2a+2b=2{\cancel {a}}^{=5}+2{\cancel {b}}^{=32}=2\cdot 5+2\cdot 32=74\qquad

FALSCH! Hier ist sogar der Wert völlig falsch! Der richtige Wert, wie wir gesehen haben, ist 16,4 dm (oder 164 cm). Man kann nicht dm und cm addieren oder subtrahieren, genauso wie man nicht dm und kg addieren kann! Addieren (oder subtrahieren) kann man nur Sachen, die genau die gleichen Einheiten haben!

Nicht nur bei Multiplikation oder Addition müssen die Einheiten übereinstimmen, sondern auch bei Division und allen anderen Rechenarten. Bei Multiplikation und Addition haben wir das Beispiel gerade eben gesehen (Fläche und Umfang des Rechtecks am letzten Beispiel). Ein Beispiel für Division, ist wenn man die Fläche eines Rechtecks durch seine Länge dividiert, um die Breite zu berechnen. Wenn die Fläche 6cm² und die Länge 30mm, dann kann man NICHT die Division so durchführen: $\textstyle b={\frac {6}{30}}$ , da 6 in cm gegeben ist und 30 in mm. Man soll zuerst z.B. die mm in cm umwandeln (30mm=3cm) und dann die Division durchführen: $\textstyle b={\frac {6}{3}}=2$ (das sind dann cm, da wir cm² durch cm dividiert haben und man die Hochzahl und dann kann man die Einheiten kürzen: $\textstyle {\frac {cm^{\cancel {2}}}{\cancel {cm}}}=cm$ .

Wir können also schreiben:

Bei Rechnungen müssen die Einheiten immer übereinstimmen!

Bei einer Rechnung (oder Gleichung) muss man immer erst kontrollieren, ob die Einheiten übereinstimmen, dann die Einheiten, die nicht übereinstimmen, in übereinstimmenden Einheiten umwandeln und erst am Ende die Rechnung durchführen! Das gilt immer (auch bei der Schluss-und Prozentrechnung)!

In Physik benutzt man sogar Einheitssysteme, das ist aber für dieses Buch ein fortgeschrittenes Thema.

Umformen in der ebenen Geometrie konkret

$\$	$\$

$\$

Beim Umformen haben wir am Anfang eine Formel, in der eine bestimmte Variable durch eine Beziehung von anderen Variablen und Zahlen ausgedrückt wird. Diese bestimmte Variable steht allein auf einer Seite (i.d.R. die rechte). Diese Formel wird dann so geändert, dass eine andere Variable der Formel allein auf einer Seite steht. Dafür benutzen wir u.A. die Gegenrechnungen (siehe Kapitel „Umformen“). Z.B. ist plus die Gegenrechnung von minus (und umgekehrt), mal von plus (und umgekehrt), Wurzel von Quadrat (und umgekehrt). „Konkret“ wird in diesem Buch das Umformen dann genannt, wenn die Variablen (außer einer) durch Zahlen ersetzt werden. Wenn dies nicht der Fall ist, wird die Rede von „abstraktem“ Umformen sein. Im letzten Fall bleiben alle Variablen (alle „Buchstaben“) vorhanden. Hier zwei Beispiele aus der Geometrie der Ebene:

Der Umfang eines Quadrats ist 12cm. Berechnen Sie die Seite und die Fläche!

Wir finden die Figur (hier Quadrat) in der Formelsammlung. Wir fangen mit der Formel der gegebenen Eigenschaft (hier Umfang) an:

u=4a

Hier ist der Umfang gegeben, man braucht die Seite. Zwischen 4 und a steht nichts, also ist mal gemeint. Die Gegenrechnung von mal ist durch und der Umfang ist 12, also:

$u=4a\quad |:4$

${\frac {u}{4}}=a$ Seiten in einer Gleichung kann man selbstverständlich umtauschen, also:

$a={\frac {u}{4}}={\frac {\cancelto {12}{u}}{4}}={\frac {12}{4}}$ also

a=3 cm

Die Formel für die Fläche, die man auch in der Formelsammlung finden kann ist dann:

$A=a^{2}$ $_{(a=3)}\ \$ $=3^{2}=9$ also $A=9\ cm^{2}$

Auch wenn die Seite erst nicht gefragt wäre, wäre es doch notwendig diese erst einmal zu berechnen, um dann mit Hilfe des Wertes für die Seite auch die Fläche berechnen zu können.

Umformen in der ebenen Geometrie abstrakt

$\$	$\$

$\$

Abstrakt umformen bedeutet hier, Umformungen nur (oder fast nur) mit Symbolen durchzuführen. Wir haben z.B. eine Formel für die Berechnung der Fläche eines Kreises, wenn sein Radius bekannt ist, aber wie sollte umgekehrt allgemein der Radius berechnet werden, wenn die Fläche gegeben ist?

Wir finden die Figur (hier Kreis) in der Formelsammlung und fangen mit der Formel der gegebenen Eigenschaft (hier Fläche) an:

$A=\pi \cdot r^{2}$

Wir brauchen eine Formel für den Radius, also das entsprechende Symbol (r) muss am Ende allein bleiben. Der erste Schritt in diesem Beispiel dafür, wäre das π von der rechten auf die linke Seite zu bringen:

$A=\pi \cdot r^{2}\quad |:\pi$

${\frac {A}{\pi }}=r^{2}$

Wir haben hier die Gegenrechnung von mal benutzt (also Division). Die Gegenrechnung fürs Quadrat ist Wurzel ziehen, das wird unser nächster Schritt sein:

${\frac {A}{\pi }}=r^{2}\quad |{\sqrt {x}}$

${\sqrt {\frac {A}{\pi }}}=r$

Seiten in einer Gleichung kann man selbstverständlich umtauschen, also:

$r={\sqrt {\frac {A}{\pi }}}$

Diese ist also die allgemeine Formel für die Berechnung des Radius eines Kreises, wenn seine Fläche gegeben ist.

Noch ein Beispiel für die Berechnung der Länge a eines Rechtecks, wenn sein Umfang u und die Breite b gegeben sind:

$u=2a+2b\quad |-2b$

$u-2b=2a|:2$

${\frac {u-2b}{2}}=a\quad$ also

$a={\frac {u-2b}{2}}$

In diesem Fall müssen wir selbstverständlich darauf aufpassen, dass die Einheiten übereinstimmen.

Ähnlichkeit von Figuren und Strahlensatz

Ähnlichkeit von Figuren

$\$	$\$

$\$

Wenn wir die beiden Bilder oben vergleichen, können wir sagen, dass es das gleiche Dreieck ist, nur von einem anderen Abstand gesehen oder, dass wir doch zwei verschiedene Dreiecke haben, die zwar ähnlich zueinander sind aber doch nicht das gleiche Dreieck, da die Seiten nicht gleich sind. Um auf diesen Unterschied aufmerksam zu machen, wird beim Vergleich zwei geometrischen Figuren nicht das Wort "gleich" (und "nicht gleich") benutzt, sondern die Worten "ähnlich" (und "nicht ähnlich") und "kongruent" (und "nicht kongruent").

Zwei geometrische Figuren sind ähnlich, wenn sie die gleiche Seitenanzahl haben und alle entsprechenden Winkel gleich zueinander sind. Wenn dazu zumindest eine Seite (und daher auch alle andere) der beiden Figuren gleich ist, dann sagt man, dass die Figuren kongruent sind.

Das Wort "gleich" wird bei geometrischen Figuren nicht benutzt, weil es dann nicht klar ist, ob nur alle Winkel oder doch auch alle Seiten gleich sind.

Bei ähnlichen Figuren gilt, dass das Verhältnis entsprechender Seiten eine Konstante Zahl ist. Wenn wir die Seiten aus dem Bild benutzen, wird es klar, was damit gemeint ist. Nehmen wir die Seite b aus dem Bild links und die entsprechende Seite b' aus dem Bild rechts. Verhältnis in Mathematik bedeutet Bruch. Der Bruch der beiden Seiten ist dann $\textstyle {b \over {b'}}$ . Werden die beiden Seiten in irgendeiner Weise gemessen, wird dann festgestellt, dass der Bruch ca. 1,5 ist. Es gilt also: $\textstyle {b \over {b'}}=1{,}5$ .

Wenn wir ein anderes Paar von entsprechenden Seiten nehmen, wird das Verhältnis (der Bruch) wieder 1,5 sein: $\textstyle {c \over {c'}}=1{,}5$ .

Das Verhältnis (der Bruch) von entprechenden Seiten (z.B. $\textstyle {b \over {b'}}$ oder $\textstyle {c \over {c'}}$ ) ist eine konstante Zahl, hier 1,5. Das gilt genauso für das dritte Paar von entsprechenden Seiten: $\textstyle {d \over {d'}}=1{,}5$ .

Diese Regel gilt nicht nur in Dreiecken sondern in allen geometrischen Figuren, die ähnlich sind. Im folgenden Bild sieht man verschiedene Figuren. Alle Figuren mit der gleichen Farbe sind ähnlich.

Alle hier gleichfarbigen Figuren sind zueinander ähnlich.

Strahlensatz

Die Ähnlichkeit von Figuren findet Anwendung im sogenannten "Strahlensatz".

Nehmen wir zwei geraden, die einander am Schnittpunkt Z schneiden, wie die Geraden BB' und AA' im Bild links. Diese Geraden werden von zwei weiteren parallel zueinander Geraden AB und A'B' geschnitten. So entstehen zwei ähnliche Dreiecke, ABZ und A'B'Z. Da die Dreiecke ähnlich sind, gilt:

${\frac {AB}{A'B'}}={\frac {AZ}{A'Z}}={\frac {BZ}{B'Z}}$

Diese Formel zeigt, was bei der Ähnlichkeit von Figuren behauptet wurde: Das Verhältnis (der Bruch) von entsprechenden Seiten bleibt konstant.

Der Strahlensatz findet zahlreiche Anwendungen in Physik und Mathematik. Hier erwähnen wir "nur" seine Anwendung bei der Vermessung des Abstandes zwischen Mond und Erde.

Eine andere Anwendung ist bei der geometrischen Erzeugung einer Dezimalzahl auf einer Zahlgerade.

Eine Bemerkung dazu: Das erste in der Geschichte bekanntes Buch, in dem Geometrie als auf wenigen Sätzen aufgebautes geordnetes Wissen dargestellt wird, ist das Werk "Elemente" von Euklid. In diesem Werk wird erst der Strahlensatz bewiesen und dann auf die Ähnlichkeit von Figuren angewendet.

Zusammengesetzte Figuren

$\$	$\$

$\$

Satz von Pythagoras

Geschichte des Satzes von Pythagoras

Obwohl der Satz nach dem griechischen Philosoph Pythagoras genannt wird, wurde er nicht von ihm entdeckt. Der Satz wurde zumindest 1000 Jahre früher benutzt. Es gibt Tontafel aus Babylonien, die sogenannte pythagoreische Tripeln beinhalten. Eine pythagoreische Tripel sind drei Zahlen, die den Satz von Pythagoras erfühlen. Die Entdeckung zeigt eine hochentwickelte antike Zivilisation, Die Berechnungen mancher Tripel ohne technische Mittel sind ziemlich kompliziert und brauchen viel Geduld und Zeit.

Formulierung des Satzes von Pythagoras

Der Satz von Pythagoras lautet:

In einem rechtwinkeligem Dreieck ist die Summe der Quadrate der Katheten gleich dem Quadrat der Hypotenuse.

Der Satz gilt daher nur bei Dreiecken, die einen rechten Winkel haben.

Selbstverständlich versteht man den Satz viel besser, wenn man eine Figur sieht:

Die Seiten an der rechten Winkel nennt man Katheten (im Bild mit a und b), die Seite gegenüber Hypotenuse (im Bild mit c).Es gilt:

a^{2}+b^{2}=c^{2}

Nehmen wir drei Zahlen: 2, 3 und 4. Sind diese eine pythagoräische Tripel? Die größte Zahl sollte die längste Seite sein, die Hypotenuse, also c. Hier ist es die Zahl 4. Dann wären die Katheten 2 und 3. Die entsprechenden Quadrate der Katheten sind 2²=4 und 3²=9, ihre Summe 4+9=13. Das Quadrat der Hypotenuse wäre 4²=16. Es gilt 2²+3²≠4² (13 ist nicht gleich 16!). Das bedeutet: Es gibt kein rechtwinkeliges Dreieck, dessen Katheten 2 und 3 und dessen Hypotenuse 4 Einheiten (z.B. Meter) sind.

2,3 und 4 sind daher keine Pythagoreische Tripel. Wie ist es mit 3, 4 und 5? Sind diese Zahlen eine Pythagoräische Tripel? 3²+4² = 25 aber auch 5² = 25. Es gilt also: 3²+4²=5². Das bedeutet nicht nur, dass es ein rechtwinkeliges Dreieck gibt, dessen Katheten 3 und 4 und dessen Hypotenuse 5 Einheiten ist, sondern auch umgekehrt, dass ein Dreieck, dessen Seiten 3, 4 und 5 Einheiten sind, einen rechten Winkel haben muss!

$\$	$\$

$\$

In den Aufgaben muss man aufpassen. Wenn die Katheten angegeben sind und die Hypotenuse gefragt, dann kann man die gegebene Formel benutzen:

Bei einem rechtwinkeligen Dreieck sind die Katheten 6 und 8 cm lang. Berechnen Sie die Hypotenuse!

$a^{2}+b^{2}=c^{2}\qquad$ wobei $a=6$ und $b=8$ also

$6^{2}+8^{2}=c^{2}\ \Rightarrow \ 36+64=c^{2}\ \Rightarrow \ 100=c^{2}\ \Rightarrow \ c={\sqrt {100\ }}=10cm$

Wenn aber die Hypotenuse und eine Kathete gegeben sind, dann muss man die Formel erst umformen:

Bei einem rechtwinkeligen Dreieck sind die eine Kathete 21mm und die Hypotenuse 0,29dm lang. Berechnen Sie die andere Kathete!

Erst müssen wir auf die Einheiten aufpassen: 0,29dm=29mm

$a^{2}+b^{2}=c^{2}\qquad |-a^{2}$

$b^{2}=c^{2}-a^{2}\qquad |-a^{2}$ also $\qquad b^{2}=29^{2}-21^{2}=841-441=400\qquad$ $b={\sqrt {400}}=20\ mm$

Also: Wenn beide Katheten angegeben sind müssen wir die Quadrate addieren, wenn nur eine Kathete und die Hypotenuse, müssen wir vom größeren Quadrat das kleinere subtrahieren. In beiden Fällen ziehen wir dann die Wurzel des Ergebnisses.

Geometrie Beweise

$\$	$\$

$\$

Geometrischer Beweis der plus und minus binomische Formeln

Ein möglicher Weg, die Geltung der plus und minus binomische Formeln zu zeigen, ist mit Hilfe der Geometrie.

Nehmen wir erst die folgende Figur, um die Geltung der plus binomischen Formel zu zeigen:

$\ \ \textstyle A_{gQ}$ ist die Fläche des großen Quadrats.
$\ \ \textstyle A_{1}$ , des Quadrats oben links, $\ \ \textstyle A_{2}$ des Rechtecks oben rechts.
$\ \ \textstyle A_{3}$ , des Rechtecks unten links, $\ \ \textstyle A_{4}$ des Quadrats unten rechts.
$\ \ \textstyle A_{gQ}=(a+b)^{2},\quad A_{1}=a^{2},\quad A_{2}=A_{3}=a\cdot b,\quad A_{4}=b^{2}$
Das Ganze (das große Quadrat) ist die Summe seiner Teilen.
$\ \ \textstyle A_{gQ}=A_{1}+A_{2}+A_{3}+A_{4}$
$\ \ \textstyle (a+b)^{2}=a^{2}+a\ b+b\ a+b^{2}$
$\ \ \textstyle (a+b)^{2}=a^{2}+2\ a\ b+b^{2}$

Ähnlich können wir die Geltung der minus binomischen Formel zeigen:

$\ \ \textstyle A_{gQ}$ ist die Fläche des großen Quadrats.
$\ \ \textstyle A_{1}$ , des Quadrats oben links, $\ \ \textstyle A_{2}$ des Rechtecks oben rechts.
$\ \ \textstyle A_{3}$ , des Rechtecks unten links, $\ \ \textstyle A_{4}$ des Quadrats unten rechts.
$\ \ \textstyle A_{gQ}=a^{2},\quad A_{1}=(a-b)^{2},\quad A_{2}=A_{3}=(a-b)\cdot b,\quad A_{4}=b^{2}$
Das Ganze (das große Quadrat) ist die Summe seiner Teilen.
$\ \ \textstyle A_{gQ}=A_{1}+A_{2}+A_{3}+A_{4}\quad |$
$\ \ \textstyle a^{2}=(a-b)^{2}+(a-b)\cdot b+(a-b)\cdot b+b^{2}\quad |$ (Klammer auflösen)
$\ \ \textstyle a^{2}=(a-b)^{2}+a\cdot b-b^{2}+a\cdot b-b^{2}+b^{2}\quad |$ (Zusammenrechnen)
$\ \ \textstyle a^{2}=(a-b)^{2}+2\cdot a\cdot b-b^{2}\quad |$
$\ \ \textstyle a^{2}-2\cdot a\cdot b+b^{2}=(a-b)^{2}\quad |$ (Seiten wechseln)
$\ \ \textstyle (a-b)^{2}=a^{2}-2\cdot a\cdot b+b^{2}$

Beweis des Satzes von Pythagoras

Der erste, der entdeckt hatte, dass es Zahlen gibt, die nicht rationale Zahlen sind, war Hippasos von Metapont, ein Schüler von Pythagoras. Diese Entdeckung war noch ein Schritt zur Forschung der Unendlichkeit, da die irrationale Zahlen unendlich viele nicht periodische Nachkommastellen haben. Zu dieser Entdeckung hat vielleicht der Satz von Pythagoras beigetragen, ein Satz der allerdings nicht von Pythagoras entdeckt wurde aber vielleicht nur bewiesen (wenn überhaupt).

Einen Beweis dieses Satzes führen wir hier mit Hilfe der folgenden Figur vor.

Für den Beweis werden wir erst einmal folgenden Zusammenhang brauchen:

$\textstyle (a+b)^{2}=(a+b)\cdot (a+b)=a^{2}+ab+ab+b^{2}=a^{2}+2ab+b^{2}$

In der Figur sieht man ein großes Quadrat, das vier kongruente (sozusagen gleiche) rechtwinkelige Dreiecke und ein kleineres Quadrat beeinhaltet. Wie man in einer Formelsammlung finden kann, ist die Fläche jedes rechtwinkeligen Dreiecks $\textstyle A_{d}={\frac {a\cdot b}{2}}$ (und es gibt 4 solche Dreiecken). Die Fläche des kleinen Quadrats in der Mitte ist $\textstyle A_{kQ}=c^{2}$ . Die Seite des großen Quadrats ist die Summe von a und b, Daher ist seine Fläche $\textstyle A_{gQ}=(a+b)^{2}$ . Das Ganze (das große Quadrat) ist aber die Summe seiner Teilen. Es gilt daher:

$\textstyle A_{gQ}=A_{kQ}+4\cdot A_{D}$

$\textstyle (a+b)^{2}=c^{2}+4\cdot {\frac {a\cdot b}{2}}$

Wie schon gezeigt, es gilt $\textstyle (a+b)^{2}=a^{2}+2ab+b^{2}.$ Wir ersetzten also in der letzten Formel $\textstyle (a+b)^{2}$ durch $\textstyle a^{2}+2ab+b^{2}.$ Dazu kürzen wir den Bruch: $\textstyle 4\cdot {\frac {a\cdot b}{2}}=2ab.$ Es gilt daher:

$\textstyle a^{2}+2ab+b^{2}=c^{2}+2ab$ und daher:

$\textstyle c^{2}=a^{2}+b^{2}\quad$ (Satz von Pythagoras)

Ähnlich ist der Beweis für die folgende Figur:

Für den Beweis werden wir erst einmal folgenden Zusammenhang brauchen:

$\textstyle (a-b)^{2}=(a-b)\cdot (a-b)=a^{2}-ab-ab+b^{2}=a^{2}-2ab+b^{2}$

Die Fläche des großen Quadrats (gesamte Fläche) ist jetzt $\textstyle A_{gQ}=c^{2}$ und des kleinen Quadrats in der Mitte $\textstyle A_{kQ}=(a-b)^{2}$ . Das Ganze (das große Quadrat) ist die Summe seiner Teilen. Es gilt daher:

$\textstyle A_{gQ}=A_{kQ}+4\cdot A_{D}$

$\textstyle c^{2}=(a-b)^{2}+4\cdot {\frac {a\cdot b}{2}}$

$\textstyle c^{2}=a^{2}-2ab+b^{2}+2ab$ und daher:

$\textstyle c^{2}=a^{2}+b^{2}\quad$

Es gibt außerdem zahlreiche andere Beweise für diesen Satz, die die Vielfalt und die Kreativität des mathematischen Denkens zeigen.

BILDERVERZEICHNIS

ÖFFNE DEIN HORIZONT!
LERNE MIT MATHEMATRIX!

\quad

\quad

\quad

$\mathbf {MATHE} \mu \alpha T\mathbb {R} ix$
LOGO	CH DE AT

SPENDEN
Der Hauptautor ggf. das Team verdient zwar nicht viel, braucht allerdings dein Geld eigentlich nicht. Wenn du aber doch meinst, dass gute Arbeit belohnt werden soll und dieses Projekt gut findest, kannst du immer in diesem Link spenden. Das ist allerdings vielleicht die einzige Einrichtung mit völliger Transparenz, wo du genau weißt, was mit deinem Geld passiert.