Digitale Schaltungstechnik/ Addierer
| Titelseite |
|---|
Wir haben im Kapitel über die Addition gelernt haben, brauchen wir zu Addition beliebiger Zahlen nur zwei Mechanismen
- Die Addition einstelliger Zahlen
- Die Handhabung der Überträge
Als erstes lernen wir, wie wir in der Digitaltechnik die Addition einstelliger Zahlen realisieren und ihm nächsten Schritt wie wir den Übertrag handhaben.
Halbaddierer
[Bearbeiten]Herleitung
[Bearbeiten]In Kapitel über die Addition von Binärzahlen haben wir diese Beziehungen gelernt:
| Addition einstelliger Binärzahlen |
|---|
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 |
Wahrheitstabelle
[Bearbeiten]Diese Beziehung können wir ohne Probleme in eine Wahrheitstabelle übertragen:
| Input | Output | ||
|---|---|---|---|
| A | B | Σ | C |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Σ ist dabei die erste Stelle des Resultats und C das Carry (also der Übertrag).
Da wir nun die Wahrheitstabelle haben, ist es auch spielend die Gleichung auszulesen:
Realisierung
[Bearbeiten]Die Realisierung als Schaltung sieht wie folgt aus:

Bei dieser Realisierung wurde genutzt, das sich als A XOR B realisieren lässt.
Blockschaltbild
[Bearbeiten]Da diese Schaltung häufiger verwendet wird, gibt es dafür auch ein Blockschaltbild:

Im weiteren Verlauf des Buches werden wir in der Regel dieses Blockschaltbild einsetzen.
Volladdierer
[Bearbeiten]Herleitung
[Bearbeiten]Für den Fall, dass es einen Übertrag gab, haben wir diese Beziehung ebenfalls angesehen:
| Addition einstelliger Binärzahlen |
|---|
0 + 0 + 0 = 0 0 + 0 + 1 = 1 0 + 1 + 0 = 1 0 + 1 + 1 = 10 1 + 0 + 0 = 1 1 + 0 + 1 = 10 1 + 1 + 0 = 10 1 + 1 + 1 = 11 |
Wahrheitstabelle
[Bearbeiten]Auch diese können wir in eine Wahrheitstabelle übertragen:
| Input | Output | |||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Wobei:
- A, B und Ci die Eingänge sind
- Co und die Ausgänge sind
- Ci bedeutet Carry in, also Übertragseingang
- Co bedeutet Carry out, also Übertragsausgang
Die Gleichung die wir auslesen können ist:
Eine alternative Darstellung mit für XOR kürzt die Funktion wesentlich:
Jedoch ist das nicht unbedingt lesbarer und die Umwandlung ist etwas aufwändig. Deshalb nur der Vollständigkeit wegen.
Realisierung
[Bearbeiten]Wir können die Schaltung nun mit der Schaltgleichung von Oben realisieren:

Eine andere Realisierung die Sich ab und an findet, ist diese:

Blockschaltbild
[Bearbeiten]Auch für den Volladdierer gibt es ein Blockschaltbild:
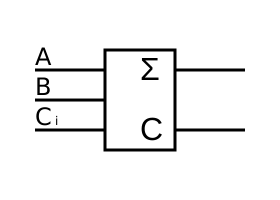
Alternative Darstellungen
[Bearbeiten]Für die Darstellung der Voll- und Halbaddierer gibt es verschiedene Zeichen:
| Volladdierer |  |
 |
 |
| Halbaddierer |  |
 |
 |
Um international lesbare Schaltungen zu zeichnen, verwenden wir die Darstellung mit Sigma und C für Carry.













