Archimedisches Axiom – Serlo „Mathe für Nicht-Freaks“
Das archimedische Axiom
[Bearbeiten]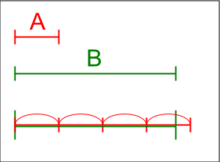
Beginnen wir das Kapitel mit dem archimedischen Axiom:
Satz (Das Archimedische Axiom)
Zu jedem und zu jedem gibt es eine natürliche Zahl , so dass ist. In Quantorenschreibweise:
Beachte, dass für uns das archimedische Axiom kein Axiom ist, sondern ein Theorem. Denn im letzten Kapitel zur Vollständigkeit der reellen Zahlen haben wir bereits ein Axiom definiert, aus dem das archimedische Axiom folgt. Da aber die meisten Lehrbücher den obigen Satz als eines der Axiome für reelle Zahlen benutzen und es somit als „archimedisches Axiom“ bezeichnen, werde ich dies auch in diesem Lehrbuch machen.
Bedeutung des archimedischen Axioms
[Bearbeiten]Die Bedeutung des archimedischen Axioms wird klar, wenn wir seine Aussage negieren. Aus
wird durch Negation
Es gibt also positive Zahlen und , so dass jedes Vielfache von kleiner als ist. Damit wäre eine in Relation zu unendlich große Zahl. Wir können also sagen
Das archimedische Axiom lautet: „Es gibt keine zwei Zahlen und , so dass in Relation zu unendlich groß ist.”
Wenn bezüglich unendlich groß ist, dann ist eine unendlich große Zahl, also eine Zahl, welche größer als jede natürliche Zahl ist. Analog ist eine unendlich kleine Zahl, welche kleiner als jede positive rationale Zahl ist. Da es aber nach dem archimedischen Axiom keine solche Zahlen und geben kann, schließt es auch die Existenz unendlich kleiner oder unendlich großer Zahlen aus. Man kann also auch sagen:
Das archimedische Axiom lautet: „Es gibt keine positiven unendlich kleinen oder unendlich großen reellen Zahlen.“
Alternative Formulierung des archimedischen Axioms
[Bearbeiten]Das Inverse einer unendlich kleinen Zahl ist unendlich groß und umgekehrt. Damit bedingen sich unendlich kleine und unendlich große Zahlen gegenseitig. Es reicht also aus, nur die Existenz der unendlich kleinen oder die Existenz der unendlich großen Zahlen auszuschließen, um eine Aussage äquivalent zum archimedischen Axiom zu erhalten.
Eine unendlich große Zahl ist eine Zahl , die größer als jede natürliche Zahl ist. Die Existenz einer unendlich großen Zahl wird also durch folgende Aussage beschrieben:
Die Negation dieser Aussage schließt damit die Existenz unendlich großer Zahlen aus. Sie lautet:
Analog kann auch die Existenz unendlich kleiner Zahlen ausgeschlossen werden. Eine unendlich kleine Zahl ist eine Zahl, die kleiner als jeder Quotient mit einer natürlichen Zahl ist. Wenn es also unendlich kleine Zahlen geben würde, würde gelten:
Die Aussage, die die Existenz unendlich kleiner Zahlen ausschließt, lautet damit:
Damit haben wir zwei Alternativformulierungen für das archimedische Axiom gefunden. Dass die beiden Aussagen auch wirklich alternative Formulierungen des archimedischen Axioms sind, können wir dadurch zeigen, dass sie äquivalent zum archimedischen Axiom sind:
Satz (Alternative Formulierungen des archimedischen Axioms)
Folgende Aussagen sind äquivalent zum archimedischen Axiom:
Beweis (Alternative Formulierungen des archimedischen Axioms)
Obigen Satz können wir beweisen, indem wir folgende Implikationskette zeigen
Beweisschritt:
Diese Implikation kann direkt gezeigt werden. Hierzu setzt man im archimedischen Axiom
für und für ein. Man erhält dann die Aussage
Beweisschritt:
Sei beliebig. Wir müssen nun zeigen, dass es eine natürliche Zahl gibt, so dass ist. Nun ist aber auch größer 0 und damit gibt es eine natürliche Zahl mit . Daraus folgt aber , was zu beweisen war.
Beweisschritt:
Seien und beliebige positive reelle Zahlen. Nun ist auch und es gibt damit eine natürliche Zahl mit . Wenn wir diese Ungleichung umstellen, kommen wir auf , was zu zeigen war. Somit ist der Beweis der Implikationskette abgeschlossen.
Beweis des archimedischen Axioms
[Bearbeiten]Wie oben bereits erwähnt, ist für uns das archimedische Axiom kein Axiom, sondern ein Satz, den wir dementsprechend auch beweisen müssen. Dies wollen wir nun tun:
Wie kommt man auf den Beweis? (Das archimedische Axiom)
Es ist egal, welche der drei vorgestellten Varianten des archimedischen Axioms wir beweisen, da sie alle äquivalent zueinander sind. Ich wähle zum Beweis die Aussage
welche die Nicht-Existenz unendlich kleiner positiver Zahlen beschreibt. Um eine Idee für einen Beweis zu bekommen, gehen wir einmal vom Gegenteil aus und nehmen an, dass es eine unendlich kleine Zahl gibt. Dies bedeutet aber, dass wir nicht von durch jede Intervallschachtelung mit rationaler Genauigkeit unterscheiden können, da der Abstand zwischen und kleiner als jede rationale Zahl ist. Jedoch haben wir im Intervallschachtelungsprinzip mit rationaler Genauigkeit definiert, dass jede solche Intervallschachtelung maximal eine Zahl approximiert.
Wir müssen also eine Intervallschachtelung mit rationaler Genauigkeit so geschickt wählen, dass wir bei der Existenz einer unendlich kleinen Zahl einen Widerspruch erhalten. Mit etwas Nachdenken kommt man hier auf die Intervallschachtelung .
Beweis (Das archimedische Axiom)
Wir beweisen die Aussage
Sei also beliebig. Betrachte nun die Intervallfolge , also die Folge
Diese Folge ist eine Intervallschachtelung mit rationaler Genauigkeit und damit existiert maximal eine reelle Zahl, die in allen Intervallen liegt. Nun liegt bereits in allen Intervallen, womit nicht in allen Intervallen liegen kann. Es gibt also ein mit . Wegen muss sein. Es gilt also , was zu beweisen war.































![{\displaystyle I_{n}=[0,{\tfrac {1}{n}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcba6e9e9bbccb5f2eb06084d388f245244f30b7)
![{\displaystyle {\begin{aligned}I_{1}&=[0,1]\\I_{2}&=\left[0,{\tfrac {1}{2}}\right]\\I_{3}&=\left[0,{\tfrac {1}{3}}\right]\\&\ \vdots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20b20688f6b056368c6581478b4ada4919bc66c7)


![{\displaystyle x\notin I_{N}=\left[0,{\tfrac {1}{N}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/743066d2da8c593c48d00b417ff0e1980ddb6687)

