Komplexe Konjugation und Betrag komplexer Zahlen – Serlo „Mathe für Nicht-Freaks“

Betrag einer komplexen Zahl

Motivation des Betrags

Im Umgang mit den reellen Zahlen haben wir die Betragsfunktion $|\cdot |\colon \mathbb {R} \to \mathbb {R} _{\geq 0}$ kennengelernt, mit der wir den absoluten Abstand zur Zahl Null angeben konnten. An der reellen Zahlengerade visualisiert sieht das wie folgt aus:

Betrag von reellen Zahlen

Auch in der komplexen Ebene können wir den Abstand einer komplexen Zahl zum Nullpunkt bestimmen. Hierzu verwenden wir den Satz des Pythagoras. Sei $z=a+b\,\mathrm {i}$ eine komplexe Zahl:

Die komplexe Zahl z mit dem Realteil a und den Imaginärteil b

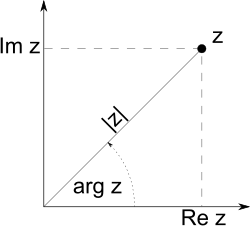
Mit dem Satz des Pythagoras gilt für den Abstand $|z|$ vom Nullpunkt die Gleichung $|z|^{2}=\operatorname {Re} (z)^{2}+\operatorname {Im} (z)^{2}=a^{2}+b^{2}$. Durch Wurzelziehen auf beiden Seiten, kann $|z|$ bestimmt werden. Es ist nämlich:

$|z|={\sqrt {{\text{Re}}(z)^{2}+{\text{Im}}(z)^{2}}}={\sqrt {a^{2}+b^{2}}}$

Mit dem Betrag können einige Konzepte der reellen Zahlen auf die komplexen Zahlen übertragen werden. So wie $|x-y|$ in den reellen Zahlen der Abstand zwischen $x$ und $y$ ist, so ist auch $|z-w|$ in den komplexen Zahlen der Abstand zwischen $z$ und $w$. Mit dem Abstand wiederum können Begriffe wie der Grenzwert definiert werden: Eine komplexe Zahl$z$ ist genau dann der Grenzwert einer Folge $(z_{n})_{n\in \mathbb {N} }$ von komplexen Zahlen, wenn der Abstand $|z-z_{n}|$ zwischen dem Grenzwert $z$ und den Folgengliedern $z_{n}$ beliebig klein wird.

Definition des komplexen Betrags

Definition (Betrag einer komplexen Zahl)

Es sei $z=a+b\,\mathrm {i} \in \mathbb {C}$. Dann setzen wir $|z|={\sqrt {{\text{Re}}(z)^{2}+{\text{Im}}(z)^{2}}}={\sqrt {a^{2}+b^{2}}}$ und nennen die Zahl $|z|\in \mathbb {R} _{\geq 0}$ den Betrag von $z$.

Hinweis

Der oben definierte Betrag auf den komplexen Zahlen stimmt für die reellen Zahlen mit dem üblichen Betrag überein. Sei $z=a+0\cdot \mathrm {i} \in \mathbb {R}$. Dann gilt:

${\begin{aligned}|z|&={\sqrt {{\text{Re}}(z)^{2}+{\text{Im}}(z)^{2}}}={\sqrt {a^{2}+0^{2}}}={\sqrt {a^{2}}}\\[0.3em]&={\begin{cases}a,&{\text{falls }}a\geq 0,\\-a,&{\text{falls }}a<0.\end{cases}}\end{aligned}}$

Komplexe Konjugation

Motivation der Konjugation

Die imaginäre Einheit $\mathrm {i}$ erfüllt als eine Wurzel von $-1$ die Gleichung $\mathrm {i} ^{2}=-1$. Wir können uns die Multiplikation $x\mapsto -1\cdot x$ als eine $180^{\circ }$-Drehung um den Nullpunkt vorstellen. Nun ist die Multiplikation $x\mapsto -1\cdot x$ wegen der Gleichung $\mathrm {i} ^{2}=-1$ dasselbe wie $x\mapsto \mathrm {i} \cdot (\mathrm {i} \cdot x)$. Damit ist $x\mapsto \mathrm {i} \cdot x$ eine Operation, die bei zweifacher Anwendung einer $180^{\circ }$-Drehung entspricht.

Es ist naheliegend, dass die Multiplikation mit $\mathrm {i}$ einer $90^{\circ }$-Drehung entspricht. Damit ist die imaginäre Einheit $\mathrm {i}$ wegen $\mathrm {i} =\mathrm {i} \cdot 1$ gleich derjenigen Zahl, die aus einer Drehung um $90^{\circ }$ der Zahl $1$ entsteht:

Rotation der 1 um 90° ergibt i

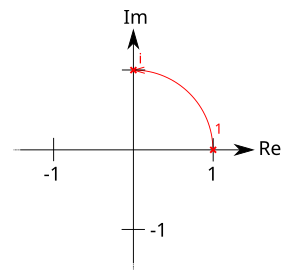
Allgemein gängig ist es, gegen den Uhrzeigersinn zu drehen. So liegt $\mathrm {i}$ dort, wo im $\mathbb {R} \times \mathbb {R}$ die $1$ auf der $y$-Achse liegt. Jedoch hätte man genau so gut im Uhrzeigersinn drehen können. Dann läge das $\mathrm {i}$ an der Stelle der $-1$ auf der $y$-Achse:

Rotation der 1 um -90° ergibt -i

Auch über diese alternative Drehung hätten wir die komplexen Zahlen herleiten können. So hätten wir eine andere Menge von komplexen Zahlen erhalten, bei der die imaginäre Einheit $\mathrm {i}$ unterhalb der $x$-Achse liegt. Bei dieser alternativen Menge von komplexe Zahlen sind die Rollen von $\mathrm {i}$ und $-\mathrm {i}$ vertauscht. Wenn wir also überall $\mathrm {i} \leftrightarrow -\mathrm {i}$ vertauschen, sollten wesentliche Eigenschaften und Strukturen, die durch die Zahlenbereichserweiterung gewonnen wurden, erhalten bleiben. Eine solche Vertauschung entspricht der Abbildung:

$a+b\,\mathrm {i} \mapsto a-b\mathrm {i}$

Bei dieser Abbildung wird der Imaginärteil mit $-1$ multipliziert. Dies entspricht einer Spiegelung der komplexen Zahl an der reellen Achse, also der $x$-Achse:

Komplexe Konjugation veranschaulicht

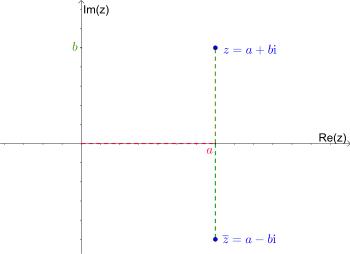
Ein Beispiel hierfür sind die Nullstellen der Funktion $f\colon \mathbb {C} \to \mathbb {C} ,f(z)=z^{2}+1$. Es ist $f(\mathrm {i} )=\mathrm {i} ^{2}+1=0$. Daher ist $\mathrm {i}$ eine Nullstelle von $f$. Andererseits gilt auch $f(-\mathrm {i} )=(-\mathrm {i} )^{2}+1=0$ und damit ist $-\mathrm {i}$ eine weitere Nullstelle. Betrachten wir $g(z)=z^{2}-2z+2$ mit der Nullstelle $1+\mathrm {i}$. Man könnte meinen, dass das Negative der Zahl, also $-1-\mathrm {i}$, eine weitere Nullstelle ist. Dies ist leider nicht der Fall. Wenn wir allerdings $\mathrm {i}$ mit $\mathrm {-} i$ austauschen, also die komplexe Zahl $1-\mathrm {i}$ betrachten, erhalten wir eine weitere Nullstelle:

${\begin{aligned}g(1-\mathrm {i} )&=(1-\mathrm {i} )^{2}-2(1-\mathrm {i} )+2\\&=(-2\mathrm {i} )-(2-2\mathrm {i} )+2=0\end{aligned}}$

Für die Nullstelle $z=a+b\,\mathrm {i}$ eines Polynoms scheint das an der reellen Achse gespiegelte $a-b\,\mathrm {i}$ eine weitere Nullstelle zu sein. Dies ist im Übrigen für alle Polynome mit rein reellen Koeffizienten der Fall. Dies weist darauf hin, dass die Abbildung $a+b\,\mathrm {i} \mapsto a-b\,\mathrm {i}$ eine Besondere ist. Diese Abbildung wird komplexe Konjugation genannt.

Definition der komplexen Konjugation

Definition (Komplexe Konjugation einer komplexen Zahl)

Es sei $z=a+b\,\mathrm {i} \in \mathbb {C}$. Dann heißt die Abbildung $\mathbb {C} \to \mathbb {C} ,z\mapsto {\bar {z}}$ komplexe Konjugation und die Zahl ${\bar {z}}=a-b\,\mathrm {i}$ die zu $z$ komplex konjugierte Zahl.

Übersicht: Eigenschaften des Betrags und der komplexen Konjugation

Eigenschaften der komplexen Konjugation

Für alle $z$ und $w\in \mathbb {C}$ gilt:

• $z={\overline {z}}\iff \operatorname {Im} (z)=0\iff z\in \mathbb {R}$
• ${\overline {\overline {w}}}=w$
• ${\overline {z+w}}={\overline {z}}+{\overline {w}}$
• ${\overline {z\cdot w}}={\overline {z}}\cdot {\overline {w}}$
• ${\overline {\sum _{k=1}^{n}z_{k}}}=\sum _{k=1}^{n}{\overline {z_{k}}}$
• ${\overline {\prod _{k=1}^{n}z_{k}}}=\prod _{k=1}^{n}{\overline {z_{k}}}$
• ${\text{Re}}(w)={\frac {1}{2}}\cdot \left(w+{\overline {w}}\right)$
• ${\text{Im}}(w)={\frac {1}{2\mathrm {i} }}\cdot \left(w-{\overline {w}}\right)$
• $|z|={\sqrt {z\cdot {\bar {z}}}}$
• $z^{-1}={\frac {\overline {z}}{|z|^{2}}}$
• ${\overline {\left({\frac {z}{w}}\right)}}={\frac {\overline {z}}{\overline {w}}}$

Eigenschaften des Betrags einer komplexen Zahl

Für alle $z$ und $w\in \mathbb {C}$ gilt:

• $|z|\geq 0$ und $|z|=0\Leftrightarrow z=0$ (positive Definitheit)
• $|wz|=|w||z|$ (Multiplikativität)
• $|{\text{Re}}(z)|\leq |z|$ und $|{\text{Im}}(z)|\leq |z|$
• $|w+z|\leq |w|+|z|$ (Dreiecksungleichung)
• $|z|\leq |{\text{Re}}(z)|+|{\text{Im}}(z)|$
• ${\big |}|w|-|z|{\big |}\leq |w-z|$

Rechenregeln der komplexen Konjugation

Konjugation verändert reelle Zahlen nicht

Satz (Konjugation verändert reelle Zahlen nicht)

Für eine Zahl $z\in \mathbb {C}$ gilt ${\bar {z}}=z$ genau dann, wenn $z$ rein reell ist, d.h. $\operatorname {Im} (z)=0$.

Beweis (Konjugation verändert reelle Zahlen nicht)

Beweisschritt: $z={\overline {z}}\implies z\in \mathbb {R}$

Sei $z=a+b\,\mathrm {i}$ mit $a,b\in \mathbb {R}$ und ${\overline {z}}=z$. Es ist dann

${\begin{array}{rrl}&z&{\overline {z}}\\\implies &a+b\,\mathrm {i} &=a-b\,\mathrm {i} \\\implies &b\,\mathrm {i} &=-b\,\mathrm {i} \\\implies &2b\,\mathrm {i} &=0\\\implies &b&=0\end{array}}$

Damit ist $\operatorname {Im} (z)=b=0$ und somit $z$ eine reelle Zahl.

Beweisschritt: $z\in \mathbb {R} \implies z={\overline {z}}$

Sei $z=a+b\,\mathrm {i}$ eine reelle Zahl. Also ist $\operatorname {Im} (z)=b=0$. Wir haben:

${\overline {z}}=a-b\,\mathrm {i} =a-0\mathrm {i} =a+0\mathrm {i} =z$

Involution

Satz (Involution)

Für eine komplexe Zahl $w\in \mathbb {C}$ gilt:

${\overline {\overline {w}}}=w$

Beweis (Involution)

Sei $w=a+b\,\mathrm {i}$ mit $a,b\in \mathbb {R}$. Dann gilt:

${\overline {\overline {w}}}={\overline {(a-b\,\mathrm {i} )}}=a+b\,\mathrm {i} =w$

Die kann auch folgendermaßen erklärt werden: ${\overline {w}}$ ist die Spiegelung von $w$ an der reellen Achse. Damit ist ${\overline {\overline {w}}}$ die Spiegelung von der Spiegelung und somit die ursprüngliche komplexe Zahl.

Verträglichkeit mit Addition

Satz (Verträglichkeit mit Addition)

Für komplexe Zahlen $z,w\in \mathbb {C}$ gilt:

${\overline {z+w}}={\overline {z}}+{\overline {w}}$

Beweis (Verträglichkeit mit Addition)

Sei $z\in \mathbb {C}$ von der Form $a+b\,\mathrm {i}$, wobei $a,b\in \mathbb {R}$ und $w\in \mathbb {C}$ von der Form $c+d\,\mathrm {i}$, wobei $c,d\in \mathbb {R}$. Dann gilt:

${\begin{aligned}{\overline {z+w}}&={\overline {(a+b\,\mathrm {i} )+(c+d\,\mathrm {i} )}}\\&={\overline {a+b\,\mathrm {i} +c+d\,\mathrm {i} }}\\&={\overline {(a+c)+(b+d)\,\mathrm {i} }}\\&=(a+c)-(b+d)\,\mathrm {i} \\&=(a+c)-b\,\mathrm {i} -d\,\mathrm {i} \\&=a-b\,\mathrm {i} +c-d\,\mathrm {i} \\&=(a-b\,\mathrm {i} )+(c-d\,\mathrm {i} )\\&={\overline {z}}+{\overline {w}}\end{aligned}}$

Verträglichkeit mit Multiplikation

Satz (Verträglichkeit mit Multiplikation)

Für komplexe Zahlen $z,w\in \mathbb {C}$ gilt:

${\overline {z\cdot w}}={\overline {z}}\cdot {\overline {w}}$

Beweis (Verträglichkeit mit Multiplikation)

Sei $z\in \mathbb {C}$ von der Form $a+b\,\mathrm {i}$, wobei $a,b1\in \mathbb {R}$ und $w\in \mathbb {C}$ von der Form $c+d\,\mathrm {i}$, wobei $c,d\in \mathbb {R}$. Dann gilt:

${\begin{aligned}{\overline {z\cdot w}}&={\overline {(a+b\,\mathrm {i} )\cdot (c+d\,\mathrm {i} )}}\\&={\overline {ac+ad\,\mathrm {i} +bc\,\mathrm {i} -bd}}\\&={\overline {(ac-bd)+(ad+bc)\,\mathrm {i} }}\\&=ac-bd-(ad+bc)\,\mathrm {i} \\&=ac-bd-ad\,\mathrm {i} -bc\,\mathrm {i} \\&=ac-ad\,\mathrm {i} -bc\,\mathrm {i} -bd\\&=(a-b\,\mathrm {i} )\cdot (c-d\,\mathrm {i} )\\&={\overline {z}}\cdot {\overline {w}}\end{aligned}}$

Verträglichkeit der Konjugation bei endlichen Summen und Produkten

Wir wissen, wie sich die Konjugation bei der Summe und dem Produkt zweier Zahlen verhält. Was passiert bei Summen und Produkten mit drei oder mehr Zahlen wie bei ${\overline {z_{1}+z_{2}+z_{3}}}$? Wir behelfen uns mit einem Trick: Wir betrachten zuerst $(z_{1}+z_{2})$ als eine einzige komplexe Zahl und benutzen zwei Mal den Satz zum Zusammenhang zwischen Konjugation und Summe:

${\overline {(z_{1}+z_{2})+z_{3}}}={\overline {(z_{1}+z_{2})}}+{\overline {z_{3}}}={\overline {z_{1}}}+{\overline {z_{2}}}+{\overline {z_{3}}}$

Es ist auch für drei Summanden egal, ob wir zuerst alles summieren und dann auf die entstandene Zahl die Konjugation anwenden, oder ob wir zuerst jede Zahl konjugieren und dann alles summieren. Dies geht allgemein für beliebig lange Summen und Produkte von komplexen Zahlen, wie wir es im Folgenden formal beweisen werden. Hierzu führen wir einen Induktionsbeweis über die Anzahl der Summanden bzw. Faktoren. Auch verwenden wir die kompakte Schreibweise für endliche Summen und Produkte.

Satz (Verträglichkeit für beliebig viele komplexe Zahlen)

Für jedes $n\in \mathbb {N}$ und alle komplexe Zahlen $z_{1},...z_{n}\in \mathbb {C}$ gilt:

1. ${\overline {\sum _{k=1}^{n}z_{k}}}=\sum _{k=1}^{n}{\overline {z_{k}}}$
2. ${\overline {\prod _{k=1}^{n}z_{k}}}=\prod _{k=1}^{n}{\overline {z_{k}}}$

Beweis (Verträglichkeit für beliebig viele komplexe Zahlen)

Wir beweisen diesen Satz für die Summe über vollständige Induktion. Der Beweis für das endliche Produkt kann analog geführt werden:

Aussageform, deren Allgemeingültigkeit für $n\in \mathbb {N}$ bewiesen werden soll:

${\overline {\sum _{k=1}^{n}z_{k}}}=\sum _{k=1}^{n}{\overline {z_{k}}}$

1. Induktionsanfang:

${\overline {\sum _{k=1}^{1}z_{k}}}={\overline {z_{1}}}=\sum _{k=1}^{1}{\overline {z_{k}}}$

2. Induktionsschritt:

2a. Induktionsvoraussetzung:

${\overline {\sum _{k=1}^{n}z_{k}}}=\sum _{k=1}^{n}{\overline {z_{k}}}$

2b. Induktionsbehauptung:

${\overline {\sum _{k=1}^{n+1}z_{k}}}=\sum _{k=1}^{n+1}{\overline {z_{k}}}$

2c. Beweis des Induktionsschritts:

${\begin{aligned}{\overline {\sum _{k=1}^{n+1}z_{k}}}&={\overline {\sum _{k=1}^{n}z_{k}+z_{n+1}}}={\color {OliveGreen}{\overline {\sum _{k=1}^{n}z_{k}}}}+{\overline {z_{n+1}}}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{Induktionsvoraussetzung}}\right.}\\[0.5em]&={\color {OliveGreen}\sum _{k=1}^{n}{\overline {z_{k}}}}+{\overline {z_{n+1}}}=\sum _{k=1}^{n+1}{\overline {z_{k}}}\end{aligned}}$

Berechnung des Real- und Imaginärteils

Satz (Real- und Imaginärteils)

Für eine komplexe Zahl $w\in \mathbb {C}$ gilt:

1. ${\text{Re}}(w)={\frac {1}{2}}\cdot \left(w+{\overline {w}}\right)$
2. ${\text{Im}}(w)={\frac {1}{2\mathrm {i} }}\cdot \left(w-{\overline {w}}\right)$

Beweis (Real- und Imaginärteils)

Sei $w=a+b\,\mathrm {i}$ mit $a,b\in \mathbb {R}$. Wir rechnen die Gleichung von der rechten Seite ausgehend nach:

${\begin{aligned}{\frac {1}{2}}\cdot \left(w+{\overline {w}}\right)&={\frac {1}{2}}\cdot (a+b\,\mathrm {i} +(a-b\,\mathrm {i} ))\\[0.3em]&={\frac {1}{2}}\cdot (a+a+b\,\mathrm {i} -b\,\mathrm {i} )\\[0.3em]&={\frac {1}{2}}\cdot (2a)=a=\mathrm {Re} (w)\\[0.3em]{\frac {1}{2\mathrm {i} }}\cdot \left(w-{\overline {w}}\right)&={\frac {1}{2\mathrm {i} }}\cdot (a+b\,\mathrm {i} -(a-b\,\mathrm {i} ))\\[0.3em]&={\frac {1}{2\mathrm {i} }}\cdot (a-a+b\,\mathrm {i} +b\,\mathrm {i} )\\[0.3em]&={\frac {1}{2\mathrm {i} }}\cdot (2b\,\mathrm {i} )=b=\mathrm {Im} (w)\end{aligned}}$

Berechnung des Betrags über die Konjugation

Satz (Berechnung des Betrags über die Konjugation)

Für alle komplexen Zahlen $z\in \mathbb {C}$ ist $|z|={\sqrt {z\cdot {\bar {z}}}}$. Damit ist $z\cdot {\overline {z}}=|z|^{2}$.

Beweis (Berechnung des Betrags über die Konjugation)

Sei $z\in \mathbb {C}$ eine beliebige komplexe Zahl mit $z=a+b\,\mathrm {i}$. Wir berechnen $z\cdot {\bar {z}}$. Es ist $z=a+b\,\mathrm {i}$ und ${\bar {z}}=a-b\,\mathrm {i}$. Also gilt

${\begin{aligned}z\cdot {\bar {z}}&=(a+b\,\mathrm {i} )\cdot (a-b\,\mathrm {i} )=a^{2}-(b\,\mathrm {i} )^{2}\\&=a^{2}-(-b^{2})=a^{2}+b^{2}=|z|^{2}\end{aligned}}$

Da $|z|^{2}$ reell ist und die Basis $|z|$ nicht negativ ist, können wir die Wurzel ziehen und erhalten die reelle Zahl $|z|={\sqrt {z\cdot {\bar {z}}}}$.

Berechnung des Reziproken mit der Konjugation

Satz (Berechnung des Reziproken mit der Konjugation)

Für alle komplexe Zahlen $z\in \mathbb {C} \setminus \{0\}$ ist $z^{-1}={\tfrac {\overline {z}}{|z|^{2}}}$.

Beweis (Berechnung des Reziproken mit der Konjugation)

Sei $z\in \mathbb {C} \setminus \{0\}$ eine beliebige komplexe Zahl. Wir wollen $z^{-1}={\tfrac {\overline {z}}{|z|^{2}}}$ zeigen. Dafür beweisen wir $z\cdot {\tfrac {\overline {z}}{|z|^{2}}}=1$. Mit $|z|^{2}=z\cdot {\bar {z}}$ folgt

$z\cdot {\frac {\overline {z}}{|z|^{2}}}={\frac {z\cdot {\overline {z}}}{|z|^{2}}}={\frac {|z|^{2}}{|z|^{2}}}=1=z\cdot z^{-1}$

Weil die Inverse in einem Körper eindeutig ist, folgt $z^{-1}={\tfrac {\overline {z}}{|z|^{2}}}$. Dies beweist, dass ${\tfrac {\overline {z}}{|z|^{2}}}$ gleich dem Reziproken von $z$ ist.

Hinweis

Beim Beweis die komplexen Zahlen bilden einen Körper haben wir auch eine multiplikative Inverse von $z=a+b\,\mathrm {i}$ hergeleitet. Dort haben wir gesehen $z^{-1}={\frac {a}{a^{2}+b^{2}}}-{\frac {b}{a^{2}+b^{2}}}\,\mathrm {i}$. Das ist konsistent mit der neuen Darstellung durch komplexe Konjugation:

$z^{-1}={\frac {a}{a^{2}+b^{2}}}-{\frac {b}{a^{2}+b^{2}}}\,\mathrm {i} ={\frac {a-b\,\mathrm {i} }{a^{2}+b^{2}}}={\frac {\overline {z}}{|z|^{2}}}.$

Konjugation bei Brüchen

Satz (Konjugation bei Brüchen)

Für alle komplexen Zahlen $z,w\in \mathbb {C}$ mit $w\neq 0$ gilt:

${\overline {\left({\frac {z}{w}}\right)}}={\frac {\overline {z}}{\overline {w}}}$

Beweis (Konjugation bei Brüchen)

Wir wissen bereits, dass für das Reziproke einer komplexen Zahl $w\in \mathbb {C} \setminus \{0\}$ gilt: ${\tfrac {1}{w}}={\tfrac {\overline {w}}{|w|^{2}}}$. Außerdem haben wir gesehen, dass reelle Zahlen durch die Konjugation nicht verändert werden und dass die Konjugation mit der Multiplikation verträglich ist. Wir zeigen zunächst: ${\overline {\left({\tfrac {1}{w}}\right)}}={\tfrac {1}{\overline {w}}}$. Hierfür benutzen wir, dass ${\tfrac {1}{|w|^{2}}}$ reell ist und dass $|w|=|{\overline {w}}|$ gilt.

${\begin{aligned}{\overline {\left({\frac {1}{w}}\right)}}&={\overline {\left({\frac {\overline {w}}{|w|^{2}}}\right)}}={\overline {\left({\overline {w}}\cdot {\frac {1}{|w|^{2}}}\right)}}={\overline {\left({\overline {w}}\right)}}\cdot {\overline {\left({\frac {1}{|w|^{2}}}\right)}}\\[0.5em]&={\overline {\left({\overline {w}}\right)}}\cdot {\frac {1}{|w|^{2}}}={\overline {\left({\overline {w}}\right)}}\cdot {\frac {1}{|{\overline {w}}|^{2}}}={\frac {\overline {\left({\overline {w}}\right)}}{|{\overline {w}}|^{2}}}={\frac {1}{\overline {w}}}\end{aligned}}$

Daraus folgt für die Konjugation von Brüchen komplexer Zahlen $z,w\in \mathbb {C}$ mit $w\neq 0$:

${\overline {\left({\frac {z}{w}}\right)}}={\overline {\left(z\cdot {\frac {1}{w}}\right)}}={\overline {z}}\cdot {\overline {\left({\frac {1}{w}}\right)}}={\overline {z}}\cdot {\frac {1}{\overline {w}}}={\frac {\overline {z}}{\overline {w}}}$

Eigenschaften der komplexen Betragsfunktion

Positive Definitheit

Satz (Positive Definitheit)

Sei $z\in \mathbb {C}$ eine komplexe Zahl, dann gilt:

$|z|\geq 0\land |z|=0\iff z=0$

Beweis (Positive Definitheit)

Sei $z=a+b\,\mathrm {i}$ in kartesischer Form gegeben. Dann gilt $|z|={\sqrt {a^{2}+b^{2}}}\geq 0$. Nun müssen wir noch die Äquivalenz beweisen. Dafür zeigen wir zwei Implikationen:

Beweisschritt: $z=0\implies |z|=0$

Sei $z=0$. Dann gilt $a=b=0$. Somit folgt $|z|={\sqrt {a^{2}+b^{2}}}={\sqrt {0+0}}=0$.

Beweisschritt: $|z|=0\implies z=0$

Diese Richtung zeigen wir durch Kontraposition. Sei dafür $z\neq 0$. Daraus folgt $a\neq 0$ oder $b\neq 0$. Wenn $a\neq 0$ gilt $|z|={\sqrt {a^{2}+b^{2}}}\geq {\sqrt {a^{2}}}=|a|>0$. Wenn $b\neq 0$ gilt $|z|={\sqrt {a^{2}+b^{2}}}\geq {\sqrt {b^{2}}}=|b|>0$. In jedem Fall folgt $|z|>0$ und damit $|z|\neq 0$.

Multiplikativität

Satz (Multiplikativität)

Für $w,z\in \mathbb {C}$ gilt $|z\cdot w|=|z|\cdot |w|$.

Beweis (Multiplikativität)

Seien $w=a+b\,\mathrm {i}$ und $z=c+d\,\mathrm {i} \in \mathbb {C}$. Dann folgt

${\begin{aligned}|z\cdot w|^{2}&=|(c+d\,\mathrm {i} )\cdot (a+b\,\mathrm {i} )|^{2}\\&=|(ac-bd)+(cb+da)\,\mathrm {i} |^{2}\\&=(ac-bd)^{2}+(cb+da)^{2}\\&=a^{2}c^{2}+b^{2}d^{2}+c^{2}b^{2}+d^{2}a^{2}\\&=(c^{2}+d^{2})(a^{2}+b^{2})\\&=|z|^{2}\cdot |w|^{2}\\&=(|z|\cdot |w|)^{2}\end{aligned}}$

Da die Basen $|z\cdot w|$ und $|z|\cdot |w|$ der beiden Quadrate auf beiden Seiten nicht negativ ist, können wir auf beiden Seiten die Wurzel ziehen. Wir erhalten dann $|z\cdot w|=|z|\cdot |w|$.

Abschätzung Real- und Imaginärteil

Satz

Für alle $z\in \mathbb {C}$ gilt $|{\text{Re}}(z)|\leq |z|$ und $|{\text{Im}}(z)|\leq |z|$.

Beweis

Sei $z=a+b\,\mathrm {i} \in \mathbb {C}$ mit $a,b\in \mathbb {R}$. Dann folgt mit $b^{2}\geq 0$:

$|z|=|a+b\,\mathrm {i} |={\sqrt {a^{2}+b^{2}}}\geq {\sqrt {a^{2}}}=|a|=|\mathrm {Re} (z)|$

Genauso folgt mit $a^{2}\geq 0$:

$|z|=|a+b\,\mathrm {i} |={\sqrt {a^{2}+b^{2}}}\geq {\sqrt {b^{2}}}=|b|=|\mathrm {Im} (z)|$

Dreiecksungleichung

Satz (Dreiecksungleichung)

Für alle $w,z\in \mathbb {C}$ gilt $|w+z|\leq |w|+|z|$.

Beweis (Dreiecksungleichung)

Seien $w$ und $z\in \mathbb {C}$. Um den Betrag abzuschätzen nutzen wir die Beziehung $|v|^{2}=v\cdot {\overline {v}}$:

${\begin{aligned}|w+z|^{2}&=(w+z){\overline {(w+z)}}\\&=(w+z)({\overline {w}}+{\overline {z}})\\&=w{\overline {w}}+w{\overline {z}}+{\overline {w}}z+{\overline {z}}z\\&=|w|^{2}+(w{\overline {z}}+{\overline {w{\overline {z}}}})+|z|^{2}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Für }}v\in \mathbb {C} {\text{ gilt }}v+{\overline {v}}=2\mathrm {Re} (v)\right.}\\[0.3em]&=|w|^{2}+2\mathrm {Re} (w{\overline {z}})+|z|^{2}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ \mathrm {Re} (w{\overline {z}})\leq |\mathrm {Re} (w{\overline {z}})|\leq |w{\overline {z}}|=|w||{\overline {z}}|=|w||z|\right.}\\[0.3em]&\leq |w|^{2}+2|w||z|+|z|^{2}\\&=(|w|+|z|)^{2}\end{aligned}}$

Abschätzung des Betrags

Satz

Für alle $z\in \mathbb {C}$ gilt $|z|\leq |\operatorname {Re} (z)|+|\operatorname {Im} (z)|$.

Beweis

Wir zeigen zuerst, dass die Ungleichung für beide Seiten im Quadrat gilt.

${\begin{aligned}|z|^{2}&=a^{2}+b^{2}=|a|^{2}+|b|^{2}\\&\leq |a|^{2}+2|a||b|+|b|^{2}\\&=(|a|+|b|)^{2}=(|\operatorname {Re} (z)|+|\operatorname {Im} (z)|)^{2}\end{aligned}}$

Die beiden Basen $|z|$ und $|\operatorname {Re} (z)|+|\operatorname {Im} (z)|$ sind nicht negative Zahlen sind, können wir die Wurzel auf beiden Seiten der Ungleichung ziehen. Diese Wurzel erhält Ungleichungen und damit ist $|z|\leq |\operatorname {Re} (z)|+|\operatorname {Im} (z)|$.

Umgekehrte Dreiecksungleichung

Satz (Umgekehrte Dreiecksungleichung)

Für komplexe Zahlen $w,z\in \mathbb {C}$ gilt ${\big |}|w|-|z|{\big |}\leq |w-z|$.

Beweis (Umgekehrte Dreiecksungleichung)

Um eine Ungleichung $|x|\leq y$ zu zeigen, können wir alternativ die beiden Ungleichungen $x\leq y$ und $-x\leq y$ beweisen. Um diese Technik in diesem Beweis anzuwenden, müssen wir die beiden Ungleichungen $|w|-|z|\leq |w-z|$ und $|z|-|w|\leq |w-z|$ beweisen.

Beginnen wir mit der ersten Ungleichung. Wir verwenden die Dreiecksungleichung des komplexen Betrag und den Trick des „Einschiebens einer $0$“:

$|w|=|(w-z)+z|\leq |w-z|+|z|$

Durch Umformung erhalten wir $|w|-|z|\leq |w-z|$. Die zweite Ungleichung zeigen wir analog, wobei die Rollen von $z$ und $w$ vertauscht sind. Zusätzlich formen wir $|z-w|$ schrittweise in $|w-z|$ um:

${\begin{aligned}|z|&=|(z-w)+w|\leq |z-w|+|w|\\&=|(-1)(w-z)|+|w|\\&=|(-1)||w-z|+|w|\\&=|w-z|+|w|\end{aligned}}$

Es folgt $|z|-|w|\leq |w-z|$. Damit haben wir die beiden Ungleichungen $|w|-|z|\leq |w-z|$ und $-(|w|-|z|)\leq |w-z|$ bewiesen. Daraus folgt die Ungleichung $||w|-|z||\leq |w-z|$.