MathemaTriX ⋅ Theorie nach Thema. Integralrechnung

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Inhalt Ein-Aus- klappen

AUFGABEN

KAPITEL Grundrechenarten Bruchrechnungen $-{\tfrac {\cdot \ +}{\ :\ }}$ Schlussrechnung Prozentrechnung Exponentialfunktion Logarithmus Arbeiten mit Termen $\mathbb {X} ^{2}$ Zahlendarstellungen Mengentheorie Aussagenlogik ${\begin{matrix}\mathbb {R} :=\\\mathbb {Q} \cup \mathbb {I} \end{matrix}}$ Einheiten $cm^{2}$ Statistik und Wahrscheinlichkeit Geometrische Konstruktionen Geometrie der Ebene Geometrie des Raums Diagramme Funktionen $f(x)$ Lineare Gleichungssysteme ${\begin{smallmatrix}{a_{1}\ b_{2}}\\{a_{2}\ b_{2}}\end{smallmatrix}}$ Trigonometrische Funktionen Vektoren Differentialrechnung $^{dy}/_{dx}$ Integralrechnung $\textstyle \int _{a}^{b}dx$ Folgen $a_{n}$ Beweise $a\rightarrow b$

Was ist ein Integral

Für jede Rechnung gibt es eine Gegenrechnung, z.B. sind Division und Multiplikation Gegenrechnungen voneinander. Das Integral ist quasi (nicht aber genau) die Gegenrechnung der Ableitung. Für die Ableitung einer Funktion müssen wir die Einheit der y-Achse durch die Einheit der x-Achse dividieren. Für die Berechnung der Einheit eines Integrals müssen wir hingegen die Einheiten der Achsen multiplizieren. Wenn wir dies tun, dann berechnen wir allerdings eine Fläche. Das Beispiel aus der geradlinigen Bewegung, das wir auch in der Erklärung der Ableitung benutzt haben, wird den Zusammenhang etwas übersichtlicher machen.

Fläche in einem v-t Diagramm

Wenn wir die Fläche des schattierten Rechtecks im v-t Diagramm berechnen wollen, können wir die Formel für die Fläche eines Rechtecks benutzen: Fläche ist Länge mal Breite, A=a⋅b. Allgemein wird eine Fläche in Flächeneinheiten berechnet, z.B. in m² oder cm². Die Fläche in einem Diagramm ist allerdings, genauso wie die Steigung, etwas Besonderes. In unserem Rechteck hier, ist die Breite des Rechtecks auf der y-Achse, die hier die Geschwindigkeit darstellt. Daher sind die Einheiten der Breite beispielsweise Meter pro Sekunde (m/s). Die Länge des Rechtecks steht auf der x-Achse und sie stellt die Zeit dar. Daher sind die Einheiten der Länge beispielsweise Sekunden (s). Wenn man die Einheiten multipliziert, ergibt sich:

${\frac {m}{s}}\cdot s=m$

Die Einheit für die Fläche in diesem Diagramm ist daher doch einfach Meter m (und nicht Quadratmeter)! Meter ist die Einheit einer Strecke. Also:

Die Fläche zwischen Kurve und x-Achse in einem v-t Diagramm zeigt uns die zurückgelegte Strecke.

In unserem Beispiel hier, wenn die Einheit für die y-Achse m/s ist und für die x-Achse s, wären es dann 2⋅3=6 m. Das bedeutet: bei einer konstanter Geschwindigkeit von 2 m/s werden nach 3 s 6m zurückgelegt. Selbstverständlich müssen in diesem Fall die Einheiten der x und der y Achse übereinstimmen, sonst müssen wir eine der beiden umrechnen.

Allgemeiner sind die Einheiten der Fläche in irgendeinem Diagramm die Einheiten der y-Achse mal die Einheiten der x-Achse.

Im Fall einer konstanten Funktion, wie im Beispiel mit dem Rechteck, entspricht die berechnete Fläche tatsächlich der Regel für die Berechnung eines Integrals:

$f(x)=a\,x^{n}\ \rightarrow \ \int f(x)\,dx={\frac {a\cdot x^{n+1}}{n+1}}+C$

Im Fall einer konstanten Funktion ist die Hochzahl Null:

$f(x)=a=a\,x^{0}\ \rightarrow \ \int f(x)\,dx={\frac {a\cdot x^{0+1}}{0+1}}=a\,x$

Es ist allerdings so, dass ein Integral zwischen zwei Werten berechnet wird. Im Beispiel mit dem Rechteck wird die Fläche zwischen den Stellen 0 und 3. In diesem Fall entfällt die Konstante (hier C), die bei der Berechnung der Integralfunktion (auch Stammfunktion genannt) immer vorkommt. Tatsächlich:

$f(x)=2\ \rightarrow \ F(x)=\int f(x)\,dx=2x+C$

Zwischen den Stellen x=0 und x=3 gilt dann:

$F(3)-F(0)=2\cdot 3+C-(2\cdot 0+C)=6\$(m)

Bei der Berechnung eines sogenannten bestimmten Integrals entfällt die Konstante.

Wie ist es bei der Berechnung des Integrals einer linearen Funktion? Nehmen wir wieder das Beispiel eines v-t Diagramms:

v-t Diagramm bei konstanter Beschleunigung

Die Steigung (nennen wir sie hier m) in diesem Fall stellt eine Beschleunigung (a) dar: $\textstyle {\text{Steigung}}\ m:{\frac {\Delta v}{\Delta t}}=a\$(Geschwindigkeitsänderungsrate, also Beschleunigung). Der y-Achsenabschnitt ist hier $v_{1}$

$v(t)=a\,t+v_{1}$

Wie ist es jetzt nach der allgemeinen Formel mit dem Integral?

$F(t)=\int v(t)\,dt={\frac {a\,t^{2}}{2}}+v_{1}\cdot t+C$

Zwischen den Stellen 0 und t gilt dann
(nicht vergessen: $\textstyle a={\frac {\Delta v}{\Delta t}}\$und die Zeitänderung: $\Delta t=t-0=t$):

$F(t)-F(0)={\frac {a\cdot t^{2}}{2}}+v_{1}\cdot t+C-\left({\frac {a\cdot 0^{2}}{2}}+v_{1}\cdot 0+C\right)={\dfrac {{\frac {\Delta v}{\Delta t}}\cdot \Delta t^{2}}{2}}+v_{1}\cdot t={\frac {\Delta v\cdot \Delta t}{2}}+v_{1}\cdot t$

Das ist allerdings ganz genau die Fläche unterhalb der linearen Funktion, also zwischen linearer Funktion und x-Achse und zwischen den zwei Stellen 0 und t. Das ist ja die Fläche des Dreiecks $\textstyle {\frac {\Delta v\cdot \Delta t}{2}}\$und des Rechtecks $v_{1}\cdot t$. Das Integral also entspricht einer Fläche: zwischen Funktion und x-Achse und zwischen zwei Stellen der Funktion. So können wir das Integral verstehen:

Dem Integral entspricht eine Fläche.

Wir haben uns bisher nur mit der Fläche in einem v-t Diagramm beschäftigt. Im Gegenteil zur Steigung, die als Änderungsrate fast immer einen physikalischen Sinn hat, ist das mit der Fläche zwischen Kurve und x-Achse nicht immer der Fall.

Fläche in einem a-t Diagramm

Was ist mit der Fläche in einem a-t Diagramm? Laut Definition der Fläche sollte sie a · t sein und das hat doch die Dimensionen der Geschwindigkeit. In einem v-t Diagramm ist die Einheit der Fläche das Produkt der Einheiten der Achsen. In einem v-t Diagramm ist das Produkt v·t eine Strecke. Die Fläche zeigt uns allerdings nicht eine Strecke, sondern eine Änderung der Strecke, eine Differenz, die zurückgelegte Strecke. Ähnlich ist es auch bei einem a-t Diagramm: die Fläche in einem a-t Diagramm zeigt uns die Differenz der Größe der Fläche, also die Differenz der Geschwindigkeit Δv (Geschwindigkeitsänderung), da a·t doch Geschwindigkeit darstellt.

In einem s-t Diagramm ist die Fläche, also das Produkt s · t, keine bekannte physikalische Größe. Daher macht es nicht Sinn, die Fläche in einem s-t Diagramm zu benutzen.

Allgemein ist die (physikalische) Größe der Fläche zwischen Kurve und x-Achse und zwischen zwei Werten von x das Produkt der Größen der beide Achsen. In Physik ist dieses Produkt oft keine sinnvolle physikalische Größe (wie z.B. in einem s-t Diagramm). Man benutzt die Fläche nur, wenn es sinnvoll ist.

Bild 2

Bild 3

Die ganze Fläche zeigt uns dann die Änderung dieser Größe zwischen den beiden Werten x₁ und x₂ auf der x-Achse (Geschwindigkeitsänderung zwischen t₁ und t₂ in einem a-t Diagramm, die Änderung der Strecke Δs zwischen t₁ und t₂ in einem v-t Diagramm usw.). Bisher haben wir vorwiegend Beispiele gesehen, wo der Wert für t₁ null war (am Koordinatenursprung), das ist aber in der Regel nicht so!

Die Fläche zu berechnen ist im Fall einer linearen Funktion (eine lineare Funktion ist im Koordinatensystem eine Gerade, siehe Bild 2) einfach (Summe der Fläche eines Dreiecks und eines Vierecks).

Allgemein (siehe beispielsweise Bild 3) kann man die Fläche mit Hilfe des sogenannten Integrals berechnen.

Die Integrale von Potenzfunktionen und ihre Kombinationen können wir mit Hilfe der Regel $\textstyle f(x)=a\,x^{n}\ \rightarrow \ \int f(x)\,dx={\frac {a\cdot x^{n+1}}{n+1}}+C\$berechnen. Für andere Funktionen gibt es entsprechende Formeln.

Schauen wir jetzt, wie wir das Integral etwas genauer (aber doch immer noch nicht streng) definieren können. Um eine Ableitung zu berechnen benutzt man die Idee des Grenzwertes eines Differenzquotienten:

$f'(x)=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}$

Der Grenzwert des Differenzquotienten wird in einer Darstellung der Ableitung als sogenannter Differentialquotient dargestellt:

$f'(x)=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}={\frac {d\ f(x)}{d\ x}}$

Obwohl man mit Differentialen nicht wie bei normalen Variablen arbeiten soll, stellen wir uns vor, dass das möglich wäre:

$f'(x)={\frac {\lim _{\Delta x\to 0}\ \left(f(x+\Delta x)-f(x)\right)}{\lim _{\Delta x\to 0}\ \Delta x}}$$={\frac {\lim _{\Delta x\to 0}\ \left(f(x+\Delta x)-f(x)\right)}{dx}}$$\Leftrightarrow f'(x)dx=\lim _{\Delta x\to 0}\ \left(f(x+\Delta x)-f(x)\right)$

Stellen wir uns dazu vor, dass die Gegenrechnung der Grenzwertberechnung (also der Ableitung) das Integral ist:

$\int \limits _{x}^{x+\Delta x}f'(x)dx=f(x+\Delta x)-f(x)$

Obwohl der Vorgang streng mathematisch gesehen nicht erlaubt ist, stimmt unseres Ergebnis schon: Das Integral der Ableitung einer Funktion zwischen zwei Stellen der Funktion $\textstyle \int \limits _{x}^{x+\Delta x}f'(x)dx$ ist soviel wie die Differenz der Werte der Funktion zwischen diesen Stellen $f(x+\Delta x)-f(x)$.

Dieses Integral der Ableitung der Funktion ist die Fläche unterhalb der Ableitungsfunktion zwischen diesen Stellen. Die Geschwindigkeit beispielsweise ist die Ableitung der zurückgelegten Strecke auf die Zeit, das Integral der Funktion der Geschwindigkeit (also die Fläche unterhalb des Diagramms der Geschwindigkeit) auf Zeit wird daher die zurückgelegte Strecke selber sein:

$\int \limits _{t}^{t+\Delta t}v(t)dt=s(t+\Delta t)-s(t)\leftrightarrow s'(t)=v(t)$

Das Integral einer linearen Funktion ist leicht zu berechnen, das ist die Summe eines Dreiecks und eines Rechtecks. Wie kann man das Integral für eine allgemeine Kurve berechnen. Eine Idee dafür sehen wir im Bild. Man teilt das Intervall auf der x-Achse zwischen den erwünschten Stellen in immer kleiner werdende Teile. Dadurch kann man Rechtecke aufbauen, die die ganze Fläche annähern. Je mehr und kleiner die Teile werden, desto genauer ist die Annäherung. Für verschwindenden Teile, also für den Grenzwert $\Delta x\to 0$, der nicht streng genommen das Differential $dx$ ist, wird die Fläche der Rechtecke genau soviel wie die gefragte Fläche unter der Kurve sein, das wird keine Annäherung mehr sein. So können wir uns das Integrieren vorstellen. Man kann tatsächlich auch dazu (sogar streng genommen) zeigen, dass das Integral etwas wie die "Gegenrechnung" der Ableitung ist.

Integral von Potenzfunktionen

Es gilt:

$\int (a\,x^{n})\,dx=a\,{\frac {x^{n+1}}{n+1}}+C\quad$für $n\neq -1\quad$und

$\int a\,x^{-1}\,dx=\ln x\,+C\quad$für $n=-1\quad$

Hier werden wir uns nur damit beschäftigen, wie wir die Stammfunktion einer Funktion finden können oder anders gesagt, wie wir eine Funktion integrieren können.

Das Integrieren können wir als die Gegenrechnung der Ableitung begreifen. Das Symbol dafür ist $\int f(x)\,dx$.Für das Integrieren der Potenzfunktionen gilt die allgemeine Regel:

$p_{n}(x)=a\,x^{n}\qquad \int p_{n}(x)\,dx=a\,{\frac {x^{n+1}}{n+1}}+C$

Die Hochzahl wird also um eins erhöht und es wird durch die neue (erhöhte) Hochzahl dividiert. Dazu wird ein Konstante addiert, die von der jeweiligen Aufgabe abhängig ist.

Die Hochzahl n kann irgendeine reelle Zahl sein mit einer einzigen Ausnahme: Wenn n=1 ist, gilt diese Regel nicht. Um der Sache etwas näher zu kommen, fangen wir mit den Ableitungen an. Die allgemeine Regel ist $p_{n}'(x)=a\cdot n\cdot x^{n-1}$. Wenden wir diese Regel für n={3, 2, 1, 0, −1 und −2}.

$p_{3}(x)=a\,x^{3}\qquad p_{3}'(x)=a\cdot 3\cdot x^{3-1}=2\,a\,x^{2}\$(Hochzahl in der Abl. = 2)

$p_{2}(x)=a\,x^{2}\qquad p_{2}'(x)=a\cdot 2\cdot x^{2-1}=2\,a\,x\$(Hochzahl in der Abl. = 1)

$p_{1}(x)=a\,x^{1}\qquad p_{1}'(x)=a\cdot 1\cdot x^{1-1}=a\$(Hochzahl in der Abl. = 0)

$p_{0}(x)=a\,x^{0}=a\qquad p_{0}'(x)=a\cdot 0\cdot x^{0-1}=0\$(Hochzahl in der Abl. wäre −1)

$p_{-1}(x)=a\,x^{-1}={\frac {1}{x}}\qquad p_{-1}'(x)=a\cdot (-1)\cdot x^{-1-1}=-a\,x^{-2}\$(Hochzahl in der Abl. = −2)

$p_{-2}(x)=a\,x^{-2}={\frac {1}{x^{2}}}\qquad p_{-2}'(x)=a\cdot (-2)\cdot x^{-2-1}=-a\,x^{-3}\$(Hochzahl in der Abl. = −3)

Wir sehen, dass in der Ableitung alle Hochzahlen außer −1 vorkommen. Es macht daher irgendwie "Sinn", dass in der "Gegenrechnung" diese Hochzahl "problematisch" sein wird. Das hat damit zu tun, dass in der Ableitung mit 0 multipliziert wird; und die Gegenrechnung (durch Null) ist nicht definierbar. Für das Integral von $a\,x^{-1}\$gibt es eine besondere Regel:

$\int a\,x^{-1}\,dx=\ln x\,+C$

Dadurch wird auch die "Lücke" in den Ableitungen ergänzt:

$f(x)=a\,\ln x\qquad f'(x)=a\,x^{-1}=a\,{\frac {1}{x}}={\frac {a}{x}}$

Warum müssen wir beim Integrieren immer eine Konstante (hier mit C geschrieben) schreiben? Dafür brauchen wir zuerst eine allgemeinere Regel:

Die Ableitung einer Summe von Funktionen ist die Summe ihrer Ableitungen:

Sei $f(x)=g(x)+h(x)$, dann ist $f'(x)=g'(x)+h'(x)$

Das Integral einer Summe von Funktionen ist die Summe ihrer Integrale:

Sei $f(x)=g(x)+h(x)$, dann ist $\int f(x)\,dx=\int g(x)\,dx+\int h(x)\,dx$

Nehmen wir jetzt die allgemeine Regel für das Integral einer Potenzfunktion (ohne die Ausnahme):

$p_{n}(x)=a\,x^{n}\qquad \int p_{n}(x)\,dx=a\,{\frac {x^{n+1}}{n+1}}+C$

Leiten wir jetzt das Ergebnis ab:

$p(x)=a\,{\frac {x^{n+1}}{n+1}}+C\qquad p'(x)=a\,(n+1)\,{\frac {x^{n+1-1}}{n+1}}+0=a\,x^{n}$

Wir stellen damit hier zwei Sachen fest:

• Die allgemeine Regel fürs Integrieren einer Potenzfunktion ist tatsächlich als Gegenrechnung des Ableitens zu konzipieren. Es gibt allerdings einen grundsätzlichen Unterschied zwischen den beiden Richtungen (Ableiten ↔ Integrieren), der erst später erklärt wird.
• Die Konstante beim Integrieren muss geschrieben werden, um den allgemeinen Fall abzudecken.

Integrale von weiteren Funktionen

Mit Hilfe der Definition als Grenzwert können wir weitere Ableitungen berechnen, wir brauchen allerdings dafür komplizierteres Wissen über trigonometrische Funktionen und sogenannte "Folgen". Mit Hilfe dieser Mittel können wir dann folgende Ableitungen bestimmen:

$f(x)=a\,\sin x\ \rightarrow \ f'(x)=a\,\cos x\qquad \qquad$$f(x)=a\,\cos x\ \rightarrow \ f'(x)=-a\,\sin x\qquad \qquad$
$f(x)=a\,e^{x}\ \rightarrow \ f'(x)=a\,e^{x}\qquad \qquad \qquad$$f(x)=a\,\ln x\ \rightarrow \ f'(x)=a\,x^{-1}\qquad$
$f(x)=a\,\tan x\ \rightarrow \ f'(x)={\frac {a}{\cos ^{2}x}}=a\left(1+\tan ^{2}x\right)$

In die Gegenrichtung gibt es die entsprechenden Stammfunktionen ("unbestimmte Integrale"):

$f(x)=a\,\sin x\ \rightarrow \ F(x)=-a\,\cos x+C\qquad \qquad$$f(x)=a\,\cos x\ \rightarrow \ F(x)=a\,\sin x+C\qquad \qquad$
$f(x)=a\,e^{x}\ \rightarrow \ F(x)=a\,e^{x}+C\qquad \qquad \qquad$$f(x)=a\,{\frac {1}{x}}\ \rightarrow \ F(x)=a\,\ln |x|+C\qquad$

Sowohl die Ableitung als auch das Integral einer Funktion ist eine neue Funktion. Im Fall der Ableitung zeigt uns diese neue Funktion die Steigung der Anfangsfunktion in Abhängigkeit von der unabhängigen Variable. Die Ableitung f'(x) einer Funktion f(x) ist eine neue Funktion, die uns die Steigung der Funktion f(x) an jeder Stelle x angibt. Das Integral allerdings weist den Unterschied zur Funktion und Ableitung auf, dass es nicht an einer Stelle sondern zwischen zwei Stellen zu berechnen ist.

Fläche zwischen zwei Funktionen

Bei der Integralrechnung kommt oft vor, dass wir die Fläche zwischen zwei Funktionen berechnen wollen. Das hat Anwendungen beispielsweise in Maschinenbau. Die Idee ist in diesem Fall nicht so kompliziert: Aus der Fläche zwischen der Funktion, die im Diagramm weiter oben ist, und x-Achse müssen wir die Fläche zwischen Funktion, die weiter unten ist, und x-Achse subtrahieren. Wir müssen daher die Fläche zwischen der Differenz der beiden Funktion berechnen. Es gibt allerdings eine Sache, auf die wir aufpassen müssen. Wenn die beiden Funktion einen Schnittpunkt haben, kann es sein, dass sie ihre Rolle wechseln. Die Funktion die vorher oben war, kann danach doch unten sein. Daher müssen wir zwei Integrale berechnen.

Berechnen Sie die Fläche zwischen den Funktionen $\ g(x)=0{,}5e^{x}-1\$ und $\ f(x)=-0{,}16x^{2}-0{,}4x+2{,}75\$ und zwischen den Stellen −2 und 2.

In solchen Aufgaben sind elektronische Mitteln notwendig (wenn wir nicht wollen, uns mit einer Aufgabe einige Stunden zu beschäftigen...). Wir haben hier mit Hilfe von Geogebra folgendes Bild für die beiden Funktionen erzeugt:

Wir sehen, dass die Funktionen einen Schnittpunkt haben. Um diesen Punkt zu berechnen, setzen wir die beiden Funktionen gleich:

$g(x)=f(x)\rightarrow 0{,}5e^{x}-1\ =-0{,}16x^{2}-0{,}4x+2{,}75\$

Diese Gleichung lässt sich allerdings auch mit elektronischen Mitteln nicht unbedingt so leicht lösen. Wenn wir aber mit den Werkzeugen von Geogebra nach dem Schnittpunkt der beiden Funktionen fragen, bekommen wir für den x-Wert des Schnittpunkts C: $x_{1}\approx 1{,}66433$. Bis zu diesem Punkt befindet sich oben die Polynomfunktion, danach die Exponentialfunktion. Um die ganze Fläche zu berechnen, müssen wir daher folgende Rechnung machen:

$A=\int _{-2}^{x_{1}}{\big (}f(x)-g(x){\big )}\,\mathrm {d} x+\int _{x_{1}}^{2}{\big (}g(x)-f(x){\big )}\,\mathrm {d} x=$
Also, bis zum Punkt x₁ berechnen wir das Integral der Differenz der Polynomfunktion minus die Exponentialfunktion, danach umgekehrt.
$\int _{-2}^{x_{1}}(-0{,}5e^{x}+1-0{,}16x^{2}-0{,}4x+2{,}75)\,\mathrm {d} x+\dots$
$\qquad \quad \dots +\int _{x_{1}}^{2}(0{,}5e^{x}-1+0{,}16x^{2}+0{,}4x-2{,}75)\,\mathrm {d} x=$
$\left[-0{,}5e^{x}+x-{\frac {0{,}16}{3}}x^{3}-0{,}2x+2{,}75x\right]_{-2}^{x_{1}}+$
$\qquad \quad \dots +\left[0{,}5e^{x}-x+{\frac {0{,}16}{3}}x^{3}+0{,}2x^{2}-2{,}75x\right]_{x_{1}}^{2}$
Bisher haben wir die unbestimmten Integrale berechnet. Wir haben die Konstante nicht geschrieben, da sie sowieso mit der Berechnung wegfallen wird. Jetzt müssen wir die Grenzwerte der Integrale einsetzen und dann berechnen.

$\left(-0{,}5e^{1{,}66..}+1{,}66..-{\frac {0{,}16}{3}}\cdot {1{,}66..}^{3}-0{,}2\cdot {1{,}66..}^{2}+2{,}75\cdot 1{,}66..\right)-\dots$
$\dots -\left(-0{,}5e^{(-2)}+1-{\frac {0{,}16}{3}}\cdot {(-2)}^{3}-0{,}2\cdot {(-2)}^{2}+2{,}75\cdot (-2)\right)+\ \ldots$
$\dots +\left(0{,}5e^{(2)}-1-{\frac {0{,}16}{3}}\cdot {(2)}^{3}+0{,}2\cdot {(2)}^{2}-2{,}75\cdot (2)\right)-\ \ldots$
$\dots -\left(0{,}5e^{1{,}66..}-1{,}66..-{\frac {0{,}16}{3}}\cdot {1{,}66..}^{3}+0{,}2\cdot {1{,}66..}^{2}-2{,}75\cdot 1{,}66..\right)-\dots$

Allein diese Rechnung zu betrachten bereitet Kopfschmerzen. Man könnte selbstverständlich das ganze Schritt zum Schritt berechnen, allderdings können wir mit elektronischen Mitteln viel schneller die Antwort berechnen. Wir müssen folgendes eintippen:

$\int _{-2}^{1{,}66433}(-0{,}5e^{x}+1-0{,}16x^{2}-0{,}4x+2{,}75)\,\mathrm {d} x+\dots$
$\qquad \quad \dots +\int _{1{,}66433}^{2}(0{,}5e^{x}-1+0{,}16x^{2}+0{,}4x-2{,}75)\,\mathrm {d} x$

Das Ergebnis sollte ca. 10,96 sein.

Wir haben schon erwähnt, dass wir Minuend und Subtrahend austauschen müssen, falls die Funktionen ihre Stellung ändern (welche oben ist). Ähnlich ist die Situation, wenn wir einfach das Integral einer Funktion berechnen wollen. Die Rolle der zweiten Funktion übernimmt dann die x-Achse (sie ist ja die konstante Funktion y=0). Was passiert, wenn wir das nicht tun und was ist die Bedeutung der beiden Berechnungen? Das können wir mit Hilfe eines einfachen Beispiels verstehen.

Wenn wir das Integral der linearen Funktion im Bild zwischen den Stellen −2 und 2 berechnen, ist das Ergebnis null. Denken wir an einen v-t Diagramm. Das Integral sollte Strecke sein. Die Geschwindigkeit ist links negativ und rechts positiv. Das bedeutet, dass wir unsere Bewegungsrichtung ändern. Wenn wir uns für eine Weile in eine Richtung bewegen und dann für die gleiche Dauer und in der gleichen Weise genau in die Gegenrichtung, dann werden wir am Ausgangspunkt gelangen. Das macht schon Sinn. Die "mittlere" zurückgelegte Strecke ist 0. Allerdings haben wir uns doch bewegt. Wie viel? Um das zu berechnen, müssen wir an der Stelle Null (x=0), wo die Gerade die x-Achse trifft, Minuend mit Subtrahend austauschen.

Ob wir Minuend mit Subtrahend austauschen, hängt daher davon ab, was wir berechnen wollen. Wenn wir allerdings Fläche zwischen zwei Funktionen berechnen wollen, dann müssen wir unbedingt Minuend mit Subtrahend austauschen, da wo es notwendig ist.

Rotationskörper

Hier werden wir erkunden, wie das Volumen eines Körpers berechnet werden kann, der durch die Rotation einer Kurve um einer Achse entsteht.

• 
• 
• 

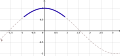
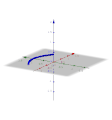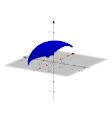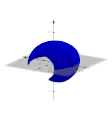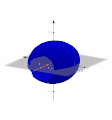
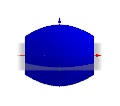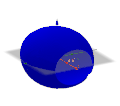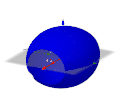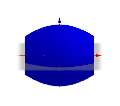
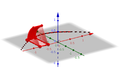
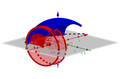
Nehmen wir hier als Beispiel die Kosinusfunktion im ersten Bild, genauer den Teil zwischen −0,9 und 0,9. Im zweiten Bild ist die Ebene des ersten Diagramms der "Boden", die x-Achse ist rot. Um diese Achse lassen wir die Kurve im zweiten Bild drehen. Dadurch entsteht der Körper im dritten Bild (hier allerdings hohl). Wie können wir das Volumen dieses Körpers berechnen? Gehen wir zurück zur Ebene:

• 
• 
• 
• 
• 
• 

Wir nehmen einen Punkt auf der Kurve und formen einen Rechteck. Die Fläche des Rechtecks ist ungefähr so viel wie die Fläche unter der Kurve, es gibt einen kleinen Teil mehr rechts von der Kurve und einen kleinen Teil weniger links (erstes Bild). Im zweiten Bild sehen wir wieder die Ebene als "Boden" und die rote x-Achse. In den restlichen Bildern sehen wir, wie durch die Drehung des Rechtecks ein Zylinder entsteht, der annähernd das gleiche Volumen hat, wie der entsprechenden Teil des blauen Körpers, der durch die Drehung der Kurve entsteht.

Wir können also die Kurve in mehreren kleinen Teilen teilen und dadurch Rechtecke konstruieren, eine Seite deren auf der x-Achse liegt. Wir Teilen die Kurve so, dass diese Seite immer gleich ist: $\Delta x$. In je mehrere Teile wir die x-Achse teilen, desto kleiner wird $\Delta x\$sein und desto genauer wird die Summe der Volumina der dadurch entstehenden Zylinder so viel wie das Volumen der Rotationskörpers sein:

• 
• 
• 

Das Volumen eines Zylinders ist allgemein die Grundfläche (ein Kreis) mal die Höhe. In diesen Zylindern ist die Höhe $\Delta x$, der Radius des Kreises der Grundfläche ist soviel wie $y$, also wie der Wert der Funktion $f(x)$ zwischen den beiden Rändern des Intervalls $\Delta x\$(in diesem Beispiel $\cos x$). Wenn wir das Intervall in n Teilen geteilt haben, ist das Volumen jedes Zylinders:

$V_{n}=\pi \left(f(x_{n})\right)^{2}\cdot \Delta x\quad$(in diesem Beispiel $V_{n}=\pi \cos ^{2}(x_{n})\cdot \Delta x$)

und das ganze Volumen:

$V=\sum _{i=1}^{n}V_{n}=\sum _{i=1}^{n}\pi \left(f(x_{n})\right)^{2}\cdot \Delta x\quad$(in diesem Beispiel $V=\sum _{i=1}^{n}\pi \cos ^{2}(x_{n})\cdot \Delta x$

Für immer größer n wird $\Delta x$ immer kleiner. Ohne hier mathematische Strenge zu verlangen, können wir schreiben:

$\lim _{n\to \infty }\Delta x=dx$

Wir können dann die Summe für verschwindendes $\Delta x$ als Integral "definieren":

$V=\int _{x_{1}}^{x_{2}}\pi \left(f(x)\right)^{2}dx$

In unserem Beispiel ist das:

$V=\int _{-0,9}^{0,9}\pi \cos ^{2}(x)dx\approx 4{,}357\$Einheiten

Rotationsfläche