MathemaTriX ⋅ Theorie. Klasse 1

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT

${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$	DEINE FESTE BEGLEITERIN
	FÜR DIE SCHULMATHEMATIK

EINFACH UND
VERSTÄNDLICH

GRATIS!^*

STARTEN!

MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS!

Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Inhalt
Ein-Aus-
klappen

AUFGABEN

Klassen

Hinweis

Hier ist zur Zeit nur eine grobe Struktur. Die schon vorhandenen entsprechenden Kaitel sind für erwachsene Personen gedacht. Für diese Klasse hier sollten erst Kapitel in einer Zentralseite entstehen, die der Altersgruppe entsprechen. Für diese Klasse sollte hier ein Kapitel mit natürlichen Zahlen entstehen (Ohne Dezimalzahlen)

Arbeiten mit Zahlen und Maßen

Stoffbeschreibung

Kenntnisse und Fähigkeiten im Umgang mit natürlichen Zahlen vertiefen, dabei auch große natürliche Zahlen verwenden und mehrstellige Multiplikationen und Divisionen durchführen können
Rechnen mit Maßen und Umwandlungen zur Bearbeitung von Sachaufgaben und geometrischen Berechnungen,
anhand von Teilern und Vielfachen Einblicke in Zusammenhänge zwischen natürlichen Zahlengewinnen;
Vorstellungen mit positiven rationalen Zahlen verbinden,
mit der Darstellung in Dezimal- und Bruchschreibweise vertraut sein,
einfache Ungleichungen zum Einschranken benutzen;
mit den positiven rationalen Zahlen Rechnungen mit leicht abschätzbaren Ergebnissen durchführen und zur Lösung von Problemen in Sachsituationen vielfältig anwenden können,
Rechnen mit Brüchen, nur in einfachen Fällen, die anschaulich deutbar sind,
grundlegende Sicherheit im Kopfrechnen gewinnen,
elektronische Rechenhilfsmittel einsetzen können,
Kenntnisse über Umkehroperationen erweitern,
die Regeln über die Reihenfolge von Rechenoperationen, einschließlich der Klammerregeln, anwenden können.

Die Grundrechenarten

Definitionen der Grundrechenarten

Die vier Grundrechenarten

Rechenart	Ausgedrückt als	Symbol	Namen der Teile	Name des Ergebnisses

Addition	plus	+	$2$ $+$ $7$ $=$	$9$
(addieren, erhöhen)			Summand $+$ Summand $=$	Summe

Subtraktion	minus	−	$65$ $-$ $22$ $=$	$43$
(subtrahieren, reduzieren, vermindern, abziehen)			Minuend $-$ Subtrahend $=$	Differenz

Multiplikation	mal	⋅ (×)	$9$ $\cdot$ $13$ $=$	$117$
(multiplizieren, vervielfachen, -fach)			Faktor ⋅ Faktor $=$	Produkt

Division	durch	: (÷, /)	$84$ $:$ $7$ $=$	$12$
(dividieren, teilen)			Dividend $:$ Divisor $=$	Quotient

Das Symbol = ist ein Gleichheitszeichen. Es steht für die Gleichheit zweier Ausdrücke. Es wird in einem eigenen Abschnitt genauer erklärt.

Das Symbol × für die Multiplikation wird kaum benutzt, weil es leicht mit dem Symbol oder dem Buchstaben x für die Variable x verwechselt werden kann. Wozu in Rechnungen Buchstaben verwendet werden, werden wir später lernen. Für die Multiplikation wird in diesem Buch das Symbol · benutzt.
Das ist ein Punkt ungefähr auf halber Höhe einer Ziffer notiert.

Für die Division benutzt man auch Punkte : Die anderen Symbole für die Division / und ÷ werden seltener benutzt.
Typisch wird allerdings / bei den Einheiten verwendet, beispielsweise in der Geschwindigkeit (km/h). In diesem Beispiel sagt man "Kilometer pro Stunde". Mit dem Wort "pro" ist Division gemeint.

Weil für Multiplikation und Division Punkte als Symbole verwendet werden, nennt man die beiden Rechenarten zusammen Punktrechnungen.

Die Symbole für die Addition + und die Subtraktion – verwenden dagegen beide Striche. Daher nennt man diese beiden Rechenarten zusammen Strichrechnungen.

Bei Addition und Multiplikation spielt jeweils die Reihenfolge keine Rolle:

5+6+11=6+11+5=\ 11+6+5\ =\ 22

Die Reihenfolge spielt keine Rolle bei der Addition.

2\cdot 5\cdot 3=5\cdot 3\cdot 2=\ 2\cdot 3\cdot 5\ =\ 30

Die Reihenfolge spielt keine Rolle bei der Multiplikation.

Bei Subtraktion und Division ist die Reihenfolge wichtig. Das Ergebnis ist nicht das Gleiche, wenn die Reihenfolge anders ist:

5-3+2=4\

aber

\ 5-2+3\ =\ 6

10\cdot 5:2=25\

aber

\ 10\cdot 2:5\ =\ 4

Weitere Ausdrücke für die vier Grundrechenarten

Im Alltag gibt es allerdings einige Worte, die irgendeine Rechenart bedeuten können:

Schneiden, Kürzen (zum Beispiel Gehalt) und so weiter könnte minus bedeuten

Wachsen, zwei Sachen zusammen, insgesamt könnte plus bedeuten

in einige gleiche Teilen schneiden könnte doch geteilt durch bedeuten

... und so weiter ...

Das Gleichheitszeichen

Ein Symbol, das bisher nicht erklärt wurde, ist das Gleichheitszeichen "=". Es wird benutzt, um zu zeigen, dass der Ausdruck links des Zeichens das Gleiche ist, wie der Ausdruck rechts des Zeichens. Dies betrifft sowohl den Wert als auch die Einheit.

$20=4\cdot 5\ \$ ✔(richtig)

$20\ {\text{Kartoffeln}}=4\cdot 5\ {\text{Kartoffeln}}\ \$ ✔(richtig)

$20\ {\text{Kartoffeln}}=4\cdot 7\ {\text{Kartoffeln}}\ \$ ✘(falsch: falscher Wert)

$20\ {\text{Birnen}}=4\cdot 5\ {\text{Kartoffeln}}\ \$ ✘(falsch: falsche Einheit)

$10m\cdot 5=50$ ✘(falsch: rechts fehlt die Einheit m)

Wie man mit Einheiten arbeitet, werden wir genauer im entsprechenden Kapitel lernen. Da werden wir auch erfahren, dass

$15m=150dm$

doch richtig ist.

Es gibt allerdings Gleichungen zwischen mehr als zwei Ausdrucken ("Gleichungsketten"), wie wir vorher gesehen haben:

$5+6+11=6+11+5=\ 11+6+5\ =\ 22$

Bei Gleichungsketten sind alle Ausdrücke gleich, daher kann man in diesem Beispiel auch schreiben:

$6+11+5=\ 22\quad$ oder $\quad 5+6+11=\ 11+6+5$

Es gilt daher allgemein:

wenn $\ a=b\$ dann auch $\ b=a\$

wenn $\ a=b=c$ dann auch $\ a=c\$

Gleichungsketten kann man allerdings in der Regel nicht bei sogenannten Äquivalenzumformungen benutzen, wie wir später lernen werden.

Die Gleichung zwischen zwei Ausdrucke spielt allerdings eine wichtige Rolle beim Einsetzen, ein Verfahren, das wir im entsprechenden Kapitel lernen werden.

Negative Zahlen

Das Minuszeichen benutzt man nicht nur bei der Subtraktion, sondern auch um sogenannte negative Zahlen zu bezeichnen. Was die negativen Zahlen sind, kann man ziemlich einfach verstehen, wenn man sich vorstellt, in einem Aufzug zu sein. Betrachten wir die folgende Bilderfolge:

\qquad \qquad \qquad

\qquad \qquad \qquad

\qquad \qquad \qquad

\qquad \qquad \qquad

\qquad \qquad \qquad

Im ersten Bild fängt man vom Erdgeschoss an, dieses kann man mit der Zahl 0 bezeichnen. Dann fährt man mit dem Aufzug 2 Stockwerke nach oben. Die Richtung nach oben kann man mit Plus (+) bezeichnen. Das ist im Bild zu sehen. 0+2=2. Im dritten Bild fährt man aus dem 2. Stock 3 Stockwerke weiter nach oben (+ Richtung). 2+3=5. Im vierten Bild fährt man 8 Stockwerke nach unten. Nach unten kann man mit Minus (−) bezeichnen, da die Stockwerke weniger werden. Wenn man aber 5−8 rechnet, kann das Ergebnis nicht 3 sein. 3 ist oberhalb des Erdgeschosses, wir sind aber jetzt in dritten Untergeschoss. Um die Stockwerke unter dem Erdgeschoss zu bezeichnen, braucht man etwas Neues: das Minuszeichen vor dem Stockwerk! Wir sind also im Stock −3, also 3 Stockwerke unterhalb des Erdgeschosses.

Im fünften Bild fährt man ein Stockwerk weiter nach unten. Wir waren im Stock −3 und nach unten bedeutet minus. Am Ende sind wir 4 Stockwerke unter der Erde, also im Stock −4: −3−1=−4. Wenn also beide Zahlen negativ sind, addiert man ihren sogenannten Betrag (3 und 1) und schreibt vor dem Ergebnis wieder ein Minus. Im sechsten Bild fährt man aus dem 4 Stock unter der Erde (−4) 5 Stockwerke nach oben (nach oben bedeutet Plus machen) und befindet sich am Ende einen Stock oberhalb des Erdgeschosses (bei +1): −4+5=1. Wenn man zwei Zahlen mit unterschiedlichem Vorzeichen hat, subtrahiert man die Beträge (größerer Betrag minus kleineren Betrag, hier: 5−4=1) und schreibt man vor dem Ergebnis das Vorzeichen des größeren Betrags (also hier von 5, da sie mehr als 4 ist). Im vierten Bild haben wir 5−8 gerechnet. Da haben wir wieder die Beträge subtrahiert (größerer minus kleineren: 8−5=3) und im Ergebnis haben wir wieder das Vorzeichen des größeren Betrags geschrieben (also das Minus, das vor 8 steht): 5−8 = −3.

Zusammengefasst: Wenn man zwei Zahlen mit dem gleichen Vorzeichen hat (z.B. 4+7 oder −3−5), dann addiert man die Beträge (4+7=11 und 3+5=8) und schreibt vor dem Ergebnis das Vorzeichen: (4+7=11 und −3−5 = −8). Wenn die eine Zahl positiv (+) ist und die andere negativ(−), subtrahiert man die Beträge und schreibt vor dem Ergebnis das Vorzeichen des größten Betrags: $\qquad \qquad \qquad$ 4−7=−3 $\qquad \qquad \qquad$ 15−9=6

Negative Zahlen werden immer mit einem Minus davor geschrieben, z.B. −6 oder −7,453 oder $-{\sqrt {87}}$ . Positive Zahlen werden mit einem Plus davor geschrieben, z.B. +6 oder +7,453 oder $+{\sqrt {87}}$ . Bei positiven Zahlen kann man das Vorzeichen auslassen. Zum Beispiel ist 6 die positive Zahl +6, mit 7,453 wird die positive Zahl +7,453 gemeint und mit ${\sqrt {87}}$ einfach $+{\sqrt {87}}$ .

Wenn allerdings das Plus oder das Minus nach der Zahl geschrieben wird, bedeutet es nicht, dass es eine positive oder negative Zahl ist. In diesem Fall erwartet man, dass noch eine Zahl folgen soll. 3− ist einfach unvollständig und auf gar keinen Fall die Zahl Minus drei ...

Weiteres über Rechnungen mit negativen Zahlen werden wir im Teilkapitel über die Plusminusregel lernen.

Das Komma bei Dezimalzahlen

Noch ein wichtiger Punkt bei der Schreibweise muss man noch kurz ansprechen. Und es geht hier genau um den Punkt.

Wenn man mit dem Taschenrechner die Division 2 durch 7 macht, kommt etwas wie folgendes vor:

$0.28571428...$

Das ist eine Zahl, die kleiner als eins ist. Auf Deutsch allerdings schreibt man:

$0{,}28571428...$

Falls der Unterschied nicht klar ist:

im ersten Fall steht zwischen 0 und dem Rest der Zahl ein Punkt:

$0\quad .\quad 28571428...$

im zweiten Fall ein Komma:

$0\quad {,}\quad 28571428...$

Man sagt auf Deutsch "Null Komma zwei acht fünf sieben...". Dieser Unterschied muss einem bewusst sein!

Auf Englisch und bei den meisten Taschenrechnern schreibt man

$8970063.4583$

oder sogar

$8{,}970{,}063.4583$ .

Auf Deutsch und in ein paar anderen Sprachen werden die beiden Teile umgekehrt durch ein Komma getrennt:

$8970063{,}4583$

oder sogar

$8.970.063{,}4583$ .

Auf diese Tatsache sollte man aufpassen!

Insbesondere wenn Menschen mit unterschiedlichen Kulturen, Sprachen oder Notationen Daten miteinander austauschen, kann dieser Unterschied für Verwirrung sorgen. Beim internationalen Datenaustausch und bei Programmiersprachen wird daher praktisch durchgehend der Punkt und nicht das Komma als Trennzeichen verwendet, in diesem Buch (wie allgemein auf Deutsch) allerdings das Komma.

Addition

Rechenart	Ausgedrückt als	Symbol	Namen der Teile	Name des Ergebnisses

Addition	plus	+	2 + 7 =	9
(addieren, erhöhen)			Summand + Summand =	Summe

Beispiele: a) 35,7 + 59367 + 95382,89 + 567332,76=? b) 56333,76 + 0,089 + 33727,727 + 9=?

Lösungen

Aufgabe a
₂	₂	₁	₂	₁	₂		₁	₀

0	0	0	0	3	5	,	1
0	5	9	3	6	7	,	0	0
0	9	5	3	8	2	,	8	9
5	6	7	3	3	2	,	7	6

7	2	2	1	1	8	,	3	5

Aufgabe b
₁	₁	₀	₂	₁		₁	₁

5	6	3	3	3	,	7	6	0
0	0	0	0	0	,	0	8	9
3	3	7	2	7	,	7	2	7
0	0	0	0	9	,	0	0	0

9	0	0	7	0	,	5	7	6

Man schreibt die Zahlen, die man addieren will, untereinander. Die Kommas müssen untereinander sein! Wenn eine Zahl kein Komma hat, dann schreibt man ein Komma am Ende der Zahl.

Um die Aufgabe übersichtlicher zu machen, schreibt man links und rechts der Zahlen Nullen(0), wenn Ziffer (im Vergleich zu den anderen Zahlen) „fehlen“.

Man addiert die Zahlen von jeder Spalte und fängt mit der rechten Spalte an (und dann immer eine Spalte nach links). Die Summe der Ziffer der Spalte schreibt man unterhalb dieser Spalte.

Wenn die Summe der Ziffer in der Spalte mehr als 9 ist, dann schreibt man unterhalb der Spalte nur die letzte Ziffer und die restlichen oberhalb der nächsten Spalte links. Z.B. bei der Aufgabe a ist die Summe der Ziffer der Spalte rechts (mit der man anfängt) 0+0+9+6=15. Man schreibt darunter 5 (die letzte Ziffer) und 1 (15 ohne 5) oberhalb der nächsten Spalte links usw. Hier ist Aufgabe a Schritt zum Schritt gezeigt:

Aufgabe a Schritt zum Schritt gelöst
35,7 + 59367 + 95382,89 + 567332,76=?

Den ganzen Vorgang kann man
auch hier als Animation sehen:

Subtraktion

Rechenart	Ausgedrückt als	Symbol	Namen der Teile	Name des Ergebnisses

Subtraktion	minus	−	65 − 22 =	43
(subtrahieren, reduzieren, vermindern, abziehen)			Minuend − Subtrahend =	Differenz

Beispiele: a) 9,2-6,7 b) 9,5-6,4 c) 4752,8–203,007

Man schreibt die Zahlen untereinander. Die Kommas müssen untereinander sein! Wenn eine Zahl kein Komma hat, dann schreibt man ein Komma am Ende der Zahl.

Die Zahl oben muss genau so viele Ziffer vor und nach dem Komma haben, wie die Zahl unten. Daher schreibt man rechts der Zahl oben Nullen(0), wenn Ziffer in den Nachkommastellen (im Vergleich zur Zahl unten) „fehlen“.

Man subtrahiert die Zahlen von jeder Spalte (oben minus unten) und fängt mit der rechten Spalte an (und dann immer eine Spalte nach links).

Wenn die Ziffer oben kleiner als die Ziffer unten ist, dann addiert man zu dieser Ziffer 10 und subtrahiert von der nächsten Ziffer oben links eins. In der nächsten Spalte links benutzt man dann oben die reduzierte Ziffer. Beispielsweise:

**Aufgaben a und b: 9,2−6,7=? 9,5-6,4=?**

Das ganze kann man hier auch als Animation sehen:

Bei größeren Zahlen macht man den ganzen Vorgang bei jedem Schritt.

**Aufgabe c: 4752,8–203,007=?**

Das Ganze kann man hier auch als Animation sehen:

**Noch ein paar gelöste Beispiele:**
Bsp. A 453,803−452,944=0,857	Bsp. B 504,6−3,6003=500,997	Bsp. C 200−199,9998=0,0002

Multiplikation

Definition der Multiplikation

Rechenart	Ausgedrückt als	Symbol	Namen der Teile	Name des Ergebnisses

Multiplikation	mal	⋅ (×)	9 ⋅ 13 =	117
(multiplizieren, vervielfachen, -fach)			Faktor ⋅ Faktor =	Produkt

Zunächst einmal erklären wir die Bedeutung der Multiplikation.

$5\cdot 3$ bedeutet, dass man $5$ mal die $3$ zueinander addiert (plus macht). Also $\textstyle \ 5\cdot 3=\underbrace {3+3+3+3+3} _{5\ mal}=15$ . Allerdings spielt bei der Multiplikation die Reihenfolge keine Rolle. $\textstyle \ 5\cdot 3=3\cdot 5$ . Letzteres ( $\textstyle 3\cdot 5$ ) bedeutet drei mal die 5 zueinander addieren: $\textstyle \ 3\cdot 5=\underbrace {5+5+5} _{3\ mal}=15$ .

Mit Hilfe der Addition kann man ein Multiplikationstabelle erstellen, sie wird das kleine Einmaleins genannt.

Multiplikation mit Hilfe der Einmaleins-Tabelle

Mit Hilfe der Einmaleinstabelle (die man allerdings schon auswendig lernen könnte) kann man Multiplikationen zwischen Zahlen mit einer Ziffer ganz schnell berechnen:

**2 mal 7 mit Hilfe der Einmaleinstabelle finden**
Zeile "2" wählen	Spalte "7" wählen	Box wo sie sich treffen wählen	Ergebnis: 14

Das Ganze auch als Animation:

Und noch ein paar Beispiele:

Multiplikation von Zahlen mit mehreren Ziffern und Nachkommastellen

a)

5\cdot 3

b)

5\cdot 30

c)

5\cdot 37

d)

4\cdot 37

e)

40\cdot 37

f)

37\cdot 45

g)

0{,}45\cdot 0{,}000037

h)

450\cdot 37000

Beispiel a haben wir im Abschnitt über Definition schon beantwortet: $5\cdot 3=3+3+3+3+3=15$

Bevor wir mit den restlichen Beispielen weitermachen, müssen wir zwei Sachen noch erklären.

Bemerkung: Multiplizieren mit Klammern
Wenn etwas in Mathematik in Klammern steht, ist es so gemeint, dass die Rechnung in den Klammern erst gemacht werden muss. Wenn wir $3\cdot (2+5)$ berechnen wollen, rechnen wir erst $\ 2+5$ aus, also was in den Klammern steht. $2+5=7$ . Dann führen wir die Multiplikation aus: $3\cdot 7=21$ . Hätten wir erst $3\cdot 2$ gerechnet und dann $+5$ , wäre das Ergebnis falsch: $3\cdot 2=6\ \ {\text{und}}\ \ 6+5=11$ .
Das bedeutet dann, dass man die Zahl außerhalb der Klammern erst mit jedem Summand in den Klammern multiplizieren muss und dann diese Produkte addieren. $3\cdot (2+5)$ ist nicht $3\cdot 2+5$ . Man muss erst die Zahl außerhalb der Klammern (3) erst mit jedem Summand in den Klammern (2 und 5) multiplizieren $3\cdot 2=6\ \ {\text{und}}\ \ 3\cdot 5=15$ und dann diese Produkte (6 und 15) addieren: $6+15=21$ (also das richtige Ergebnis). Man schreibt:
$3\cdot (2+5)=3\cdot 2+3\cdot 5=6+15=21$
oder
$3\cdot (2+5)=3\cdot 7=21$
Bemerkung: Multiplizieren mit 10
Wenn man eine Zahl mit 10 multipliziert, ist das Ergebnis diese Zahl mit einer Null auf ihren rechten Seite geschrieben. Das haben wir in der einmaleins-Tabelle gesehen: $\textstyle 2\cdot 10=20\quad 3\cdot 10=30\quad 3\cdot 10=30\$ usw. Leicht denkt man dann, dass das Gleiche mit $\textstyle \ 15\cdot 10$ passiert. Tatsächlich ist $15\cdot 10$ gleich einer $15$ mit einer $0$ dahinter, also $15\cdot 10=150$ .

Im Beispiel b ist es möglich, $30$ als Produkt von $3$ und $10$ zu schreiben. Es steht tatsächlich in der einmaleins-Tabelle, dass $\textstyle \ 3\cdot 10=30$ ist, also

$\textstyle \ 30=3\cdot 10$

Daher

$\textstyle \ 5\cdot 30=5\cdot 3\cdot 10=15\cdot 10$

(wir haben gerade eben im Beispiel a gesehen, dass $\textstyle \ 5\cdot 3=15$ ist).

Wir wir in der zweiten Bemerkung (Multiplizieren mit 10) gerade eben gelernt haben, gilt für $\textstyle 15\cdot 10$

$\textstyle 15\cdot 10=150$

Man kann also zusammenfassen:

$\textstyle \ 5\cdot 30=5\cdot 3\cdot 10=15\cdot 10=150$ , also $\textstyle \ 5\cdot 30=150$ .

Um Beispiel c zu lösen, können wir die erste Bemerkung (Multiplikation mit Klammern) benutzen:

$\textstyle \ 5\cdot 37=5\cdot (30+7)=5\cdot 30+5\cdot 7$ ist

$5\cdot 30=150$

wie wir eben im Beispiel b gesehen haben.

$\textstyle \ 5\cdot 7=35$

wie man aus der Einmaleins-Tabelle ablesen kann. Somit ist

$\textstyle \ 5\cdot 37=5\cdot (30+7)=5\cdot 30+5\cdot 7=150+35=185$ ,

also

$\textstyle \ 5\cdot 37=185$ .

In der gleichen Weise und mit den gleichen Schritten kann man Beispiel d berechnen:

$\textstyle \ 4\cdot 37=4\cdot (30+7)=4\cdot 30+4\cdot 7=120+28=148$ ,

also

$\textstyle \ 4\cdot 37=148$ .

Aber auch Beispiel e ist dann nicht so schwer, man soll einfach eine Null zum Ergebnis von d dazu schreiben, wie wir in der Bemerkung über Multiplikation mit 10 gelernt haben:

$\textstyle \ {\color {blue}4}{\color {red}\mathbf {0} }{\color {blue}\cdot 37}={\color {blue}168}{\color {red}\mathbf {0} }$

Wenn jetzt $37$ mit $45$ multipliziert wird, wie im Beispiel f, dann werden die folgenden Schritte gemacht:

${\begin{alignedat}{2}37\cdot 45&=37(40+5)\\&=37\cdot 40&&+37\cdot 5\\&=1480\ ^{\text{(Bsp. e)}}&&+185\ ^{\text{(Bsp. c)}}\end{alignedat}}$

(Wir haben hier die Ergebnisse aus den Beispielen e und c benutzt)

$1480+185$ ist

${\begin{array}{c|c|c|c|c}&1&4&8&0\\+&&1&8&5\\\hline &1&6&6&5\\\end{array}}$

wie wir schon bei der Addition gelernt haben. Also:

$37\cdot 45=1665$

Es gibt verschiedene Schreibweisen, die diesen Prozess beschreiben.

${\begin{array}{c\|c\|c\|c\|c}&45&\times &37&\\\hline &1&4&8&0\\+&&1&8&5\\\hline &1&6&6&5\\\end{array}}$	oder	(ohne Null) ${\begin{array}{c\|c\|c\|c\|c}&45&\times &37&\\\hline &1&4&8&\\+&&1&8&5\\\hline &1&6&6&5\\\end{array}}$	und
${\begin{array}{c\|c\|c\|c\|c}&&45&&\\&\times &37&&\\\hline &&1&8&5\\+&1&4&8&0\\\hline &1&6&6&5\\\end{array}}$	oder	${\begin{array}{c\|c\|c\|c\|c}&&45&&\\&\times &37&&\\\hline &&1&8&5\\+&1&4&8&\\\hline &1&6&6&5\\\end{array}}$

Wenn man Kommas hat, lässt man die Kommas und die Nullen am Anfang aus und macht die Multiplikation. Im Beispiel g ( $\textstyle \ 0{,}45\cdot 0{,}000037$ ) haben wir insgesamt 8 Nachkommastellen (zwei bei $\textstyle \ 0{,}\overbrace {45} ^{2\ St.}$ und sechs bei $\textstyle \ 0{,}\overbrace {000037} ^{6\ Stellen}$ , also 2+6=8 Stellen nach dem Komma insgesamt). Beim Ergebnis der Multiplikation ohne Kommas ( $166{\color {red}5}$ ) fängt man dann mit der Ziffer rechts (hier ${\color {red}5}$ ) an und zählt nach links so viele Stellen, wie die gesamten Nachkommastellen (hier 8 Stellen). Dort muss beim neuen Ergebnis das Komma stehen. $1665$ hat aber nur vier Ziffer. Wenn die Zahl weniger Ziffer als die Nachkommastellen hat wie hier, schreibt man erst mehrere Nullen links der Zahl:

$000000001665\qquad \qquad 00000|\overbrace {0001665} ^{7\ Stellen}\qquad$ Komma 7 Stellen nach links stellen → $0{,}0001665$

Daher:

$0{,}45\cdot 0{,}000037=0{,}0001665$

Wenn man Nullen am Ende der Zahlen hat, dann lässt man diese Nullen aus. Man macht die Multiplikation und schreibt dann wieder die ausgelassenen Nullen dazu. Im Beispiel h ( $450\cdot 37000$ ) haben wir 4 Nullen (eine bei $650$ und drei bei $38000$ ). Also zum Ergebnis $1865$ schreibt man noch 4 Nullen dazu: $\textstyle \ 16650000$ . Also $450\cdot 37000=18650000$ .

Das Folgende Beispiel zeigt die Vorgangsweise genauer und Schritt zum Schritt:

Das ganze kann man hier
auch als Animation sehen:

Und noch ein Beispiel, diesmal mit zwei Zahlen mit jeweils drei Ziffern:

Division

Definition der Division

Rechenart	Ausgedrückt als	Symbol	Namen der Teile	Name des Ergebnisses

Division	durch	: (÷, /)	84 : 7 =	12
(dividieren, teilen)			Dividend : Divisor =	Quotient

Einfache Division mit Hilfe der Einmaleins-Tabelle

Mit diesem Vorgang kann man Divisionen durchführen, wenn der Divisor höchstens (also kleiner oder gleich) 10 ist und der Dividend höchsten das 10-fache des Divisors (also wenn der Divisor 4 ist, höchsten 40, wenn der Divisor 7 ist, höchstens 70 und so weiter.)

**Zum Beispiel 17 : 5**
Zeile des Divisors wählen	17 liegt zwischen 15 und 20 Beide Spalten wählen
Schauen, welche Zahlen oben in den Spalten stehen	Von beiden Zahlen (3 und 4) die kleinste wählen. Das ist das Ergebnis 17 : 5 = 3
Aber 3 mal 5 ist doch nicht 17	Es gibt einen Rest. Diesen berechnen wir dann: 3 mal 5 = 15 und 17−15=2 also 17 : 5 = 3 mit Rest 2 Man schreibt: 17:5=3 R 2

Hier als Animation

Der Haupt(vor)gang der Division

Dividend mit Nullen am Ende

Wenn der Dividend Nullen am Ende hat, kann man sich ein paar Schritte sparen. Schauen wir ein Beispiel:

Schauen wir jetzt, wie die richtige Regel lautet:

Man kann also die Division aufhören und die restlichen Nullen erst dann schreiben, wenn der Rest zum ersten Mal Null ist!

Wenn der Divisor auch Nullen am Ende hat, kann man vom beiden Divisor und Dividend so viele Nullen streichen, wie die Nullen des Divisors und erst dann die Division durchführen. Beispielsweise ist 7910000:400=79100:4 (in beiden Fällen ist das Ergebnis 19775). Warum das so ist, kann man erst verstehen, wenn man das Kürzen von Brüchen gelernt hat, daher lernen wir es hier zunächst einmal einfach so, als Regel...

Division mit Null in der Mitte des Ergebnisses

Ein Fehler, der oft vorkommt, ist die Nullen in der Mitte des Ergebnisses auszulassen.
Im ersten Bild sieht man den richtigen Vorgang.

Für jede Ziffer des Dividenden, die runtergebracht wird,
muss eine Ziffer im Ergebnis geschrieben werden!

Das richtige Ergebnis ist daher 2008. Im zweiten Bild sieht man den falschen Vorgang.
Selbstverständlich ist 28 nicht gleich 2008 und daher ein falsches Ergebnis!

Division mit Null am Anfang des Ergebnisses

Was ist aber, wenn die Null (oder die Nullen) ganz am Anfang des Ergebnisses stehen? In diesem Fall spielt es keine Rolle, ob die Null da steht oder nicht. 059 bedeutet genau die gleiche Zahl wie 59 (allerdings auch genau wie 59,000 und 00059, auf gar keinen Fall aber wie 590 oder 59000...).

Wenn man Nullen vor dem Anfang einer Zahl oder nach der letzten Nachkommastelle schreibt, ändert sich die Zahl nicht.

47,03=00047,03=47,030000=0047,03000.

Das gilt allerdings nur für den Anfang der Zahl oder nach der letzten Nachkommastelle. Wenn man Nullen irgendwo in der Mitte der Zahl schreibt, dann hat man nicht mehr die gleiche Zahl.
47,03 ≠ 407,03 ≠ 470,03 ≠ 47,003 Alle diese Zahlen sind nicht gleich!
Aus diesem Grund kann man am Anfang (und nur am Anfang) der Division mit den ersten zwei (oder drei und so weiter) Ziffern anfangen, wenn die erste kleiner als der Divisor ist. Dieser Vorgang wird im zweiten Bild dargestellt.

Dividend mit Komma (einfach)

Was ist, wenn der Divident schon Nachkommastellen hat? In diesem Fall wird die Division, wie wir sie bisher gelernt haben, mit einer Änderung durchgeführt:

Wenn zur nächsten Ziffer nach dem Komma gesprungen werden muss, dann muss man erst ein Komma im Ergebnis schreiben.

In unserem Fall ist es nicht wenn man die Ziffer 9 im Dividend erreicht. Das Komma muss geschrieben werden, erst bevor man die nächste Ziffer nach dem Komma (hier die Ziffer 2) runter bringen muss. Erst dann schreibt man das Komma und dann macht man die Rechnung (12:3) und dann schreibt man das Ergebnis dieser Rechnung (4) nach dem Komma. Es gibt kein anderes Komma in der Zahl (also auf gar keinen Fall irgendwo ein zweites Komma schreiben).
Eine Bemerkung noch: Den letzten Rest haben wird hier mit (R) in Klammern geschrieben. Den Begriff Rest benutzt man eigentlich bei ganzzahligen Divisionen (mit Zahlen ohne Nachkommastellen)^[1]. 0 ist hier der Teilrest der letzten Teildivision (12:4=3 R 0). Wenn bei einer Division mit Nachkommastellen im Ergebnis Teilrest 0 hat, kann man mit der Division aufhören. Das ist allerdings nur selten der Fall, wie wir gleich lernen werden.

↑ Der genaue Begriff ist allerdings in diesem Fall Modulo

Divisor mit Komma (einfach)

Was ist, wenn der Divisor Nachkommastellen hat, wie zum Beispiel in 236,2875:0,5? In diesem Fall wird das Komma sowohl im Divisor als auch im Dividenden so oft nach rechts verschoben, bis der Divisor keine (notwendige) Kommastelle mehr hat. In unserem Beispiel, wenn das Komma im Divisor (0,5) ein Mal nach rechts verschoben wird, bekommt man die Zahl 5, die keine Nachkommastellen hat. Das Komma wird dann auch im Dividenden (236,2875) ein Mal nach rechts verschoben (also der neue Dividend wird 2362,875 sein). Mit diesen neuen Zahlen kann man die Division ganz normal fortführen, wie im Bild am Rand. Der Prozess ist also:

Komma in Divisor verschieben, bis er keine Nachkommastelle hat: $0{\color {red},}5\ \to \ 0\underbrace {_{\color {red}{\xcancel {,}}}5{,}} _{1\ mal}...\ \to \ 5$ →
Komma genauso oft (hier einmal) im Divident verschieben: $236{\color {red},}2875\ \to \ 236\underbrace {_{\color {red}{\xcancel {,}}}2{,}} _{1\ mal}875\ \to \ 2362{,}875\$ →
Division mit den neuen Zahlen durchführen (siehe Bild)

Was ist, wenn der Dividend keine Nachkommastellen hat, beispielsweise 205:0,04?

In diesem Fall denkt man, dass ein Komma am Ende des Dividenden steht, und schreibt so viele Nullen wie notwendig nach dem Komma: 205=205,00 (allerdings gilt auch 205=205,00000 und so weiter). Dann wird der Vorgang wie vorher durchgeführt:

Komma im Divisor verschieben: $0{\color {red},}04\to 0\underbrace {_{\color {red}{\xcancel {,}}}04{,}} _{2\ mal}\to 4$ →
Komma genauso oft (hier zweimal) im Dividenden verschieben, bis er keine Nachkommastelle hat: $205{\color {red},}00\ \to \ 205\underbrace {_{\color {red}{\xcancel {,}}}00{,}} _{2\ mal}...\ \to \ 20500\$ →
Division mit den neuen Zahlen durchführen (siehe Bild)

Ein letztes Beispiel: 205:0,0004. Hier muss man das Komma sogar viermal verschieben:

Komma im Divisor verschieben: $0{\color {red},}0004\ \to \ 0\underbrace {_{\color {red}{\xcancel {,}}}0004{,}} _{4\ mal}...\ \to \ 4$ \ →
Komma genauso oft (hier zweimal) im Dividenden verschieben, bis er keine Nachkommastelle hat: $205{\color {red},}000000\ \to \ 205\underbrace {_{\color {red}{\xcancel {,}}}0000{,}} _{4\ mal}...\ \to \ 2050000\$ →
Division mit den neuen Zahlen durchführen (siehe Bild)

Dividend ohne Komma, Ergebnis mit Komma (mit Null Rest)

Was ist, wenn die Division nicht genau aufgeht. wie zum Beispiel in 935:4?
		In diesem Beispiel ist es klar, dass ein Rest geben wird. Die Division kann man aber doch weiter fortsetzen, wie wir bei Zahlen mit Nachkommastellen schon gelernt haben. In diesem Beispiel können wir 935 als Zahl mit Nachkommastellen schreiben (freilich alle Nullen), wie wir schon gelernt haben: 935=935,00... Dann führen wir die Division in der gewöhnlichen Weise durch (siehe Bild). Allerdings kann man in diesem Fall die Nullen im Dividenden gar nicht schreiben, wie im Bild links unten zu sehen ist. In diesem Fall werden Nullen weiter unten geschrieben, bis der Teilrest irgendwann Null wird. Vorsicht aber: Wenn der Dividend zu Ende ist und die erste Null dazu benutzt wird, muss man ein Komma im Ergebnis schreiben!

			Diesen Prozess (weiter Nullen schreiben) kann man auch benutzen, wenn der Dividend zwar schon Nachkommastellen hat, der Teilrest am Ende aber doch nicht Null ist. In diesem Fall schreibt man Nullen weiter, selbstverständlich ohne ein zweites Komma im Ergebnis zu schreiben!

Dividend ohne Komma, Ergebnis mit Komma (periodisch)

Division Kombinationen

Hier finden wir ein paar weiterführende Beispiele zur Vertiefung der Kenntnissen.

Probieren wir erst die Division 3706,1:0,00007. Wenn der Divisor ein Komma hat (wie hier 0,00007), dann muss man das Komma sowohl im Divisor also auch im Dividenden so oft nach rechts verstellen, bis der Divisor keine Nachkommastellen mehr hat. Falls der Dividend dann nicht genügende Nachkommastellen hat, werden sie mit Nullen nachgefüllt. Daher ist 3706,1:0,00007 gleich so viel wie 370610000:7

3706,1:0,00007=370610000:7

Letztere Division führen wir auch im Bild durch. Wir fangen dann mit dem Hauptvorgang (in verkürzter Darstellung) an. Da die erste Stelle des Dividenden (3) kleiner als der Divisor ist, kann man weitere Ziffer des Dividenden benutzen (also 37), weil Nullen am Anfang des Ergebnisses (und nur dort) keine Rolle spielen. Diese zwei Stellen wurden mit Hellblau markiert. Da, wo die rote Stelle und der rote rechts-Pfeil im Bild ist, kann man weitere Nullen einführen, nachdem erst ein Komma im Ergebnis geschrieben wird (roter nach-oben-Pfeil und Komma im Ergebnis). Mit Lila (um dem Teildividenden 30) wird darauf aufmerksam gemacht, dass das Ergebnis doch periodisch ist (also der Teildividend 30 und alle andere Teildividenten, die nach ihm kommen, in der gleichen Reihe immer wiederholt vorkommen). Die Periode, wie im Ergebnis wieder mit Lila notiert, ist die Zifferfolge 428591.

Da man aber die Periode im Ergebnis erst nach dem Komma notiert wird, schreibt man nicht

$3706,1:0,00007=5295{\overline {4285{,}91}}\$ (falsch), sondern

$3706,1:0,00007=52954285{,}{\overline {914285}}\$ (richtig).

Im vorherigen Beispiel haben wir eine Division durch 11 gesehen. Da bestand die Periode aus zwei Ziffern (27). Im letzten Beispiel (Division durch 7) bestand die Periode aus sechs Ziffern (914285). Bei einer anderen Division (durch 4), gab es wieder keine Periode. Es kann also eine Periode geben oder nicht, und sie kann lang oder kurz sein. Im folgenden Beispiel (938:23) haben wir die Periode nicht mal angegeben, da sie schon aus 22 Ziffern(!) besteht. Es gibt einen Beweis dafür, dass wenn der Divisor und der Dividend ganze Zahlen sind (oder sein können), immer eine Periode entsteht (also eine wiederholte Reihenfolge von Ziffern nach dem Komma) oder ein Teilrest Null (also die Division kann aufhören). Diese Periode kann sehr lang sein, es gibt sie aber in diesem Fall immer.

Im folgenden Beispiel lernen wir allerdings auch dazu genauer, wie man die Division durchführt, wenn der Divisor größer als 10 ist. Wir haben schon eine solche Division gesehen, aber noch nicht erklärt, wie das funktioniert.

Grundsätzlich gibt es hier nichts Neues. Man soll wieder die Grundschritten durchführen:

↓ Ziffer runter (ganz links anfangen)

÷ was runter Steht durch den Divisor dividieren ("wie oft der Divisor in den Teildividenden hineinpasst")

× das Ergebnis der Division mit dem Divisor multiplizieren

− dieses Produkt von dem, was "runter steht" subtrahieren.

Nun aber werden diese Schritte irgendwo am Rand durchgeführt und jeweils unter dem Teildividenden das Ergebnis der Subtraktion am Ende geschrieben.

Schritt ↓ Ziffer runter: Weil die erste Ziffer im Dividend (9) kleiner als der Divisor (23) ist, nehmen wir am Anfang die ersten zwei Ziffer des Dividenden (93)

Schritt ÷ dividieren: 23 passt in 93 viermal hinein (das kann man allerdings bei größeren Zahlen nur raten und ausprobieren). Wie erste Ziffer des Ergebnisses wird daher 4 sein.

Schritt × multiplizieren: Die letzte Ziffer des Ergebnisse (4) wird mit dem Divisor multipliziert: 4×23=92.

Schritt − subtrahieren: Das Ergebnis der Multiplikation (92) wird aus dem vorläufigen Teildividenden (93) subtrahiert (93−92=1). Allein das Ergebnis der Subtraktion (hier 1) wird dann unter den Teildividenden geschrieben. Im Bild haben wir allerdings die zwei letzten Schritten am Rand links zusammengefasst (93−4×23=1).

Diese Schritte werden dann wiederholt, bis man irgendwann die Periode entdeckt. Hier haben wir allerdings schon ziemlich bald aufgehört (wie schon erwähnt, ist die Periode in diesem Beispiel sehr lang...).

Im folgenden Beispiel ist der Divisor wieder größer als 10, wir haben aber hier die Teilschritte des Hauptvorgangs (↓ ÷ × −) nicht am Rand geschrieben. Die Division lautet 4,52:1,3, man soll also erst das Komma verschieben: 4,52:1,3=45,2:13. Letztere Division wird im Bild gezeigt. Wieder muss man mit zwei Ziffern anfangen. Sofort nach der ersten Ziffer im Ergebnis muss man ein Komma schreiben (roter Pfeil). Und wieder gibt es eine Periode (wenn der Teildividend 100 wiederholt wird), die Ziffernfolge 769230. Die Periode besteht hier (wie bei der Division durch 7 am Anfang dieses Teilkapitels) aus sechs Ziffern. Also $\ 4,52:1,3=3{,}4{\overline {769230}}$ . Hier ist zu beachten, dass nicht alle Ziffern nach dem Komma die Periode sind! Die Periode fängt in diesem Fall erst nach der ersten Nachkommastelle an.

Wenn allerdings die Division 0,0452:13 durchgeführt wird, muss man im Ergebnis schon mit Null und Komma anfangen (Bild links)! Der Rest des Vorgangs bleibt unverändert. Vorsicht aber: in diesem Fall (wenn Komma schon am Anfang steht), darf man Nullen nicht auslassen! Die Periode allerdings fängt in diesem Fall noch weitere Stellen nach dem Komma an: $0{,}0452:13=0{,}00034{\overline {769230}}$ .

Bei der Division 330,103:11 (links) finden wir noch ein paar Neuigkeiten. Die Periode besteht zwar wieder aus zwei Ziffern wie in der vorherigen Division durch 11, diesmal sind es aber die Ziffern 36 (und nicht 27). Es gibt in dieser Division einige Nullen dazwischen, die man selbstverständlich NICHT auslassen darf und dazu ein Komma unter diesen Nullen.

Bei der Division 391,204:11 (rechts) stellt man fest, dass die Division durch 11 sogar auch genau ausgehen kann (das stimmt ja für alle Divisoren, die ganzzahlig, also ohne Komma, sind). Wenn der Teilrest Null ist, ist der Vorgang fertig. Wann die Division durch bestimmte Zahlen genau aufgeht, lernt man im Kapitel über Teilbarkeit.

Im letzten Beispiel können wir sehen, dass die Periode auch nur eine Ziffer sein kann (hier 6). In diesem Beispiel fängt die Periode wieder erst an der dritten Nachkommastelle an. Man schreibt: $7,43:3=2,47{\dot {6}}$

Punktrechnungen mit 10, 100, 1000 und so weiter

Wenn man eine Zahl mit 10, 100, 1000 und so weiter multipliziert, dann verschiebt sich das Komma der Zahl einfach nach rechts (die Zahl wird größer), so oft, wie es Nullen gibt:

3,45 · 10 = 34,5 (Mal 10; in 10 gibt es eine Null, Komma wird einmal nach rechts verschoben)

54 · 10000 = 54,0000 · 10000 = 540000 (Mal 10000; in 10000 gibt es vier Nullen, Komma wird 4 Mal nach rechts verschoben; Allerdings gibt es kein Komma am Ende der Zahl 54; man schreibt ein Komma am Ende der Zahl und dazu nach dem Komma so viele Nullen, wie man will, und schiebt dann das Komma)

0,008 · 100 = 0,8 (Mal 100; in 100 gibt es 2 Nullen, Komma wird 2 Mal nach rechts verschoben)

Wenn man eine Zahl mit 10, 100, 1000 und so weiter dividiert, dann verschiebt sich das Komma der Zahl einfach nach links (die Zahl wird kleiner), so oft, wie es Nullen gibt:

3,45:10 = 0,345 (Durch 10; in 10 gibt es eine Null, Komma wird einmal nach links verschoben; allerdings gibt es links vor 3,4 keine Null, man schreibt also links von der Zahl so viele Nullen, wie man will, und schiebt dann das Komma)

54:10000 = 0,0054 (Durch 10000; in 10000 gibt es 4 Nullen, Komma wird 4 Mal nach links verschoben; allerdings gibt es links vor 54 kein Komma, man schreibt also links von der Zahl ein Komma und so viele Nullen, wie man will, und schiebt dann das Komma)

0,008:100 = 0,00008 (Durch 10; in 10 gibt es eine Null, Komma wird 1 Mal nach links verschoben; allerdings muss man zuerst am Ende der Kommazahl weitere Nullen schreiben)

900000:100 = 9000,00 = 9000 (Durch 100; in 100 gibt es 2 Nullen, Komma wird 2 Mal nach links verschoben; da es kein Komma am Ende der Zahl gibt, muss man erst das Komma schreiben)

Textaufgaben zu den Grundrechenarten

$\$	$\$

$\$

Rechenart	Ausgedrückt als	Symbol	Namen der Teile	Name des Ergebnisses

Addition	plus	+	$2$ $+$ $7$ $=$	$9$
(addieren, erhöhen)			Summand $+$ Summand $=$	Summe

Subtraktion	minus	−	$65$ $-$ $22$ $=$	$43$
(subtrahieren, reduzieren, vermindern, abziehen)			Minuend $-$ Subtrahend $=$	Differenz

Multiplikation	mal	⋅ (×)	$9$ $\cdot$ $13$ $=$	$117$
(multiplizieren, vervielfachen, -fach)			Faktor ⋅ Faktor $=$	Produkt

Division	durch	: (÷, /)	$84$ $:$ $7$ $=$	$12$
(dividieren, teilen)			Dividend $:$ Divisor $=$	Quotient

Mit den Grundrechenarten kann man auch Textaufgaben bilden. Bei diesen Aufgaben ist in der Regel die Bedeutung der Wörter nicht so wichtig, wie der Aufbau des Satzes:

Dividieren Sie die Differenz von 125 und 20 mit der Summe von 4 und 3.

Schauen wir mal, wie der Satz aufgebaut ist. Erst steht, dass man dividieren muss (also durch machen). Was muss man aber dividieren? Was steht nach dem Wort dividieren? Die Zahlen 125 und 20? NEIN! Nach dem Wort dividieren (durch machen) steht das Wort Differenz! Man muss also erst eine Differenz berechnen! Welche Differenz? Die Differenz von 125 und 20(was nach dem Wort Differenz steht)! Das steht ja auch da! Die Differenz (Minus) von 125 und 20 ist 125−20=105. Diese Differenz muss man durch irgendwas dividieren. Ist das durch 4, durch 3 oder doch was anderes? Doch was anderes! Die Differenz muss man mit der Summe (Plus machen) dividieren. Man muss also erst eine Summe berechnen, die Summe von 4 und 3 (was nach dem Wort Summe steht), 4+3=7. Man soll also die Differenz (105) durch die Summe (7) dividieren:

105:7=15. 15 ist also die Antwort zur Aufgabe!

Vorrang der Rechenarten

Grundrechenartenvorrang

$\$	$\$

$\$

Bei einer Rechnung muss die Reihenfolge der Rechnungen klar sein, sonst ist das Ergebnis nicht eindeutig:

$6+3-7+5$ :

Wenn man von links nach rechts liest, dann: $\ 6+3=9,\ 9-7=2,\ 2+5=7\quad$ also Ergebnis 7.
Wenn man von rechts nach links liest, dann: $\ {\overleftarrow {{\color {red}12}=7+5}},\ {\overleftarrow {{\color {lime}9}=3-{\color {red}12}}},\ {\overleftarrow {15=6+{\color {lime}9}}}\quad$ also Ergebnis 15.

Das Ergebnis ist nicht das Gleiche! In den meisten Sprachen der Welt fängt man links an. Dann ist das richtige (und eindeutige) Ergebnis 7. Nur bei Addition oder Multiplikation spielt die Leserichtung und allgemein die Reihenfolge keine Rolle:

$6+5+11=5+6+11=11+5+6=5+11+6=22$

$2\cdot 4\cdot 5=4\cdot 2\cdot 5=2\cdot 5\cdot 4=40$

In diesem Buch wird die Deutsche Leserichtung benutzt, also von links nach rechts.

Was ist, wenn man Strich- und Punktrechnungen gleichzeitig hat? Spielt hier die Reihenfolge wieder keiner Rolle, wie bei der Addition oder der Multiplikation?

$2+3\cdot 4$

Machen wir die Rechnung einfach von links nach rechts, ist das Ergebnis: $2+3=5\ \to \ 5\cdot 4=20$

Ändern wir die Reihenfolge der Multiplikation: $2+4\cdot 3$

und machen wir die Rechnung einfach von links nach rechts, bekommen wir ein anderes Ergebnis: $2+4=6\ \to \ 6\cdot 3=18$

Es gilt auch:

Wenn man erst die Strichrechnung macht, ist das Ergebnis: $2+3=5\ \to \ 5\cdot 4=20$
Wenn man erst die Punktrechnung macht, ist das Ergebnis: $3\cdot 4=12\ \to 2+12=14$

Das Ergebnis ist wieder unterschiedlich.Ein unterschiedliches Ergebnis kommt auch dann vor, wenn die Reihenfolge bei der Addition geändert wird und die Multiplikation erst gemacht wird:

$2+3\cdot 4\$ und $\ 3+2\cdot 4$

Hier haben wir die Reihenfolge bei der Addition geändert (einmal steht 2+3 und dann 3+2). Machen wir in beiden Fällen erst die Multiplikation:

$2+3\cdot 4\ =2+12=14\$ und $\ 3+2\cdot 4=3+8=11$

Das Ergebnis ist wieder unterschiedlich. Wenn wir aber einen mathematischen Ausdruck haben, wollen wir ein eindeutiges Ergebnis. Damit das Ergebnis eindeutig ist, muss es eine Regel geben. In Mathematik haben die Punktrechnungen (mal und durch) immer Vorrang vor den Strichrechnungen (Plus und Minus). Man muss zuerst die Punktrechnungen machen und dann die Strichrechungen. Also ist hier 14 das richtige Ergebnis. Wenn es also in einer Rechnung Strich- und Punktrechnungen gibt, dann muss man zuerst die Punktrechnungen machen!

Wenn es aber eine Klammer gibt, dann muss man erst die Rechnung in der Klammer machen:

$(2+3)\cdot 4=5\cdot 4=20\$ Hier ist das Ergebnis doch $20$

$2+(3\cdot 4)=2+12=14\$ ...und hier ist das Ergebnis wieder $14$ .

Wenn in einem mathematischen Ausdruck mehrere Rechenarten vorkommen, dann muss eine Regel gelten, damit das Ergebnis eindeutig ist. Die grundlegende Regel lautet:

Klammer vor Punkt vor Strich.

(Zu Erinnerung: Punktrechnungen sind mal und durch, Strichrechnungen sind plus und minus)

Wenn es wiederum innerhalb einer Klammer mehrere Rechnungen gibt, dann muss man die Klammer erst machen und in der Klammer an die Regeln halten:

$5+36:(3\cdot 5-6)-(56:7-2)\cdot 3=?$

Unterstreichen wir zuerst die Rechnungen in den Klammern:

$5+$	$36:$	${\underline {({\underline {3\cdot 5}}-6)}}\ -$	${\underline {({\underline {56:7}}-2)}}$	$\cdot 3$	$=$	In beiden Klammern muss man zuerst die Punktrechnung machen
		$15-6\quad$	$8-2$			und dann die Strichrechnung in Klammer
		$9$	$6$			Man kann also die Klammer durch das jeweilige Ergebnis ersetzen

$5+$	$36:$	${\cancelto {9}{(3\cdot 5-6)}}\ -$	${\cancelto {6}{(56:7-2)}}$	$\cdot 3=$
$5+$	$36:$	$9-$	$6$	$\cdot 3=$	Kompakter geschrieben ist die Rechnung jetzt:

$5+36:9-6\cdot 3\qquad \qquad$ Hier muss man erst die Punktrechnungen machen

$5+{\cancelto {4}{36:9}}-{\cancelto {18}{6\cdot 3}}=$

$5+4-18=-9$

Hier das Ganze noch einmal übersichtlicher und in einer Animation:

Alle Schritte kompakt dargestellt:

{\begin{array}{c}5+36:\underbrace {(\underbrace {3\cdot 5} _{15}-6)} _{9}-\underbrace {(\underbrace {56:7} _{8}-2)} _{6}\cdot 3=\\5+\underbrace {36:9} _{4}-\underbrace {6\cdot 3} _{18}=\\5+4-18=-9\end{array}}

Einheiten

Einheiten und physikalische Größen

$\$	$\$

$\$

Unsere Umgebung, die Natur, wir selber haben viele Eigenschaften: ein Wald kann schön sein, ein Berg kann groß oder klein sein, das Meer blau usw. Manche Eigenschaften, die man messen kann, sind für die Physik wichtig. Solche Eigenschaften sind z.B. die Länge (oder der Abstand, der Weg usw.), die Masse (grob gesagt: das Gewicht), die Zeit, die Geschwindigkeit, die Kraft, die elektrische Ladung usw. Alle diese Eigenschaften, die für die Physik wichtig sind und die man messen kann, nennt man physikalische Größen.

Jede Größe kann man mit verschiedenen Einheiten messen. Für den Abstand z.B. benutzt man Meter (oder auch Zolle, Kilometer, Millimeter usw.), für die Zeit Sekunde (oder Stunden, Tagen, Minuten usw.) für die Masse Kilogramm (oder Gramm, Tonne usw.), für die Kraft Newton usw..

Vorsätze von Einheiten

Für jede Einheit gibt es verschiedene Vorsätze, also kleine Wörter, die einen gewissen Anteil der Einheit zeigen:

Milli (m) bedeutet ein Tausendstel, Zenti (c) ein Hundertstel, Deci (d) ein Zehntel, Kilo (k) bedeutet Tausend. Ein Milligramm (mg) bedeutet daher ein Tausendstel eines Gramms, ein Zentimeter (cm) bedeutet ein Hundertstel eines Meters, ein Kilogramm (kg) Tausend Gramms, ein Decivolt (dV) ein Zehntel eines Volts, ein Zentiliter (cL) ein Hundertstel eines Liters, ein Kilowatt (kW) Tausent Watts.

Einheiten umrechnen

Abstand

Für die Umrechnungen eines Abstandes benutzt man folgendes Schema:

In diesem Bild:

Wenn ein Abstand z.B. in km gegeben ist und in dm umgerechnet werden soll (von links nach rechts, vom größten zum kleinsten) muss man multiplizieren, in diesem Beispiel einmal mit 1000 und einmal mit 10:

2,35km= 2,35 ·1000 ·10 dm = 23500 dm

wenn ein Abstand z.B. in cm gegeben ist und in m umgerechnet werden soll (von rechts nach links, vom kleinsten zum größten) muss man dividieren, in diesem Beispiel zwei mal durch 10:

0,054cm= 0,054:10:10 m = 0,00054m

Masse

Für die Umrechnungen einer Masse benutzt man folgendes Schema:

In diesem Bild:

wenn eine Masse z.B. in kg gegeben ist und in mg umgerechnet werden soll (von links nach rechts, vom größten zum kleinsten) muss man multiplizieren, in diesem Beispiel zwei mal mit 1000:

0,087kg= 0,087 ·1000 ·1000 mg = 87000mg

wenn eine Masse z.B. in g gegeben ist und in Tonnen (t) umgerechnet werden soll (von rechts nach links, vom kleinsten zum größten) muss man dividieren, in diesem Beispiel zwei mal durch 1000:

36530g= 36530:1000:1000 t = 0,03653t

Zeit

Für die Umrechnungen der Zeit benutzt man folgendes Schema:

In diesem Bild:

wenn eine Zeit z.B. in Minuten gegeben ist und in Sekunden umgerechnet werden soll (von links nach rechts, vom größten zum kleinsten) muss man multiplizieren, in diesem Beispiel einmal mit 60:

0,08min= 0,08·60 s = 4,8s

wenn eine Zeit z.B. in Minuten gegeben ist und in Tage umgerechnet werden soll (von rechts nach links, vom kleinsten zum größten) muss man dividieren, in diesem Beispiel einmal durch 60 und einmal durch 24:

36630 min= 36630:60:24 Tage = 25,4375 Tage

Bruchrechnungen

Was ist ein Bruch?

Bruch: $\textstyle {\begin{array}{ccc}10&\leftarrow {\text{Zähler}}\\{\boldsymbol {-}}&\leftarrow \mathrm {Bruchstrich} \\5&\leftarrow \mathrm {Nenner} \end{array}}$

Es gilt: $\textstyle {\frac {10}{5}}=10:5=2$ (Ein Bruch ist wie eine Division)

Unterschied: Ein Bruch ist eine Zahl. Eine Division ist eine Rechenart zwischen zwei Zahlen.

Echter Bruch: Wenn der Nenner größer als der Zähler ist: $\textstyle {\frac {5}{11}}$

Unechter Bruch: Wenn der Zähler größer als der Nenner ist: $\textstyle {\frac {11}{5}}$

Gleichnamige Brüche: Brüche, die den gleichen Nenner haben (z.B. $\textstyle {\frac {10}{5}}$ , $\textstyle {\frac {3}{5}}$ aber NICHT $\textstyle {\frac {5}{10}}$ und $\textstyle {\frac {5}{9}}$ , wo der Zähler gleich ist, oder $\textstyle {\frac {10}{5}}$ und $\textstyle {\frac {5}{9}}$ )

Arbeiten mit Variablen

Stoffbeschreibung

Mit Variablen allgemeine Sachverhalte beschreiben können, zB gleichartige Rechenabläufe, die sich nur durch unterschiedliche Zahlen unterscheiden, oder allgemeine Beziehungen zwischen Größen,
insbesondere Formeln bzw. Gleichungen aufstellen,
Lösungen zu einfachen linearen Gleichungen finden können,
Formeln anwenden und interpretieren können.

Umformen

Die Gegenrechungen

$\$	$\$

$\$

Nachdem Vassili Lisa drei Äpfel gibt, hat er fünf Äpfel. Wie viele Äpfel hatte er vorher?

Wie kann man diese Aufgabe in der mathematischen Sprache schreiben? Für das Gefragte (wie viele Äpfel) wird in Mathematik irgendein Symbol benutzt, als Stellvertreter für die noch unbekannte Zahl. In der Regel wird als Symbol ein Buchstabe verwendet und nicht allzu selten x.
Mit x sind also die Äpfel gemeint, die Vassili am Anfang hatte. Wir wissen noch nicht, wie viele sie waren, daher schreiben wir ein Symbol dafür, ein Buchstabe, also x.

Wenn Vassili drei Äpfel der Lisa gibt, dann hat er weniger Äpfel als zuvor, es geht um eine Subtraktion. Von den x Äpfeln am Anfang sind drei Äpfel zu subtrahieren. Dass dann noch fünf Äpfel bleiben, wird durch den folgenden mathematischen Ausdruck geschrieben:

x−3=5

Man kann für x verschiedene Zahlen ausprobieren, z.B. 2, 3, 7, 8 oder 9. So kann man schon feststellen, dass nur acht minus drei gleich fünf ist. „x“ muss also 8 sein, damit die Rechnung stimmt. Vassili hatte also 8 Äpfel am Anfang.

Die ganze Zeit ausprobieren ist allerdings nicht gerade geschickt. Besonders bei größeren Zahlen wird es sogar ziemlich schwer. Es gibt in der Mathematik einen geschickteren Weg, die Aufgabe zu lösen. Man benutzt die sogenannte Gegenrechnung. Bei allen Gleichungen gibt es zwei Teile, ein Teil links vom „=“ und ein Teil rechts vom „=“. Bringt man einen Term von einer Seite zur anderen, dann muss man die Gegenrechnung benutzen.

Die Gegenrechnung der Subtraktion ist die Addition und umgekehrt.

Wenn x−3=5 ist, dann kann man die 3 auf die andere Seite vom „=“ bringen und statt minus die Gegenrechnung (plus) benutzen:

x=5+3 also x=8

Bei der Aufgabe c+4452 = 341 bringt man 4452 auf die andere Seite und benutzt die Gegenrechnung von minus. Die Lösung ist daher:

c+4452 = 341 → c= 341−4452 → c = −4111

Die Gegenrechnung der Multiplikation ist die Division und umgekehrt.

3f=114

Zwischen 3 und f steht nichts.

Wenn in Mathematik zwischen zwei Ausdrucken (zum Beispiel einer Zahl und einem Symbol, einer Klammer und einer Zahl und so weiter) nichts steht, dann ist Multiplikation gemeint (einzige Ausnahme: die gemischten Zahlen).

Da zwischen 3 und f nichts steht, ist mal gemeint. f ist ein Symbol und steht für irgendeine Zahl. Die Aufgabe ist herauszufinden, wie viel f sein soll, damit die Rechnung stimmt. In diesem fall soll 3 auf die andere Seite gebracht und die Gegenrechnung von mal (also durch) benutzt werden:

3f=114 (nichts zwischen 3 und f, also mal gemeint):

3·f=114 (3 auf die andere Seite von „=“ bringen und Gegenrechnung, also hier Division, benutzen)

f=114:3 und daher

f = 38.

Man kann auch einen Bruch statt einer Division benutzen:

$f={\frac {114}{3}}=38$

Entsprechend ist die Gegenrechnung der Division die Multiplikation:

$\textstyle {\frac {k}{5}}=11$ also k:5 = 11 und daher k = 11 · 5

k = 55

Was ist aber die Gegenrechnung vom Quadrat?

Die Gegenrechnung von Quadrat ist die sogenannte „Wurzel“:

z² = 81 also z = ${\sqrt {81}}$ und daher z=9

9 ist die Zahl, deren Quadrat 81 ist, daher ist die Wurzel von 81 gleich 9. Wenn wir in der Gleichung z² = 81 z durch 9 ersetzen, dann stimmt die Gleichung tatsächlich: 9² = 81

Selbstverständlich ist die Gegenrechnung der Wurzel das Quadrat.

${\sqrt {m}}$ = 13 also m = 13² und daher m=169

Obwohl es für das Niveau dieses Buches nicht absolut notwendig ist, können wir doch auf eine Tatsache aufmerksam machen: Die Gleichung z² = 81 hat noch eine Lösung, wenn z gleich −9 ist. Freilich stimmt die Gleichung (−9)² = 81. (−9)² bedeutet (−9)·(−9). Minus mal minus ist plus und daher:

(−9)² =(−9)·(−9)= + 9·9 = 81 also

(−9)² = 81

Arbeiten mit Figuren und Körpern

Stoffbeschreibung

ausgehend von Objekten der Umwelt durch Idealisierung und Abstraktion geometrische Figuren und Körper sowie ihre Eigenschaften erkennen und beschreiben können,
aufbauend auf die Grundschule Kenntnisse über grundlegende geometrische Begriffe gewinnen,
Skizzen von Rechtecken, Kreisen, Kreisteilen, Quadern und ihren Netzen anfertigen können,
Zeichengeräte zum Konstruieren von Rechtecken, Kreisen und Schrägrissen gebrauchen können,
Maßstabszeichnungen anfertigen und Längen daraus ermitteln können;
Umfangs- und Flächenberechnungen an Rechtecken (und einfachen daraus zusammengesetzten Figuren),
sowie Volums- und Oberflächenberechnungen an Quadern (und einfachen daraus zusammengesetzten Körpern) durchführen können,
Formeln für diese Umfangs-, Flächen- und Volumsberechnungen aufstellen können;
Winkel im Umfeld finden und skizzieren,
Gradeinteilung von Winkeln kennen,
Winkel mit dem Winkelmesser (Geodreieck) zeichnen können;
einfache symmetrische Figuren erkennen und herstellen können.

Ebene Geometrie

Grundbegriffe der Geometrie

Strecke

Strecke ist der kürzeste Weg zwischen zwei Punkten. Z.B von den beiden gezeichneten Möglichkeiten zwischen A und B im Bild "Strecken Definition", welche ist die kürzeste?

Gerade und Strahl

Wenn ich eine Strecke auf einer Seite unendlich lang verlängere, dann habe ich einen Strahl. Wenn ich das an beiden Seiten tue, dann hab ich eine Gerade.

Winkel

Winkel Darstellung

Zwischen zwei Strahlen, die vom gleichen Punkt ausgehen, entsteht ein Winkel. Mit einem Winkel misst man eine Drehung.

Rechter Winkel

vier rechte Winkel

Wenn sich zwei Geraden einander so schneiden, dass vier gleichen Winkel entstehen, dann ist jeder von diesen Winkeln ein rechter Winkel.

Parallelen

Wenn zwei Geraden so nebeneinander liegen, dass sie nie einander schneiden und immer den Gleichen Abstand haben, dann sind sie parallel zueinander.

Punkt

Um alle Begriffe bisher zu definieren, haben wir den Punkt gebraucht. Was ist aber wieder ein Punkt? Diese ist die schwerste Definition. Wenn man beispielsweise den Abstand zwischen Wien und Linz berechnen will, muss man einen Ort in jeder Stadt wählen, sonst kann der Abstand bis 15km mehr oder weniger sein! Dieser Ort könnte z.B. eine Säule in der Mitte von jeder Stadt sein. Für so einen großen Abstand reicht eine Säule schon. Sie ist sozusagen ein Punkt.

Wenn man aber die Säule selber messen will, geht es nicht mehr. Man nimmt dann zwei winzigen Flächen am Rand der Säule. Je kleiner das Objekt ist, das wir messen wollen, desto kleiner muss der „Punkt“ sein.

Im idealen Fall ist der Punkt gar nichts, hat selber keine Länge, keine Breite und keine Höhe! So kann man sich einen Punkt vorstellen und so wird er auch definiert.

Eckpunkt

In einer ebenen Figur sind die Eckpunkte, die Punkte bei denen sich zwei Seiten einander schneiden.

Seite und Diagonale

Die Seiten einer ebenen Figur sind die Abgrenzungen der Figur vom Rest der Ebene. Im folgenden Bild eines Quadrats werden alle seine Seiten mit a bezeichnet, im Bild des Rechtecks werden zwei Seiten mit a und zwei mit b bezeichnet. Eine Seite verbindet zwei Punkte die nacheinander liegen. Die Diagonale verbindet hingegen zwei gegenüberliegenden Eckpunkte, die sich nicht am Rand der gleichen Seite befinden. Ein Quadrat und ein Rechteck haben jeweils zwei Diagonalen, die gleich lang sind, in einem Parallelogramm hingegen sind sie nicht gleich lang.

Figuren

Quadrat

Ein Quadrat ist eine viereckige geschlossene Figur, deren Seiten als auch deren Winkel gleich zu einander sind. Formeln: u=4a, A=a² (u ist der Umfang, a die Seite, A die Fläche). Mit d ist hier die sogenannte Diagonale gezeigt (verbindet zwei gegenüberliegende Eckpunkte).

Rechteck

Ein Rechteck ist eine viereckige geschlossene Figur, deren Winkel gleich zueinander sind und deren gegenüberliegenden Seiten auch gleich sind. Formeln: u=2a+2b oder u=2(a+b), A=a·b. Mit d ist wieder die Diagonale bezeichnet, mit a und b die Seiten (in der Figur ist a für die Länge, also die längere Seite und b für die Breite, also die kürzere Seite).

Parallelogramm

Ein Parallelogramm ist eine viereckige geschlossene Figur, deren gegenüberliegenden Seiten gleich sind. Daher sind sie auch parallel. Formeln: u=2a+2b oder u=2(a+b), A=a·h_a oder A=b·h_b. In der Figur ist h_a die Höhe zur Seite a und h_b die Höhe zur Seite b. Mit d wird eine der beiden Diagonalen bezeichnet (hier die kürzeste).

Raute (Rhombus)

Eine Raute ist eine viereckige geschlossene Figur, deren Seiten gleich sind. Daher sind auch alle Winkeln gleich. Formeln: u=4a, A= $\textstyle {\frac {e\cdot f}{2}}$ . Mit e und f sind die beiden Diagonale bezeichnet, mit a die Seite.

Trapez

Ein Trapez ist eine viereckige geschlossene Figur mit zwei gegenüberliegenden parallele Seiten. Formeln: u=a+b+c+d, $\textstyle A={\frac {a+c}{2}}\cdot h$ . Mit a, b, c und d werden die vier (nicht unbedingt gleichen) Seiten bezeichnet, mit h die Höhe auf die Basis (Basis ist nicht nur beim Trapez, sondern bei jeder Figur die untere Seite, beim Trapez im Bild hier die Seite a, also die Seite die im Bild unten steht). In der Figur sieht man auch die Diagonalen (ohne Symbol).

Deltoid

Ein Deltoid ist eine viereckige geschlossene Figur mit zwei Paaren nacheinander liegenden gleichen Seiten.

Vieleck (regelmäßiges)

Ein Vieleck ist eine Figur mit mehreren Winkeln. Wenn die Figur geschlossen ist und alle Seiten (und Winkel) gleich zueinander, dann ist das Vieleck regelmäßig. Im Bild sieht man ein regelmäßiges Siebeneck, die Seite ist hier mit s bezeichnet.

Fragen zu Figuren

Ist jedes Rechteck ein Parallelogramm? Umgekehrt?

Ist jede Raute ein Quadrat? Umgekehrt?

Ist jedes Trapez ein Parallelogramm? Umgekehrt?

Ist jedes Quadrat auch ein Rechteck? Umgekehrt?

Dreieck, Besondere Dreiecke

spitz
gleichseitiges
gleichschenkliges
rechtwinkeliges
stumpfwinkeliges

Ein Dreieck ist eine geschlossene Figur mit drei Winkel. Ist einer Winkel mehr als 90°, dann heißt das Dreieck stumpfwinkeliges, wenn alle Winkel kleiner als 90° sind, dann spitzwinkeliges.

Bei allen Dreiecken gilt für den Umfang: u=a+b+c, wobei a, b und c die Symbole für die Seiten sind. Die allgemeinen Formeln für die Fläche sind $\textstyle A={\frac {a\cdot h_{a}}{2}}={\frac {b\cdot h_{b}}{2}}={\frac {c\cdot h_{c}}{2}}$ , wobei h_a, h_b und h_c die Höhen zu den entsprechenden Seiten sind (im Bild nicht zu sehen).

Ist einer der Winkeln 90°, dann wird das Dreieck rechtwinkelig genannt. Die Formel für die Fläche ist in diesem Fall $\textstyle A={\frac {a\cdot b}{2}}$ , wobei hier a und b die kleineren Seiten sind (Katheten genannt). Die größte Seite (dem rechten Winkel gegenüber) nennt man Hypotenuse.

Sind zwei der drei Winkel (und auch zwei Seiten) gleich, dann nennt man das Dreieck gleichschenklig. Sind alle Winkel (und Seiten) gleich, dann ist es ein gleichseitiges Dreieck (mit Seite a). Für die Fläche des gleichseitigen Dreiecks gilt: $\textstyle A={\frac {\sqrt {3}}{4}}\cdot a^{2}$ .

Kreis, Kreissektor, Kreisring

Kreis
Kreisteile
Kreisring

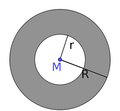
Ein Kreis ist die Menge aller Punkten, die von einem Punkt M (Mittelpunkt genannt) den gleichen Abstand r (Radius genannt) haben. Formeln: u=2πr, A=πr². r ist der Radius. Hier wird mit d der Durchmesser bezeichnet. π ist eine Zahl (wie 2 oder 5,632), mit dem Unterschied, dass man diese Zahl (π) nicht genau angeben kann. π ist ungefähr 3,14159... Sie ist das Verhältnis (also der Bruch) des Umfangs zum Durchmesser $\textstyle ({\boldsymbol {\pi }}={\frac {\boldsymbol {u}}{\boldsymbol {d}}})$ .

Schneidet man einen Kreis wie einen Torten-schnitt (also zwei Schnitte von Mittelpunkt aus bis am Rand), dann hat man einen Kreissektor. Schneidet man ein Stück mit einer Strecke von einem zu einem anderen Punkt des Kreises, hat man ein Kreissegment. Im Bild steht für den Bogen das englische Wort "arc". Schneidet man von der Mitte eines Kreises einen kleineren Kreis mit den selben Mittelpunkt ab, dann bekommt man ein Kreisring.

Ellipse

Schneidet man einen Zylinder schief, dann entsteht eine Ellipse. Die sieht wie ein zerquetschter Kreis aus. Die genauere Definition ist kompliziert:

Man nimmt zwei Punkte, die Brennpunkte (im Bild B₁ und B₂). Jeder Punkt der Ellipse (im Bild z.B. X) hat zu jedem Brennpunkt einen gewissen Abstand (im Bild z.B. ist der Abstand zum Brennpunkt B₁ mit s bezeichnet und zum B₂ mit p). In einer Ellipse ist die Summe der beiden Abständen (also s+p) immer gleich (im Bild gleich 2a, wobei a die sogenannte große Halbachse ist). Mit b wird hier die sogenannte kleine Halbachse bezeichnet.

Fläche

Definition des Quadratzentimeters

Ein Zentimeter Quadrat (1 cm², ein Zentimeter hoch zwei) ist ganz einfach ein Quadrat, dessen Seite ein Zentimeter ist (erstes Bild).

Fläche des Rechtecks

Im zweiten Bild sieht man ein Rechteck, dass aus mehreren Quadrat Zentimeter besteht. Hier haben wir zwei Zeilen, jede mit 3 Quadraten. Insgesamt 2x3=6 (cm²). Man kann offenbar sagen, dass der Flächeninhalt A eines Rechtecks die Länge a der einer Seite mal die Länge b der anderen ist.

A = a · b

Sonderfall: Das Quadrat. Da gilt A = a · a = a², da die Seiten gleich sind.

Raumgeometrie

Grundbegriffe

Dimension

Wir haben schon in der Geometrie der Ebene den Begriff der Strecke als auch verschiedene Figuren auf einer ebenen Fläche (z.B. Quadrat, Kreis, Dreieck, Rechteck) kennengelernt. Für eine Strecke braucht man nur die Länge angeben (z.B. 2,4dm), dann hat man sie vollständig beschrieben. Alle Strecken mit dieser Länge sind die gleiche Sache (man sagt in Mathematik: Sie sind Kongruent).

Verschiedene Rechtecke
mit gleicher Länge
und anderer Breite

Bei einem Rechteck hingegen reicht die Länge nicht aus. Es gibt unendlich viele Rechtecke mit der gleichen Länge und eine andere Breite. Diese Rechtecke sind nicht mehr die gleiche Sache. Sie haben auch einen anderen Flächeninhalt. Sie sind nicht kongruent. Man braucht daher bei Flächen zwei Zahlen, die Abstände beschreiben, beim Rechteck ist das die Länge und die Breite.

Wenn man jetzt eine Figur im Raum betrachtet, z.B. einen Quader, dann reichen die Länge und die Breite wieder nicht aus. Da braucht man noch einen Abstand, die Höhe. Wenn die Höhe anders ist, dann ist auch das Volumen anders.

Die Anzahl der Abstandswerte, die man braucht, um eine Figur vollständig zu beschreiben, nennt man Dimension.^[1]

Eine Strecke ist eine eindimensionale Figur: Allein ein Abstand (die Länge), reicht aus, um sie zu beschreiben. Ein Rechteck (und alle ebene Figuren) ist eine zweidimensionale Figur: Man braucht zwei Abstände (Länge und Breite), um sie zu beschreiben. Ein Quader (und alle Figuren, die Raum besetzen) ist eine dreidimensionale Figur: Man braucht drei Abstände (Länge, Breite und Höhe), um sie zu beschreiben. In unserem Bild eines Quaders wird die Länge mit a, die Breite mit b und die Höhe mit c bezeichnet.

Obwohl wir Menschen uns nicht mehrere Dimensionen vorstellen können, gibt es in der Physik theoretische Modelle, die noch mehrere Dimensionen haben. Beispielsweise setzt die allgemeine Relativitätstheorie die Zeit als eine weitere Dimension des sogenannten Zeitraums voraus! Die Stringtheorie kann sogar 11 Dimensionen voraussetzen!

↑ _{Allerdings wird in der Physik nicht nur der Abstand, sondern auch andere Größen als Dimensionsgrundlagen benutzt, z.B. ist in der Relativitätstheorie die Zeit eine vierte Dimension der sogenannten Raumzeit}

Körper

Ein Gegenstand in der Geometrie wird Körper genannt, wenn für seine Beschreibung drei Abstände notwendig und hinreichend sind.

Notwendig bedeutet, dass weniger Abstände nicht genügend sind, um den Körper zu beschreiben. Man kann nicht einen Quader nur mit Länge und Breite vollständig beschreiben.

Hinreichend bedeutet, dass man nicht mehrere Abstände oder eine andere Dimension für die Beschreibung braucht. Wenn die Länge, die Breite und die Höhe des Quaders gegeben sind, braucht man nicht auch die Raumdiagonale angeben (sie wird schon von den anderen drei Abständen bestimmt).

Jede dreidimensionale Figur ist ein (geometrischer) Körper. In diesem Text wird auch das Wort „Raumfigur“ dafür benutzt.

Kante

Im Kapitel über die Geometrie der Ebene haben wir den Begriff der Seite einer ebenen Fläche gesehen. Bei einem Quadrat sind alle Seiten gleich, bei einem Rechteck gibt es eine Länge und eine Breite. Die Strecken am Rand einer ebene Figur wurden also Seiten genannt.

Die Strecken am Rand eine Raumfigur werden aber doch Kanten genannt. Das Wort „Seite“ wäre in diesem Fall verwirrend: man wüsste dann nicht, ob mit „Seite“ die Seitenfläche oder die Seitenstrecke gemeint ist. Daher benutzt man das Wort „Kante“ für die Strecken. In unserem Bild eines Quaders wird die Länge mit a, die Breite mit b und die Höhe mit c bezeichnet. a,b und c sind daher Kanten des Quaders. Es gibt in diesem Bild 4 Kanten, die so lang wie a sind, 4 Kanten, die so lang wie b sind, und 4 Kanten, die so lang wie c sind.

Für die ebenen Flächen, die die Figur begrenzen, benutzt man die Worte „Grundfläche“, „Seitenfläche“ und „Deckfläche“. Es gibt selbstverständlich auch Raumfiguren, die von keinen ebenen Flächen begrenzt werden, wie beispielsweise die Kugel.

Ecke und Raumdiagonale

Den Punkt, wo drei Grenzflächen aufeinander treffen, nennt man Ecke (Eckpunkt). Die Strecke zwischen zwei Eckpunkten, die nicht auf der gleichen Grenzfläche liegen, nennt man Raumdiagonale (mit d im Bild des Quaders bezeichnet).

Oberfläche

Grundfläche

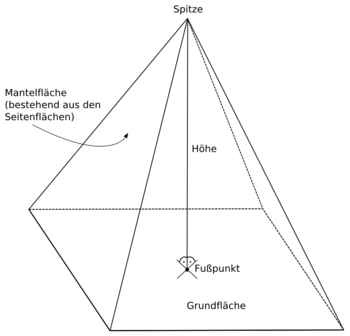
Grundfläche ist die Fläche, die im Bild unten (am Grund) steht. Bei Figuren deren Grenzflächen alle die gleiche Form haben (wie z.B. in einem Quader, wo alle Grenzflächen Rechtecke sind), kann jede beliebige Fläche der Figur als Grundfläche benutzt werden.

Wenn es eine Grenzfläche gibt, die sich von den anderen unterscheidet (wie z.B. bei der Pyramide in unserem Bild: alle Flächen außer einer sind Dreiecke), dann wird i.d.R. diese Fläche als Grundfläche bezeichnet.

Wenn es eine Grundfläche gibt, dann kann ihr gegenüber nur ein Punkt oder eine ganze Fläche stehen. Wenn ihr gegenüber eine ganze Fläche steht, dann nennt man diese Fläche Deckfläche (da sie an der „Decke“ ist). Die Deckfläche kann auch rund sein. Wenn der Grundfläche gegenüber nur ein Punkt liegt (wie in der Pyramide am Bild), dann nennt man diesen Punkt Spitze.

Seitenfläche und Mantel

Wenn es eine Grundfläche gibt, dann nennt man jede der restlichen Flächen Seitenfläche (außer der Deckfläche, wenn es eine gibt). Alle Seitenflächen zusammen nennt man Mantel. Der Mantel kann allerdings auch aus runden und nicht nur ebenen Flächen bestehen, wie z.B. in einem Zylinder (der auch eine Deckfläche hat, die ebenfalls ein Kreis ist) oder einem Kegel (der keine Deckfläche hat, dafür eine Spitze).

Gerade und schiefe Körper

A: gerades Prisma
B: schiefes Prisma
Gerade Pyramide
Schiefe Pyramide
Gerader Kegel
Schiefer Kegel

Wenn es bei einem Körper eine Grundfläche gibt, dann gibt es gegenüber entweder eine Fläche oder einen Punkt. Wenn der gegenüberliegende Punkt oder der Mittelpunkt der gegenüberliegenden Fläche direkt oberhalb (also senkrecht nach oben) vom Mittelpunkt der Grundfläche liegen, dann sagt man, dass der Körper gerade ist, sonst dass er schief ist.

Körper

Würfel

Würfel
Würfelnetz
Spielwürfel

Definition

Eine geschlossene Raumfigur, deren Grenzfläche aus 6 kongruente („gleiche“) Quadrate besteht, nennt man Würfel.

Formeln

Mit $a$ wird die Länge der Kante bezeichnet.

Volumen: $V=a^{3}$

Oberfläche: $A_{O}=6a^{2}$

Kantensumme: $K=12a$

Raumdiagonale(rot im Bild): $d_{R}={\sqrt {3}}\ a$

Flächendiagonale(grün im Bild): $d_{F}={\sqrt {2}}\ a$

Quader

Quader
Netz eines Quader
Eine quaderförmige
Mauerziegel

Definition

Eine geschlossene Raumfigur, deren Grenzfläche aus 3 Paare paarweise kongruente („gleiche“) gegenüberliegende Rechtecke besteht, nennt man Quader.

Formeln

Mit $a$ wird hier die Länge, mit $b$ die Breite und mit $c$ die Höhe bezeichnet (wie im Bild).

Volumen: $V=abc$

Oberfläche: $A_{O}=2ab+2ac+2bc$

Kantensumme: $K=4a+4b+4c$

Raumdiagonale: $d_{R}={\sqrt {a^{2}+b^{2}+c^{2}}}$

Flächendiagonalen: $d_{F1}={\sqrt {a^{2}+b^{2}}}$ , $d_{F2}={\sqrt {a^{2}+c^{2}}}$ , $d_{F3}={\sqrt {b^{2}+c^{2}}}$

Prisma

Prisma
Prismanetz
Optisches Prisma

Definition

Eine geschlossene Raumfigur, die durch Parallelverschiebung eines ebenen Vielecks entlang einer nicht in dieser Ebene liegenden Geraden im Raum entsteht, nennt man Prisma. Die Höhe ist der Abstand zwischen Grund- und Deckfläche.

Formeln

Es gibt viele verschiedenen Prismen, daher sollte man dafür die allgemeineren Formeln benutzen, die sich am Ende dieses Teilkapitels befinden.

Pyramide

Pyramide
Pyramidennetz
Einer der ältesten
bekannten Pyramiden
Maya Pyramide

Definition

Wenn man alle Punkte des Umfangs eines Vieleckes mit einem Punkt (genannt „Spitze“ oder „Scheitel“) außerhalb der Ebene des Vieleckes verbindet, dann entsteht die Grenzfläche einer Pyramide. Das Vieleck bildet dann i.d.R. die Grundfläche, die Dreiecke, die durch die Verbindung des Punktes mit dem Umfang entstehen, sind dann die Seitenflächen. Höhe ist der Abstand zwischen Spitze und Grundfläche.

Formeln

Es gibt viele verschiedenen Pyramiden, daher sollte man dafür die allgemeineren Formeln benutzen, die sich am Ende dieses Teilkapitels befinden.

Zylinder

Zylinder
Zylindernetz
Ein klappbarer (fast) zylinderförmiger Hut

Definition

Eine geschlossene Raumfigur, die durch Parallelverschiebung einer ebenen runden Figur (z.B. eines Kreises oder einer Ellipse) entlang einer nicht in dieser Ebene liegenden Geraden im Raum entsteht, nennt man allgemeinen Zylinder. Das Wort Zylinder allein wird i.d.R. für den Körper benutzt, der durch Parallelverschiebung eines Kreises entsteht. Die Höhe ist der Abstand zwischen Grund- und Deckfläche.

Formeln (für einen geraden Kreiszylinder)

Mit $h$ wird hier die Höhe, mit $r$ der Radius der Grundfläche $\ A_{G}\$ bezeichnet (wie im Bild), $\ A_{M}\$ ist die Mantelfläche:

Volumen: $V=\pi r^{2}\ h$

Oberfläche: $A_{O}=2\ A_{G}+A_{M}=2\pi r^{2}+2\pi r\ h=2\pi r(r+h)$

Kegel

Gerader Kegel
Kegelnetz
Spielkegel ^[1]

↑ (die allerdings nicht die Form eines Kegels haben...)

Definition

Wenn man alle Punkte des Umfangs einer runden ebenen Figur mit einem Punkt (genannt „Spitze“ oder „Scheitel“) außerhalb der Figurebene verbindet, entsteht die Grenzfläche eines (allgemeinen) Kegels. Die runde Figur ist dann die Grundfläche und die Fläche, die durch die Verbindung des Punktes mit dem Umfang entsteht, ist der Mantel. Wenn die runde ebene Figur ein Kreis ist, dann spricht man von einem Kreiskegel (in der Schulmathematik oft einfach Kegel genannt). Höhe ist der Abstand zwischen Spitze und Grundfläche. Mit s bezeichnet man die „Mantellinie“ bei einem geraden Kegel.

Formeln (für einen geraden Kegel)

Mit $h$ wird hier die Höhe, mit $r$ der Radius der Grundfläche $\ A_{G}\$ bezeichnet (wie im Bild), $\ A_{M}\$ ist die Mantelfläche:

Volumen: $\textstyle V={\frac {1}{3}}\pi r^{2}\ h$

Oberfläche: $A_{O}=A_{G}+A_{M}=\pi r^{2}+2\pi r\ s=\pi r(2r+s)$

(wobei s die sogenannte „Mantellinie“ $s={\sqrt {r^{2}+h^{2}}}$ ist)

Kugel

Kugel
Kugel mit Längen- und Breitenkreisen
Die Erde mit Längen- und Breitenkreisen
Kugelförmige Murmeln
Gewehrkugel^[1]
Ein kugelförmiger Basketball
Flächentreue Projektion der Erde^[2]

↑ (die allerdings nicht kugelförmig sind)
↑ (die allerdings nicht winkeltreu ist)

Für einen Kugel kann man nicht ein Netz auf einer Ebene zeichnen (nur näherungsweise), was der berühmte Mathematiker und Physiker Carl Friedrich Gauß bewiesen hat.

Definition

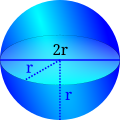
Eine Raumfigur mit einer Grenzfläche, deren Punkte alle von einem Punkt in der Mitte der Raumfigur (Mittelpunkt genannt) den gleichen Abstand haben (Radius genannt), nennt man Kugel.

Formeln

Mit $r$ wird der Radius bezeichnet (wie im Bild).

Volumen: $\textstyle V={\frac {4}{3}}\pi r^{3}$

Oberfläche: $A_{O}=4\pi r^{2}$

Die platonischen Körper

Die fünf platonischen Körper und ihre Netze

Die fünf platonischen Körper und ihre Netze

Tetraeder
Würfel^[1]
Oktaeder
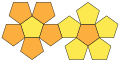
Dodekaeder
Ikosaeder

↑ (auch Hexaeder genannt)

Die platonischen Körper sind Raumfiguren, dessen Grenzflächen kongruent („gleich“) zueinander regelmäßige Vielecke sind. Man hat schon in Altertum bewiesen, dass es genau 5 davon gibt: der Würfel, den wir schon gelernt haben (mit 6 Quadrate als Grenzflächen), das Tetraeder (mit vier gleichseitigen Dreiecke als Grenzflächen), das Oktaeder (mit acht gleichseitigen Dreiecke als Grenzflächen), das Dodekaeder (mit zwölf regelmäßigen Fünfecke als Grenzflächen) und das Ikosaeder (mit zwanzig gleichseitigen Dreiecke als Grenzflächen). Da alle Grenzflächen kongruent sind, kann man nicht durch irgendein Merkmal eine Fläche von der anderen oder eine Kante von den andern unterscheiden. Wegen dieser und anderer Eigenschaften haben diese Körper die Philosophen und Wissenschaftler seit der antiken Zeit interessiert.

Eine schöne Animation der Körper und ihrer Körpernetze findet man hier!^[1]

↑ (Vorsicht:dieses Link kann den Browser bei alten Computer verlangsamen)

Volumen und Flächenberechnung

Volumen- und Oberflächenregeln

Für alle Körper, die eine Grund- und eine (parellele zur Grundfläche) kongruente („gleiche“) Deckfläche haben, gilt, dass das Volumen $\ V\$ die Grundfläche $\ A_{G}\$ mal die Höhe $\ h\$ ist:

$V=A_{G}\cdot h$

Genauer formuliert gilt diese Regel für alle Körper, die durch Parallelverschiebung einer ebenen Fläche entstehen. Für diese Körper gilt dann, dass die Mantelfläche $A_{M}$ die Summe deren Teilflächen ist und die gesamte Oberfläche $\ A_{O}=A_{M}+2A_{G}$ . Für die Teilflächen sollte dann man die Formeln aus der Geometrie der Ebene benutzen.

Für alle Körper, die eine Grundfläche $A_{G}\$ und eine gegenüber liegende Spitze haben, gilt, dass das Volumen ein drittel des Produkts der Grundfläche und der Höhe $\ h\$ ist:

$\textstyle V={\frac {1}{3}}A_{G}\ h$

Genauer gesagt muss dazu gelten, dass die Abstände zwischen Spitze und den Punkten auf dem Umfang der Grundfläche gerade sein sollen. Für diese Körper gilt dann, dass die Mantelfläche $A_{M}$ die Summe deren Teilflächen ist und die gesamte Oberfläche $\ A_{O}=A_{M}+A_{G}\$ . Für die Teilflächen sollte dann man die Formeln aus der Geometrie der Ebene benutzen.

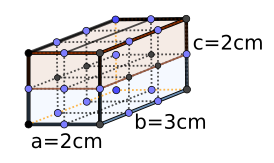
Intuitiver Beweis der Formel des Volumens des Quaders

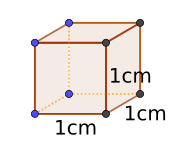
1 cm³ (auch „Kubikzentimeter“ genannt, Bild links) ist ein Würfel, dessen Kante 1cm ist.

Das Wort „Kubik“ stammt aus dem griechischen Wort für Würfel. Als Hochzahl bedeutet „Kubik“ hoch 3, also Kubikzentimeter (cm³), Kubikmeter (m³) usw.

Wie man jetzt im Bild rechts sehen kann, wenn man einen Quader hat, dessen Länge 3cm, dessen Breite 2cm und dessen Höhe 2cm ist, dann beinhaltet dieser Quader 12 Würfel, je 1cm³, also ist das Volumen 12cm³. Man kann daraus folgen, dass das Volumen eines Quaders allgemein die Länge mal die Breite mal die Höhe ist:

$V=a\cdot b\cdot c$

Arbeiten mit Modellen, Statistik

Stoffbeschreibung

direkte Proportionalitäten erkennen (zB Warenmenge-Geld, Zeit-Weg),
entsprechende Fragestellungen finden und Berechnungen durchführen können,
Modelle mit realen Gegebenheiten vergleichen,
grundlegende Überlegungen zur Sinnhaftigkeit von Modellen für die Praxis anstellen,
Tabellen und graphische Darstellungen zum Erfassen von Datenmengen verwenden können.

Direkte Proportionalität

$\$	$\$

$\$

Fangen wir direkt mit einem Beispiel an.

5 Tische kosten 315€. Wie viel kosten 2 Tische?

Hier spricht man von einer sogenannten direkte Proportionalität. Weniger Tische werden weniger Geld kosten. Das Beispiel besteht aus zwei Sätze:

was gegeben ist: „5 Tische kosten 315€“. Diese Daten schreibt man auf ein Zeile nebeneinander. Man schreibt also am Anfang:

5 Tische ... 315€

was gefragt ist: „Wie viel kosten 2 Tische?“ Hier ist der Preis der Tische in € gefragt. Man schreibt eine zweite Zeile unter die erste: Dabei schreiben wir das Gefragte (Preis der Tische) als x und die Anzahl der Tische unter der Anzahl Tische von der ersten Zeile:

5 Tische ... 315€

2 Tische ... x

Man fängt mit der gefragten Größe an (hier €), also mit der Zahl, die an der gleichen
Spalte mit x steht, und multipliziert diese Zahl mit der Zahl schräg gegenüber.

315·2=630.

Das Ergebnis dividiert man mit der verbliebenden Zahl (hier 5).

630:5=126

Jetzt kommt die Frage: 126 was? Was haben wir hier gerechnet? Sicherlich nicht Frösche und auch nicht Äpfel. Wie kann man herausfinden, was hier gerechnet wurde? Eine Möglichkeit ist es, die folgende Frage zu stellen: „Wieviel kosten 2 Tische?“ Kosten sind gefragt, also €. Das Ergebnis ist daher der Wert in €. Ein anderer Weg ist es darauf zu schauen, wo x steht: Es steht unterhalb von „315€“. Wir haben gesagt, dass in jeder Spalte die Sachen (in Mathematik „Einheiten“ genannt) übereinstimmen müssen. Unterhalb von € müssen € stehen. Daher sollte die Einheit von x auch € sein. Somit ist die Antwort:

„Zwei Tische kosten 126€.“

Der ganze Prozess noch einmal Schritt für Schritt:

und die entsprechende Animation:

Noch ein Beispiel:

3,5 Liter eines Stoffes wiegen 14,7 kg.

a) Wie viel wiegen 0,0175 Liter?

b) Wie viel Liter sind 3850kg?

Hier gibt es zwei Fragen, das gegebene ist aber in beiden Fällen das gleiche, nämlich der erste Satz.

a) Für die erste Frage schreiben wir das gegebene an einer Zeile und das gefragte darunter (gleiche Sachen unter gleichem):

${\begin{matrix}{\text{3,5 Liter}}\\\uparrow :\\{\text{0,0175 Liter}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{14,7 kg}}\\{}\\x\end{matrix}}$

Die Zahl, die an der gleichen
Spalte mit x steht, mal die Zahl schräg
gegenüber und durch die andere Zahl:

\left({\frac {14{,}7\cdot 0{,}0175}{3{,}5}}\right)\qquad x=0{,}735\ \ kg

Noch einmal stellt sich die Frage: 0,735 was? Was haben wir hier gerechnet? Wieso haben wir kg geschrieben? Die Frage war „Wie viel wiegen 0,0175 Liter?“ Also muss die Einheit vom Ergebnis kg sein. Wenn wir die Schlussrechnung betrachten, sehen wir ebenfalls, dass x unterhalb von „14,7 kg“ steht. In einer Spalte müssen die Einheiten übereinstimmen, unterhalb von kg müssen gleichfalls kg stehen. Somit ist die Antwort:

„0,0175 Liter des Stoffes wiegen 0,735kg.“

b) Für die zweite Frage schreiben wir wieder das gegebene in einer Zeile und das gefragte darunter (gleiche Sachen (Einheiten) unter gleiche):

${\begin{matrix}{\text{3,5 Liter}}\\{}\\x\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\searrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{14,7 kg}}\\:\uparrow \\{\text{3850 kg}}\end{matrix}}$ $\left({\frac {3{,}5\cdot 3850}{14{,}7}}\right)\qquad x\approx 916{,}7\ {\text{ Liter}}$

Ob man die Liter links oder rechts schreibt oder das gegebene oben oder unten, spielt keiner Rolle. Wichtig ist: das Gegebene in einer Zeil und gleiche Sachen (Einheiten) in der gleichen Spalte!

${\begin{matrix}{\text{14,7 kg}}\\\uparrow :\\{\text{3850 kg}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{3,5 Liter}}\\{}\\x\end{matrix}}$ $\left({\frac {3{,}5\cdot 3850}{14{,}7}}\right)\qquad x\approx 916{,}7\ {\text{Liter}}$

In diesen Aufgaben ist es wichtig zu verstehen: Man braucht nicht wissen, was die Wörter bedeuten! Man soll einfach die Struktur der Sätze der Aufgabe verstehen!

Diagramme

Was ist ein Diagramm

In Diagrammen kann man verschiedene Daten in einem Bild darstellen, die man dann schnell ablesen kann. Diagramme können helfen, einen schnellen Überblick zu bekommen, werden aber auch oft benutzt, um einen falschen Eindruck zu bewirken. Hier werden das Säulendiagramm, das Liniendiagramm, das Kreisdiagramm und das Boxplotdiagramm präsentiert, es gibt aber auch zahlreiche andere Diagrammarten, wie z.B. Punktdiagramm, Balkendiagramm usw.

Säulendiagramm

$\$	$\$

$\$

Das Diagramm mit den Farben gibt die Anzahl der Steine in einem Kinderspiel, die eine gewisse Farbe haben. 4 Steine sind rot, 1 ist orange, 1 ist gelb, keine ist grün, es gibt 6 türkis usw. So ein Diagramm nennt man Säulendiagramm, weil es aus „Säulen“ besteht, wie in einem alten Tempel (Bild rechts). Die Farben sind sogenannte nominale Variablen. Nominale Variablen können wir zwar voneinander unterscheiden, wir können aber nicht z.B. sagen, dass rot "größer" als blau ist, wie z.B. wir sagen können, dass 4 mehr als 1 ist. Nominalen Variablen können wir also nicht der Größe nach ordnen. In diesem Diagramm können wir allerdings den sogenannten Modus ablesen, also welche Farbe am häufigsten vorkommt (Türkis).

Das folgende Diagramm gibt die Anzahl der Packungen, die eine gewisse Anzahl von Bananen pro Packung beinhalten. Die Anzahl der Bananen pro Packung ist eine sogenannte kardinale Größe (genauer gesagt: Variable einer Verhältnisskala). Wir können die einzelne Werte addieren, wir können auch dadurch einen Durchschnitt finden. Das geht allerdings nicht mit den Werten, die auf der x-Achse stehen (hier Bananen pro Packung), sondern nur mit den einzelnen Werten.

Wenn die Frage z.B. ist, wie viele Packungen 4 Bananen haben, geht man so vor:

Auf der Achse unten (waagerechte Achse, x-Achse, auch Abszissenachse oder einfach Abszisse genannt) kann man die Bananen pro Packung ablesen, also kann man Bananen ablesen. Da wo 4 Bananen stehen (unten am Diagramm) befindet sich eine Säule. Man kann sehen, wie hoch diese Säule ist. Sie ist so hoch wie 5 Packungen. Die Anzahl der Packungen kann man links ablesen (auf der senkrechte Achse, der y-Achse, auch Ordinatenachse oder einfach Ordinate genannt). Also es gibt 5 Packungen mit 4 Bananen.

Wie viele Packungen haben 3 Bananen? Da, wo 3 Bananen stehen (unten, x-Achse), gibt es keine Säule! Die Höhe der Säule ist daher 0. Es gibt also keine (0) Packung, die 3 Bananen hat!

Wie viele Packungen haben keine Banane? Da, wo 0 Bananen stehen (unten, x-Achse), gibt es eine Säule, die 4 Packungen hoch ist. Es gibt also 4 Packungen mit keiner Banane!

Wie viele Packungen haben höchstens 3 Bananen? Höchstens bedeutet bis, also so viel wie 3 Bananen oder weniger (also 2, 1 oder keine Banane). Es gibt keine Packung mit 3 Bananen, 3 Pack. mit 2 Ban., 2 Pack. mit 1 Banane und 4 Pack. mit keiner Banane, also insgesamt 0+3+2+4=9 Pack..

Wie viele Packungen haben mindestens 3 Bananen? Mindestens bedeutet ab, also so viel wie 3 Bananen oder mehr (also 4, 5, 6 oder mehr Bananen). Es gibt keine Packung mit 3 Bananen, 5 Pack. mit 4 Ban. und 1 Pack. mit 5 Ban., also insgesamt 0+5+1=6 Pack..

Liniendiagramm

$\$	$\$

$\$

Die Kurve in einem Liniendiagramm kann irgendeine Form haben (und nicht nur eine Gerade). Das folgende Beispiel zeigt die Körpertemperatur von einer Person (namens Gregor) am 12.3.15. Man kann sich aber vorstellen, was im Diagramm dargestellt wird. Man kann z.B. sehen welche Temperatur Gregor um 6 oder um 22.15 Uhr hatte, oder am welchen Zeitpunkten seine Temperatur z.B. 36,45°C oder 36,6°C war.

Kreisdiagramm

$\$	$\$

$\$

Ein Kreisdiagramm zeigt Anteile des Ganzen. Es kann benutzt werden, um einen schnellen Überblick von statistischen Daten zu bekommen.

Ein Beispiel: In einer Klasse sind 8 Personen aus Österreich, 2 aus Deutschland, 2 aus der Türkei, 2 aus Serbien und 2 aus Tschechien. Diese Information kann man so wie im Bild in einem Kreisdiagramm darstellen. Die Hälfte des Kreises sind die 8 Personen aus Österreich. Die andere Hälfte ist in vier gleichen Teilen geteilt, also jeweils 2 Personen für Türkei, Deutschland, Serbien und Tschechien.

[1] Der genaue Begriff ist allerdings in diesem Fall Modulo

[2] _{Allerdings wird in der Physik nicht nur der Abstand, sondern auch andere Größen als Dimensionsgrundlagen benutzt, z.B. ist in der Relativitätstheorie die Zeit eine vierte Dimension der sogenannten Raumzeit}

[3] (die allerdings nicht die Form eines Kegels haben...)

[4] (die allerdings nicht kugelförmig sind)

[5] (die allerdings nicht winkeltreu ist)

[6] (auch Hexaeder genannt)

[7] (Vorsicht:dieses Link kann den Browser bei alten Computer verlangsamen)

[1]

[1]

[1]

[1]

[2]

[1]

[1]

${\begin{array}{c\|c\|c\|c\|c}&45&\times &37&\\\hline &1&4&8&0\\+&&1&8&5\\\hline &1&6&6&5\\\end{array}}$	oder	(ohne Null) ${\begin{array}{c\|c\|c\|c\|c}&45&\times &37&\\\hline &1&4&8&\\+&&1&8&5\\\hline &1&6&6&5\\\end{array}}$	und
${\begin{array}{c\|c\|c\|c\|c}&&45&&\\&\times &37&&\\\hline &&1&8&5\\+&1&4&8&0\\\hline &1&6&6&5\\\end{array}}$	oder	${\begin{array}{c\|c\|c\|c\|c}&&45&&\\&\times &37&&\\\hline &&1&8&5\\+&1&4&8&\\\hline &1&6&6&5\\\end{array}}$