MathemaTriX ⋅ Theorie. Klasse 2

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Inhalt Ein-Aus- klappen

AUFGABEN

Klassen Klasse 1 Klasse 2 Klasse 3 Klasse 4 Klasse 5 Klasse 6 Klasse 7 Klasse 8

Hinweis

Hier ist zur Zeit nur eine grobe Struktur. Die schon vorhandenen entsprechenden Kaitel sind für erwachsene Personen gedacht. Für diese Klasse hier sollten erst Kapitel in einer Zentralseite entstehen, die der Altersgruppe entsprechen. Für diese Klasse sollte hier ein Kapitel mit natürlichen Zahlen entstehen (Ohne Dezimalzahlen)

Arbeiten mit Zahlen und Maßen

Stoffbeschreibung

• Arbeiten mit Zahlen und Maßen: Klasse 1
• Festigen und Vertiefen der Fähigkeiten beim Arbeiten mit positiven rationalen Zahlen, um vielfältigeund komplexere Probleme in Sachsituationen bearbeiten zu können,
• Rechnen mit Brüchen (mit kleinen Zählern und Nennern), damit die Rechenregeln im Hinblick auf dieAlgebra sicher beherrscht werden,
• diese Rechenregeln für das Bruchrechnen begründen können,
• Bruchdarstellung in Dezimaldarstellung überführen und umgekehrt,
• wichtige Teilbarkeitsregeln kennen und anwenden können;
• Rechnen mit Prozenten in vielfältigen Zusammenhängen;
• Maße verwenden und Umwandlungen durchführen können in dem Ausmaß, wie es die Bearbeitung von Sachaufgaben und geometrischen Aufgaben erfordert und es dem Vorstellungsvermögen der Schülerinnen und Schüler entspricht.

Vorrang mit Klammern in Klammern

$5+6\cdot 7-55:$	$(21-4\cdot 8)$	$-3\cdot$	$[7+$	$2\cdot (6\cdot 3-39:3)]$	$-57$	$=$	In der großen Klammer hat die kleine Klammer Vorrang (Klammer vor Punkt vor Strich)
	↓		$7+$	$2\cdot (18-13)$			In der kleinen Klammer erst Punkt und dann Strichrechnung
	↓		7   +   $2\cdot 5$				Kleine Klammer durch ihr Ergebnis in der großen Klammer ersetzen
	$21-32$		$7$   +   $10$				In den verbliebenen Klammern erst Punkt- und dann Strichrechnungen
	$-11$		$17$				Man kann also die Klammer durch das jeweilige Ergebnis ersetzen

${\begin{array}{c}5+6\cdot 7-55:{\cancelto {21-32=-11}{(21-4\cdot 8)}}-3\cdot \underbrace {{\Bigl [}7+{\color {blue}\overbrace {2\cdot {\color {red}({\cancelto {18}{6\cdot 3}}-{\cancelto {13}{39:3)}}}} ^{2\cdot {\color {red}{\cancelto {5}{(18-13)}}}=\ \ 10}{\color {black}{\Bigr ]}}}} _{7+{\color {blue}10}=17}-57=\\\\5+{\cancelto {42}{6\cdot 7}}-{\cancelto {-5}{55:(-11)}}+{\cancelto {51}{3\cdot 17}}-57\\\\5+42+5-51-57=-56\end{array}}$

(an Plus-Minus Regeln halten!)

(an Plus-Minus Regeln halten!)

Einheiten

• Einheiten: Klasse 1

Einheiten umrechnen

Fläche

Volumen

Für die Umrechnungen eines Volumens benutzt man wieder das Schema des Abstandes:

Volumen ist immer Kubik: km³, m³, dm³, cm³, mm³

Es ist immer hoch 3. Daher muss man jeden Schritt (oder alle Schritte zusammen) hoch 3 machen! Daher kann man folgendes Bild benutzen:

In diesem Bild:

• Wenn das Volumen z.B. in km³ gegeben ist und in dm³ umgerechnet werden soll (von links nach rechts, vom größten zum kleinsten) muss man multiplizieren, in diesem Beispiel einmal mit 1000³ und einmal mit 10³.

2,35 km³ = 2,35 ·1000³ ·10³ dm³ = 2,35 ·1000000000·1000 dm³ = 2350000000000 dm³ (=2,35·10¹² dm³)

• Wenn das Volumen z.B. in cm³ gegeben ist und in m³ umgerechnet werden soll (von rechts nach links, vom kleinsten zum größten) muss man dividieren, in diesem Beispiel zwei mal durch 10³.

0,054cm³ = 0,054:10³:10³ m³ = 0,054:1000 :1000 m³ = 0,000000054 m³ (= 5,4 ·10^-8 m³)

Eine Einheit, die oft am Alltag für das Volumen benutzt wird, ist der Liter. Ein Liter ist genau so viel wie ein dm³. Daher ist ein$\ m\ell \$(Milliliter) so viel wie ein cm³.

Bruchrechnungen

• Bruchrechnungen: Klasse 1

Gemischte Zahlen

Eine gemischte Zahl besteht aus einer natürlichen Zahl und einem echten Bruch:  $\textstyle 6{\frac {4}{5}}$

Mathematrix: Werkzeuge/ LinksEine gemischte Zahl besteht aus einer natürlichen Zahl und einem echten Bruch:  $\textstyle 6{\frac {4}{5}}$

Gemischte Zahl in unechten Bruch umwandeln

Um eine gemischte Zahl in einen Bruch umzuwandeln, multipliziert man die natürliche Zahl mit dem Nenner des Bruches und addiert das Ergebnis zum Zähler. Das neue Ergebnis ist dann der Zähler des neuen Bruches, der Nenner bleibt der gleiche:

$6{\frac {4}{5}}={\frac {6\cdot 5+4}{5}}={\frac {34}{5}}$

Unechten Bruch in gemischte Zahl umwandeln

Um einen unechten Bruch in eine gemischte Zahl umzuwandeln, dividiert man den Zähler mit dem Nenner (ohne Nachkommastellen). Das Ergebnis der Division ist der „Zahlteil“ der gemischten Zahl, der Rest ist der Zähler des „Bruchteils“, der Nenner bleibt der gleiche:

    (siehe Division)

Folgendes Beispiel setzt die Anwendung eines Taschenrechners voraus:

${\frac {1895}{23}}=?\qquad \qquad {\begin{array}{rrl}1895&:{\boldsymbol {2}}3&={\color {red}{\boldsymbol {8}}2}{,}\dots \\\ {\color {red}{\boldsymbol {8}}2}&\cdot \ {\boldsymbol {2}}3&={\color {YellowOrange}1886}\\1895&-{\color {YellowOrange}1886}&={\color {blue}{\boldsymbol {9}}}\end{array}}\qquad \qquad {\text{ also }}\quad {\frac {1895}{23}}={\color {red}{\boldsymbol {8}}2}{\frac {\color {blue}{\boldsymbol {9}}}{{\boldsymbol {2}}3}}$

Eintausend-achthundert-fünfundneunzig Dreiundzwanzigstel sind so viel wie zweiundachtzig Ganzen und neun Zwanzigstel.

Das Ergebnis der Division 1895:23 mit dem Taschenrechner ist 82 Komma einige Nachkommastellen. Dieses Ergebnis ohne Nachkommastellen (82) wird die ganze Zahl in der gemischte Zahl sein. Das Ergebnis ohne Nachkommastellen (82) wird dann mit den Nenner (hier 23) multipliziert: 82·23=1886. Dieses Produkt (1886) wird dann vom Zähler (1895) subtrahiert: 1895-1886=9. Diese Differenz (9) stellt den neuen Zähler in der gemischten Zahl dar, der Nenner bleibt unverändert (23).

Der Prozess also mit Anwendung eines Taschenrechners könnte so aussehen:

${\frac {1895}{23}}=?$

Division mit dem Taschenrechner durchführen (1895:23=82 Komma einige Nachkommastellen). Ergebnis nach dem Gleichzeichen samt Bruchstrich und Nenner (23) schreiben:

${\frac {\color {red}1895}{23}}={\color {red}81}{\frac {?}{\color {red}23}}$

Die Diagonale (hier oben mit roten Zahlen markiert:) Zähler links (1895) minus ganze Zahl (81) mal Nenner rechts (23) wie im folgenden benutzen und Ergebnis in den Zähler rechts schreiben:

$1895-81\cdot 23={\color {red}9}$

also

${\frac {1895}{23}}=81{\frac {\color {red}9}{23}}$

Gemischte Zahl in unechten Bruch umwandeln

Um eine gemischte Zahl in einen Bruch umzuwandeln, multipliziert man die natürliche Zahl mit dem Nenner des Bruches und addiert das Ergebnis zum Zähler. Das neue Ergebnis ist dann der Zähler des neuen Bruches, der Nenner bleibt der gleiche:

$6{\frac {4}{5}}={\frac {6\cdot 5+4}{5}}={\frac {34}{5}}$

Unechten Bruch in gemischte Zahl umwandeln

Um einen unechten Bruch in eine gemischte Zahl umzuwandeln, dividiert man den Zähler mit dem Nenner (ohne Nachkommastellen). Das Ergebnis der Division ist der „Zahlteil“ der gemischten Zahl, der Rest ist der Zähler des „Bruchteils“, der Nenner bleibt der gleiche:

    (siehe Division)

Folgendes Beispiel setzt die Anwendung eines Taschenrechners voraus:

${\frac {1895}{23}}=?\qquad \qquad {\begin{array}{rrl}1895&:{\boldsymbol {2}}3&={\color {red}{\boldsymbol {8}}2}{,}\dots \\\ {\color {red}{\boldsymbol {8}}2}&\cdot \ {\boldsymbol {2}}3&={\color {YellowOrange}1886}\\1895&-{\color {YellowOrange}1886}&={\color {blue}{\boldsymbol {9}}}\end{array}}\qquad \qquad {\text{ also }}\quad {\frac {1895}{23}}={\color {red}{\boldsymbol {8}}2}{\frac {\color {blue}{\boldsymbol {9}}}{{\boldsymbol {2}}3}}$

Eintausend-achthundert-fünfundneunzig Dreiundzwanzigstel sind so viel wie zweiundachtzig Ganzen und neun Zwanzigstel.

Das Ergebnis der Division 1895:23 mit dem Taschenrechner ist 82 Komma einige Nachkommastellen. Dieses Ergebnis ohne Nachkommastellen (82) wird die ganze Zahl in der gemischte Zahl sein. Das Ergebnis ohne Nachkommastellen (82) wird dann mit den Nenner (hier 23) multipliziert: 82·23=1886. Dieses Produkt (1886) wird dann vom Zähler (1895) subtrahiert: 1895-1886=9. Diese Differenz (9) stellt den neuen Zähler in der gemischten Zahl dar, der Nenner bleibt unverändert (23).

Der Prozess also mit Anwendung eines Taschenrechners könnte so aussehen:

${\frac {1895}{23}}=?$

Division mit dem Taschenrechner durchführen (1895:23=82 Komma einige Nachkommastellen). Ergebnis nach dem Gleichzeichen samt Bruchstrich und Nenner (23) schreiben:

${\frac {\color {red}1895}{23}}={\color {red}81}{\frac {?}{\color {red}23}}$

Die Diagonale (hier oben mit roten Zahlen markiert:) Zähler links (1895) minus ganze Zahl (81) mal Nenner rechts (23) wie im folgenden benutzen und Ergebnis in den Zähler rechts schreiben:

$1895-81\cdot 23={\color {red}9}$

also

${\frac {1895}{23}}=81{\frac {\color {red}9}{23}}$

Erweitern und Kürzen

Erweitern

Erweitern ist, wenn man sowohl Zähler als auch Nenner eines Bruches mit der gleichen Zahl multipliziert. Der neue Bruch bleibt dann doch gleich:

${\frac {4}{7}}={\frac {4\cdot 5}{7\cdot 5}}={\frac {20}{35}}$

Bruchkürzen

Kürzen ist, wenn man sowohl Zähler als auch Nenner eines Bruches mit der gleichen Zahl dividiert. Der neue Bruch bleibt dann doch gleich:

${\frac {12}{8}}={\frac {12:4}{8:4}}={\frac {3}{2}}$

In all diesen Fällen arbeitet man mit natürlichen Zahlen (positive Zahlen ohne Komma).

Erklärung des Erweiterns und des Kürzens

7 2         5

Vergleichen wir die beiden Bilder. Im ersten Bild wird das Ganze im $5$ geteilt, zwei Teile davon werden dunkel dargestellt. Das ist also eine Repräsentation des Bruches $\textstyle \ {\frac {2}{5}}$. Im zweiten Bild wird das Ganze nicht nur in $5$ (waagerecht) sondern auch in $7$ (senkrecht) geteilt. Dadurch entstehen im Ganzen $\ 5\cdot 7=35\$ kleine "Quadrate". Jedes kleines Quadrat ist daher $\textstyle \ {\frac {1}{35}}\$ des Ganzen. Die dunkle Region ($\textstyle \ {\frac {2}{5}}$) beinhaltet allerdings $\ 2\cdot 7=14\$ solche "Quadrate" also $\textstyle \ {\frac {14}{35}}$. Man folgt daraus, dass $\textstyle \ {\frac {2}{5}}={\frac {14}{35}}\$ ist. Man hat in diesem Fall sowohl den Zähler als auch den Nenner mit der gleichen Zahl (hier $7$) multipliziert: $\textstyle \ {\frac {2}{5}}={\frac {2\cdot 7}{5\cdot 7}}={\frac {14}{35}}\$. Diesen Prozess nennt man erweitern.

Der Gegenprozess ist dann das Kürzen. Im ersten Bild wird das Ganze in $5$ Zeilen und $7$ Spalten also insgesamt in $\ 7\cdot 5=35\$ kleine "Quadrate" geteilt (das könnte selbstverständlich eine andere Austeilung sein). Die blaue Region ist $\ 3\cdot 5=15\$ solche Teile, also $\textstyle \ {\frac {15}{35}}$. Wenn man jetzt die waagerechte Austeilung (in Fünf Zeilen geteilt) entfernt (zweites Bild), dann ist das ganze nur in $7$ (Spalten) geteilt, wobei jetzt die blaue Region $3$ Spalten davon ist also $\textstyle \ {\frac {3}{7}}$. In diesem Fall haben wir sowohl Zähler als auch Nenner durch die gleichen Zahl (hier $5$) dividiert: $\textstyle \ {\frac {15}{35}}={\frac {15:5}{35:5}}={\frac {3}{7}}$. Diesen Prozess nennt man kürzen.

Erweitern

Mathematrix: Werkzeuge/ LinksErweitern ist, wenn man sowohl Zähler als auch Nenner eines Bruches mit der gleichen Zahl multipliziert. Der neue Bruch bleibt dann doch gleich:

${\frac {4}{7}}={\frac {4\cdot 5}{7\cdot 5}}={\frac {20}{35}}$

Bruchkürzen

Mathematrix: Werkzeuge/ Links Kürzen ist, wenn man sowohl Zähler als auch Nenner eines Bruches mit der gleichen Zahl dividiert. Der neue Bruch bleibt dann doch gleich:

${\frac {12}{8}}={\frac {12:4}{8:4}}={\frac {3}{2}}$

In all diesen Fällen arbeitet man mit natürlichen Zahlen (positive Zahlen ohne Komma).

Erklärung des Erweiterns und des Kürzens

7 2         5

Vergleichen wir die beiden Bilder. Im ersten Bild wird das Ganze im $5$ geteilt, zwei Teile davon werden dunkel dargestellt. Das ist also eine Repräsentation des Bruches $\textstyle \ {\frac {2}{5}}$. Im zweiten Bild wird das Ganze nicht nur in $5$ (waagerecht) sondern auch in $7$ (senkrecht) geteilt. Dadurch entstehen im Ganzen $\ 5\cdot 7=35\$ kleine "Quadrate". Jedes kleines Quadrat ist daher $\textstyle \ {\frac {1}{35}}\$ des Ganzen. Die dunkle Region ($\textstyle \ {\frac {2}{5}}$) beinhaltet allerdings $\ 2\cdot 7=14\$ solche "Quadrate" also $\textstyle \ {\frac {14}{35}}$. Man folgt daraus, dass $\textstyle \ {\frac {2}{5}}={\frac {14}{35}}\$ ist. Man hat in diesem Fall sowohl den Zähler als auch den Nenner mit der gleichen Zahl (hier $7$) multipliziert: $\textstyle \ {\frac {2}{5}}={\frac {2\cdot 7}{5\cdot 7}}={\frac {14}{35}}\$. Diesen Prozess nennt man erweitern.

Der Gegenprozess ist dann das Kürzen. Im ersten Bild wird das Ganze in $5$ Zeilen und $7$ Spalten also insgesamt in $\ 7\cdot 5=35\$ kleine "Quadrate" geteilt (das könnte selbstverständlich eine andere Austeilung sein). Die blaue Region ist $\ 3\cdot 5=15\$ solche Teile, also $\textstyle \ {\frac {15}{35}}$. Wenn man jetzt die waagerechte Austeilung (in Fünf Zeilen geteilt) entfernt (zweites Bild), dann ist das ganze nur in $7$ (Spalten) geteilt, wobei jetzt die blaue Region $3$ Spalten davon ist also $\textstyle \ {\frac {3}{7}}$. In diesem Fall haben wir sowohl Zähler als auch Nenner durch die gleichen Zahl (hier $5$) dividiert: $\textstyle \ {\frac {15}{35}}={\frac {15:5}{35:5}}={\frac {3}{7}}$. Diesen Prozess nennt man kürzen.

Strich und Punkt Bruchrechnungen

Strichbruchrechnungen

Wenn man zwei Brüche addiert oder subtrahiert, dann muss man auf den Nenner aufpassen:

Brüche mit gleichem Nenner:

${\frac {5}{4}}+{\frac {2}{4}}={\frac {5+2}{4}}={\frac {7}{4}}$

Brüche mit unterschiedlichen Nennern: Zähler und Nenner des ersten Bruches mit Nenner des zweiten erweitern (blaue Pfeile) und entsprechend für den zweiten Bruch (rote Pfeile)!

$={\frac {5\cdot 3}{4\cdot 3}}+{\frac {2\cdot 4}{3\cdot 4}}$$\textstyle \color {CadetBlue}{\left(={\frac {5\cdot 3+2\cdot 4}{3\cdot 4}}\right)}$$={\frac {15}{12}}+{\frac {8}{12}}={\frac {15+8}{12}}={\frac {23}{12}}$

Dabei ist es nicht wichtig, ob man minus oder plus zwischen den Brüchen hat. Allein der Nenner (ob er der gleiche oder nicht ist) spielt einer Rolle.

Erklärung der Strichbruchrechnungen

Wenn man den gleichen Nenner hat, ist es leicht mit einer Figur zu verstehen, warum die angegebene Regel gilt. Man kann sehen:

wenn zwei gleiche Schokoladentafeln in 7 geteilt werden und von einer Schokoladentafel 3 Teile (drei Siebtel) und von der anderen 2 Teile (zwei Siebtel) genommen werden, hat man insgesamt 5 Teile (also fünf Siebtel).

Was ist aber, wenn man nicht den gleichen Nenner hat (ungleichnamige Brüche), wie z.B. mit $\textstyle \ {\frac {2}{5}}+{\frac {3}{7}}$ ?

• 
• 

Das Ergebnis ist:

$\ {\frac {2}{5}}+{\frac {3}{7}}={\frac {2\cdot 7+5\cdot 3}{5\cdot 7}}={\frac {29}{35}}.$

Um dies zu zeigen, haben wir das erste Rechteck horizontal in 5 Teile geteilt und das zweite senkrecht in 7. Wir teilen jetzt dazu die erste Figur auch in 7 senkrechte Teile und die zweite in 5 horizontale:

• 
• 

Wir haben in jedem der beiden (gleichen) Rechtecken 5 mal sieben, also 35 kleine Quadrate. Jedes kleines Quadrat in den neuen Figuren ist daher $\textstyle \ {\frac {1}{35}}\$ des Ganzen. Wie man sehen kann, sind die $\textstyle {\frac {2}{5}}\$ gleich so viel wie $\textstyle \ {\frac {2\cdot 7}{5\cdot 7}}={\frac {14}{35}}\$ und die $\textstyle \ {\frac {3}{7}}\$ gleich so viel wie $\textstyle \ {\frac {3\cdot 5}{7\cdot 5}}={\frac {15}{35}}.\$ Da wir jetzt gleichnamigen Brüchen haben, kann man die Zähler addieren:

${\frac {2}{5}}+{\frac {3}{7}}={\frac {2\cdot 7}{5\cdot 7}}+{\frac {3\cdot 5}{7\cdot 5}}={\frac {14}{35}}+{\frac {15}{35}}={\frac {14+15}{35}}={\frac {29}{35}}$

Aus unserer alltäglichen Erfahrung können wir vermuten, dass wir diesen Vorgang auch bei allen anderen Paaren von ungleichnamigen Brüchen übertragen können (wenn auch mit viel mehr Aufwand für größeren Nennern). Das können wir dann auch auf mehrere Brüche übertragen, da wir den Vorgang erst am ersten Paar anwenden können und dann mit dem Ergebnis mit dem nächsten Bruch arbeiten können usw. Dies gilt auch für die Subtraktion von Brüchen (wenn das Ergebnis positiv ist).

Erklärung der Punktbruchrechnungen

Arbeiten mit ganzen Zahlen und Brüchen

Die Rechnungen mit ganzen Zahlen und Brüchen sind leicht, wenn man den vorherigen Stoff schon verstanden hat.

Strichrechnungen

Um eine ganze Zahl in einen Bruch umzuwandeln, reicht das Produkt der ganzen Zahl mit dem Nenner des Bruches als Zähler im Bruch zu schreiben:

$3={\frac {5\cdot 3}{5}}={\frac {15}{5}}$

Das sollte schon klar sein, da 15:5=3 ist... Um das zu veranschaulichen reicht es 3 ganzen jeweils in 5 geteilt nebeneinander zu stellen. Dann werden genau 3×5=15 Fünftel aufgezählt!

Hat man einmal die ganze Zahl als (gleichnamigen) Bruch, kann man auch eine entsprechende Strichrechnung durchführen, z.B.:

$3+{\frac {2}{7}}={\frac {3\cdot 7}{7}}+{\frac {2}{7}}={\frac {23}{7}}\qquad \qquad 5-{\frac {5}{9}}={\frac {5\cdot 9}{9}}-{\frac {5}{9}}={\frac {40}{9}}$

Punktrechnungen

Genau so leicht ist die entsprechende Multiplikation. Im ersten Bild werden zwei Fünftel dargestellt und diese werden 4 mal nebeneinander dargestellt. Insgesamt sind es daher 4×2=8 Fünftel.

$4\cdot {\frac {2}{5}}={\frac {4\cdot 2}{5}}={\frac {8}{5}}$

Um das Produkt einer ganzen Zahl mit einem Bruch zu berechnen, reicht es das Produkt der ganzen Zahl mit dem Zähler des Bruches in einem neuen gleichnamigen Bruch zu schreiben.

Die Division ist dann auch leicht:

$4:{\frac {3}{13}}=4\cdot {\frac {13}{3}}={\frac {52}{3}}\ (=17{\frac {1}{3}})$

Um den Quotient einer ganzen Zahl durch einem Bruch zu berechnen, reicht es das Produkt der ganzen Zahl mit dem Kehrwert des Bruches zu berechnen.

Textaufgaben zu den Bruchrechnungen

Die Textaufgaben mit Bruchrechnungen werden i.d.R. leicht in die mathematische Sprache umgewandelt:

In einem Staat mit 8,46 Millionen Einwohner trinkt jeder Einwohner durchschnittlich vier Neuntel Liter Milch täglich.

1. 1. Wie viel Liter werden dann täglich konsumiert?
   2. Der Gewinn für die Eigentümer ist 0,8¢/Liter Milch. Wie viel ist der tägliche Gewinn? Finden Sie ihn gerechtfertigt?
2. Im einem anderen Staat gibt es 4 Supermarktketten. Zusammen gewinnen die Eigentümer 105000€ täglich. Eigentümer A bekommt zwei Fünftel des Gewinns, Eigentümer B ein Drittel und den Rest teilen die anderen zwei Eigentümer C und D. Wie viel gewinnt täglich jeder Eigentümer? Finden Sie den Gewinn gerechtfertigt?

Aufgabe a lässt sich leicht berechnen:

$8{,}46\cdot {\frac {4}{9}}=3,76\ {\text{(Millionen Liter)}}$

Da der Gewinn pro Liter 0,8¢ ist, soll man 0,8 mit 3,76 Mil. multiplizieren (dann hat man ¢) und dann durch 100 dividieren (dann hat man €):

$3{,}76\cdot {\frac {0{,}8\cdot 1000000}{100}}=30080\ {\text{(€)}}$

Ob dieser Gewinn gerechtfertigt ist, soll jeder für sich entscheiden (die Eigentümer werden ihn sicherlich gerechtfertigt finden, sonst würden sie ihn nicht machen...).

Aufgabe b ist ebenfalls nicht besonders schwer:

Eigentümer A: $105000\cdot {\frac {2}{5}}=44000\ {\text{(€)}}$

Eigentümer B: $105000\cdot {\frac {1}{3}}=35000\ {\text{(€)}}$

Eigentümer C und D teilen den Rest: $105000-44000-35000=26000\qquad 26000:2=13000\ {\text{(€ jeweils für Eigentümer C und D)}}$

Doppelbrüche

Ein Doppelbruch ist wie die Division zwischen zwei Brüchen. Der Bruch oben wird durch den Bruch unten dividiert, also mit dem Kehrwert des Bruches unten multipliziert:

${\dfrac {\ \ {\frac {7}{12}}\ \ }{\frac {3}{20}}}={\frac {7}{12}}:{\frac {3}{20}}={\frac {7}{\cancelto {3}{12}}}\cdot {\frac {\cancelto {5}{20}}{3}}={\frac {35}{9}}$

Teilbarkeit

Durch 2

Wenn eine Zahl in 0, 2, 4, 6, 8 endet (gerade Zahl), dann ist sie durch 2 teilbar:

2004 und 33338 sind durch 2 teilbar: 2004 endet in 4, 33338 in 8.

2005 oder 486863 sind nicht durch 2 teilbar: 2005 endet in 5 und 486863 in 3.

Durch 5

Wenn eine Zahl in 0 oder 5 endet, dann ist sie durch 5 teilbar:

409 und 85923 sind nicht durch 5 teilbar (sie enden in 9 bzw. in 3).

490 und 89235 hingegen sind durch 5 teilbar (sie enden in 0 bzw. in 5)

Durch 3 (oder 9)

Wenn die Summe der Ziffer einer Zahl durch 3 (bzw. 9) teilbar ist, dass ist die Zahl auch durch 3 (bzw. 9) teilbar:

135 ist durch 3 teilbar: 1+3+5=9 (9:3=3, die Summe der Ziffer 9 ist durch 3 teilbar, also auch die Zahl 135). Sie ist auch durch 9 teilbar (9 ist durch 9 teilbar)

3564825 ist durch 3 teilbar: 3+5+6+4+8+2+5=33, 33:3=11. 33 ist durch 3 teilbar, daher auch 3564825. 33 ist aber nicht durch 9 teilbar, also 3564825 auch nicht.

3564824 ist nicht durch 3 oder 9 teilbar: 3+5+6+4+8+2+4=32, 32 ist nicht durch 3 oder 9 teilbar.

35644825 ist sowohl durch 3 als auch durch 9 teilbar: 3+5+6+4+4+8+2+4=32, 32 ist durch 3 und 9 teilbar.

Durch 7

Um zu verstehen, wie man herausfindet, ob eine Zahl durch 7 teilbar ist, machen wir ein Beispiel. Nehmen wir die Zahl 4445. Man teilt sie in Teilen am Ende anfangend und jedes mal zwei Ziffer nehmend: 44 | 45. Wenn die Summe vom doppelten des linken teils und vom rechten Teil durch 7 teilbar ist, dann ist auch die ganze Zahl: 2·44+45=133. Wenn man nicht sofort sehen kann, ob 133 durch 7 teilbar ist, kann man den Vorgang wiederholen: 133 in zwei Teilen → 1 | 33 2·1+33=35. 35 ist durch 7 teilbar, daher auch 133 und 4445. Bei größeren Zahlen muss man den Vorgang wiederholen. Probieren wir es mit einer größeren Zahl: 437381 43 | 73 | 81 2·43+73=159 2·159+81=399 → 3 | 99 3·2+99= 105 → 1 | 05 1·2+05=7 7 ist offenbar durch 7 teilbar also auch 105 und 399 und 437381! Man muss sagen: diese Regel kann doch länger dauern, als die eigentliche Division zu machen...

Durch 11

Für die Teilbarkeit durch 11 gibt es eine Regel: wenn die Differenz der alternierenden Summe der Ziffer einer Zahl 0 oder durch 11 teilbar ist, dann ist die Zahl auch durch 11 teilbar. Beispiel: 981607. Man nimmt die Summe der ersten, der dritten und der fünften (alternierend) Ziffer 9+1+0= 10 und die Summe der zweiten, der vierten und der sechsten (alternierend) Ziffer 8+6+7=21. Die Differenz der beiden Summen ist 21-10=11, was durch 11 teilbar ist. Daher ist auch 981607 durch 11 teilbar!

Primfaktorzerlegung =

Was sind Primzahlen

Primzahlen sind die natürlichen Zahlen (Zahlen ohne Komma und Minus), die nur durch 1 und sich selbst geteilt werden können. (teilbar: dividieren, ohne dass eine Kommazahl entsteht)

	2	3	4	5	6	7	8	9	10	11	12	13
geht auch durch			2		2 3		2 4	3	2 5		2 3 4 6
Prim- zahl	✔	✔	✘	✔	✘	✔	✘	✘	✘	✔	✘	✔

Z.B.:

2 ist nur durch 2 und 1 teilbar und daher eine Primzahl.

3 ist nur durch 3 und 1 teilbar und daher eine Primzahl.

4 ist nur durch 4 und 1, aber auch durch 2 teilbar und daher keine Primzahl.

5 ist nur durch 5 und 1 teilbar und daher eine Primzahl.

6 ist nur durch 6 und 1, aber auch durch 2 und 3 teilbar und daher keine Primzahl.

usw.

Was bedeutet in diesen Sätzen "teilbar"? Eine Zahl ist durch eine andere Zahl teilbar, wenn das Ergebnis der Division kein Nachkommastellen enthält.

Nehmen wir die Zahl 5.

$5:1=5$

$5:2=2{,}5$

$5:3=1{,}{\dot {3}}$ 

$5:4=1{,}25$

$5:5=1$

Dividiert man 5 durch jede größere natürlich Zahl (also: 6,7,8…), erhält man als Ergebnis eine Kommazahl kleiner als 1 (also Null-Komma-irgendwas). Beispielsweise:

$5:6=0{,}8{\dot {3}}$

Teilbar ist die Zahl 5 also nur durch eins (5:1=5) und sich selbst (5:5=1). Da bei unserem Beispiel alle anderen Ergebnisse ein Komma enthalten ist die Zahl 5 eine Primzahl.

Für 6 hingegen ist das nicht der Fall. 6 ist selbstverständlich durch 1 und 6 teilbar, aber eben auch durch 2 (6:2=3) und durch 3 (6:3=2). Daher ist 6 KEINE Primzahl.

Die ersten Primzahlen sind also 2, 3, 5, 7, 11, 13, 17, 19, 23 ...

Faktor ist ein Teil einer Multiplikation.

Primfaktorzerlegung (PFZ) bedeutet daher, eine Zahl als Produkt von Primzahlen auszudrücken (die dann Faktoren sind; Primzahlen die auch Faktoren sind, nennt man Primfaktoren; wenn man eine Zahl in Primfaktoren zerlegt, hat man die PFZ).

Primfaktorzerlegung Vorgangsweise

Nehmen wir die Zahl 7800. Wir versuchen sie durch die Primzahlen der Reihe nach und soweit es jedes Mal geht zu dividieren. Die erste Primzahl ist 2 7800 : 2 = 3900. Geht es weiter durch 2? Ja! 3900 : 2 = 1950. Geht es noch weiter? Ja! 1950:2=975. Weiter durch 2 geht es aber nicht.

Probieren wir dann durch 3. Geht es? Ja! 975:3=325. Geht es weiter durch 3? Nein! (325:3 = 108,33

Probieren wir die nächste Primzahl: 325:5=65. Das geht nochmal: 65:5=13.

Die nächsten Primzahlen sind 7 und 11, da geht es nicht. Es geht wieder durch 13 13:13=1.

Hier sind wir fertig. Wir haben 7800 drei mal durch 2, ein mal durch 3, zwei mal durch 5 und ein mal durch 13 dividiert und dann war das Ergebnis 1. Es gilt daher: 7800:2:2:2:3:5:5:13=1 und umgekehrt (Gegenrechnung) 7800=2·2·2·3·5·5·13.

Primfaktorzerlegung Schreibweise

Den ganzen Prozess Schritt zum Schritt kann man so darstellen:

7800

7800	2
3900

7800	2
3900	2
1950

7800	2
3900	2
1950	2
975	3
325

7800	2
3900	2
1950	2
975	3
325	5
65

7800	2
3900	2
1950	2
975	3
325	5
65	5
13

7800	2
3900	2
1950	2
975	3
325	5
65	5
13	13
1

Kürzen mit Primfaktorzerlegung

Wir haben schon das Kürzen von Brüchen gesehen:

${\frac {45}{35}}={\frac {45:5}{35:5}}={\frac {9}{7}}$

Hier sieht man sofort, dass man sowohl den Zähler als auch den Nenner durch 5 teilen kann. Was ist aber, wenn man große Zahlen hat. In diesem Fall ist es besser, die PFZ der Zahlen erst durchzuführen:

${\frac {6664}{8820}}=$?

6664	2
3332	2
1666	2
833	7
119	7
17	17
1

8820	2
4410	2
2205	3
735	3
245	5
49	7
7	7
1

Man schreibt Zähler und Nenner als Produkt von Primzahlen und kürzt den Bruch (also Primzahlen, die oben und unten vorkommen, werden gestrichen)

${\frac {6664}{8820}}={\frac {{\cancel {2}}\cdot {\cancel {2}}\cdot 2\cdot {\cancel {7}}\cdot {\cancel {7}}\cdot 17}{{\cancel {2}}\cdot {\cancel {2}}\cdot 3\cdot 3\cdot 5\cdot {\cancel {7}}\cdot {\cancel {7}}}}={\frac {2\cdot 17}{3\cdot 3\cdot 5}}={\frac {34}{45}}$

Bruchstrichrechnungen mit Primfaktorzerlegung

Schauen wir folgendes Beispiel an:

$2{\frac {11}{36}}-3{\frac {13}{24}}+{\frac {44}{45}}-{\frac {1}{40}}$

Wir haben schon gesehen, wie man zwei Brüche addiert oder subtrahiert. Was ist es aber, wenn man mehrere Brüche hat? Man könnte selbstverständlich erst die zwei Brüche machen, das Ergebnis mit dem nächsten Bruch usw. Das kann lang dauern und Brüche mit sehr große Nennern als Ergebnis haben. Es gibt eine Methode, die schneller ist und die Primfaktorzerlegung (PFZ) benutzt. Schauen wir ein Beispiel an. In unserem Beispiel wandeln wir erst die gemischte Zahlen in „unechten“ Brüchen um:

$2{\frac {11}{36}}-3{\frac {13}{24}}+{\frac {44}{45}}-{\frac {1}{40}}={\frac {83}{36}}-{\frac {85}{24}}+{\frac {44}{45}}-{\frac {1}{40}}$

Jetzt machen wir die PFZ der Nenner:

36	2
18	2
9	3
3	3
1

24	2
12	2
6	3
3	3
1

45	3
15	3
5	5
1

40	2
20	2
10	2
5	5
1

also:

36 = 2·2·3·3

24 = 2·2·2·3

45 = 3·3·5

40 = 2·2·2·5

Als nächstes sollen wir das sogenannte „kleinste gemeinsame Vielfache“ (kgV) bilden. Das geht so: Wir schauen welche Faktoren in den Nennern vorkommen. In unserem Fall sind es 2, 3 und 5. Dann schauen wir, wo jeder von diesen Faktoren am häufigsten vorkommt.

2 kommt in 36 zwei mal vor, in 24 drei mal vor, in 45 kein mal und in 40 wieder drei mal vor. Am häufigsten also kommt 2 drei mal vor (in 36 oder in 40, das spielt keine Rolle, wichtig ist, dass 2 am häufigsten in irgendeinem Nenner drei mal vorkommt). In diesem Fall müssen wir für das kgV die 2 drei mal benutzen.

3 kommt in 36 zwei mal vor, in 24 ein mal, in 45 zwei mal und 40 kein mal vor. Am häufigsten kommt 3 also zwei mal vor (in 36 oder in 45, wir benutzen also nur 36 oder nur 45, also die 3 zwei mal). In diesem Fall müssen wir für das kgV die 3 zwei mal benutzen.

5 kommt in 36 kein mal, in 24 auch kein mal, in 45 ein mal und 40 auch ein mal vor. Am häufigsten kommt 5 also ein mal vor (in 45 oder in 40, das spielt keine Rolle, wichtig ist, dass 5 am häufigsten in irgendeinem Nenner ein mal vorkommt). In diesem Fall müssen wir für das kgV die 5 ein mal benutzen.

Also die 2 kommt in kgV als drei mal Faktor vor, die 3 zwei mal und die 5 ein mal vor:

kgV=2·2·2·3·3·5=360

Für den nächsten Schritt gibt es verschiedene Wege, wir schreiben hier den Weg, den wir für den einfachsten halten. Unsere Rechnung nach dem ersten Schritt (gemischte Zahlen in unechten Brüchen umwandeln) ist jetzt:

${\frac {83}{36}}-{\frac {85}{24}}+{\frac {44}{45}}-{\frac {1}{40}}$

Wir multiplizieren unser kgV jeweils mit dem Zähler und dividieren jeweils durch den Nenner für jeden Bruch. Die Ergebnisse schreiben wir in einem Zähler auf, mit den jeweiligen Strichrechnungen dazwischen. Im Nenner kommt das kgV (hier 360) vor. Also:

Für den ersten Bruch: 360⋅83:36=830
Für den zweiten Bruch: 360⋅85:24=1275
Für den dritten Bruch: 360⋅44:45=352
Für den vierten Bruch: 360⋅1:40=9

Diese vier Zahlen kommen im Zähler mit den jeweiligen Strichrechnungen dazwischen vor, im Nenner kommt das kgV vor. Im Zähler machen wir dann auch die Strichrechnungen:

${\frac {830-1275+352-9}{360}}=-{\frac {102}{360}}$

In diesem Fall können wir den Bruch auch weiter kürzen (hier mit 6). Daher ist das Ergebnis:

$-{\frac {102}{360}}=-{\frac {17}{60}}$

Wiederholen wir das Ganze:

$\ 2{\frac {11}{36}}-3{\frac {13}{24}}+{\frac {44}{45}}-{\frac {1}{40}}=\qquad \qquad (kgV=360)$ $\ =\overbrace {\frac {83}{36}} ^{360\cdot 83:36=830}-\overbrace {\frac {85}{24}} ^{360\cdot 85:24=1275}+\overbrace {\frac {44}{45}} ^{360\cdot 44:45=352}-\overbrace {\frac {1}{40}} ^{360\cdot 1:40=9}=$ $={\frac {830-1275+352-9}{360}}=-{\frac {102}{360}}=-{\frac {17}{60}}$

Berechnung kgV: 36=2⋅2⋅3⋅3 24=2⋅2⋅2⋅3 45=3⋅3⋅5 40=2⋅2⋅2⋅5 kgV=2⋅2⋅2⋅3⋅3⋅5 =360

Textaufgaben Primfaktorzerlegung

Prozentrechnung

• Schlussrechnung: Klasse 1

Prozentrechnung Begriffe

Das Wort „Prozent“ kommt aus dem lateinischen und bedeutet pro Hundert. Ein Prozent IST ein Hundertstel.

$1\%=\textstyle {\frac {1}{100}}=0{,}01$

In diesem Sinn ist z.B.:

$5\%=\textstyle {\frac {5}{100}}=0{,}05\qquad \quad 20\%={\frac {20}{100}}=0{,}20=0{,}2\qquad \quad {\frac {1}{4}}=0{,}25={\frac {25}{100}}=25\%$

Bei Aufgaben, die mit Prozentrechnung zu tun haben, ist der Wert am Anfang immer 100%.

100% ist gleich 1, also das „Ganze“:

100%=1

Diesen Anfangswert nennt man Grundwert. Es gibt dazu auch den Prozentwert (oder Prozentanteil) und den Prozentsatz. Um zu verstehen, was die Begriffe bedeuten, nehmen wir folgendes Beispiel:

Wie viel % von 55 Personen sind 11 Personen?

Wir wollen einen Teil von den 55 Personen in Prozent (in Hundertstel) berechnen. Dieser Teil sind die 11 Personen. Die 11 Personen sind der Prozentanteil oder Prozentwert.

Das Ganze (100%, Anfangswert) sind die 55 Personen. Der Grundwert ist "55 Personen".

Herauszufinden welcher Wert der Grundwert ist, ist in der Prozentrechnung eine entscheidende Aufgabe. Um den Grundwert im Satz zu erkennen, schaut man in der Regel, welches Wort im Genitiv steht. Wenn man sagt "des Gewichts", "der Bevölkerung", "von 55 Personen", dann sind diese Ausdrücke der Grundwert (100%). Der andere Wert ist der Prozentanteil.

Es kann aber sein, dass kein Wort in der Aufgabe im Genitiv steht, sondern, dass eine zeitliche Reihenfolge vorkommt. Wenn nichts anderes angegeben wird, ist der Wert in der früheren Zeit der Wert am Anfang, der Grundwert (100%). Beispielsweise, wenn ein Baum wächst, ist der Wert am zeitlichen Anfang der Grundwert, der Prozentwert kann dann variieren, je nachdem was gefragt ist: Er kann die Höhe am Ende sein oder der Höhenunterschied.

Wenn beides vorkommt (zeitliche Folge und Genitiv), dann ist der Genitiv der Grundwert. Im Beispiel mit dem Baum kann gefragt werden, wie viel Prozent der Höhe am Ende die Höhe am Anfang ist. In diesem Fall ist die Höhe am Ende der Anfangswert (Genitiv ist "stärker" als die zeitliche Reihenfolge).

Der Prozentsatz beschreibt, wie viele Hundertstel des Ganzen der Prozentanteil ist. In unserem Beispiel:

${\frac {11}{55}}\ \ {\stackrel {\text{kürzen}}{=}}\ \ {\frac {1}{5}}\ \ {\stackrel {\text{erweitern}}{=}}\ \ {\frac {20}{100}}\ =\ 20\%$

Grundaufgaben der Prozentrechnung

Nicht vergessen: Der Wert am Anfang (das „Ganze“) ist immer 100%

• Wie viel % von 55 Personen sind 11 Personen?

Der Wert am Anfang (das „Ganze“) ist immer 100%. Hier ist der Prozentsatz eines Teils von 55 Personen gefragt. 55 Personen sind 100%. (Nach dem Wort „von“ steht der Wert, der 100% ist). Wir schreiben das so auf, wie wir es in der Schlussrechnung (genauer in der direkten Proportionalität) gelernt haben:

${\begin{matrix}{\text{55 Personen }}\\\uparrow :\\{\text{11 Personen }}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\{}\\x\end{matrix}}$      $\left({\frac {100\cdot 11}{55}}\right)\qquad x=20\%$.

• Wie viele Personen sind 11% von 55 Personen?

Der Wert am Anfang (das „Ganze“) ist immer 100%. Hier ist ein Prozentsatz von 55 Personen gefragt, also haben wir am Anfang 55 Personen, die dann 100% sind! (Also nach dem Wort „von“ steht der Wert, der 100% ist). Wir schreiben das auf, wie wir es in der Schlussrechnung (genauer in der direkten Proportionalität) gelernt haben:

${\begin{matrix}{\text{55 Personen }}\\{}\\x\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\searrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\:\uparrow \\11\%\end{matrix}}$      $\left({\frac {55\cdot 11}{100}}=6{,}05\right)\qquad x\approx 6\ {\text{Personen}}$.

• Wie viel % von 23 kg sind 5329kg?

Hier steht nach „von“ 23 kg, also sind 23kg 100%

${\begin{matrix}{\text{23 kg}}\\\uparrow :\\{\text{5329 kg}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\{}\\x\end{matrix}}$      $\left({\frac {100\cdot 5329}{23}}\right)\qquad x\approx 23170\%$.

• Wie viel ist 0,3% von 0,26 Liter?

${\begin{matrix}{\text{0,26 Liter}}\\{}\\x\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\searrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\:\uparrow \\0{,}3\%\end{matrix}}$      $\left({\frac {0{,}26\cdot 0{,}3}{100}}\right)\qquad x=0{,}00078\ {\text{Liter}}$.

• Von wie vielen Personen sind 55 Personen 11%?

Hier steht nach dem Wort „von“ eine Frage. Das Gefragte schreibt man in der Mathematik mit x. Daher ist x 100%. Das Gefragte ist 100%.

${\begin{matrix}x\\{}\\{\text{55 Personen }}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\nearrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\:\downarrow \\11\%\end{matrix}}$      $\left({\frac {55\cdot 100}{11}}\right)\qquad x=500\ {\text{Personen}}$.

Prozentrechnung und Brüche

Prozent bedeutet durch Hundert. Also:

$50\%={\frac {50}{100}}={\frac {1}{2}}={\frac {3}{6}}={\frac {7}{14}}=...=0{,}50=0{,}5={\sqrt {0{,}25}}\$

${\tfrac {50}{100}}\$haben wir mit 50 gekürzt. Wir merken, dass in allen Brüchen (auch bei ${\tfrac {50}{100}}$) der Nenner doppelt so viel ist wie der Zähler. ${\tfrac {1}{2}}\$haben wir erst mit 3 erweitert (also sowohl Zähler als auch Nenner mit 3 multipliziert) und das Ergebnis war ${\tfrac {3}{6}}$, dann auch mit 7 erweitert (Ergebnis ${\tfrac {7}{14}}$). Alle diese Brüche sind gleich zueinander und gleich 0,5. Das ist immer die gleiche Zahl. Also 50% ist 0,50 also 0,5. Wir merken auch, dass bei der Verwandlung des Prozentsatzes in eine einfache Dezimalzahl (Zahl ohne % daneben), wir das Komma einfach zwei mal verschieben.

daher ist:
20%:$\ 20\%={\frac {20}{100}}={\frac {1}{5}}={\frac {4}{20}}={\frac {13}{65}}=...=0{,}2$	25%:$\ 25\%={\frac {25}{100}}={\frac {1}{4}}={\frac {7}{28}}...=0{,}25$
5%:$\ 5\%={\frac {5}{100}}={\frac {1}{20}}={\frac {7}{140}}...=0{,}05$	350%:$\ 350\%={\frac {350}{100}}=...=3{,}5$
175%:$\ 175\%={\frac {175}{100}}={\frac {7}{4}}=...=1{,}75$	300%:$\ 300\%={\frac {300}{100}}=...=3$

In den letzten zwei Beispielen merken wir auch: Wenn etwas 75% mehr wird, dann ist das Ergebnis 175% (100%+75%), also das 1,75-fache des Anfangswerts; Wenn etwas 200% mehr wird, dann ist das Ergebnis 300% (100%+200%), also das 3-fache des Anfangswerts.

Noch eine Anmerkung zu den Verhältnissen:

Wenn z.B. 25% eine Eigenschaft haben (z.B. sind Schwarz) und der Rest nicht (sind also nicht Schwarz), dann ist das Verhältnis der Schwarzen zum ganzen 25%, also ${\tfrac {50}{100}}={\tfrac {1}{4}}\$also 1:4 (man sagt: „eins zu vier), das Verhältnis allerdings der Schwarzen zu den nicht Schwarzen ist 25% zu 75%, also ${\tfrac {25}{75}}={\tfrac {1}{3}}\$, also 1:3 (eins zu drei).

Noch eine Anmerkung: Das Verschieben des Kommas gilt bei allen Multiplikationen und Divisionen mit Potenzen von 10 (z.B. 100, 10000, 1000, 100000000 usw.) und nicht nur bei der Prozentrechnung. Wenn wir durch so ein Potenz dividieren, dann verschieben wir das Komma nach links, und zwar so oft, wie die Nullen sind (z.B. bei Division durch 10000000 verschieben wir 7 mal nach links). Bei Multiplikation verschieben wir nach rechts (die Zahl wird ja größer).

Prozentrechnung bei Wachstum und Abnahme

In diesem Absatz werden wir uns mit Aufgaben beschäftigen, bei denen irgendeine Größe mehr oder weniger wird.

• Das Gehalt eines Beamten war 1800€ und wurde um 2,5% gekürzt. Berechnen sie das neue Gehalt! Um wie viel € wurde das Gehalt gekürzt?

Es gibt zumindest zwei Wege, um diese Aufgabe zu lösen. Wir werden hier nur den Weg lernen, der für die Umkehraufgaben (die wir im nächsten Absatz lernen werden) notwendig ist.

Zur Erinnerung: der Wert am Anfang (das „Ganze“) ist immer 100%. Das Gehalt am Anfang war 1800€, daher sind 1800€ (der Wert am Anfang) 100%. Das Gehalt wurde gekürzt, also wurde es um 2,5% weniger. Daher bleibt dann 100%-2,5%=97,5% des Gehaltes. Wir wollen wissen, wie viel Geld in € diesen 97,5% ist:

${\begin{matrix}{\text{1800 €}}\\{}\\x\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\searrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\:\uparrow \\97{,}5\%\end{matrix}}$      $\left({\frac {1800\cdot 97{,}5}{100}}\right)\qquad x=1755{\text{ €}}$

Das Gehalt wurde daher um 1800€-1755€= 45€ gekürzt. Diese 45€ sind 2,5% des Gehalts (also 2,5% von 1800€).

Wenn die einzige Frage ist, wie viel das Gehalt gekürzt wurde, dann soll 2,5% bei der Schlussrechnung benutzt werden:

${\begin{matrix}{\text{1800 €}}\\{}\\x\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\searrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\:\uparrow \\2{,}5\%\end{matrix}}$$\qquad \left({\frac {1800\cdot 2{,}5}{100}}\right)\qquad x=45{\text{ €}}$

Es ist dann auch möglich, in dieser Weise das Gehalt am Ende zu berechnen: 1800€-45€= 1755€. Diesen Weg kann man aber in den Umkehraufgaben (nächster Absatz) nicht mehr benutzen.

• Ein Baum ist 5,6m groß und wächst in einem Jahr auf 6m. Um wie viel % ist er gewachsen?

Zur Erinnerung: der Wert am Anfang (das „Ganze“) ist immer 100%. Der Baum war am Anfang 5,6m, daher sind 5,6m (der Wert am Anfang) 100%. Er ist auf 6m gewachsen, also um 6m-5,6m= 0,4m größer geworden. Wir wollen wissen, wie viel % (von 5,6m) diese 0,4m sind:

${\begin{matrix}{\text{5,6 m}}\\\uparrow :\\{\text{0,4 m}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}100\%\\{}\\x\end{matrix}}$      $\left({\frac {100\cdot 0{,}4}{5{,}6}}\right)\qquad x\approx 7{,}14\%$.

Arbeiten mit Variablen

Stoffbeschreibung

• Arbeiten mit Variablen: Klasse 1
• mit Variablen allgemeine Sachverhalte beschreiben,
• Gleichungen und Formeln aufstellen, insbesondere auch in Sachsituationen,
• unter Verwendung von Umkehroperationen einfache lineare Gleichungen mit einer Unbekannten lösen und Formeln umformen,
• Formeln interpretieren.

Umformen

• Umformen: Klasse 1

Arbeiten mit Figuren und Körpern

Stoffbeschreibung

• Arbeiten mit Figuren und Körpern: Klasse 1
• Dreiecke, Vierecke und regelmäßige Vielecke untersuchen, wesentliche Eigenschaften feststellen,
• die Figuren skizzieren und konstruieren können,
• Erkennen, ob Angaben mehrdeutig sind oder überhaupt nicht in Konstruktionen umgesetzt werden können,
• kongruente Figuren herstellen können, die Kongruenz begründen können;
• Eigenschaften von Strecken- und Winkelsymmetralen kennen und für Konstruktion anwenden können;
• Flächeninhalte von Figuren berechnen können, die sich durch Zerlegen oder Ergänzen auf Rechtecke zurückführen lassen,
• Volumina von Prismen berechnen, möglichst in Anwendungsaufgaben.

Ebene Geometrie

• Ebene Geometrie: Klasse 1

Dreieckskonstruktionen Einführung

Ein Dreieck ist eine geschlossene ebene Figur mit drei Strecken als Seiten. Die Dreieckkonstruktion ist von selber aus eine Herausforderung und ein Weg, einige Fertigkeiten zu üben. Sie gilt als Vorbereitung und Einführung allgemein für die Geometrie. Ziel ist ein Dreieck mit drei vorgegebenen Größen nur mit Hilfe eines Zirkels und eines Lineals zu konstruieren. Solche Konstruktionen waren sehr beliebt schon in der Antike. Wichtig ist zu wissen, dass die Summe aller Winkel genau 180° und jeder Winkel kleiner als 180° ist und dass keine Seite größer als die Summe der anderen zwei sein darf.

Es gibt vier verschiedenen Aufgabensorten, je nachdem, was gegeben ist. Wenn drei Seiten gegeben sind, dann spricht man von der SSS (Seite-Seite-Seite) Konstruktion. Wenn zwei Seiten und der dazwischen liegender Winkel gegeben sind, spricht man von der SWS (Seite-Winkel-Seite) Konstruktion. Wenn zwei Seiten und ein Winkel, der nicht zwischen den Seiten liegt, gegeben sind, dann spricht man von der SSW Konstruktion (Seite-Seite-Winkel). Wenn zwei Winkel und eine Seite gegeben sind, dann spricht man von der WSW Konstruktion (Winkel-Seite-Winkel).

Konventionen

Die Seiten jedes Dreiecks werden klein geschrieben (mit a, b und c). Die gegenüber liegenden Eckpunkte werden entsprechend groß geschrieben mit (A, B und C). Für die entsprechenden Winkel werden die griechischen klein Buchstaben α, β und γ benutzt (Alpha, Beta und Gamma). Also, wenn A der Eckpunkt ist, ist der Winkel an diesem Punkt α und die gegenüberliegende Seite a. Man zeichnet die Seiten nacheinander im Gegenuhrzeigersinn. Unten zeichnet man i.d.R. die Seite a.

SSS Konstruktion

Wenn drei Seiten gegeben sind, geht man wie in den folgenden Bildern vor. Die Schritte sieht man am Rand jedes Bildes.

Die ganzen Schritten kann man in der folgenden Animation sehen:

SWS Konstruktion

Wenn zwei Seiten und der Winkel dazwischen gegeben sind, geht man wie in den folgenden Bildern vor. Die Schritte sieht man am Rand jedes Bildes.

Die ganzen Schritten kann man in der folgenden Animation sehen:

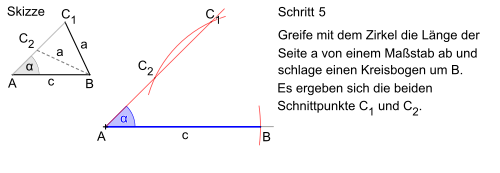
SSW Konstruktion

Wenn zwei Seiten und ein Winkel, der nicht zwischen diesen Seiten steht, gegeben sind, geht man wie in den folgenden Bildern vor. Die Schritte sieht man am Rand jedes Bildes.

Die ganzen Schritten kann man in der folgenden Animation sehen:

WSW Konstruktion

Wenn zwei Winkel und eine Seite gegeben sind, gibt es zwei Möglichkeiten. Wenn die zwei Winkel am Rand der gegebenen Seite stehen, dann geht man wie in den folgenden Bildern vor. Wenn einer der gegebenen Winkel, der Winkel gegenüber der gegebenen Seite ist, dann berechnet man erst den dritten Winkel (180°− die anderen beiden Winkel) und geht dann vor, wie in den folgenden Bildern. Die Schritte sieht man am Rand jedes Bildes.

Die ganzen Schritten kann man in der folgenden Animation sehen:

Herzlichem Dank an Petrus3743, der die Seite vorbereitet hat und die Erlaubnis gegeben hat, sie hier zu benutzen. Für weitere Konstruktionen kann man seinem Link folgen

Flächen

Fläche des Parallelogramms

Parallelogramm

Im Fall eines Parallelogramms kann man sich vorstellen, dass ein Stück der Figur so wie im Bild geschnitten und auf der anderen Seite wieder hinzugefügt werden kann. Dadurch entsteht wieder ein Rechteck, dessen Seiten jetzt die Basis a und die Höhe h_a des Parallelogramms sind. Die Fläche des dadurch entstandenen Rechtecks ist daher der Flächeninhalt des Parallelogramms:

A= a · h_a

Variablen in der Geometrie

Bei allen Formeln gibt es sogenannten „Variablen“. Es geht in der Regel um ein Buchstabe, der für irgendwas steht. Hier schreiben wir, wofür diese Symbole in der Geometrie stehen.

• Ein großes A, steht in der Regel für die Fläche (genauer für den Flächeninhalt)

• Ein u steht i.d.R. für den Umfang (also wie lang das Rum-herum der Figur ist)

• a, b, c usw. stehen i.d.R. für die Seiten (auch Länge oder Breite) von Figuren

• h (oder H) steht i.d.R. für die Höhe einer Figur. Oft gibt es dann ein Index, z.B. h_b, was dann bedeutet, dass diese die Höhe für die Seite b ist.

• r (oder R) steht i.d.R. für den Radius eines Kreises.

• d steht bei einem Kreis für den Durchmesser des Kreises, bei einem Parallelogramm (oder Rechteck, Quadrat, Trapez, Vieleck) aber für die Diagonale!

• Griechische kleine Buchstaben (α, β, γ, δ, ε, θ, φ) stehen i.d.R. für Winkel.

• Allerdings ist mit dem griechischen Buchstabe π die Kreiszahl bezeichnet (π≈3,1415...).

Formel Einsetzen in der ebenen Geometrie

Bei einer Aufgabe sind immer gewisse Informationen gegeben, z.B.:

• Ein Zimmer ist 4m lang und 2,8m breit. Finden Sie seinen Umfang und seine Fläche heraus!

In solchen Problemen soll man die gegebenen Zahlen in die Formel sinnvoll einsetzen. Das bedeutet, dass man die Buchstaben in der Formel durch Zahlen ersetzt. In diesem Beispiel sucht man in einer Formelsammlung das Rechteck (da ein Zimmer die Form eines Rechtecks hat).

Rechteck

In der Figur, die man in der Formelsammlung finden kann, kann man sehen, dass mit a die Länge und mit b die Breite bezeichnet wird. In der Formelsammlung kann man auch die Formel für den Umfang finden:

u=2a+2b

Die Länge a ist gegeben: 4m. Die Breite b auch: 2,8m. Wenn nichts zwischen einer Zahl und einer Variable steht (hier z.B. 2a), dann ist mal gemeint (2 mal a). Man schreibt also an der Stelle von a und b die Zahlen 4 und 2,8:

$u=2a+2b=2{\cancel {a}}^{=4}+2{\cancel {b}}^{=2{,}8}=2\cdot 4+2\cdot 2,8=13,6\ (m$, da wie m mit m addiert haben)

In der Spalte für die Fläche steht beim Rechteck:

A=a·b   also

$A=a\cdot b={\cancel {a}}^{=4}\cdot {\cancel {b}}^{=2{,}8}=4\cdot 2,8=11,2\ (m^{2}$, da wie m mit m multipliziert haben)

Man soll auch auf die Einheiten aufpassen:

Der Umfang ist eine Strecke, also er wird in Streckeneinheiten gemessen (hier m), die Fläche hingegen in Flächeneinheiten (hier in m²).

Andererseites kann es sein, dass eine Größe in verschiedenen Einheiten gegeben wird, z.B.:

• Die Länge eines Rechtecks ist 5dm und seine Breite 32cm. Finden Sie seinen Umfang und seine Fläche heraus!

Das Einsetzen von Werten in einer Formel setzt voraus, dass die Einheiten übereinstimmen. Man muss z.B. überall in der Formel Werte in Stunden haben und nicht irgendwo Stunden, an einer anderen Stelle Minuten usw. Hier muss man den Wert einer der beiden Seiten umwandeln, z.B.:

32cm=32:10 dm = 3,2 dm

Jetzt sind beide Seiten (Länge und Breite) in dm und es kann weiter berechnet werden:

u=2a+2b und A=a·b

Die Länge a ist gegeben: a=5dm. Die Breite b haben wir jetzt auch in dm umgerechet: b=3,2dm:

$u=2a+2b=2{\cancel {a}}^{=5}+2{\cancel {b}}^{=3{,}2}=2\cdot 5+2\cdot 3{,}2=16{,}4\ (dm$, da wie hier dm mit dm addiert haben)      und

$A=a\cdot b={\cancel {a}}^{=5}\cdot {\cancel {b}}^{=3{,}2}=5\cdot 3{,}2=16\ (dm^{2}$,da wie hier dm mit dm multipliziert haben)

Hätten wir die Einheiten (die 32cm) nicht umgewandelt, hätten wir Probleme mit dem Einheit am Ende oder sogar ein völlig falsche Antwort:

• Bei der Multiplikation hätten wir:

$\textstyle A=a\cdot b={\cancel {a}}^{=5}\cdot {\cancel {b}}^{=32}=5\cdot 32=160\qquad$FALSCH! Wenn man hier dm² oder cm² als Einheit schreibt, ist das Ergebnis völlig falsch, die Einheit, die wir schreiben hätten sollen, wäre dm⋅cm, das wäre zwar richtig, aber diese Einheit wird für die Fläche nie benutzt.

• Bei der Addition hätten wir:

$u=2a+2b=2{\cancel {a}}^{=5}+2{\cancel {b}}^{=32}=2\cdot 5+2\cdot 32=74\qquad$FALSCH! Hier ist sogar der Wert völlig falsch! Der richtige Wert, wie wir gesehen haben, ist 16,4 dm (oder 164 cm). Man kann nicht dm und cm addieren oder subtrahieren, genauso wie man nicht dm und kg addieren kann! Addieren (oder subtrahieren) kann man nur Sachen, die genau die gleichen Einheiten haben!

Nicht nur bei Multiplikation oder Addition müssen die Einheiten übereinstimmen, sondern auch bei Division und allen anderen Rechenarten. Bei Multiplikation und Addition haben wir das Beispiel gerade eben gesehen (Fläche und Umfang des Rechtecks am letzten Beispiel). Ein Beispiel für Division, ist wenn man die Fläche eines Rechtecks durch seine Länge dividiert, um die Breite zu berechnen. Wenn die Fläche 6cm² und die Länge 30mm, dann kann man NICHT die Division so durchführen:  $\textstyle b={\frac {6}{30}}$, da 6 in cm gegeben ist und 30 in mm. Man soll zuerst z.B. die mm in cm umwandeln (30mm=3cm) und dann die Division durchführen:  $\textstyle b={\frac {6}{3}}=2$ (das sind dann cm, da wir cm² durch cm dividiert haben und man die Hochzahl und dann kann man die Einheiten kürzen:  $\textstyle {\frac {cm^{\cancel {2}}}{\cancel {cm}}}=cm$.

Wir können also schreiben:

Bei Rechnungen müssen die Einheiten immer übereinstimmen!

Bei einer Rechnung (oder Gleichung) muss man immer erst kontrollieren, ob die Einheiten übereinstimmen, dann die Einheiten, die nicht übereinstimmen, in übereinstimmenden Einheiten umwandeln und erst am Ende die Rechnung durchführen! Das gilt immer (auch bei der Schluss-und Prozentrechnung)!

In Physik benutzt man sogar Einheitssysteme, das ist aber für dieses Buch ein fortgeschrittenes Thema.

Raumgeometrie

• Raumgeometrie: Klasse 1

Formel Einsetzen in der Raumgeometrie

Arbeiten mit Modellen, Statistik

Stoffbeschreibung

• Arbeiten mit Modellen, Statistik: Klasse 1
• charakteristische Kennzeichen von indirekten und direkten Proportionalitäten an Beispielen angebenkönnen,
• einfache Fragestellungen dazu formulieren, sie graphisch darstellen und lösen können,
• Fragen zu sinnvollen Anwendungsbereichen für solche Proportionalitäten stellen;
• relative Häufigkeiten ermitteln können,
• entsprechende graphische Darstellungen lesen, anfertigen und kritisch betrachten können,
• Manipulationsmöglichkeiten erkennen.

Schlussrechnung

• Schlussrechnung: Klasse 1

Indirekte Proportionalität

In der direkten Proportionalität haben wir gesehen, wie man vorgeht, wenn zwei Größen gleichzeitig größer oder kleiner werden. Wenn man mehr von einer Ware kaufen will, dann muss man auch mehr bezahlen. Wenn man weniger kaufen will, dann zahlt man auch weniger. Wenn man mehr kg von einem Stoff hat, dann hat man auch mehr Liter des Stoffes. Es gibt aber auch Fälle, bei denen die Erhöhung einer Größe die Verminderung einer anderen bedeutet:

• 3 Arbeiter brauchen 15 Stunden, um ein Haus mit Fliesen zu verlegen. Wie viel Zeit brauchen dann 5 Arbeiter?

1 Arbeiter würde in diesem Fall mehr Zeit brauchen. Es gibt für einen Arbeiter viel mehr Boden zu verlegen, wenn er alleine arbeitet. Also weniger Arbeiter brauchen mehr Zeit. Das ist also KEINE direkte sondern eine indirekte Proportionalität.

Wie bei der direkten Proportionalität schreibt man hier auch die gegebenen Größen nebeneinander und gleiche Größen untereinander.

${\begin{matrix}{\text{3 Arbeiter}}\\{\text{5 Arbeiter}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{15 Stunden}}\\x\end{matrix}}$

In diesem Fall multipliziert man mit der Zahl gerade gegenüber (und NICHT schräg gegenüber, wie in der direkten Proportionalität) und dividiert dann durch die andere Zahl:

${\begin{matrix}{\text{3 Arbeiter}}\\\downarrow :\\{\text{5 Arbeiter}}\end{matrix}}\quad {\begin{matrix}{\dot {\longleftarrow }}\\\\{}\end{matrix}}\quad {\begin{matrix}{\text{15 Stunden}}\\{}\\x\end{matrix}}$      $\left({\frac {15\cdot 3}{5}}\right)\qquad x=9\ {\text{Stunden}}\ \$  (die die Arbeiter in diesem Fall brauchen).

Um zu unterscheiden, ob man eine direkte oder indirekte Proportionalität hat, muss man schon die Sprache und die Zusammenhänge gut verstehen können!

Vergleich direkter und indirekter Proportionalität

Wie wir in den vorherigen Absätzen gesehen haben, muss man sowohl bei der direkten als auch bei der indirekten Proportionalität die Daten, die (in der Regel in einem Satz) in Verbindung gebracht werden, in einer Zeile nebeneinander schreiben (hier bei der direkten Proportionalität 3,5 Liter und 14,7 kg und bei der indirekten 3 Arbeiter und 15 Stunden) und dafür sorgen, dass in jeder Spalte die gleichen Einheiten geschrieben werden.

${\begin{matrix}{\text{3,5 Liter}}\\\\{\text{0,0175 Lit}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\{}\\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{14,7 kg}}\\{}\\x\end{matrix}}$

${\begin{matrix}{\text{3 Arbeiter}}\\{}\\{\text{5 Arbeiter}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{15 Stunden}}\\{}\\x\end{matrix}}$

Bei beiden Vorgängen fängt man dann mit der Zahl an, die nur an der gleichen Spalte mit x steht (hier 14,7 kg in der direkten und 15 Stunden in der indirekten Proporionalität). Der Unterschied ist: bei der direkten Proportionalität geht man dann schräg, bei der indirekten gerade gegenüber, und multiplitiert mit dieser Zahl (hier 0,0175 Liter in der direkten und 3 Arbeiter in der indirekten Proporionalität). Am Ende dividiert man in beiden Fällen mit der übriggebliebenen Zahl (hier 3,5 Liter in der direkten und 5 Arbeiter in der indirekten Proporionalität).

${\begin{matrix}{\text{3,5 Liter}}\\\uparrow :\\{\text{0,0175 Lit}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{14,7 kg}}\\{}\\x\end{matrix}}$

${\begin{matrix}{\text{3 Arbeiter}}\\\downarrow :\\{\text{5 Arbeiter}}\end{matrix}}\quad {\begin{matrix}{\dot {\longleftarrow }}\\\\{}\end{matrix}}\quad {\begin{matrix}{\text{15 Stunden}}\\{}\\x\end{matrix}}$

Wie kann man verstehen, ob eine direkte oder eine indirekte Proportionalität vorliegt?

Nehmen wir den folgenden Bruch b:  $\textstyle b={\frac {z}{n}}$,  wobei z der Zähler und n der Nenner ist. Wenn z=20 und n=5 ist, dann ist der Bruch b=4: $\textstyle b={\frac {20}{5}}=4$. Wenn jetzt der Zähler z größer wird (z.B. z=30), dann wird der ganze Bruch b auch größer:  $\textstyle b={\frac {30}{5}}=6$. Wenn der Zählerz kleiner wird (z.B. z=10), dann wird der ganze Bruch auch kleiner:  $\textstyle b={\frac {10}{5}}=2$. Je größer der Zähler, desto größer der Bruch. Je kleiner der Zähler, desto kleiner der Bruch. Diesen Zusammenhang nennt man direkte Proportionalität.

Wenn jetzt der Nenner größer wird (z.B. n=10), dann wird der ganze Bruch das Gegenteil, also kleiner:

Wenn der Zähler z=20 und der Nenner n=5 ist, dann ist der Bruch b=4: $\textstyle b={\frac {20}{5}}=4$. Wird der Nenner n größer, z.B. 10, dann wird der Bruch b kleiner:  $\textstyle b={\frac {20}{10}}=2$. Wenn der Nenner kleiner wird (z.B. n=2), dann wird der ganze Bruch das Gegenteil, also größer:  $\textstyle b={\frac {20}{2}}=10$. Je größer der Nenner, desto kleiner der Bruch. Je kleiner der Nenner, desto größer der Bruch. Diesen Zusammenhang nennt man indirekte Proportionalität.

Wenn zwei Größen (z.B. Volumen und grob gesagt Gewicht) gleichzeitig wachsen oder gleichzeitig weniger werden, dann liegt eine direkte Proportionalität vor (z.B. wenn man mehr Wasser hat, ist sowohl das Volumen als auch das Gewicht mehr). Wenn das Wachstum einer Größe zur Verminderung einer anderen führt, dann liegt eine indirekte Proportionalität vor (z.B. mehr Arbeiter brauchen weniger Zeit, um die gleiche Arbeit zu erledigen). So kann man verstehen, ob man direkte oder indirekte Proportionalität benutzen soll. Beim nächsten Kapitel allerdings (Prozentrechnung) kommt nur die direkte Proportionalität vor!

Diagramme

• Diagramme: Klasse 1