MathemaTriX ⋅ Theorie. Klasse 6
| ||||||||||||||||||
|
Inhalt
Ein-Aus- klappen |
| AUFGABEN | |
|
|
Vorgabe des Ministeriums
[Bearbeiten]Potenzen, Wurzeln, Logarithmen
[Bearbeiten]- Definieren von Potenzen mit natürlichen, ganzen, rationalen und reellen Exponenten, Definieren von Wurzeln und Logarithmen
- Formulieren und Beweisen von Rechengesetzen für Potenzen, Wurzeln und Logarithmen; Umformen entsprechender Terme
Folgen
[Bearbeiten]- rekursives und explizites Darstellen von Folgen
- Untersuchen von Folgen auf Monotonie, Beschränktheit und Konvergenz, intuitives Erfassen und Definieren des Begriffes Grenzwert
- Definieren der Eulerschen Zahl
- Arbeiten mit arithmetischen und geometrischen Folgen und Reihen, Erkennen des Zusammenhangs zwischen arithmetischen Folgen und linearen Funktionen sowie zwischen geometrischen Folgen und Exponentialfunktionen
- Verwenden von Folgen zur Beschreibung diskreter Prozesse in anwendungsorientierten Bereichen (insbesondere Geldwesen)
Gleichungen, Ungleichungen, Gleichungssysteme
[Bearbeiten]- Arbeiten mit einfachen Ungleichungen (Abschätzungen, Umformungen, Fallunterscheidungen)
- Lösen von linearen Gleichungssystemen mit drei Gleichungen in drei Variablen
- Kennenlernen von Näherungsverfahren zum Lösen von Gleichungen Reelle
Funktionen
[Bearbeiten]- Definieren, Darstellen und Untersuchen von Potenzfunktionen, von Exponential-und Logarithmusfunktionen sowie von Winkelfunktionen (Bogenmaß)
- Untersuchen von Eigenschaften reeller Funktionen (Monotonie, globale und lokale Extremstellen, Symmetrie, Periodizität) und von Beziehungen zwischen Funktionen (Umkehrfunktionen)
- Beschreiben von Änderungen durch Änderungsmaße (absolute und relative Änderung, Differenzenquotient)
- Anwenden von Funktionen zur Beschreibung kontinuierlicher Prozesse, Vergleichen von Modellen, Erkennen der Grenzen von Modellbildungen
- Kennenlernen von Verallgemeinerungen des Funktionsbegriffs
- Verketten von Funktionen
Analytische Geometrie des Raumes
[Bearbeiten]- Übertragen bekannter Begriffe und Methoden aus der zweidimensionalen analytischen Geometrie, Erkennen der Grenzen dieser Übertragbarkeit
- Ermitteln von Normalvektoren, Definieren des vektoriellen Produkts
- Beschreiben von Geraden und Ebenen durch Parameterdarstellungen bzw. Gleichungen
- Schneiden von Geraden und Ebenen, Untersuchen von Lagebeziehungen
- Lösen von geometrischen Aufgaben, gegebenenfalls unter Einbeziehung der Elementargeometrie und der Trigonometrie
Stochastik
[Bearbeiten]- Arbeiten mit Darstellungsformen und Kennzahlen der beschreibenden Statistik
- Kennen des Begriffes Zufallsversuch, Beschreiben von Ereignissen durch Mengen
- Kennen der Problematik des Wahrscheinlichkeitsbegriffs; Auffassen von Wahrscheinlichkeiten als relative Anteile, als relative Häufigkeiten und als subjektives Vertrauen
- Berechnen von Wahrscheinlichkeiten aus gegebenen Wahrscheinlichkeiten; Arbeiten mit der Multiplikations- und der Additionsregel; Kennen des Begriffs der bedingten Wahrscheinlichkeit
- Arbeiten mit dem Satz von Bayes
Arbeiten mit Termen
[Bearbeiten]Term Definition
[Bearbeiten]Ein Term ist ein mathematischer Ausdruck. , , , , sind alles Terme, wobei aus mehreren Teiltermen besteht.
Potenzen
[Bearbeiten]Potenz Definition
[Bearbeiten]Jeder Term der Form mn ist eine Potenz. Was unten steht (hier m) nennt man Basis, was oben rechts (hier n) Hochzahl.
Potenz Was bedeutet diese Schreibweise?
Wenn man 4+4+4 hat, kann man auch 3·4 schreiben: . Eine Multiplikation zeigt, wie oft man eine Zahl mit sich selbst addiert.
Wenn man 4·4·4 hat, dann kann man 4³ schreiben. Eine Potenzzahl (hier 4³) zeigt, wie oft (so oft, wie die Hochzahl, hier 3) man eine Zahl (die Basis, hier 4) mit sich selbst multipliziert.
Potenzen Erklärung
[Bearbeiten]Strichrechnungen unter Potenzzahlen
[Bearbeiten]Wir haben gelernt, dass eine Multiplikation uns zeigt, wie oft die gleiche Zahl innerhalb einer Summe vorkommt. Beispielsweise ist . Das bedeutet allerdings auch, dass ist, weil
Eine Potenzzahl zeigt, wie oft die gleiche Zahl innerhalb eines Produktes vorkommt. Beispielsweise: .
Was ist jetzt, wenn wir Potenzzahlen addieren (oder subtrahieren)?
Nehmen wir ein Beispiel: .
Bei 3a² und 7a² hat die Potenzzahl a² die gleiche Basis a und die gleiche Hochzahl 2. Diese Potenzen können zusammengerechnet werden:
Entsprechend können wir mit a⁴ arbeiten:
a² und a⁴ können wir hingegen nicht zusammenrechnen, da sie zwar die gleiche Basis a aber nicht die gleiche Hochzahl (2 bzw. 4) haben.
a² und b² können wir auch nicht zusammenrechnen, da sie zwar die gleiche Hochzahl 2 aber nicht die gleiche Basis (a bzw. b) haben.
Daher ist:
Warum ist es so? Wie schon erwähnt, können nur gleiche Summanden durch eine Multiplikation ersetzt werden:
Wenn wir 3⁴ und 3² anstatt 3 haben, sind die Summanden nicht gleich, da 3⁴=3·3·3·3=81 und 3²=3·3=9 ist:
Noch ein Beispiel:
Multiplikation von zwei Potenzen mit der gleichen Basis
[Bearbeiten]
Warum das so ist, ist leicht zu erklären:
Die Hochzahlen addiert man, auch wenn sie negativ sind:
Allgemein kann man daher folgern:
wobei n und m irgendwelche positive oder negative reelle Zahlen sein können. Für den Fall von natürlichen Hochzahlen können wir schreiben:
Division von zwei Potenzen mit der gleichen Basis
[Bearbeiten]
Warum das so ist, ist leicht zu erklären:
Die Hochzahlen subtrahiert man (oben minus unten), auch wenn sie negativ sind:
Da ein Bruch (fast) gleichbedeutend mit einer Division ist, kann man auch sagen, dass bei der Division von Potenzzahlen mit gleicher Basis das Ergebnis die gleiche Basis ist, mit einer Hochzahl, die die Differenz aus der Hochzahl des Dividends und der Hochzahl des Divisors ist. Allgemein kann man daher schreiben:
wobei n und m irgendwelche positive oder negative reelle Zahlen sein können.
Null als Hochzahl
[Bearbeiten]
und nach der Regel gilt auch:
Also ist gleichzeitig gleich 1 und gleich . Daher gilt:
Potenzen mit negativer Hochzahl
[Bearbeiten]
Nach der Regel gilt:
Also ist gleichzeitig und . Daher gilt:
und allgemein:
Es muss auch klar sein: x² ist nicht das Gleiche wie y² (kann ausnahmsweise sein, ist es in der Regel aber nicht!)! Wenn die Basis anders ist, kann man mit den Hochzahlen keine Strichrechnung machen, z.B.:
oder etwas Ähnliches. Man kann einfach diesen Ausdruck NICHT vereinfachen!
Potenz einer Potenzzahl
[Bearbeiten]
Warum das so ist, kann man wie im Folgenden erklären:
- Kurze Erklärung zum Schritt : . Hier haben wir die eben erklärte Multiplikationsregel benutzt: .
Die Hochzahlen multipliziert man, auch wenn sie negativ sind:
Allgemein kann man daher schreiben:
wobei n und m irgendwelche positive oder negative reelle Zahlen sein können.
Potenz eines Produktes oder eines Bruches
[Bearbeiten]Mit einem Beispiel kann auch dieser Zusammenhang schnell erklärtwerden:
und entsprechend für einen Bruch:
Es gilt also allgemein:
Weitere Beispiele:
{{#ifeq:Mathematrix: AT AHS/ Theorie/ Klasse 6|Mathematrix: AT PSA Theorie nach Thema/ Arbeiten mit Termen
|
|
Potenzen mit Bruchhochzahl
[Bearbeiten]
Versuchen wir jetzt diesen Zusammenhang zu erklären.
Im Kapitel über Kubikwurzel lernen wir, dass die Gegenrechnung einer Hochzahl die entsprechende Wurzel ist:
und allgemein:
Es gilt allgemein, dass wenn eine Rechnung und ihre Gegenrechnung verwendet werden, das Ergebnis der Anfangswert sein wird:
(Die Gegenrechnung von +6 ist −6)
(Die Gegenrechnung von ⋅5 ist ÷5)
(Die Gegenrechnung von Quadrat ist die Quadratwurzel)
und allgemein für die Gegenrechnung einer Wurzel, wie eben gezeigt:
Benutzten wir jetzt die eben gelernte Regel über Potenz einer Potenz. Wie sollen die Hochzahlen aussehen, damit das Ergebnis der Anfangswert ist?
da ist
Es soll also für die Hochzahlen und gelten:
und daher
Ersetzen wir dann durch im Ausdruck und vergleichen wir folgende zwei Ausdrücke:
Beide Ausdrücke sind gleich a und daher gleich zueinander. Damit die Ausdrücke gleich sind, muss die Basis in beiden Fällen gleich sein:
Allgemeiner gilt also:
und:
}}
Arbeiten mit Potenzen Die Rechenregel zusammengefasst
[Bearbeiten]Komplexe Beispiele mit Potenzzahlen
[Bearbeiten]|style="padding: 0.5em; margin: 0.3em"| | |style="padding: 0.5em; margin: 0.3em"| |- |style="padding: 0.5em; margin: 0.3em"| | |style="padding: 0.5em; margin: 0.3em"| |- |style="padding: 0.5em; margin: 0.3em"| | |style="padding: 0.5em; margin: 0.3em"| |- |style="padding: 0.5em; margin: 0.3em"| | |style="padding: 0.5em; margin: 0.3em"| |- |style="padding: 0.5em; margin: 0.3em"| | |style="padding: 0.5em; margin: 0.3em"| |}
In diesem Absatz erklären wir anhand von Beispielen, wie wir die Rechenregeln der Potenzzahlen anwenden können.
Wenn wir im Ausdruck eine Wurzel haben, ist es unsere erste Aufgabe, diese Wurzel als Potenzzahl zu schreiben. Die Wurzelpotenz soll als Nenner eines Bruches in der entsprechenden Hochzahl geschrieben werden (oder im Nenner eines Bruches, wenn die entsprechende Hochzahl schon ein Bruch ist):
oder auf einmal:
In diesem Ausdruck haben wir keinen Bruch oder Produkt von Potenzzahlen. Es geht um die Potenz einer Potenz (einer weiteren Potenz) und daher müssen wir nach der entsprechenden Regel die Hochzahlen einfach multiplizieren:
oder einfacher:
Jetzt wenden wir einfach die Multiplikationsregel von Zahlen an (minus mal minus ist plus) und führen diese Multiplikation aus:
Hier brauchen wir nur den zweiten und dritten Schritt der vorherigen Aufgabe durchführen. Am Ende haben wir allerdings in die Gegenrichtung gearbeitet und den Nenner im Bruch als Wurzelpotenz in einer Wurzel geschrieben.
Dieses Beispiel sieht kompliziert aus. Das sollte uns nicht aus der Fassung bringen. Die Schritten bleiben doch die gleichen:
Erst schreiben wir die Wurzel als Potenzzahl, also die Wurzelpotenz als Nenner in der entsprechenden Hochzahl:
Hier haben wir allerdings auch die Klammer in der Klammer aufgelöst (der erster Ausdruck links auf der linken Seite), indem wir die Regel der Potenz einer Potenz angewandt haben (Hochzahlen multiplizieren):
Wir haben also ein Produkt aus Potenzen mit der gleichen Basis, wir sollen daher die Regel anwenden und die Hochzahlen addieren:
und am Ende die Regel für die Potenz einer Potenz anwenden, also die Hochzahlen multiplizieren:
Dieser Ausdruck sieht noch komplizierter aus, das sollte uns aber immer noch nicht aus der Fassung bringen. Wir sollen ganz gemütlich und ruhig die Regeln anwenden. Um die Lösung klarer zu machen, bearbeiten wir im Folgenden erst den Zähler und dann den Nenner.
Wie in den vorherigen Beispielen, haben wir hier erst die Wurzel als Potenz ausgedrückt, indem wir die Wurzelpotenz in den Nenner der Hochzahl geschrieben haben. Wir haben daher die Potenz einer Potenz und wir müssen die Hochzahlen multiplizieren:
In der Hochzahl haben wir eine Multiplikation von Brüchen und diese führen wir aus (indem wir kürzen): . Es gilt daher für den Zähler:
Zähler
Im Nenner haben wir einen Bruch von Potenzzahlen mit der gleichen Basis, wir müssen daher die Hochzahl oben minus die Hochzahl unten berechnen:
Nenner
Wir schreiben also jetzt zusammen den Zähler und den Nenner in einem Bruch, wie es dazu gehört. Wir haben dann einen Bruch von Potenzen mit der gleichen Basis, wir müssen also die Hochzahl oben minus die Hochzahl unten berechnen:
Umformen
[Bearbeiten]Umformen Grundwissen Gegenrechnungen
[Bearbeiten]Wie kann man diese Aufgabe in der mathematischen Sprache schreiben? Für das Gefragte (wie viele Äpfel) wird in Mathematik irgendein Symbol benutzt, als Stellvertreter für die noch unbekannte Zahl. In der Regel wird als Symbol ein Buchstabe verwendet und nicht allzu selten x.
Mit x sind also die Äpfel gemeint, die Vassili am Anfang hatte. Wir wissen noch nicht, wie viele sie waren, daher schreiben wir ein Symbol dafür, ein Buchstabe, also x.
Wenn Vassili drei Äpfel der Lisa gibt, dann hat er weniger Äpfel als zuvor, es geht um eine Subtraktion. Von den x Äpfeln am Anfang sind drei Äpfel zu subtrahieren. Dass dann noch fünf Äpfel bleiben, wird durch den folgenden mathematischen Ausdruck geschrieben:
x−3=5
Man kann für x verschiedene Zahlen ausprobieren, z.B. 2, 3, 7, 8 oder 9. So kann man schon feststellen, dass nur acht minus drei gleich fünf ist. „x“ muss also 8 sein, damit die Rechnung stimmt. Vassili hatte also 8 Äpfel am Anfang.
Die ganze Zeit ausprobieren ist allerdings nicht gerade geschickt. Besonders bei größeren Zahlen wird es sogar ziemlich schwer. Es gibt in der Mathematik einen geschickteren Weg, die Aufgabe zu lösen. Man benutzt die sogenannte Gegenrechnung. Bei allen Gleichungen gibt es zwei Teile, ein Teil links vom „=“ und ein Teil rechts vom „=“. Bringt man einen Term von einer Seite zur anderen, dann muss man die Gegenrechnung benutzen.
Die Gegenrechnung der Subtraktion ist die Addition und umgekehrt.
Wenn x−3=5 ist, dann kann man die 3 auf die andere Seite vom „=“ bringen und statt minus die Gegenrechnung (plus) benutzen:
x=5+3 also x=8
Bei der Aufgabe c+4452 = 341 bringt man 4452 auf die andere Seite und benutzt die Gegenrechnung von minus. Die Lösung ist daher:
c+4452 = 341 → c= 341−4452 → c = −4111
Die Gegenrechnung der Multiplikation ist die Division und umgekehrt.
3f=114
Zwischen 3 und f steht nichts.
Wenn in Mathematik zwischen zwei Ausdrucken (zum Beispiel einer Zahl und einem Symbol, einer Klammer und einer Zahl und so weiter) nichts steht, dann ist Multiplikation gemeint (einzige Ausnahme: die gemischten Zahlen).
Da zwischen 3 und f nichts steht, ist mal gemeint. f ist ein Symbol und steht für irgendeine Zahl. Die Aufgabe ist herauszufinden, wie viel f sein soll, damit die Rechnung stimmt. In diesem fall soll 3 auf die andere Seite gebracht und die Gegenrechnung von mal (also durch) benutzt werden:
3f=114 (nichts zwischen 3 und f, also mal gemeint):
3·f=114 (3 auf die andere Seite von „=“ bringen und Gegenrechnung, also hier Division, benutzen)
f=114:3 und daher
f = 38.
Man kann auch einen Bruch statt einer Division benutzen:
Entsprechend ist die Gegenrechnung der Division die Multiplikation:
also k:5 = 11 und daher k = 11 · 5
k = 55
Was ist aber die Gegenrechnung vom Quadrat?
Die Gegenrechnung von Quadrat ist die sogenannte „Wurzel“:
z² = 81 also z = und daher z=9
9 ist die Zahl, deren Quadrat 81 ist, daher ist die Wurzel von 81 gleich 9. Wenn wir in der Gleichung z² = 81 z durch 9 ersetzen, dann stimmt die Gleichung tatsächlich: 9² = 81
Selbstverständlich ist die Gegenrechnung der Wurzel das Quadrat.
= 13 also m = 13² und daher m=169
Obwohl es für das Niveau dieses Buches nicht absolut notwendig ist, können wir doch auf eine Tatsache aufmerksam machen: Die Gleichung z² = 81 hat noch eine Lösung, wenn z gleich −9 ist. Freilich stimmt die Gleichung (−9)² = 81. (−9)² bedeutet (−9)·(−9). Minus mal minus ist plus und daher:
(−9)² =(−9)·(−9)= + 9·9 = 81 also
(−9)² = 81
Umformen einfache Kombinationen
[Bearbeiten]5x − 7 = 3x + 11
Wir wählen die linke Seite als die Seite, in der die Teilterme (Summanden) mit der gesuchten Variable (x) sein werden. Wir haben zwei solchen Teilterme, 5x und 3x. 5x ist schon auf der linken Seite, wir müssen also noch 3x auf die andere Seite bringen. Vor 3x steht das Symbol „=“. Ist 3x jetzt positiv oder negativ? Wenn man b=4 schreibt, ist +4 oder −4 gemeint? Die Antwort ist +4. Daher auch hier, wenn nach dem Symbol „=“ kein plus oder minus steht, dann ist ein plus gemeint. Wenn man 5x − 7 = 3x + 11 schreibt, ist es das Gleiche wie + 5x − 7 = + 3x + 11. Wenn man den Term 3x auf die andere Seite bringt, muss man die Gegenrechnung benutzen, also Subtraktion (minus).
5x − 7 − 3x = 11
7 hat kein x neben sich, sie muss auch auf die rechte Seite gebracht werden, wieder mit der Gegenrechnung, also diesmal mit Addition (plus):
5x − 3x = 11 + 7
Das Ganze kann man in einem Schritt machen:
5x − 7 = 3x + 11
5x − 3x = 11 +7
2x = 18
(Hier haben wir einfach die Rechnungen gemacht: 5x-3x ist 2x und 11+7 ist 18).
Es bleibt noch, 2 auf die andere Seite zu bringen. Zwischen 2 und x steht nichts, daher ist eine Multiplikation gemeint. Die Gegenrechnung ist eine Division:
x = und daher x = 9
Man kann das ganze auch so erklären:
5x − 7 = 3x + 11
Man will, dass auf der rechten Seite 3x verschwindet. Das kann passieren, indem man 3x subtrahiert. Ein Gleichung aber ist wie eine Waage. Das Gleichungssymbol (=) teilt die Gleichung in zwei Teilen, links und rechts. Was auf der einen Seite passiert, muss auch auf der anderen stattfinden, damit das Gleichgewicht erhalten bleibt. Man benutzt folgende Schreibweise:
5x − 7 = 3x + 11 | −3x (Man schreibt am Rand, was auf beiden Seiten zu tun ist)
5x − 7 − 3x = 3x + 11 − 3x
2x − 7 = 11
Man will aber auf der linken Seite nur Teilterme (Summanden) mit x haben, deshalb muss die -7 dort verschwinden. Das geht, indem man 7 auf beiden Seiten addiert.
2x − 7 = 11 | +7
2x − 7 + 7 = 11 + 7
2x = 18
Jetzt bleibt nur die Division:
2x = 18 | :2
x = 18 : 2 (Man kann auch schreiben)
x = 9
Sofern mehrere Teilrechnungen oder Zwischenschritte im Kopf durchgeführt werden, wird zusammengefasst und kürzer notiert:
5x − 7 = 3x + 11 | −3x+7
2x = 18 | :2
x =
x = 9
Wenn die Variable innerhalb einer Klammer steht, ist der erste Schritt, die Klammer aufzulösen, sonst geht man wie vorher vor:
4y + 3 (7 − 5y) = 11 − 6y
4y + 21 − 15y = 11 − 6y | −21
4y − 15y = 11 − 6y −21 | +6y
4y − 15y + 6y = 11 − 21
− 5y = −10 | : (−5)
y=2
Wenn man y durch 2 in der Anfangsgleichung 4y + 3 (7 − 5y) = 11 − 6y ersetzt, stellt man fest, dass die Gleichung tatsächlich stimmt.
4y + 3 (7 − 5y) = 11 − 6y
4·2 + 3 (7 − 5·2) = 11 − 6·2
8 + 3 ·(−3) = 11 − 12
8 − 9 = − 1
In der Tat ist 2 der einziger Wert von y, für den die Gleichung wirklich stimmt. Die LeserInnen können andere Werte ausprobieren und feststellen, dass die Gleichung dann nicht mehr stimmt.
Kubikwurzel und weitere Wurzeln
[Bearbeiten]Das Volumen eines Würfels ist 530cm³. Wie viel ist seine Fläche?
Diese Aufgabe ist ähnlich zur Aufgabe im letzten Unterkapitel über Umformen. Die Formeln für den Würfel sind:
.
Man muss erst die Kante des Würfels berechnen, um seine Fläche berechnen zu können. Man kann dafür die Formel fürs Volumen benutzen, , da der Wert des Volumens auch gegeben ist. Welche ist aber die Gegenrechnung von „hoch 3“? Diese Gegenrechnung nennt man Kubikwurzel oder noch besser dritte Wurzel:
Dann kann man leicht die Oberfläche berechnen:
Entsprechend zur Wurzel (die besser Quadratwurzel genannt wird), ist die dritte Wurzel (auch Kubikwurzel genannt) nur dann eine genaue Zahl, wenn die Zahl unter der Wurzel eine sogenannte Kubikzahl ist, wie z.B.:
1(=1³), 8(=2³), 27(=3³), 64(=4³), 125(=5³), 216(=6³), 343(=7³), 512(=8³), 729(=9³), 1000(=10³), 0,008(=0,1³), 9,261(=2,1³)...
Daher gilt:
Die Kubikwurzel von jeder anderen Zahl (die keine Kubikzahl ist) ist eine irrationale Zahl.
Diese Idee der Gegenrechnung kann man auf alle Hochzahlen erweitern:
oder sogar (!):
Zur Vereinfachung der Symbole benutzt man keine Zahl am Anfang des Wurzelzeichens, nur wenn es um die Quadratwurzel geht:
ist gleichbedeutend wie
Herzlichen Dank an alle, deren Bilder ich in diesem Kapitel benutzt habe!
Komplexe Umformungen
[Bearbeiten]
Wenn hier m gefragt ist, ist es völlig irrelevant, wie kompliziert der Rest aussieht. In unserem Kopf sollen wir folgendes Bild haben:
Dieses Bild wird noch einfacher, wenn wir in unserem Kopf A1 und A5 als ein Box denken und entsprechend A2 und A3. Das geht, weil die ersten zwei Summanden sind, die auf die andere Seite gehen sollen, und die letzten zwei ein Produkt sind:
Wir brauchen die Fassung nicht verlieren. Wir sollen einfach die Strukturen erkennen. Dann ist es eher einfach. Es gibt allerdings keine Regel der Form "Klammer vor Punkt vor Strich". Wichtig ist zu erkennen, was bei einer "Verschachtelung" "innen" oder was "außen" ist. Beispiel:
und
Im ersten Fall ist der Bruch innerhalb der Wurzel, also müssen wir erst die Gegenrechnung für die Wurzel und dann für den Bruch benutzen:
Im zweiten Fall ist die Wurzel innerhalb des Bruches, also müssen wir erst die Gegenrechnung für den Bruch und dann für die Wurzel benutzen:
Beim Umformen ist unsere erste Aufgabe den Term (oder die Terme) mit der gesuchten Variable zu isolieren (allein auf einer Seite lassen).
In den folgenden Gleichungen ist immer m die gefragte Variable. In der ersten Spalte sieht man eine Gleichung. Für jede Gleichung haben wir in der zweiten Spalte den Term (bzw. die Terme) mit der gesuchten Variable in einem Rahmen und die gesuchte Variable mit Rot hervorgehoben. In der letzten Spalte sieht man dann diesen Term (bzw. diese Terme) allein auf einer Seite, während alle andere Terme sich auf der anderen Seite befinden.
|
|
| ||||||||
|
|
| ||||||||
|
|
| ||||||||
|
|
| ||||||||
|
|
|
Man sieht in diesen Beispielen, dass der Term mit der gesuchten Variable von den anderen Summanden isoliert wird. Wenn man diesen Schritt schon gemacht hat, sind die weiteren Schritten viel einfacher. Im Folgenden werden wir immer mit der Gleichung der jeweiligen letzten Spalte anfangen.
- Im ersten Fall haben wir die gesuchte Variable im Nenner. Man multipliziert jede Seite als Ganzes mit der gesuchten Variable.
Als Ganzes bedeutet also hier die linke Summe in Klammer zu setzen. Man dividiert dann durch die Klammer und dann haben wir schon das Ergebnis!
oder in einem Bruch:
- Im zweiten Fall
muss man zuerst durch a dividieren und dann Wurzel ziehen. Das Ergebnis ist dann:
oder in einem Bruch geschrieben:
- Im dritten Fall steht die gesuchte Variable in einer Summe im Nenner.
Es gibt verschiedenen Möglichkeiten das Minus weg zu kriegen (z.B. mit -1 multiplizieren). Wir ziehen aber hier vor, das Minus in den Nenner zu bringen, was dazu führt, dass sich die Vorzeichen ändern (also anstatt haben wir ). Wir arbeiten dann wie im ersten Fall aber mit dem Nenner als Ganzes:
und das Ergebnis ist:
- Im viertel Fall befindet sich die gesuchte Variable in mehreren Termen:
Man muss also die gesuchte Variable zuerst herausheben:
und dann durch die dadurch entstandenen Klammer dividieren. Das Endergebnis (wenn man auch den Doppelbruch vereinfacht) ist:
- Im fünften Fall befindet sich die gesuchte Variable innerhalb einer Wurzel im Nenner.
Man soll zuerst den Nenner "oben" bringen, also mit dem Nenner multiplizieren
Als zweites soll die Wurzel allein auf einer Seite bleiben:
Dann soll man die Wurzel "auflösen", in dem man beide Seiten quadriert:
Jetzt steht die gefragte Variable m (quadriert) in einer Summe rechts. Man soll sie erst "isolieren":
und dann einfach Wurzel ziehen:
Exponential und Logarithmus Funktion
[Bearbeiten]Exponentialfunktion und Logarithmus
[Bearbeiten]Zusammenhang Exponentialfunktion und Logarithmus
[Bearbeiten]Wenn wir Voraussagen über die Bevölkerung in einem Staat machen wollen, benutzen wir eine sogenannte Exponentialfunktion. Nehmen wir beispielsweise an, dass die Bevölkerung in einem Staat mit 30 Millionen EinwohnerInnen um 2% jedes Jahr wächst. Das bedeutet, dass jedes Jahr die Bevölkerung 102% der Bevölkerung des vorherigen Jahres sein wird, also das 1,02-fache. Um die Bevölkerung nach Jahren zu berechnen, müssen wir daher die Bevölkerung am Anfang mit 1,02 mal multiplizieren:
Im konkreten Beispiel wäre das dann nach 20 Jahren:
(Millionen Menschen)
In dieser Funktion wird die Bevölkerung (in Millionen Personen) in Bezug auf die Zeit (in Jahren) ausgedrückt. Die Zeit (hier mit dem Symbol x dargestellt) ist die unabhängige Variable.
Was ist aber, wenn wir die Frage umkehren wollen? Wie können wir berechnen, nach wie vielen Jahren die Bevölkerung mit diesem Wachstum 100 Millionen sein wird? Wir sollen in diesem Fall eine Gegenrechnung benutzen. Die Gegenrechnung von minus ist plus, von mal durch und von hoch die entsprechende Wurzel. Die zwei ersten Paare können wir als Möglichkeit hier schon ausschließen. Kommt die Wurzel als Möglichkeit vor? Für Wurzel und Potenzzahl gilt:
Probieren wir das in unserem Beispiel. Wir wollen berechnen, nach wie vielen Jahren () die Bevölkerung () 100 Millionen sein wird. Hier ist also nicht die Zeit x angegeben, sondern die Bevölkerung (=100 Millionen). Die Bevölkerung am Anfang bleibt immer noch 30 Millionen:
Was können wir jetzt tun? Können wir x berechnen? Die Antwort ist nein. x steht als Wurzelpotenz. Wir können es nicht berechnen. Wir brauchen eine neue Gegenrechnung. Was ist hier der Unterschied zu den Potenzfunktion? Die unabhängige Variable ist nicht mehr die Basis, wie bei der Potenzfunktion . Wenn die unabhängige Variable als Hochzahl in der Funktion vorkommt, dann ist die Gegenrechnung der entsprechende sogenannte Logarithmus. In unserem Beispiel:
(Jahren)
Das bedeutet: Mit diesem Wachstum (2%) wird die Bevölkerung nach fast 61 Jahren 100 Millionen sein. Man sagt: „x ist der Logarithmus von zur Basis 1,02“. Der Logarithmus zu einer Basis b ist daher die Gegenrechnung der Potenzzahl mit gleicher Basis b und Hochzahl die Variable.
Für zwei Zahlen als Basis eines Logarithmus gibt es in der mathematischen Gesellschaft entsprechende Schreibweisekonventionen.
- Wenn die Basis 10 ist schreiben wir einfach ohne Basis. Also, wenn einfach da steht, dann ist als Basis 10 gemeint.
Dieser wird Zehner- oder Dekadischer Logarithmus genannt. Bei Taschenrechnern wird dafür nicht das Symbol oder sondern einfach ohne Basis benutzt. Das Symbol bedeutet also bei Taschenrechnern den Zehnerlogarithmus. - Es gibt dazu eine ganz besondere Zahl, die sogenannte eulersche Zahl . gehört zu den berühmtesten mathematischen Konstanten, wie die Kreiszahl π. Die Kreiszahl π wird als das Verhältnis (der Bruch) des Umfangs eines Kreises zu seinem Durchmesser. π ist ungefähr (aber nicht genau...) 3,14… . Die Definition für die Zahl e ist nicht so leicht und wird an dieser Stelle nicht erklärt. Es reicht zu wissen, dass e eine besondere Zahl und ungefähr gleich 2,718… ist. Wenn jetzt e die Basis einer Potenz ist, dann schreiben wir für die Gegenrechnung anstatt :
Dieser wird natürliche (viel seltener "napiersche") Logarithmus genannt.
Lambda
[Bearbeiten]
Arbeiten mit Logarithmen
[Bearbeiten]Rechenregeln zwischen Logarithmen
[Bearbeiten]|
|
Hier ein paar Beispiele der Anwendung dieser Regeln:
- Zerlegen Sie folgende Ausdrücke unter Verwendung der Logarithmusregeln in den möglichst einfachsten Logarithmanden.
Da der ganze Numerus mit einer Hochzahl versehen ist, können wir die zweite Regel benutzen:
Für das, was noch in Klammern bleibt, können wir die vierte und die fünfte Regel benutzen:
Im ersten und im dritten Summand haben wir wieder eine Hochzahl, wir können wieder die zweite Regel benutzen:
Wenn der Numerus eine Summe ist , können wir nichts machen, allerdings ist nach der ersten Regel , daher ist das Ergebnis insgesamt:
.
Benutzen wir die vierte und die fünfte Regel um die Produkte bzw. den Bruch zu zerlegen:
Der Numerus des ersten Summanden ist eine Potenz von 5: . Die Wurzel im Numerus des zweiten und des letzten Summanden kann man als Hochzahl schreiben: und . Daher:
Unter Anwendung der zweiten und der ersten Regel bekommen wir dann:
Mit Anwendung der vierten und der zweiten Regel und Zusammenrechnen bekommen wir schließlich:
- Fassen Sie folgenden Ausdruck unter Verwendung der Logarithmusregeln in einen Logarithmanden.
Nach der ersten Regel ist und nach der zweiten , und . Mit Anwendung der vierten und fünften Regel bekommen wir schließlich;
Beweise der Rechenregeln zwischen Logarithmen
[Bearbeiten]Wenn wir bei einem mathematischen Ausdruck eine Rechnung und ihre Gegenrechnung oder eine Funktion und ihre Umkehrfunktion anwenden, bleibt der Ausdruck unverändert. Hier sind ein paar Beispiele[1]:
Der Logarithmus ist die Gegenfunktion der unabhängigen Variable als "Hochzahl", genauer gesagt, der Exponentialfunktion:
(hier für den natürlichen Logarithmus)
Wenn wir also gleichzeitig Funktion und Umkehrfunktion anwenden, dann bleibt der Ausdruck unverändert. Ersetzen wir also in den letzten Ausdrucken durch bzw. durch :
also
Setzten wir in der letzten Gleichung :
also oder
Allgemeiner bedeutet das:
Der Logarithmus seiner Basis ist 1:
Gehen wir zurück zur vorherigen Formel und Benutzen wir letzteres Ergebnis:
Der Logarithmus einer Potenzzahl ist die Hochzahl dieser Potenzzahl mal den Logarithmus ihrer Basis:
Beweis.
Laut Definition des Logarithmus:
(b für Basis, p für Potenzzahl, h für Hochzahl)
Da ist, können wir in der Gleichung dadurch ersetzten:
Mit anderen Symbolen:
Es gilt:
Mit Hilfe der Definition des Logarithmus können wir auch leicht zeigen, dass der Logarithmus von Null gleich 1 ist (für jede Basis):
Der Logarithmus hat irgendwas mit den Hochzahlen zu tun. Wenn wir zwei Potenzzahlen mit der gleichen Basis multiplizieren, dann ist das Ergebnis eine neue Potenzzahl mit der gleichen Basis und Hochzahl die Summer der Hochzahlen: . Mit dieser Tatsache hat die nächste Regel für Logarithmen zu tun:
Der Logarithmus eines Produkts ist die Summe der Logarithmen der Faktoren:
Beweis. Es gilt:
Entsprechend gilt die Regel für die Division:
Der Logarithmus eines Quotients ist die Differenz der Logarithmen des Zählers und des Nenners:
Beweis. Es gilt:
Für eine Basisänderung des Logarithmus gilt:
Beweis: Es gilt:
- ↑ Es gibt immer wieder Voraussetzungen für diese Regeln, die mit den Definitionsmengen zu tun haben, wir werden sie aber hier nicht erwähnen, damit die Sache nicht zu kompliziert wird.
Mathematische Folgen
[Bearbeiten]Eine Zahlenfolgelegende und die geometrische Summenformel
[Bearbeiten]Nach einer alten Legende schuf in Indien ein Brahmane (etwas wie Priester) das Schachspiel, um die Aufmerksamkeit seines grausamen Herrschers abzulenken. Der Herrscher war so begeistert, dass er dem Brahmanen belohnen wollte. Der Brahmane fragte dann als Belohnung die folgende Summe von Weizenkörnern. Auf das erste Feld des Schachbretts sollte ein Korn sein, am zweiten sollten doppelt so viele Körner sein usw. bis zum letzten Feld. Der Herrscher kannte keine Exponentialfunktionen und hat gedacht, dass diese Belohnung nicht so hoch wäre. Bald hat sich allerdings herausgestellt,dass er sich enorm geirrt hatte.
Versuchen wir zu berechnen, wie viele Körner das wären. Jedes mal muss mit zwei multipliziert werden. Dadurch bekommen wir die Zahlen 1, 2, 4, 8, 16, 32, 64, 128... Mit 128 sind wir noch beim 8. Feld. Wie wird die Zahl am 64. Feld aussehen?
Dafür müssen wir eine andere Darstellung dieser Zahlenreihe benutzen. Das erste Feld hat Korn, das zweite , das dritte , das vierte , das fünfte usw.. Es wird also klar, dass die Hochzahl von 2 jedes mal um 1 weniger als die Anzahl des Feldes ist. Das Schachbrett hat 64 Felder, daher werden am letzten Feld , also 9 Trillionen Körner sein. Gefragt ist allerdings die Summe. Es gibt einen Weg diese Summe mit einer Formel zu berechnen. Um diese Formel zu finden, benutzen wir den allgemeinen Fall. Wir fangen mit einem Wert w (hier 1) an und jedes mal wird das vorherige Ergebnis mit der gleichen Zahl a multipliziert. Das n-te Glied diese Zahlenfolge wird dann . Bei der Summe der Folgeglieder kann w herausgehoben werden: . Wir wollen die Summe in Klammer berechnen. Fangen wir mit der einfachen Tatsache an, dass diese Summe gleich sich selbst sein wird:
Multiplizieren wir jetzt beide Seiten mit a:
Multiplizieren wir jetzt die rechte Seite der Gleichung aus. Dadurch wird die Hochzahl bei jedem Summand um eins mehr:

Subtrahieren wir jetzt von beiden Seiten die Zahlenfolge vom Anfang :
Auf der linke Seite können wir die zweite Klammer mit 1 multiplizieren, auf der rechten die Klammer ausmultiplizieren, dadurch werden alle plus zu minus:
Auf der linken Seite können wir jetzt die Klammer herausheben und auf der rechten die Subtraktionen durchführen, wodurch alle Potenzen mit zwei Ausnahmen verschwinden:
Umformen (durch ):
Letzteres Ergebnis ist die Summenformel einer sogenannten geometrischen Folge (geometrische Summenformel). Etwas abstrakter schreibt man in Mathematik:
In der antiken Legende ist a gleich 2, die Summe der ganzen Körner ist daher:
Körner!
Diese Menge entspricht mehr als das 1000-fache der Jahresproduktion heutzutage. Was sollte der König machen? Ein Berater von ihm, hat ihm die Lösung gegeben. Er sollte die Körner eins zu eins zahlen lassen ![]() .
.
Folgen
[Bearbeiten]Definition
Einfache Definition: Eine Folge in der Mathematik ist eine (endliche oder unendliche) Reihenfolge von Objekten, die man aufzählen und möglicherweise auch einordnen kann.Zwei formelle Definitionen von Folgen sind:
Als Folge oder Sequenz wird in der Mathematik eine Auflistung von endlich oder unendlich vielen fortlaufend nummerierten Objekten (beispielsweise Zahlen) bezeichnet.[1]
Eine Folge ist eine eindeutige Zuordnung zwischen den natürlichen Zahlen und den reellen Zahlen :
Nehmen wir jetzt als Beispiel eine Anzahl von Farben: {Rot, Blau, Grün, Blau, Schwarz}. Das ist schon eine Folge, in diesem Fall eine endliche. Könnte man eine unendliche Folge mit den Farben machen? Das ist eher eine physikalische als eine mathematische Frage. Da die Wahrnehmungszellen im Auge vermutlich stufenweise funktionieren (was von Quantenphysik bestimmt wird), wird wahrscheinlich die Antwort zu dieser Frage eher so sein: "Man kann wirklich eine riesige Zahl von Farben definieren, sie wird aber nicht unendlich sein". Das ist nicht der Fall mit Zahlen. Da kann man immer eine unendliche Folge aufbauen. Nehmen wir als Beispiel die Brüche von Fünf.
- Wir können eine endliche Folge definieren:
Die erste 8 Brüche von 5 mit einer positive ganze Zahl als Zähler: . - Wir können auch eine unendliche Folge definieren:
Alle Brüche von 5 mit einer positive ganze Zahl als Zähler: . - Wir können allerdings keine Folge definieren, wenn wir in unsere Definition alle Brüche von 5 benutzen. Das würde dann bedeuten, dass wir alle reelle Zahlen als Zähler benutzen sollen. Für die reellen Zahlen gibt es einen Beweis, dass es nicht möglich ist, sie aufzuzählen. Allein sogar die reellen Zahlen zwischen 0 und 1 lassen sich nicht aufzählen!
In diesen Beispielen können wir die Glieder der Folge auch einordnen. Das erste Glied der Folge mit den 5 Farben ist Rot, das zweite Blau usw.. Diese Einordnung ist allerdings willkürlich. Bei der Folge mit den Brüchen kann die Einordnung sowohl willkürlich als auch nach einer Regel sein:
- willkürlich: .
- nach einer Regel (vom kleinsten zum größten): .
Die arithmetische Folge
[Bearbeiten]Eine arithmetische Folge ist eine mathematische Folge, die eingeordnet ist und in der zwei nacheinander folgenden Glieder immer die gleiche Differenz aufweisen. Nehmen wir die erste 8 Brüche von 5 mit einer positive ganze Zahl als Zähler:
Die Folge ist eingeordnet und die Differenz zwei einander folgenden Glieder ist immer . Die gleiche Folge können wir auch so schreiben:
Eine andere arithmetische Folge kann beispielsweise mit 4,1 anfangen, die Differenz 3,3 aufweisen und unendlich sein:
Die gleiche Folge können wir auch so schreiben:
Wie kann man diese Folgen ohne Auflistung ihrer Elemente definieren? Es gibt dafür zumindest zwei Wege:
- Jedes Glied als Funktion angeben:
wobei d die Differenz ist. Im Fall einer endlichen Folge muss man auch die Anzahl der Glieder angeben: - Das erste Glied und jedes folgende Glied mit einer sogenannten rekursiven Formel angeben:
wobei d die Differenz ist. Im Fall einer endlichen Folge muss man auch die Anzahl der Glieder angeben:
Für die Folge mit den 8 Brüchen ist in diesem Sinne die Definition mit einer Formel:
Für die Folge mit 3,3 als Anfangsglied ist in diesem Sinne die Definition mit einer rekursiven Formel:
Die geometrische Folge
[Bearbeiten]Eine geometrische Folge ist eine mathematische Folge, die eingeordnet ist und in der zwei nacheinander folgenden Glieder immer den gleichen Quotient aufweisen. Nehmen wir die erste 7 Potenzen von 3 mit einer positive ganze Zahl als Hochzahl:
Die Folge ist eingeordnet und der Quotient zwei einander folgenden Glieder ist immer 3. Die gleiche Folge können wir auch so schreiben:
Eine andere geometrische Folge kann beispielsweise mit 4 anfangen, den Quotient 1,5 aufweisen und unendlich sein:
Die gleiche Folge können wir auch so schreiben:
Wie kann man diese Folgen ohne Auflistung ihrer Elemente definieren? Es gibt dafür zumindest zwei Wege:
- Jedes Glied als Funktion angeben:
wobei d die Differenz ist. Im Fall einer endlichen Folge muss man auch die Anzahl der Glieder angeben: - Das erste Glied und jedes folgende Glied mit einer sogenannten rekursiven Formel angeben:
wobei d die Differenz ist. Im Fall einer endlichen Folge muss man auch die Anzahl der Glieder angeben:
Für die Folge mit Quotient 3 ist in diesem Sinne die Definition mit einer Formel:
Für die Folge mit Quotient 1,5 ist in diesem Sinne die Definition mit einer rekursiven Formel:
Die Fibonacci Folge und der goldene Schnitt
[Bearbeiten]
Die Fibonacci Folge ist eine berühmte mathematische Zahlenfolge, die sich leicht(er) durch eine rekursive Formel definieren lässt. Das nächste Glied wird als die Summe der zwei vorherigen Glieder definiert. Die zwei ersten Glieder sind entweder 0 und 1 oder 1 und 1:
Die Definition durch eine rekursive Formel lautet daher (wenn wir mit 1 und nicht mit 0 anfangen):
Das dritte Glied ist daher , das vierte , das fünfte usw..
Die Folge wurde nach einem berühmten Mathematiker des 11.-12. Jahrhunderts genannt, die Folge war allerdings schon seit langem bekannt. Fibonacci hat die Formel benutzt, um Wachstumsprozesse bei Kaninchen zu beschreiben, dass diese Wachstumsprozesse und andere Vorgänge in der Natur diesem Muster folgen war allerdings auch schon bekannt.
Eine interessante Eigenschaft der Folge ist, dass der Quotient zwei nacheinander folgenden Glieder der Folge immer näher zum sogenannten goldenen Schnitt sind. Der goldene Schnitt ist eine Zahl. Wenn man eine Strecke in zwei Teilstrecken so teilt, dass der Quotient der Länge der ganzen Strecke zum größten Teil soviel ist, wie der Quotient des größten Teils zum kleinsten, dann ist dieser Quotient der goldene Schnitt. Seine Wert ist:

Man kann also beweisen:
Das ist das gleiche, wie der unendliche Kettenbruch:
Fibonacci Zahlen werden oft in Kryptographie benutzt. Allerdings kommen in einer großen Anzahl von Phänomenen vor:
- In der Natur:
Die Blätter (Phyllotaxis) oder Fruchtstände vieler Pflanzen sind in Spiralen angeordnet, wobei die Anzahl dieser Spiralen den Fibonacci-Zahlen entsprechen.
Die Fibonacci-Folge beschreibt die Ahnenmenge einer männlichen (n = 1) Honigbiene (Apis mellifera) usw.. - In Mathematik:
Die Summe in bestimmte Diagonalen im Pascalschen Dreieck sind Fibonacci Folgen usw..
Die eulersche und die Kreiszahl als Folgen
[Bearbeiten]Die eulersche Zahl ist die Basis der natürlichen Logarithmen:

Die Logarithmusfunktion ist das Integral der Kehrwertfunktion :
Dadurch können wir die eulersche Zahl definieren:
Also die Fläche zwischen der Kurve und der x-Achse von 1 bis ist genau dann gleich 1, wenn z gleich ist.
Für die eulersche Zahl gibt es allerdings noch einige andere Definitionen. Hier ist nur eine begrenzte Anzahl davon:
- Sie ist der Grenzwert der Folge .
- Sie ist so viel wie die unendliche Folgesumme (Reihe)
. - Sie lässt sich durch folgende unendliche Kettenbruchentwicklung berechnen
Die Kreiszahl lässt sich als der Quotient des Umfangs eines Kreises durch seinen Durchmesser definieren. Die Formeln für die Berechnung der Kreiszahl sind i. d. R. kompliziert. Hier ist nur eine begrenzte Anzahl der einfachsten davon:
- Sie ist der Grenzwert der folgenden Produktfolge:
- Ein viertel der Kreiszahl ist der Grenzwert der folgenden Folgesumme (Reihe):
- Sie lässt sich durch das folgende unendliche Produkt berechnen:
- Sie lässt sich durch folgende unendliche Kettenbruchentwicklung berechnen:
Lineare Gleichungssysteme mehrerer Variablen
[Bearbeiten]Das gaußsche Eliminationsverfahren
[Bearbeiten]Als linear wird eine Gleichung bezeichnet, wenn alle in ihr vorkommenden Variablen nur mit der Hochzahl 1 vorkommen. Beispielsweise ist eine lineare Gleichung, da alle Variablen (x, d und m) ohne Hochzahl, also mit der Hochzahl 1 vorkommen. Die Gleichung ist linear, was die Variablen x und m betrifft, nicht aber was die Variablen d und c betrifft. Die Gleichung ist nicht linear.
Ein lineares Gleichungssystem besteht aus mehreren linearen Gleichungen mit mehreren Variablen. Eine, eindeutige Lösung für so ein System, gibt es, wenn es möglich ist, jede Variable durch jeweils eins Zahl zu ersetzen, so dass alle Gleichungen stimmen. In der Regel wird es in den Aufgaben so viele Gleichungen wie Variablen geben, das muss aber nicht sein. Betrachten wir zunächst einmal ein Beispiel mit 2 Variablen und 2 Gleichungen:
Es gibt zumindest 4 Wege, dieses System zu lösen: graphisch (was ohne Computer ungenau ist) und mit dem Gleichsetzungs-, Einsetzungs- und Additionsverfahren.
- Graphisch
Beide lineare Funktionen mit Hilfe von jeweils 2 Punkten abzeichnen:
|
Der Schnittpunkt L:(2|6) der beiden Geraden ist die Lösung
- Mit dem Gleichsetzungsverfahren
- Mit dem Einsetzungsverfahren
- Mit dem Additionsverfahren
Wenn am Anfang neben der zweiten Gleichung geschrieben wird, ist damit gemeint, das von jeder Seite in der zweiten Gleichung 3 mal die entsprechende Seite der ersten Gleichung subtrahiert wird. Dadurch wird in der zweiten Gleichung die x Variable wegfallen ().
Das Gleichsetzungsverfahren benutzen wir oft, wenn wir die Schnittpunkte zweier Funktionen finden wollen (also die Lösung des entsprechenden oft nicht linearen Gleichungssystems). Des Ersetzungsverfahren wird oft in Physik und anderen Wissenschaften benutzt, wenn mehrere Formel nacheinander benutzt werden müssen. Für die Lösung allerdings von linearen Gleichungssystemen mit 3 oder mehreren Variablen wird fast ausschließlich ein das gaußsche Verfahren benutzt, das dem Additionsverfahren sehr ähnelt. Nehmen wir folgendes Beispiel eines LGS mit 3 Variablen und 3 Gleichungen:
Es ist übersichtlicher, nur die Koeffizienten der Variablen a, b und c in einer sogenannten "Matrix" zu schreiben. Jede Spalte der Matrix entspricht einer Variable: in der ersten Spalte sind die Koeffizienten von a, in der zweiten von b und in der dritten von c. Separat in einer Spalte rechts werden die rechten Seiten der Gleichungen geschrieben (die keine Koeffizienten sind).
Die Matrix kann mit elektronischen Hilfsmitteln
oder mit dem gaußschen Verfahren gelöst werden.
Ziel des Verfahrens ist, durch Addition und Subtraktion
von Vielfachen der verschiedenen Zeilen folgende
("diagonale") Form der Matrix zu erreichen:
Die erste Spalte ist für die Variable a, die zweite für
die Variable b und die dritte für die Variable c. Als
lineares Gleichungssystem wird daher die letzte
Matrize wie im Folgenden dargestellt:
was gleichbedeutend ist, wie:
Das bedeutet wiederum, dass wir die Lösung
des LGS in der diagonalen Matrize sofort ablesen können.
Schauen wir den ganzen Prozess mit Hilfe des Beispiels. Bei
jedem Schritt soll noch eine Koeffizient null werden, bis wir
die Diagonale Form erreichen.
|
|
|
|
|
|
|
|
|
|
Wir haben vereinbart, dass die dritte Spalte die c-Koeffizienten beinhaltet. Die erste Zeile in der letzten Matrize zeigt uns dann:
Entsprechend für die zweite und dritte Spalte:
Somit haben wir eine eindeutige Lösung für dieses LGS gefunden. Wenn wir die Lösungen für a, b und c in den Anfangsgleichungen einsetzen, werden alle drei Gleichungen stimmen. Wenn wir andere Zahlen dafür benutzen, werden die drei Gleichungen nicht mehr (gleichzeitig) stimmen.
Dieses Verfahren ist das einfachste, wenn wir ein LGS mit 3 oder mehreren Variablen lösen wollen, daher wird es auch bei mehreren Variablen benutzt.
Textaufgaben zu linearen Gleichungssystemen
[Bearbeiten]|
Eine Bootverleihfirma hat insgesamt 43 Boote, |
Hier sind drei Sachen gefragt: die Anzahl der Tretboote, die Anzahl der Ruderboote und die Anzahl der Kanus. Schreiben wir t für die Anzahl der Tretboote, r für die Ruderboote und k für die Kanus (selbstverständlich können wir auch andere Symbole benutzen, z.B. a, b und c usw.). Versuchen wir jetzt die Angabe in die mathematische Sprache zu "übersetzten".
- Nach Angabe sind alle Boote zusammen 43. Wenn wir die Boote zusammenrechnen (addieren) wird daher das Ergebnis 43 sein. Wir müssen also die Symbole für die Anzahl der verschiedenen Bootarten addieren:
- Allerdings kann die Firma höchstens 159 Personen bedienen. Wenn alle Tretboote (t) unterwegs sind, dann sind in diesen Booten 5t Personen, für die Ruderboote sind es 3r Personen und für die Kanus 2k Personen. Allesamt gilt daher für die Personen, die die Firma höchstens bedienen kann:
- Die Firma verdient 8 €/h für jedes der t Tretboote, also für alle zusammen 8·t €/h. Entsprechend sind die Einnahmen pro Stunde für die Ruderboote 7r € und für die Kanus 4k €. Daher gilt für die maximalen Einnahmen der Firma (pro Stunde), die laut Angabe 271 € sind:
Schreiben wir die drei Gleichungen, die wir durch die "Übersetzung" des Textes erzeugt haben, als ein Gleichungssystem auf:
|
|
Dieses LGS können wir mit Hilfe eines elektronischen Mittels lösen. Wenn keines vorhanden ist, dann können wir am einfachsten das gaußsche Eliminationsverfahren benutzten:
|
|
Die dritte Spalte ist die Anzahl der Kanus, die zweite die Anzahl der Ruderboote und die erste die Anzahl der Tretboote.
Es gibt daher 24 Tretboote, 1 Ruderboot und 18 Kanus.
Funktionen
[Bearbeiten]Schnittpunkte von Funktionen
[Bearbeiten]
| Diagramm |
| Text |

Hier sind ein paar Beispiele von Funktionen:
f(x)=3x−5 K(s)=3s+1,5 V(r,h)=πr²(r+h)
h(t)=14− 3t ρ(m,V)=
Oft haben wir erwähnt, dass wenn nichts zwischen zwei mathematischen Ausdrücken steht, eine Multiplikation gemeint ist. In diesen Fällen ist allerdings nicht so. Mit dem Symbol f(x) ist eine Funktion f gemeint, wo die abhängige Variable durch f (in diesem Fall auch y) und die unabhängige durch x symbolisiert wird. f(x) bedeutet so viel wie „f in Abhängigkeit von x“. Entsprechend könnte K(s) die Kosten einer Taxifahrt in Abhängigkeit vom Abstand s bedeuten, V(r,h) das Volumen V eines zusammengesetzten geometrischen Körpers in Abhängigkeit von dem Radius r und der Höhe h, h(t) die Höhe einer Kerze in Abhängigkeit von der Zeit oder ρ(m,V) die Dichte in Abhängigkeit von der Masse und das Volumen. Selbstverständlich können alle diese Symbole auch etwas anderes als Kosten, Volumen, Radius, Zeit usw. bedeuten und jedes Symbol kann mal die unabhängige und mal die abhängige Variable sein (wie hier mit dem Volumen). In der Symbolik a(u) ist das (oder die) Symbol im Klammer (hier u) die unabhängige Variable, die auf der x-Achse dargestellt wird und das Symbol außerhalb (vor) der Klammer (hier a) die abhängige.

In einer Funktion kann es für jeden Wert der unabhängigen Variable genau einen Wert der abhängigen geben, für jeden Wert der abhängigen allerdings keine, eine oder mehrere Werte der unabhängigen. Die Menge der Werte der unabhängigen Variable wird Definitionsmenge genannt, die Menge der Werte der abhängigen Zielmenge. Obwohl für die Zielmenge oft das Wort Wertemenge benutzt wird, sind in der Schulmathematik i.d.R. nur die Werte der Zielmenge, die tatsächlich einem Wert der Definitionsmenge entsprechen, mit Wertemenge gemeint. Im Bild ist A die Definitionsmenge, B die Zielmenge und {b,c,d} die Wertemenge. B kann in diesem Fall nicht die Definitionsmenge sein, da {b} zwei Werten von A entspricht. Mit dem Wort „Stelle“ ist ein Wert aus der Definitionsmenge gemeint („x-Wert“), mit dem Ausdruck „Wert der Funktion“ ein Wert aus der Zielmenge („y-Wert“). Wenn der Wert einer Funktion (y-Wert) an einer gewissen Stelle gefragt wird, dann muss man die unabhängige Variable in der Funktion durch ihren angegebenen Wert („Stelle“, x-Wert) ersetzen. Wenn z.B. die Funktion g(a)=a²+4a−11 ist, dann ist der Wert der Funktion an der Stelle 2 gleich g(2)=2²+4·2−11 also 1. Wie zu sehen ist, haben wir bei g(2) überall, wo in der Funktion g(a)=a²+4a−11 das a steht, dieses durch 2 ersetzt und damit den Wert der Funktion an dieser Stelle berechnet. Es gilt daher in dieser Funktion: g(2)=1.
Mit dem Begriff „Lösungen“ einer Funktion sind die Stellen (x-Werte) der Funktion gemeint, wo die Funktion gleich Null ist, also wo die x-Achse von der Funktion geschnitten oder berührt wird und wo der y-Wert Null ist. Im Diagramm sind die Punkte B, C, D und E Lösungen der Funktion, die durch die Kurve dargestellt wird. Der Punkt F ist die Lösung der Funktion, die mit einer Gerade dargestellt wird. Wenn nicht ein Diagramm sondern der "algebraische" Ausdruck der Funktion gegeben ist, dann sollen wir die Funktion gleich Null setzen, um die Lösungen zu finden. Beispielsweise müssen wir die Funktion k(x)=x4−5x3+4x gleich Null setzen, u ihre Lösungen (Nullstellen) zu finden:
0=x4−5x3+4x
Diese Gleichung stimmt für x gleich ca. −0,83, 0, 1 und ca. 4,83. Diese Stellen (: Werte von x) sind die Lösungen der Funktion (Nullstellen: Stellen, also Werten von x, wo die Funktion, also die Werte von y, Null ist).
Der y-Achsenabschnitt für eine Gerade haben wir schon gelernt, für die Kurve im Diagramm ist er der Punkt A. An diesem Punkt ist der x-Wert Null (wie allerdings auf der ganzen y-Achse). Wenn wir den Wert der Funktion g(a)=a²+4a−11 a an der Stelle 0 (x-Wert, also die unabhängige Variable ist Null, also hier a=0), dann bekommen wir den Wert g(0)=0²+4∙0−11=−11. Alle Teilterme, die x haben, werden bei der Berechnung des y-Achsenabschnitts einfach ausgelassen (da sie mit Null multipliziert werden). Der y-Achsenabschnitt der Kurve im Diagramm ist 1 (Punkt A), der Gerade 13 (nicht sichtbar).
Lösung eines Gleichungssystems sind die Punkte, wo die Funktionen einander schneiden. Im Bild sind es die Punkte G, H, I. Da schneiden die Kurve und die gerade einander. Um diese Punkte zu finden, werden die beide Funktionen gleich zueinander gestellt. Wenn z.B. die Kurve k(x)=x⁵+4x³-3x²+1 wäre und die Gerade f(x)=−2x+13, dann schreibt man: k(x)=f(x) also x⁵+4x³-3x²+1=−2x+13 und löst diese Gleichung. Das funktioniert, weil die beiden Funktionen an den Schnittpunkten die gleichen y-Werte haben (also ist an diesen Punkten tatsächlich k(x)=f(x)) und auch die gleichen x-Werte.
Der Punkt K gehört zur Kurve aber nicht zur Gerade, Punkt J gehört zu keiner der beiden Funktionen. Um herauszufinden, ob ein Punkt zu einer Funktion gehört, setzen wir in der Funktion den Wert von x ein und vergleichen wir das Ergebnis (y-Wert) mit dem y-Wert des Punktes. Wenn diese dann übereinstimmen, dann gehört der Punkt zur Funktion, sonst nicht.
Polynomfunktionen Diagramm
[Bearbeiten]Eine Polynomfunktion ist eine Funktion von einer Summe von Potenzfunktionen, deren Hochzahlen natürliche Zahlen sind:
n ist die größte Hochzahl und bestimmt den sogenannten Grad der Funktion (für an≠0), an, an-1, … , a0 sind die sogenannten Koeffizienten.
Ist die höchste Hochzahl null, dann haben wir die sogenannten "konstanten" Funktionen (Polynomfunktionen 0. Grades) , wie im Diagramm A. Sie sind Geraden, die parallel zu x-Achse laufen und daher keine "Lösung" haben (keine Nullstelle, also sie treffen die x-Achse nie). Einzige Ausnahme die konstante Funktion , die die x-Achse selber ist und daher sozusagen unendlich viele "Lösungen" hat.
Ist die höchste Hochzahl eins, dann haben wir die sogenannten "linearen" Funktionen (Polynomfunktionen 1. Grades) , wie im Diagramm B. Sie sind Geraden, die die x-Achse genau ein mal treffen und daher genau eine "Lösung" haben (eine Nullstelle, also sie treffen die x-Achse ein mal). ist die Steigung der Funktion, der y-Achsenabschnitt. Ist positiv, läuft die Gerade "nach oben" (also von links unten nach rechts oben), wenn negativ dann nach unten.
Ist die höchste Hochzahl 2, dann haben wir die sogenannten "quadratischen" Funktionen (Polynomfunktionen 2. Grades), wie im Diagramm C. Ihre Form ist eine sogenannte Parabel. Im Diagramm C können wir zwei solche Funktionen die nach oben gerichtet sind. In diesem Fall ist positiv, in der anderen Funktion (nach unten) ist diese Koeffizient negativ. Eine Polynomfunktion kann zwei Lösungen haben (wie beide Funktionen, die nach oben gerichtet sind), eine oder sogar keine (wie die Funktion, die nach unten gerichtet ist).
Ist die höchste Hochzahl 3, dann haben wir die sogenannten "kubischen" Funktionen (Polynomfunktionen 3. Grades), wie im Diagramm D und E. Ist positiv, läuft die Funktion "nach oben", sonst "nach unten". An dieser Stelle können wir den Begriff des Monotonieverhaltens erklären als auch, wie wir den Grad der Funktion erkennen können. Wenn die Funktion "nach oben" geht, also von links unten nach rechst oben, dann wird sie als "steigend" bezeichnet, was ihr Monotonieverhalten betrifft. Wenn sie "nach unten" läuft, wird sie als "fallend" bezeichnet. Eine Funktion hat nicht unbedingt (und eher seltener) ein festes Monotonieverhalten. Die Funktion in Diagramm D ist bis zur Stelle ca. −3 fallend, dann bis +3 steigend und dann wieder fallend. Die Funktion in Diagramm E, die auch wie im D 3. Grades ist, ist hingegen überall steigend (wie es auch der Fall bei Geraden ist, die "nach oben" laufen). Das Monotonieverhalten kann uns also nichts über den Grad der Funktion sagen. Man merkt allerdings, dass die Funktion im Diagramm E keine Gerade ist. Was sich da ändert, ist die sogenannte Krümmung der Funktion. Die Funktion biegt einmal in eine Richtung und dann wieder in der anderen. Wir haben also zwei "Abbiegungen". Allgemein gilt:
- Der Grad einer Polynomfunktion ist zumindest um 1 größer, als die Anzahl der "Abbiegungen".
Um den Begriff der Krümmung etwas besser zu verstehen, stellen wir uns vor, dass die Kurve in Diagramm D eine Straße wäre und wir mit einem Fahrzeug von links oben fahren. Wir müssen schon am Anfang ein bisschen nach links abbiegen, um auf der "Straße" zu bleiben und dann immer abrupter, bis ungefähr an der Stelle −3. Dann müssen wir immer weniger abbiegen und ungefähr ab der Stelle null müssen wir anfangen, rechts abzubiegen. Wir haben an diese Stelle eine Krümmungsänderung. Auf einer Gerade hingegen (Diagramm B) brauchen wir (dürfen wir sogar) nicht abbiegen.
Diagramme F und G sind Polynomfunktionen 4. Grades, H 5. Grades, K 6.Grades und L 7.Grades. Wenn wir diese Diagramme betrachten, kommen wir zu weiteren Schlüssen:
- Ist das Monotonieverhalten an den Rändern der Funktion unterschiedlich, dann ist die Hochzahl eine gerade Zahl. Wenn die Funktion am Rand links fallend und am Rand rechts steigend ist (wie in den beide "oberen" Funktionen in Diagramm C, als auch in Diagramm G und Diagramm K), dann ist die Koeffizient der höchsten Potenz positiv, sonst ist sie negativ.
- Ist das Monotonieverhalten an den Rändern der Funktion gleich, dann ist die Hochzahl eine ungerade Zahl. Wenn die Funktion links und rechts steigend ist (wie in den Diagrammen E, H und L), dann ist die Koeffizient der höchsten Potenz positiv, sonst ist sie negativ.
Die Abbiegungen (um 1 erhöht) können uns nur zur Erschließung des minimalen möglichen Grades der Funktion helfen. Wir wissen ja nicht, wie die Funktion außerhalb des sichtbaren Bereiches läuft und auch andere Sachen nicht. Im Diagramm H beispielsweise können wir mit Sicherheit sagen, dass die Funktion zumindest von 5. Grad ist (es gibt 4 sichtbaren Abbiegungen; 4+1=5). Im Diagramm K gibt es 5 sichtbare Abbiegungen, die Funktion ist zumindest 6. Grades. Wenn wir Diagramme H und K vergleichen, stellen wir fest, dass die Änderung des Monotonieverhaltens eine Krümmung voraussetzt (zumindest in den Funktionen, die wir hier behandeln). Das Gegenteil ist allerdings nicht der Fall. Im Diagramm H folgt nach jeder Abbiegung eine Änderung des Monotonieverhaltens (also von fallend zu steigend oder umgekehrt). Im Diagramm K hingegen gibt es in der Umgebung der Lösung III zwei Abbiegungen, die nicht zu einer Änderung des Monotonieverhaltens führt. Das gleiche gilt in Diagramm E, wo wir zwei Abbiegungen haben ohne dass sich das Monotonieverhalten überhaupt ändert (die Funktion ist immer steigend).
Über die Anzahl der Lösungen können wir mit Hilfe der Diagrammen Folgendes schließen:
- Eine Polynomfunktion hat höchstens so viele Lösungen wie ihr Grad. Ist der Grad eine ungerade Zahl, dann hat sie zumindest eine Lösung. Ist der Grad eine Gerade Zahl, dann kann sie doch auch keine Lösung haben.
Wenn der Grad ungerade ist, ist das Monotonieverhalten an den Rändern der Funktion das gleiche, beispielsweise steigend. Das bedeutet dann, dass die Kurve mit Sicherheit zumindest einmal die x-Achse treffen wird. Das ist nicht der Fall beim geraden Grad, wo die ganze Funktion sich unterhalb oder oberhalb der x-Asche befinden kann (wie im Diagramm C für die "untere" Funktion und in Diagramm F).
Noch eine Information zu der Ableitung von Polynomfunktionen:
- Die Ableitung einer Polynomfunktion ist eine neue Polynomfunktion mit einem Grad um 1 reduziert. Einzige Ausnahme die konstante Funktion, deren Ableitung null ist (also der Grad bleibt in diesem Fall null).
Umkehrfunktionen mit Umformen finden
[Bearbeiten](t in Minuten, T in °C)
Das bedeutet in diesem Fall, dass die Temperatur am Anfang 35°C ist und jede Minute um 2°C fällt. In diesem Fall ist die Zeit die sogenannte unabhängige Variable, die Temperatur die abhängige. Die Frage in diesem Fall ist: "Wie viel ist die Temperatur nach so und so viele Minuten?" Wenn wir die Temperatur nach 195 s messen wollen, müssen wir erst die s in min umrechnen: . Diese Zahl setzen wir dann in die Formel ein, um die entsprechende Temperatur zu finden:
Die Temperatur wird daher 28,5°C sein.
Was ist aber, wenn wir die Frage umkehren? "Wann ist die Temperatur 10°C?"
Um diese Frage zu beantworten, müssen wir die Funktion auf die Variable t (Zeit) umformen. Wir vergessen kurz die Funktionsdarstellung T(t), wir schreiben für die Temperatur einfach T und formen auf diese Variable um:
Jetzt können wir wieder die Funktionsdarstellung benutzen:
(t in Minuten, T in °C)
Hier ist die Temperatur die unabhängige Variable und die Zeit die abhängige. Wir wollen wissen, "wie viel" die Zeit, "bei" einer gewissen Temperatur ist. Diese Funktion ist die sogenannte Umkehrfunktion der Funktion am Anfang.
Die Angabe der Einheiten ist immer notwendig, wenn die Variablen Einheiten aufweisen, um Fehler bei den Berechnungen zu vermeiden. In diesem Beispiel hätten wir ein anderes Ergebnis, wenn wir 195 statt 3,25 benutzt hätten. Wenn allerdings die Variablen reine Zahlen sind, dann brauchen wir auch keine Einheiten angeben (es gibt ja dann keine). Hier sind einige Gegenrechnungen, die beim Umformen notwendig sein können. Manche davon haben wir gelernt, manche vielleicht auch noch nicht. Letztere werden wir erst später erklären.
|
|
|
|
Definition von Sinus Kosinus und Tangens
[Bearbeiten]
| Definitionen |
Trigon. Umkehrf. |
| Pythagoras abstrakt |
Pythagoras konkret |


An jedem rechtwinkeligen Dreieck gilt eine gewisse Regel, die schon seit zumindest 4000 Jahren bekannt ist. Diese Regel wurde nach einem griechischen Philosophen genannt: der Pythagoräische Lehrsatz.
In einem rechtwinkeligem Dreieck ist die Summe der Quadrate der Katheten gleich dem Quadrat der Hypotenuse.
Dieser Satz ist verständlicher, wenn wir das erste Dreieck für einen Entwurf des Satzes mit Symbolen benutzen. Wenn a und b die zwei kleineren Seiten des rechtwinkeligen Dreiecks (Katheten genannt) und c die größere (Hypotenuse genannt) sind, ist der entsprechende mathematische Ausdruck:
Genauso seit tausenden Jahren bekannt ist eine andere Eigenschaft der geometrischen Figuren und in diesem Fall der rechtwinkeligen Dreiecke. Bei ähnlichen Dreiecken (wenn alle Winkel gleich sind) ist das Verhältnis (der Bruch der Längen) der entsprechenden Seiten konstant. im ersten Dreieck im Bild ist genauso viel wie im zweiten. Besonders in rechtwinkeligen Dreiecken bedeutet diese Tatsache, dass:
- Das Verhältnis der dem kleinsten Winkel gegenüberliegenden Seite (hier a) zu Hypotenuse (hier c) eine konstante Zahl für alle ähnlichen rechtwinkeligen Dreiecke ist.
- Das Verhältnis der dem kleinsten Winkel anliegenden Kathete (hier b) zu Hypotenuse eine konstante Zahl für alle ähnlichen rechtwinkeligen Dreiecke ist.
Das entsprechende gilt für den anderen nicht rechten Winkel.
Mit Buchstaben ist dieser Satz viel verständlicher. Im ersten Dreieck gilt: und sind konstant, für alle ähnlichen rechtwinkeligen Dreiecke.
Der erste Bruch wurde Sinus genannt, der zweite Kosinus. Für den kleinsten Winkel (nennen wir ihn ) des ersten Bildes gilt also:
und
Die zwei Dreiecke im Bild sind ähnlich. Die kleinste Kathete a im ersten Dreieck durch seine Hypotenuse, wird so viel sein, wie die kleinste Kathete c im zweiten Dreieck durch seine Hypotenuse:
und
Somit werden Sinus und Kosinus definiert. Sinus und Kosinus sind die zwei wichtigsten trigonometrischen Funktionen. Formell:
|
und |
|
wobei irgendein nicht rechter Winkel |
Für den anderen nicht rechten Winkel des ersten Dreiecks (nennen wir ihn ) gilt dann:
und ,
da gegenüber von die Seite b ist.
Alle Winkel zusammen in einem Dreieck sind 180°. In einem rechtwinkeligen Dreieck ist einer Winkel 90°, daher sind die anderen zwei zusammen auch 90°. Daher gilt:
und .
Mit Hilfe des Pythagoräischen Lehrsatzes ist auch leicht zu zeigen, dass:
.
und bedeuten bzw. .
Es gibt allerdings noch eine wichtige Trigonometrische Funktion, der Tangens. Er ist das Verhältnis der Gegen- zu Ankathete:
Die Symbole für manche weiteren trigonometrischen Funktionen sind: und . Es gibt allerdings auch die Umkehrfunktionen. Von und werden sie mit den Symbolen bzw. oder bzw. (besonders bei Taschenrechnern) dargestellt.
Einheitskreis
[Bearbeiten]Einheitskreis und trigonometrische Funktionen
[Bearbeiten]Der Einheitskreis ist ein in einem Koordinatensystem gezeichneter Kreis. Sein Mittelpunkt ist der Koordinatensystemanfang (also der Punkt (0|0)) und sein Radius ist die Einheit (also 1). Der Radius steht am Anfang auf der x Achse rechts und wird im Gegenuhrzeigesinn gedreht. Dadurch entsteht ein Winkel im Kreis (und ein Punkt P auf dem Kreis), wie im ersten Bild zu sehen ist. Im zweiten Bild sehen wir genauer diese Drehung. Wir sehen auch, dass ein viertel Kreis Drehung einen 90°, ein halber Kreis einen 180°, drei viertel Kreis 270° und ein ganzer Kreis 360° Winkel entsprechen.
Im dritten Bild sehen wir, dass der Sinus gleich der Seite gegenüber dem Winkel ist und der Kosinus gleich der Ankathete. Sinus wird als Gegenkathete durch Hypotenuse definiert: , da die Hypotenuse c in diesem Fall gleich 1 ist. Das Entsprechende gilt für Kosinus: . Die Länge der Seite a ist allerdings auch so viel wie die y-Koordinate des entsprechenden Punktes. Das bedeutet, dass auf der y-Achse der Sinus des Winkels dargestellt wird. Entsprechend wird auf die x-Achse der Kosinus des Winkels dargestellt (die Seite b, also die x-Koordinate des entsprechenden Punktes auf dem Kreis).
Im vierten Bild sehen wir, dass ein Winkel und sein Gegenwinkel den gleichen Kosinus haben. Da ein ganzer Kreis 360° ist, haben und den gleichen Kosinus. Im fünften Bild sehen wir, dass ein Winkel und sein Supplementwinkel math>180^\circ -\omega\ </math>den gleichen Sinus haben. Im letzten Bild sehen wir, dass wenn wir eine ganze Drehung (oder mehrere ganzen Drehungen) dazu machen, der neue Winkel sowohl den gleichen Sinus als auch den gleichen Kosinus hat.
Im letzten Bild wird allerdings eine ganze Drehung mit 2π und nicht mit 360° bezeichnet. Das ist eine andere Einheit für die Messung von Winkeln, Radiant genannt. Genauso wie es auf der Welt für die Messung von einer Länge verschiedene Einheiten, wie km oder Meile gibt, gibt es verschiedene Einheiten auch für die Messung einer Drehung (eines Winkels). 2π rads entsprechen einer ganzen Drehung, also 360°.
Radiant
[Bearbeiten]Für die Messung einer Drehbewegung verwenden wir in der Regel den Winkelgrad. Ein Grad ist einer ganzen Drehung. Eine ganze Drehung ist damit 360°. Bei Rechnungen in der höheren Mathematik und in der Physik hat sich allerdings gezeigt, dass eine andere Einheit notwendig ist, der Radiant (rad). Eine ganze Drehung ist rad. Mit Schlussrechnung können wir daher sehr einfach zwischen den beiden Einheiten [1]umrechnen:
- ↑ (die allerdings dimensionslos sind)
Einheitskreis wichtige Punkte
[Bearbeiten]
 | |
Der Einheitskreis wird durch die beiden Achsen des Koordinatensystems in vier gleichen Teilen geteilt. Diese Teile werden Quadrante genannt und werden in einer ähnlichen Weise wie der Winkel in diesem Kreis definiert (Gegenuhrzeigersinn, Aufzählungsanfang oben rechts), d.h. der Teil oben rechts (zwischen 0° und 90°) wird erstes, oben links (zwischen 90° und 180°) zweites, unten links (zwischen 180° und 270°) drittes und unten rechts (zwischen 270° und 360° bzw. wieder 0°) viertes Quadrant genannt.
Im Einheitskreis wird der Sinus auf der y-Achse dargestellt. Tatsächlich ist zumindest im ersten Quadrant die Länge der Gegenkathete des Winkels so viel wie die y-Koordinate des entsprechenden Punktes auf dem Einheitskreis. Das gilt für alle Quadrante, allerdings nur für den Betrag der y-Koordinate (die unterhalb der x-Achse doch negativ ist). Das bedeutet:
Der Sinus ist im ersten und zweiten Quadrant positiv, im dritten und vierten negativ.
Entsprechend liegt die Ankathete des Winkels auf der x-Achse, die links von der y-Achse ihre negativen Werte hat. Daher gilt:
Der Kosinus ist im ersten und vierten Quadrant positiv und im zweiten und dritten negativ.
Da der Tangens auch als das Verhältnis von Sinus durch Kosinus definiert kann, ist es leicht auch sein Vorzeichen in den verschiedenen Quadranten zu finden. Im ersten Quadrant sind Sinus und Kosinus positiv, also auch der Tangens, im zweiten ist Sinus positiv und Kosinus negativ, daher ist dort der Tangens negativ ("Plus durch minus ist minus"). Es gilt daher:
Der Tangens ist im ersten und dritten Quadrant positiv und im zweiten und vierten negativ.
Am Einheitskreis gibt es einige besondere Punkte, wie wir im letzten Bild links sehen können. Bei 0 rad (und 0°) ist die y-Koordinate, also Sinus, gleich null und die x-Koordinate, also der Kosinus, so viel wie der Radius, also 1. Bei rad (90°) ist Kosinus null und Sinus 1. Bei rad (180°) ist Kosinus −1 und Sinus wieder null, bei rad (270°) ist wiederum Kosinus null und Sinus −1.
Von der Natur der Definition von Sinus und Kosinus im Einheitskreis wird sichtbar, dass Sinus und Kosinus Werte im Intervall zwischen −1 und 1 annehmen.
Sinus und Kosinus nehmen Werte im Intervall zwischen −1 und 1 an.
Es gibt keinen Winkel (im Bereich der reellen Zahlen) der Sinus oder Kosinus mehr als 1 oder weniger als −1 hat. Das gilt allerdings nicht für den Tangens, der jeden Wert annehmen kann. Beispielsweise, wenn der Winkel nah zu rad (90°) ist, dann nimmt Sinus Werte immer näher zu 1 und Kosinus immer näher zu null an. Daher nimmt Tangens Werte gegen Unendlichkeit an. Bei rad ist allerdings der Tangens nicht mehr definierbar, da Kosinus (der Nenner) null ist.
Ein weiterer interessanter Winkel ist rad (45°). In diesem Fall hat das rechtwinkelige Dreiecke zwei gleichen Winkel, es ist also gleichschenklich. Der Sinus ist in diesem Fall so viel wie der Kosinus und lässt sich einfach mit Hilfe des Satzes von Pythagoras berechnen. Bei rad (30°) haben wir die Hälfte eines gleichseitigen Dreiecks, die Gegenkathete ist daher die Hälfte der Hypotenuse und der Sinus daher , so viel wie der Kosinus des Komplementwinkels rad (60°). Der Kosinus von rad (30°) (und der Sinus von rad also von 60°) lässt sich dann leicht mit Hilfe des Pythagorassatzes für Trigonometrie :
.
Mit Hilfe des Einheitskreises und Beachtung des Vorzeichens lassen sich dadurch die trigonometrische Zahlen der entsprechenden Winkel in den anderen Quadranten berechnen, also auch die entsprechenden Tangens.
Trigonometrische Funktionen Diagramm
[Bearbeiten]Sinus Diagramm und Einheitskreis
[Bearbeiten]Nehmen wir an, dass ein Punkt PK sich auf einem Kreis mit konstanter (Winkel- oder Bahn-) Geschwindigkeit bewegt („gleichförmige“ Kreisbewegung) (siehe Animation). PY ist die Projektion des Punktes auf der y-Achse. Stellen wir uns vor, dass sich an Punkt PY eine Füllfeder befindet und darunter ein bewegendes Papier. Die Füllfeder hinterlässt eine Spur (Punkt PF) auf dem Papier. Das Ergebnis würde wie auf den folgenden Bildern aussehen.
 |
 |
 |
 |


Die Kurve die entsteht nennt man Kosinusfunktion. Sie (als auch die Sinusfunktion) ist eine sogenannte Winkelfunktion. Winkelfunktionen und Kreisbewegung sind also ganz stark miteinander verbunden. Eigentlich ist die Kreisfunktion eine Kombination von zwei Winkelfunktionen (Sinus und Cosinus) in zwei verschiedenen Richtungen (Senkrecht und Waagerecht). Hier ist noch ein dreidimensionales Bild zur Entstehung der Kosinus Funktion (links) und ein Bild zur Entstehung der Sinus Funktion (rechts).
Winkelfunktionen stellen die Basis für die Beschreibung und das Verständnis der Schwingungen und daher auch der Wellen dar. Eine genauere Beschreibung der Mathematik der Wellen ist aber außerhalb der Ziele dieses Buches. Dafür soll man sich an anderen Quellen wenden, z.B. Wellenfunktion oder Wellengleichung.
Parameter im Diagramm der Sinusfunktion
[Bearbeiten]
Hier werden wir erkunden, wie sich das Diagramm der Sinusfunktion ändert, wenn wir sogenannten Parameter der Grundfunktion modifizieren. Allgemein (mit solchen Parametern) ist die Formel für die Sinusfunktion (genauer gesagt: für eine Wellenfunktion in der Mechanik):

ist die sogenannte Amplitude. Sie zeigt uns wie weit nach oben und nach unten der Wert der Funktion schwankt. Sinus (und Kosinus) nehmen Werte zwischen 1 und −1. Das können wir mit Hilfe des Einheitskreises sofort sehen. Wenn wir Sinus mit multiplizieren (und nichts anderes machen) wird die Funktion Werte zwischen und aufnehmen. Im Bild ist (schwarz, Amplitude ), (blau, Amplitude ), (rot, Amplitude ), (grün, Amplitude ).

ist die sogenannte Winkelfrequenz. Sie zeigt uns wie oft innerhalb eines Intervalls des x-Wertes von der y-Wert wieder seinen Anfangswert bekommt. Zwischen Winkelfrequenz und Frequenz gilt: . Der Kehrwert der Frequenz ist die Periode: . Daher gilt auch: . Sinus (und Kosinus) nehmen wiederholt Werte zwischen 1 und −1. Die Periode zeigt uns, nach welcher Änderung des x-Wertes der Wert der Funktion (y-Wert) wieder der gleiche sein wird. Ist (und daher ), dann kommt die Welle im Diagramm öfters vor. Im Bild ist (schwarz, Winkelfrequenz , Periode , Intervall ), (blau, Winkelfrequenz , Periode ), (rot, Winkelfrequenz , Periode .

ist die sogenannte Phase. Sie zeigt uns an welcher Stelle die Funktion "anfängt". Die Sinusfunktion fängt normalerweise mit null und steigend an. Wenn die Phase nicht null ist, dann ist der Wert der Funktion null (und die Funktion steigend) bei . Im Bild ist (schwarz, Phase ), (rot, Phase , der Wert der Funktion ist 0 bei ), (blau, Phase , der Wert der Funktion ist 0 bei .

ist eine Konstante, die das ganze Diagramm nach oben ( positiv) oder nach unten ( negativ) verschiebt. Im Bild ist (schwarz, ), (rot, , Funktion um 0,8 senkrecht nach oben verschoben), (blau, , Funktion um 1,4 senkrecht nach unten verschoben).

Hier sehen wir ein Beispiel, wo alles kombiniert wird. Die Funktion nimmt Werte von −3 bis 1,4. Die gesamte Schwankung (das doppelte der Amplitude) ist daher 4,4 und die Amplitude selber . Die Funktion ist allerdings nach unten verschoben, die Werte schwanken um den Wert −0,8, daher ist die Konstante . Die Phase zu finden ist in diesem Fall ein bisschen komplizierter. Da die Funktion nach unten verschoben ist, müssen wir den Anfang etwas nach unten (bei −0,8) suchen. Dann können wir entdecken, dass der "Anfang" an der Stelle −0,5 ist, daher ist die Phase +0,5. Die rote Funktion lautet daher:
Funktionserkennung
[Bearbeiten]Funktionserkennung in Diagramm
[Bearbeiten]| Diagramm erkennen |
Diagramm Eigenschaften |
Es gibt unendlich viele Funktionen und es macht daher keinen Sinn, sie alle einzeln zu besprechen. Hier werden wir uns nur mit einer begrenzten Anzahl von Funktionen beschäftigen: Polynomfunktionen, Wurzelfunktionen, trigonometrische Funktionen, indirekte Proportionalität, Logarithmus und Exponentialfunktion. Wir werden manche von denen paarweise vergleichen. Dadurch können wir besondere Merkmale einer Funktion erkennen, die uns zu entscheiden helfen können, ob eine Funktion durch ein bestimmtes Diagramm dargestellt wird (und umgekehrt).
Polynomfunktion höheren Grades und Sinusfunktion.
|
Links sehen wir eine Sinusfunktion und zwei Polynomfunktionen. Die Mitte der beiden Polynomfunktionen ist kaum von der Sinusfunktion zu unterscheiden. Das bedeutet nicht, dass jede Polynomfunktion wie eine Sinusfunktion aussieht, aber dass es Polynomfunktionen geben kann, die teilweise stark wie eine Sinusfunktion aussehen. In der Regel sehen allerdings Polynomfunktionen nicht so stark wie eine Sinusfunktion aus (Bilder rechts). Das Merkmal, das diese der Sinusfunktion ähnlichen Polynomfunktionen von der Sinusfunktion selber unterscheidet, ist in den Diagramm leicht erkennbar: ihre Ränder. |
|
Wurzel und Logarithmusfunktion
|
Links sehen wir eine Wurzelfunktion und eine (leicht verschobene) Logarithmusfunktion. Beide Funktionen sind nur für positiven Werten von x definierbar (außer wenn sie "verschoben" sind, wie der Fall mit der Logarithmusfunktion hier ist). Wenn wir hier einen bestimmten Bereich vergleichen (Vergleich A), sind die Funktionen wieder kaum voneinander zu unterscheiden, was allerdings bei größeren Bereichen nicht der Fall ist (Vergleich B). Es gibt drei grundsätzliche Unterscheide zwischen den beiden Funktionen: 

Wir haben gesehen, dass die beide Funktionen (Logarithmus und Wurzelfunktion) bei einem gewissen Bereich übereinstimmen. Das bedeutet nicht, dass jede Logarithmusfunktion bei einem bestimmten Bereich mit jeder Wurzelfunktion übereinstimmt, sondern dass es eine Logarithmus und eine Wurzelfunktion geben kann, die bei einem bestimmten Intervall übereinstimmen. |
Quadratische und Exponentialfunktion
|
Links sehen wir eine quadratische und zwei exponentiellen Funktionen (beide im zweiten Diagramm). Die eine exponentielle ist fallend (von links oben nach rechts unten) und die andere steigend. Sie werden auf der y-Achse "gespiegelt". Die quadratische ist links der Achse fallend und rechts steigend. Hier sehen wir wieder, dass die von uns gewählten Funktionen bei einem bestimmten Intervall übereinstimmen (Vergleich A). Allerdings weisen sie auch erhebliche Unterschiede:
Die Asymptote einer Funktion ist eine Gerade (in irgendeine Richtung und nicht nur die x- oder y-Achse). Für diese Gerade ist es beweisbar, dass die Werte der Funktion ihr immer näher werden (aber sie nie berühren). |
Indirekte Proportionalität und Exponentialfunktion
|
Links sehen wir eine Exponentialfunktion und eine indirekte Proportionalität. Im zentralen Bereich um die y-Achse gibt es in diesem Fall keine Übereinstimmung (nur 2 Schnittpunkte, Vergleich A). Allerdings verlaufen weiter rechts von der y-Achse beide Funktionen fast parallel zur x-Achse. Daher geht es einfach, mit einer kleinen Verschiebung (einer Änderung von irgendeinem Parameter), dass die Funktionen in einem (sogar großen) Intervall fast übereinstimmen (Vergleich B). Hier wollen wir uns auf die Unterschiede konzentrieren.
|
Tangens und kubische Funktion
|
Links sehen wir eine Tangensfunktion und eine Polynomfunktion 3. Grades ("kubische Funktion"). In angezeigtem Bereich ("Intervall") sind sie kaum von einander zu unterscheiden (Vergleich A). Es gibt allerdings wieder eindeutige Unterschiede (Vergleich B):
|
Umkehrfunktionen in Diagramm erkennen
[Bearbeiten]


Im Bild "y-Achse als Spiegel" ist zu erkennen, dass jeder der beiden dargestellten Funktionen das Spiegelbild der anderen auf der y-Achse ist. Die (blaue) Funktion f ist steigend, die (rote) Funktion g ist fallend und ihre Punkte entsprechen genau einander, wenn wir an der y-Achse als Spiegel denken. Beispielsweise entspricht der Punkt (1|2) der Funktion g dem Punkt (−1|2) der Funktion f. Der y-Wert ist genau der gleiche, der Betrag der x-Werte auch und nur das Vorzeichen der x-Werte ist anders. Wenn wir eine Spiegelung auf der y-Achse haben können wir daher schreiben:
Die Werte der Funktionen sind gleich für die Gegenstellen.
Im Bild "x-Achse als Spiegel" können wir eine ähnliche Situation erkennen, nun jetzt mit der x-Achse als Spiegel. Die Kurve kann nach der Definition der Funktion nicht eine einzige Funktion darstellen, das es (mit der Ausnahme der Stelle 0) jeder Stelle zwei Werte entsprechen (eine oberhalb und einer unterhalb der x-Achse). Wir haben daher zwei Funktionen, die auf der x-Achse gespiegelt werden. Dem Punkt (4|2) der Funktion oben entspricht Beispielsweise der Punkt (4|−2) der Funktion unten. Wenn wir eine Spiegelung auf der x-Achse haben können wir daher schreiben:
An jeder Stelle hat eine Funktion den Gegenwert der anderen.
Im Bild "Indirekte Proportionalität" können wir zwei Funktionen sehen, die beide eine indirekte Proportionalität darstellen. Jede Funktion ist ihr eigener Spiegel und zwar auf zwei Achsen. Diese Achsen sind auch im Bild dargestellt und sie entsprechen den Funktionen y=x (steigende Diagonale) und y=−x (fallende Diagonale). Wenn wir beispielsweise die (rote) Funktion beobachten, stellen wir fest, dass der Punkt (2|1) auf der Diagonale y=x gespiegelt wird und dem Punkt (1|2) entspricht. Man sagt in diesem Fall, dass die indirekte Proportionalität ihre eigene Umkehrfunktion ist.
Wenn eine Funktion die Spiegelung einer anderen Funktion über die Achse y=x ist, dann ist sie ihre Umkehrfunktion. Das Umgekehrte gilt auch: Umkehrfunktionen werden auf der Diagonale y=x gespiegelt. Umkehrfunktionen werden oft mit Hochzahl −1 dargestellt. Beispielsweise wird die Umkehrfunktion von mit dargestellt. Für die Umkehrfunktionen allgemeiner gilt:
Wenn dann
Um die Umkehrfunktion zu finden, müssen wir auf die unabhängige Variable umformen. Um die Umkehrfunktion darzustellen, müssen wir die Funktion auf der Diagonale y=x spiegeln. In den folgenden Bildern sehen wir jeweils ein Paar von Umkehrfunktionen:
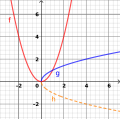

In vielen Fällen kommt es vor, dass die Umkehrfunktion einer Funktion aus mehreren Teilefunktionen besteht, da sie sonst keine Funktion mehr ist. Das gilt z.B. für die zwei Funktionen um die x-Achse im Bild "Quadrat und Wurzel", die wir auch am Anfang dieses Teils gesehen haben. Sie sind die Funktionen und . Zusammen sind sie die Umkehrung der Funktion , die im Bild auch zu sehen ist. Man sagt daher, dass die Umkehrung der Funktion aus zwei "Zweige" besteht, die Funktion und die Funktion . Im Bild "Umkehrung mit drei Zweigen" sehen wir ein ähnliches Beispiel (für eine kubische Funktion und die entsprechende Umkehrung, die einer kubischen Wurzel entspricht und aus drei Zweigen besteht).
Die Darstellung mit mehreren Zweigen macht allerdings nicht immer Sinn. Die Umkehrfunktionen der trigonometrischen Funktionen beständen in diesem Fall aus unendlich vielen Zweigen. In den folgenden Bildern sehen wir die Umkehrfunktionen von Sinus, Kosinus und Tangens. Der Definitionsbereich für Sinus und Kosinus beschränkt sich auf das Intervall , der Wertebereich auf das Intervall bzw. .
-
sin und arcsin
-
cos und arccos
-
arctan
Funktionserkennung in Text
[Bearbeiten]Lineare und Exponentialfunktion
[Bearbeiten]Vergleichen wir zunächst einmal folgende Texte:
- Ein 40 cm hoher Baum wächst jedes Jahr um 30 cm.
- Ein 40 cm hoher Baum wächst jedes Jahr um 30%.
- Die Höhe eines 40 cm hohen Baum wird jedes Jahr das 1,3-fache des vorherigen Jahrs.
- Ein 40 cm hoher Baum wächst jedes Jahr um 130%.
- Ein 40 cm hoher Baum wächst jedes Jahr 12 cm.
Es gibt einen entscheidenden Unterschied in den Texten.
- Im ersten und fünften Text wird die Änderung in Einheiten gegeben. Es gibt bei der Änderung keinen Vergleich zum Anfangswert. In diesem Fall haben wir eine lineare Funktion. Jede Änderung der unabhängigen Variablen (hier der Zeit) um eine Einheit, bewirkt die Änderung der abhängigen Variable um immer die gleichen Anzahl ihrer Einheiten. Im ersten Beispiel: Jedes Jahr (eine Einheit der unabhängigen Variable), wird die Höhe (abhängige Variable) genau 30 cm ändern. Diese Änderungsrate (30 cm/Jahr) wird die Steigung der Funktion sein und bleibt vom Jahr zum Jahr gleich. Der Wert am Anfang wird der y-Achsenabschnitt sein.
- Im zweiten, dritten und vierten Text wird die Änderung als Anteil angegeben ("Prozent", "-fach"). Die Änderung in Einheiten bleibt daher vom Jahr zum Jahr nicht die gleiche. Der Anfangswert für den Vergleich wird jedes Jahr ein neuer Wert sein. Beispielsweise sind 30% von 40 cm 12 cm. Der Baum wird daher nach einem Jahr 52 cm sein. Am nächsten Jahr wird er wieder 30% wachsen, das sind aber nicht mehr 12 cm sondern 30% von 52 cm, also 15,6 cm. Der Baum wächst jedes Jahr nicht um den gleichen Wert sondern um den gleichen Anteil. Es gibt keine feste Steigung, wir haben daher sicherlich keine lineare Funktion. In diesem Fall geht es um eine Exponentialfunktion.
Vertiefen wir jetzt etwas mehr in den Eigenschaften dieser beiden Funktionen.
- Bei der linearen Funktion ist die Steigung s durch eine Änderungsrate angegeben. Wenn sie positiv ist, ist die Funktion steigend, wenn negativ fallend. Wenn noch eine Zahl in der Textaufgabe angegeben ist, sollte sie der Wert am Anfang sein, also der y-Achsenabschnitt Ay. Selbstverständlich müssen wir darauf aufpassen, dass die Einheiten übereinstimmen. Die Funktion ist dann:
In unserem Beispiel: - Bei der Exponentialfunktion ist die Sache teilweise etwas komplizierter. Das einfachste ist der y-Achsenabschnitt Ay. Er ist so viel wie der Anfangswert, genauso wie bei der linearen Funktion. In der Exponentialfunktion wird er allerdings addiert, sondern mit der Potenzzahl multipliziert. Die Hochzahl wird die unabhängige Variable sein. Die Basis der Potenz müssen wir erst berechnen. Sie ist der Wachstumsanteil WA(als Zahl und nicht als Prozent) um 1 erhöht. In unserem Beispiel ist der Jahreswachstum 30% also 0,3. 0,3 um 1 erhöht ist 1,3. Diese Zahl wird die Basis sein:
In unserem Beispiel:
Ob die Exponentialfunktion steigend oder fallend ist, hängt sowohl vom Vorzeichen des Anfangswert als auch von der Basis der Potenz ab:- Wenn der Anfangswert positiv ist, ist die Darstellung der Funktion im ganzen Diagramm oberhalb der x-Acshe.
- Ist die Basis mehr als 1, dann ist die Funktion steigend, mit Basis weniger als 1 ist sie fallend.
- Ist die Basis weniger als 1, dann ist die Funktion fallend, mit Basis mehr als 1 ist sie steigend.
- Wenn der Anfangswert negativ ist, ist die Darstellung der Funktion im ganzen Diagramm unterhalb der x-Acshe.
- Ist die Basis mehr als 1, dann ist die Funktion fallend, mit Basis weniger als 1 ist sie steigend.
- Ist die Basis weniger als 1, dann ist die Funktion steigend, mit Basis mehr als 1 ist sie fallend.
- Trivialfall: Basis 1, dann ist ja die Funktion eine Konstante...
- Wenn der Anfangswert positiv ist, ist die Darstellung der Funktion im ganzen Diagramm oberhalb der x-Acshe.
Noch drei Sachen:
- Im fünften Text ist das Wachstum das erste Jahr 30%. Der Baum wächst das erste Jahr 12 cm und 12 cm sind 30% von 40%. Das zweite Jahr ist allerdings das Wachstum in Prozent doch weniger. Der Baum ist jetzt 52 cm und wächst wieder 12 cm, was ca. 23% ist!
- Im vierten Text ist das Wachstum 130%, also 1,3. Das wird NICHT die Basis der Potenz in der Exponentialfunktion sein. Diese Zahl müssen wir erst um 1 erhöhen. Die Basis wird daher in diesem Fall 2,3 sein.
- Die Funktion im zweiten und dritten Text ist genau die gleiche Exponentialfunktion: . Wenn der Wert jedes nächste das 1,3-fache des vorherigen Jahres ist, dann ist 0,3 (also 30%) mehr. Wenn die Aufgabe mit einem Vielfachen ausgedrückt wird, ist die Basis dieses Vielfache.
Periodische Funktionen und Polynomfunktionen
[Bearbeiten]Wie der Name schon andeutet, sind periodische Funktionen Funktionen die sich wiederholen. Es gibt viele verschiedene periodische Funktionen, hier werden wir uns mit den trigonometrischen Funktionen Sinus, Kosinus und Tangens beschäftigen. Die allgemeine Formel für die Sinusfunktion ist:
ist die maximale Ablenkung, Amplitude genannt. ist die sogenannte Winkelfrequenz. Die wird mit Hilfe der Periode T berechnet:
Daher können wir die Formel auch in Bezug auf die Periode schreiben:
Die Formeln für Kosinus und Sinus entsprechen der Formel für Sinus:
Teile einer Polynomfunktion können auch wie eine Sinusfunktion aussehen. Bei Textaufgaben ist es allerdings leicht zu erkennen, wann eine trigonometrische Funktion vorkommt. Das Wort Wiederholung oder Periode oder was ähnliches wird vorkommen. Von den Polynomfunktionen kommt die lineare Funktion oft vor, sie ist allerdings sehr leicht im Text von einer periodische Funktion zu erkennen. Die Polynomfunktionen von einem höheren Grad kommen in allen Wissenschaften oft vor. Sie werden in der Regel explizit erwähnt, entweder in der Angabe oder durch eine Formel.
Indirekte Proportionalität
[Bearbeiten]Die indirekte Proportionalität kommt in der Wissenschaft oft in Formeln der Form . In dieser Formel besteht eine indirekte Proportionalität zwischen a und c. Zwischen a und b wie auch zwischen b und c besteht eine direkte Proportionalität. Hier sind ein paar Beispiele aus der Physik:
- Dichte:
m steht für die Masse und V fürs Volumen. Bei gleicher Masse ist die Dichte desto kleiner, je größer das Volumen ist. Wenn 1 kg Wasser und 1 kg Eisen verglichen werden, wird das Wasser viel mehr Volumen haben, also eine kleine Dichte. - Druck:
F steht für die Kraft, A für die Fläche. Bei gleicher Kraft ist der Druck desto kleiner, je größer die Fläche ist. Wenn wir einen Nagel mit dem Kopf an die Wand einschlagen, wird er kaum oder gar nicht eindringen. - Geschwindigkeit:
s steht für die zurückgelegte Strecke, t für die Zeit. Bei gleicher Strecke ist die Geschwindigkeit desto kleiner, je größer die Zeit ist. Wenn wir mehr Zeit brauchen, sind wir langsamer. - Stromstärke:
U steht für die Spannung, R für den Widerstand. Bei gleicher Spannung ist die Stromstärke desto kleiner, je größer der Widerstand ist. Der elektrische Widerstand wirkt ja gegen den elektrischen Strom.
Logarithmusfunktion
[Bearbeiten]Die Logarithmusfunktion ist die Umkehrfunktion der Exponentialfunktion. Sie wird nur für x>0 definiert. Ihre Wertebereich ist allerdings die ganzen reellen Zahlen. Logarithmus wird bei der Einheiten von verschiedenen Größen benutzt, die sich exponentiell ändern. Solche logarithmische Skalas sind z.B. die "Lautstärke" (logarithmische Einheit: Dezibel, dB), der saure oder basische Charakter einer wässrigen Lösung (logarithmische Größe: pH-Wert), die stärke eines Erdbebens (logarithmische Richterskala), die Helligkeit von Sternen usw.. In der Regel wird es explizit erwähnt, dass es gerade um eine logarithmische Größe geht.
Statistik und Wahrscheinlichkeitsrechnung
[Bearbeiten]Baumdiagramm
[Bearbeiten]
Denken wir an das folgende mathematische Problem:
|
In einer Urne gibt es 5 schwarze und 4 rote Kugeln. Wir ziehen drei mal zufällig
|
Am Anfang haben wir 4 roten Kugeln und 9 insgesamt, daher ist die Wahrscheinlichkeit, dass wir eine rote Kugel ziehen . Wenn wir ein rote ziehen, dann gibt es noch 3 roten von insgesamt 8, also sie die Wahrscheinlichkeit . Wir können allerdings alle mögliche Ergebnisse in ein sogenanntes "Baumdiagramm" darstellen, wie im Bild links. Der einzige Pfad, wo drei rote Kugeln gezogen werden, ist der ganz links. Um die Wahrscheinlichkeit, dass drei roten Kugeln gezogen werden, zu berechnen, müssen wir das Produkt der Wahrscheinlichkeiten von jedem Schritt bilden.
Warum multiplizieren wir in diesem Fall? Wir können an ein ganz einfaches Beispiel denken. Denken wir einfach an eine Schokoladentafel. Wenn wir davon nehmen, dann haben dieses Bild: . Wenn wir von diesen nehmen, dann haben wir ein neues Bild: . Jeder kleiner Teil in diesem neuen Bild ist der Schokolade und wir haben 6 solchen Teil. Daher haben wir die beiden Brüchen multipliziert: . Genauso ist es mit der Wahrscheinlichkeit. Bei jedem Schritt nehmen wir einen Teil des neuen Teils, wir müssen daher multiplizieren. Somit ist die Antwort zur ersten Frage: . Genauso können wir die Antwort zur Frage B finden:
Für jeden Pfad müssen wir das Produkt der Wahrscheinlichkeit von jedem Schritt bilden. Wenn aber eine Frage durch verschiedene Pfade erfüllt wird, dann müssen wir die Wahrscheinlichkeiten der unterschiedlichen Pfade addieren. Im Beispiel mit der Schokolade können wir so denken, dass verschiedene Personen die ganze Schokolade (Wahrscheinlichkeit 1) teilen und dass wir dann die Teile von mehrere Personen zusammenrechnen wollen. Das ist der Fall in Fragen C und D. In beiden Fragen gibt es drei Pfade, die das gefragte erfüllen:
- C)
- D)
Für die letzte Fragen müssen wir einfach dazu denken, dass in diesem Fall bei jedem Schritt die Wahrscheinlichkeit gleich bleibt:
- E)
Satz von Bayes
[Bearbeiten]Satz von Bayes konkretes Beispiel
[Bearbeiten]
|
Die Sensitivität des gewöhnlichen AIDS Tests ist ca. 99,9%, die |
Im deutschsprachigen Raum zuerst. Von 100 Millionen Menschen sind
Personen krank.
Von denen werden als positiv
positiv diagnostiziert, die restlichen 150 als negativ.
Gesund sind die restlichen
Personen. Von denen werden als
negativ diagnostiziert, die restlichen 199700 als positiv.
Die Schritten können wir in der folgenden Abbildung zusammengefasst sehen:
Stellen wir die Ergebnisse in einer Tabelle dar:
| Positiv | Negativ | Teilsummen | |
| Krank | 149850 | 150 | 150000 |
| Gesund | 199700 | 99650300 | 99850000 |
| Teilsummen | 349550 | 99650450 | 100000000 |
Wenn wir die Spalte mit den positiven Ergebnissen beobachten, stellen
wir fest, dass von den 349550 positiven Tests 149850 tatsächlich krank
sind, also
In Südafrika hingegen sieht die Tabelle so aus:
| Positiv | Negativ | Teilsummen | |
| Krank | 10989000 | 11000 | 11000000 |
| Gesund | 88000 | 43912000 | 44000000 |
| Teilsummen | 11077000 | 43923000 | 55000000 |
Wenn wir die Spalte mit den positiven Ergebnissen beobachten, stellen
wir fest, dass von den 11077000 positiven Tests 10989000 tatsächlich krank
sind, also
Wir können daher den Schluss ziehen, dass die Aussagekraft eines Krankheitstests
stark von der Häufigkeit der Krankheit in einer Gruppe abhängig sein kann.
Wir sehen daher, dass der Satz von Bayes zu Folgerungen führen kann, die intuitiv nicht so leicht zu verstehen sind.
Satz von Bayes abstraktes Beispiel
[Bearbeiten]|
Die bedingte Wahrscheinlichkeit eines Ereignisses A unter |
|
|
Nun, um diesen Satz zu verstehen, können wir ein einfaches Beispiel bringen.
|
In der Klasse W gibt es 15 Mädchen, davon sind 60% Blond, |
In der Klasse W sind 60% der 15 Mädchen blond, also 0,6·15=9 Blondinen.
In der Klasse S sind 35% der 20 Mädchen blond, also 0,35·20=7 Blondinen.
Daher sind in der Party insgesamt 9+7=16 Blondinen von insgesamt 15+20=
35 Mädchen. Lass uns die ganzen Zahlen in einer Tabelle schreiben:
|
P(S|B) ist die gefragte Wahrscheinlichkeit. In der Party gibt es 16 Blondinen, von denen 7 aus der Klasse S kommen. Wenn jemand mit einer Blondine schon spricht, ist die Wahrscheinlichkeit, dass sie aus der Klasse S kommt: . Diese Wahrscheinlichkeit ist nicht die gleiche mit der Wahrscheinlichkeit, dass irgendein Mädchen (blond oder nicht) aus der Klasse S kommt. Für diese Wahrscheinlichkeit brauchen wir die ganze Anzahl der Mädchen (35) und die Anzahl der Mädchen in der S Klasse (20): . Wir sehen also: die Wahrscheinlichkeit, dass ein Mädchen aus der Klasse S kommt, unter der Voraussetzung, dass sie Blond ist, hängt von drei Sachen ab:
Schreiben wir den Satz für diesen konkreten Fall:
Benutzen wir konkrete Zahlen, um diesen Satz zu erklären. Fangen wir mit der gefragten Wahrscheinlichkeit an:
Von den 16 Mädchen, die in der Party sind, sind 7 aus der Klasse S. Zähler und Nenner können wir als Bruch (beides durch 1) schreiben und wir können den Zähler mit der Anzahl der Mädchen in der S Klasse (20) erweitern. Daraus entsteht ein Doppelbruch:
Der Bruch im Zähler ist die Wahrscheinlichkeit P(B|S), dass ein Mädchen Blond ist, wenn es aus der Klasse S kommt: von den 20 Mädchen in der Klasse S sind 7 Blond. Wir können also diesen Bruch durch P(B|S) ersetzten und den Bruch etwas mehr bearbeiten, indem wir Zähler und Nenner des Doppelbruches mit erweitern:
Der Bruch im Zähler ist nichts anders, als die Wahrscheinlichkeit P(S), dass ein Mädchen (blond oder nicht) aus der Klasse S kommt. Es sind ja insgesamt 35 Mädchen, von denen 20 aus der Klasse S sind. Der Bruch im Zähler ist nichts anders, als die Wahrscheinlichkeit P(B), dass ein Mädchen blond ist. Es sind ja insgesamt 35 Mädchen, von denen 16 Blond sind. Wenn wir die Brüche durch die entsprechenden Wahrscheinlichkeiten ersetzten, kommen wir zum Satz von Bayes:
|
Im allgemeinen Fall wird das Symbol A anstatt B und B anstatt S benutzt:
| Satz von Bayes |
|
|
|
Die bedingte Wahrscheinlichkeit eines Ereignisses A unter der |
Diesen Satz können wir dann direkt in einem abstrakten Beispiel benutzten:
|
Die Sensitivität des gewöhnlichen AIDS Tests ist ca. 99,9%, die |
Wir suchen die Wahrscheinlichkeit P(K|T+), dass eine Person Krank (K) ist unter der Voraussetzung, dass der Test Positiv (T+) ist. Nach dem Satz von Bayes brauchen wir dafür:
- Die Wahrscheinlichkeit P(T+|K) dass ein Test positiv ist, wenn die Person krank ist. Das ist die Sensitivität 99,9%, also 0,999.
- Die Wahrscheinlichkeit P(K) dass eine Person Krank ist. Das ist die Häufigkeit der Krankheit in der Bevölkerung, Prävalenz genannt: 0,15% also 0,0015.
- Die Wahrscheinlichkeit P(T+) dass ein Test allgemein in der Bevölkerung positiv ist. Das ist 0,34955 %, also 0,0034955.
Diese Wahrscheinlichkeit weicht stark von der Sensitivität ab. Intuitiv denken wir, dass wir sicher krank sind, wenn der Test positiv ist, wenn seine Sensitivität so hoch ist (hier 99,9%). Die Sensitivität zeigt allerdings nur wie viel Prozent der Kranken mit dem Test tatsächlich erwischt werden. Das ist aber etwas anderes als der Anteil der Personen mit positivem Test, die tatsächlich krank sind. Nicht nur (fast) alle Kranke werden positiv gezeigt, sondern auch einige Gesunde. Das könnte z.B. daran liegen, dass ein anderer Virus, der keine Krankheit verursacht, Ähnlichkeiten mit dem Krankheitsvirus aufweist. Daher kann der Test manchmal positiv sein, auch wenn die Person nicht krank ist und daher gibt es mehrere Positive als Kranke. Wenn die Krankheit wirklich selten vorkommt, ist die Wahrscheinlichkeit, dass jemand beim positiven Test krank ist, nicht unbedingt so hoch. In unserem (tatsächlichen) Beispiel ist sie weniger als 50%!

































































![{\displaystyle \textstyle a^{1 \over m}={\sqrt[{m}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fea6f5273a124a9040ac9a26a48c1b641b2fee32)
![{\displaystyle {\begin{aligned}{\sqrt {a}}&=b&&\rightarrow \quad a=b^{2}\\{\sqrt[{-5}]{m}}&=n&&\rightarrow \quad m=n^{-5}\\{\sqrt[{4,3}]{m}}&=n&&\rightarrow \quad m=n^{4,3}\\{\sqrt[{\sqrt {6}}]{x}}&=z&&\rightarrow \quad x=z^{\sqrt {6}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e817daca16798c8dce8f4260b45ac53419d7b8f)
![{\displaystyle {\sqrt[{m}]{a}}=b\quad \rightarrow \quad a=b^{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f5e730a5129a881eaff79b220dc1a6ea326ed54)



![{\displaystyle ({\sqrt[{n}]{a}})^{n}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84e72f3f41f93d141f4e8df331367846c1b3c856)









![{\displaystyle ({\sqrt[{n}]{a}})^{n}={(a^{1 \over n})}^{n}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98f416c685cc71862c3aad3f9e3d909444904823)
![{\displaystyle {\sqrt[{n}]{a}}=a^{1 \over n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eb00d02a7cdd73d845e32f7a648aa75e297e93d)
![{\displaystyle {\sqrt[{m}]{a^{n}}}=({\sqrt[{m}]{a}})^{n}=a^{n \over m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6419cb1b8600ea98519e7c274a6a091d06c5b22)
![{\displaystyle {\sqrt[{n}]{a^{n}}}=({\sqrt[{n}]{a}})^{n}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af274240c4278adde49b27adf3aec8844f4fadbb)
![{\displaystyle a^{1 \over m}={\sqrt[{m}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81b4d6953524a07958bc266d9659c2af38fa4730)
![{\displaystyle {\left({\sqrt[{35}]{w^{-5}}}\right)}^{-14}={\left[{(w^{-5})}^{1 \over 35}\right]}^{-14}=w^{(-5)\cdot {1 \over 35}\cdot {(-14)}}=w^{70 \over 35}=w^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09d003e6edb8db67f9b6539e446c9c7052c0f7dc)
![{\displaystyle {\left({\sqrt[{35}]{w^{-5}}}\right)}^{-14}={\left[{(w^{-5})}^{1 \over 35}\right]}^{-14}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/946b53d72917eb518fc6703a71c3b1d40f11a248)

![{\displaystyle {\left[{(w^{-5})}^{1 \over 35}\right]}^{-14}=w^{(-5)\cdot {1 \over 35}\cdot {(-14)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/984f233022bc759bf4fcec545b6c3a0276e22463)


![{\displaystyle {\left(b^{3 \over 7}\right)}^{28 \over 9}=b^{{\frac {3}{7}}\cdot {\frac {28}{9}}}=b^{\frac {4}{3}}\left(={\sqrt[{3}]{b^{4}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b78068f1ad9bc755f945b02959c02dd1a14c7476)
![{\displaystyle \left(\left(b^{3 \over 5}\right)^{3}\cdot {\sqrt[{5}]{b^{6}}}\cdot b^{-2}\right)^{29}=\left(b^{{\frac {3}{5}}\cdot 3}\cdot {b^{6 \over 5}}\cdot b^{-2}\right)^{29}=\left(b^{{\frac {9}{5}}+{\frac {6}{5}}-2}\right)^{29}=\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/97585b67800a1cf4001bdbd1740e03a7676001a4)

![{\displaystyle \left(\left(b^{3 \over 5}\right)^{3}\cdot {\sqrt[{5}]{b^{6}}}\cdot b^{-2}\right)^{29}=\left(b^{{\frac {3}{5}}\cdot 3}\cdot {b^{6 \over 5}}\cdot b^{-2}\right)^{29}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dda6c22b695620816cd53096fdee0a6f60554e1)



![{\displaystyle {\dfrac {\sqrt[{3}]{{\Bigl (}b^{15 \over 7}{\Bigr )}^{28}}}{b^{3} \over b^{-8}}}={\frac {\left(b^{\frac {15}{7}}\right)^{28 \over 3}}{b^{3-(-8)}}}={\frac {b^{{\frac {15}{7}}\cdot {\frac {28}{3}}}}{b^{3+8}}}={\frac {b^{20}}{b^{11}}}=b^{9}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ad337a347bc7a74f1ca8e8f230490838fd06c34)
![{\displaystyle {\sqrt[{3}]{{\Bigl (}b^{15 \over 7}{\Bigr )}^{28}}}={\left(b^{\frac {15}{7}}\right)^{28 \over 3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0da10f6a4e890d81881d5b5bfc7b7fa0d9893311)














![{\displaystyle a^{3}=V\quad \Leftrightarrow a={\sqrt[{3}]{V}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13e089531b0b849c30e68a58e08ec463f735480f)
![{\displaystyle a={\sqrt[{3}]{530}}\approx 8,1\ (cm)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49655481613f3158bf6b0ebfed724cac6bc75745)

![{\displaystyle {\begin{aligned}{\sqrt[{3}]{1}}&=1\\{\sqrt[{3}]{27}}&=3\\{\sqrt[{3}]{343}}&=7\\{\sqrt[{3}]{9{,}261}}&=2{,}1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ead9293b8d5c52aa98cd099bb701bcace3f323db)
![{\displaystyle {\begin{aligned}{\sqrt[{4}]{a}}&=b&&\rightarrow \quad a=b^{4}\\{\sqrt[{5}]{m}}&=n&&\rightarrow \quad m=n^{5}\\{\sqrt[{-10}]{x}}&=z&&\rightarrow \quad x=z^{-10}\\{\sqrt[{35}]{p}}&=q&&\rightarrow \quad p=q^{35}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f92aae84faa1f8fc8e22c1bff0579f406f9362fd)
![{\displaystyle {\begin{aligned}{\sqrt[{4,3}]{a}}&=b&&\rightarrow \quad a=b^{4,3}\\{\sqrt[{0,3}]{m}}&=n&&\rightarrow \quad m=n^{0,3}\\{\sqrt[{\sqrt {6}}]{x}}&=z&&\rightarrow \quad x=z^{\sqrt {6}}\\{\sqrt[{x}]{p}}&=q&&\rightarrow \quad p=q^{x}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10a01830f5a736aaff92414b26ff4f0c34067d7b)
![{\displaystyle {\sqrt[{2}]{m}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4650b423e45e729f221a0e20f736a031e38bfbd)

































![{\displaystyle {\boldsymbol {m}}={\frac {2\cdot c_{L}\cdot k_{B}\cdot T\cdot d}{[d\cdot (2{,}2-a)+l]\cdot v^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8df884a41b99e6f4f04586aa26a1e15fafc78d86)





















![{\displaystyle {\sqrt[{n}]{x}}=a\Rightarrow x=a^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/561512a576d22165e0db8467433081aff8a29a9a)


![{\displaystyle B_{x}=B_{0}\cdot 1{,}02^{x}\ \Rightarrow \ 100=30\cdot 1{,}02^{x}\ \Rightarrow \ {\frac {100}{30}}=1{,}02^{x}\ \Rightarrow \ {\sqrt[{x}]{\frac {100}{30}}}=1{,}02}](https://wikimedia.org/api/rest_v1/media/math/render/svg/470b7dd91177167e40233a3b1c3f726511d3ac2f)






























![{\displaystyle \log _{5}\left({\frac {0{,}04}{{\sqrt[{3}]{d^{5}\cdot 5^{d}\cdot 5^{5}}}\ \ }}\cdot 125{\sqrt[{5}]{5}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e02c115ef7d44b4a7e3a5a8ae2c67d80ded2a950)
![{\displaystyle \log _{5}\left({\frac {0{,}04}{{\sqrt[{3}]{d^{5}\cdot 5^{d}\cdot 5^{5}}}\ \ }}\cdot 125{\sqrt[{5}]{5}}\right)=\log _{5}0{,}04-\log _{5}{\sqrt[{3}]{d^{5}\cdot 5^{d}\cdot 5^{5}}}+\log _{5}125+\log _{5}{\sqrt[{5}]{5}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4a658c60599986f263bf68a86b31a761b01dd7a)

![{\displaystyle {\sqrt[{3}]{d^{5}\cdot 5^{d}\cdot 5^{5}}}=\left(d^{5}\cdot 5^{d}\cdot 5^{5}\right)^{\tfrac {1}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05bc2f2d8579b6dd40e9c664424f9c2315cd6d72)
![{\displaystyle {\sqrt[{5}]{5}}=5^{\tfrac {1}{5}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/496f39137be415280f48e09c1342a3e6a38decdd)
![{\displaystyle \log _{5}0{,}04-\log _{5}{\sqrt[{3}]{d^{5}\cdot 5^{d}\cdot 5^{5}}}+\log _{5}125+\log _{5}{\sqrt[{5}]{5}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c3e87867e65d7999c4a8fb3d9264c66c694eccc)












![{\displaystyle a+3-3=a\qquad b\cdot t:t=b\qquad ({\sqrt[{n}]{w\ }})^{n}=w\qquad {\sqrt[{n}]{w^{n}\ }}=w}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65ef697e5968913ecf080be618d33517bf5f6a55)




















































































![{\displaystyle \phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{\;\,\ddots }}}}}}}}=[1;{\overline {1}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e491fb1128692468f14dcb61d34513a796aa07b6)



































![{\displaystyle \left[{\begin{matrix}9&3&1\\2{,}25&1{,}5&1\\4&2&0\end{matrix}}\left|{\begin{matrix}5\\4{,}5\\0\end{matrix}}\right.\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e18390e2731f54e621fba0f9005555af0115614)
![{\displaystyle \left[{\begin{matrix}1&0&0\\0&1&0\\0&0&1\end{matrix}}\left|{\begin{matrix}\textstyle {L_{a}}\\\textstyle {L_{b}}\\\textstyle {L_{c}}\end{matrix}}\right.\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0bb8f6580fd09bd0c2f745438fb0191be185e9)



![{\displaystyle \left[{\begin{matrix}9&3&1\\2{,}25&1{,}5&1\\4&2&0\end{matrix}}\left|{\begin{matrix}5\\4{,}5\\0\end{matrix}}\right.\right]{\begin{matrix}\textstyle {\frac {\qquad }{}}\\I-II\\\textstyle {\frac {\qquad }{}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5efec2cb32ec2cf47220af9b3fe24c2a1b83cf9)






![{\displaystyle \left[{\begin{matrix}9&3&1\\6{,}75&1{,}5&0\\4&2&0\end{matrix}}\left|{\begin{matrix}5\\0{,}5\\0\end{matrix}}\right.\right]{\begin{matrix}\textstyle {\frac {\qquad }{}}\\\textstyle {\frac {\qquad }{}}\\{4\,II-3\,III}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/555940a7b8a02e3e9335379a6e6f9b10db95ec5b)
![{\displaystyle \left[{\begin{matrix}9&3&1\\6{,}75&1{,}5&0\\15&0&0\end{matrix}}\left|{\begin{matrix}5\\0{,}5\\2\end{matrix}}\right.\right]{\begin{matrix}\textstyle {\frac {\qquad }{}}\\II\,-0{,}45\,III\\:15\qquad \qquad \end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c49c925d8595d992dc332be21c7987d739a5d1b7)
![{\displaystyle \left[{\begin{matrix}9&3&1\\0&1{,}5&0\\1&0&0\end{matrix}}\left|{\begin{matrix}5\\-0{,}4\\\textstyle {\frac {2}{15}}\end{matrix}}\right.\right]{\begin{matrix}-2\,II-9\,III\\:1{,}5\qquad \qquad \\\textstyle {\frac {\qquad }{}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46d71bfe49235220a236a90c2b1a762514a3dd5a)
![{\displaystyle \left[{\begin{matrix}0&0&1\\0&1&0\\1&0&0\end{matrix}}\left|{\begin{matrix}\textstyle {\frac {23}{5}}\\\textstyle {-{\frac {4}{15}}}\\\textstyle {\frac {2}{15}}\end{matrix}}\right.\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b22be5fe05d5281549c8d41e2e3f12b60707144)










































![{\displaystyle +\leftrightarrow -\qquad \cdot \leftrightarrow :\qquad {\sqrt[{n}]{\ a\ }}\leftrightarrow a^{n}\qquad \sin \leftrightarrow \arcsin \qquad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/02ac63f6bf5cbcffab5dc26ea4299e2dd1647491)


















































































































































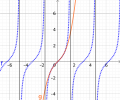















![{\displaystyle [-1,\ 1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af00b66b52652ce32454518d1223d68508bd1aed)
![{\displaystyle \textstyle [-{\frac {\pi }{2}},\ {\frac {\pi }{2}}]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8312161c0da8a8efb637b656681f50cd92348725)
![{\displaystyle [0,\ \pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d344e727733ee1859f2b80cb08efe2f4a59b38d2)






































































