Lim sup und Lim inf – Serlo „Mathe für Nicht-Freaks“
Der Limes superior und der Limes inferior ist der größte und der kleinste Häufungspunkt einer Folge. Diese dienen als partiellen Ersatz für den Grenzwert, wenn dieser nicht existiert.
Motivation
[Bearbeiten]Der Grenzwert einer Folge ist diejenige Zahl, gegen die eine Folge im Unendlichen strebt. In jeder Umgebung um den Grenzwert liegen fast alle Folgenglieder und damit befinden sich nur endlich viele Folgenglieder außerhalb einer beliebigen Umgebung:

Auch, wenn nicht jede Folge einen Grenzwert besitzt, kann man sowohl bei konvergenten als auch bei divergenten Folgen einiges über ihr Verhalten im Unendlichen aussagen. Im Kapitel „Häufungspunkt einer Folge“ haben wir bereits das Konzept des Häufungspunkts als Verallgemeinerung des Grenzwerts kennengelernt. Der Häufungspunkt ist eine Zahl, gegen die ein Teil der Folge strebt und um die sich deswegen die Folgenglieder „häufen“. Damit können sie benutzt werden, um das Verhalten einer Folge im Unendlichen zu beschreiben.
Durch Angabe des größten und des kleinsten Häufungspunkts können wir den Bereich einschränken, wo sich diese Häufungspunkte befinden. Der größte Häufungspunkt wird dabei Limes superior und der kleinste Limes inferior genannt. Dabei verwenden wir für den größten Häufungspunkt einer Folge den Ausdruck und für den kleinsten Häufungspunkt .
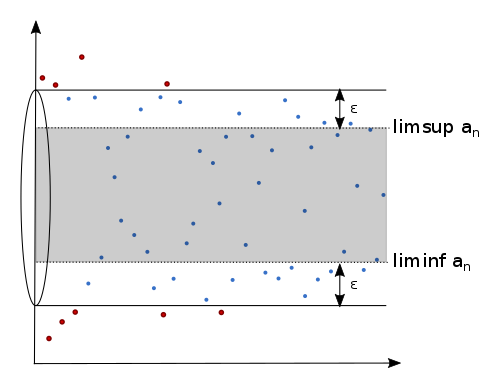
Das abgeschlossene Intervall zwischen dem kleinsten und größten Häufungspunkt ist eine Art „verallgemeinertes Grenzwertintervall“. Wir können nämlich zeigen, dass sich bei beschränkten Folgen in jeder Umgebung um dieses Intervall fast alle Folgenglieder befinden. Außerhalb einer solchen Umgebung befinden sich nur endlich viele Folgenglieder. In der folgenden Abbildung ist dies für eine Epsilon-Umgebung um dieses Intervall illustriert. Außerhalb dieses "Schlauchs" befinden sich nur endlich viele Folgenglieder und innerhalb fast alle:
Definition
[Bearbeiten]Wir wollen eine Folge genauer durch die Bestimmung des kleinsten und größten Häufungspunkts beschreiben. Dadurch schwächen wir den Grenzwertbegriff ab und gewinnen einen anderen Blick auf die Folge. Der größte Häufungspunkt wird Limes superior genannt und wird bei einer Folge mit bezeichnet. Der kleinste Häufungspunkt ist der Limes inferior und wird als beschrieben:
Definition (Limes superior)
Der Limes superior einer Folge ist bei nach oben beschränkten Folgen der größte Häufungspunkt dieser Folge und wird mit bezeichnet. Bei nach oben unbeschränkten Folgen schreiben wir .
Definition (Limes inferior)
Der Limes inferior einer Folge ist bei nach unten beschränkten Folgen der kleinste Häufungspunkt dieser Folge und wird mit bezeichnet. Bei nach unten unbeschränkten Folgen setzen wir .
Beispiele
[Bearbeiten]Beispiel
Wir zerlegen die Folge in ihre eigenen Bestandteile, indem wir dazu die Folgen und definieren.
Die Teilfolgen der divergenten Folge haben die Häufungspunkte und .
Die Folge ist dahingegen bestimmt divergent mit .
Wir fügen nun die "Grenzwerte" von und zusammen. Aufgrund von ergibt sich die nach unten unbeschränkte Folge . Da gilt, erhalten wir die nach oben unbeschränkte Folge .
Somit gilt und .
Beispiel
Ist , so ist . Da die Folge konvergiert, hat sie nur den Häufungspunkt . Daher ist
Beispiel
Ist , so ist . Also ist nach oben unbeschränkt. Somit ist . Des Weiteren ist nach unten (durch ) beschränkt und besitzt keine Häufungspunkte, da fast alle sind. Daher ist auch .
Zusammenhang mit Grenzwert
[Bearbeiten]Eine Folge konvergiert genau dann, wenn der Limes superior und der Limes inferior existieren und übereinstimmen:
Satz (Limes superior/inferior und Konvergenz)
Eine Folge konvergiert genau dann, wenn gilt:
Wie kommt man auf den Beweis? (Limes superior/inferior und Konvergenz)
Wir müssen die Äquivalenz
zeigen.
Die Hin-Richtung "" des Beweises ist einfach. Da jede konvergente Folge beschränkt ist, folgt sie unmittelbar aus der Definition von und .
Für die Rück-Richtung "" verwenden wir die alternativen Umgebungs-Definitionen von Grenzwert und Häufungspunkt. Zur Erinnerung:
Eine Folge konvergiert genau dann gegen , wenn fast alle , und eine Folge hat den Häufungspunkt , wenn unendlich viele .
Beweis (Limes superior/inferior und Konvergenz)
Beweisschritt 1: ""
Konvergiert gegen , so ist beschränkt, und ist der einzige Häufungspunkt der Folge. Nach Definition ist daher
Beweisschritt 2: ""
Gelte .
Da der größte Häufungspunkt von ist, liegen nach den alternativen Definitionen eines Häufungspunktes und des Grenzwertes für alle unendlich viele Folgenglieder in und fast alle Folgenglieder in .
Da der kleinste Häufungspunkt von ist, liegen für alle unendlich viele Folgenglieder in und fast alle Folgenglieder in .
Also liegen für alle fast alle Folgenglieder in , d.h. konvergiert gegen .
An ursprünglichen Autor: Alternativen Widerspruchsbeweis für eine Richtung ergänzen, evtl. Skizze zum Satz ergänzen
Hinweis
Der Satz lässt sich auch auf bestimmt divergente Folgen übertragen. Es gilt
Aufgabe (Limes superior/inferior und unbestimmte Divergenz)
Beweise die Aussage für .
Wie kommt man auf den Beweis? (Limes superior/inferior und unbestimmte Divergenz)
Wieder müssen wir beide Richtungen zeigen. Die Hinrichtung "" folgt wieder direkt aus der Definition. Die Rückrichtung "" ist hier auch wieder etwas aufwendiger.
Beweis (Limes superior/inferior und unbestimmte Divergenz)
Beweisschritt 1: . Gelte . Dann ist nach oben unbeschränkt und nach unten beschränkt. Damit ist (und ). Außerdem kann keinen Häufungspunkt haben. Daher gilt auch .
Beweisschritt 2: . Gelte . Dann ist nach oben unbeschränkt und nach unten beschränkt. Da ist, hat keine Häufungspunkte. Daraus können wir nun folgern. Wir müssen also zeigen:
Sei eine nach unten beschränkt reelle Folge, die keinen Häufungspunkt in besitzt, dann konvergiert uneigentlich gegen .
Dies können wir am bestem mit einem Widerspruchsbeweis machen: Gelte sei nach unten beschränkt und konvergiert nicht uneigentlich gegen , d.h.
Also gibt es unendlich viele mit . Aus diesen kann man eine beschränkte Teilfolge bilden. Nach dem Satz von Bolzano-Weierstraß gibt es eine konvergente Teilfolge von . Da eine Teilfolge einer Teilfolge wieder eine Teilfolge (der ursprünglichen Folge) ist, besitzt damit eine konvergente Teilfolge und somit einen Häufungspunkt.
Diese Aufgabe in Aufgabenteil auslagern, und evtl. Hilfsaufgabe als eigene Teilaufgabe formulieren
Alternative Charakterisierung von Limes Superior und Limes Inferior
[Bearbeiten]Ist beschränkt, so lassen sich und auch wie folgt charakterisieren:
Satz (Alternative Definition von lim sup und lim inf)
Ist eine beschränkte reelle Folge, so gilt
Beispiele
[Bearbeiten]Da diese Charakterisierungen von und am Anfang etwas abstrakt wirken, wollen wir sie zunächst an zwei Beispielen veranschaulichen:
Beispiel
Sei zunächst . Entscheidend ist es nun, und zu bestimmen. Dies ist hier aber nicht allzu schwer. Da die Folge nur die Werte annimmt, und beide unendlich oft, ist und für alle . Damit ergibt sich
und
Beispiel
Ist , so ist
Daraus folgt dann
Verständnisaufgabe: Bestimme analog .
Es gilt
Und daher ist ebenfalls
Beweis des Satzes
[Bearbeiten]Wie kommt man auf den Beweis? (Alternative Charakterisierung von lim sup und lim inf)
Zunächst zeigen wir, dass konvergiert. Da monoton fallend und beschränkt ist, folgt dies aus dem Monotoniekriterium. Anschließend müssen wir noch zeigen, dass tatsächlich gegen , also den größten Häufungswert von , konvergiert. Dies machen wir, indem wir und zeigen.
Analog zeigen wir, dass monoton steigend und beschränkt ist und gegen , also den kleinsten Häufungspunkt von , konvergiert.
Beweis (Alternative Charakterisierung von lim sup und lim inf)
Da nach Voraussetzung beschränkt ist, ist auch insbesondere nach unten beschränkt. Weiter gilt
Also ist monoton fallend. Nach dem Monotoniekriterium konvergiert . Wir nennen den Grenzwert .
Weiter setzen wir (größter Häufungspunkt von ). Nun müssen wir noch zeigen: . Dies machen wir, indem wir und zeigen.
Da Häufungspunkt von ist, existiert zu jedem ein mit , so dass . Da beliebig war, ist daher für alle . Nach dem Monotoniekrieterium für Grenzwerte ist auch .
Verständnisaufgabe: Zeige ähnlich .
Da Häufungspunkt von ist, existiert zu jedem ein mit , so dass . Daher ist für alle . (Vorsicht: Da in das Supremum gebildet wird, kann hier nicht gefolgert werden!) Da aber beliebig war, folgt daraus .
Alternativ kann man, an Stelle von , auch direkt zeigen, dass ein Häufungspunkt von ist. Zusammen mit folgt dann, dass es der größte Häufungspunkt von ist.
Die Aufgabe sollte kein Teil des Beweises sein
Rechenregeln für Limes Superior und Limes Inferior
[Bearbeiten]Satz (Monotonieregel)
Seien und beschränkte reelle Folgen mit für alle . Dann gilt
Beweis (Monotonieregel)
Sei der größte Häufungspunkt von und der größte Häufungspunkt von . Diese existieren nach Bolzano-Weierstraß, da die Folgen nach Voraussetzung beschränkt sind. Sei gegeben. Da der größte Häufungspunkt von ist, gibt es ein , so dass für alle : . Wegen gilt aber auch für alle : . Also muss gelten. Da beliebig war, folgt .
Aufgabe (Monotonieregel)
Zeige analog .
Satz (Zusammenhang limsup und liminf)
Sei eine beschränkte reelle Folge. Dann gilt
Beweis (Zusammenhang limsup und liminf)
Sei der größte Häufungspunkt von . Wir müssen zeigen, dass gilt, also dass der kleinste Häufungspunkt von ist. Dies tun wir in zwei Schritten:
- Wir zeigen: ist ein Häufungspunkt von
- Wir zeigen: ist der kleinste Häufungspunkt von
Beweisschritt 1: Wegen gibt es eine Teilfolge von mit . Mit den Rechenregeln für Grenzwerte gilt dann . Also konvergiert die Teilfolge von gegen , d.h. ist Häufungspunkt von .
Beweisschritt 2: Sei ein beliebiger Häufungspunkt von , dann gibt es eine Teilfolge von mit . Mit den Grenzwertregeln folgt dann aber . Also ist ein Häufungspunkt von . Da der größte Häufungspunkt von war, folgt . Dies ist äquivalent zu .
Da ein beliebiger Häufungspunkt von war, folgt daraus, dass der kleinste Häufungspunkt von ist. Also gilt , und genau das wollten wir zeigen.
Satz (Summenregel)
Seien und reelle Folgen. Dann gilt
Beweis (Summenregel)
Beweisschritt 1: Zunächst zeigen wir die 2. Ungleichung :
Sei , und ein beliebiger Häufungspunkt von . Dann gibt es eine Teilfolge von mit .
Sei nun beliebig. Da der größte Häufungspunkt von und der größte Häufungspunkt von ist, gibt es ein , so dass für alle gilt: und . Also gilt für alle auch . Nach der Monotonieregel für Grenzwerte gilt damit . Da beliebig war, folgt daraus . Da nun ein beliebiger Häufungspunkt von war, gilt
Beweisschritt 2: Nun zeigen wir die erste Ungleichung . Dafür verwenden wir die 2. Ungleichung, die wir gerade bewiesen haben, und die limsup/liminf-Regel () von oben. Es gilt
Dies ist aber äquivalent zur ersten Ungleichung .
Aufgabe (Beispiel zur Summenregel)
Finde konkrete Folgen und mit
Lösung (Beispiel zur Summenregel)
Beispielsweise können wir
und
wählen. Dann ist
und
Also haben und jeweils die Häufungspunkte und . Außerdem ist
Somit hat die Häufungspunkte und . Damit gilt






![{\displaystyle \left[\liminf _{n\to \infty }a_{n},\limsup _{n\to \infty }a_{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2a2b0fd61588e79528ba95b8c2b52a3c81605a0)
![{\displaystyle \left[\liminf _{n\to \infty }a_{n}-\epsilon ,\limsup _{n\to \infty }a_{n}+\epsilon \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/576f2658eb188c81bd420861f039a581578b8f8a)























































































































































