Satz von Bolzano-Weierstraß – Serlo „Mathe für Nicht-Freaks“
In diesem Kapitel besprechen wir einen Satz, der für viele Beweise hilfreich ist: Der Satz von Bolzano-Weierstraß, welcher nach Bernard Bolzano und Karl Weierstraß benannt ist.
Dieser Satz garantiert die Existenz von Häufungspunkten bei beschränkten Folgen und wird oft verwendet, um die Existenz von Grenzwerten oder Häufungspunkten zu zeigen. Zwar könnte zum Nachweis dieser Existenz auch das Intervallschachtelungsprinzip herangezogen werden, der Weg über den Satz von Bolzano-Weierstraß ist aber oftmals einfacher.
So wird in einigen Lehrbüchern mit Hilfe des Satzes von Bolzano-Weierstraß das Monotoniekriterium für Folgen und Reihen gezeigt. Auch kann mit ihm das Theorem bewiesen werden, dass stetige Funktionen auf abgeschlossenen Intervallen der Form mit beschränkt sind und ihr Maximum und Minimum annehmen.
Der Satz von Bolzano-Weierstraß
[Bearbeiten]Der Satz von Bolzano-Weierstraß lautet:
Satz (Satz von Bolzano-Weierstraß)
Jede beschränkte Folge von reellen Zahlen besitzt mindestens einen Häufungspunkt. Es gibt also eine reelle Zahl , so dass mindestens eine Teilfolge von gegen konvergiert.
Diesen Satz kannst du so nachvollziehen: Eine Folge ist genau dann beschränkt, wenn es ein Intervall gibt, so dass alle Folgenglieder in diesem Intervall liegen. Nun hat eine Folge unendlich viele Glieder. Wenn man sie alle in das endliche Intervall sperrt, gibt es ein ziemliches Gedränge und die Folgenglieder müssen sich zwangsweise zum Teil sehr nah kommen. Nun sagt der Satz von Bolzano-Weierstraß, dass es mindestens eine reelle Zahl gibt, der die Glieder einer Teilfolge beliebig nah kommen. Diese Zahl ist Häufungspunkt der Folge. Beachte, dass selbst kein Glied der Folge sein muss. Auch könnte es insgesamt mehr als einen Häufungspunkt geben.
Wie bereits erwähnt, wird der Satz von Bolzano-Weierstraß bei Existenzbeweisen genutzt. So kann mit diesem Satz ein gesuchter Grenzwert oder ein gesuchter Häufungspunkt gefunden werden. Dabei ist die Anwendung dieses Satzes oft einfacher als die Benutzung des Supremumaxioms oder des Intervallschachtelungsprinzips. Der Grund liegt darin, dass die Beschränktheit einer Folge oft leicht nachgewiesen werden kann. Demgegenüber lässt sich das Supremumaxiom nur dann gut anwenden, wenn die gesuchte Zahl Supremum einer gegebenen Menge ist und beim Intervallschachtelungsprinzip muss man eine geeignete Intervallschachtelung konstruieren bzw. finden, die die gesuchte Zahl beliebig genau approximiert.
Hinweis
In der Literatur wird manchmal der Satz von Bolzano-Weierstraß in der Form „Jede reelle beschränkte Folge besitzt eine konvergente Teilfolge“ formuliert. Der Satz „Jede beschränkte Folge reeller Zahlen besitzt einen Häufungspunkt“ wird dann als Satz vom Häufungspunkt bezeichnet.
Notwendigkeit des Vollständigkeitsaxioms
[Bearbeiten]Für den Satz von Bolzano-Weierstraß ist die Vollständigkeit der reellen Zahlen eine notwendige Eigenschaft. Um dies zu sehen, nehmen wir als Grundmenge die rationalen Zahlen. Hier betrachten wir eine Folge rationaler Zahlen, die gegen eine irrationale Zahl konvergieren würde. Weil diese Folge konvergiert, muss sie auch beschränkt sein (wir hatten bereits nachgewiesen, dass jede konvergente Folge beschränkt ist). Außerdem ist der irrationale Grenzwert der einzige Häufungspunkt der Folge (jeder Grenzwert ist alleiniger Häufungspunkt einer Folge).
Nun besitzt die gewählte Folge keinen Häufungspunkt mehr, weil wir beim Wechsel von nach den einzigen Häufungspunkt der Folge entfernt haben. Damit kann für die Grundmenge der rationalen Zahlen der Satz von Bolzano-Weierstraß nicht gelten. Schließlich kann es beschränkte rationale Folgen geben, die keine rationalen Häufungspunkte besitzen. Dieses Beispiel zeigt, wie wichtig die Grundmenge für den Satz ist und dass wir zum Beweis das Vollständigkeitsaxiom der reellen Zahlen benötigen werden. Schließlich ist die Vollständigkeit die wesentliche Eigenschaft, die die reellen von den rationalen Zahlen unterscheidet.
Beweis (mit Intervallschachtelung)
[Bearbeiten]Beweis (Satz von Bolzano-Weierstraß)
Sei eine beschränkte Folge. Wir wissen, dass es ein und ein gibt, so dass alle Folgenglieder in liegen (die Folge ist beschränkt):

Nun müssen wir einen Häufungspunkt der Folge finden. Wir wissen bereits, dass wir hierfür die Vollständigkeit von benötigen, welche wir über das Intervallschachtelungsprinzip eingeführt haben. Zur Erinnerung: Eine Intervallschachtelung ist eine Möglichkeit, eine Zahl durch eine Folge von immer kleiner werdenden Intervallen zu approximieren. Die gesuchte Zahl ist dabei Element jedes Intervalls der Intervallschachtelung. Dabei ist eine Abschätzung nach unten und eine Abschätzung nach oben von , also .
Wenn die Breite der Intervalle gegen konvergiert (also die Approximation beliebig genau wird), dann garantiert das Intervallschachtelungsprinzip, dass durch die Intervallschachtelung genau eine reelle Zahl beschrieben wird. Es gibt also genau eine reelle Zahl, die in allen Intervallen liegt.
Fazit: Um den gesuchten Häufungspunkt von zu finden, können wir eine Intervallschachtelung konstruieren, bei der jedes Intervall approximiert. Das Intervallschachtelungsprinzip garantiert uns dann die Existenz von . Wie gehen wir bei der Konstruktion der Intervallschachtelung vor?
Zunächst setzen wir als erstes Intervall . Wir wissen ja bereits, dass in diesem Intervall alle Folgenglieder liegen und damit sich auch der gesuchte Häufungspunkt in diesem Intervall befinden muss:

Jetzt teilen wir das Intervall in zwei gleich große Intervalle:

Da die Folge unendlich viele Folgenglieder besitzt, müssen in mindestens einem der beiden Intervalle unendlich viele Folgenglieder von liegen. Dieses Intervall setzen wir als das zweite Intervall der Intervallschachtelung. Da unendlich viele Folgenglieder der ursprünglichen Folge besitzt, sollte sich in diesem Intervall ein Häufungspunkt der ursprünglichen Folge befinden:

Nun können wir wiederum in zwei gleich große Teilintervalle aufteilen:
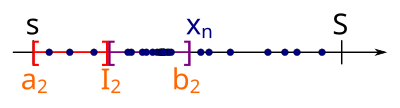
Als nächstes Intervall wählen wir das Teilintervall von , welches wiederum unendlich viele Folgenglieder der ursprünglichen Folge besitzt. Wir wissen, dass existiert, weil sich bereits in unendlich viele Folgenglieder der ursprünglichen Folge befinden und damit auch in mindestens einem der zwei Teilintervalle unendlich Folgenglieder von liegen müssen:
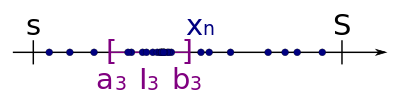
Dieses Verfahren wiederholen wir beliebig oft, so dass wir am Ende eine Intervallschachtelung erhalten. Formal können wir die Intervallschachtelung wie folgt beschreiben: Setze . Ist gegeben, so setze und
Die Breite der Intervalle halbiert sich bei jedem Schritt. Es ist
Dabei ist die Breite des -ten Intervalls. Es folgt
Die Breite der Intervalle konvergiert gegen und damit gibt es nach dem Intervallschachtelungsprinzip genau einen Punkt , der in allen Intervallen liegt. Dieser Punkt sollte Häufungspunkt der Folge sein. Das müssen wir aber noch beweisen.
Betrachten wir hierzu für ein beliebiges die -Umgebung von . Weil ist, gibt es ein mit . Wegen ist damit aber . Nun hatten wir die Intervalle so konstruiert, dass in jedem Intervall unendlich viele Folgenglieder von liegen. Also liegen auch in unendlich viele Folgenglieder der ursprünglichen Folge. Wegen sind alle Elemente von auch Elemente von . Damit müssen aber auch in der -Umgebung unendlich viele Folgenglieder von liegen (nämlich mindestens diejenigen, die bereits in liegen).
Weil beliebig gewählt wurde, liegen in jeder -Umgebung von unendlich viele Folgenglieder von . Dies beweist, dass Häufungspunkt von ist, womit diese Folge mindestens einen Häufungspunkt besitzt.
Alternativer Beweis (mit Monotoniekriterium)
[Bearbeiten]@Stephan Kulla: Dieser Abschnitt muss noch überarbeitet werden.
Eine weitere Möglichkeit, den Satz von Bolzano-Weierstraß zu zeigen, lässt sich mit Hilfe des Monotoniekriteriums erläutern. Zur Wiederholung: Dieses besagt, dass jede monotone und beschränkte Folge reeller Zahlen konvergiert.
Da die Beschränktheit in der Voraussetzung von Bolzano-Weierstraß steckt, ist der wesentliche Teil des Beweises, den folgenden Hilfssatz zu zeigen, der in der Literatur auch als Auswahlprinzip von Bolzano-Weierstraß bezeichnet wird:
Satz (Auswahlprinzip von Bolzano-Weierstraß)
Jede reelle Folge besitzt eine monotone Teilfolge.
Wie kommt man auf den Beweis? (Auswahlprinzip von Bolzano-Weierstraß)
Am besten lässt sich dieser Satz beweisen, indem wir die "Gipfelstellen" unserer Folge betrachten. Dabei heißt ein Folgenindex Gipfelstelle der Folge , falls für gilt: . Wichtig: Die Gipfelstellen sind die Indizes , nicht die Folgenglieder .
Betrachten wir zunächst ein Beispiel:
Sei die Folge mit , also die Folge .
Sizze zur Folge
Diese hat alle ungeraden Zahlen als Gipfelstellen, denn für alle , für alle und so weiter. Sie hat also unendlich viele Gipfelstellen für . Was helfen uns nun diese Gipfelstellen für unsere monotone Teilfolge? Ganz einfach: Die zu den Gipfelstellen gehörenden Folgenglieder bilden eine (streng) monoton fallende Teilfolge
Dies ist auch kein Zufall, sondern liegt an der Charakterisierung der Gipfelstellen. Ist nämlich eine Gipfelstelle, so ist per Definition kleiner als die vorherigen zu den Gipfelstellen gehörenden Folgenglieder , also . So erhalten wir immer eine (streng) monoton fallende Teilfolge , von , falls die Folge unendlich viele Gipfelstellen hat.
Was machen wir nun aber im anderen Fall, wenn die Anzahl der Gipfelstellen unserer Folge endlich ist? Betrachten wir wieder ein konkretes Beispiel:
Sei nun die Folge mit , also die Folge .
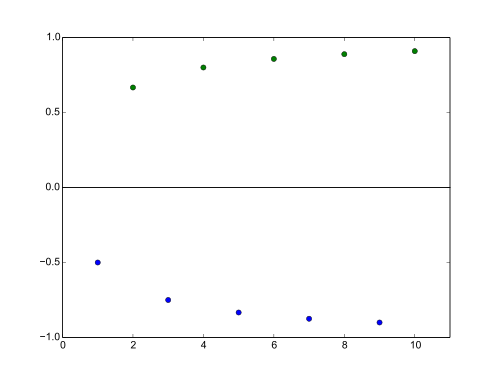
Diese Folge hat keine Gipfelstellen. Denn die ungeraden Indizes sind keine Gipfelstellen, da für alle geraden Indizes gilt , also gibt es immer ein mit . Die geraden Indizes sind aber auch keine Gipfelstellen, da die Teilfolge der geraden Folgenglieder (streng) monoton steigend ist: . Also gibt es immer ein mit . Nun haben wir aber auch hier eine monotone Teilfolge. Denn die Folge der geraden Glieder bildet eine (streng) monoton steigende Teilfolge von .
Auch dies ist kein Zufall, sondern immer der Fall, wenn die Anzahl der Gipfelstellen endlich ist. Sind allgemein die (endlich vielen) Gipfelstellen von , dann ist keine Gipfelstelle von . Da keine Gipfelstelle ist, gibt es aber mit . Da nun ebenfalls keine Gipfelstelle von ist, gibt es mit . Dies können wir nun sukzessive weiterführen und erhalten so immer eine monoton steigende Teilfolge von .
Beweis (Auswahlprinzip von Bolzano-Weierstraß)
1.Fall: besitzt unendlich viele Gipfelstellen . Dann ist die Teilfolge per Definiton (streng) monoton fallend.
2.Fall: besitzt endlich viele Gipfelstellen . Stetze . Wähle mit , und danach rekursiv für alle : mit . Dann ist die Teilfolge per Definiton monoton steigend.
Damit ist es nun kein Problem mehr, den Satz von Weierstraß mit Hilfe des Monotoniekriteriums zu beweisen:
Beweis (Alternativbeweis von Bolzano-Weierstraß)
Sei eine beschränkte reelle Folge. Nach dem Hilfssatz von oben besitzt sie eine monotone Teilfolge . Da beschränkt ist, ist auch beschränkt. Nach dem Monotoniekriterium konvergiert . Also besitzt eine konvergente Teilfolge und daher einen Häufungspunkt.



![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)






![{\displaystyle [s,S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa89eaacbc711abc21f726338470978db420e117)




![{\displaystyle I_{n}=[a_{n},b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c37f3e46f5c868cfdd53ab13ff0c30b69aa8c293)
![{\displaystyle [a_{n},b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e30ce1f218c7164247ad32fbbcde76c02c817bd1)








![{\displaystyle I_{1}=[s,S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58be63fbf6d3dff28ca6747569a558d5af61740e)
![{\displaystyle I_{k}=[a_{k},b_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/242d0e8ba6e5da6f32782b09ef11aa02bdd82eb6)

![{\displaystyle I_{k+1}=[a_{k+1},b_{k+1}]={\begin{cases}\;[a_{k},M]&{\text{in }}[a_{k},M]{\text{ liegen unendlich viele }}a_{n}\\\;[M,b_{k}]&{\text{sonst}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21c7b7e4a12c43313173867faad446e6f260b861)





























































